A Closer Earth and the Faint Young Sun Paradox: Modification of the Laws of Gravitation or Sun/Earth Mass Losses?
Abstract
:1. Introduction
2. A Working Hypothesis: Was the Earth Closer to the Sun than Now?
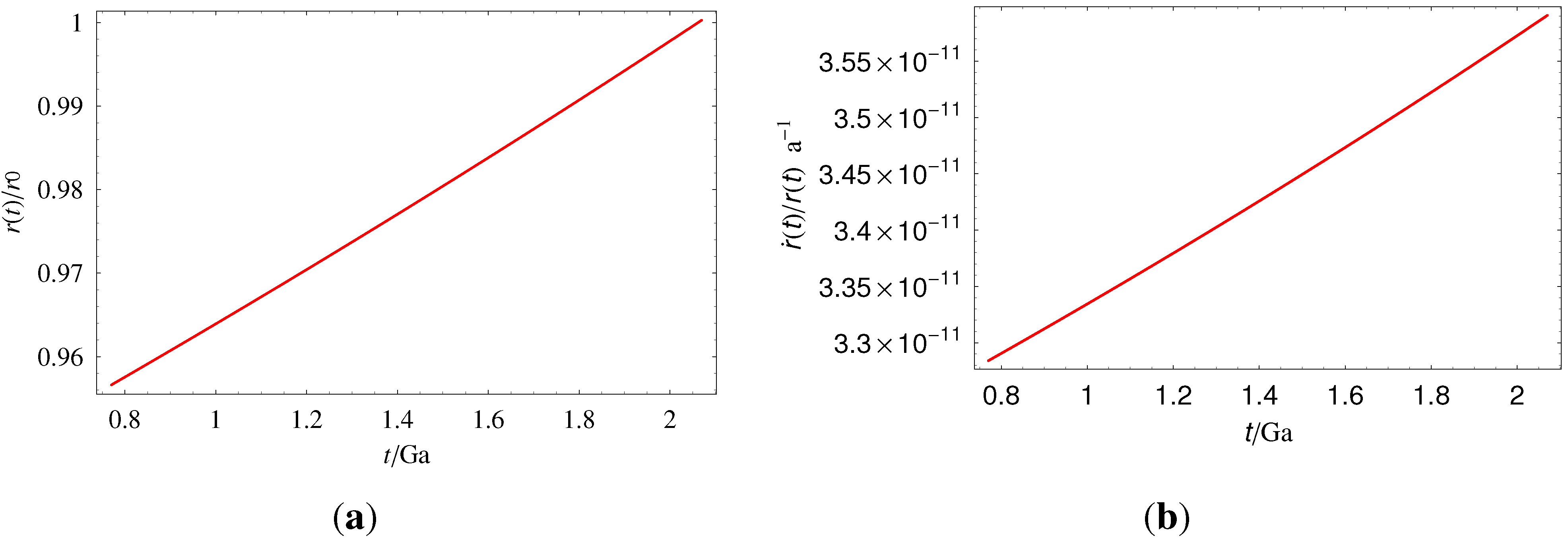
3. Ruling Out Cosmological Explanations
3.1. The Accelerated Expansion of the Universe
3.2. A Time-Dependent Varying Gravitational Parameter, G
4. Unconventional Orbital Effects
4.1. Modified Gravitational Theories with Nonminimal Coupling
4.2. The Secular Increase of the Astronomical Unit
5. Some Non-Climatic, Classical Orbital Effects
5.1. Gravitational Billiard
5.2. Mass Losses
5.2.1. Isotropic Mass Loss of the Sun
5.3. Non-Isotropic Mass Loss of the Earth, Due to a Possible Erosion of Its Hydrosphere Driven by the Solar Wind
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Sagan, C.; Mullen, G. Earth and Mars: Evolution of atmospheres and surface temperatures. Science 1972, 177, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Feulner, G. The faint young Sun problem. Rev. Geophys. 2012, 50, RG2006. [Google Scholar] [CrossRef]
- Kopp, G.; Lean, J.L. A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 2011, 38, L01706. [Google Scholar] [CrossRef]
- Gough, D.O. Solar interior structure and luminosity variations. Solar Phys. 1981, 74, 21–34. [Google Scholar] [CrossRef]
- Ribas, I. The Sun and Stars as the Primary Energy Input in Planetary at Mospheres. In Solar and Stellar Variability (IAU S264): Impact on Earth and Planets; Kosovichev, A.G., Andrei, A.H., Rozelot, J.-P., Eds.; Cambridge University Press: Cambridge, UK, 2010; Volume 264, pp. 3–18. [Google Scholar]
- Bahcall, J.N.; Pinsonneault, M.H.; Basu, S. Solar models: Current epoch and time dependences, neutrinos, and helioseismological properties. Astrophys. J. 2001, 555, 990–1012. [Google Scholar] [CrossRef]
- Driese, S.; Jirsa, M.; Ren, M.; Brantley, S.; Sheldon, N.; Parker, D.; Schmitz, M. Neoarchean paleoweathering of tonalite and metabasalt: Implications for reconstructions of 2.69 Ga early terrestrial ecosystems and paleoatmospheric chemistry. Precambrian Res. 2011, 189, 1–17. [Google Scholar] [CrossRef]
- Wordsworth, R.; Pierrehumbert, R. Hydrogen-nitrogen greenhouse warming in Earth’s early atmosphere. Science 2013, 339, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Cohen, O.; Drake, J.J.; Kóta, J. The cosmic-ray intensity near the archean earth. Astrophys. J. 2012, 760, 85–91. [Google Scholar] [CrossRef]
- Güdel, M. The Sun in time: Activity and environment. Living Rev. Solar Phys. 2007, 4. [Google Scholar] [CrossRef]
- Wood, B.E. Astrospheres and solar-like stellar winds. Living Rev. Solar Phys. 2004, 1. [Google Scholar] [CrossRef]
- Kasting, J.F. Early Earth: Faint young Sun redux. Nature 2010, 464, 687–689. [Google Scholar] [CrossRef] [PubMed]
- Goldblatt, C.; Zahnle, K.J. Faint young Sun paradox remains. Nature 2011, 474, E1. [Google Scholar] [CrossRef] [PubMed]
- Kienert, H.; Feulner, G.; Petoukhov, V. Faint young Sun problem more severe due to ice-albedo feedback and higher rotation rate of the early Earth. Geophys. Res. Lett. 2012, 39, L23710. [Google Scholar] [CrossRef]
- Rosing, M.T.; Bird, D.K.; Sleep, N.H.; Bjerrum, C.J. No climate paradox under the faint early Sun. Nature 2010, 464, 744–747. [Google Scholar] [CrossRef] [PubMed]
- Kasting, J.F. How was early earth kept warm? Science 2013, 339, 44–45. [Google Scholar] [CrossRef] [PubMed]
- Haqq-Misra, J.D.; Domagal-Goldman, S.D.; Kasting, P.J.; Kasting, J.F. A revised, hazy methane greenhouse for the archean earth. Astrobiology 2008, 8, 1127–1137. [Google Scholar] [CrossRef] [PubMed]
- Schultz, C. More greenhouse gases needed to explain warm Archean Earth. Trans. Am. Geophys. Union 2013, 94, 76. [Google Scholar] [CrossRef]
- Gaidos, E.J.; Güdel, M.; Blake, G.A. The faint young Sun paradox: An observational test of an alternative solar model. Geophys. Res. Lett. 2000, 27, 501–503. [Google Scholar] [CrossRef] [PubMed]
- Minton, D.A.; Malhotra, R. Assessing the massive young Sun hypothesis to solve the warm young Earth puzzle. Astrophys. J. 2007, 660, 1700–1706. [Google Scholar] [CrossRef]
- Minton, D. Was the Earth always at 1 AU (and Was the Sun always One Solar Mass)? Available online: http://realserver4.stsci.edu/t/data/2012/04/2983/Minton.pdf (accessed on 11 June 2013).
- Budyko, M.I. The effect of solar radiation variations on the climate of the Earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef]
- Sellers, W.D. A global climatic model based on the energy balance of the earth-atmosphere system. J. Appl. Meteorol. 1969, 8, 392–400. [Google Scholar] [CrossRef]
- Gerard, J.C.; Hauglustaine, D.A.; François, L.M. The faint young Sun climatic paradox: A simulation with an interactive seasonal climate-sea ice model. Glob. Planet. Chang. 1992, 5, 133–150. [Google Scholar] [CrossRef]
- Jenkins, G.S. A general circulation model study of the effects of faster rotation rate, enhanced CO2 concentration, and reduced solar forcing: Implications for the faint young Sun paradox. J. Geophys. Res. 1993, 98, 20803–20811. [Google Scholar] [CrossRef]
- Longdoz, B.; Francois, L.M. The faint young Sun climatic paradox: Influence of the continental configuration and of the seasonal cycle on the climatic stability. Glob. Planet. Chang. 1997, 14, 97–112. [Google Scholar] [CrossRef]
- Williams, G.E. Geological constraints on the Precambrian history of Earth’s rotation and the Moon’s orbit. Rev. Geophys. 2000, 38, 37–60. [Google Scholar] [CrossRef]
- Eriksson, K.A.; Simpson, E.L. Quantifying the oldest tidal record: The 3.2 Ga Moodies Group, Barberton Greenstone Belt, South Africa. Geology 2000, 28, 831–834. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Lei, Y. Experimental measurement of growth patterns on fossil corals: Secular variation in ancient Earth-Sun distances. Chin. Sci. Bull. 2010, 55, 4010–4017. [Google Scholar] [CrossRef]
- Křížek, M. Dark energy and the anthropic principle. New Astron. 2012, 17, 1–7. [Google Scholar] [CrossRef]
- Collaboration, P.; Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; et al. Planck 2013 results. XVI. Cosmological parameters. ArXiv E-Prints 2013. [Google Scholar]
- Padmanabhan, T. Gravitation: Foundations and Frontiers; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia supernova discoveries at z > 1 from the hubble space telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665–687. [Google Scholar] [CrossRef]
- Carrera, M.; Giulini, D. Influence of global cosmological expansion on local dynamics and kinematics. Rev. Mod. Phys. 2010, 82, 169–208. [Google Scholar] [CrossRef]
- Giulini, D. Does cosmological expansion affect local physics? ArXiv E-Prints 2013. [Google Scholar] [CrossRef]
- Adkins, G.S.; McDonnell, J. Orbital precession due to central-force perturbations. Phys. Rev. D 2007, 75, 082001. [Google Scholar] [CrossRef]
- Kopeikin, S.M. Celestial ephemerides in an expanding universe. Phys. Rev. D 2012, 86, 064004. [Google Scholar] [CrossRef]
- Iorio, L. Local cosmological effects of the order of H in the orbital motion of a binary system. Mon. Not. R. Astron. Soc. 2013, 429, 915–922. [Google Scholar] [CrossRef]
- Kerr, A.W.; Hauck, J.C.; Mashhoon, B. Standard clocks, orbital precession and the cosmological constant. Class. Quantum Gravity 2003, 20, 2727–2736. [Google Scholar] [CrossRef]
- Milne, E.A. Relativity, Gravitation and World-Structure; The Clarendon Press: Oxford, UK, 1935. [Google Scholar]
- Milne, E.A. Kinematics, dynamics, and the scale of time. R. Soc. Lond. Proc. Ser. A 1937, 158, 324–348. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Jordan, P. Die physikalischen Weltkonstanten. Naturwissenschaften 1937, 25, 513–517. (in Germany). [Google Scholar] [CrossRef]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Progress in lunar laser ranging tests of relativistic gravity. Phys. Rev. Lett. 2004, 93, 261101. [Google Scholar] [CrossRef] [PubMed]
- Müller, J.; Biskupek, L. Variations of the gravitational constant from lunar laser ranging data. Class. Quantum Gravity 2007, 24, 4533–4538. [Google Scholar] [CrossRef]
- Murphy, T. Lunar laser ranging: The millimeter challenge. Rep. Progr. Phys. 2013, 76, 076901. [Google Scholar] [CrossRef] [PubMed]
- Uzan, J.P. Varying constants, gravitation and cosmology. Living Rev. Relativ. 2011, 14, 2. [Google Scholar] [CrossRef]
- Puetzfeld, D.; Obukhov, Y.N. Covariant equations of motion for test bodies in gravitational theories with general nonminimal coupling. Phys. Rev. D 2013, 87, 044045. [Google Scholar] [CrossRef]
- Goenner, H.F.M. Theories of gravitation with nonminimal coupling of matter and the gravitational field. Found. Phys. 1984, 14, 865–881. [Google Scholar] [CrossRef]
- Bertolami, O.; Páramos, J. Mimicking the cosmological constant: Constant curvature spherical solutions in a nonminimally coupled model. Phys. Rev. D 2011, 84, 064022. [Google Scholar] [CrossRef]
- Bertotti, B.; Farinella, P.; Vokrouhlický, D. Physics of the Solar System; Kluwer Academic Press: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Pitjeva, E. Use of Optical and Radio Astrometric Observations of Planets, Satellites and Spacecraft for Ephemeris Astronomy. In A Giant Step: From Milli- to Micro-Arcsecond Astrometry; Jin, W., Platais, I., Perryman, M., Eds.; Cambridge University Press: Cambridge, UK, 2007; Volume 248, pp. 20–22. [Google Scholar]
- Krasinsky, G.A.; Brumberg, V.A. Secular increase of astronomical unit from analysis of the major planet motions, and its interpretation. Celest. Mechan. Dyn. Astron. 2004, 90, 267–288. [Google Scholar] [CrossRef]
- Standish, E.M. The Astronomical Unit Now. In Transits of Venus: New Views of the Solar System and Galaxy; Kurtz, D.W., Ed.; Cambridge University Press: Cambridge, UK, 2005; pp. 163–179. [Google Scholar]
- Anderson, J.D. Astrometric solar-system anomalies. ArXiv E-Prints 2009. [Google Scholar] [CrossRef]
- Holzwarth, V.; Jardine, M. Theoretical mass loss rates of cool main-sequence stars. Astron. Astrophys. 2007, 463, 11–21. [Google Scholar] [CrossRef]
- Ehrenreich, D.; Désert, J.-M. Mass-loss rates for transiting exoplanets. Astron. Astrophys. 2011, 529, A136. [Google Scholar] [CrossRef]
- Suzuki, T. Solar wind and its evolution. Earth Planets Space 2012, 64, 201–206. [Google Scholar] [CrossRef]
- Iorio, L. Orbital effects of Sun’s mass loss and the Earth’s fate. Nat. Sci. 2010, 2, 329–337. [Google Scholar] [CrossRef]
- Adams, F.C.; Anderson, K.R.; Bloch, A.M. Evolution of planetary systems with time-dependent stellar mass-loss. Mon. Not. R. Astron. Soc. 2013, 432, 438–454. [Google Scholar] [CrossRef]
- Li, L.S. Secular influence of the evolution of orbits of near-Earth asteroids induced by temporary variation of G and solar mass-loss. Mon. Not. R. Astron. Soc. 2013, 431, 2971–2974. [Google Scholar] [CrossRef]
- Iorio, L. Orbital effects of non-isotropic mass depletion of the atmospheres of evaporating hot Jupiters in extrasolar systems. New Astron. 2012, 17, 356–361. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and dark matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin, Germany, 1994. [Google Scholar]
- Drake, J.J.; Cohen, O.; Yashiro, S.; Gopalswamy, N. Implications of mass and energy loss due to coronal mass ejections on magnetically active stars. Astrophys. J. 2013, 764, 170. [Google Scholar] [CrossRef]
- Brumberg, V.A. Essential Relativistic Celestial Mechanics; Adam Hilger: Bristol, UK, 1991. [Google Scholar]
- Iorio, L. Classical and relativistic orbital motions around a mass-varying body. SRX Phys. 2010, 2010, 261249. [Google Scholar] [CrossRef]
- Meščerskii, I. Mass Variable Particle Dynamics; St. Petersburg university: Saint Petersburg, Russia, 1897. [Google Scholar]
- Sommerfeld, A. Mechanics. Lectures on Theoretical Physics; Academic Press: New York, NY, USA, 1952; Volume 1. [Google Scholar]
- Hadjidemetriou, J.D. Two-body problem with variable mass: A new approach. Icarus 1963, 2, 440–451. [Google Scholar] [CrossRef]
- Hadjidemetriou, J. Secular variation of mass and the evolution of binary systems. Adv. Astron. Astrophys. 1967, 5, 131–188. [Google Scholar]
- Razbitnaya, E.P. The problem of two bodies with variable masses. Classification of different cases. Astron. Zhurnal 1985, 62, 1175–1181. [Google Scholar]
- Plastino, A.R.; Muzzio, J.C. On the use and abuse of Newton’s second law for variable mass problems. Celest. Mech. Dyn. Astron. 1992, 53, 227–232. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA) Web Page. Earth Fact Sheet. Available online: http://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html (accessed on 11 June 2013).
- Zahnle, K.; Schaefer, L.; Fegley, B. Earths earliest atmospheres. Cold Sprinh Harbor Perspect. Biol. 2010, 2, a004895. [Google Scholar] [CrossRef]
- Marty, B.; Meibom, A. Noble gas signature of the late heavy bombardment in the Earth’s atmosphere. eEarth 2007, 2, 43–49. [Google Scholar] [CrossRef]
- Ryder, G.; Koeberl, C.; Mojzsis, S.J. Heavy Bombardment on the Earth at ∼ 3.85 Ga: The Search for Petrographic and Geochemical Evidence. In Origin of the Earth and Moon; Canup, R.M., Righter, K., Eds.; University of Arizona Press: Tucson, AZ, USA, 2000; pp. 475–492. [Google Scholar]
- Brož, M.; Morbidelli, A.; Bottke, W.F.; Rozehnal, J.; Vokrouhlický, D.; Nesvorný, D. Constraining the cometary flux through the asteroid belt during the late heavy bombardment. Astron. Astrophys. 2013, 551, A117. [Google Scholar] [CrossRef]
- Tarduno, J.A.; Cottrell, R.D.; Watkeys, M.K.; Hofmann, A.; Doubrovine, P.V.; Mamajek, E.E.; Liu, D.; Sibeck, D.G.; Neukirch, L.P.; Usui, Y. Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 2010, 327, 1238–1240. [Google Scholar] [CrossRef] [PubMed]
- Sterenborg, M.G.; Cohen, O.; Drake, J.J.; Gombosi, T.I. Modeling the young Sun’s solar wind and its interaction with Earth’s paleomagnetosphere. J. Geophys. Res. 2011, 116, A01217. [Google Scholar] [CrossRef]
© 2013 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Iorio, L. A Closer Earth and the Faint Young Sun Paradox: Modification of the Laws of Gravitation or Sun/Earth Mass Losses? Galaxies 2013, 1, 192-209. https://doi.org/10.3390/galaxies1030192
Iorio L. A Closer Earth and the Faint Young Sun Paradox: Modification of the Laws of Gravitation or Sun/Earth Mass Losses? Galaxies. 2013; 1(3):192-209. https://doi.org/10.3390/galaxies1030192
Chicago/Turabian StyleIorio, Lorenzo. 2013. "A Closer Earth and the Faint Young Sun Paradox: Modification of the Laws of Gravitation or Sun/Earth Mass Losses?" Galaxies 1, no. 3: 192-209. https://doi.org/10.3390/galaxies1030192
APA StyleIorio, L. (2013). A Closer Earth and the Faint Young Sun Paradox: Modification of the Laws of Gravitation or Sun/Earth Mass Losses? Galaxies, 1(3), 192-209. https://doi.org/10.3390/galaxies1030192




