Combining Faraday Tomography and Wavelet Analysis
Abstract
1. Introduction
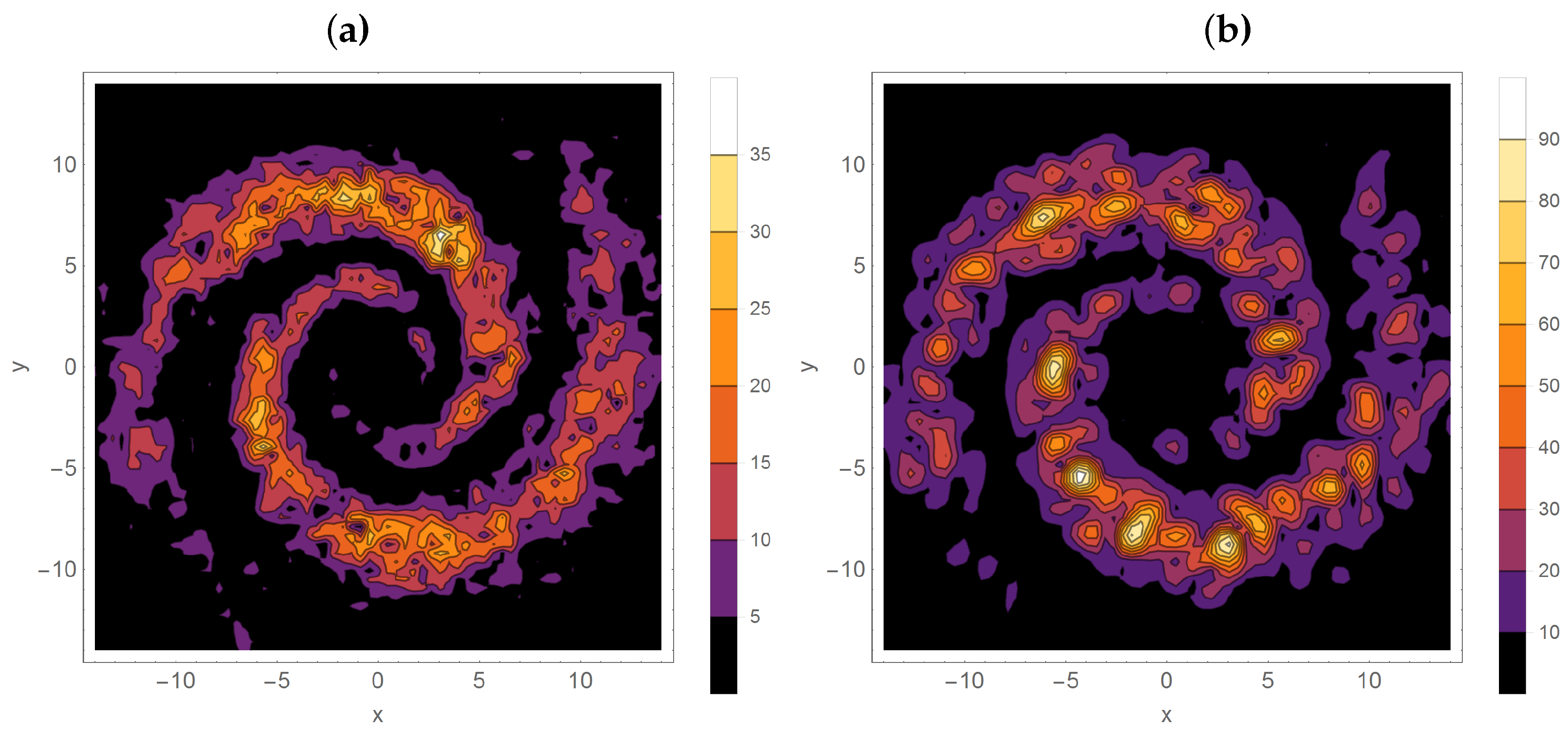
2. Idea of the Method Applied to the NGC 6946 Data
3. Synthetic Data Analysis
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NGC | New General Catalogue |
| SKA | Square Kilometre Array |
| RM | Rotation measure |
References
- Beck, R.; Frick, P.; Stepanov, R.; Sokoloff, D. Recognizing magnetic structures by present and future radio telescopes with Faraday rotation measure synthesis. Astron. Astrophys. 2012, 543, A113. [Google Scholar] [CrossRef]
- Weżgowiec, M.; Ehle, M.; Beck, R. Hot gas and magnetic arms of NGC 6946: Indications for reconnection heating? Astron. Astrophys. 2016, 585, A3. [Google Scholar] [CrossRef]
- Beck, R. Magnetic fields in spiral galaxies. Astron. Astrophys. Rev. 2015, 24, 4. [Google Scholar] [CrossRef]
- Chamandy, L.; Shukurov, A.; Subramanian, K. Magnetic spiral arms and galactic outflows. Mon. Not. R. Astron. Soc. 2015, 446, L6–L10. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Sun, X.H.; Rudnick, L.; Akahori, T.; Anderson, C.S.; Bell, M.R.; Bray, J.D.; Farnes, J.S.; Ideguchi, S.; Kumazaki, K.; O’Brien, T.; et al. Comparison of Algorithms for Determination of Rotation Measure and Faraday Structure. I. 1100–1400 MHz. Astron. J. 2015, 149, 60. [Google Scholar] [CrossRef]
- Heald, G.; Braun, R.; Edmonds, R. The Westerbork SINGS survey. II Polarization, Faraday rotation, and magnetic fields. Astron. Astrophys. 2009, 503, 409–435. [Google Scholar] [CrossRef]
- Chupin, A.; Beck, R.; Frick, P.; Heald, G.; Sokoloff, D.; Stepanov, R. Magnetic arms of NGC6946 traced in the Faraday cubes at low radio frequencies. Astron. Nachr. 2018, 339, 440–446. [Google Scholar] [CrossRef]
- Schwinn, J.; Baugh, C.M.; Jauzac, M.; Bartelmann, M.; Eckert, D. Uncovering substructure with wavelets:proof of concept using Abell 2744. Mon. Not. R. Astron. Soc. 2018, 481, 4300–4310. [Google Scholar] [CrossRef]
- Frick, P.; Sokoloff, D.; Stepanov, R.; Beck, R. Wavelet-based Faraday rotation measure synthesis. Mon. Not. R. Astron. Soc. 2010, 401, L24–L28. [Google Scholar] [CrossRef]
- Frick, P.; Sokoloff, D.; Stepanov, R.; Beck, R. Faraday rotation measure synthesis for magnetic fields of galaxies. Mon. Not. R. Astron. Soc. 2011, 414, 2540–2549. [Google Scholar] [CrossRef]
- Stepanov, R.; Arshakian, T.G.; Beck, R.; Frick, P.; Krause, M. Magnetic field structures of galaxies derived from analysis of Faraday rotation measures, and perspectives for the SKA. Astron. Astrophys. 2008, 480, 45–59. [Google Scholar] [CrossRef]
- Stepanov, R.; Shukurov, A.; Fletcher, A.; Beck, R.; La Porta, L.; Tabatabaei, F. An observational test for correlations between cosmic rays and magnetic fields. Mon. Not. R. Astron. Soc. 2014, 437, 2201–2216. [Google Scholar] [CrossRef]
- Ferrière, K. Faraday tomography: A new, three-dimensional probe of the interstellar magnetic field. J. Phys. Conf. Ser. 2016, 767, 012006. [Google Scholar] [CrossRef]
- Lazarian, A.; Yuen, K.H. Gradients of Synchrotron Polarization: Tracing 3D Distribution of Magnetic Fields. Astrophys. J. 2018, 865, 59. [Google Scholar] [CrossRef]
- Frick, P.; Stepanov, R.; Beck, R.; Sokoloff, D.; Shukurov, A.; Ehle, M.; Lundgren, A. Magnetic and gaseous spiral arms in M83. Astron. Astrophys. 2016, 585, A21. [Google Scholar] [CrossRef]
- Ossenkopf-Okada, V.; Stepanov, R. Measuring the filamentary structure of interstellar clouds through wavelets. arXiv, 2018; arXiv:1811.02082. [Google Scholar]
- Van Eck, C.L.; Haverkorn, M.; Alves, M.I.R.; Beck, R.; de Bruyn, A.G.; Enßlin, T.; Farnes, J.S.; Ferrière, K.; Heald, G.; Horellou, C.; et al. Faraday tomography of the local interstellar medium with LOFAR: Galactic foregrounds towards IC 342. Astron. Astrophys. 2017, 597, A98. [Google Scholar] [CrossRef]





© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokoloff, D.; Beck, R.; Chupin, A.; Frick, P.; Heald, G.; Stepanov, R. Combining Faraday Tomography and Wavelet Analysis. Galaxies 2018, 6, 121. https://doi.org/10.3390/galaxies6040121
Sokoloff D, Beck R, Chupin A, Frick P, Heald G, Stepanov R. Combining Faraday Tomography and Wavelet Analysis. Galaxies. 2018; 6(4):121. https://doi.org/10.3390/galaxies6040121
Chicago/Turabian StyleSokoloff, Dmitry, Rainer Beck, Anton Chupin, Peter Frick, George Heald, and Rodion Stepanov. 2018. "Combining Faraday Tomography and Wavelet Analysis" Galaxies 6, no. 4: 121. https://doi.org/10.3390/galaxies6040121
APA StyleSokoloff, D., Beck, R., Chupin, A., Frick, P., Heald, G., & Stepanov, R. (2018). Combining Faraday Tomography and Wavelet Analysis. Galaxies, 6(4), 121. https://doi.org/10.3390/galaxies6040121





