Detection of Periodic Radio Signal from the Blazar J1043+2408
Abstract
1. Introduction
2. Data Acquisition
3. Analysis and Results
3.1. Periodicity Search
3.1.1. Epoch Folding
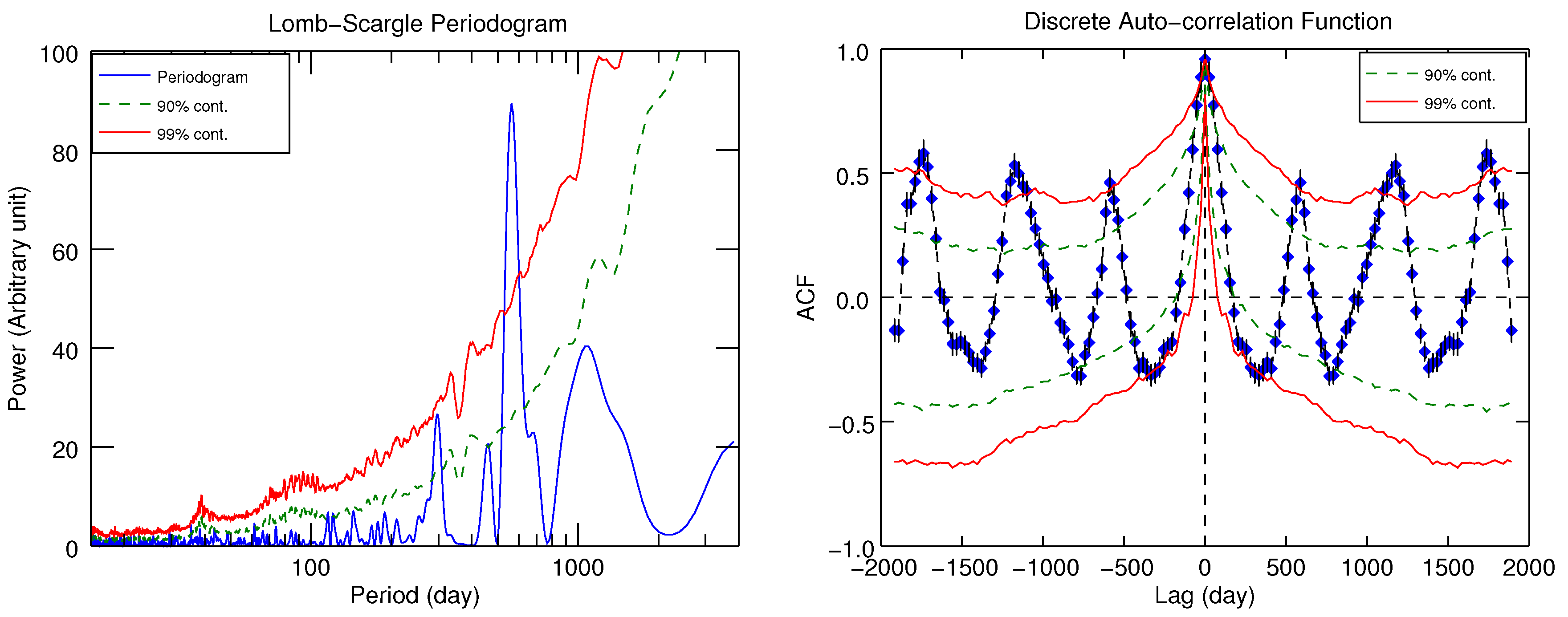
3.1.2. Lomb–Scargle Periodogram
3.1.3. Discrete Auto-Cross-Correlation Function
3.1.4. Significance Estimation and Monte Carlo Simulation
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| AGN | Active Galactic Nuclei |
| ACF | Autocorrelation function |
| BL Lac | BL Lacertae object |
| BH | Black hole |
| FSRQ | Flat Spectrum Radio Quasar |
| LSP | Lomb–Scargle Periodogram |
| MC | Monte Carlo |
| OVRO | Owens Valley Radio Observatory |
| PSD | Power spectral density |
| QPO | Quasiperiodic oscillation |
| SMBH | Supermassive black hole |
References
- Meier, D.L. Black Hole Astrophysics: The Engine Paradigm; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A jet model for the gamma-ray emitting blazar 3C 279. Astrophys. J. 1992, 397, L5–L9. [Google Scholar] [CrossRef]
- Bloom, S.D.; Marscher, A.P. An Analysis of the Synchrotron Self-Compton Model for the Multi-Wave Band Spectra of Blazars. Astrophys. J. 1996, 461, 657. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R. Thermal Comptonization Model for the High Energy Emission of Seyfert Active Galactic Nuclei. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Sikora, M. High-energy radiation from active galactic nuclei. Astrophys. J. Suppl. Ser. 1994, 90, 923. [Google Scholar] [CrossRef]
- Błażejowski, M.; Sikora, M.; Moderski, R.; Madejski, G.M. Comptonization of Infrared Radiation from Hot Dust by Relativistic Jets in Quasars. Astrophys. J. 2000, 545, 107. [Google Scholar] [CrossRef]
- Mannheim, K.; Biermann, P.L. Gamma-ray flaring of 3C 279—A proton-initiated cascade in the jet? Astron. Astrophys. 1992, 253, L21. [Google Scholar]
- Aharonian, F.A. TeV gamma rays from BL Lac objects due to synchrotron radiation of extremely high energy protons. New Astron. 2000, 5, 377. [Google Scholar] [CrossRef]
- Mücke, A.; Protheroe, R.J.; Engel, R.; Rachen, J.P.; Stanev, T. BL Lac objects in the synchrotron proton blazar model. Astropart. Phys. 2003, 18, 593. [Google Scholar] [CrossRef]
- Bhatta, G.; Mohorian, M.; Bilinsky, I. Hard X-ray Properties of NuSTAR Blazars. Astron. Astrophys. 2018, 619, A93. [Google Scholar] [CrossRef]
- Bhatta, G.; Stawarz, L.; Markowitz, A.; Balasubramaniam, K.; Zola, S.; Zdziarski, A.A.; Jamrozy, M.; Ostrowski, M.; Kuzmicz, A.; Ogloza, W.; et al. Signatures of the disk-jet coupling in the Broad-line Radio Quasar 4C+74.26. Astrophys. J. 2018, 866, 132. [Google Scholar] [CrossRef]
- Bhatta, G.; Ostrowski, M.; Markowitz, A.; Akitaya, H.; Arkharov, A.A.; Bachev, R.; Benítez, E.; Borman, G.A.; Carosati, D.; Cason, A.D.; et al. Multifrequency Photo-polarimetric WEBT Observation Campaign on the Blazar S5 0716+714: Source Microvariability and Search for Characteristic Timescales. Astrophys. J. 2016, 831, 92B. [Google Scholar] [CrossRef]
- Gupta, A. Multi-Wavelength Intra-Day Variability and Quasi-Periodic Oscillation in Blazars. Galaxies 2018, 6, 1. [Google Scholar] [CrossRef]
- Bhatta, G. Radio and γ-Ray Variability in the BL Lac PKS 0219-164: Detection of Quasi-periodic Oscillations in the Radio Light Curve. Astrophys. J. 2017, 487, 7B. [Google Scholar] [CrossRef]
- Bhatta, G.; Zola, S.; Ostrowski, M.; Winiarski, M.; Ogłoza, W.; Dróżdż, M.; Siwak, M.; Liakos, A.; Kozieł-Wierzbowska, D.; Gazeas, K.; et al. Detection of Possible Quasi-periodic Oscillations in the Long-term Optical Light Curve of the BL Lac Object OJ 287. Astrophys. J. 2016, 832, 47. [Google Scholar] [CrossRef]
- Zola, S.; Valtonen, M.; Bhatta, G.; Goyal, A.; Debski, B.; Baran, A.; Krzesinski, J.; Siwak, M.; Ciprini, S.; Gopakumar, A.; et al. A Search for QPOs in the Blazar OJ287: Preliminary Results from the 2015/2016 Observing Campaign. Galaxies 2016, 4, 41. [Google Scholar] [CrossRef]
- Liu, F.K.; Zhao, G.; Wu, X.-B. Harmonic QPOs and Thick Accretion Disk Oscillations in the BL Lacertae Object AO 0235+164. Astrophys. J. 2006, 650, 749. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Villata, M.; Aller, H.D.; Aller, M.F.; Heidt, J.; Kurtanidze, O.M.; Lanteri, L.; Maesano, M.; Massaro, E.; Montagni, F.; et al. Optical and radio variability of the BL Lacertae object AO 0235+16: A possible 5-6 year periodicity. Astron. Astrophys. 2001, 377, 396. [Google Scholar] [CrossRef]
- King, O.G.; Hovatta, T.; Max-Moerbeck, W.; Meier, D.L.; Pearson, T.J.; Readhead, A.C.; Reeves, R.; Richards, J.L.; Shepherd, M.C. A quasi-periodic oscillation in the blazar J1359+4011. Mon. Not. R. Astron. Soc. 2013, 436, L114. [Google Scholar] [CrossRef]
- Xie, G.Z.; Yi, T.F.; Li, H.Z.; Zhou, S.B.; Chen, L.E. Periodicity analysis of the radio curve of PKS 1510-089 and implications for its central structure. Astrophys. J. 2008, 135, 2212. [Google Scholar] [CrossRef]
- An, T.; Baan, W.A.; Wang, J.-Y.; Wang, Y.; Hong, X.-Y. Periodic radio variabilities in NRAO 530: A jet–disc connection? Mon. Not. R. Astron. Soc. 2013, 434, 3487. [Google Scholar] [CrossRef]
- Wang, J.-Y.; An, T.; Baan, W.A.; Lu, X.-L. Periodic radio variabilities of the blazar 1156+295: Harmonic oscillations. Mon. Not. R. Astron. Soc. 2014, 443, 58. [Google Scholar] [CrossRef]
- Hovatta, T.; Tornikoski, M.; Lainela, M.; Lehto, H.J.; Valtaoja, E.; Torniainen, I.; Aller, M.F.; Aller, H.D. Statistical analyses of long-term variability of AGN at high radio frequencies. Astron. Astrophys. 2007, 469, 899. [Google Scholar] [CrossRef]
- Hovatta, T.; Lehto, H.J.; Tornikoski, M. Wavelet analysis of a large sample of AGN at high radio frequencies. Astron. Astrophys. 2008, 488, 897. [Google Scholar] [CrossRef]
- Hewett, P.C.; Wild, V. Improved redshifts for SDSS quasar spectra. Mon. Not. R. Astron. Soc. 2010, 405, 2302. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- Massaro, E.; Giommi, P.; Leto, C.; Marchegiani, P.; Maselli, A.; Perri, M.; Piranomonte, S.; Sclavi, S. Roma-BZCAT: A multifrequency catalogue of blazars. Astron. Astrophys. 2009, 495, 691. [Google Scholar] [CrossRef]
- Pursimo, T.; Ojha, R.; Jauncey, D.L.; Rickett, B.J.; Dutka, M.S.; Koay, J.Y.; Lovell, J.E.; Bignall, H.E.; Kedziora-Chudczer, L.; Macquart, J.P. The Micro-Arcsecond Scintillation-Induced Variability (MASIV) Survey. III. Optical Identifications and New Redshifts. Astrophys. J. 2013, 767, 14. [Google Scholar] [CrossRef]
- Richards, J.L.; Max-Moerbeck, W.; Pavlidou, V.; King, O.G.; Pearson, T.J.; Readhead, A.C.; Reeves, R.; Shepherd, M.C.; Stevenson, M.A.; Weintraub, L.C.; et al. Blazars in the Fermi Era: The OVRO 40 m Telescope Monitoring Program. Astrophys. J. Suppl. Ser. 2011, 194, 29. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271. [Google Scholar] [CrossRef]
- Bhatta, G.; Webb, J. Microvariability in BL Lacertae: “Zooming” into the Innermost Blazar Regions. Galaxies 2018, 6, 2. [Google Scholar] [CrossRef]
- Leahy, D.A.; Elsner, R.F.; Weisskopf, M.C. On searches for periodic pulsed emission—The Rayleigh test compared to epoch folding. Astrophys. J. 1983, 272, 256. [Google Scholar] [CrossRef]
- Davies, S.R. An improved test for periodicity. Mon. Not. R. Astron. Soc. 1990, 244, 93–95. [Google Scholar]
- Davies, S.R. Davies Periodicity Test Revisited. Mon. Not. R. Astron. Soc. 1991, 251, 64P. [Google Scholar] [CrossRef]
- Larsson, S. Parameter estimation in epoch folding analysis. Astron. Astrophys. Suppl. Ser. 1996, 117, 197. [Google Scholar] [CrossRef]
- Zhang, B.-K.; Zhao, X.-Y.; Wang, C.-X.; Dai, B.-Z. Optical quasi-periodic oscillation and color behavior of blazar PKS 2155-304. Res. Astron. Astrophys. 2014, 14, 933–941. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II—Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb–Scargle Periodogram. Astrophys. J. Suppl. Ser. 2018, 236, 16. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H. The discrete correlation function—A new method for analyzing unevenly sampled variability data. Astrophys. J. 1988, 333, 646. [Google Scholar] [CrossRef]
- Villata, M.; Raiteri, C.M.; Aller, H.D.; Aller, M.F.; Teräsranta, H.; Koivula, P.; Wiren, S.; Kurtanidze, O.M.; Nikolashvili, M.G.; Ibrahimov, M.A.; et al. The WEBT campaigns on BL Lacertae. Time and cross-correlation analysis of optical and radio light curves 1968–2003. Astron. Astrophys. 2004, 424, 497. [Google Scholar] [CrossRef]
- Press, W.H. Flicker noises in astronomy and elsewhere. Comments Astrophys. 1978, 7, 103. [Google Scholar]
- Uttley, P.; McHardy, I.M.; Papadakis, I.E. Measuring the broad-band power spectra of active galactic nuclei with RXTE. Mon. Not. R. Astron. Soc. 2002, 332, 231. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Emmanoulopoulos, D.; McHardy, I.M.; Papadakis, I.E. Generating artificial light curves: Revisited and updated. Mon. Not. R. Astron. Soc. 2013, 433, 907. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Takalo, L.O.; Sillanpaa, A. Testing the 1995 binary black hole model of OJ287. Astrophys. J. 2011, 729, 33–38. [Google Scholar] [CrossRef]
- Komossa, S. Observational evidence for binary black holes and active double nuclei. Mem. Soc. Astron. Ital. 2006, 77, 733. [Google Scholar]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307. [Google Scholar] [CrossRef]
- Sillanpaa, A.; Haarala, S.; Valtonen, M.J.; Sundelius, B.; Byrd, G.G. OJ 287—Binary pair of supermassive black holes. Astrophys. J. 1988, 325, 628. [Google Scholar] [CrossRef]
- Peters, P.C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. 1964, 136, 1224. [Google Scholar] [CrossRef]
- Kharb, P.; Lal, D.V.; Merritt, D. A candidate sub-parsec binary black hole in the Seyfert galaxy NGC 7674. Nat. Astron. 2017, 1, 727. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. Lett. 2015, 813, L41. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883. [Google Scholar] [CrossRef]
- Rieger, F.M. Supermassive binary black holes among cosmic gamma-ray sources. Astrophys. Space Sci. 2007, 309, 271. [Google Scholar] [CrossRef]
- Camenzind, M.; Krockenberger, M. The lighthouse effect of relativistic jets in blazars—A geometric origin of intraday variability. Astron. Astrophys. 1992, 255, 59. [Google Scholar]
- Mohan, P.; Mangalam, A. Kinematics of and Emission from Helically Orbiting Blobs in a Relativistic Magnetized Jet. Astrophys. J. 2015, 805, 91. [Google Scholar] [CrossRef]
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-Ray Binaries. Astrophys. J. Lett. 1998, 492, L59. [Google Scholar] [CrossRef]
- Motta, S.; Muñoz-Darias, T.; Casella, P.; Belloni, T.; Homan, J. Low-frequency oscillations in black holes: A spectral-timing approach to the case of GX 339-4. Mon. Not. R. Astron. Soc. 2011, 418, 2292. [Google Scholar] [CrossRef]
- Liska, M.; Hesp, C.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Glikman, E.; Larson, S.; Christensen, E. A systematic search for close supermassive black hole binaries in the Catalina Real-time Transient Survey. Mon. Not. R. Astron. Soc. 2015, 453, 1562. [Google Scholar] [CrossRef]
- Li, L.-X.; Narayan, R. Quasi-periodic Oscillations from Rayleigh-Taylor and Kelvin-Helmholtz Instability at a Disk-Magnetosphere Interface. Astrophys. J. 2004, 601, 414. [Google Scholar] [CrossRef]
- Fu, W.; Lai, D. Dynamics of the innermost accretion flows around compact objects: Magnetosphere-disc interface, global oscillations and instabilities. Mon. Not. R. Astron. Soc. 2012, 423, 831. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083. [Google Scholar] [CrossRef]



© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatta, G. Detection of Periodic Radio Signal from the Blazar J1043+2408. Galaxies 2018, 6, 136. https://doi.org/10.3390/galaxies6040136
Bhatta G. Detection of Periodic Radio Signal from the Blazar J1043+2408. Galaxies. 2018; 6(4):136. https://doi.org/10.3390/galaxies6040136
Chicago/Turabian StyleBhatta, Gopal. 2018. "Detection of Periodic Radio Signal from the Blazar J1043+2408" Galaxies 6, no. 4: 136. https://doi.org/10.3390/galaxies6040136
APA StyleBhatta, G. (2018). Detection of Periodic Radio Signal from the Blazar J1043+2408. Galaxies, 6(4), 136. https://doi.org/10.3390/galaxies6040136




