Influence of the Longitudinal Magnetic Field on the Formation of the Bead in Narrow Gap Gas Tungsten Arc Welding
Abstract
:1. Introduction
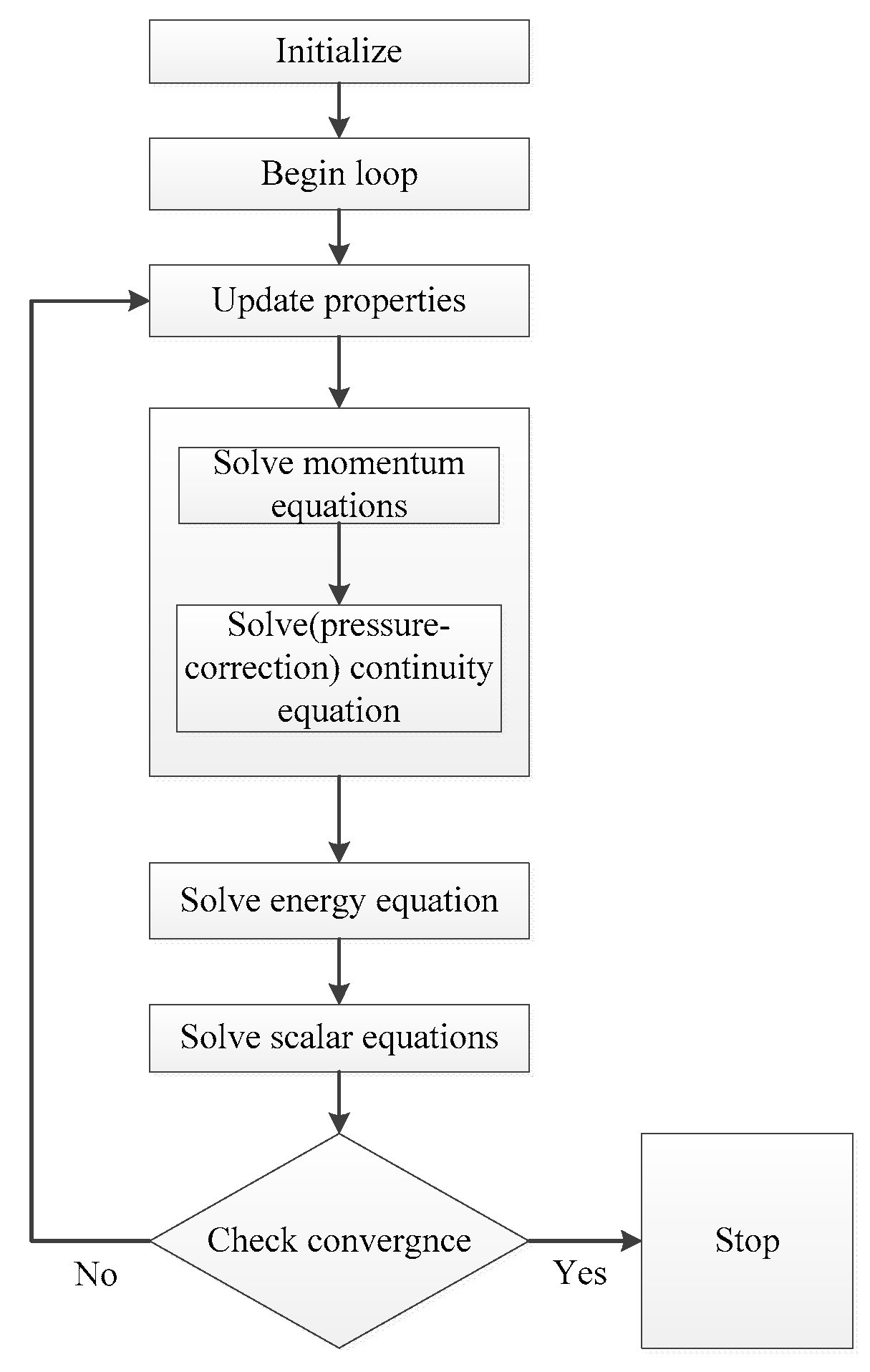
2. Mathematical Model
2.1. Computational Domain
2.2. Governing Equations
2.3. Treatment of Interface
2.4. External Boundary Conditions and Material Properties
3. Results and Discussion
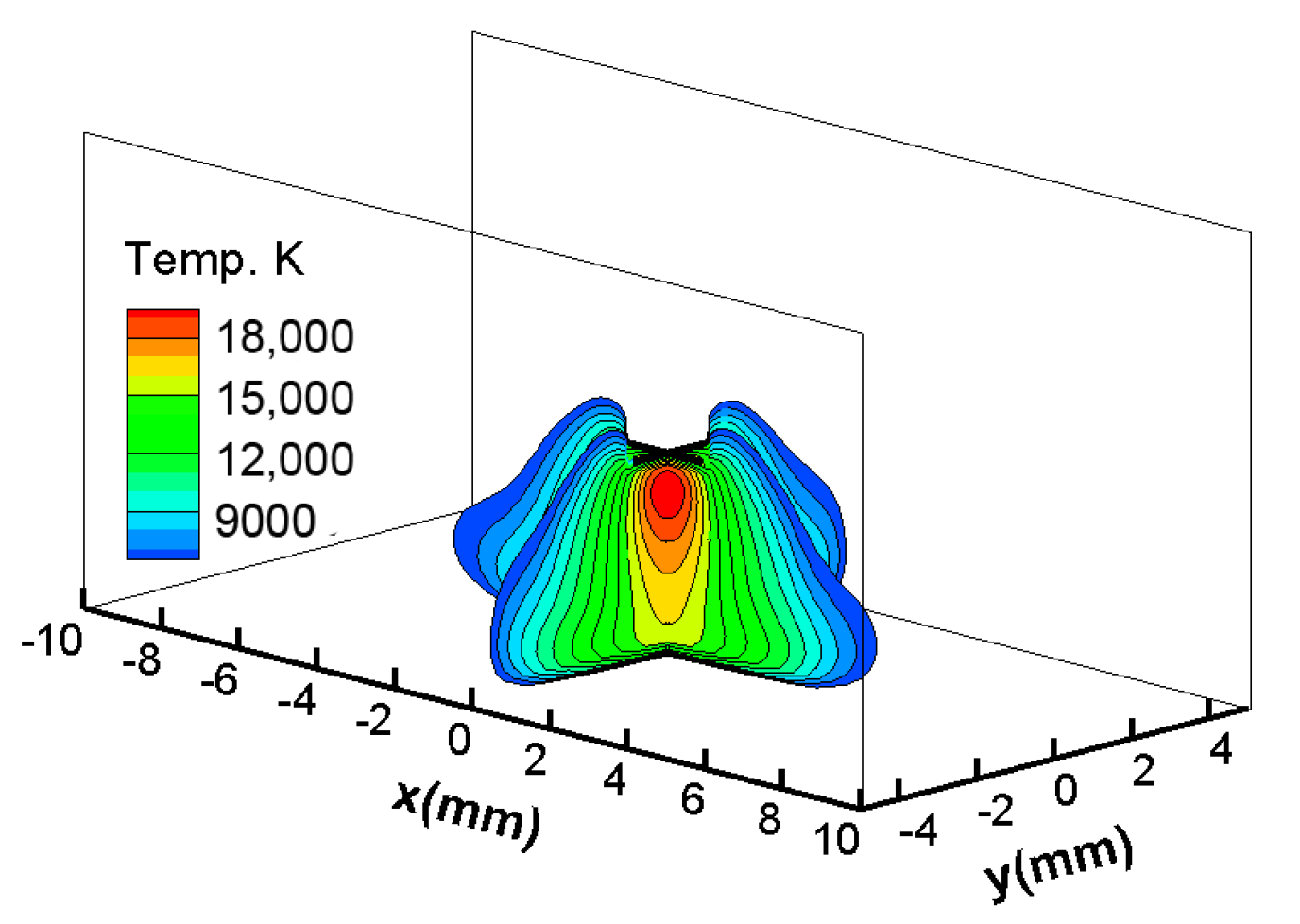
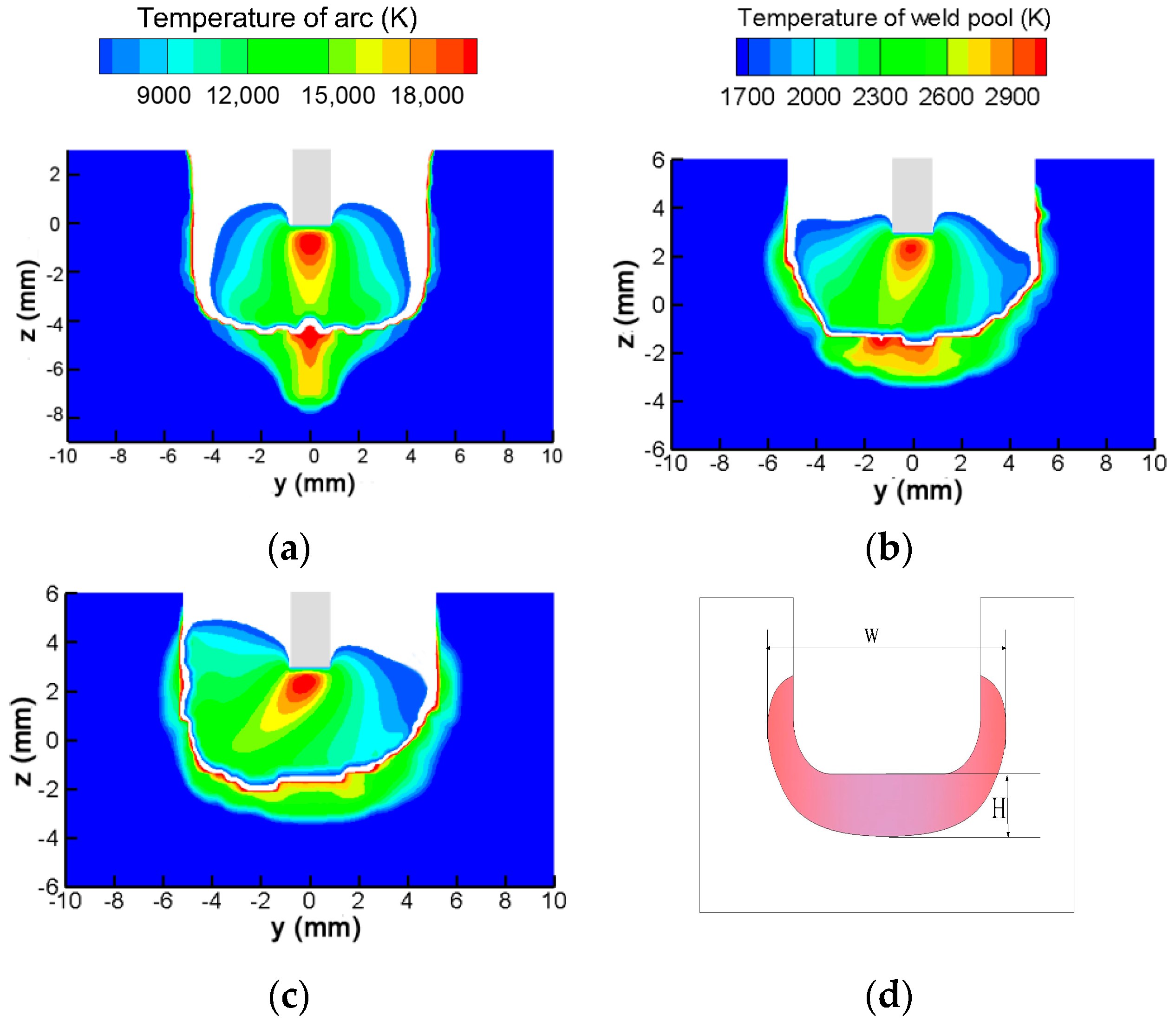
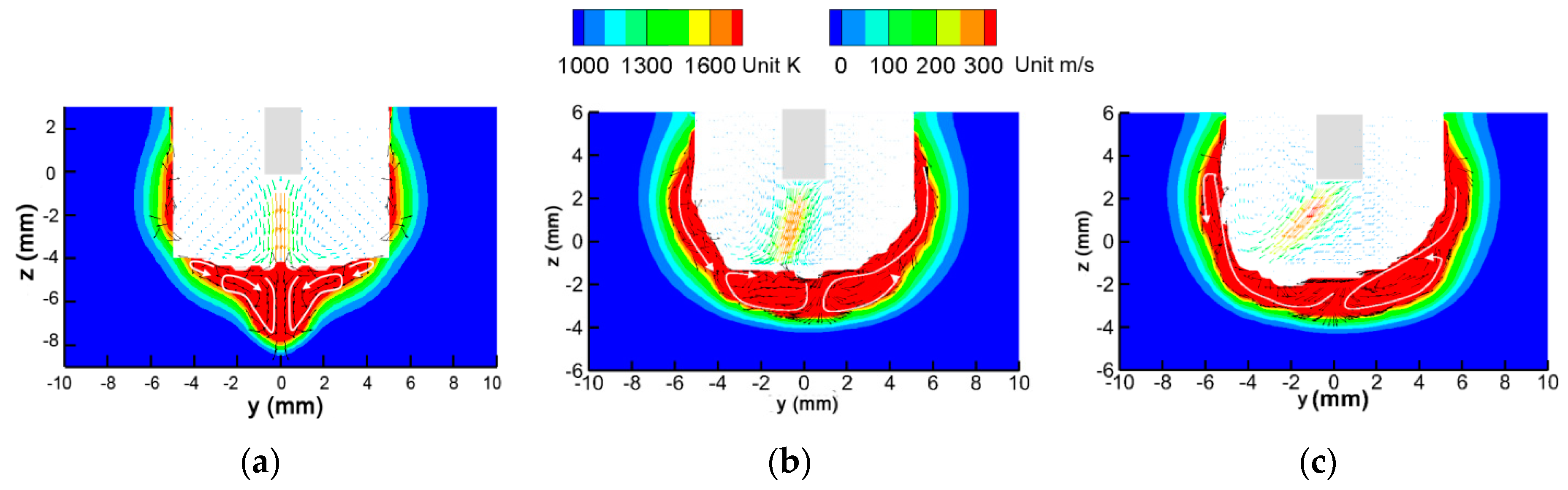
3.1. Welding Arc Behavior under LMF
3.2. Molten Pool Behavior under LMF
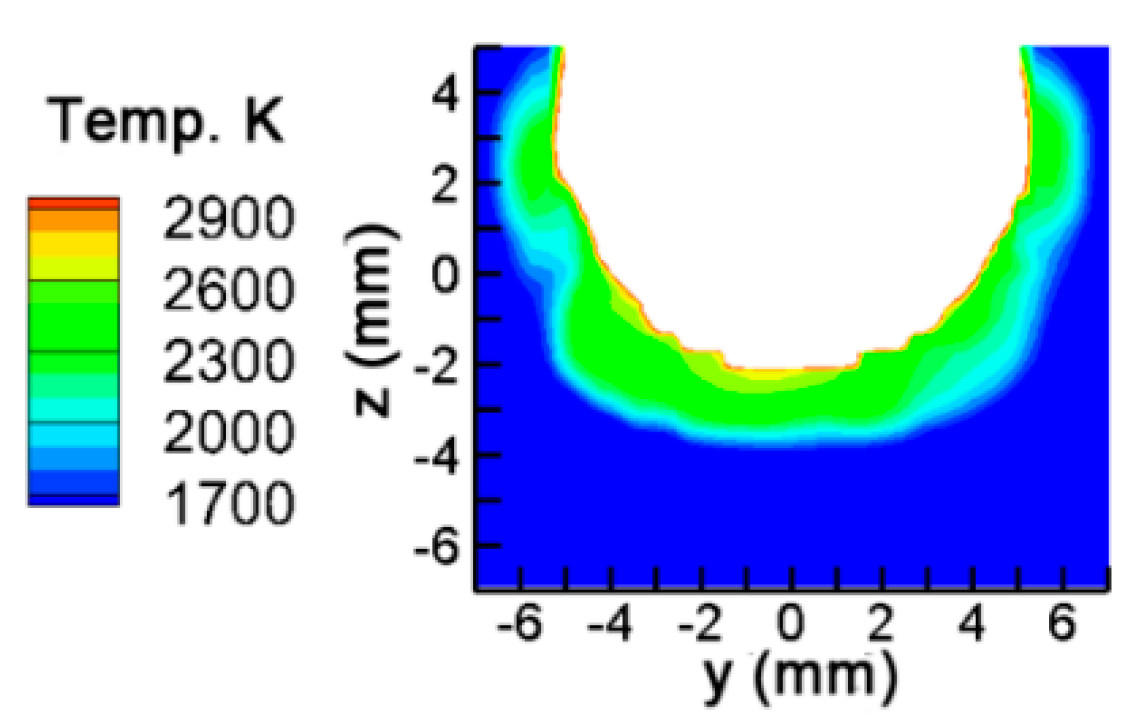
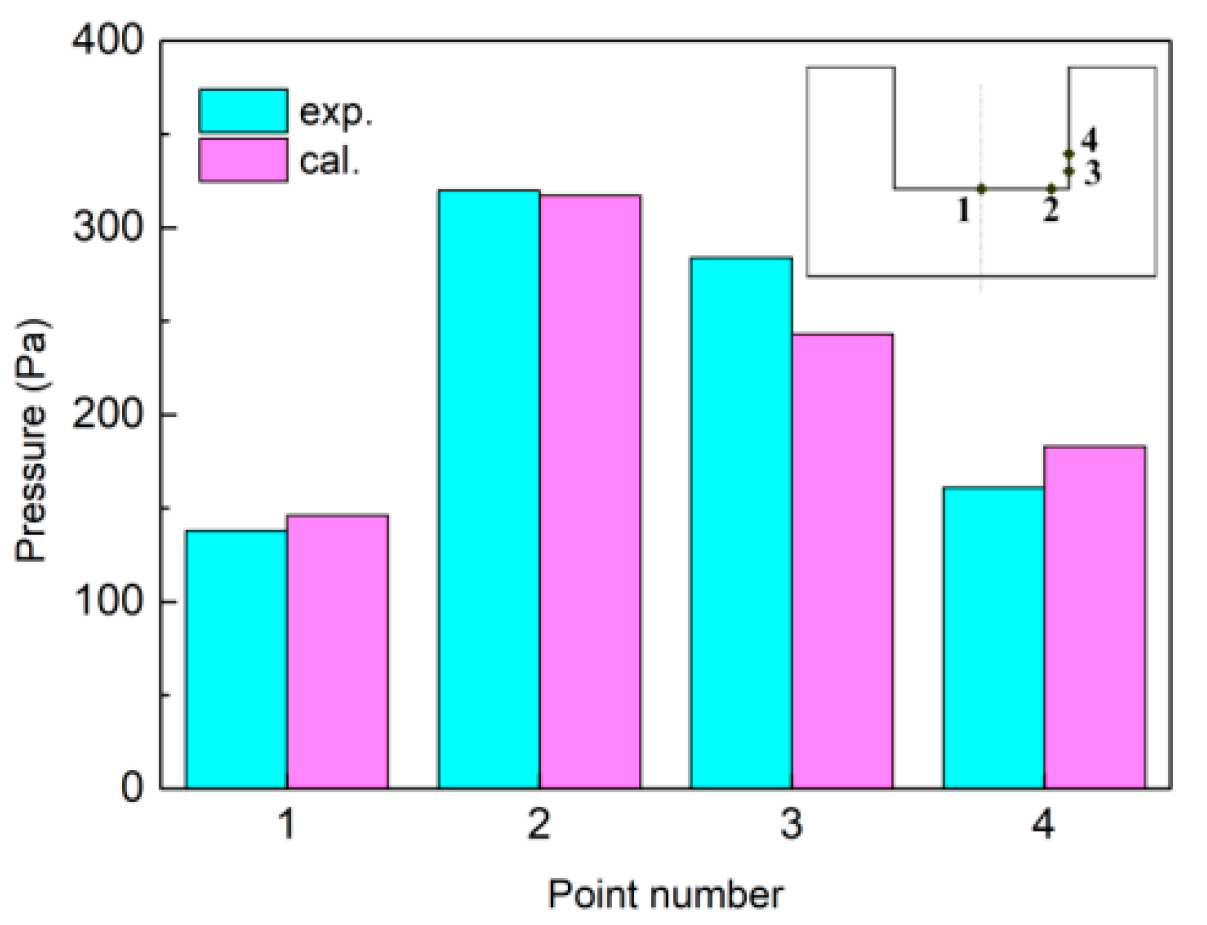
3.3. Validation of the Model
4. Conclusions
- (1)
- A unified 3D simulation model for LMF-NG-GTAW is developed including the electrode, welding arc, weld pool, and work piece; it can simulate the arc behavior and the weld pool formation process.
- (2)
- The profile of the deflecting welding arc has a big effect on the heat flux distribution. When the magnetic-field strength is 6 mT, the axis of the arc column moves from the bottom to the side wall; the decrease of the maximum heat flux at the bottom is about one-half, and the maximum heat flux at the side wall is increased by a factor of 10. The heat flux is dispersed along the narrow groove face, and this is helpful to form a uniform penetration weld.
- (3)
- The flow pattern in the weld pool is different with different magnetic-field strength. When the magnetic field is suitable, the flow pattern can transfer heat from the bottom to the side wall.
- (4)
- The model is validated by experimental data from references. Both the percentage deviations of the simulation weld penetration at the side wall and at the bottom from the experimental results are lower than 10%.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, G.; Shi, Y.; Zhu, M.; Fan, D. Arc characteristics and metal transfer behavior in narrow gap gas metal arc welding process. J. Mater. Process. Technol. 2017, 245, 15–23. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, J.; Fu, P.; Su, R.; Han, W.; Yang, F. A Swing arc system for narrow gap GMA welding. ISIJ Int. 2012, 52, 110–114. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhu, J.; Zhang, C.; Xu, G.; Li, W. Effect of arc swing parameters on narrow gap vertical GMA weld formation. ISIJ Int. 2016, 56, 844–850. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Wang, J.; Li, P.; Zhu, J.; Cao, Q. Numerical analysis of heat transfer and fluid flow in swing arc narrow gap GMA welding. J. Mater. Process. Technol. 2018, 252, 260–269. [Google Scholar] [CrossRef]
- Huang, J.; Chen, H.; He, J.; Yu, S.; Pan, W.; Fan, D. Narrow gap applications of swing TIG-MIG hybrid weldings. J. Mater. Process. Technol. 2019, 271, 609–614. [Google Scholar] [CrossRef]
- Guo, N.; Wang, M.; Guo, W.; Yu, J.; Feng, J. Study on forming mechanism of appearance defects in rotating arc narrow gap horizontal GMAW. Int. J. Adv. Manuf. Technol. 2014, 75, 15–20. [Google Scholar] [CrossRef]
- Wei, B.; Jia, C.; Wu, W.; Fang, C.; Wu, C. Stirring effect of the rotating arc on the molten pool during non-axisymmetric tungsten NG-GTAW. J. Mater. Process. Technol. 2020, 285, 116769. [Google Scholar] [CrossRef]
- Cai, X.Y.; Lin, S.; Fan, C.L.; Yang, C.L.; Zhang, W.; Wang, Y.W. Molten pool behaviour and weld forming mechanism of tandem narrow gap vertical GMAW. Sci. Technol. Weld. Join. 2016, 21, 124–130. [Google Scholar] [CrossRef]
- Cai, X.; Dong, B.; Lin, S.; Murphy, A.B.; Fan, C.; Yang, C. Heat source characteristics of ternary-gas-shielded tandem narrow-gap GMAW. Materials 2019, 12, 1397. [Google Scholar] [CrossRef] [Green Version]
- Sharma, P.; Chattopadhyaya, S.; Singh, N.K. A review on magnetically supported gas metal arc welding process for magnesium alloys. Mater. Res. Express 2019, 6, 082002. [Google Scholar] [CrossRef]
- Belous, V.Y. Conditions for formation of defect-free welds in narrow-gap magnetically controlled arc welding of low titanium alloys. Paton Weld. J. 2011, 3, 16–18. [Google Scholar]
- Kang, Y.H.; Na, S.J. Characteristics of welding and arc signal in narrow groove gas metal arc welding using electromagnetic arc oscillation. Weld. J. 2003, 82, 93S–99S. [Google Scholar]
- Sun, Q.; Wang, J.; Cai, C.; Li, Q.; Feng, J. Optimization of magnetic arc oscillation system by using double magnetic pole to TIG narrow gap welding. Int. J. Adv. Manuf. Technol. 2015, 86, 761–767. [Google Scholar] [CrossRef]
- Sun, Q.; Hun, H.F.; Li, W.J.; Liang, Y.C.; Feng, J.C. Electrode tips geometry and penetrating in narrow gap welding. Sci. Technol. Weld. Join. 2013, 18, 198–203. [Google Scholar] [CrossRef]
- Wang, J.; Feng, J.; Zhao, H.; Sun, Q.; Wang, S. Characteristics of welding and arc pressure in TIG narrow gap welding using novel magnetic arc oscillation. Int. J. Adv. Manuf. Technol. 2016, 90, 413–420. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Zhang, T.; Zhang, S.; Liu, Y.; Feng, J. Arc characteristics in alternating magnetic field assisted narrow gap pulsed GTAW. J. Mater. Process. Technol. 2018, 254, 254–264. [Google Scholar] [CrossRef]
- Nomura, K.; Ogino, Y.; Hirata, Y. Shape control of TIG arc plasma by cusp-type magnetic field with permanent magnet. Weld. Int. 2012, 26, 759–764. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Su, Y. Simulation and analysis of heat transfer and fluid flow characteristics of arc plasma in longitudinal magnetic field-tungsten inert gas hybrid welding. Int. J. Adv. Manuf. Technol. 2018, 98, 2015–2030. [Google Scholar] [CrossRef]
- Wang, L.; Chen, J.; Wu, C.; Luan, S. Numerical analysis of arc and droplet behaviors in gas metal arc welding with external compound magnetic field. J. Mater. Process. Technol. 2020, 282, 116638. [Google Scholar] [CrossRef]
- Lowke, J.J.; Tanaka, M. ‘LTE-diffusion approximation’ for arc calculations. J. Phys. D Appl. Phys. 2006, 39, 3634–3643. [Google Scholar] [CrossRef]
- Murphy, A.B.; Arundelli, C.J. Transport coefficients of argon, nitrogen, oxygen, argon-nitrogen, and argon-oxygen plasmas. Plasma Chem. Plasma Process. 1994, 14, 451–490. [Google Scholar] [CrossRef]
- Cram, L.E. Statistical evaluation of radiative power losses from thermal plasmas due to spectral lines. J. Phys. D Appl. Phys. 1985, 18, 401–411. [Google Scholar] [CrossRef]

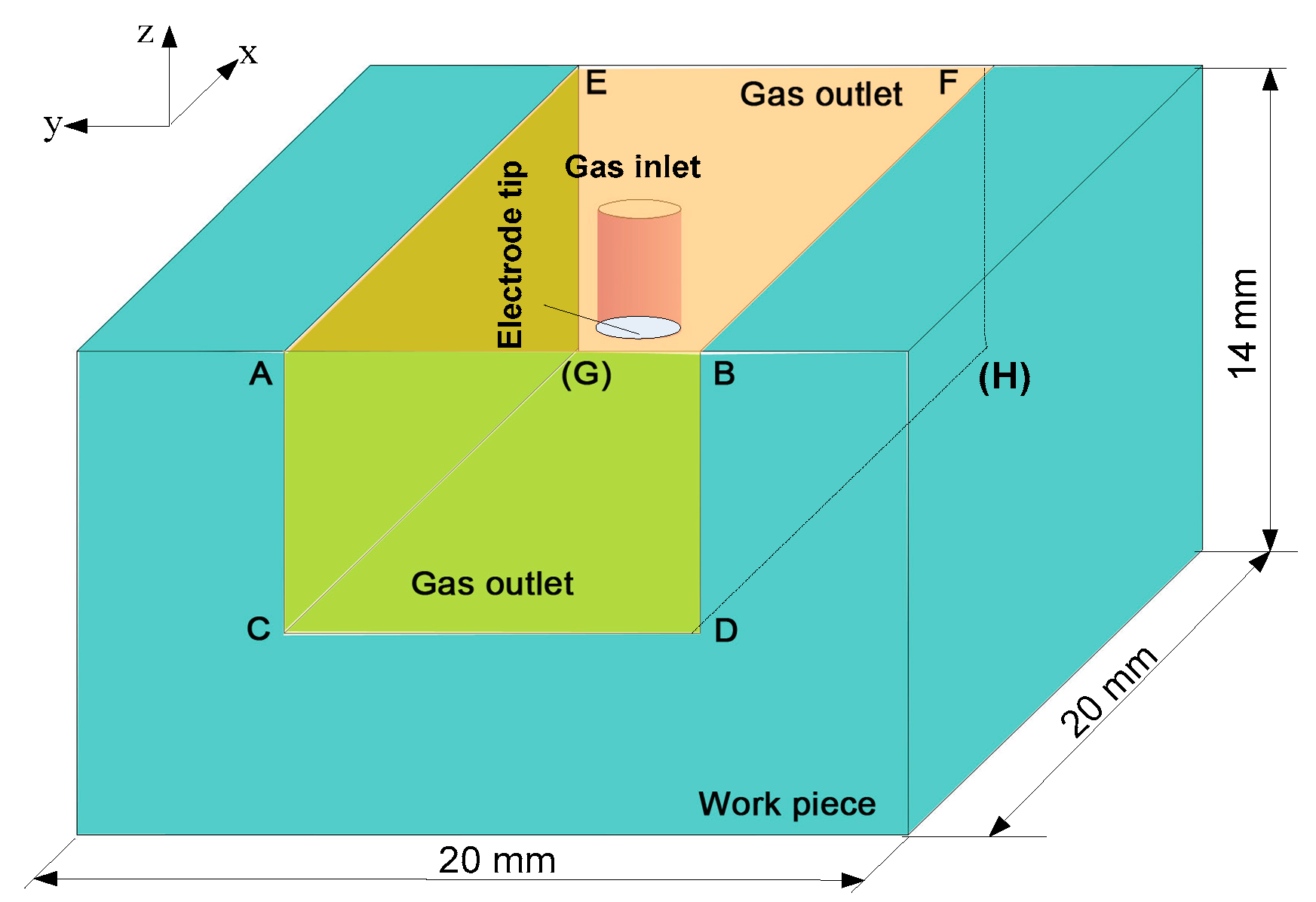
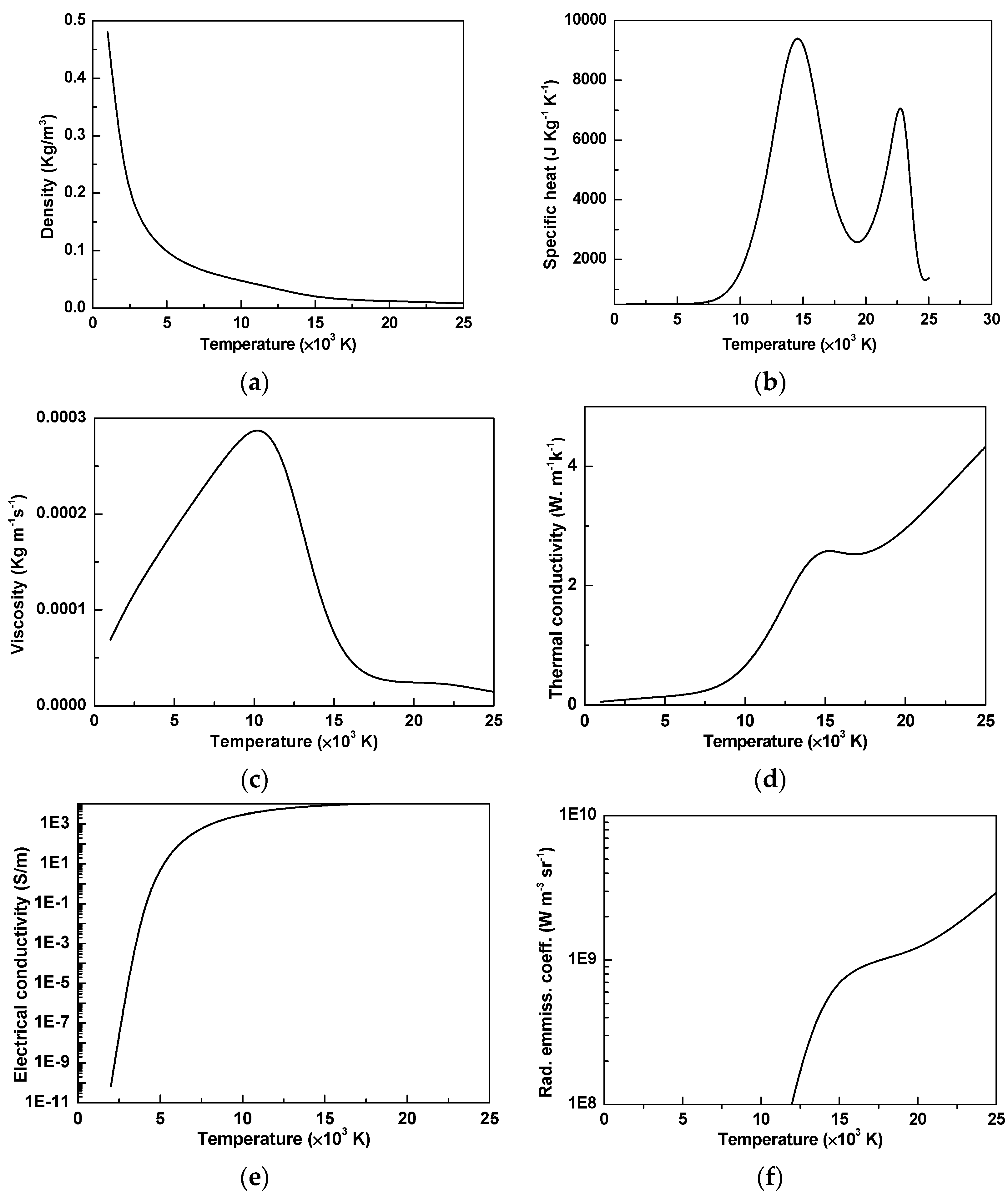
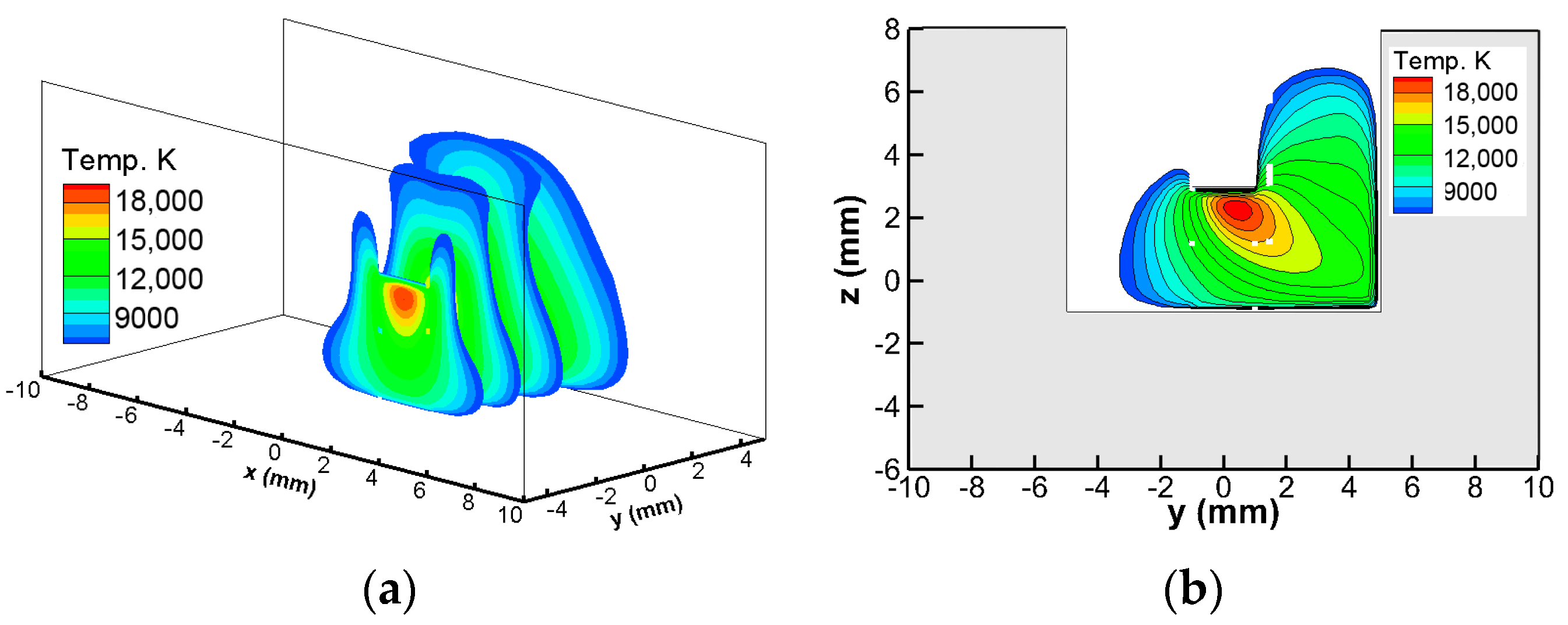

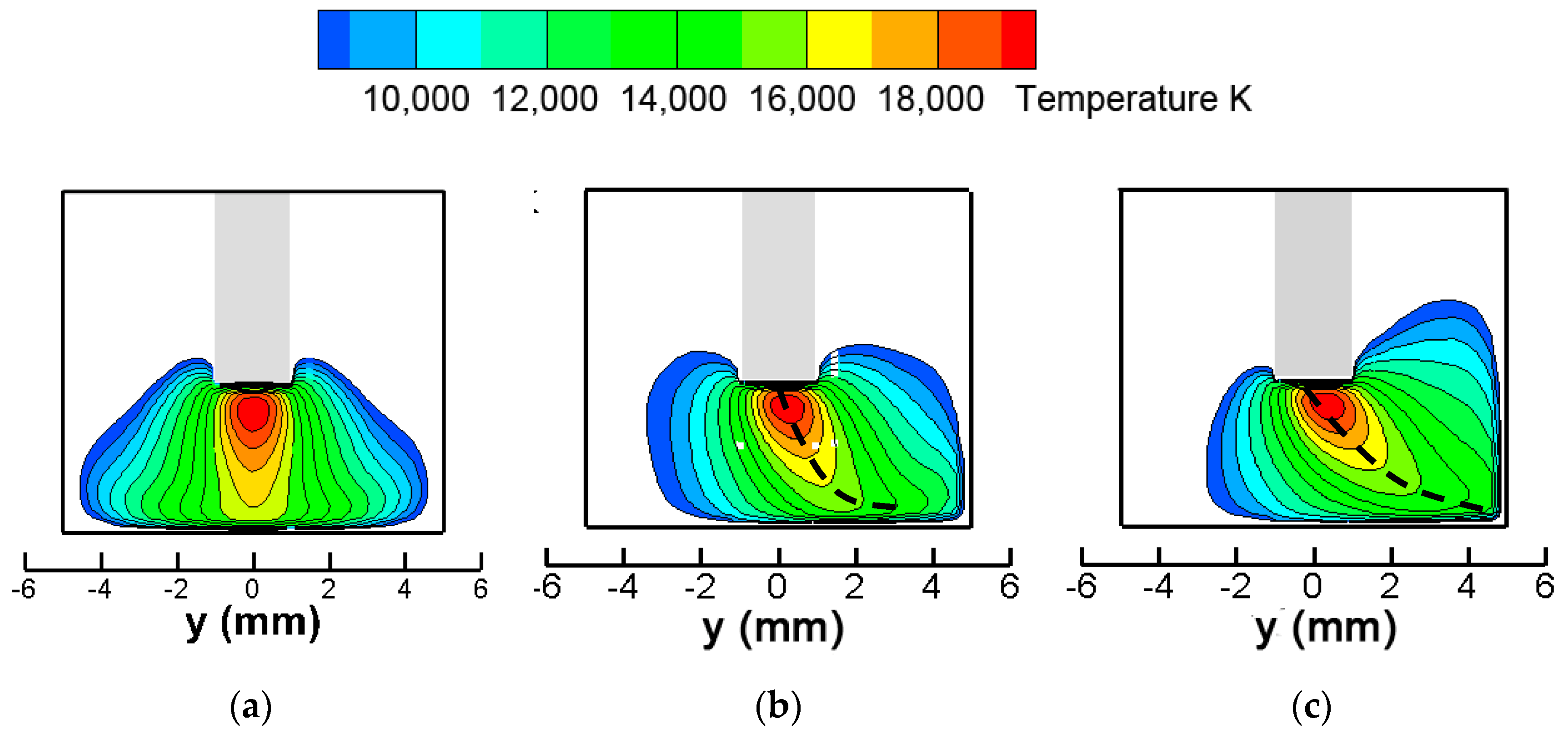
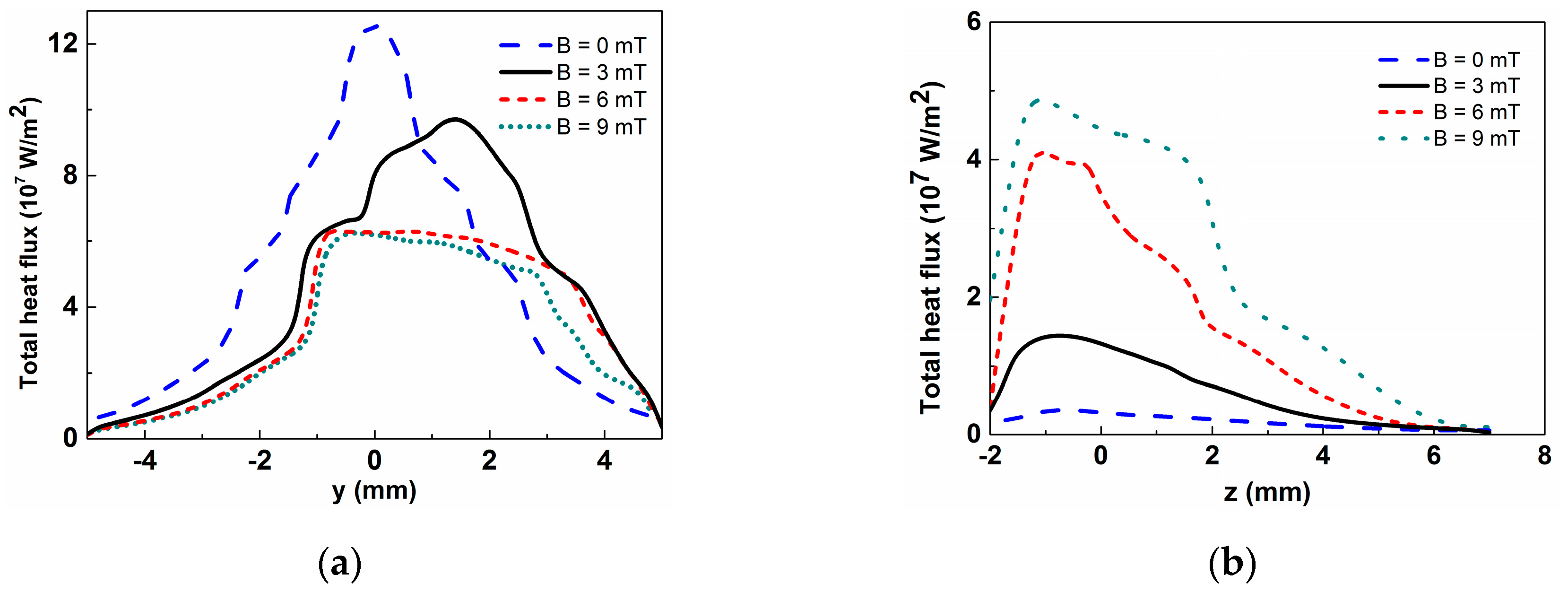
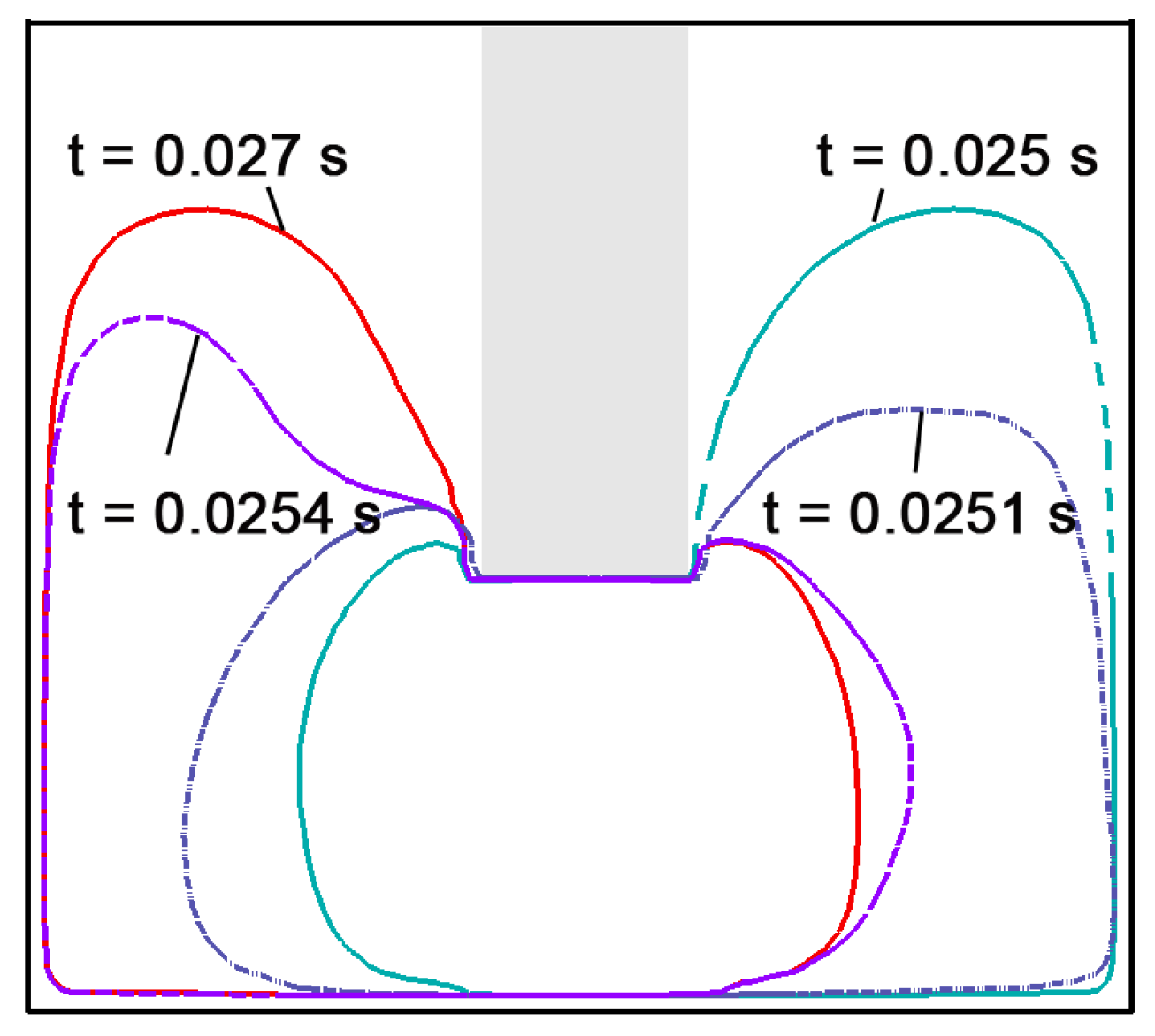

| Boundary | T (K) | V (m/s) | Φ (V) | A |
|---|---|---|---|---|
| Gas inlet | 500 | vx = vy = 0, vz = vg | ||
| Electrode tip | 3000 | - | ||
| Electrode surface | 1000 | - | ||
| Gas outlet | 1000 | - | 0 | |
| External surfaces of work piece | - | ϕ = 0 |
| Nomenclature | Value |
|---|---|
| freezing point | 1670 K |
| melting point | 1727 K |
| density | 7200 kg·m−3 |
| electric conductivity | 7.7 × 105 S/m |
| surface tension coefficient | 1.2 N·m−1 |
| surface tension temperature gradient | 1 × 10−4 N·m−1·K−1 |
| work function | 4.65 eV |
| Magnetic Field Strength (mT) | Weld Pool Width (mm) | Weld Pool Depth (mm) |
|---|---|---|
| B = 0 | 10.9 | 3.9 |
| B = 3 | 12.1 | 2.6 |
| B = 9 | 12.8 | 2.3 |
| Experimental [13] | Simulation | Deviation | |
|---|---|---|---|
| Weld width (mm) | 14.6 | 14.2 | 2.8% |
| Weld depth (mm) | 2 | 1.8 | 8.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, X.; Wu, H. Influence of the Longitudinal Magnetic Field on the Formation of the Bead in Narrow Gap Gas Tungsten Arc Welding. Metals 2020, 10, 1351. https://doi.org/10.3390/met10101351
Jian X, Wu H. Influence of the Longitudinal Magnetic Field on the Formation of the Bead in Narrow Gap Gas Tungsten Arc Welding. Metals. 2020; 10(10):1351. https://doi.org/10.3390/met10101351
Chicago/Turabian StyleJian, Xiaoxia, and Hebao Wu. 2020. "Influence of the Longitudinal Magnetic Field on the Formation of the Bead in Narrow Gap Gas Tungsten Arc Welding" Metals 10, no. 10: 1351. https://doi.org/10.3390/met10101351




