Manufacture of Defined Residual Stress Distributions in the Friction-Spinning Process: Investigations and Run-to-Run Predictive Control
Abstract
:1. Introduction
2. Materials and Methods
3. Experimental Investigations
3.1. Process Characteristics of Flange Forming by the Friction Spinning of Tubes
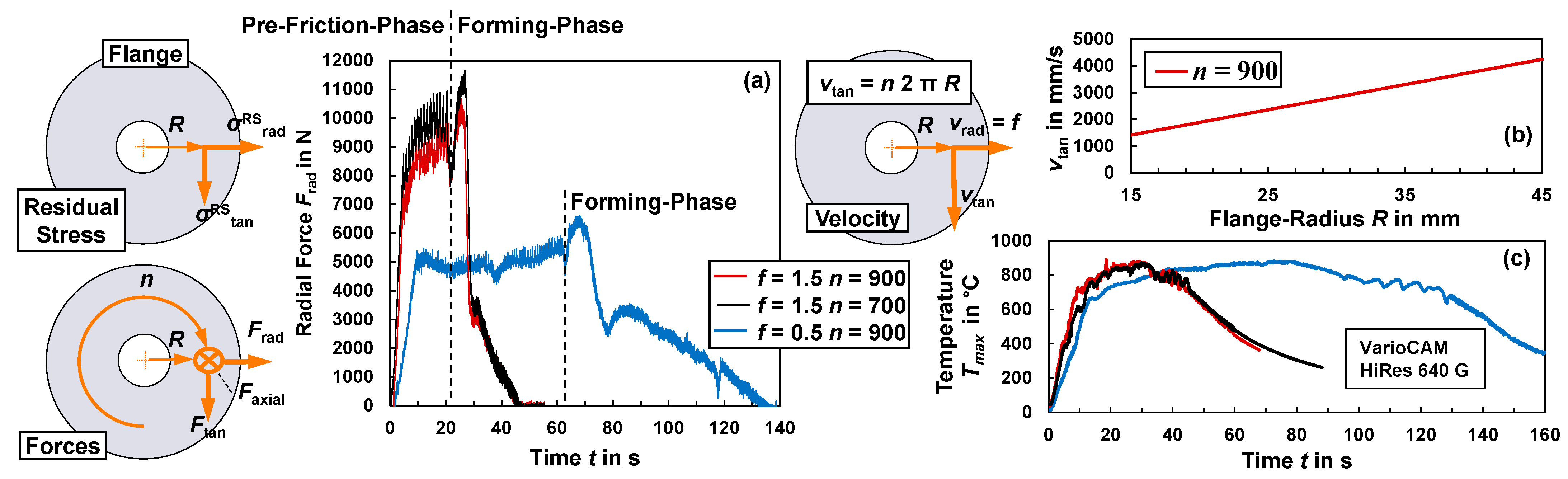
3.1.1. Process Forces in the Steel-Forming Process
3.1.2. Stress States during Aluminium and Steel Flange Forming
3.1.3. Thermal Profile of Steel Flange Forming
3.1.4. Softening and Recrystallisation in Steel Flange Forming (1.0308)
3.1.5. Thermal Stresses
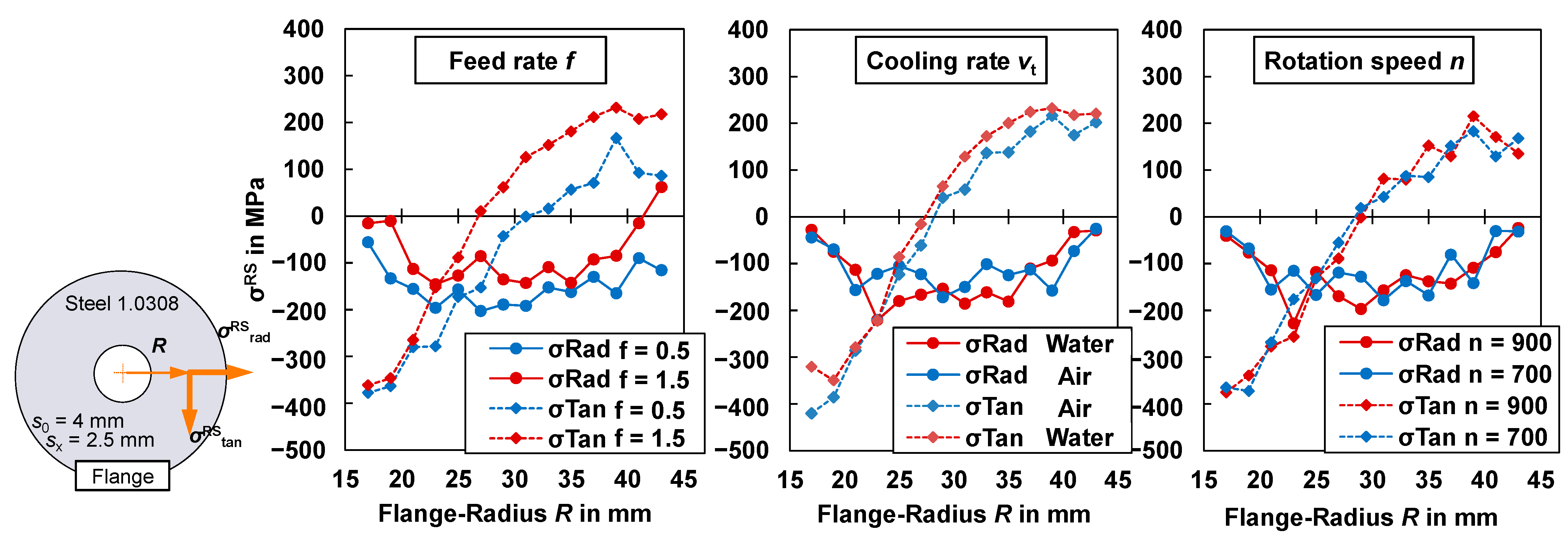
3.2. Near-Surface Residual Stress in Flanges Formed by the Friction Spinning of Steel Tubes 1.0308
3.3. Residual Stress Depth Profile in Flanges Formed by the Friction-Spinning of Steel Tubes (1.0308)
Interactions and Effects of the Parameters (1.0308)
3.4. Discussion of Residual-Stress Generation in Steel Flange Forming
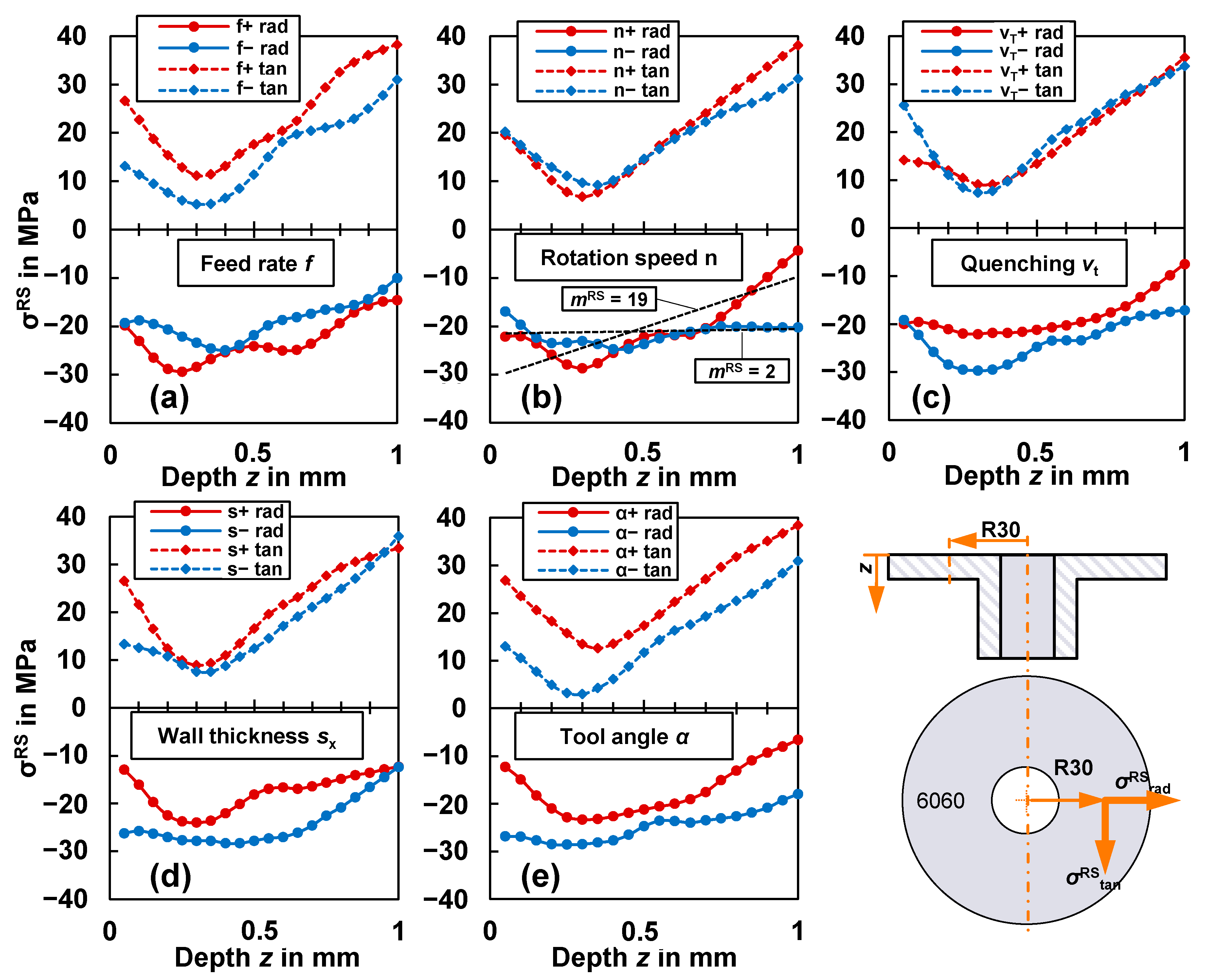
3.5. Residual Stress Profile in Flanges Formed by the Friction Spinning of Aluminium 6060 Tubes
3.5.1. Residual Stress Depth Distribution in Aluminium
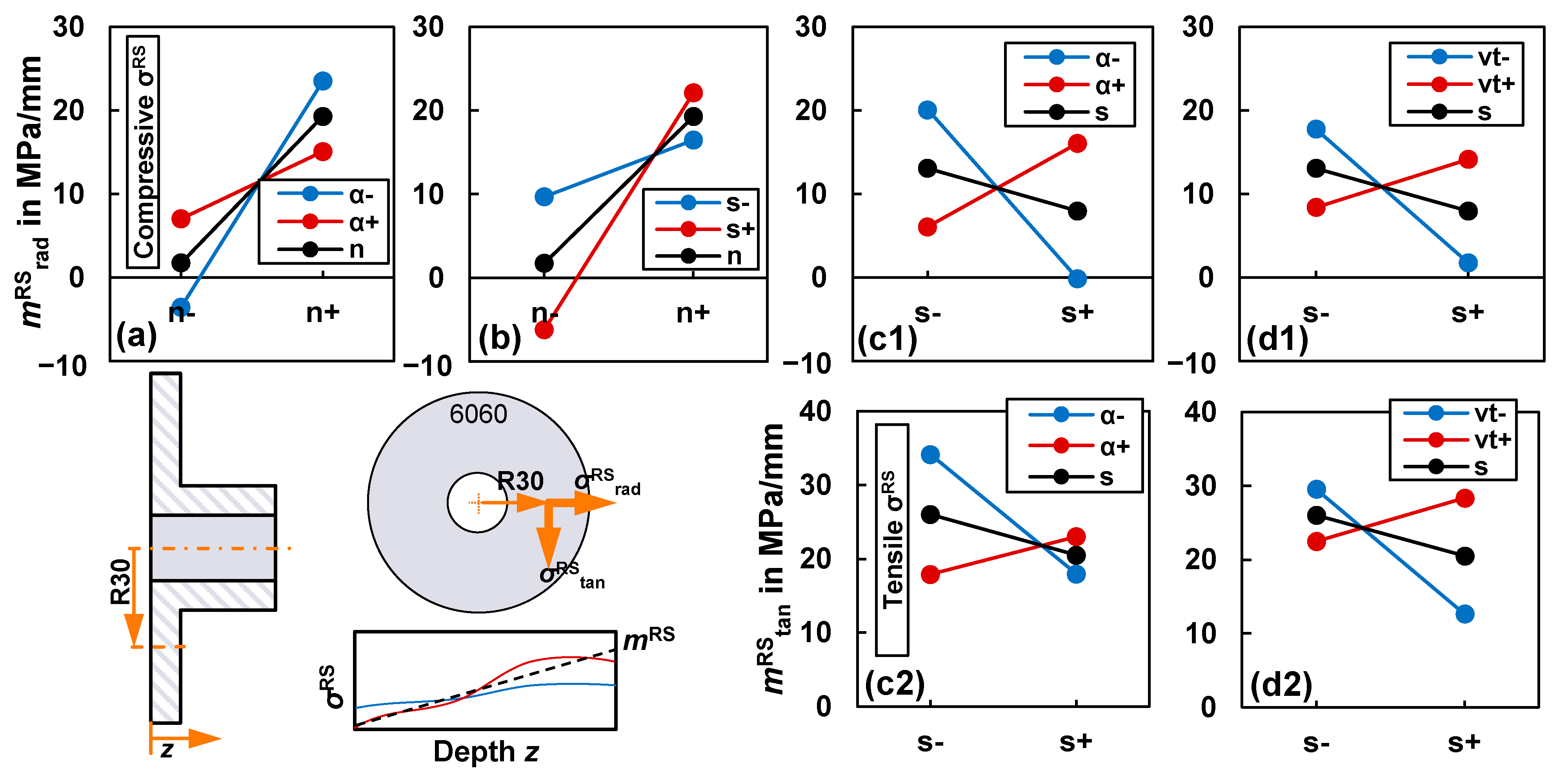
3.5.2. Interactions and Effects of the Parameters (Aluminum 6060)
3.6. Discussion of Residual Stress’ Generation in Aluminium Flange Forming
4. Process Control for Residual Stress Adjustments in Flange Forming
Residual Stress Adjustment by Run-to-Run Predictive Control (Steel 1.0308)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Processing Technol. 2010, 210, 3–23. [Google Scholar] [CrossRef]
- Runge, M. Spinning and Flow forming: Spinning and flow forming technology, product design, equipment, control systems. Verl. Mod. Ind. 1994, 72, 1–70. [Google Scholar]
- Li, W.; Vairis, A.; Preuss, M.; Ma, T. Linear and rotary friction welding review. Int. Mater. Rev. 2016, 61, 71–100. [Google Scholar] [CrossRef]
- Lossen, B.; Andreiev, A.; Stolbchenko, M.; Homberg, W.; Schaper, M. Friction-Spinning—Grain Structure Modification and the Impact on Stress/Strain Behaviour. J. Mater. Processing Technol. 2018, 261, 242–250. [Google Scholar] [CrossRef]
- Lossen, B.; Homberg, W. Friction-spinning—Interesting Approach to Manufacture of Complex Sheet Metal Parts and Tubes. Procedia Eng. 2014, 81, 2379–2384. [Google Scholar] [CrossRef] [Green Version]
- Homberg, W.; Hornjak, D.; Beerwald, C. Manufacturing of Complex Functional Graded Workpieces with the Friction-Spinning Process. Int. J. Mater. Form. 2010, 3, 943–946. [Google Scholar] [CrossRef]
- Schajer, G.S.; Whitehead, P.S. Hole-Drilling Method for Measuring Residual Stresses. Synth. SEM Lect. Exp. Mech. 2018, 1, 1–186. [Google Scholar] [CrossRef]
- Withers, P.J. Residual stress and its role in failure. Rep. Prog. Phys. 2007, 70, 2211–2264. [Google Scholar] [CrossRef] [Green Version]
- Sticchi, M.; Schnubel, D.; Kashaev, N.; Huber, N. Review of Residual Stress Modification Techniques for Extending the Fatigue Life of Metallic Aircraft Components. Appl. Mech. Rev. 2014, 67, 10801. [Google Scholar] [CrossRef]
- Maeder, G. The use of residual stresses in automotive industry. Rev. De Metall.-Cah. D Inf. Tech. 1997, 94, 199. [Google Scholar]
- Withers, P.J.; Bhadeshia, H. Residual stress. Part 1—Measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H. Residual stress. Part 2—Nature and origins. Mater. Sci. Technol. 2001, 17, 366–375. [Google Scholar] [CrossRef]
- Robinson, J.S.; Pirling, T.; Truman, C.E.; Panzner, T. Residual stress relief in the aluminium alloy 7075. Mater. Sci. Technol. 2017, 33, 1765–1775. [Google Scholar] [CrossRef]
- Lossen, B.; Homberg, W. Friction spinning—Twist phenomena and the capability of influencing them. In ESAFORM 2016, Proceedings of the 19th International ESAFORM Conference on Material Forming, Nantes, France, 27–29 April 2016; AIP Publishing LLC: Melville, NY, USA, 2016; p. 70001. [Google Scholar] [CrossRef]
- LI, Z.; SHU, X. Residual stress analysis of multi-pass cold spinning process. Chin. J. Aeronaut. 2021, 35, 259–271. [Google Scholar] [CrossRef]
- Wong, C.; Dean, T.; Lin, J. A review of spinning, shear forming and flow forming processes. Int. J. Mach. Tools Manuf. 2003, 43, 1419–1435. [Google Scholar] [CrossRef]
- Tsivoulas, D.; Da Quinta Fonseca, J.; Tuffs, M.; Preuss, M. Effects of flow forming parameters on the development of residual stresses in Cr-Mo-V steel tubes. Mater. Sci. Eng. A 2015, 624, 193–202. [Google Scholar] [CrossRef]
- Maaß, F.; Hahn, M.; Tekkaya, A.E. Adjusting residual stresses by flexible stress superposition in incremental sheet metal forming. Arch. Appl. Mech. 2021, 91, 3489–3499. [Google Scholar] [CrossRef]
- Franceschi, A.; Stahl, J.; Kock, C.; Selbmann, R.; Ortmann-Ishkina, S.; Jobst, A.; Merklein, M.; Kuhfuß, B.; Bergmann, M.; Behrens, B.-A.; et al. Strategies for residual stress adjustment in bulk metal forming. Arch. Appl. Mech. 2021, 91, 3557–3577. [Google Scholar] [CrossRef]
- Allwood, J.M.; Duncan, S.R.; Cao, J.; Groche, P.; Hirt, G.; Kinsey, B.; Kuboki, T.; Liewald, M.; Sterzing, A.; Tekkaya, A.E. Closed-loop control of product properties in metal forming. CIRP Annals-Manufacturing Technology 2016, 65, 573–596. [Google Scholar] [CrossRef] [Green Version]
- ASTM E837-20. Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method; ASTM International: West Conshohocken, PA, USA, 2020; Available online: www.astm.org (accessed on 12 February 2021).
- Schajer, G.S. Compact Calibration Data for Hole-Drilling Residual Stress Measurements in Finite-Thickness Specimens. Exp. Mech. 2020, 60, 665–678. [Google Scholar] [CrossRef]
- Fitzpatrick, M.E.; Fry, A.T.; Holdway, P.; Kandil, F.A.; Shackleton, J.; Suominen, L. Determination of Residual Stresses by X-ray Diffraction: Issue 2. Measurement Good Practice Guide; National Physical Laboratory: Teddington, UK, 2005; Volume 52. [Google Scholar]
- Schajer, G.S.; Steinzig, M. Full-Field Calculation of Hole Drilling Residual Stresses from Electronic Speckle Pattern Interferometry Data. Exp. Mech. 2005, 45, 526–532. [Google Scholar] [CrossRef]
- Dahms, F.; Homberg, W. Investigations and Improvements in 3D-DIC Optical Residual Stress Analysis—A New Temperature Compensation Method. In FORMING THE FUTURE: Proceedings of the 13th International Conference on the Technology of Plasticity, Virtual Event (Ohio State University, USA), July 25-30, 2021; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; Springer International Publishing: Cham, The Netherlands; Volume 21, pp. 2249–2259. ISBN 978-3-030-75380-1.
- DIN EN 10305-1:2016-08. Präzisionsstahlrohre—Technische Lieferbedingungen—Teil1: Nahtlose kaltgezogene Rohre; Deutsche Fassung EN 10305-1:2016; Beuth Verlag GmbH: Berlin, Germany, 2016. [Google Scholar]
- DIN EN 755-2:2016-10. Aluminium und Aluminiumlegierungen—Stranggepresste Stangen, Rohre und Profile—Teil 2: Mechanische Eigenschaften; Deutsche Fassung EN 755-2:2016; Beuth Verlag GmbH: Berlin, Germany, 2016. [Google Scholar]
- Homberg, W.; Lossen, B. Thermal assisted incremental forming of tubes and sheets with process-integrated heat generation: In Functionally Graded Materials in Industrial Mass Production|Volume 2; Heim, H.P., Biermann, D., Homberg, W., Eds.; Verlag Wissenschaftliche Scripten: Auerbach, Germany, 2013; pp. 113–128. ISBN 978-3-942267-91-5. [Google Scholar]
- Doherty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jonas, J.J.; Jensen, D.; Kassner, M.E.; King, W.E.; McNelley, T.R.; McQueen, H.J.; Rollett, A.D. Current issues in recrystallization: A review. Mater. Sci. Eng. A 1997, 238, 219–274. [Google Scholar] [CrossRef] [Green Version]
- Stein, T.; Brueckner-Foit, A.; Lossen, B.; Homberg, W. Fatigue Crack Extension in an Incrementally Formed Tube. In Proceedings of the Procedia Materials Science of 20th European Conference on Fracture, Trondheim, Norway, 30 June–4 July; Volume 3, pp. 1884–1889. [CrossRef] [Green Version]
- Homberg, W.; Hornjak, D. Friction-spinning of tubular components—Basic research on parameter influence and process design. Int. Conf. Technol. Plast. 2011, 10, 548–553. [Google Scholar]
- Lossen, B.; Andreiev, A.; Homberg, W.; Schaper, M. Friction-Spinning—Possibility of Grain Structure Adjustment. Procedia Eng. 2017, 207, 1749–1754. [Google Scholar] [CrossRef]









| Alloy | Si | Fe | Cu | Mn | Mg | Cr | Ni | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|---|
| 6060 | 0.432 | 0.174 | 0.049 | 0.044 | 0.490 | 0.010 | 0.005 | 0.023 | 0.008 | 98.71 |
| Alloy | C | Si | Mn | P | S | Al | ||||
| S235 | 0.17 | 0.35 | 1.20 | 0.025 | 0.025 | 0.015 |
| Parameter Coded | Rotation Speed n [rpm] | Feed Rate f [mm/s] | Quenching vt |
|---|---|---|---|
| +1 | 900 | 1.5 | Water |
| −1 | 700 | 0.5 | Air |
| Parameter Coded | Rotation Speed n [rpm] | Feed Rate f [mm/s] | Quenching vt | Wall Thickness sx [mm] | Tool Angle α [°] |
|---|---|---|---|---|---|
| +1 | 900 | 3 | Water | 2.5 | 55 |
| −1 | 500 | 1.5 | Air | 2 | 45 |
| Residual Stresses | avg. | n | F | vt | n f | n vt | f vt | n f vt | ||
|---|---|---|---|---|---|---|---|---|---|---|
| mRSrad | [MPa/mm] | Grad. | 135 | 65 | −156 | −51 | 31 | −4 | 6 | −48 |
| mRStan | [MPa/mm] | Grad. | 200 | 23 | −159 | 48 | −55 | −35 | −5 | 28 |
| Residual Stresses | z [mm] | avg. | n | f | n f | sx | n sx | f sx | α vt | α | n α | f α | sxvt | sx α | f vt | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σRSrad,0.2 | MPa | 0.2 | −25 | −2 | −8 | 1 | 5 | −4 | −1 | −4 | 8 | 2 | −4 | −3 | −3 | −2 |
| σRStan,0.2 | MPa | 0.2 | 12 | −3 | 8 | −4 | 2 | 1 | −1 | 0 | 13 | 1 | 0 | 1 | −5 | 2 |
| σRSrad,0.8 | MPa | 0.8 | −18 | 5 | −3 | −3 | 6 | −1 | 4 | −8 | 10 | −6 | −4 | 2 | 5 | −4 |
| σRStan,0.8 | MPa | 0.8 | 27 | 4 | 11 | −6 | 4 | 0 | 6 | 0 | 9 | 0 | −3 | 6 | 3 | 1 |
| mRSrad | MPa/mm | Grad. | 11 | 18 | 1 | 1 | −5 | 11 | 5 | −7 | 1 | −10 | 3 | 11 | 15 | 0 |
| mRStan | MPa/mm | Grad. | 23 | 10 | −1 | 3 | −6 | 4 | 3 | 3 | −6 | 3 | −3 | 11 | 11 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahms, F.; Homberg, W. Manufacture of Defined Residual Stress Distributions in the Friction-Spinning Process: Investigations and Run-to-Run Predictive Control. Metals 2022, 12, 158. https://doi.org/10.3390/met12010158
Dahms F, Homberg W. Manufacture of Defined Residual Stress Distributions in the Friction-Spinning Process: Investigations and Run-to-Run Predictive Control. Metals. 2022; 12(1):158. https://doi.org/10.3390/met12010158
Chicago/Turabian StyleDahms, Frederik, and Werner Homberg. 2022. "Manufacture of Defined Residual Stress Distributions in the Friction-Spinning Process: Investigations and Run-to-Run Predictive Control" Metals 12, no. 1: 158. https://doi.org/10.3390/met12010158





