Effect of Ni Doping on the Embrittlement of Liquid Zinc at Σ5 Fe Austenite Grain Boundary
Abstract
:1. Introduction
2. Experimental Methods
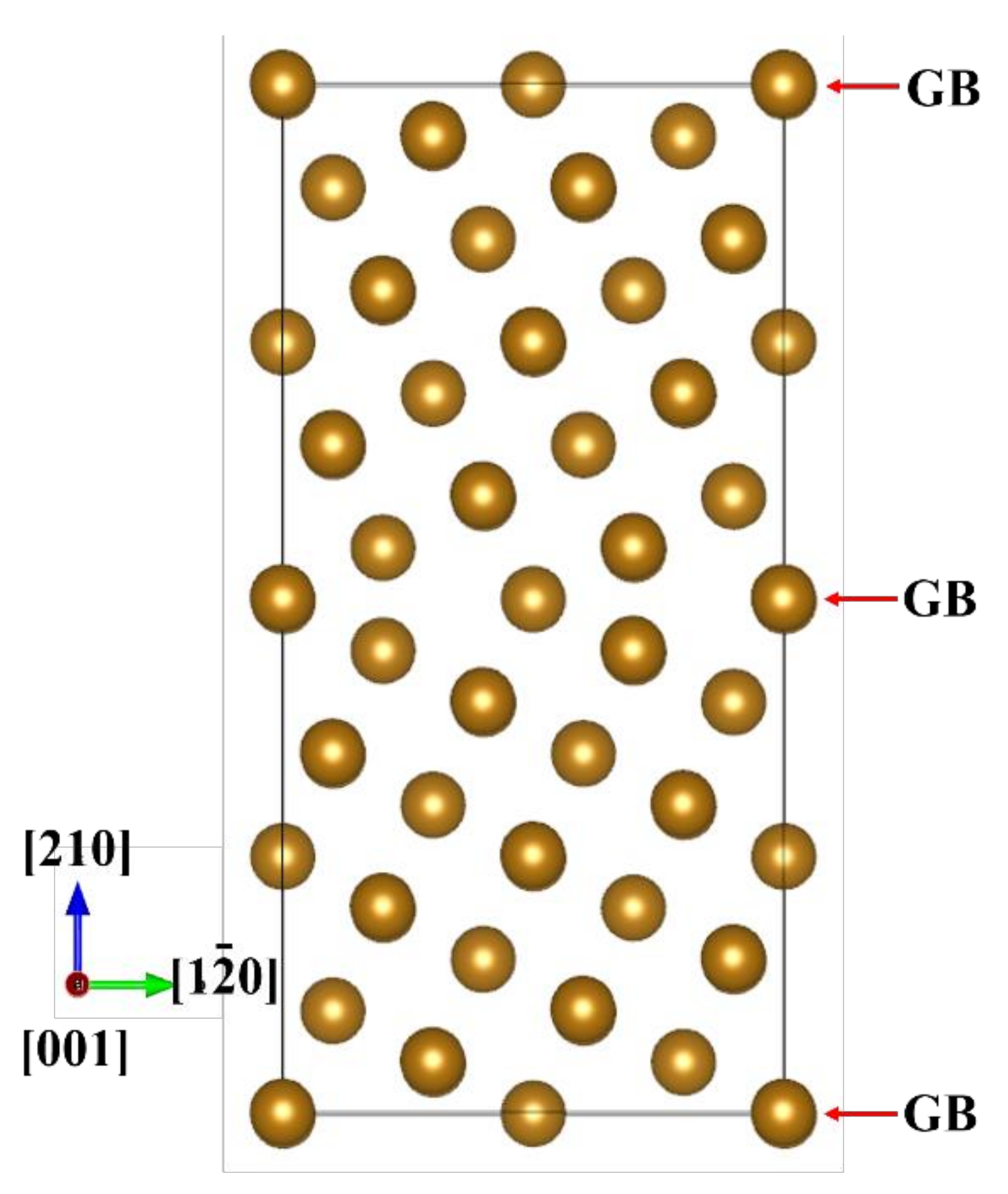
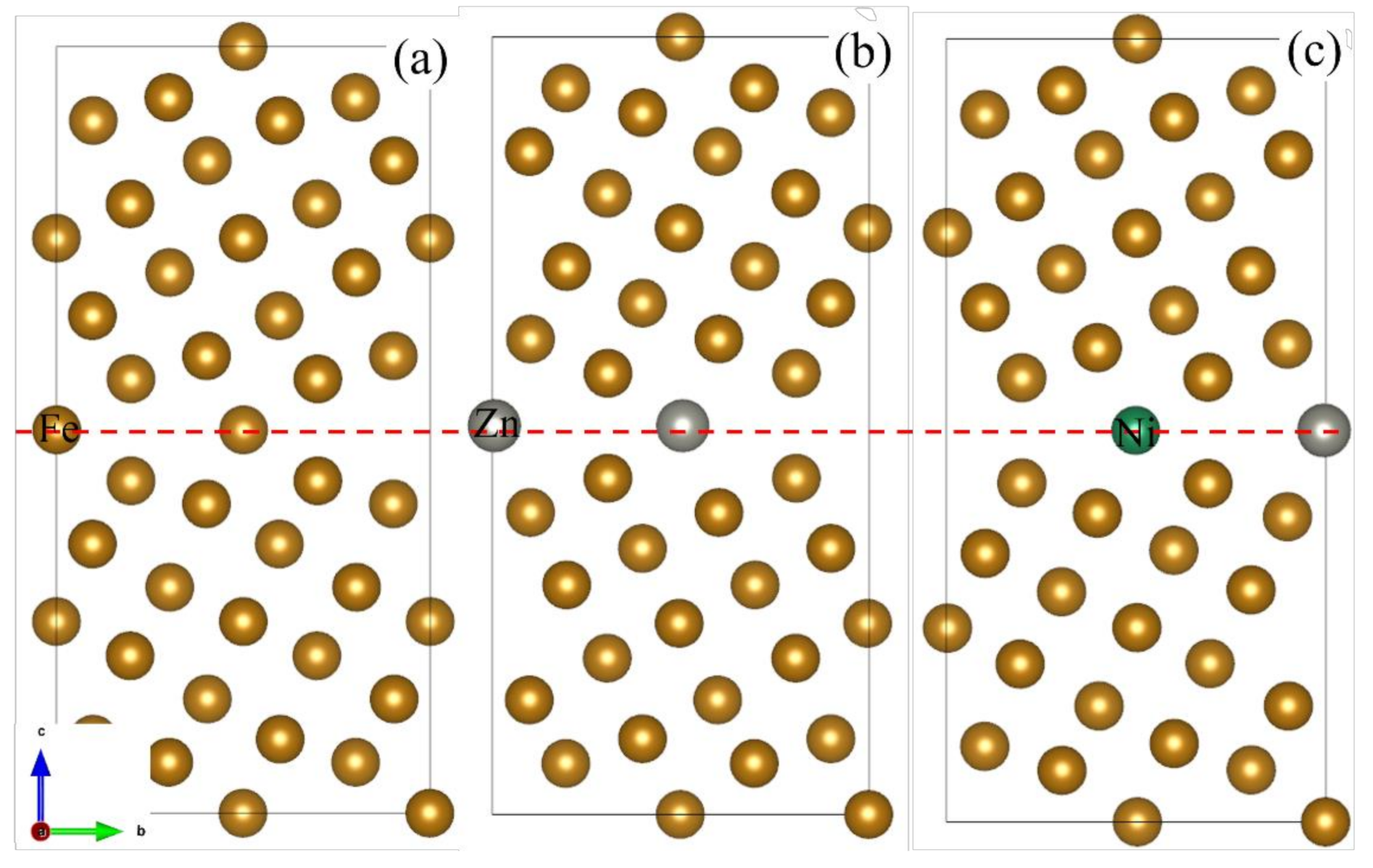
2.1. Grain Boundary Models
2.2. Calculation Method and Parameter Setting
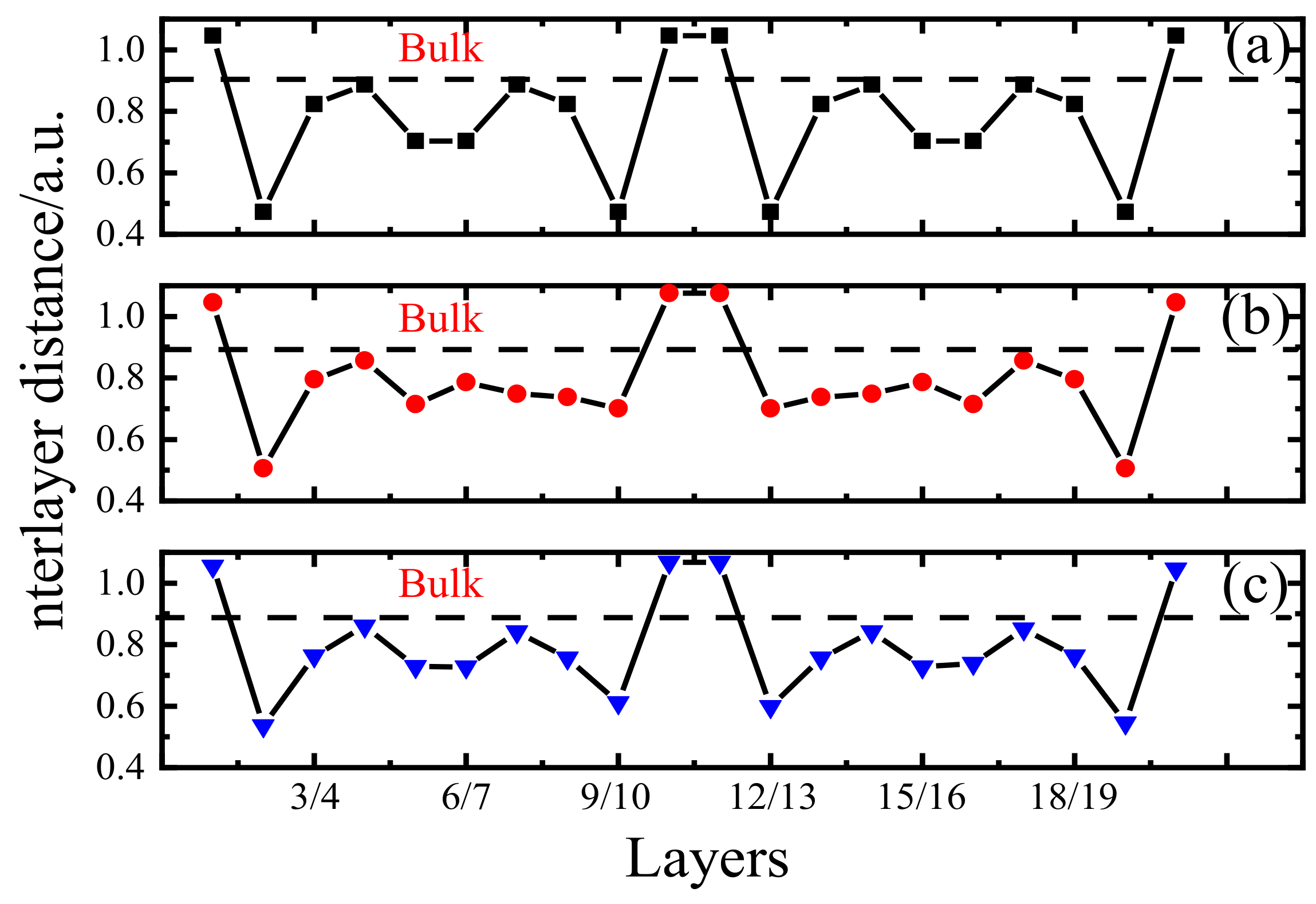
2.3. Model Optimization
- The Poisson’s ratio was ignored as suggested in previous studies [39]. In other words, the material was not deformed along the vertical strain direction (z-axis), and the unit cell parameters along the x and y-directions remained unchanged.
- The atom at the fixed twin boundary did not move. In fact, the unit cell contained two twin boundaries (z = 0 (1) and z = 0.5), and only the z = 0 (1) boundary was fixed during calculations. There were no restrictions for the movements of the two atoms with z = 0.5; however, they did not produce any displacements during the calculation process.
- The structure with a strain of 0% was fully relaxed as the initial stable configuration. The applied strain changed the c value of the unit cell parameter according to the following formula:where is the magnitude of strain equal to 2%, 4%, 6% …; is the c-axis unit cell parameter of the POSCAR file corresponding to strain; and is the c-axis unit cell parameter at a strain of 0%.
3. Results and Discussion
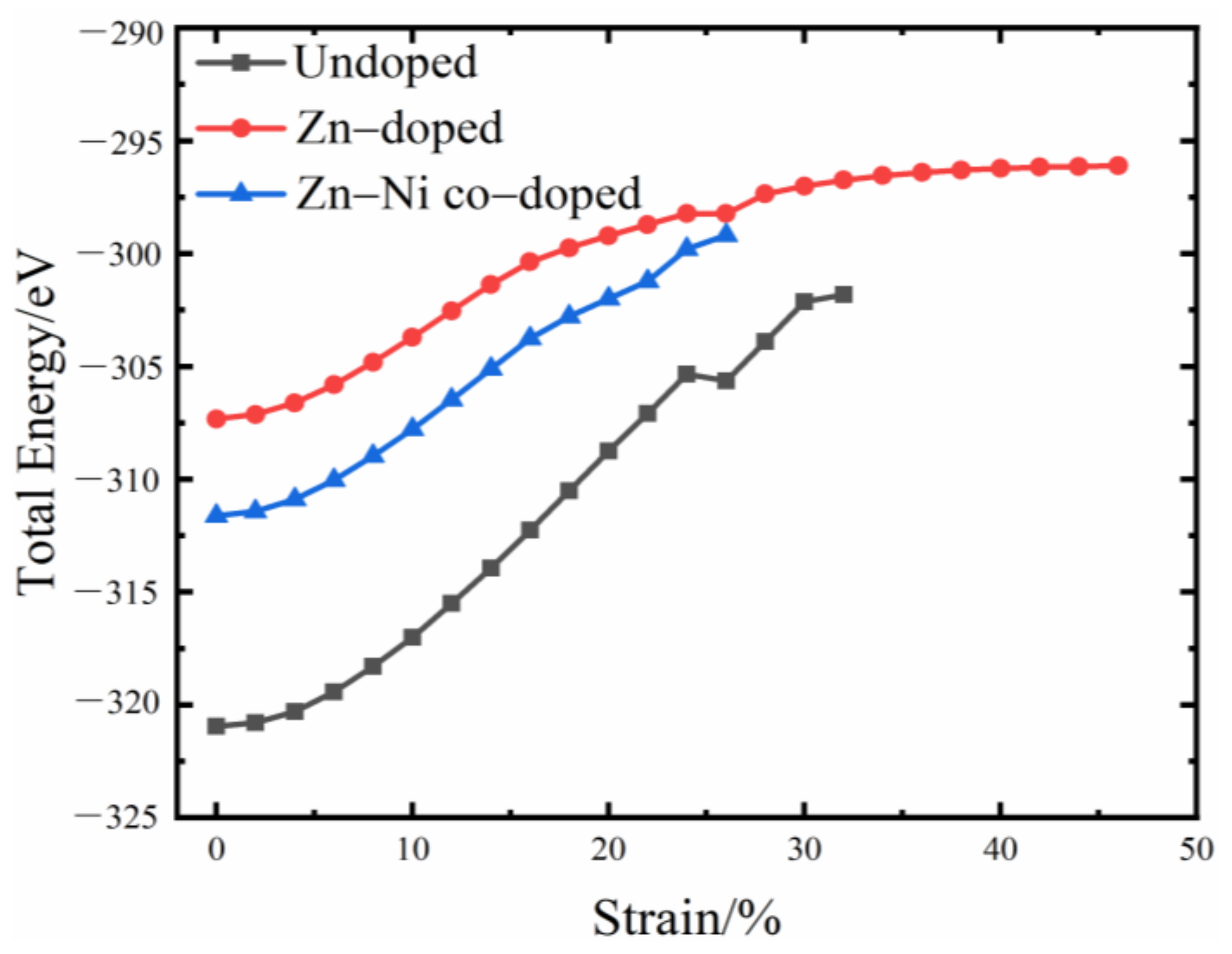
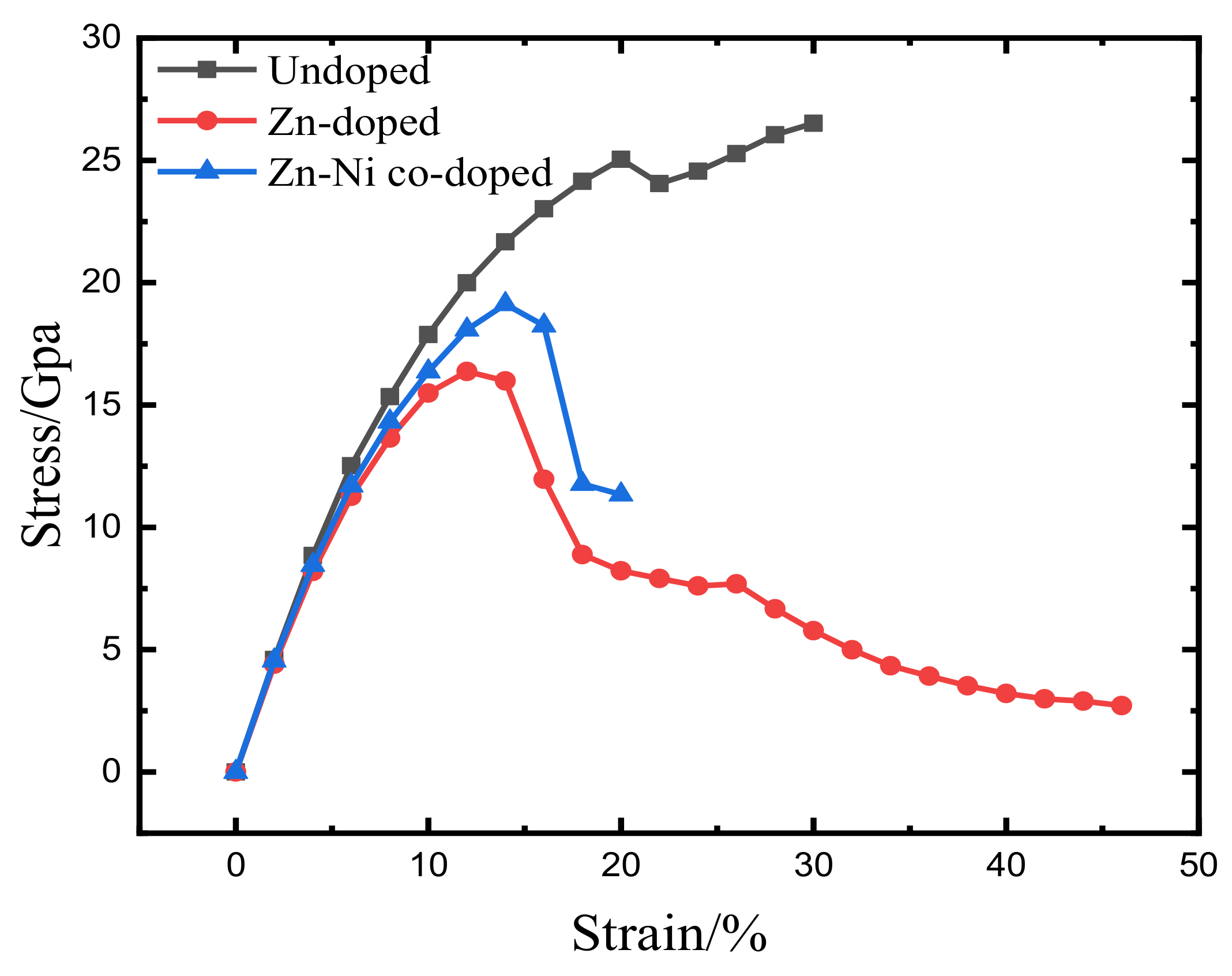
3.1. Total Energy and Theoretical Tensile Strength
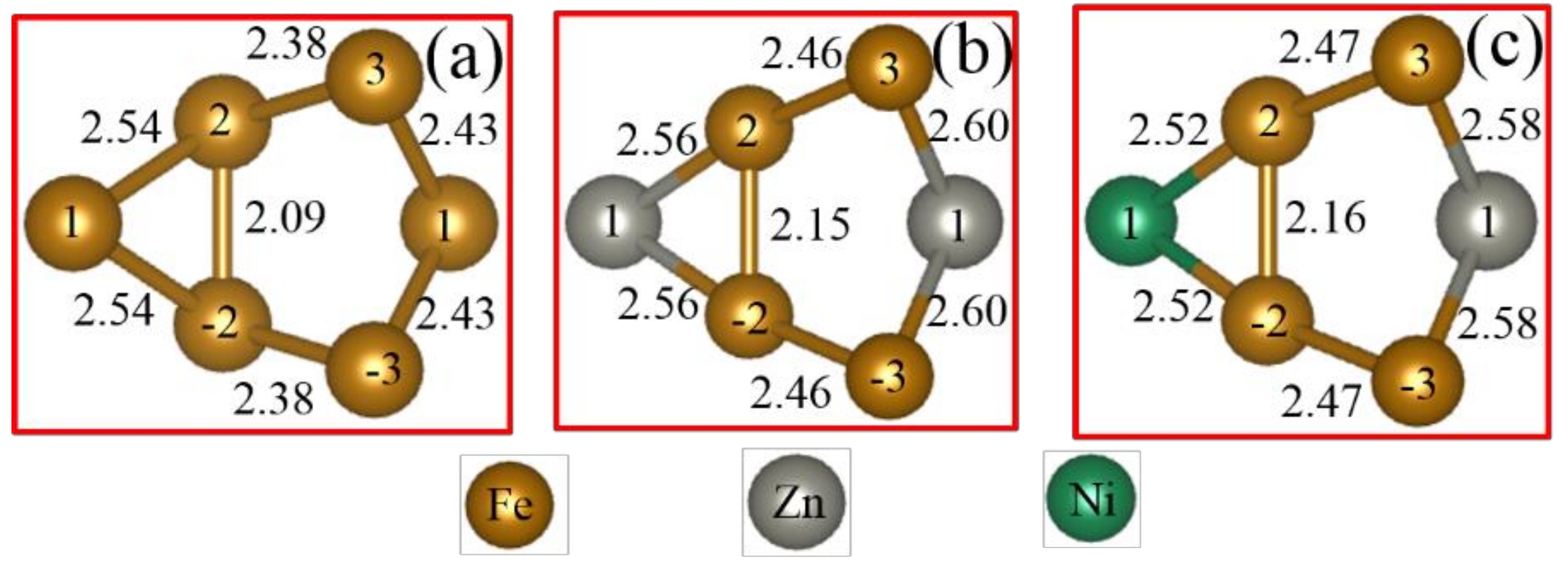
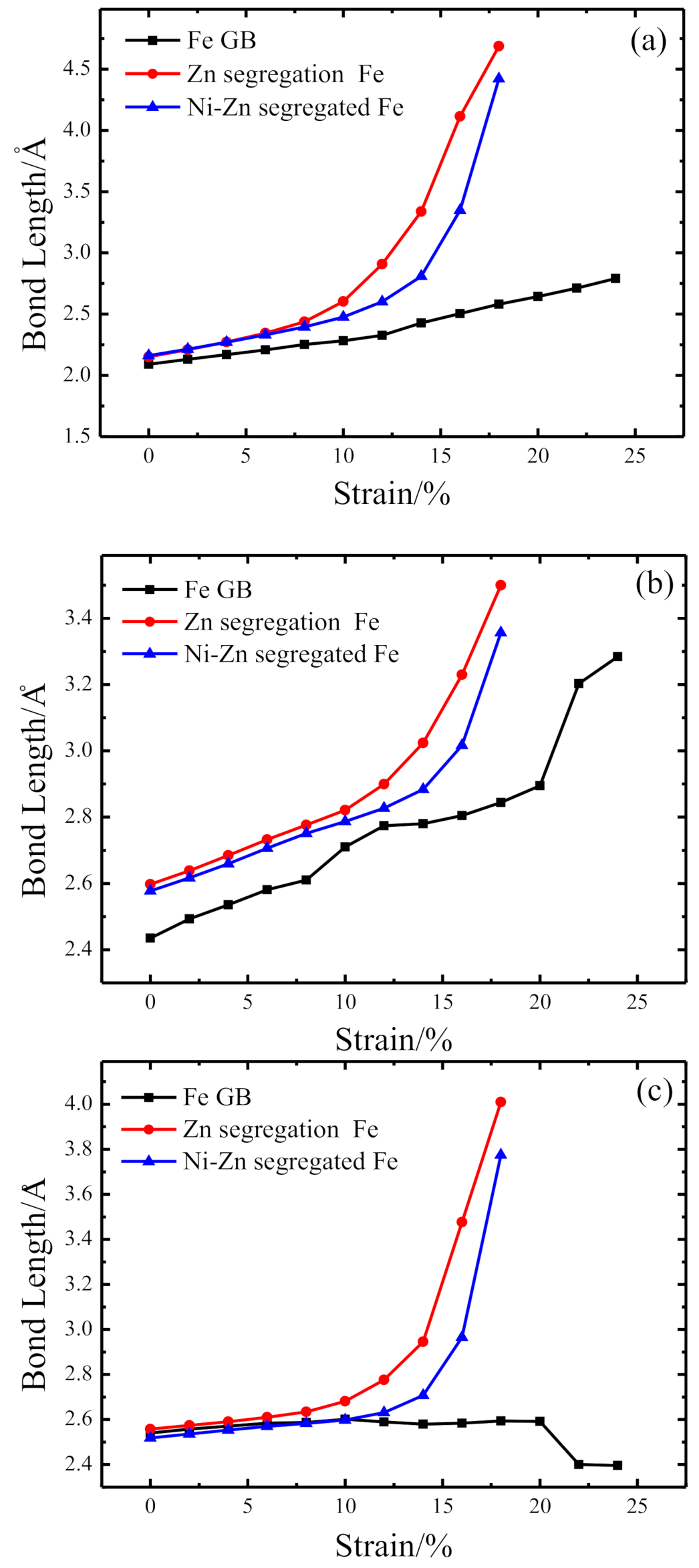
3.2. Chemical Bond Structure
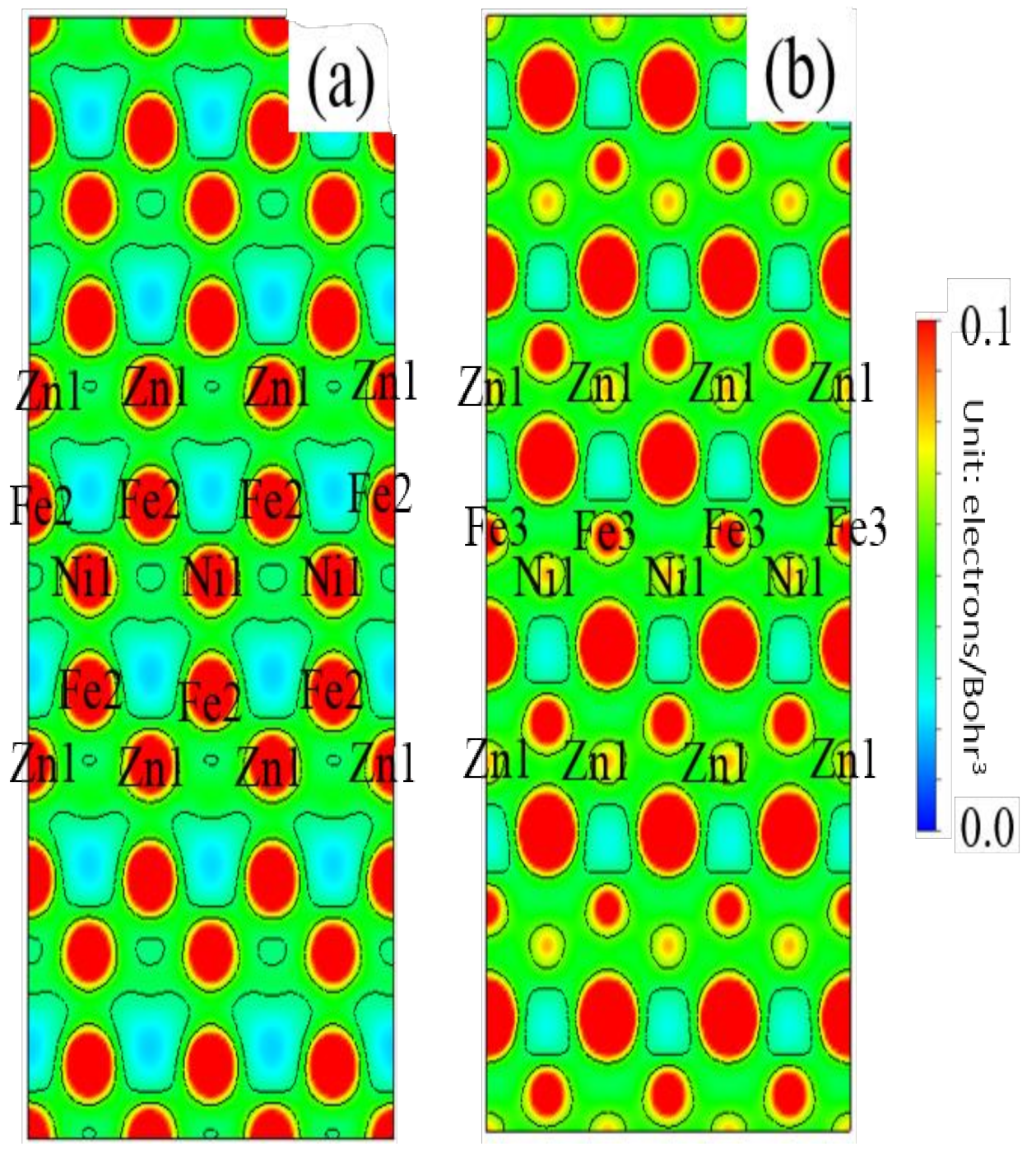
3.3. Electronic Structure
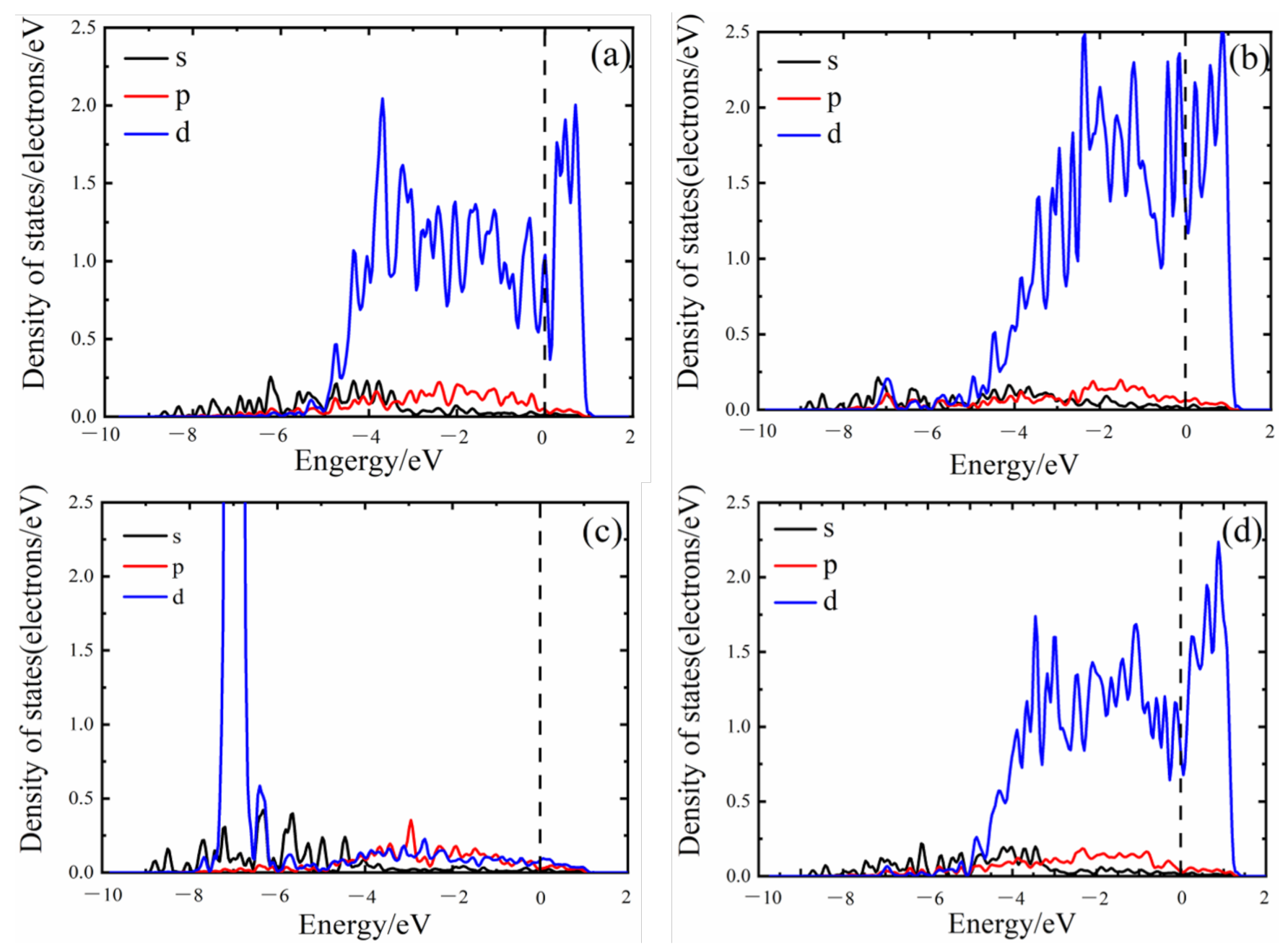
3.4. Density of States
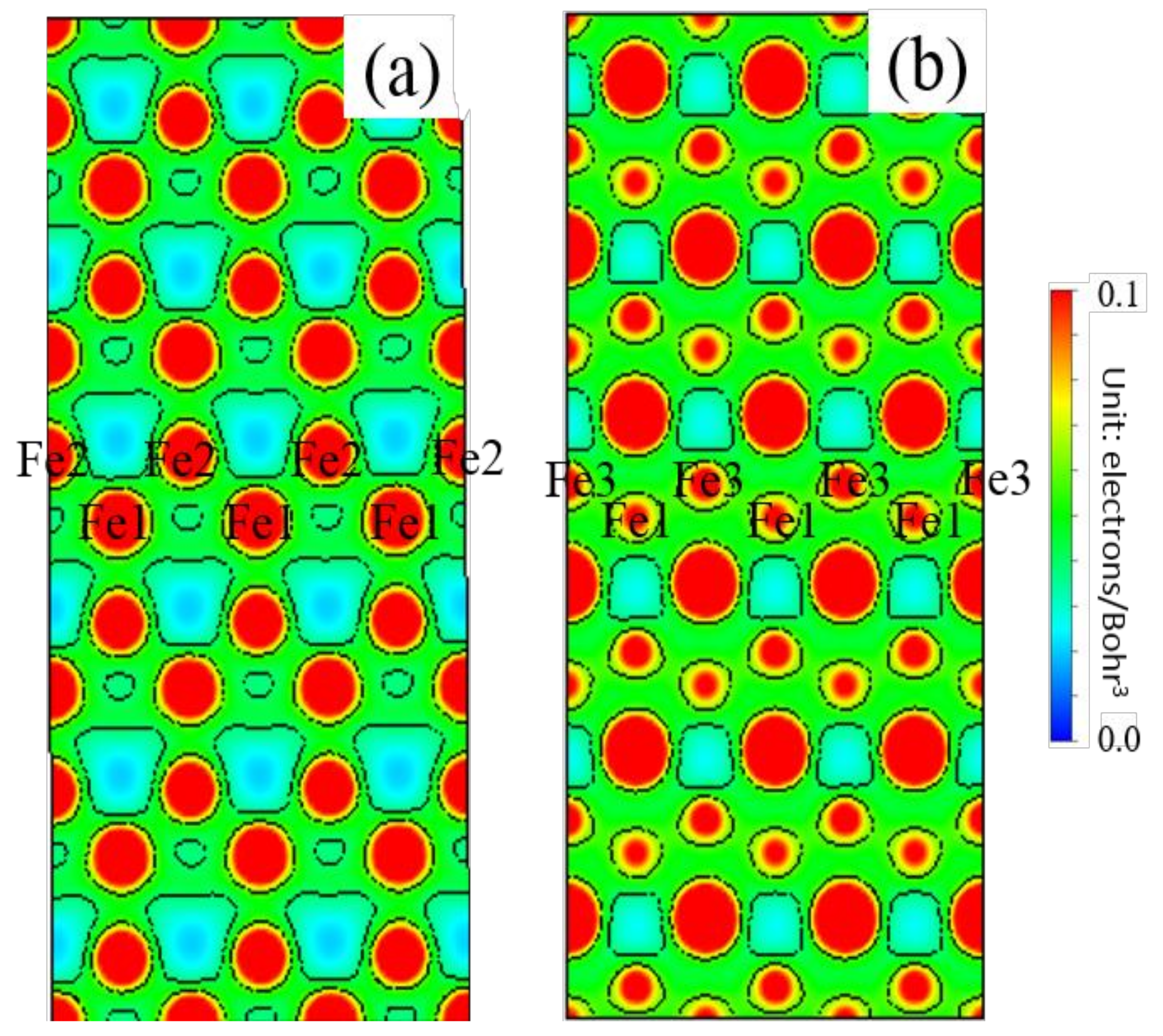
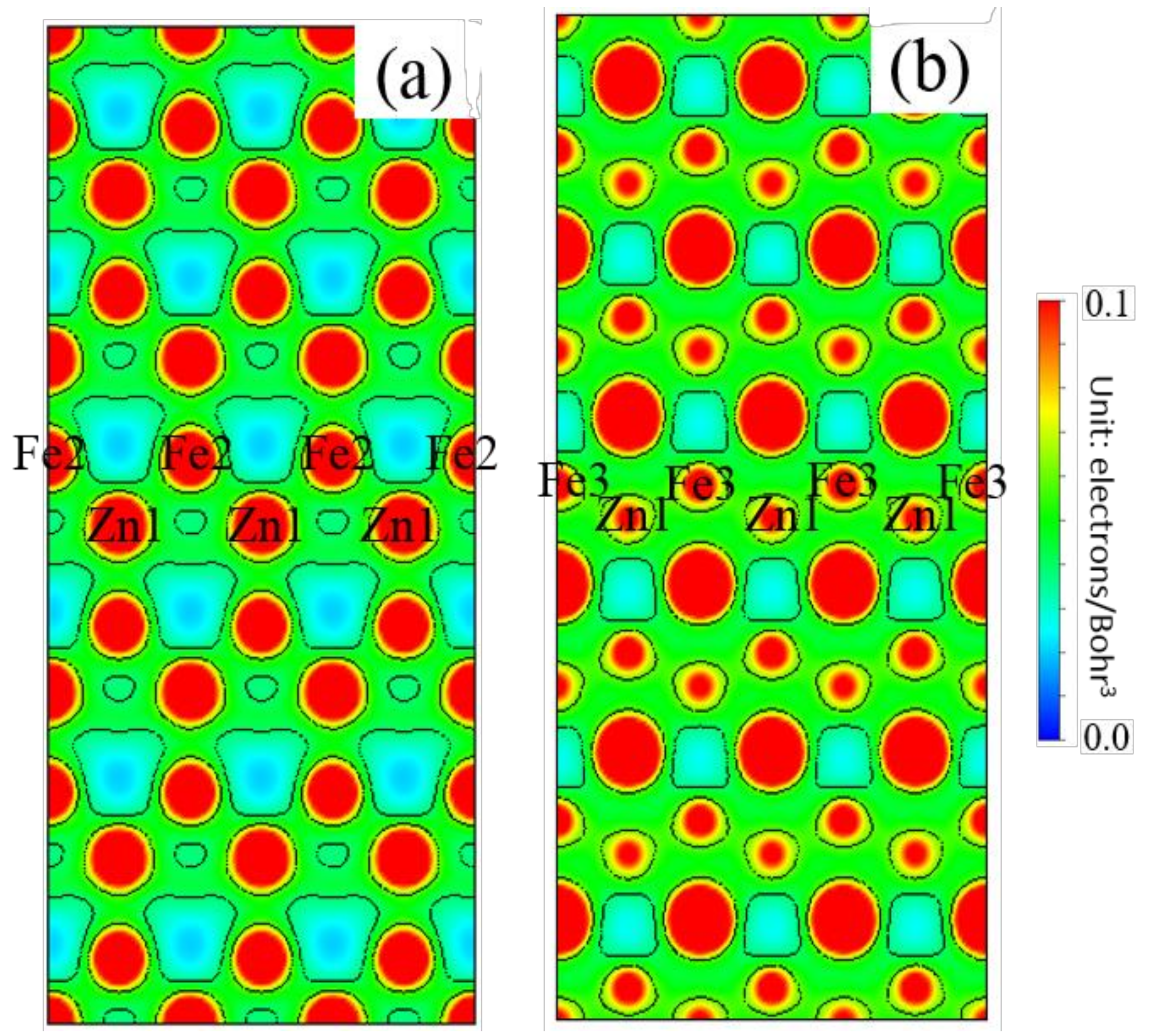
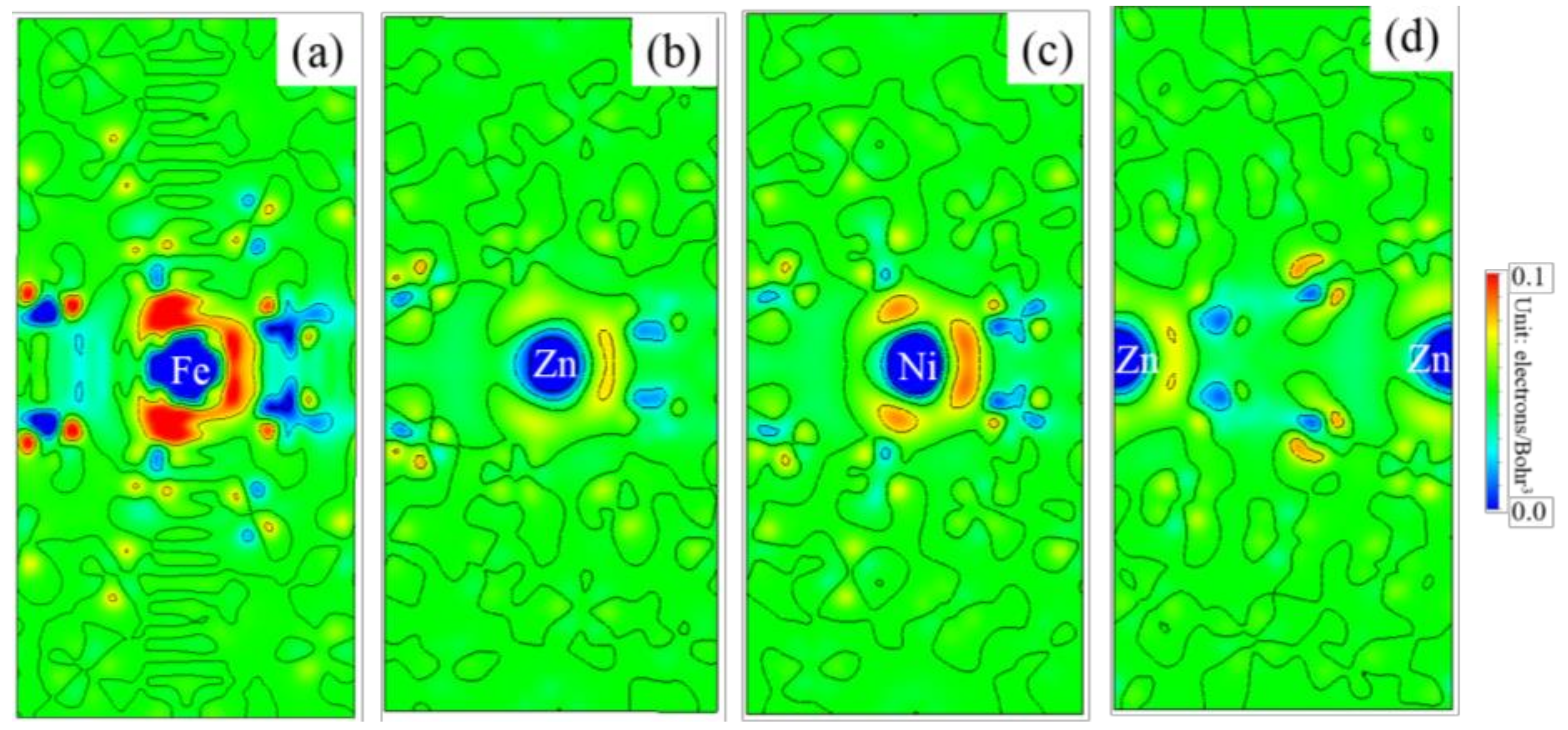
3.5. Differential Charge Density
4. Conclusions
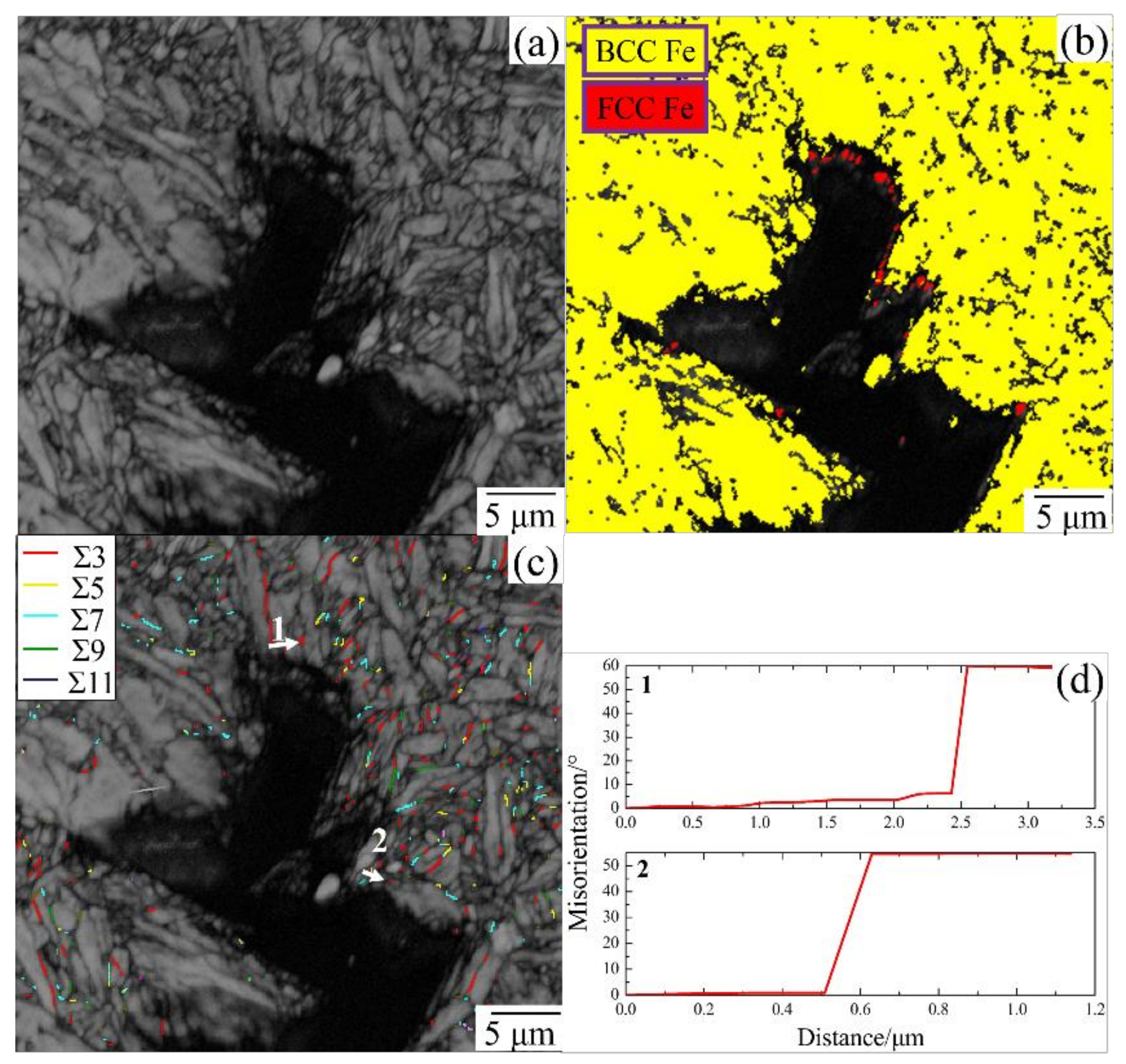
- EBSD was used to establish an appropriate grain boundary model to further explain the brittle fracture induced by liquid zinc.
- Because the sizes of Zn and Fe atoms are not the same, doping the pure Fe grain boundary leads to its expansion, which increases the lengths of Fe-Fe bonds, leading to their weakening, and reduces the overall boundary strength.
- The Zn doping of the grain boundary results in the formation of Zn-Fe covalent bonds, which decrease the charge density of Fe-Fe bonds and weakens them. Meanwhile, the Fe-Zn bonds are oriented at a certain angle with respect to the grain boundary direction and possess very low strengths. After the weakened Fe-Fe bonds are broken, the strength of the grain boundary drops significantly.
- After the Zn-Ni co-doping of the grain boundary, Ni atoms form metallic bonds with Fe atoms, which increase the charge density and strength of Fe-Fe bonds with respect to that of the Fe-Fe bonds in the Zn-doped grain boundary.
- The Fe-Ni bonds at the Zn-Ni co-doped grain boundary are stronger than the Fe-Zn bonds and, therefore, can potentially suppress the fcc Fe grain boundary fracture.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Drillet, P.; Grigorieva, R.; Leuillier, G.; Vietoris, T. Study of cracks propagation inside the steel on press hardened steel zinc based coatings. La Metall. Ital. 2012. [Google Scholar] [CrossRef] [Green Version]
- Kondratiuk, J.; Kuhn, P.; Labrenz, E.; Bischoff, C. Zinc coatings for hot sheet metal forming: Comparison of phase evolution and microstructure during heat treatment. Surf. Coat. Technol. 2011, 205, 4141–4153. [Google Scholar] [CrossRef]
- Lee, C.W.; Choi, W.S.; Cho, L.; Cho, Y.R.; De Cooman, B.C. Liquid-metal-induced embrittlement related microcrack propagation on Zn-coated press hardening steel. ISIJ Int. 2015, 55, 264–271. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.W.; Fan, D.W.; Sohn, I.R.; Lee, S.J.; De Cooman, B.C. Liquid-metal-induced embrittlement of Zn-coated hot stamping steel. Metall. Mater. Trans. A 2012, 43, 5122–5127. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.; Peng, W.; Lu, R.; Wu, G.; Zhang, J. Diffusion and cracking behavior involved in hot press forming of Zn coated 22MnB5. J. Alloys Compd. 2019, 806, 195–205. [Google Scholar] [CrossRef]
- Chang, J.K.; Lin, C.S.; Wang, W.R.; Cheng, W.J. Microstructural evaluation and property change of 5 wt pct Al-Zn coating on press hardening steel during austenitization. Metall. Mater. Trans. A 2018, 49, 3715–3728. [Google Scholar] [CrossRef]
- Chang, J.K.; Lin, C.S. Microstructural Evolution of 11Al-3Mg-Zn Ternary Alloy-Coated Steels During Austenitization Heat Treatment. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2017, 48, 3734–3744. [Google Scholar] [CrossRef]
- Schino, A. Di Manufacturing and Applications of Stainless Steels. Metals 2020, 10, 327. [Google Scholar] [CrossRef] [Green Version]
- Bauer, K.D.; Todorova, M.; Hingerl, K.; Neugebauer, J. A first principles investigation of zinc induced embrittlement at grain boundaries in bcc iron. Acta Mater. 2015, 90, 69–76. [Google Scholar] [CrossRef]
- Miyazawa, N.; Hakamada, M.; Mabuchi, M. Atomic bond-breaking behaviour during grain boundary fracture in a C-segregated Fe grain boundary. Philos. Mag. Lett. 2017, 97, 311–319. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.H.; Deng, S.; Wang, T.; Kohyama, M.; Yamamoto, R. Theoretical tensile strength of an Al grain boundary. Phys. Rev. B 2004, 69, 134106. [Google Scholar] [CrossRef]
- Lu, G.H.; Zhang, Y.; Deng, S.; Wang, T.; Kohyama, M.; Yamamoto, R.; Liu, F.; Horikawa, K.; Kanno, M. Origin of intergranular embrittlement of Al alloys induced by Na and Ca segregation: Grain boundary weakening. Phys. Rev. B 2006, 73, 224115. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Lu, G.H.; Wang, T.; Deng, S.; Kohyama, M.; Yamamoto, R. Effects of segregated Ga on an Al grain boundary: A first-principles computational tensile test. Mater. Trans. 2006, 47, 2678–2681. [Google Scholar] [CrossRef] [Green Version]
- Yuasa, M.; Mabuchi, M. Bond mobility mechanism in grain boundary embrittlement: First-principles tensile tests of Fe with a P-segregated Σ 3 grain boundary. Phys. Rev. B 2010, 82, 94108. [Google Scholar] [CrossRef]
- Yuasa, M.; Mabuchi, M. Effects of segregated Cu on an Fe grain boundary by first-principles tensile tests. J. Phys. Condens. Matter 2010, 22, 505705. [Google Scholar] [CrossRef]
- Nyyssönen, T.; Isakov, M.; Peura, P.; Kuokkala, V.T. Iterative determination of the orientation relationship between austenite and martensite from a large amount of grain pair misorientations. Metall. Mater. Trans. A 2016, 47, 2587–2590. [Google Scholar] [CrossRef]
- Hutchinson, B.; Hagström, J.; Karlsson, O.; Lindell, D.; Tornberg, M.; Lindberg, F.; Thuvander, M. Microstructures and hardness of as-quenched martensites (0.1–0.5% C). Acta Mater. 2011, 59, 5845–5858. [Google Scholar] [CrossRef]
- Ryde, L. Application of EBSD to analysis of microstructures in commercial steels. Mater. Sci. Technol. 2006, 22, 1297–1306. [Google Scholar] [CrossRef]
- Razmpoosh, M.H.; Macwan, A.; Biro, E.; Chen, D.L.; Peng, Y.; Goodwin, F.; Zhou, Y. Liquid metal embrittlement in laser beam welding of Zn-coated 22MnB5 steel. Mater. Des. 2018, 155, 375–383. [Google Scholar] [CrossRef]
- Martin, S.; Wolf, S.; Martin, U.; Krüger, L.; Rafaja, D. Deformation mechanisms in austenitic TRIP/TWIP steel as a function of temperature. Metall. Mater. Trans. A 2016, 47, 49–58. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Estrin, Y.; De Cooman, B.C. Application of a dislocation density-based constitutive model to Al-alloyed TWIP steel. Metall. Mater. Trans. A 2013, 44, 4168–4182. [Google Scholar] [CrossRef] [Green Version]
- Razmpoosh, M.H.; Biro, E.; Chen, D.L.; Goodwin, F.; Zhou, Y. Liquid metal embrittlement in laser lap joining of TWIP and medium-manganese TRIP steel: The role of stress and grain boundaries. Mater. Charact. 2018, 145, 627–633. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Cho, L.; Van der Aa, E.; Ghassemi-Armaki, H.; Pichler, A.; Findley, K.O.; Speer, J.G. Transgranular cracking in a liquid Zn embrittled high strength steel. Scr. Mater. 2020, 175, 49–54. [Google Scholar] [CrossRef]
- Li, Y.; Han, C.; Zhang, C.; Jia, K.; Han, P.; Wu, X. Effects of alloying on the behavior of B and S at Σ5 (2 1 0) grain boundary in γ-Fe. Comput. Mater. Sci. 2016, 115, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Peng, W.; Peng, H.; Wu, G.; Zhang, J. Effect of zinc-doping on tensile strength of Σ5 bcc Fe symmetric tilt grain boundary. Comput. Mater. Sci. 2020, 171, 109204. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Cho, L.; Van Der Aa, E.; Pichler, A.; Pottore, N.; Ghassemi-Armaki, H.; Findley, K.O.; Speer, J.G. Influence of the starting microstructure of an advanced high strength steel on the characteristics of Zn-Assisted liquid metal embrittlement. Mater. Sci. Eng. A 2021, 804, 140391. [Google Scholar] [CrossRef]
- Cho, L.; Kang, H.; Lee, C.; De Cooman, B.C. Microstructure of liquid metal embrittlement cracks on Zn-coated 22MnB5 press-hardened steel. Scr. Mater. 2014, 90, 25–28. [Google Scholar] [CrossRef]
- Kang, H.; Cho, L.; Lee, C.; De Cooman, B.C. Zn penetration in liquid metal embrittled TWIP steel. Metall. Mater. Trans. A 2016, 47, 2885–2905. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Ramíarez, R.; Böhm, M.C. Simple geometric generation of special points in brillouin-zone integrations. Two-dimensional bravais lattices. Int. J. Quantum Chem. 1986, 30, 391–411. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef] [PubMed]
- Makov, G.; Shah, R.; Payne, M.C. Periodic boundary conditions in ab initio calculations. II. Brillouin-zone sampling for aperiodic systems. Phys. Rev. B 1996, 53, 15513. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Basinski, Z.S.; Hume-Rothery, W.; Sutton, A.L. The lattice expansion of iron. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 229, 459–467. [Google Scholar]
- Zhang, Y.; Lu, G.-H.; Deng, S.; Wang, T.; Xu, H.; Kohyama, M.; Yamamoto, R. Weakening of an aluminum grain boundary induced by sulfur segregation: A first-principles computational tensile test. Phys. Rev. B 2007, 75, 174101. [Google Scholar] [CrossRef]
- Nielsen, O.H.; Martin, R.M. Quantum-mechanical theory of stress and force. Phys. Rev. B 1985, 32, 3780. [Google Scholar] [CrossRef]
- Sun, S.N.; Kioussis, N.; Lim, S.P.; Gonis, A.; Gourdin, W.H. Impurity effects on atomic bonding in Ni 3 Al. Phys. Rev. B 1995, 52, 14421. [Google Scholar] [CrossRef] [PubMed]

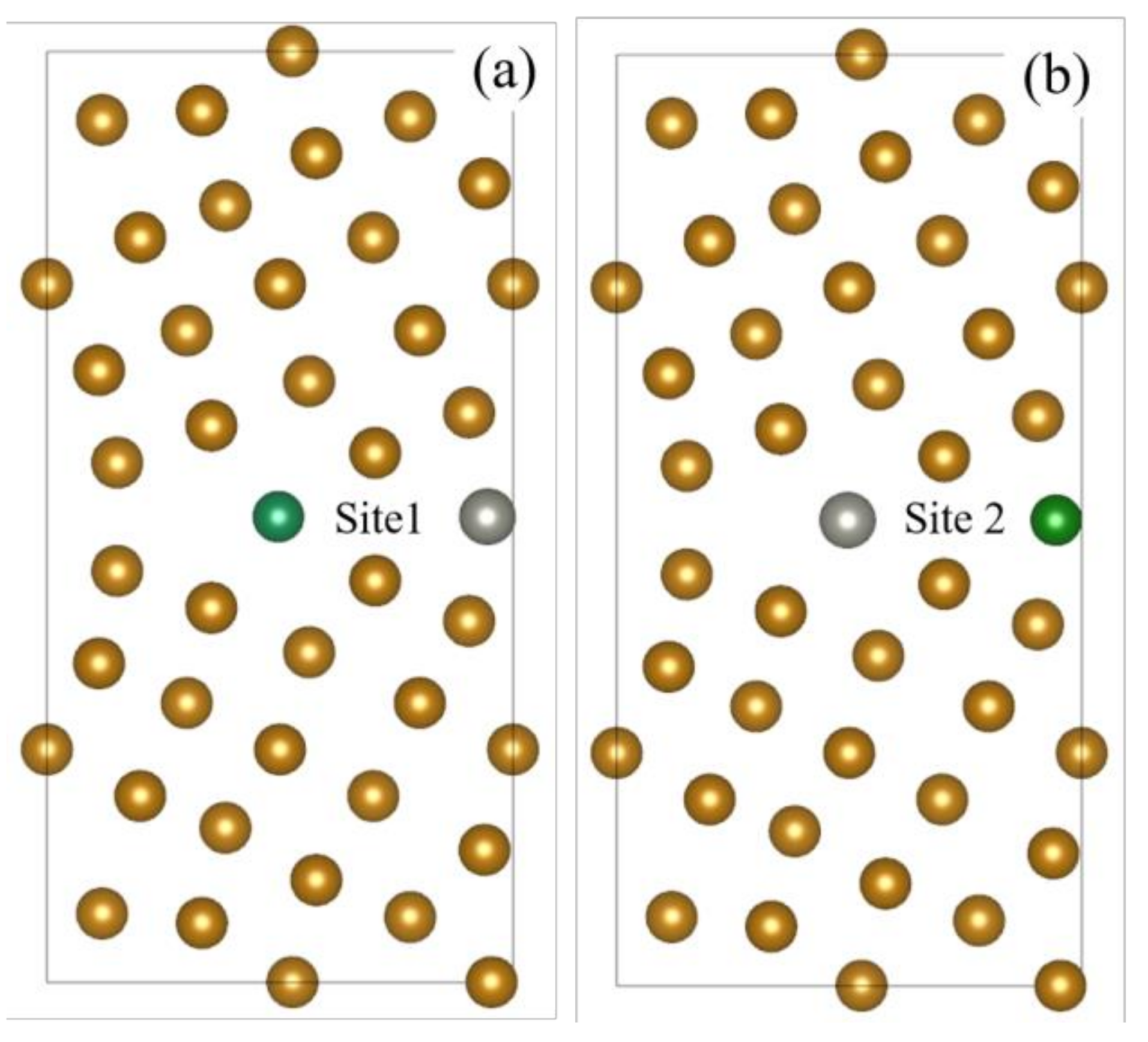

| Site | Site 1 | Site 2 |
|---|---|---|
| Total Free Energy/eV | −305.129 | −305.128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, C.; Peng, W.; Ma, Z.; Zhao, Y.; Teng, H.; Wu, G. Effect of Ni Doping on the Embrittlement of Liquid Zinc at Σ5 Fe Austenite Grain Boundary. Metals 2022, 12, 27. https://doi.org/10.3390/met12010027
Ding C, Peng W, Ma Z, Zhao Y, Teng H, Wu G. Effect of Ni Doping on the Embrittlement of Liquid Zinc at Σ5 Fe Austenite Grain Boundary. Metals. 2022; 12(1):27. https://doi.org/10.3390/met12010027
Chicago/Turabian StyleDing, Chengfa, Wangjun Peng, Zheng Ma, Yan Zhao, Huaxiang Teng, and Guangxin Wu. 2022. "Effect of Ni Doping on the Embrittlement of Liquid Zinc at Σ5 Fe Austenite Grain Boundary" Metals 12, no. 1: 27. https://doi.org/10.3390/met12010027
APA StyleDing, C., Peng, W., Ma, Z., Zhao, Y., Teng, H., & Wu, G. (2022). Effect of Ni Doping on the Embrittlement of Liquid Zinc at Σ5 Fe Austenite Grain Boundary. Metals, 12(1), 27. https://doi.org/10.3390/met12010027





