Static Strength of Tubular K-Joints Reinforced with Outer Plates under Axial Loads at Ambient and Fire Conditions
Abstract
:1. Introduction
2. Literature Review
2.1. Tubular Joints Reinforced with the Outer Plate
2.2. Joints Reinforced with Other Methods
2.3. K-Joints under Fire Conditions
2.4. Concluding Remarks
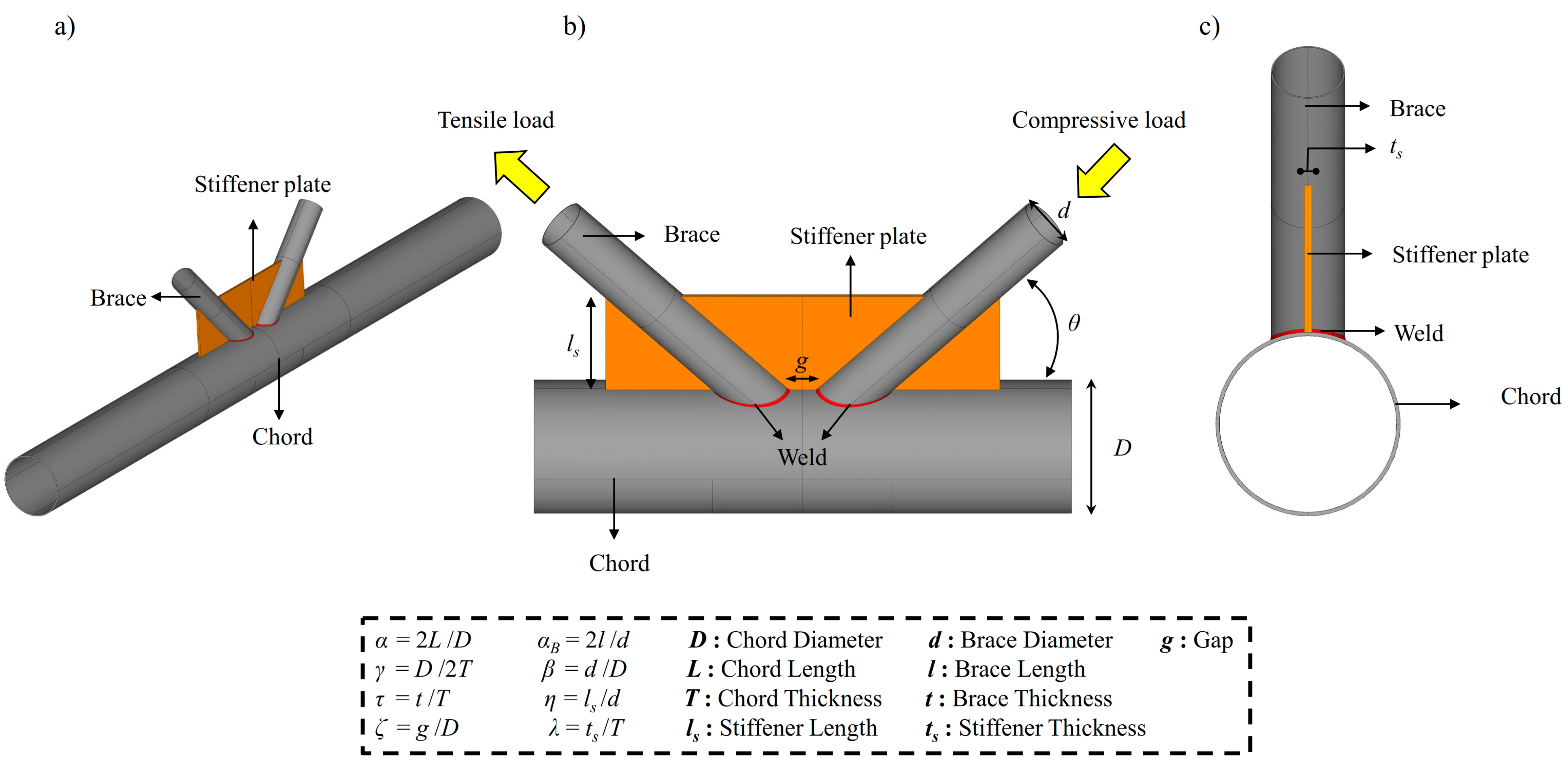
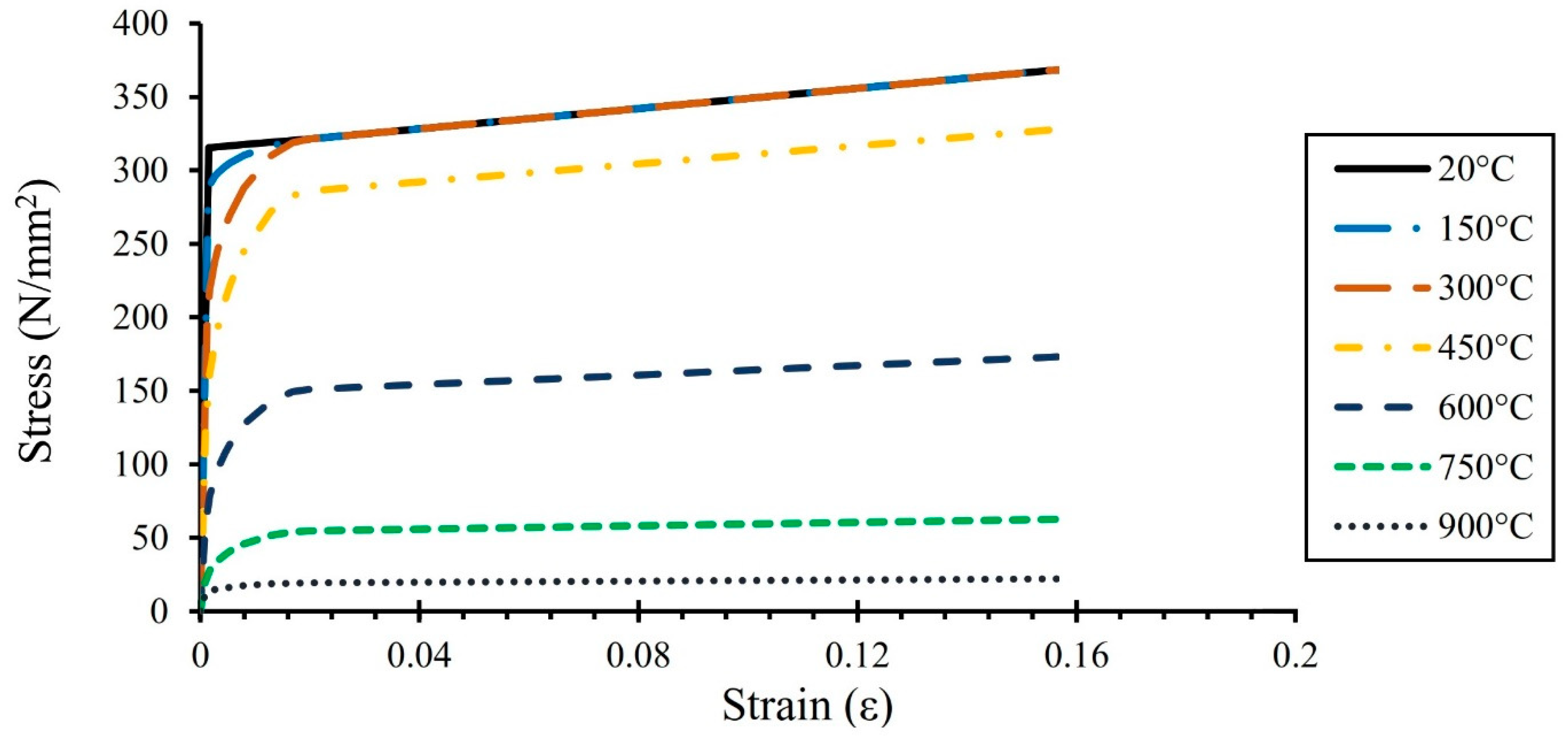
3. FE Modeling
4. Validation and Parametric Study
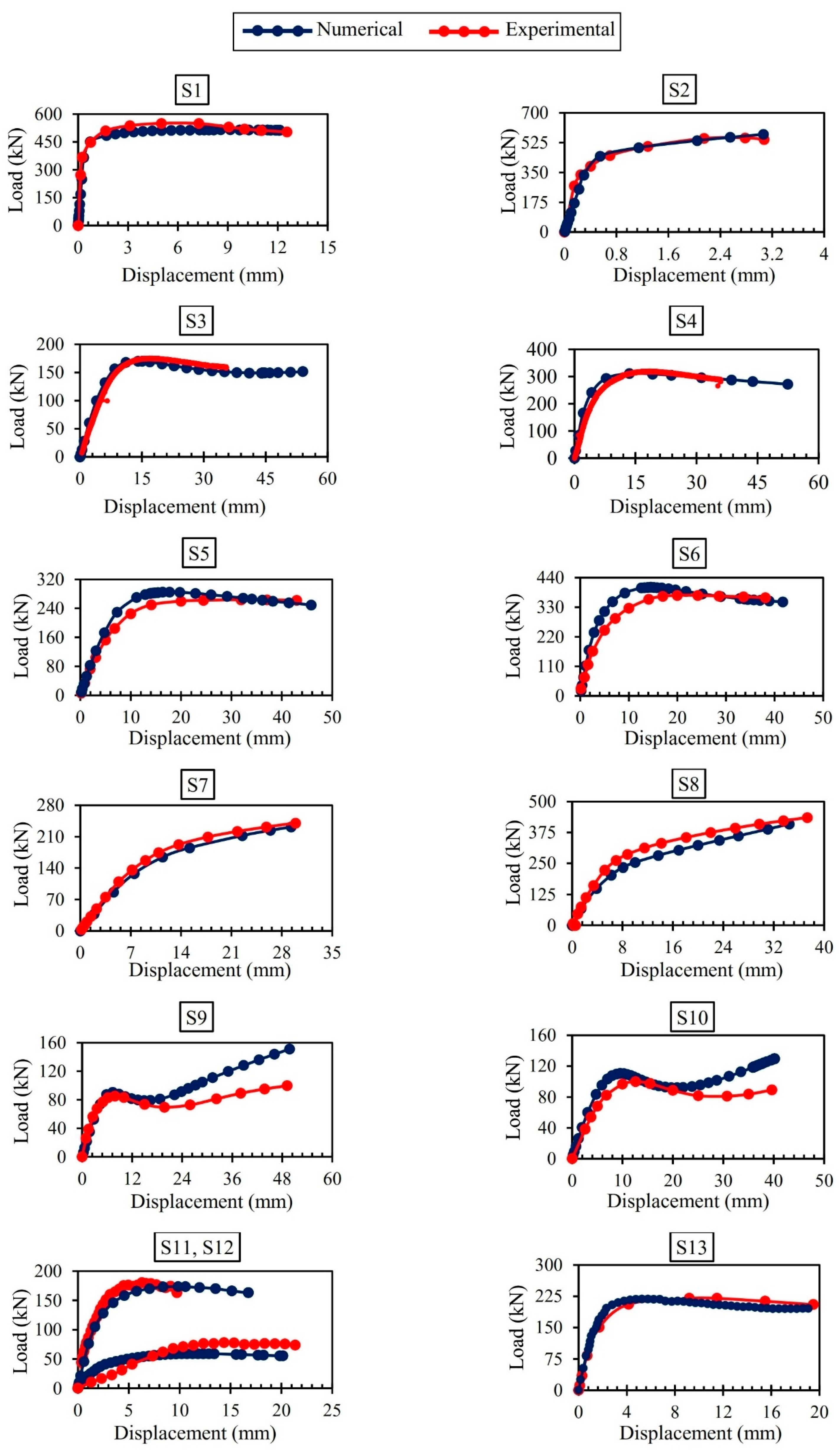
4.1. Validation of the FE Model
4.2. Details of the Parametric Study
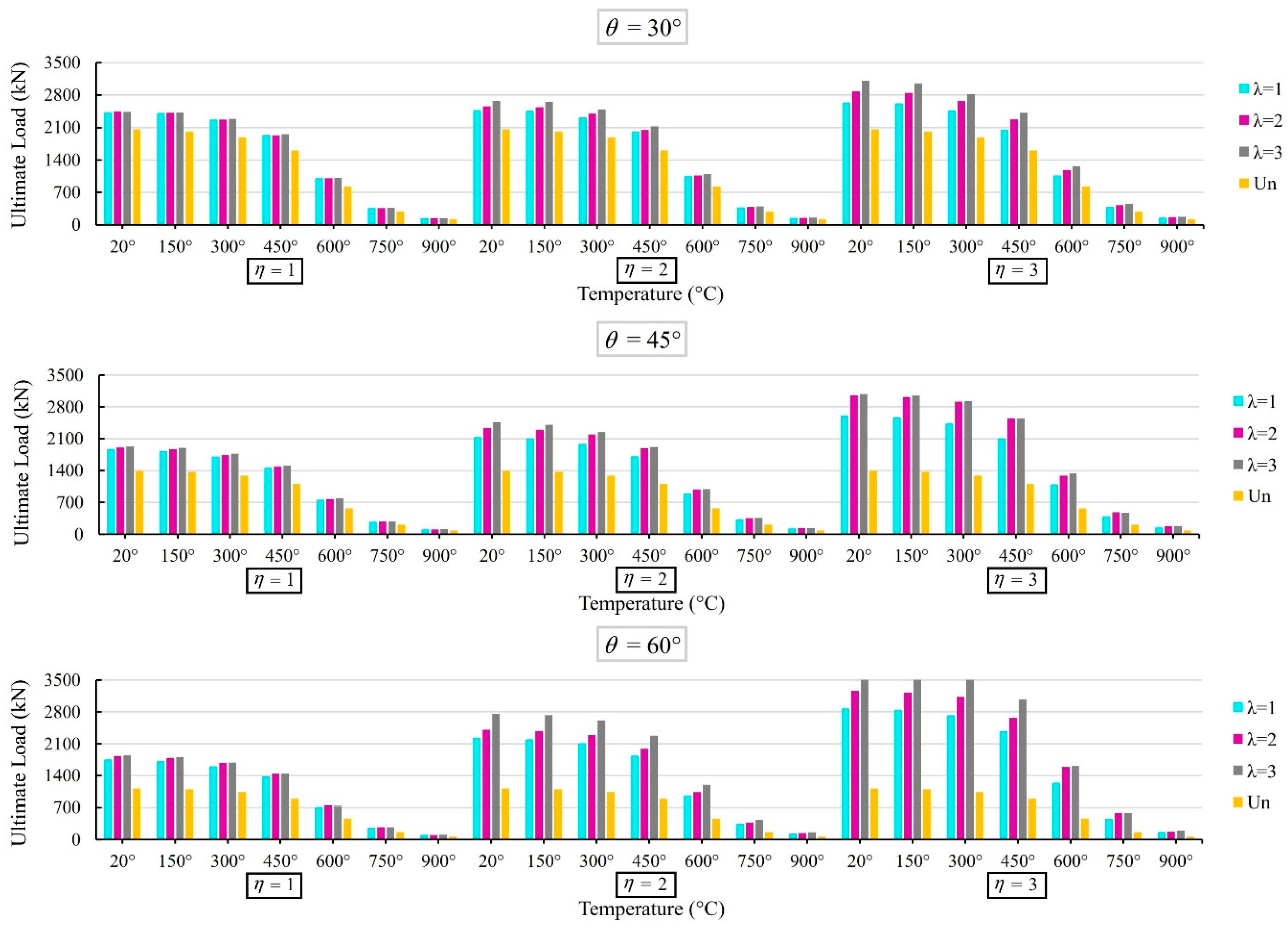
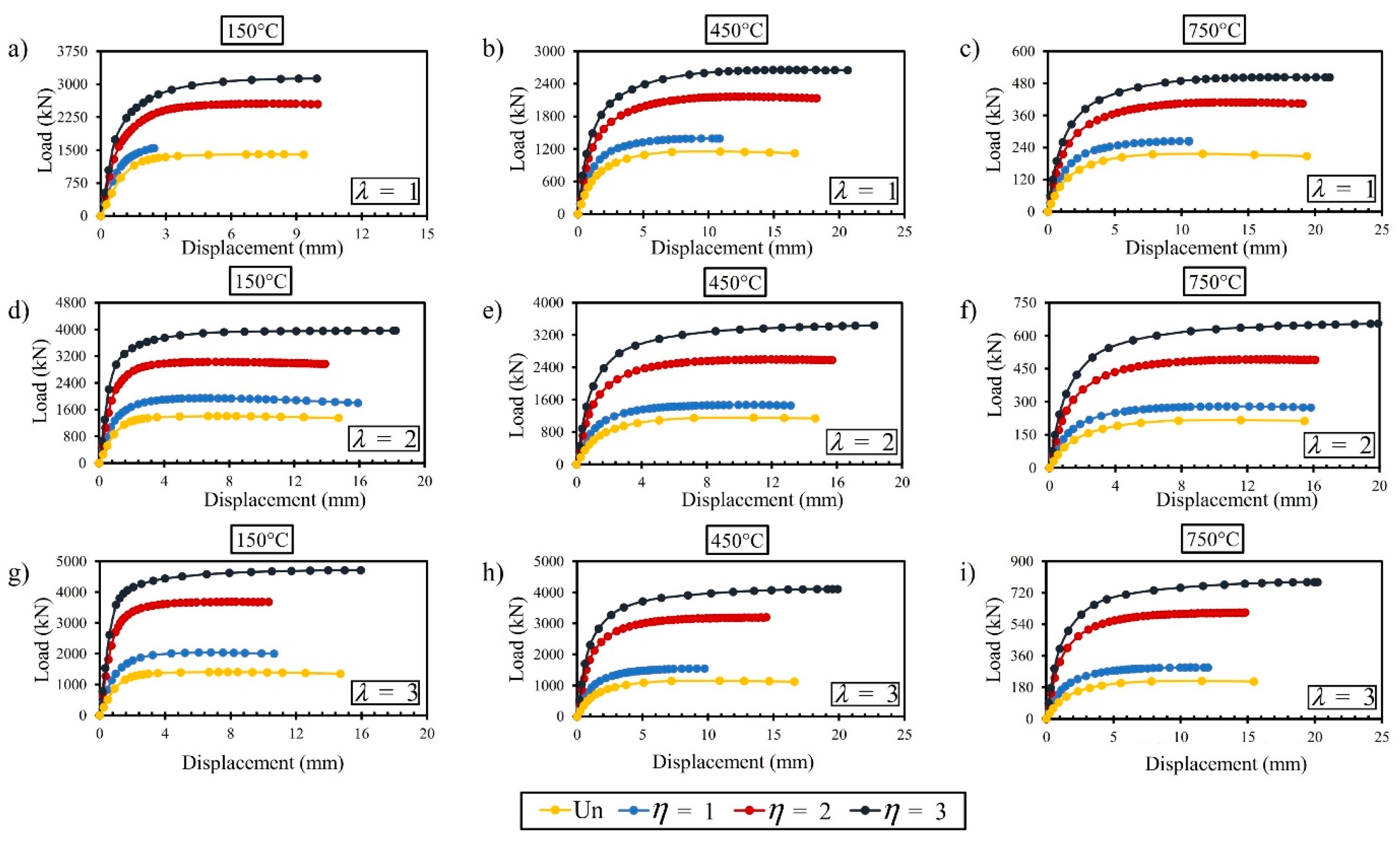
4.3. Efffect of the θ, Plate Size (λ, η), and High Temperatures
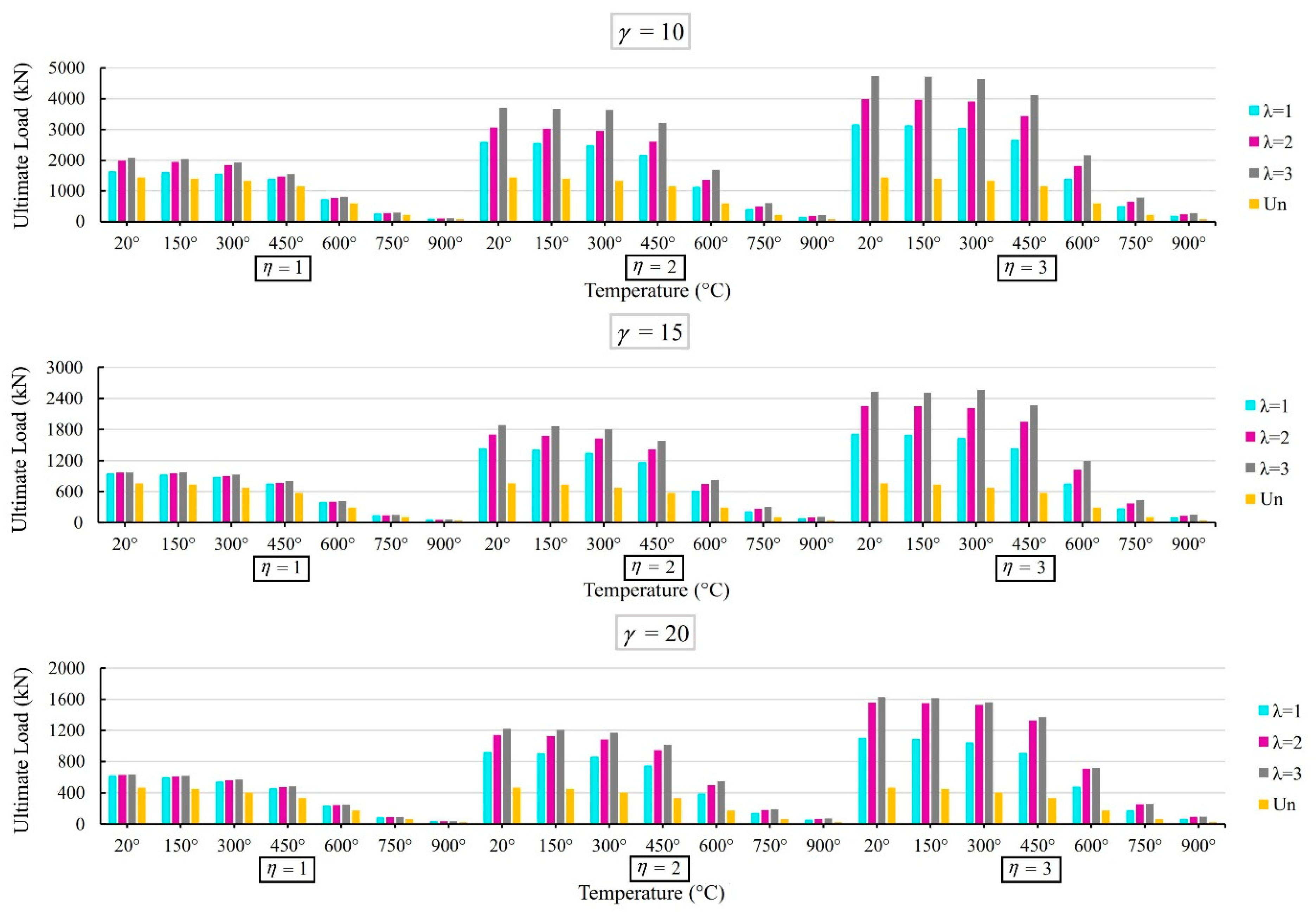
4.4. Effect of the γ, Plate Size (λ, η), and High Temperatures
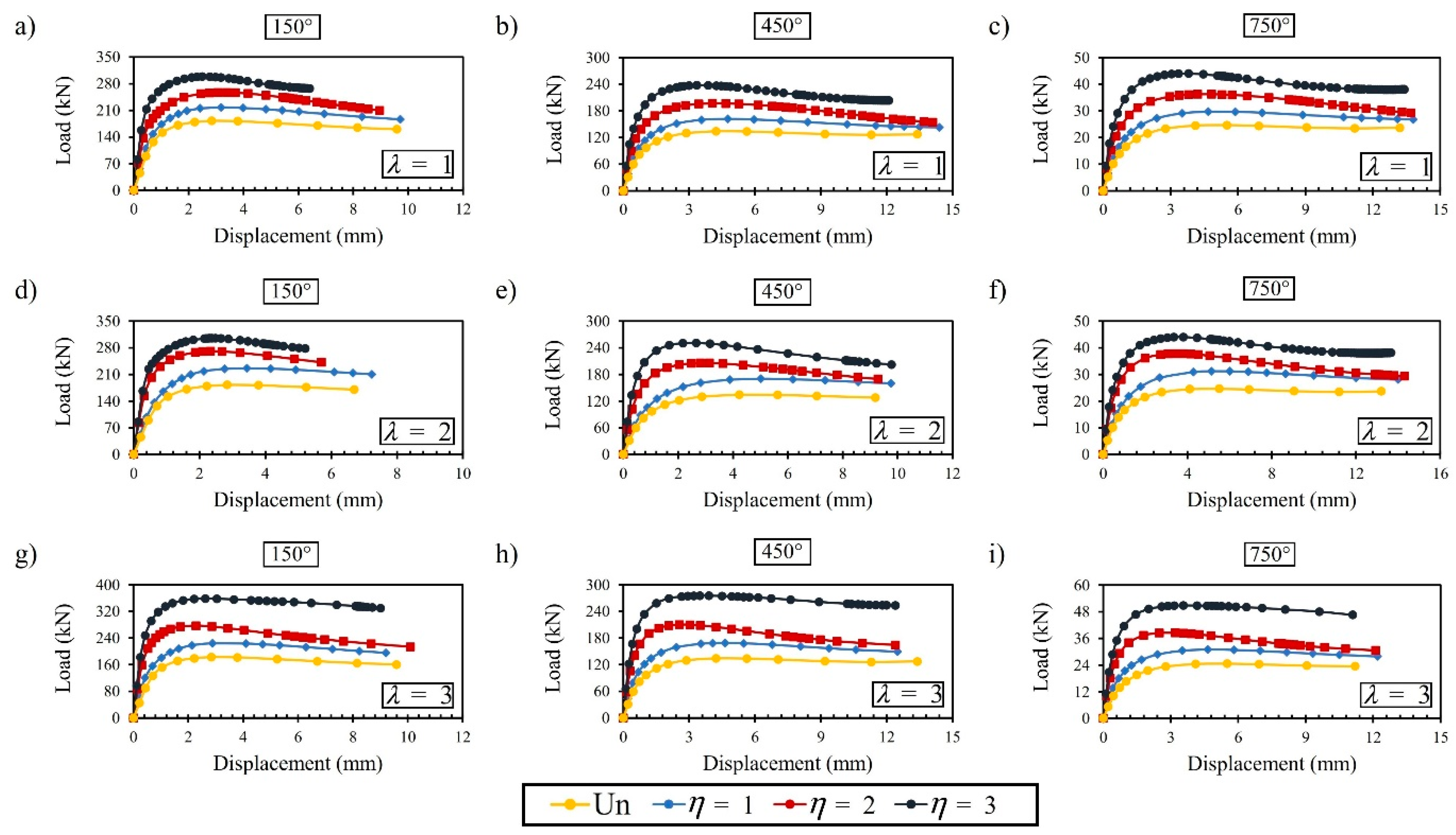
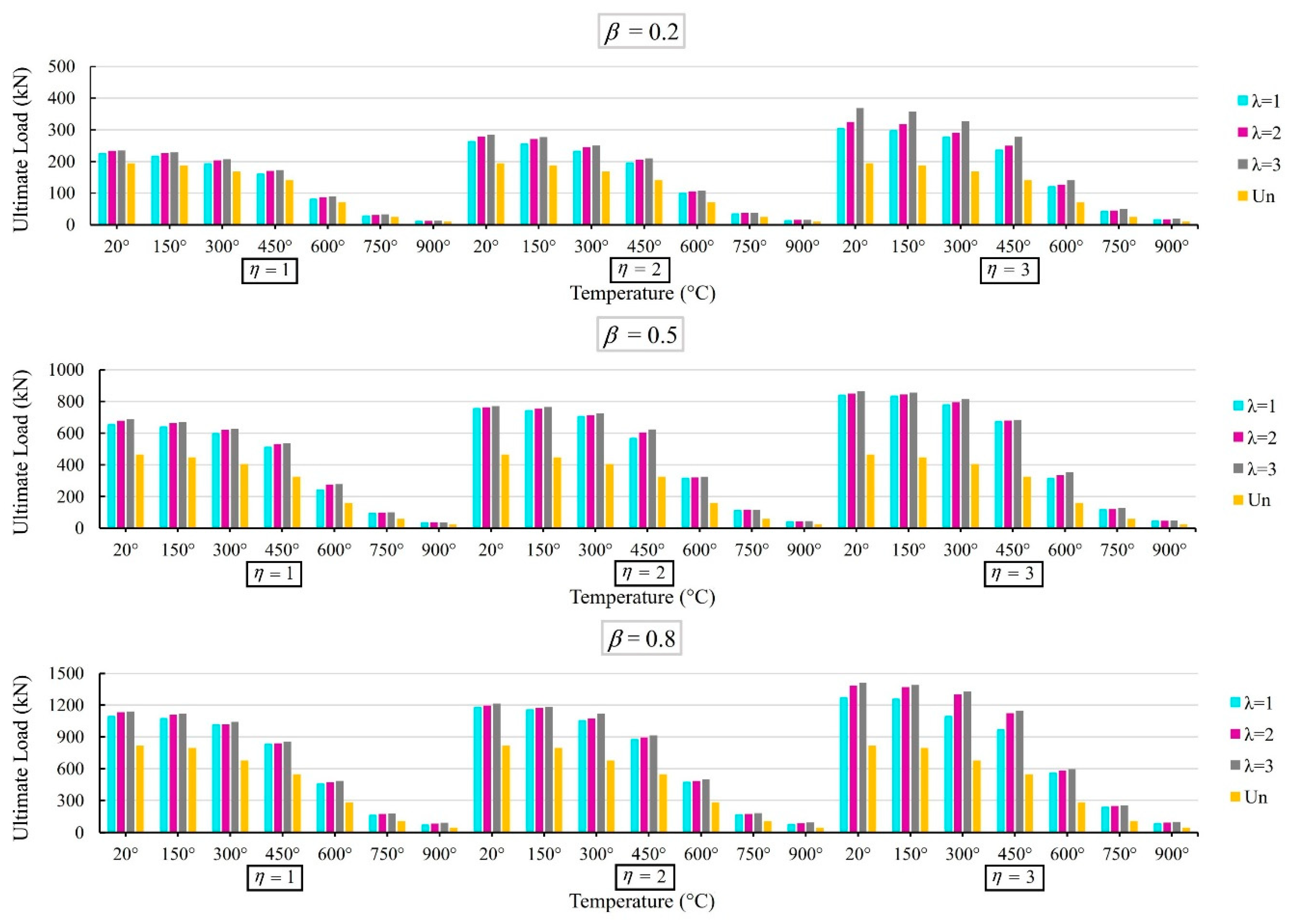
4.5. Effect of the β, Plate Size (λ and η), and High Temperatures
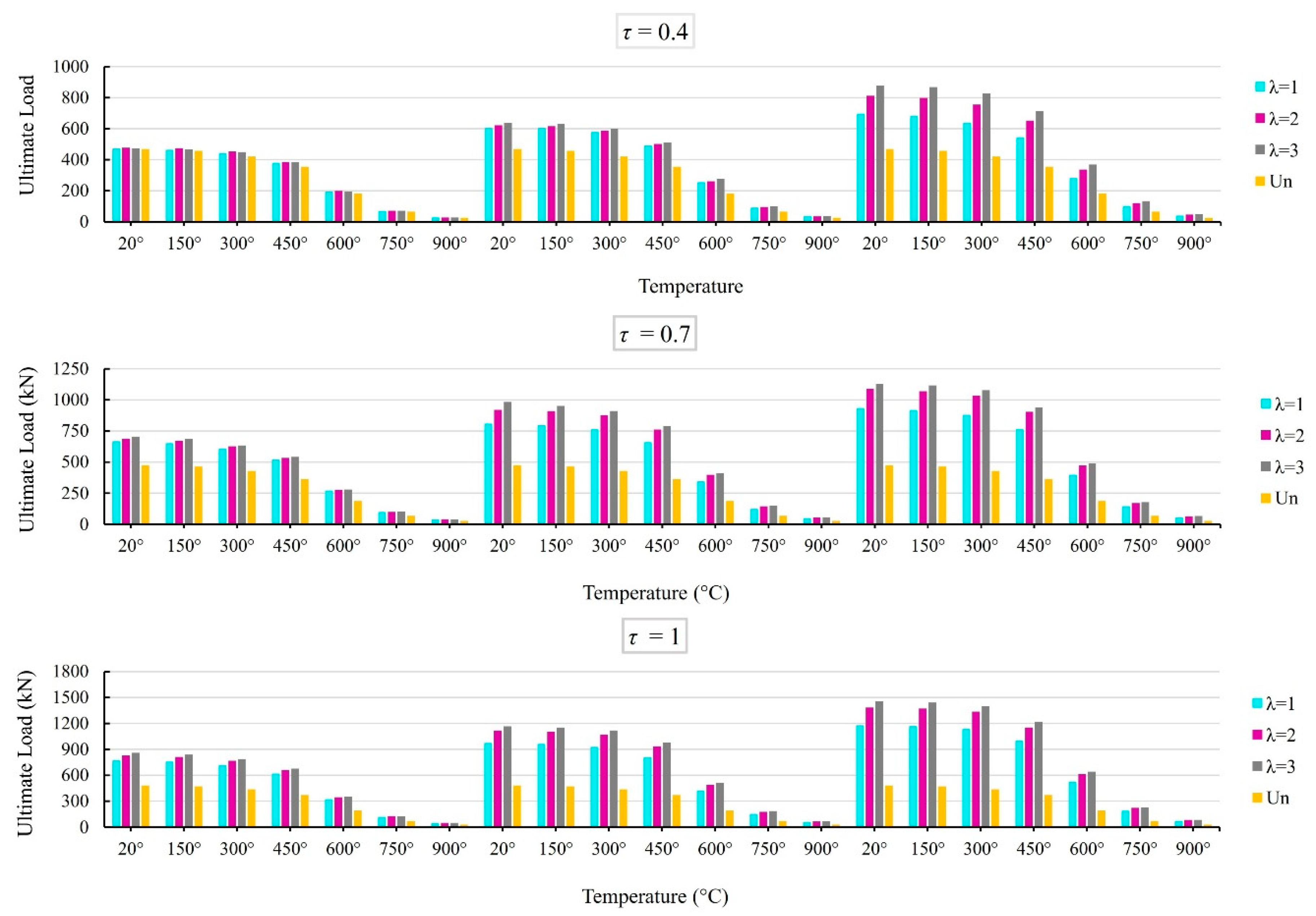
4.6. Effect of the τ, Plate Size (λ and η), and High Temperatures
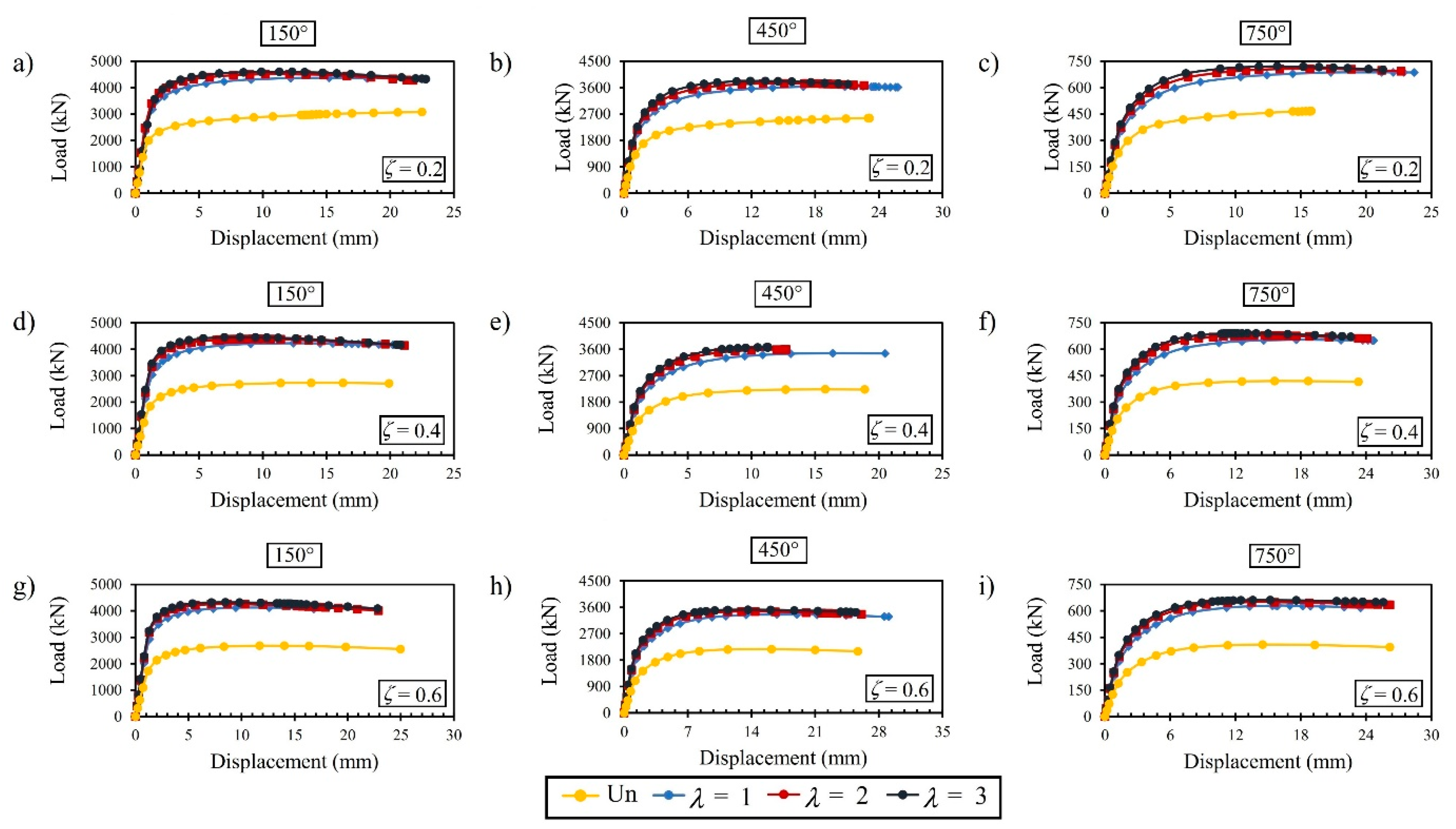
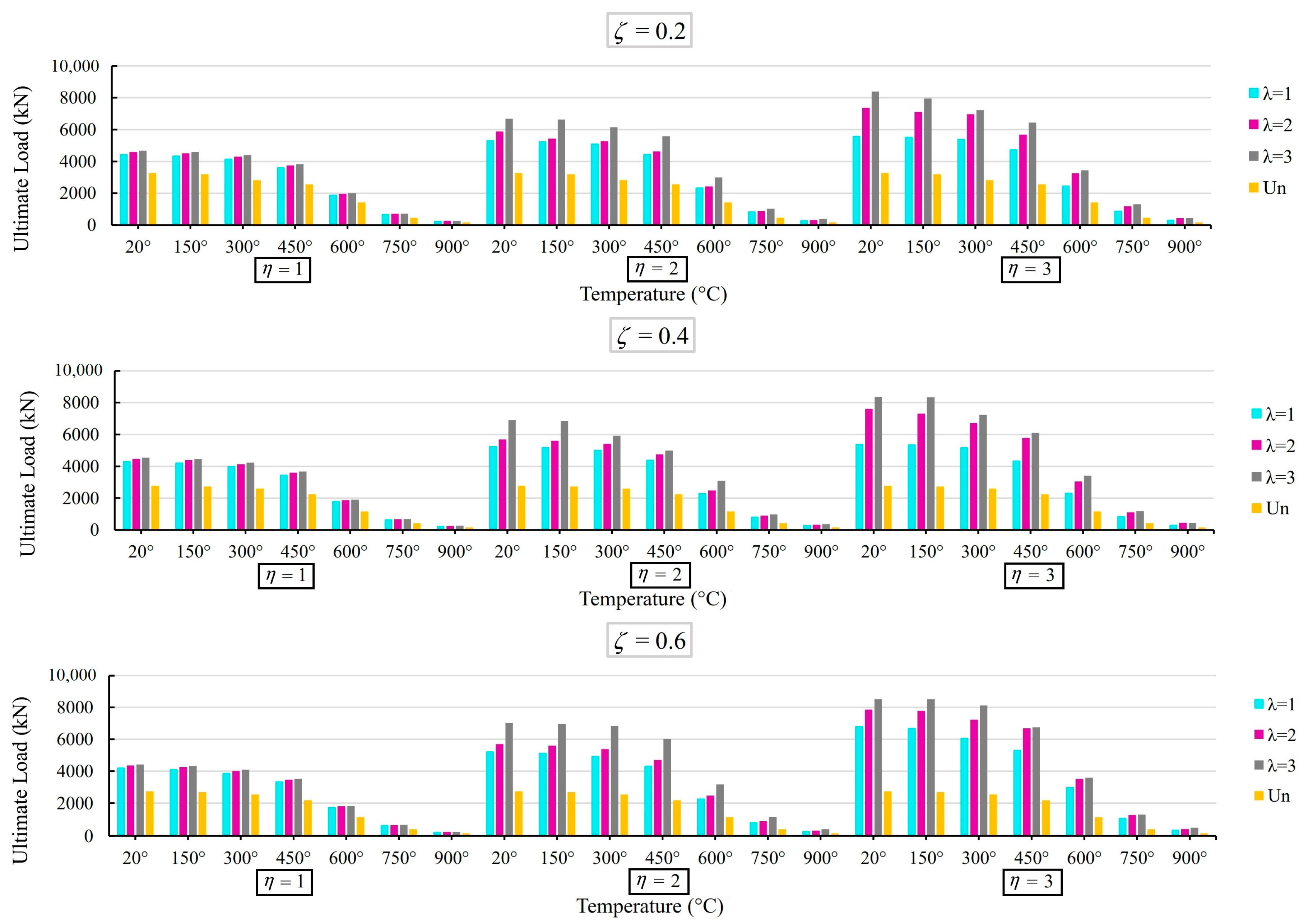
4.7. Effect of the ξ, Plate Size (λ and η), and High Temperatures
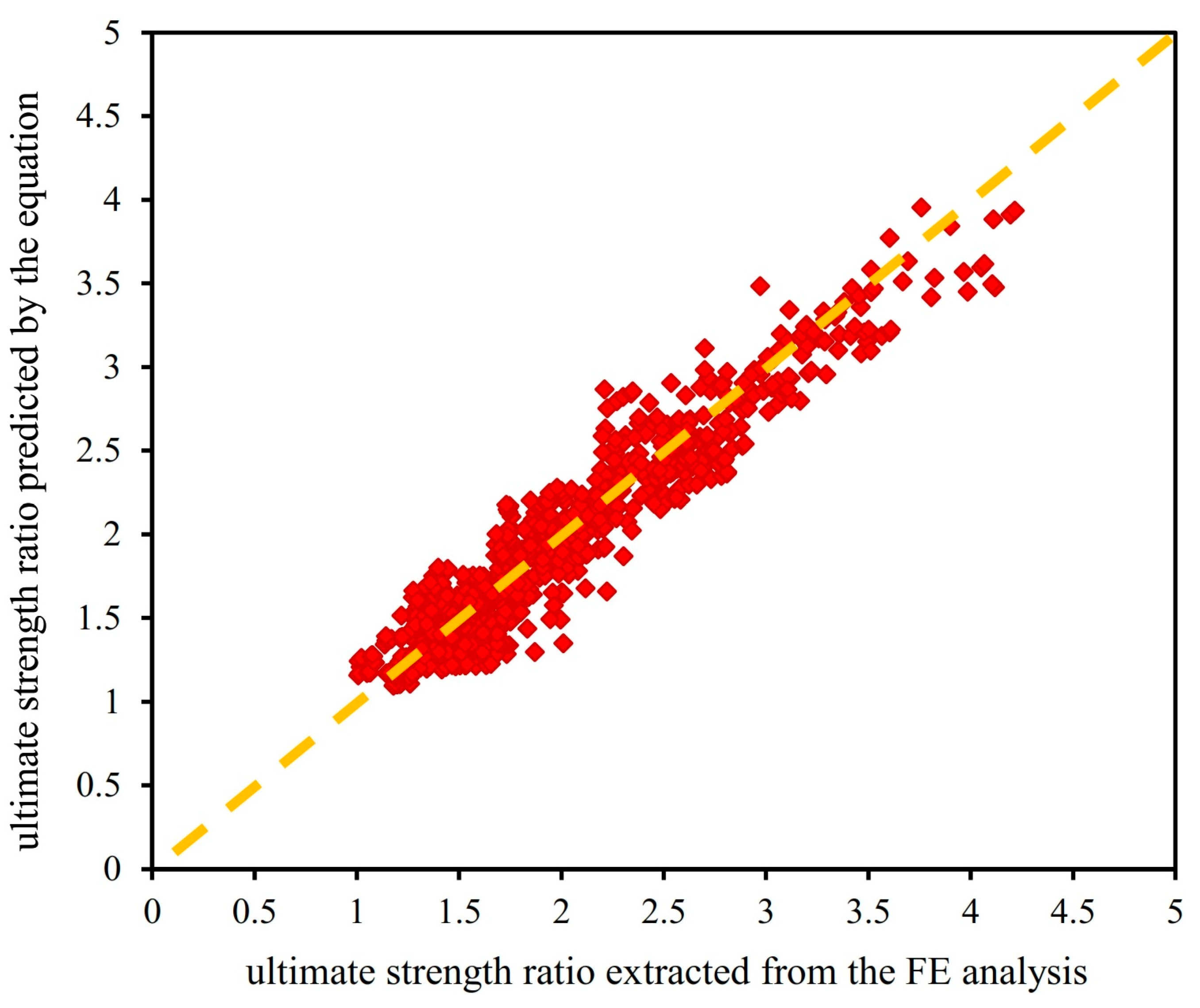
5. The Practical Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Z.; Wu, G.; Si, F.; Shang, J.; Zhou, H.; Li, Q.; Zhou, T. Parametric study on SCF distribution along the weld toe of internally ring-stiffened two-planar tubular KK joints under axial loading. Ocean Eng. 2022, 248, 110826. [Google Scholar] [CrossRef]
- He, S.; Shao, Y.; Zhang, H.; Wang, Q. Parametric study on performance of circular tubular K-joints at elevated temperature. Fire Saf. J. 2015, 71, 174–186. [Google Scholar] [CrossRef]
- Li, W.; Zhang, S.; Huo, W.; Bai, Y.; Zhu, L. Axial compression strength of steel CHS X-joints retrofittedwith external stiffeners. J. Construct. Steel Res. 2018, 141, 156–166. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, K.; Bai, Y.; Sun, H. CHS X-joints retrofittedby external stiffeners under brace axial tension. Eng. Struct. 2018, 171, 445–452. [Google Scholar] [CrossRef]
- Zhu, L.; Han, S.; Song, Q.; Ma, L.; Wei, Y.; Li, S. Experimental study of the axial compressive strength of CHS T-joints reinforced with external stiffening rings. Thin-Walled Struct. 2016, 98, 245–251. [Google Scholar] [CrossRef]
- Nassiraei, H.; Yara, A. Numerical analysis of local joint flexibility of K-joints with external plates under axial loads in offshore tubular structures. J. Mar. Sci. Appl. 2022, 21, 134–144. [Google Scholar] [CrossRef]
- Azari-Dodaran, N.; Ahmadi, H. A numerical study on the ultimate load of offshore two-planar tubular TT-joints reinforced with internal ring stiffeners at fire-induced elevated temperatures. Ocean Eng. 2021, 230, 108797. [Google Scholar] [CrossRef]
- Fu, Y.; Tong, L.; He, L.; Zhao, X.L. Experimental and numerical investigation on behavior of CFRP-retrofittedcircular hollow section gap K-joints. Thin-Walled Struct. 2016, 102, 80–97. [Google Scholar] [CrossRef]
- Gao, F.; Tang, Z.; Guan, X.; Zhu, H.; Chen, Z. Ultimate strength of tubular T-joints reinforced with doubler plates after fire exposure. Thin-Walled Struct. 2018, 132, 616–628. [Google Scholar] [CrossRef]
- Yang, J.; Shao, Y.; Chen, C. Static strength of chord reinforced tubular Y-joints under axial loading. Mar. Struct. 2012, 29, 226–245. [Google Scholar] [CrossRef]
- Wu, Q.; Zheng, Q.; Chen, K.; Nakamura, S. Study on fatigue performance of concrete-filled steel tubular K-joints with internal studs. J. Const. Steel Res. 2023, 200, 107662. [Google Scholar] [CrossRef]
- Nassiraei, H. Static strength of tubular T/Y-joints reinforced with collar plates at fire induced elevated temperature. Mar. Struct. 2019, 67, 102635. [Google Scholar] [CrossRef]
- Nassiraei, H. Probability distribution models for the ultimate strength of tubular T/Y-joints reinforced with collar plates at room and different fire conditions. Ocean Eng. 2023, 270, 113557. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Probabilistic analysis of the ultimate strength of tubular X-joints stiffened with outer ring at ambient and elevated temperatures. Ocean Eng. 2022, 248, 110744. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, Y.; Wang, W.; Xie, W.; Ying, T.; Yue, G. Investigation of hot spot stress for welded tubular K-joints with stiffeners. J. Constr. Steel Res. 2022, 197, 107452. [Google Scholar] [CrossRef]
- He, S.; Shao, Y.; Zhang, H. Evaluation on fire resistance of tubular K-joints based on critical temperature method. J. Constr. Steel Res. 2015, 115, 398–406. [Google Scholar] [CrossRef]
- He, S.B.; Shao, Y.B.; Zhang, H.Y.; Yang, D.P.; Long, F.L. Experimental study on circular hollow section (CHS) tubular K-joints at elevated temperature. Eng. Fail. Anal. 2013, 34, 204–216. [Google Scholar] [CrossRef]
- Ozyurt, E.; Wang, Y.C.; Tan, K.H. Elevated temperature resistance of welded tubular joints under axial load in the brace member. Eng. Struct. 2014, 59, 574–586. [Google Scholar] [CrossRef]
- Ozyurt, E.; Wang, Y.C. Resistance of T-and K-joints to tubular members at elevated temperatures. In Applications of Structural Fire Engineering; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Xu, J.; Wu, S.; Han, J.; Wang, J.; Li, Z. Post-earthquake fire resistance of stainless steel K-joints considering gradient temperature effect. J. Constr. Steel Res. 2022, 192, 107219. [Google Scholar] [CrossRef]
- Shao, Y.; He, S.; Yang, D. Prediction on static strength for CHS tubular K-joints at elevated temperature. KSCE J. Civ. Eng. 2017, 21, 900–911. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Shao, Y.; Chung, K.F.; Hu, Y. Fire resistance and design assessment of Q355 circular hollow section joints. J. Constr. Steel Res. 2023, 201, 107702. [Google Scholar] [CrossRef]
- Lan, X.; Huang, Y.; Chan, T.M.; Young, B. Static strength of stainless steel K-and N-joints at elevated temperatures. Thin-Walled Struct. 2018, 122, 501–509. [Google Scholar] [CrossRef]
- Bharti, K.; Kumaraswamidhas, L.A.; Das, R.R. A novel optimization approach for bonded tubular gap K-type connections made of FRP composites. Structures 2020, 28, 2135–2145. [Google Scholar] [CrossRef]
- Tan, K.H.; Fung, T.C.; Nguyen, M.P. Structural behavior of CHS T-joints subjected to brace axial compression in fire conditions. J. Struct. Eng. 2013, 139, 73–84. [Google Scholar] [CrossRef]
- Dodaran, N.A.; Ahmadi, H.; Lotfollahi-Yaghin, M.A. Parametric study on structural behavior of tubular K-joints under axial loading at fire-induced elevated temperatures. Thin-Walled Struct. 2018, 130, 467–486. [Google Scholar] [CrossRef]
- Azari-Dodaran, N.; Ahmadi, H.; Zhu, L.; Li, P. Experimental and numerical study of the ultimate load for collar-plate-reinforced tubular K-joints at fire-induced elevated temperatures. Ships Offshore Struct. 2022, 17, 1159–1177. [Google Scholar] [CrossRef]
- American Welding Society (AWS). Structural Welding Code: AWS D 1.1; American Welding Society (AWS): Miami, FL, USA, 2015. [Google Scholar]
- EN 1993-1-2; Eurocode 3: Design of Steel Structures—Part 1-2: General Rules—Structural Fire Design. British Standard Institute: London, UK, 2005.
- Van der Vegte, G.J.; Choo, Y.S.; Liang, J.X.; Zettlemoyer, N.; Liew, J.Y.R. Static strength of T-joints reinforced with doubler or collar plates. II: Numerical simulations. J. Struct. Eng. 2005, 131, 129–138. [Google Scholar] [CrossRef]
- Nassiraei, H.; Zhu, L.; Lotfollahi-Yaghin, M.A.; Ahmadi, H. Static strength of tubular X-joints reinforced with collar plate subjected to brace compression. Thin-Walled Struct. 2017, 119, 256–265. [Google Scholar] [CrossRef]


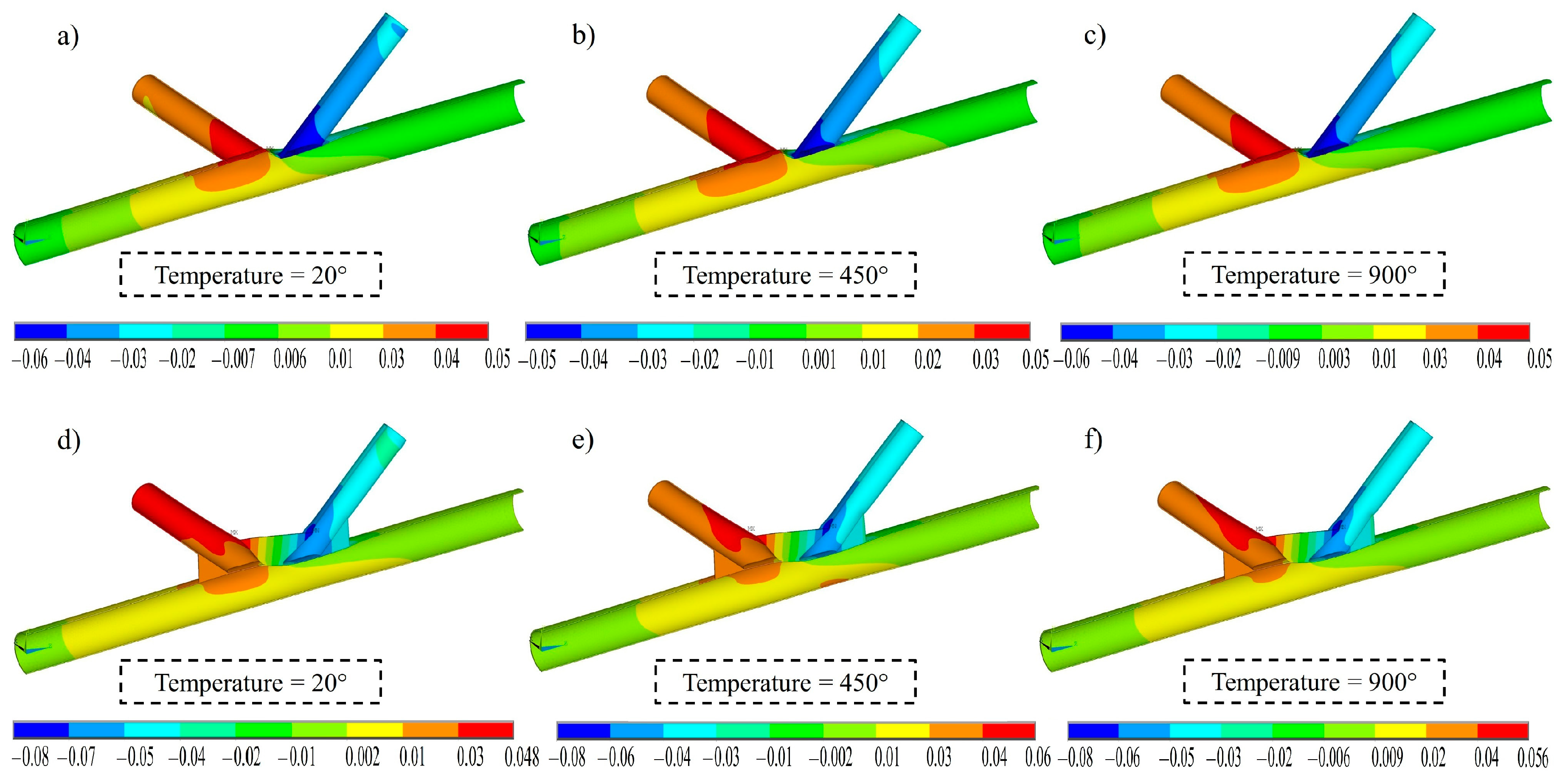


| Specimen | Joint Type | Researchers | D (mm) | ls (mm) | ts (mm) | α | θ (°) | β | γ | τ | Temperature (°C) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | K | Fu et al. [8] | 219 | - | - | 22.83 | 55 | 0.60 | 13.68 | 0.75 | 20 |
| S2 | 219 | - | - | 22.83 | 55 | 0.60 | 13.68 | 0.75 | 20 | ||
| S3 | X | Nassiraei et al. [31] | 300.03 | - | - | 12.0 | 90 | 0.25 | 16.4 | 0.90 | 20 |
| S4 | 300.00 | - | - | 12.0 | 90 | 0.73 | 17.9 | 0.99 | 20 | ||
| S5 | X | Li et al. [3] | 299.60 | 303.50 | 7.80 | 12.06 | 90 | 0.51 | 18.68 | 1.01 | 20 |
| S6 | 300.40 | 437.3 | 7.90 | 11.96 | 90 | 0.73 | 18.70 | 1.00 | 20 | ||
| S7 | X | Ding et al. [4] | 304.00 | 152 | 8 | 11.86 | 90 | 0.25 | 18.68 | 0.71 | 20 |
| S8 | 298.03 | 302 | 8 | 12.06 | 90 | 0.51 | 17.90 | 1.04 | 20 | ||
| S9 | T | Zhu et al. [5] | 298.00 | - | - | 12.08 | 90 | 0.25 | 24.03 | 1.10 | 20 |
| S10 | 298.20 | 71.50 | 5.3 | 12.07 | 90 | 0.25 | 24.04 | 1.10 | 20 | ||
| S11 | T | Tan et al. [25] | 244.5 | - | - | 18 | 90 | 0.69 | 19.4 | 1 | 550 |
| S12 | 244.5 | - | - | 18 | 90 | 0.69 | 19.4 | 1 | 700 | ||
| S13 | 244.5 | - | - | 18 | 90 | 0.8 | 19.4 | 1 | 550 |
| Specimen | fu0 (MPa) | fu1 (MPa) | fu2 (MPa) | fy0 (MPa) | fy1 (MPa) | fy2 (MPa) | E0 (GPa) | E1 (GPa) | E2 (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| S1 | 473 | 480 | - | 310 | 298 | - | - | - | - |
| S2 | 473 | 480 | - | 310 | 298 | - | - | - | - |
| S3 | 460 | 470 | 474 | 270 | 358 | 285 | 206 | 218 | 213.3 |
| S4 | 460 | 469 | 474 | 270 | 298 | 285 | 206 | 203 | 213.3 |
| S5 | 194 | 192 | 212 | 325 | 316 | 301 | 466 | 493 | 414 |
| S6 | 194 | 200 | 212 | 325 | 321 | 301 | 466 | 489 | 414 |
| S7 | 200.3 | 222.3 | 246.5 | 267.7 | 313.3 | 358.3 | - | - | - |
| S8 | 200.3 | 240 | 246.5 | 267.7 | 295 | 358.3 | - | - | - |
| S9 | 227 | 224 | - | 345 | 470 | - | - | - | - |
| S10 | 227 | 224 | 229 | 345 | 470 | 322 | - | - | - |
| S11 | 355 | 355 | - | 380.3 | 380.3 | - | 201 | 201 | - |
| S12 | 355 | 355 | - | 380.3 | 380.3 | - | 201 | 201 | - |
| S13 | 355 | 355 | - | 355 | 355 | - | 210 | 210 | - |
| Specimen | Fu, test (kN) | Fu, num (kN) | Fu, num/Fu, test |
|---|---|---|---|
| S1 | 542 | 515.63 | 0.95 |
| S2 | 542 | 573.63 | 1.05 |
| S3 | 174.63 | 170 | 0.97 |
| S4 | 319.41 | 311.44 | 0.97 |
| S5 | 256.20 | 285.17 | 0.89 |
| S6 | 374.65 | 404.474 | 1.07 |
| S7 | 194.7 | 211.31 | 1.08 |
| S8 | 308.1 | 354.99 | 1.15 |
| S9 | 85 | 90.20 | 1.06 |
| S10 | 100.2 | 110.442 | 1.10 |
| S11 | 180.9 | 173.4 | 0.95 |
| S12 | 76.4 | 77.90 | 1.01 |
| S13 | 216.5 | 220 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nassiraei, H.; Yara, A. Static Strength of Tubular K-Joints Reinforced with Outer Plates under Axial Loads at Ambient and Fire Conditions. Metals 2023, 13, 1857. https://doi.org/10.3390/met13111857
Nassiraei H, Yara A. Static Strength of Tubular K-Joints Reinforced with Outer Plates under Axial Loads at Ambient and Fire Conditions. Metals. 2023; 13(11):1857. https://doi.org/10.3390/met13111857
Chicago/Turabian StyleNassiraei, Hossein, and Amin Yara. 2023. "Static Strength of Tubular K-Joints Reinforced with Outer Plates under Axial Loads at Ambient and Fire Conditions" Metals 13, no. 11: 1857. https://doi.org/10.3390/met13111857
APA StyleNassiraei, H., & Yara, A. (2023). Static Strength of Tubular K-Joints Reinforced with Outer Plates under Axial Loads at Ambient and Fire Conditions. Metals, 13(11), 1857. https://doi.org/10.3390/met13111857





