Numerical Study on Metal Transverse Flow Law and Model of Rolled Strip under Variable Specification in Hot Rolling
Abstract
:1. Introduction
2. Flatness Calculation Model and Metal Transverse Flow
2.1. Flatness Calculation Model
2.2. Description of Metal Transverse Flow
2.3. Establishment of Metal Transverse Flow Simulation Model
2.4. Simulation Parameter Setting
3. The Influence of Rolling Production Factors on Metal Transverse Flow
3.1. Metal Transverse Flow under Different Contact Interface Friction States
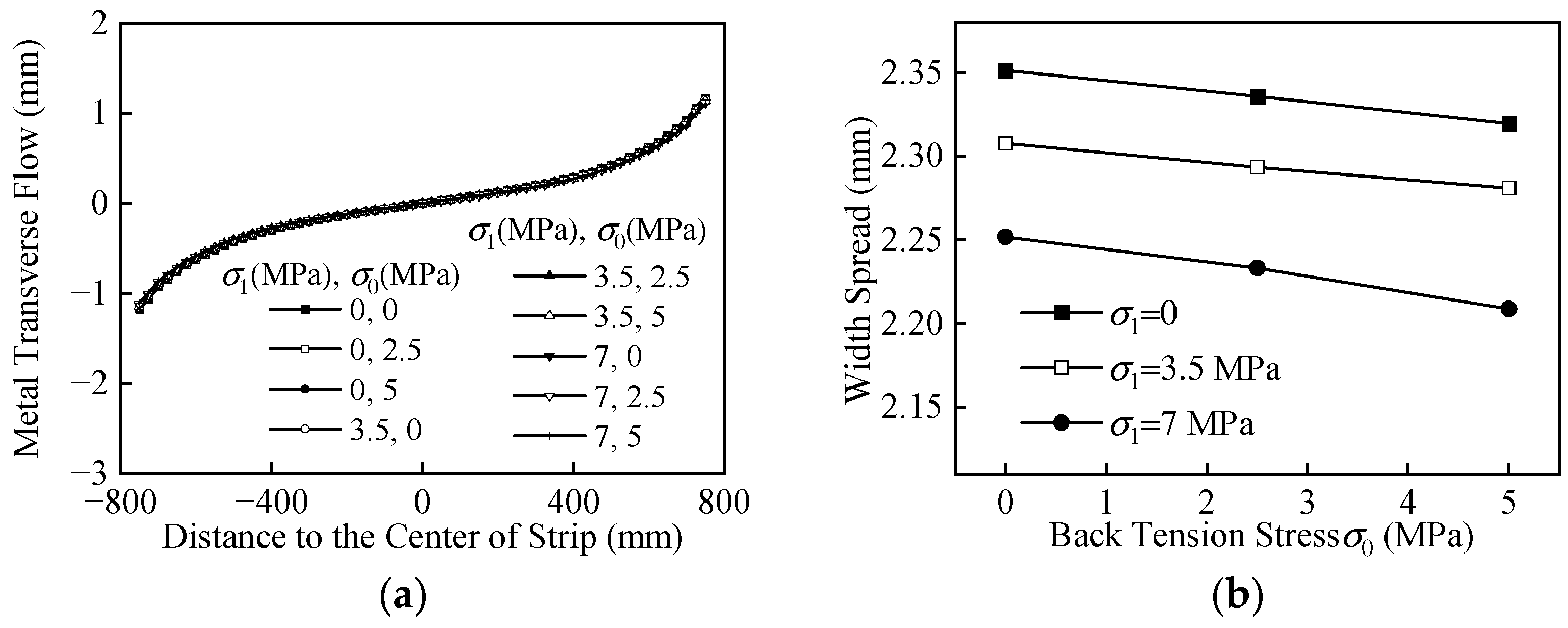
3.2. Metal Transverse Flow under Different Average Front and Back Tension Stresses
4. Study on the Metal Transverse Flow under Variable Specifications
4.1. Study on Metal Transverse Flow under Different Width Specifications
4.2. Study on Metal Transverse Flow under Different Thickness Specifications
4.2.1. The Effect of Entry Thickness
4.2.2. The Effect of Reduction Rate
5. Establishment of Metal Transverse Flow Prediction Model
6. Conclusions
- (1)
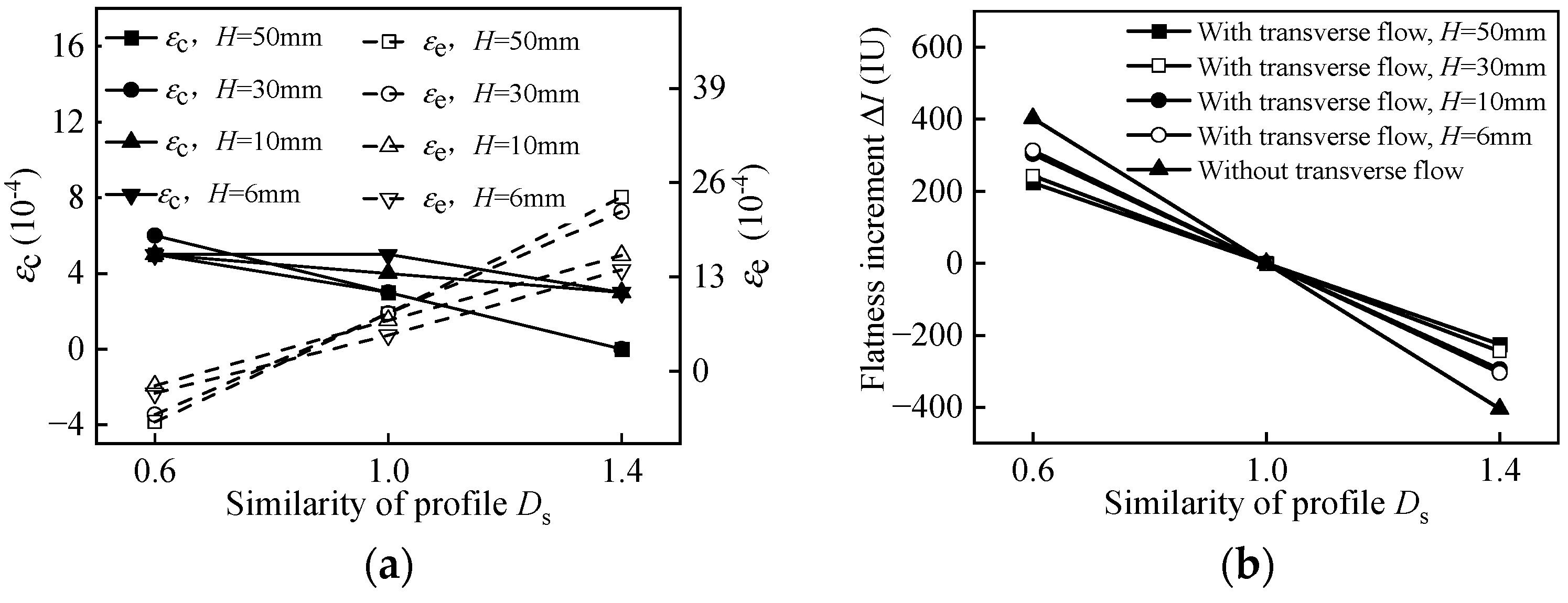
- Two parameters of metal transverse flow affecting the flatness of a rolled strip are put forward: central transverse strain εc and edge transverse strain εe. A finite element model is established to analyze the variation in metal transverse flow and εc and εe under different strip specifications. According to the theory of metal plastic deformation and simulation results, the influence of unknown parameters in the finite element model is determined, which provides a reference for the setting of parameters in simulation models.
- (2)
- Combined with the theory of metal plastic deformation and simulation results, the influence of strip specifications on its spread and metal transverse flow is analyzed, and the shape evolution mechanism of the rolling deformation process is further clarified. The similarity of profile Ds has a linear effect on εc and εe, and the influence slope changes nonlinearly with the strip width, entry thickness and reduction rate. Due to the metal transverse flow, the strip exhibits the ability of flatness self-correction. The ksc of the strip with B = 700 mm is 0.87, which is significantly greater than the 0.45 ksc value of the strip with B = 2100 mm. Priority can be given to ensure the crown requirements during narrow strip rolling. The ksc of the strip with H = 50 mm is 0.45, which is higher than the 0.22 ksc value of the strip with H = 6 mm, and the ksc of the strip with ε = 50% is 0.52, which is higher than the 0.30 ksc value of the strip with ε = 10%. It is more reasonable to adjust the crown to a greater extent in the upstream stand to meet the requirement of both flatness and crown for the large entry thickness reduction rate and self-correction ability.
- (3)
- Combined with the simulation results of the linear influence of the similarity of profile on the center transverse strain and edge transverse strain, a prediction model is established. The model can meet the requirement of crown setting at the exit of each stand and the rapid calculation of online flatness control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, X.; Ma, B.; Li, J.; Chen, P.; Peng, Y.; Ren, Z. Effect of Strip Profile of Hot-rolled Silicon Steel on Transverse Thickness Difference of Cold-rolled Strip. Ironmak. Steelmak. 2023, 50, 921–935. [Google Scholar] [CrossRef]
- Shkarin, A.N.; Bel’Skii, S.M.; Pimenov, V.A. Influence of the Cross-Sectional Shape of Hot Semifinished Rolled Products on the Formation of the Plot of Specific Tension in Cold-Rolled Strips. Metallurgist 2020, 64, 699–708. [Google Scholar] [CrossRef]
- Safronov, A.A.; Shopin, I.I.; Belskiy, S.M. Influence of the Variation of Mechanical Properties and Thickness in Hot-Rolled Strips of Electrical Anisotropic Steel to Stabilize Cold Rolling. Metallurgist 2023, 66, 1557–1561. [Google Scholar] [CrossRef]
- Wang, Q.; Song, L.; Zhao, J.; Wang, H.; Dong, L.; Wang, X.; Yang, Q. Application of the Gradient Boosting Decision Tree in the Online Prediction of Rolling Force in Hot Rolling. Int. J. Adv. Manuf. Technol. 2023, 125, 387–397. [Google Scholar] [CrossRef]
- Servin-Castañeda, R.; Garcia-Lara, A.M.; Mercado-Solís, R.D.; Vega-Lebrun, C.A. Development of Mathematical Model for Control Wear in Backup Roll for Hot Strip Mill. J. Iron Steel Res. Int. 2014, 21, 46–51. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Liu, X. Thermal Crown Model and Shifting Effect Analysis of Work Roll in Hot Strip Mills. J. Iron Steel Res. Int. 2015, 22, 777–784. [Google Scholar] [CrossRef]
- Okinaka, N. Temperature Buffered Work Roll Using Phase Change Material (PCM) in Hot Rolling. J. Iron Steel Inst. Jpn. 2020, 106, 542–548. [Google Scholar] [CrossRef]
- Byon, S.M.; Roh, Y.H.; Yang, Z.; Lee, Y. A Roll-bending Approach to Suppress the Edge Cracking of Silicon Steel in the Cold Rolling Process. Proc. Inst. Mech. Eng. Part B 2021, 235, 112–124. [Google Scholar] [CrossRef]
- Liu, H. Three-Dimensional Rolling Theory and Its Application: Strip Element Method for Simulating Rolling Process; Science Press: Beijing, China, 1999; pp. 3–5. [Google Scholar]
- Matsumoto, H. 2-Dimensional Lateral-Material-Flow Model Reduced from 3-Dimensional Theory for Flat Rolling. ISIJ. Int. 1991, 31, 550–558. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Xie, H.; Liu, H.; Sun, L.; Liu, T.; Liu, X.; Shi, K.; Jiang, Z. Novel Three-dimensional Multi-objective Numerical Modeling for Hot Strip Tandem Rolling. Int. J. Mater. Form. 2021, 14, 589–1004. [Google Scholar] [CrossRef]
- Cavaliere, M.A.; Goldschmit, M.B.; Dvorkin, E.N. Finite Element Simulation of the Steel Plates Hot Rolling Process. Int. J. Numer. Meth. Engng. 2001, 52, 1411–1430. [Google Scholar] [CrossRef]
- Gangolu, S.; Rao, A.G.; Prabhu, N.; Deshmukh, V.P.; Kashyap, B.P. Microstructure Evolution and Flow Behavior of Hot-rolled Aluminum-5% B4C Composite. Mater. Des. 2014, 53, 581–587. [Google Scholar] [CrossRef]
- Peng, K.; Zhong, H.; Zhao, L.; Xue, K.; Ji, Y. Strip Shape Modeling and its Setup Strategy in Hot Strip Mill Process. Int. J. Adv. Manuf. Technol. 2014, 72, 589–605. [Google Scholar] [CrossRef]
- Shohet, K.; Townsend, N. Flatness control in plate rolling. J. Iron Steel Inst. 1971, 209, 769–775. [Google Scholar]
- Yang, L. Research on the Strip Element Method of Three Thermo-Mechanical Coupling of Plate and Strip Rolling and Development of the Simulation System. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2006. [Google Scholar]
- Wang, X.; Liu, Y.; Zhao, X.; Jin, X. Unsymmetrical Situation for Analyzing the Function of Metal Lateral Displacement. Steel Rolling 2007, 24, 12–14. [Google Scholar]
- Kim, K.S.; Hong, W.K.; Barlat, F. Effect of Rolling Parameters on Surface Strain Variation in Hot Strip Rolling. Steel Res. Int. 2017, 88, 1600492. [Google Scholar] [CrossRef]
- Kumar, A.; Rath, S.; Kumar, M. Simulation of Plate Rolling Process Using Finite Element Method. Mater. Today Proc. 2021, 42, 650–659. [Google Scholar] [CrossRef]
- Liu, C.; He, A.; Qiang, Y.; Guo, D.; Shao, J. Effect of Internal Stress of Incoming Strip on Hot Rolling Deformation Based on Finite Element and Infinite Element Coupling Method. Metals 2018, 8, 92. [Google Scholar] [CrossRef]
- Peng, W.; Chen, X.; Wang, Q.; Wan, Z.; Sun, J.; Zhang, D. Mathematical Modeling and Simulated Analysis of Metal Flow Behavior during the FGC of ESP Rolling Process. Int. J. Adv. Manuf. Technol. 2023, 127, 5031–5047. [Google Scholar] [CrossRef]
- Moazeni, B.; Salimi, M. Investigations on Relations between Shape Defects and Thickness Profile Variations in Thin Flat Rolling. Int. J. Adv. Manuf. Tech. 2015, 77, 1315–1330. [Google Scholar] [CrossRef]
- Yang, C.; Li, Z.; Zhang, G.; Guo, B. FEM Simulation on Width Spread during the Multi-pass and Reversing Process of Roughing Horizontal Rolling for Hot Strip Mills. J. Univ. Sci. Technol. Beijing 2011, 33, 227–231. [Google Scholar]
- Li, C.; Wang, X.; Yang, Q.; Wang, L. Metal Transverse Flow and its Influence Factors of Hot Rolled Strips. J. Univ. Sci. Technol. Beijing 2013, 35, 222–227. [Google Scholar]
- Zhao, J.; Wang, X.; Yang, Q.; Wang, Q.; Wang, Y.; Li, W. Mechanism of lateral metal flow on residual stress distribution during hot strip rolling. J. Mater. Process. Technol. 2021, 288, 116838. [Google Scholar] [CrossRef]
- Chai, X.; Li, H.; Zhang, J.; Zhou, Y.; Ma, H.; Zhang, P. Flatness Analysis and Control of Strips with Different Thickness in 2250 mm Hot Tandem Rolling. Steel Res. Int. 2018, 89, 1800104. [Google Scholar] [CrossRef]
- Zhou, J.; Guan, K. Resistance to Plastic Deformation of Metals; China Machine Press: Beijing, China, 1989; pp. 211–230. [Google Scholar]
- Feng, G. Fem Study on Metal Deformation Law of Hot Strip Rough Rolling. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2003. [Google Scholar]
- Peng, D. The Principle of Metal Plasticity Processing; Central South University Press: Changsha, China, 2004; pp. 112–113. [Google Scholar]
- Wang, Y. Three-Dimensional Strip Element Method and Its Simulation of Hot Plate and Strip Rolling Process. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2003. [Google Scholar]

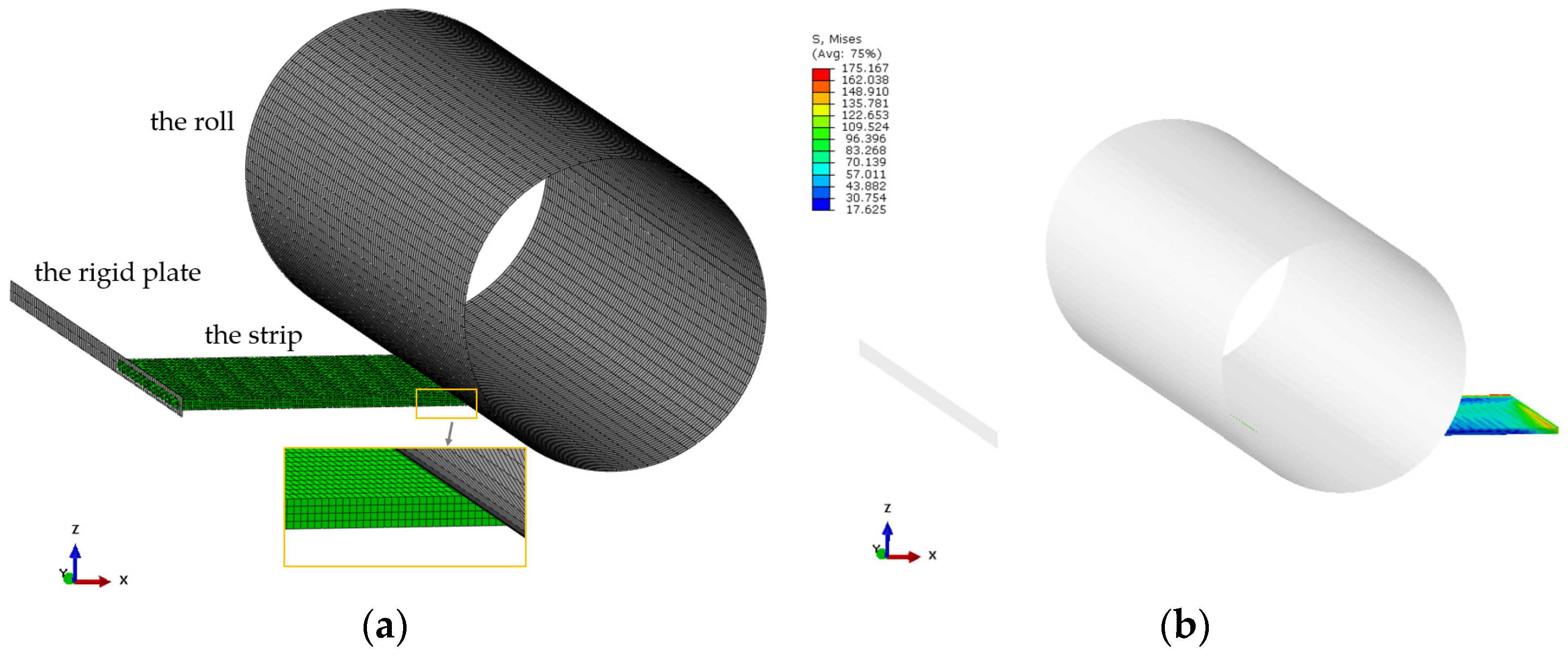







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| roll diameter | 800 mm | strip entry thickness | 30 mm |
| roll length | 2550 mm | strip exit thickness | 18 mm |
| strip width | 1500 mm | strip velocity | 1.5 m/s |
| strip temperature | 933 °C | Poisson’s ratio | 0.3 |
| front tension stress | 0~7 MPa | back tension stress | 0~5 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, X.; Li, Y.; Shang, F. Numerical Study on Metal Transverse Flow Law and Model of Rolled Strip under Variable Specification in Hot Rolling. Metals 2023, 13, 1876. https://doi.org/10.3390/met13111876
Chai X, Li Y, Shang F. Numerical Study on Metal Transverse Flow Law and Model of Rolled Strip under Variable Specification in Hot Rolling. Metals. 2023; 13(11):1876. https://doi.org/10.3390/met13111876
Chicago/Turabian StyleChai, Xiaojun, Yanlin Li, and Fei Shang. 2023. "Numerical Study on Metal Transverse Flow Law and Model of Rolled Strip under Variable Specification in Hot Rolling" Metals 13, no. 11: 1876. https://doi.org/10.3390/met13111876




