Optimization of Processing Parameters of Aluminum Alloy Cylindrical Parts Based on Response Surface Method during Hydromechanical Deep Drawing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Performance Parameters and Structural Characteristics of the Parts
2.2. Establishment and Simulation of the Finite Element Model
3. Simulation Results and Discussion
3.1. Effect of Friction Coefficient on Part Forming
3.2. Effect of Pressure Rate on Part Forming
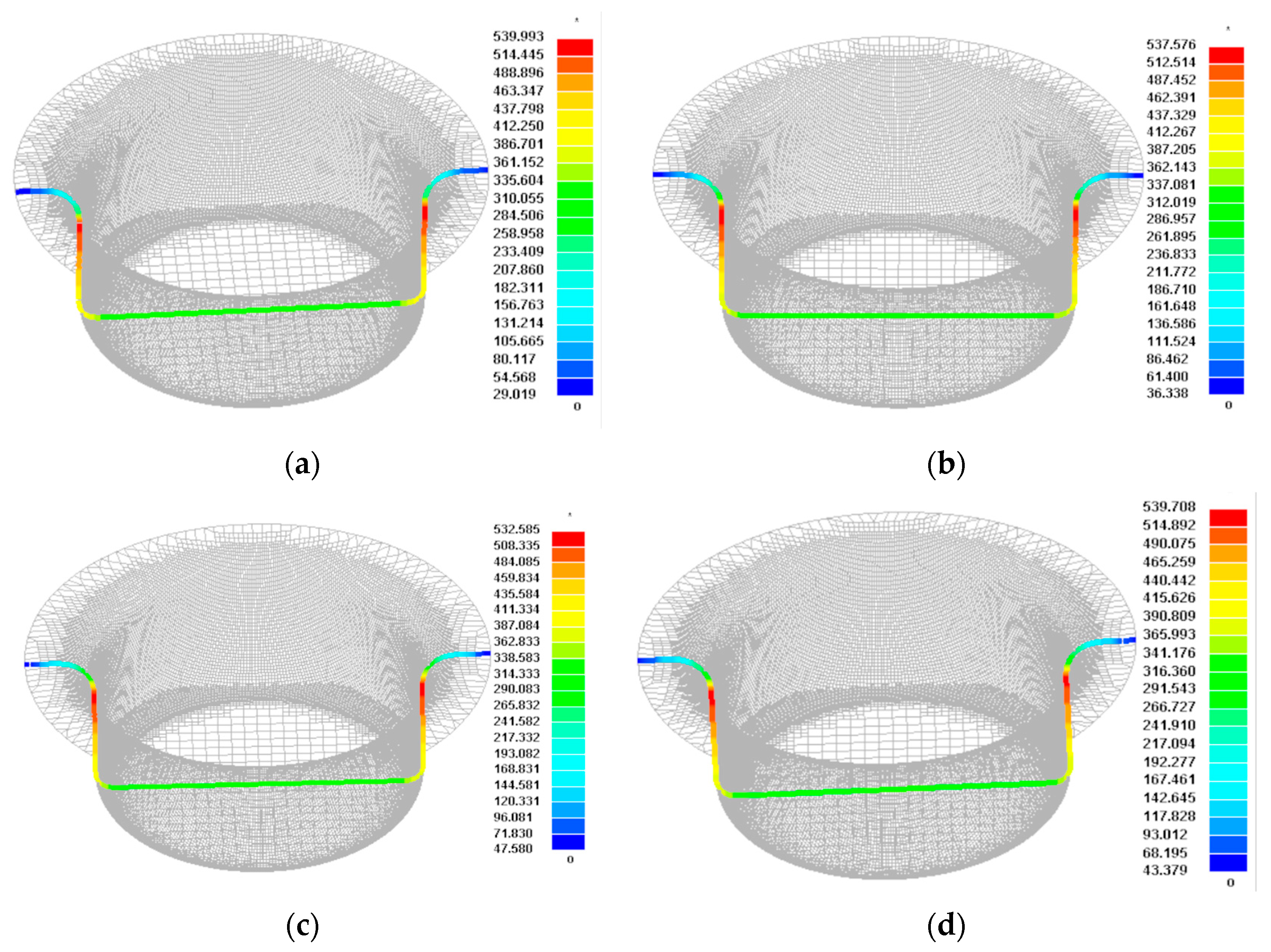
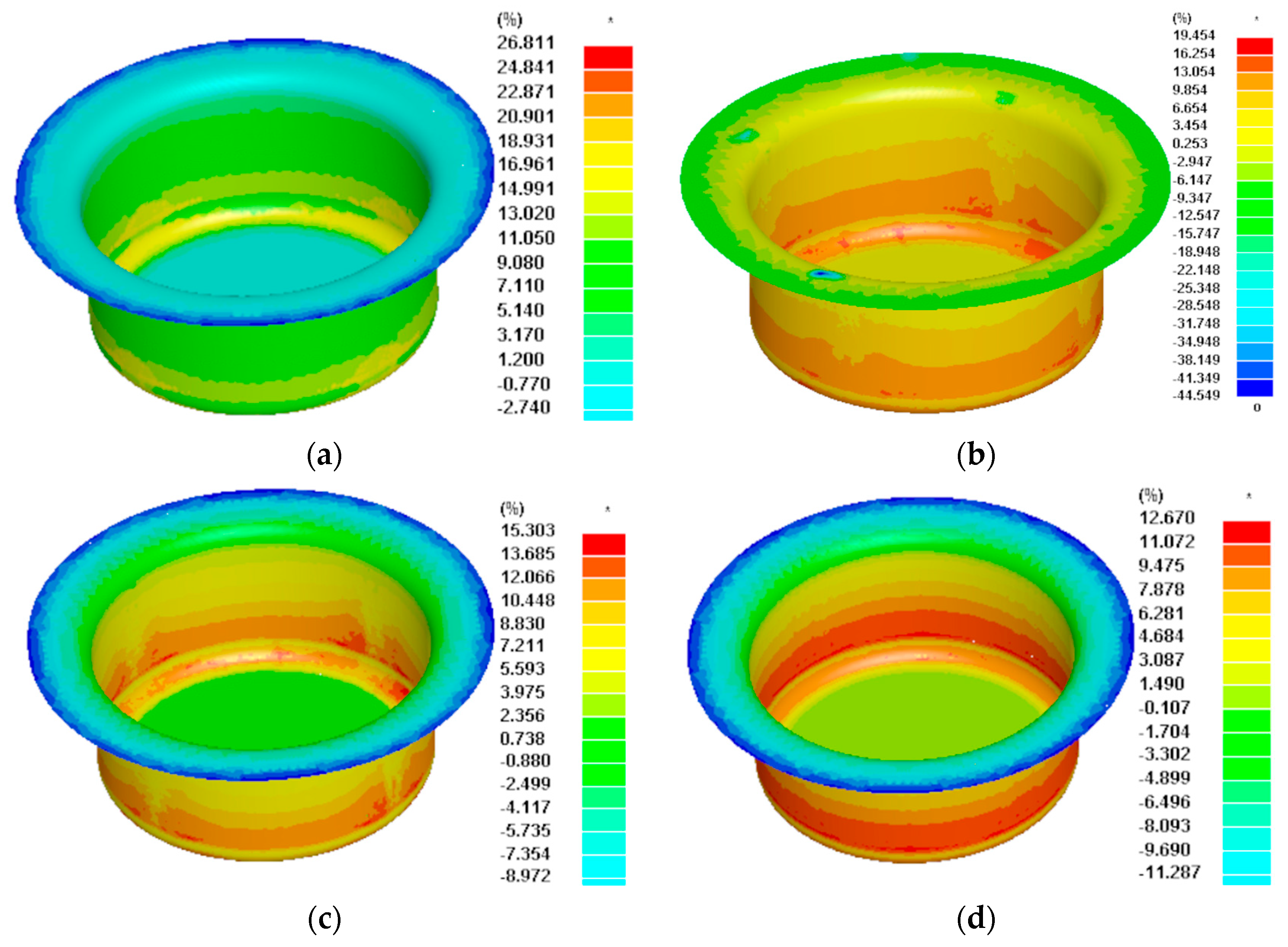
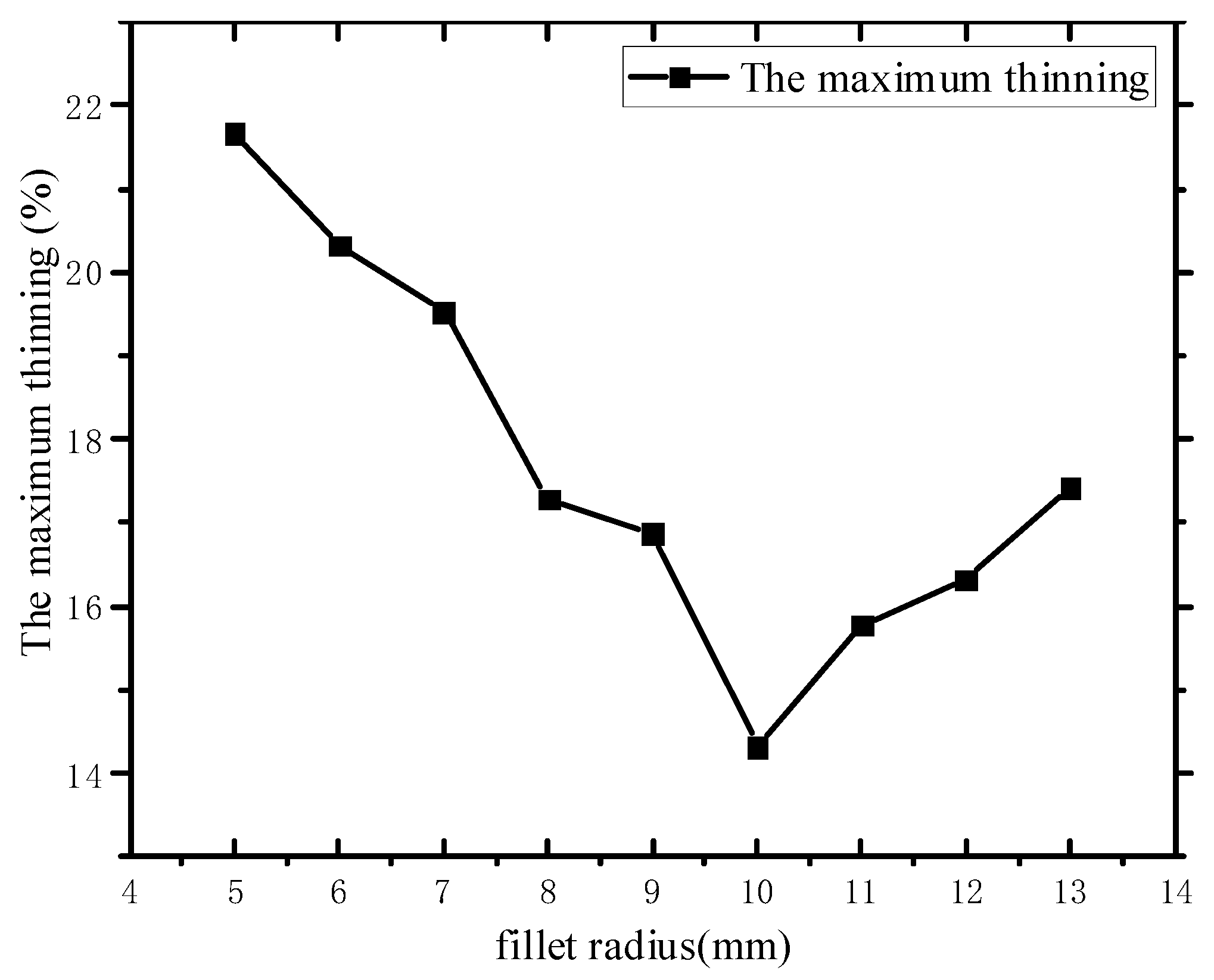
3.3. Effect of Fillet Radius on Part Forming
4. Experimental Results and Discussion
4.1. Experimental Factors and Design
4.2. Experimental Results of the Box–Behnken Design
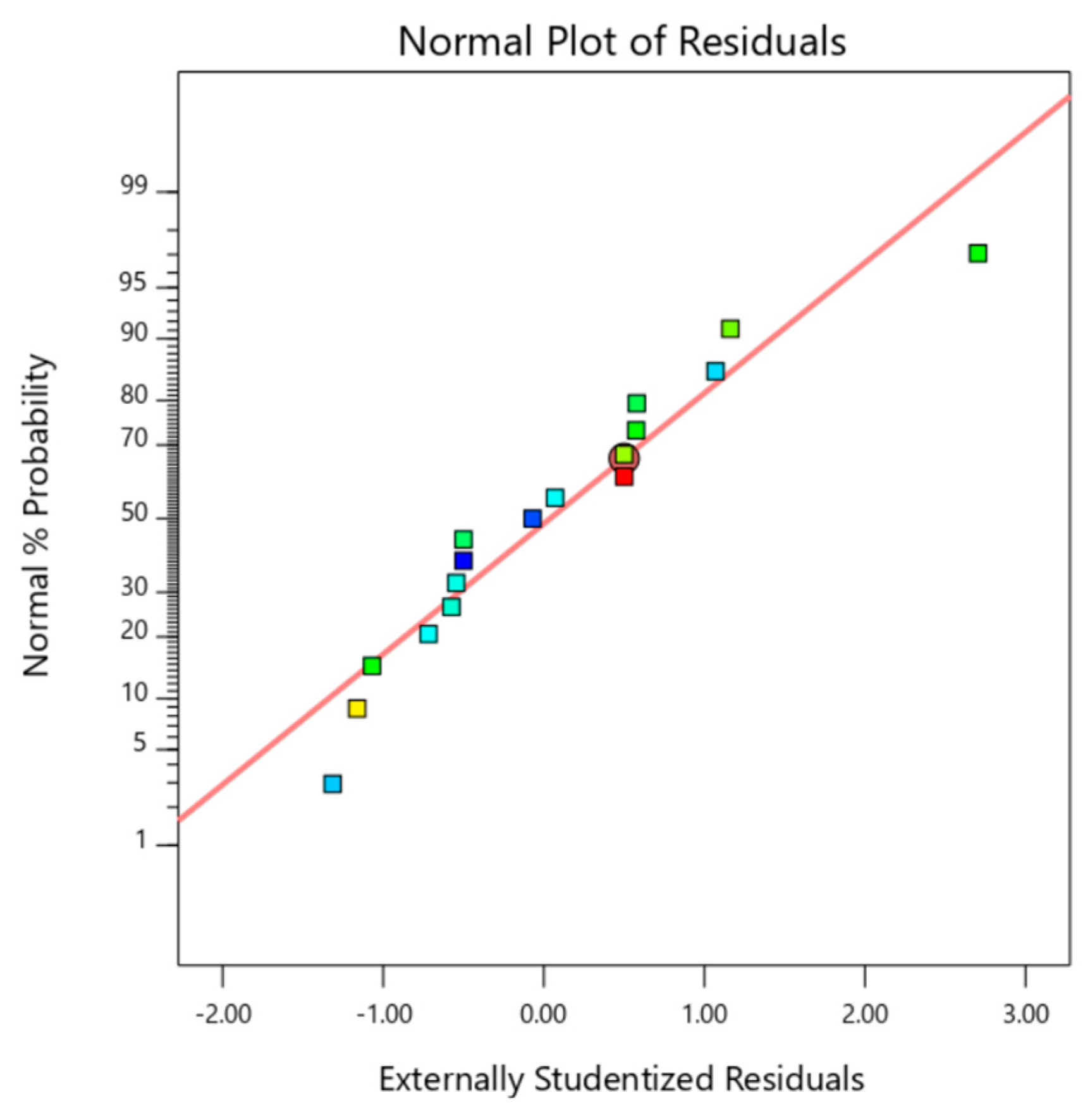
4.3. Analysis of Variance
4.4. Response Surface Results and Interaction Effects Analysis
4.5. Experimental Verification and Optimization
5. Conclusions
- (1)
- The friction coefficient, pressure rate, and fillet radius of the die have a significant influence on the maximum thinning rate and axial stress distribution of the parts. With the increase of the friction coefficient and fillet radius of the die, the maximum thinning rate of the parts decreases first and then increases. With the increase in the pressure rate, the maximum axial stress and the maximum thinning rate of the parts decrease and finally remain unchanged;
- (2)
- The quadratic response model between the maximum thinning rate and processing parameters was established. Through the quadratic response model, the optimal combination of processing parameters was obtained: the pressure rate was 11.6 MPa/s, the friction coefficient between the blank holder and the sheet was 0.15, and the fillet radius of the die was 8 mm;
- (3)
- The experimental results show that the quadratic regression model can satisfactorily estimate the correlation between formability and the considered process parameters, and the error range is less than ±5%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Xu, J. Advanced lightweight materials for Automobiles: A review. Mater. Des. 2022, 221, 110994. [Google Scholar] [CrossRef]
- Der, A.; Kaluza, A.; Reimer, L.; Herrmann, C.; Thieds, S. Integration of Energy Oriented Manufacturing Simulation into the Life Cycle Evaluation of Lightweight Body Parts. Int. J. Precis. Eng. Manuf. Green Technol. 2022, 9, 899–918. [Google Scholar] [CrossRef]
- Du, B.; Li, Q.C.; Zheng, C.Q.; Wang, S.Z.; Gao, C.; Chen, L.L. Application of Lightweight Structure in Automobile Bumper Beam: A Review. Materials 2023, 16, 967. [Google Scholar] [CrossRef] [PubMed]
- Churiaque, C.; Sanchez-Amaya, J.M.; Caamano, F.; Vazquez-Martinez, J.M.; Botana, J. Springback Estimation in The Hydroforming Process of UNS A92024-T3 Aluminum Alloy by FEM Simulations. Metals 2018, 8, 404. [Google Scholar] [CrossRef] [Green Version]
- Shen, G.W.; Chen, X.L.; Yan, J.; Fan, J.; Yang, Z.; Zhang, J.; Guan, R.G. A Review of Progress in the Study of Al-Mg-Zn(-Cu) Wrought Alloys. Metals 2023, 13, 345. [Google Scholar] [CrossRef]
- Zhe, H.H.; Lin, Y.L.; Chen, K.L.; He, Z.B. Forming Limit Analysis of Thin-Walled Extruded Aluminum Alloy Tubes under Nonlinear Loading Paths Using an Improved M-K Model. Materials 2023, 16, 1647. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.P.; Wang, B.; Lu, J.; Wang, C.; Li, Y.M.; Luo, F.H. Microstructure, mechanical properties, and corrosion resistance of continuous heating aging 6013 aluminum alloy. J. Mater. Res. Technol. 2022, 18, 370–383. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.M.; Chen, J.; Peng, X.D.; Chen, D.L.; Pan, F.S. Research advances in magnesium and magnesium alloys worldwide in 2020. J. Magnes. Alloys 2021, 9, 705–747. [Google Scholar] [CrossRef]
- Piccininni, A.; Palumbo, G.; Zaheer, O.; Ingarao, G.; Fratini, L. Reshaping End-of-Life components by sheet hydroforming: An experimental and numerical analysis. J. Mater. Process. Technol. 2022, 306, 117650. [Google Scholar] [CrossRef]
- Zhang, B.; Endelt, B.; Lang, L.H.; Zhao, Y.; Yan, S.; Nielsen, K.B. An inverse strategy to determine constitutive parameters of tubular materials for hydroforming processes. Chin. J. Aeronaut. 2022, 35, 379–390. [Google Scholar] [CrossRef]
- He, Z.B.; Zhang, K.; Zhu, H.H.; Lin, Y.L.; Fu, M.; Yuan, S.J. An anisotropic constitutive model for forming of aluminum tubes under both biaxial tension and pure shear stress states. Int. J. Plast. 2022, 152, 103259. [Google Scholar] [CrossRef]
- Jiao, Z.H.; Lang, L.H.; Zhao, X.N. 5A06-O aluminium-magnesium alloy sheet warm hydroforming and optimization of process parameters. Trans. Nonferrous Met. Soc. China 2021, 31, 2939–2948. [Google Scholar] [CrossRef]
- Cui, X.L.; Chu, R.H.; He, J.Q.; Han, C.; Yuan, S.J. Less-loading hydroforming process for large-size hollow components of aluminum alloy. J. Mater. Res. Technol. JMRT 2021, 15, 1935–1948. [Google Scholar] [CrossRef]
- Shi, C.S.; Li, J.P.; Juan, D. Research on the hydroformed metal stator bushing based on full restraint at both ends. Eng. Fail. Anal. 2021, 128, 105591. [Google Scholar] [CrossRef]
- Yuan, S.J. Fundamentals and Processes of Fluid Pressure Forming Technology for Complex Thin-Walled Components. Engineering 2021, 7, 358–366. [Google Scholar] [CrossRef]
- Chen, D.Y.; Xu, Y.; Zhang, S.H.; Ma, Y. A novel method to evaluate the high strain rate formability of sheet metals under impact hydroforming. J. Mater. Process. Technol. 2021, 287, 116553. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Manabe, K.I. Latest hydroforming technology of metallic tubes and sheets. Metals 2021, 11, 1360. [Google Scholar] [CrossRef]
- Cui, X.L.; Yuan, S.J. Analysis of thickness variation and stress state in hydroforming of complex T-shaped tubular part of nickel-based superalloy. Arch. Civ. Mech. Eng. 2021, 21, 111. [Google Scholar] [CrossRef]
- Liu, K.N.; Lang, L.H.; Zhang, W.S.; Marai, M.; Liu, B.S. Coupled eulerian–lagrangian simulation of granular medium sheet forming process and experimental investigation at elevated temperature. Int. J. Adv. Manuf. Technol. 2017, 88, 2871–2882. [Google Scholar] [CrossRef]
- Reddy, R.V.; Reddy, T.A.J.; Reddy, G.C.M. Optimization of blank holder force to control wrinkling and fracture of cylindrical cups in deep drawing. Int. J. Eng. Technol. 2012, 3, 669–676. [Google Scholar] [CrossRef]
- Lang, L.H.; Wang, Y.M.; Xie, Y.S.; Yang, X.Y.; Xu, Y.Q. Pre-bulging effect during sheet hydroforming process of aluminum alloy box with unequal height and flat bottom. Trans. Nonferrous Met. Soc. China 2012, 22, s302–s308. [Google Scholar] [CrossRef]
- Han, T.C.; Liu, Q.; Lu, H.; Gao, G.L.; Xie, W.C.; Yuan, S.J. Thickness improvement in hydroforming of a variable diameter tubular component by using wrinkles and preforms. J. Adv. Manuf. Technol. 2018, 99, 2993–3003. [Google Scholar] [CrossRef]
- Cai, G.S.; Wu, C.Y.; Gao, Z.P.; Lang, L.H.; Alexandrov, S. Investigation on the effect of pressure rate on formability of aluminum alloy during warm/hot sheet hydroforming. AIP Adv. 2018, 8, 095313. [Google Scholar] [CrossRef] [Green Version]
- Reddy, P.V.; Reddy, B.V.; Ramulu, P.J. An investigation on tube hydroforming process considering the effect of frictional coefficient and corner radius. Adv. Mater. Process. Technol. 2020, 6, 84–103. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.F.; Chen, D.Y. Determination of the forming limit of impact hydroforming by frictionless full zone hydraulic forming test. Int. J. Mater. Form. 2021, 14, 1221–1232. [Google Scholar] [CrossRef]
- Cheng, D.M.; Teng, B.G.; Guo, B.; Yuan, S.J. Thickness distribution of a hydroformed Y-shape tube. Mater. Sci. Eng. A-Struct. 2009, 499, 36–39. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, G.H.; Wang, W.Q.; Jing, X.K. Evaluation and optimization on the formability of an AZ31B Mg alloy during warm incremental sheet forming assisted with oil bath heating. Measurement 2020, 157, 107673. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Zhang, H.G.; Luo, Z.A.; Wu, Q.L. Loading path optimization of T tube in hydroforming process using response surface method. Int. J. Adv. Manuf. Technol. 2019, 101, 1979–1995. [Google Scholar] [CrossRef]
- Hu, C.L.; Yin, Q.; Zhao, Z. A novel method for determining friction in cold forging of complex parts using a steady combined forward and backward extrusion test. J. Mater. Process. Technol. 2017, 249, 57–66. [Google Scholar] [CrossRef]
- Lang, L.H.; Du, P.M.; Liu, B.S.; Cai, G.S.; Liu, K.N. Pressure rate controlled unified constitutive equations based on microstructure evolution for warm hydroforming. J. Alloys Compd. 2013, 574, 41–48. [Google Scholar] [CrossRef]
- Cai, G.S.; Fu, J.B.; Wu, C.Y.; Liu, K.N.; Lang, L.H. Simulation and Experimental Investigation of Granular Medium Forming Technology on Titanium Alloy Sheet at 500 °C. Metals 2021, 11, 114. [Google Scholar] [CrossRef]









| Material Name | Poisson Ratio μ | Anisotropic Parameters | Hardening Index n | Hardening Factor K/MPa | |||||
|---|---|---|---|---|---|---|---|---|---|
| AA6013 | 69,000 | 380 | 350 | 0.33 | 0.684 | 0.684 | 0.684 | 0.226 | 608.8 |
| Level | Factor | ||
|---|---|---|---|
| A Friction Coefficient | B Pressure Rate/ MPa/s | C Fillet Radius/mm | |
| −1 | 0.09 | 1.25 | 5 |
| 0 | 0.295 | 6.75 | 9 |
| 1 | 0.5 | 12.5 | 13 |
| Test Number | A Friction Coefficient | B Pressure Rate (MPa/s) | C Fillet Radius (mm) | The Maximum Thinning (%) |
|---|---|---|---|---|
| 1 | 0.09 | 1.25 | 9 | 16.7 |
| 2 | 0.5 | 1.25 | 9 | 19.8 |
| 3 | 0.09 | 12.25 | 9 | 16.3 |
| 4 | 0.5 | 12.25 | 9 | 17.6 |
| 5 | 0.09 | 6.75 | 5 | 18.3 |
| 6 | 0.5 | 6.75 | 5 | 20.2 |
| 7 | 0.09 | 6.75 | 13 | 19.7 |
| 8 | 0.5 | 6.75 | 13 | 21.4 |
| 9 | 0.295 | 1.25 | 5 | 18.6 |
| 10 | 0.295 | 12.25 | 5 | 17.4 |
| 11 | 0.295 | 1.25 | 13 | 18.6 |
| 12 | 0.295 | 12.25 | 13 | 17.4 |
| 13 | 0.295 | 6.75 | 9 | 18.6 |
| 14 | 0.295 | 6.75 | 9 | 17.8 |
| 15 | 0.295 | 6.75 | 9 | 18.4 |
| 16 | 0.295 | 6.75 | 9 | 17.3 |
| 17 | 0.295 | 6.75 | 9 | 17.6 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 25.20 | 9 | 2.80 | 6.40 | 0.00115 (significant) |
| A-friction | 8.00 | 1 | 8.00 | 18.29 | 0.0037 |
| B-pressure rate | 2.65 | 1 | 2.65 | 0.00435 | |
| C-fillet radius | 1.13 | 1 | 1.13 | 2.57 | 0.00152 |
| AB | 0.8100 | 1 | 0.8100 | 1.85 | 0.2158 |
| AC | 0.0100 | 1 | 0.0100 | 0.0229 | 0.8841 |
| BC | 0.0400 | 1 | 0.0400 | 0.0914 | 0.7711 |
| A2 | 1.95 | 1 | 1.95 | 4.45 | 0.0728 |
| B2 | 5.28 | 1 | 5.28 | 12.07 | 0.0103 |
| C2 | 5.86 | 1 | 5.86 | 13.40 | 0.0081 |
| Residual | 3.06 | 7 | 0.4374 | ||
| Lack of fit | 0.7300 | 3 | 0.2433 | 0.7506 | not significant |
| Pure Error | 2.33 | 4 | 0.5830 | ||
| Cor Total | 28.26 | 16 | |||
| R2 = 0.9427 | R2adjust = 0.9345 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Cai, G. Optimization of Processing Parameters of Aluminum Alloy Cylindrical Parts Based on Response Surface Method during Hydromechanical Deep Drawing. Metals 2023, 13, 1406. https://doi.org/10.3390/met13081406
Pan Y, Cai G. Optimization of Processing Parameters of Aluminum Alloy Cylindrical Parts Based on Response Surface Method during Hydromechanical Deep Drawing. Metals. 2023; 13(8):1406. https://doi.org/10.3390/met13081406
Chicago/Turabian StylePan, Yufeng, and Gaoshen Cai. 2023. "Optimization of Processing Parameters of Aluminum Alloy Cylindrical Parts Based on Response Surface Method during Hydromechanical Deep Drawing" Metals 13, no. 8: 1406. https://doi.org/10.3390/met13081406




