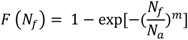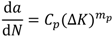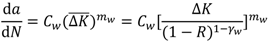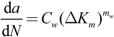1. Introduction
AM60B magnesium alloy is increasingly used in the auto industry. This material offers attractive properties to designers. For instance, lower density (quarter of steel and two third of aluminum), high specific strength, and excellent castability and machinability are some of the positive attributes of this alloy. The increase in the use of the alloy requires more knowledge and base-line data on the microstructure and its effect on the mechanical properties of the material.
In the real world, fatigue fracture is a dominant and catastrophic failure mode in the auto industry. That is a major reason why the fatigue and fracture response of this alloy should be carefully studied. This response is strongly influenced by microstructural defects.
2. Micro-Structural Study
Porosities play a significant role in microstructure of cast magnesium alloy AM60B. These are a by-product of non-uniform solidification during the casting process. Pores and voids, due to both gas encapsulation and shrinkage, act as stress intensifiers, generating sites that facilitate fatigue crack initiation and propagation. In this part, the influence of microstructure of the alloy on the basic material response is reviewed.
2.1. Monotonic and Cyclic Behavior of the Alloy
The mechanical behavior of AM60B under monotonic and cyclic loading conditions was studied in detail by Lu
et al. [
1]. As previously mentioned, uneven cooling in a typically high-pressure die-casting process produces non-uniform porosity distribution in the material. It is an established fact that voids and porosities undermine mechanical properties of metals.
Casting-induced heating and subsequent cooling usually produce different micro-structural layers. Variation in the mechanical properties of skin and core of cast magnesium alloy has been reported by Weiler [
2]. The cooling process may also result in formation of residual stresses, in turn forming micro-cracks. Variable cooling rates are chiefly responsible for such phenomena. Lu
et al. [
1] captured scanning electron microscopy (SEM) images of AM60B as shown in
Figure 1. They reported different particles in the material. The micro-structural components are clearly visible in
Figure 1b. The darkest (or the main part) represents the α-Mg matrix, while the bright parts represent the β-Mg
17Al
12. In addition to these two materials, some other particles, such as AlMnSi intermetallics, are also seen, identified as the brightest parts.
Figure 1.
(
a) Overall view of micro-structure; (
b) Higher magnification of the micro-structure [
1].
2.1.1. Experimental Investigations
Lu
et al. [
1] experimentally investigated the effect of micro-structure of different layers within the thickness of the alloy. The alloy used by our research group, provided by Meridian Technology Inc. (Strathroy, Ontario, Canada), has a chemical composition listed in
Table 1. In order to investigate the effect of the spatial variation in the micro-structure, the specimens were cut from different instrument panels or different regions of one panel.
Figure 2 shows some typical selected regions of a panel. The experimental investigation presented here focused on region 2.
Table 1.
Chemical composition of AM60B [1].
| Mg | Al | Mn | Si | Zn | Fe | Cu | Ni | Other |
|---|
| Bal. | 5.5–6.5 | 0.25 min | 0.1 max | 0.22 max | 0.005 max | 0.01 max | 0.002 max | 0.003 max (total) |
In order to study the mechanical behavior of the skin and core separately, the skin with the thickness of 0.45 mm was separated from the core using an electrical discharge machine (EDM). Both parts (skin and core) were tensile-tested and their responses compared.
Figure 2.
Identification of the investigated regions [
1].
2.1.2. Experimental Results
The stress-strain curve obtained from a tensile test of two different panels at the same region (26-2 and 32-2) is shown in
Figure 3. For each specimen, the first number is in reference to the panel number and the second one references the region from which that specimen was taken. Comparison of the two curves discloses greater ductility in specimen 32-2. The difference is attributed to variable micro-structure of the specimens, particularly the area hosting the porosities on the fractured surface.
Figure 3.
Stress-strain curve for specimens 26-2 and 32-2 [
1].
Lu
et al. [
1] have also shown (see
Figure 4) that the area fraction of porosities of specimen 26-2 is significantly higher than that of specimen 32-2. An increase in the percentage of porosity results in reduction of the surface normal to the applied load; accordingly, the stress will increase. The pore also acts as a stress intensifier, thus fostering crack initiation and propagation.
Figure 4.
Fractograph of fractured surface of specimens 26-2 and 32-2 [
1].
2.1.3. Micro-Structural Layers (Skin and Core)
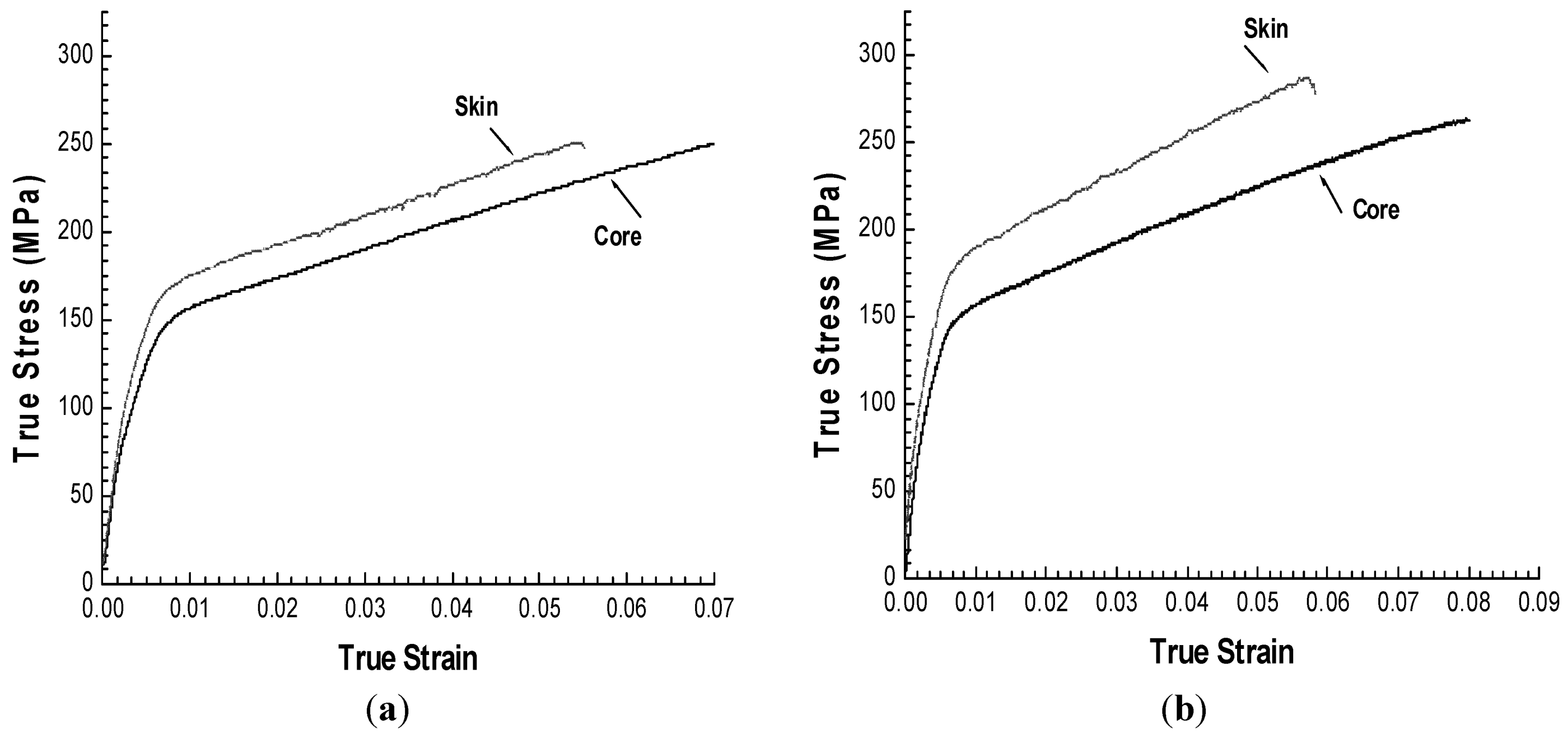
The results of the tensile test applied to the separated skin and core are presented in
Figure 5. The difference between the material behavior in skin and core confirms the significant variation in the microstructure of these layers. According to the results presented in
Figure 5, in comparison to the skin, the core material exhibited greater ductility, but offered less ultimate strength. This response is attributed to the grain size and porosity of the material.
Figure 5.
Stress-strain curves of skin and core of specimens extracted from two different regions [
1].
The SEM image of the skin and core microstructure of the AM60B alloy is shown in
Figure 6. The figure shows a large variation in grain size of the skin and core. The skin contains fine-grained microstructure. Not only does the core host large grain size, but it also contains α-Mg dendritic structure. It has also been reported by other researchers [
3,
4] that the amount of β-phase Mg
17Al
12 in the skin layer is relatively higher than in the core layer. The β-phase is a brittle material, and it is obvious that an increase in the amount of this particle in the skin would result in higher stiffness and brittleness of the layer. This confirms the responses shown in
Figure 5.
Figure 6.
SEM observation of (
a) skin; and (
b) core’s micro-structure [
1].
2.1.4. Cyclic Stress-Strain Curve
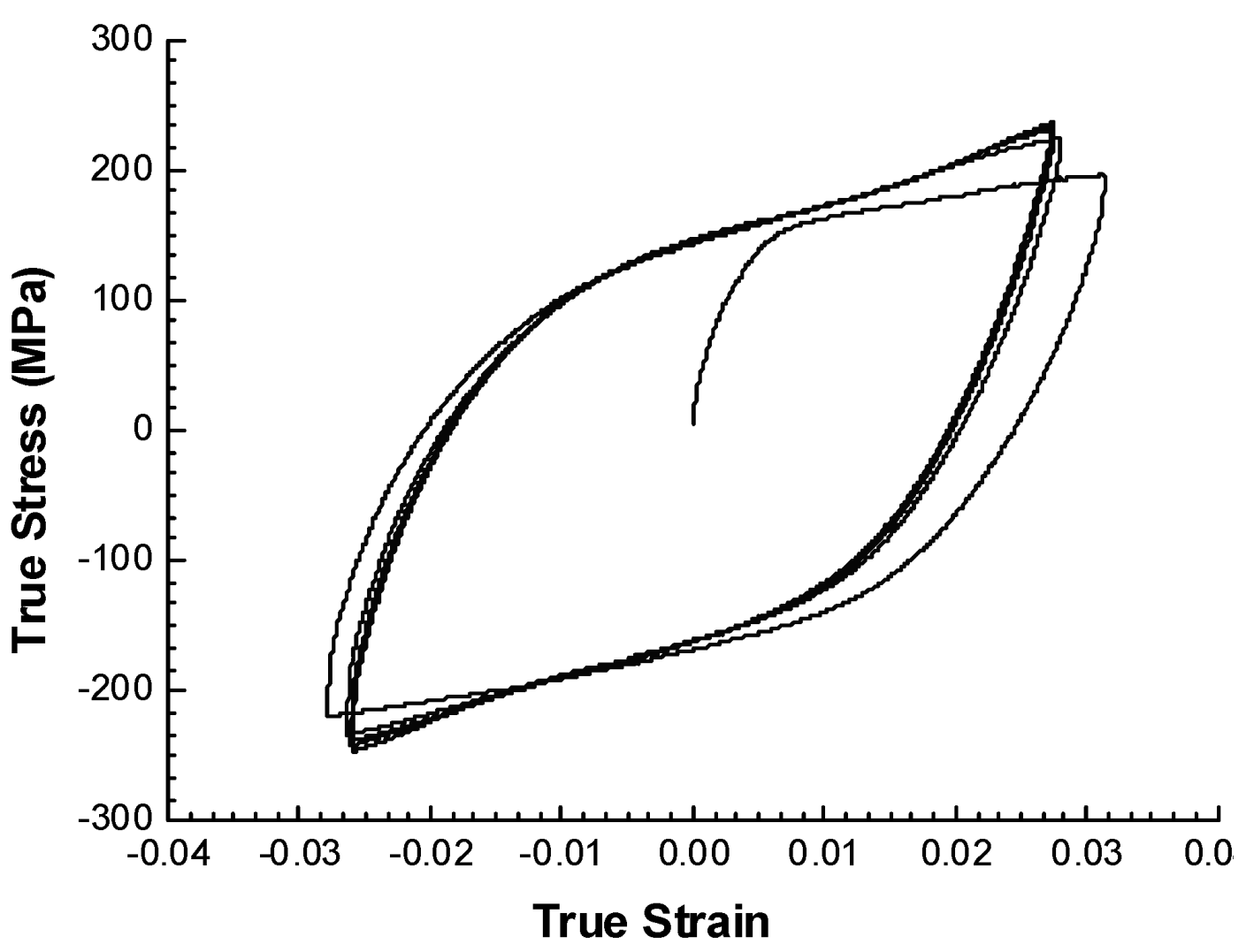
In continuation of their previous effort, In order to investigate the cyclic hardening of the alloy, Lu
et al. [
1] also subjected the alloy to cyclic tensile loading under a strain range of 6.4%. The resulting response is shown in
Figure 7. As seen, the stress-strain hysteresis became saturated after three to five cycles, and its loop’s width decreased as the cyclic hardening occurred after certain number of cycles.
Figure 7.
Cyclic stress-strain curve [
1].
Lu
et al. [
1] divided the hysteresis loop into compression and tension parts and showed the variation in the true stress as a function of the accumulated strain (see
Figure 8). The results shown in
Figure 8 confirm the kinematic hardening response of the alloy. As can be seen, the yield strength changed significantly when the loading direction was reversed (
i.e., from compression to tension and vice-versa).
Figure 8.
(
a) One complete cycle; (
b) One and half cycle; and (
c) Two complete cycles [
1].
2.2. The Mechanism of Fatigue Crack Incubation and Propagation in AM60B
Lu
et al. [
5] furthered their investigation into the influence of microstructure on the crack initiation and propagation of the alloy. As noted earlier, the alloy’s microstructure has a significant effect on its strength, as well as the location of crack initiation.
2.2.1. Fatigue Tests Procedure and the Results
Lu
et al. [
5] carried out a set of low-cycle fatigue tests on the AM60B. The observed fatigue life for the specimen, taken from different parts of the panels (shown in
Figure 2), were compared. The fatigue tests were conducted under a stress ratio of 0.1 and loading frequency of 30 Hz. The specimens were tested over several stress ranges.
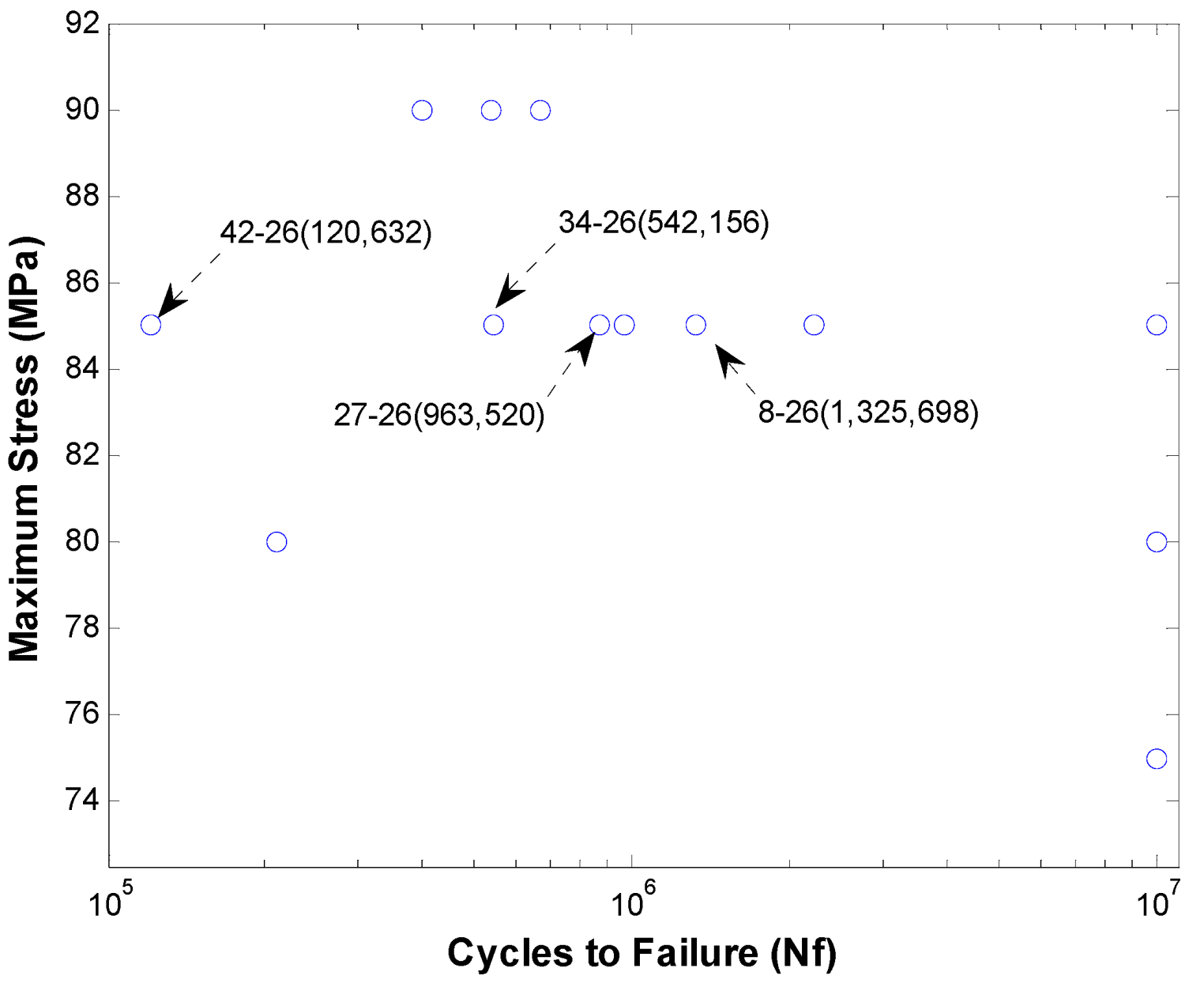
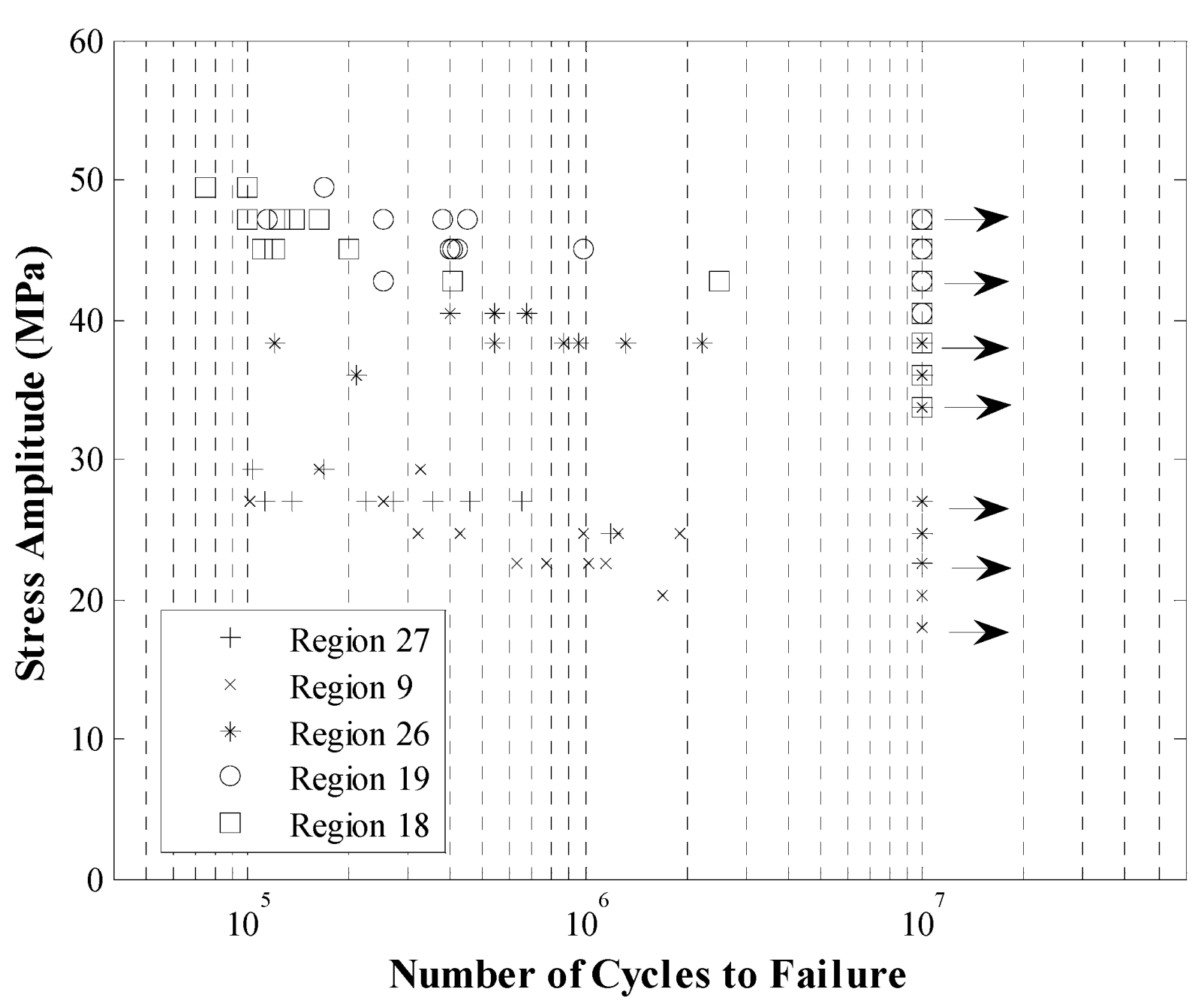
The staircase method was used in conducting the fatigue tests. In this method the stress range in a given test stage was determined based on the results obtained in the previous stage of testing. If the specimen survived the set fatigue life (usually 10 million cycles) in the first test stage, then the stress range would be increased in the following test stage to induce a shorter fatigue life. The fatigue life results of specimens extracted from region 26 are shown in
Figure 9. The results show a large variation (by two orders of magnitude) in the fatigue life for a given constant stress range. This further confirms the variations in the microstructure of the alloy from one specimen to another. It shows that the fatigue life of a specimen depends highly on the micro-structural components, such as porosity, brittle β-phase and other initial induced anomalies, as well as the stress range.
Figure 9.
Specimen’s fatigue life subjected to several stress ranges [
5].
2.2.2. Micro-Structural Analysis
McDowell
et al. [
6] divided the fatigue life of a material into three stages: crack initiation, small crack (micro-structurally and physically) propagation, and long crack propagation. They have reported that under high cycle fatigue, the first stage (referred to as crack incubation) controls the entire fatigue life of a specimen.
SEM observations of the fracture surface close to the crack initiation sites for two different specimens (taken from two different panels) are shown in
Figure 10 and
Figure 11. As can be seen in
Figure 10, the crack started from a casting pore of approximately 170 μm × 540 μm in specimen 34-26, while
Figure 11 exhibits the crack initiating from a smaller initial pore size (
i.e., 50 μm × 140 μm in specimen 27-26). Therefore, specimen 34-26 has a shorter fatigue life because of its larger pore size compared with specimen 27-26.
Figure 10.
SEM image of a crack initiation site in specimen 34-26 (Fatigue life = 542,156 cycles) [
5].
Figure 11.
SEM image of a crack initiation site in specimen 27-26 (Fatigue life = 963,520 cycles) [
5].
Interactions of two pores with different distances from each other are shown in
Figure 12 and
Figure 13.
Figure 12 shows two small casting pores at a very close distance of 156 μm, while, as shown in
Figure 13, the pores are located about 800 μm from each other. Shorter fatigue life was observed for the specimen with the pores at closer distance. This confirms that the fatigue life of a material depends highly on the distance between the pores, as well as their size. Moreover, it was concluded from these observations that the crack was initiated due to casting pores located far from the free surface, which could be indicative of the influence of the existence of compressive residual stress in the skin.
Figure 12.
SEM image of a crack initiation site in specimen 42-26 (Fatigue life = 120,632 cycles) [
5].
Figure 13.
SEM image of a crack initiation site in specimen 8-26 (Fatigue life = 1,325,698 cycles) [
5].
2.3. Influence of Porosity on the Fatigue Life
In this part, the experimental and numerical study of Lu
et al. [
7], conducted with the aim of assessing the effect of casting pores on the fatigue life of the alloy is discussed. The specimens tested in this part of their investigation were taken from regions 9, 18, 19, 26 and 27 (see
Figure 2). As a result of the casting induced heating and the subsequent cooling, specimens 18 and 19 had very low porosity, while regions 9 and 27, which were the last regions to be filled in the casting mold, showed higher levels of porosity. The fatigue test was carried out under the stress ratio of
R = 0.1, under several maximum stress amplitudes, ranging from 50 MPa to 110 MPa. The experimental results were analyzed using the Weibull distribution method.
2.3.1. Weibull Distribution Analysis
According to Wang
et al. [
8] the scatter high cycle fatigue data of alloys with variable microstructures could be presented using a two-parameter Weibull model, represented by the following relation:
where
F(
Nf),
Nf,
Na and m are the failure probability, fatigue life, the characteristic fatigue life at which 63% of the specimens have failed, and the Weibull modulus respectively. The fatigue lives of the specimens subjected to various stress amplitudes are depicted in
Figure 14.
Figure 14.
Fatigue test results obtained at different stress amplitude [
7].
Figure 15 illustrates the plot of double natural logarithm of the Weibull distribution against the natural logarithm of fatigue life. As can be seen, the experimental data could be presented by a two parameter linear Weibull model. As reported by other researchers (e.g., see Reference [
8]), the linear variation indicates the strong influence of porosity on the fatigue life of the material. It also indicates that the influence of this parameter overrides the influence of other parameters, such as the β-phase and inter-metallic particles; otherwise, the variation trend would have been nonlinear. The Weibull modulus and the characteristic fatigue life of the experimental test data were found to be 1.08 and 6.11 × 10
5, respectively.
Figure 15.
The two-parameter Weibull model [
7].
2.3.2. Numerical Investigation
A finite element analysis was also carried out (see Reference [
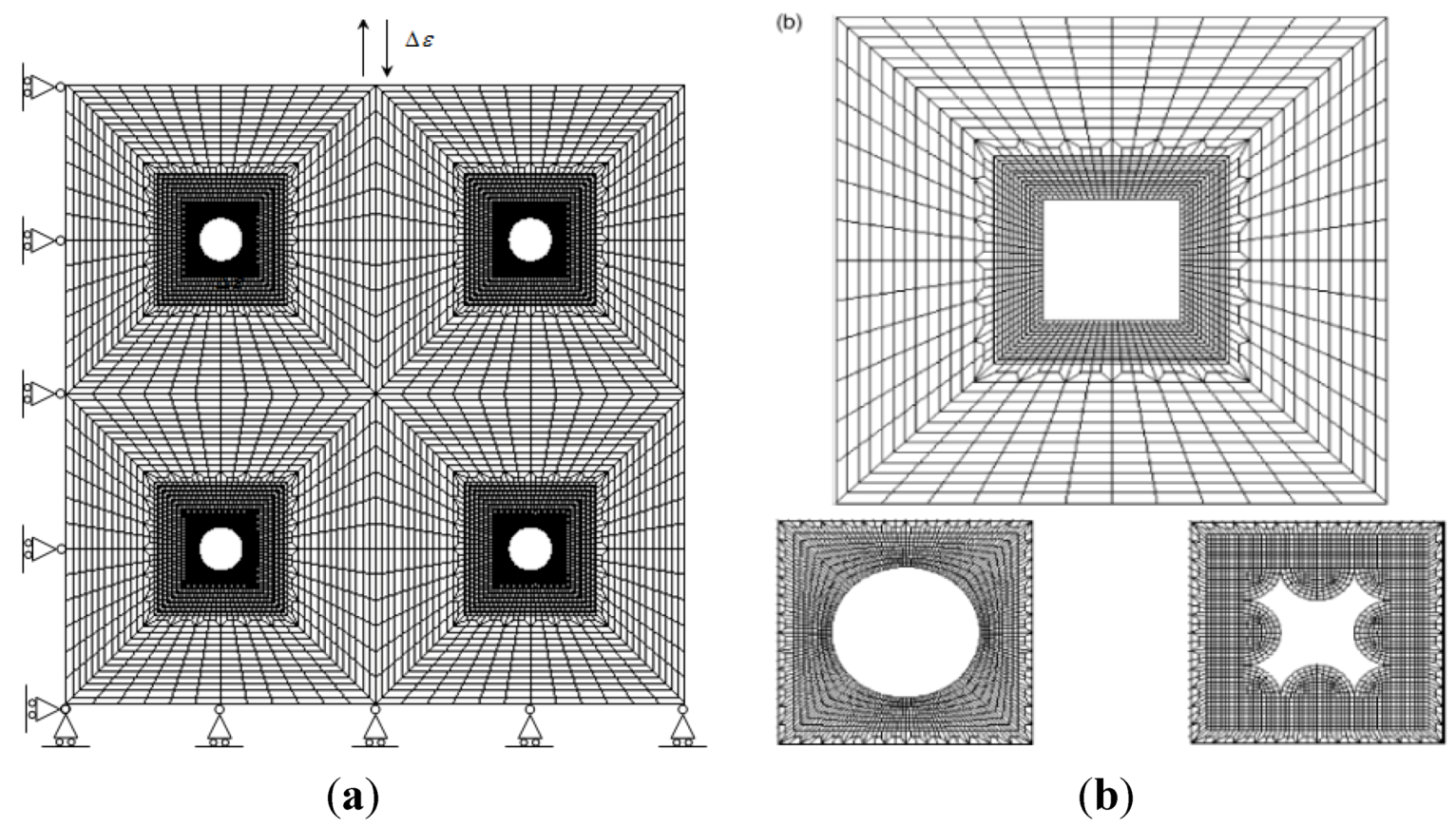
7]) to study the influence of microstructural defects on the local plastic strain and stress concentration around the defects. A representative microscopic volumetric (RMV) region of a specimen having micro-defects was modelled using the four node plane strain element of the Abaqus software. Different micro-defect (pore) shapes, as shown in
Figure 16, were considered. Each RMV’s was subjected to a far-field strain range with different amplitudes, and due to symmetry, a quarter of the RMV was analyzed. It should be emphasized that although a specimen containing such micro-voids would be under plane stress state, the RMV itself is considered to be under a plane strain state (since the pores go through the entire RMV).
Figure 16.
(
a) Overall view of the plate with micro-defects and mesh configuration; (
b) Defect shape [
7].
The model used to describe alloy’s nonlinear response was based on a nonlinear kinematic hardening model developed by the authors, based on the model originally developed by Ohno and Wang [
9].
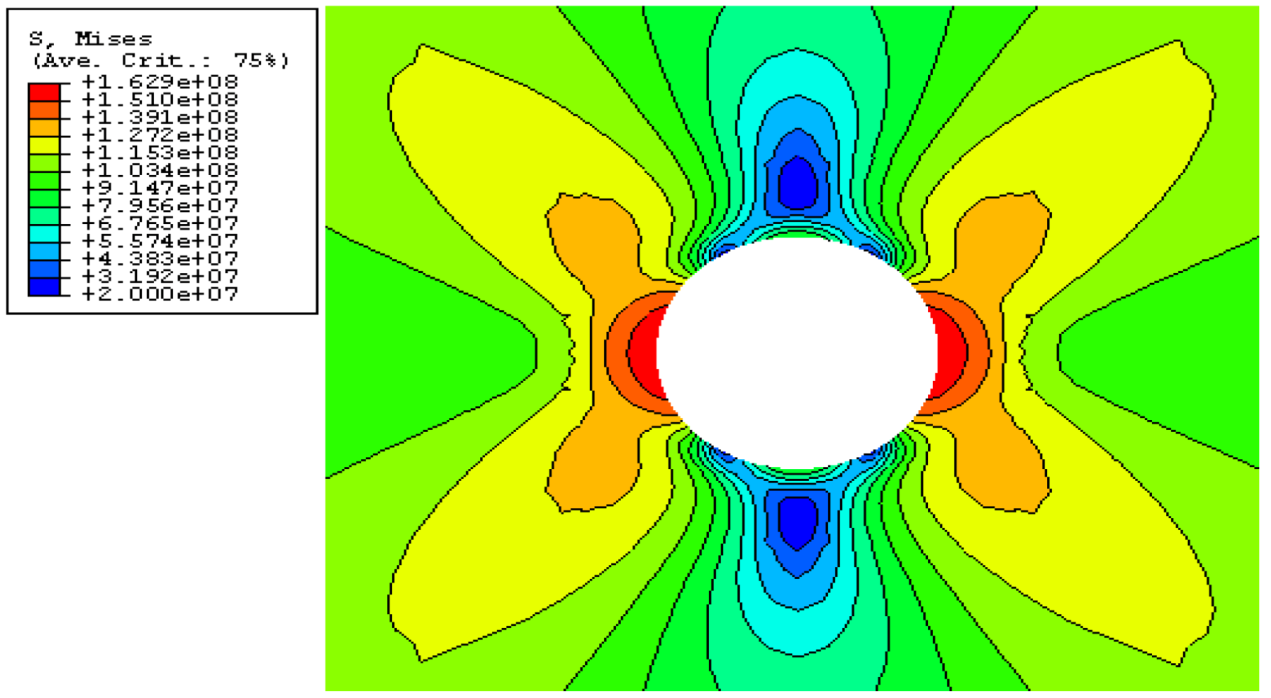
The von-Mises stress distribution in a plate hosting awkward star-shaped pores under a monotonic loading is shown in
Figure 17.
Fatemi and Socie [
10] and McDowll [
11] reported the maximum shear strain range (∆γ
max) as the driving force of fatigue crack initiation. In this part, the average maximum shear strain range is considered. This was also proposed by Gall
et al. [
12].
Figure 17.
The von-Mises stress distribution around a circular shape pore [
7].
2.3.3. Results and Discussions
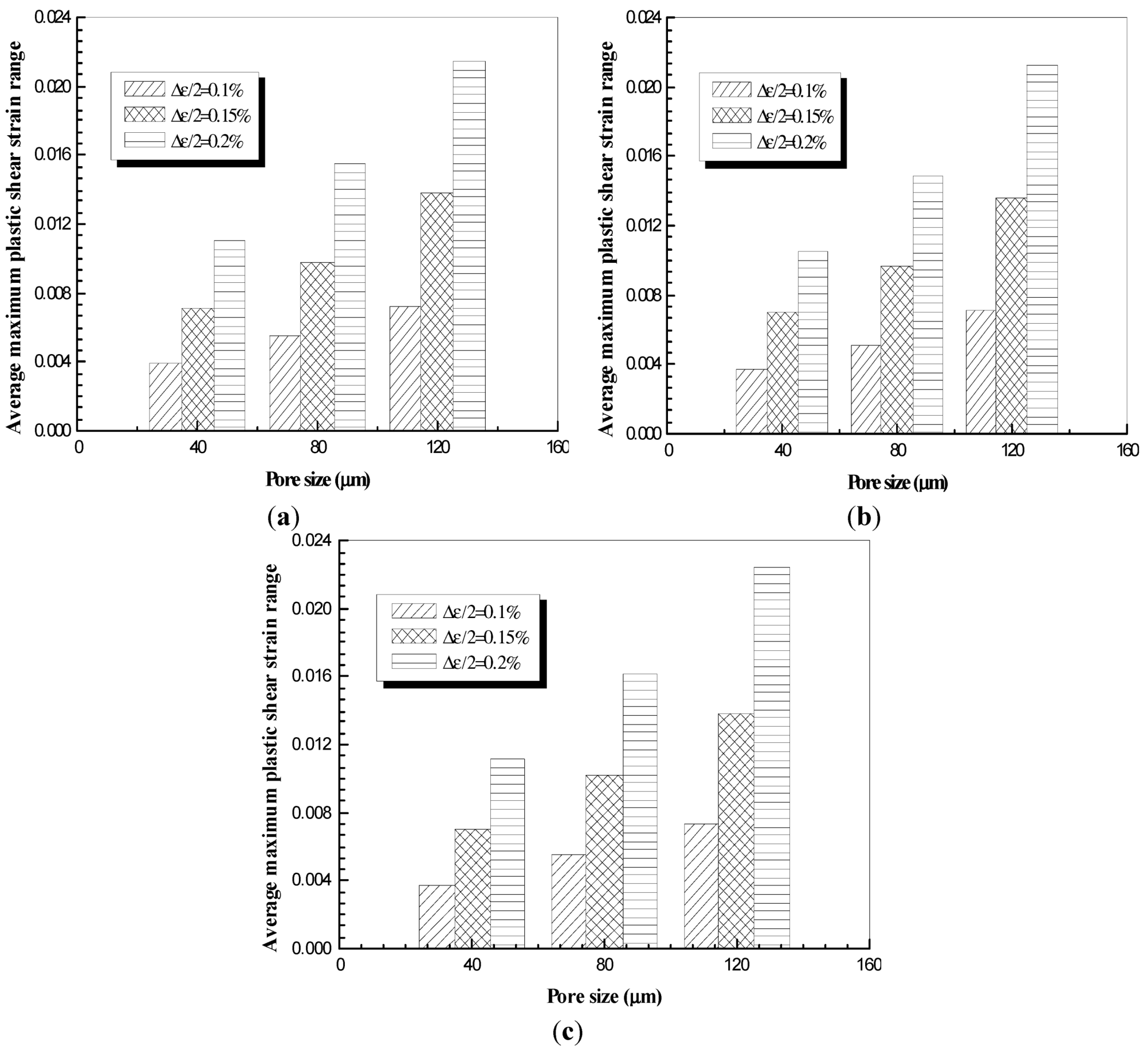
The influence of pore size on the local average maximum shear strain after ten cycles of fatigue strain loading with different strain ratios is depicted in
Figure 18. It should be mentioned that three loading strain amplitudes of ∆ε/2 = 0.1%, 0.15% and 0.2%, and three pore sizes of 40 μm, 80 μm and 120 μm, were investigated. The pore spacing was consistent and equal to 560 μm. According to the results shown in
Figure 18, the driving force behind the crack initiation is highly dependent on the pore size, such that the average maximum shear strain increases when the plate is hosting larger pores. Additionally, the sensitivity is higher at higher strain amplitude.
Figure 18.
Pore size effect the average maximum shear under the loading ratio of (
a)
R = 0.5; (
b)
R = 0; and (
c)
R = −1 [
7].
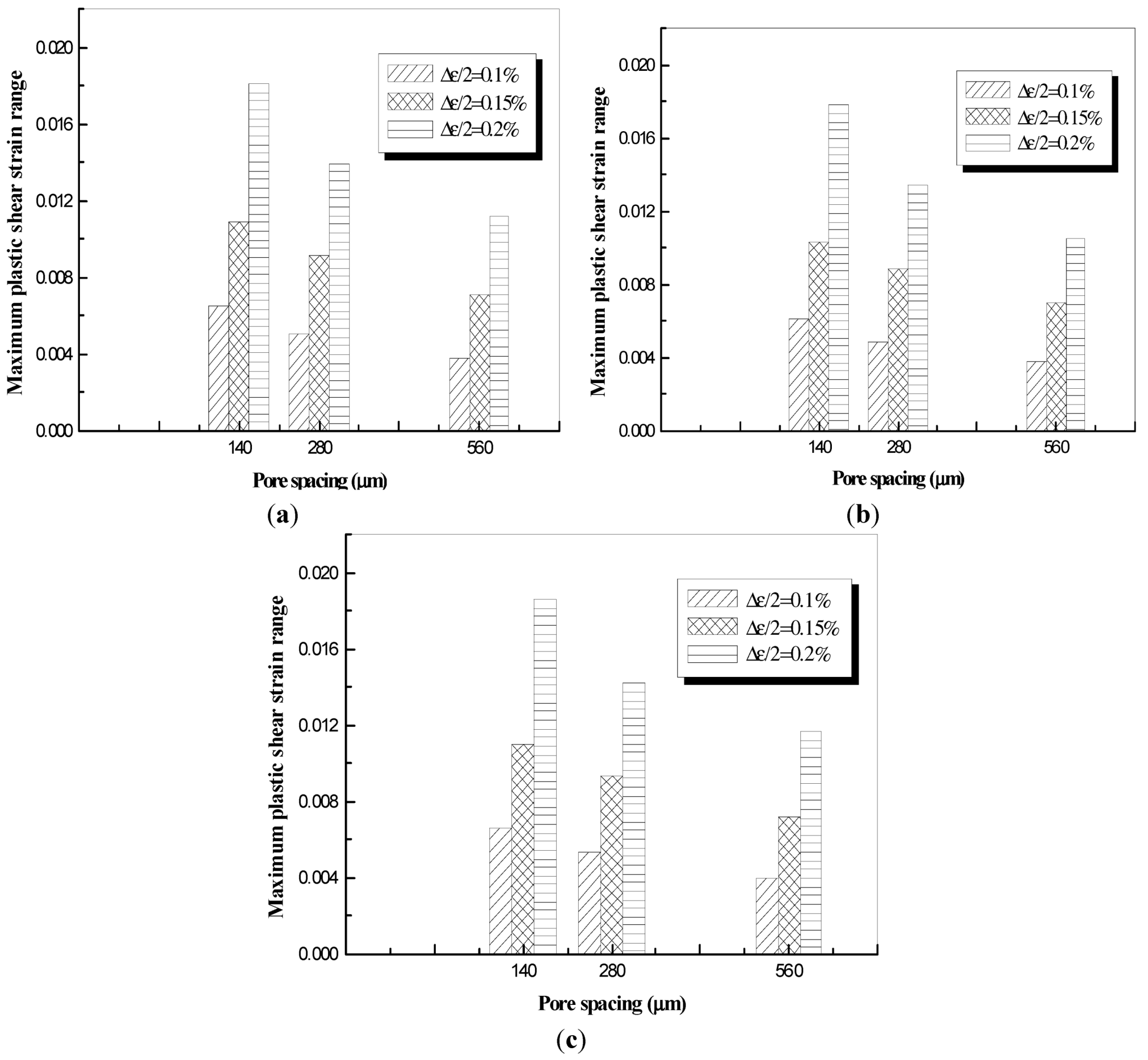
The influence of pores spacing (three different spacings of 140 μm, 280 μm and 560 μm for a uniform pore size of 40 μm in this study) on the average maximum shear strain is shown in
Figure 19. The Figure shows that the average maximum shear strain will decrease when the pores are at a larger distance from one another. These results justify the shorter fatigue life in specimen 42-26, which contains two small casting pores within a very close distance.
Figure 19.
Pore spacing effect on the average maximum shear strain under the loading ratio of (
a)
R = 0.5; (
b)
R = 0; and (
c)
R = −1 [
7].
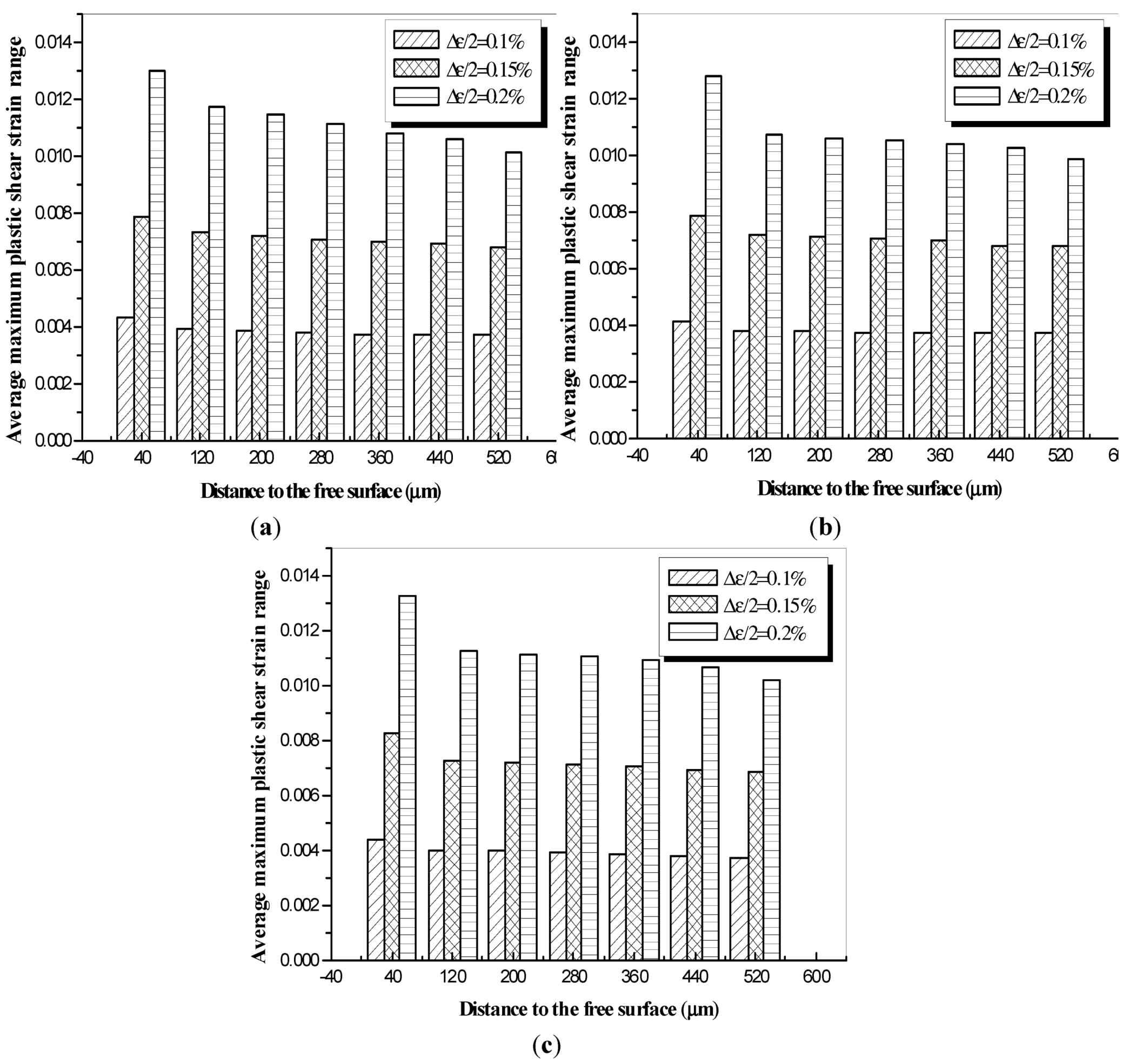
The other important factor considered, which was postulated to have a significant effect on crack initiation, was the distance of the pores from the free surface. This effect was studied, and the results are summarized in
Figure 20. A greater average maximum shear strain can be observed for the casting pores which were closer to the free surface. Moreover, in the case of the higher strain range (∆ε = 0.2%), results indicate that the free surface would have larger influence on the crack initiation.
Figure 20.
The effect of pores distance from free surface on the average maximum shear strain under the loading ratio of (
a)
R = 0.5; (
b)
R = 0; and (
c)
R = −1 [
7].
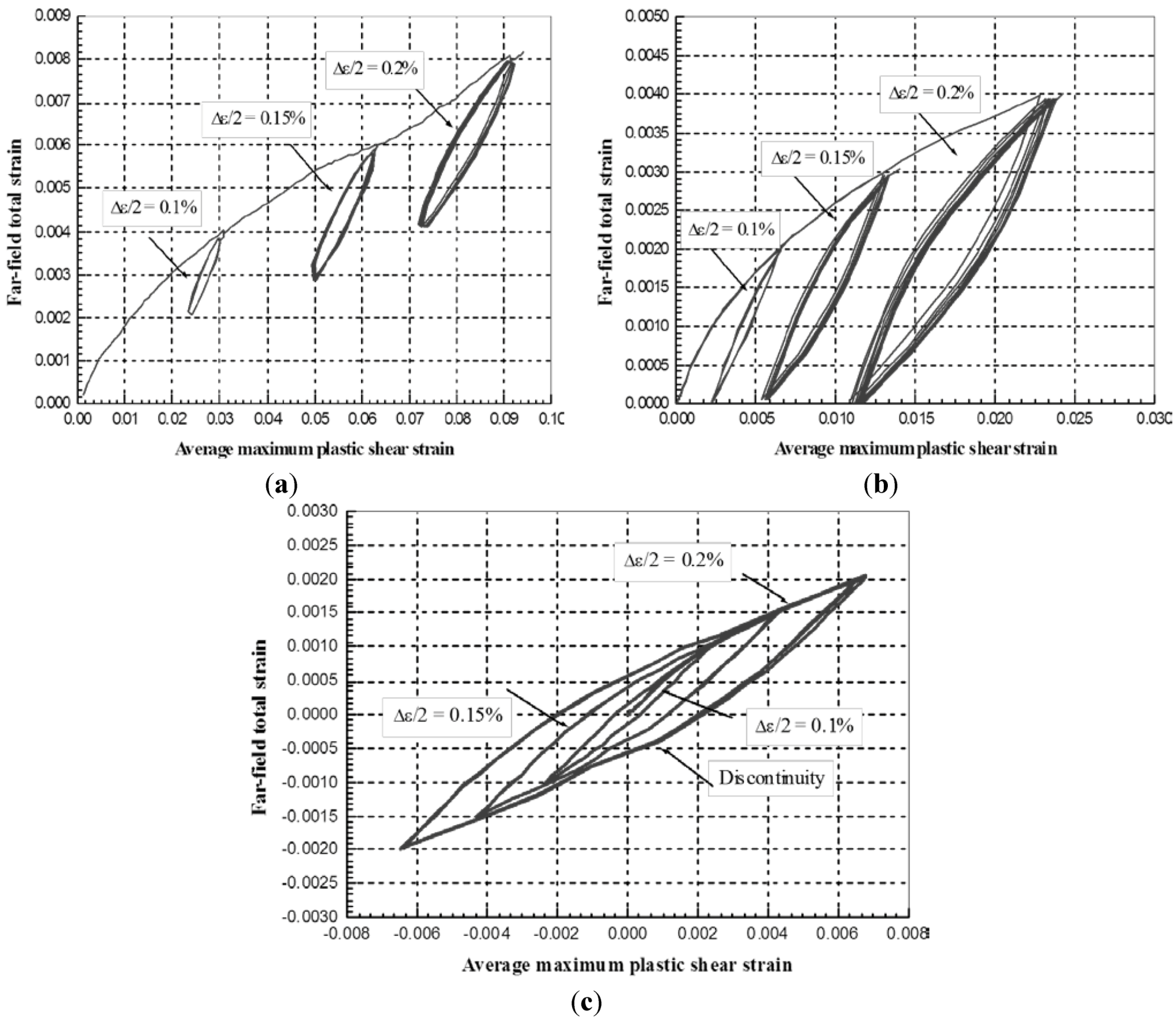
In order to illustrate the effect of the pore’s shape on crack initiation, the far field total strain is plotted against the average maximum shear strain range for two different pore’s shapes, as depicted in
Figure 21 and
Figure 22. The results are for the idealized circular and awkward star-shaped pores, respectively. It is believed that the width of the hysteresis loop is proportional to the magnitude of the driving force causing crack initiation. Since the awkward star shape pore has a wider hysteresis loop, it was concluded that the irregular shape of pore would have a beneficial effect on fatigue crack initiation since it produce larger driving force for crack initiation.
Figure 21.
Hysteresis loop for idealized pore shape under the loading ratio of (
a)
R = 0.5; (
b)
R = 0; and (
c)
R = −1 [
7].
Lu
et al. [
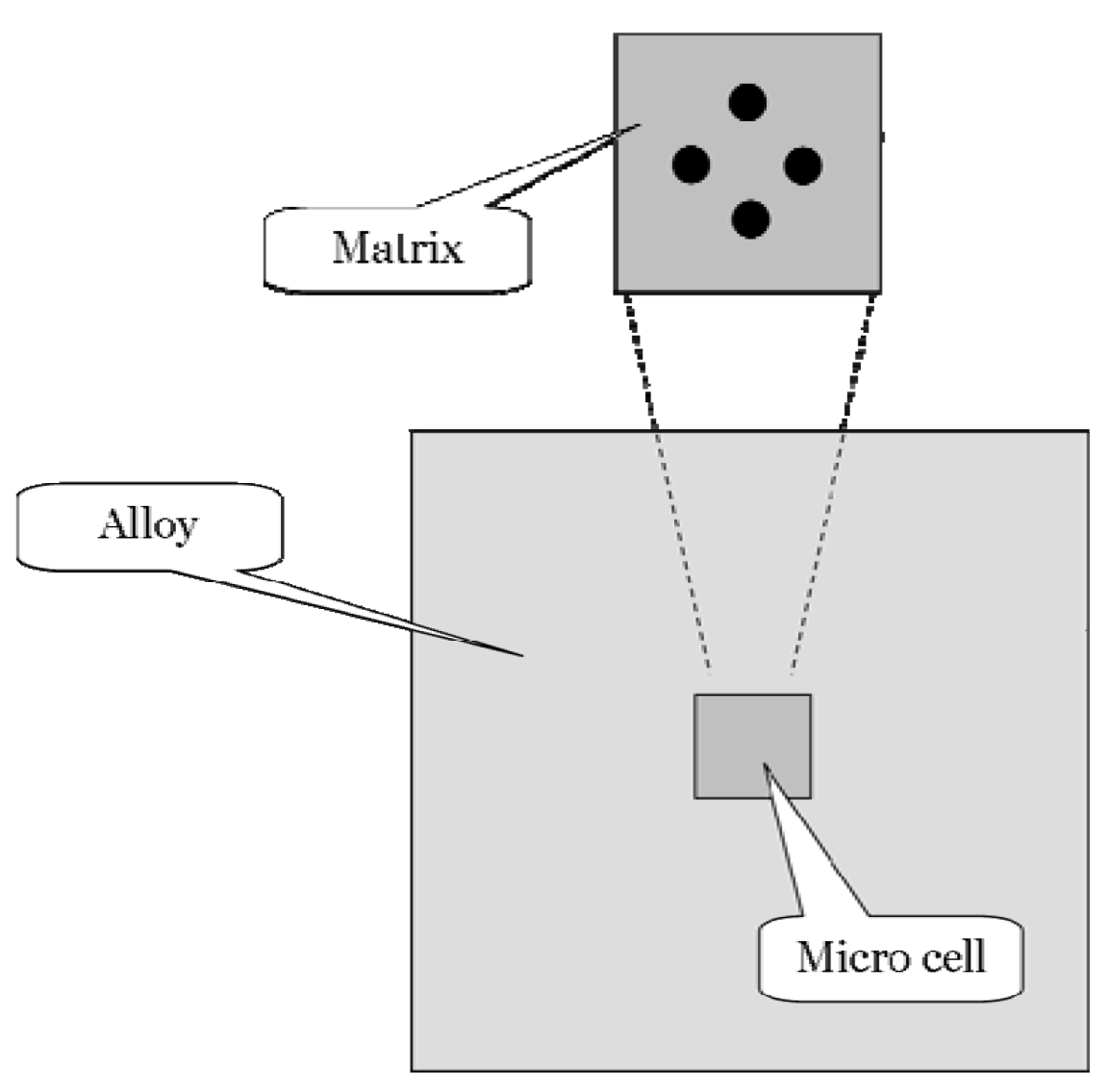
13] continued their investigation and examined the influence of casting features on fracture and debonding of β-phase particles under high cycle fatigue loading. A micro-cell finite element was developed and employed in that study. Configuration of a micro-cell considered in their investigation is shown in
Figure 23, which contains two different regions: the alloy region and a cell region containing the casting feature. As can be seen, the cell region has four Mg
17Al
12 in α-Mg matrix environment.
Figure 22.
Hysteresis loop for awkward star pore shape under the loading ratio of (
a)
R = 0.5; (
b)
R = 0; and (
c)
R = −1 [
7].
Figure 23.
Schematic configuration of a micro-cell [
13].
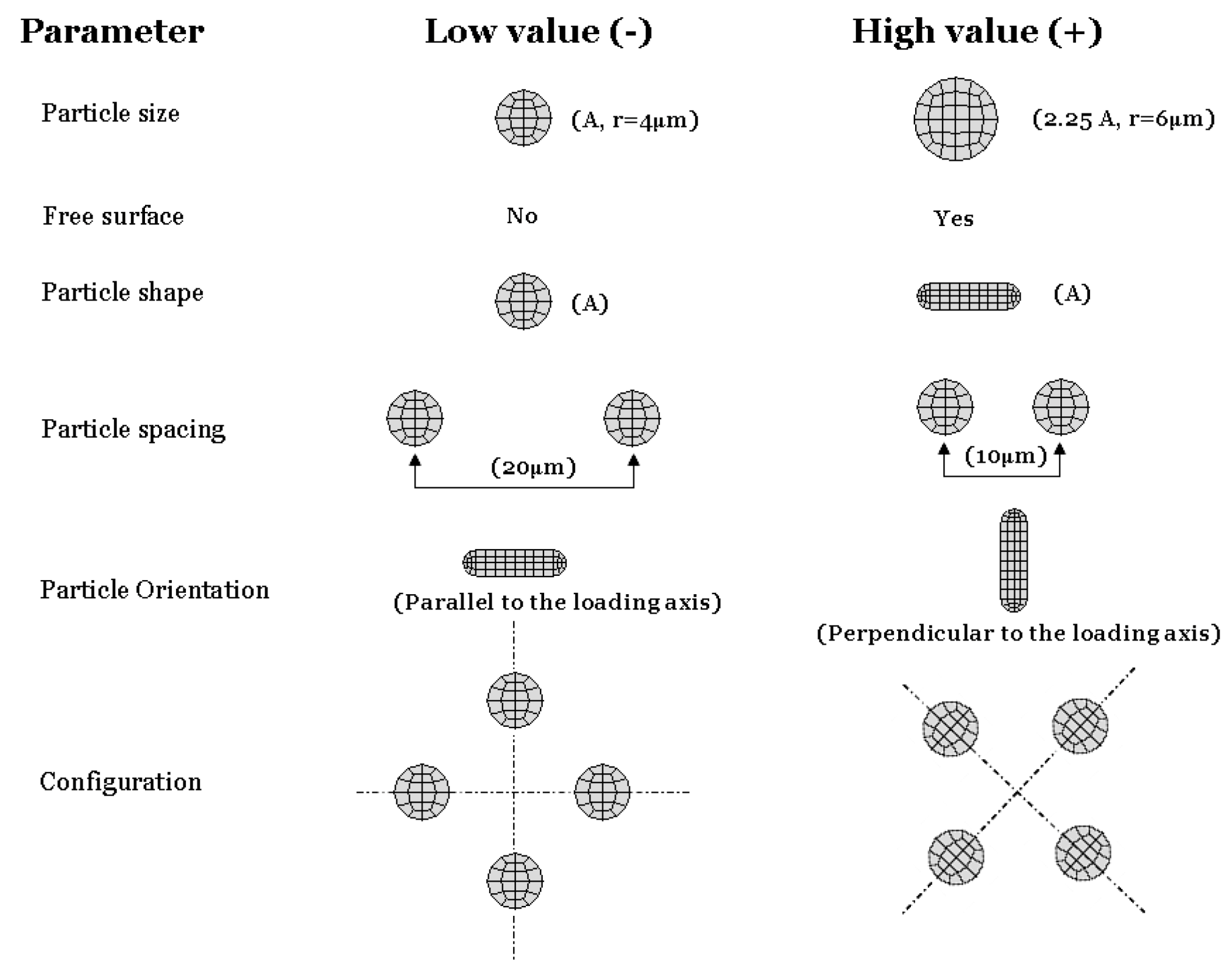
Several casting parameters (particle size, shape, orientation, spacing, distance from free surface and cluster configuration), which are schematically shown in
Figure 24 were also considered. A two level design of experiment (DOE) approach was used to analyze the influence of each feature. Particles were assumed to have been either pre-fractured or pre-debonded in some of the models, using the “seam” command in the ABAQUS software. Assigning the seam on the boundary of the particles produces the pre-debonding situation, while assigning it to the center of a particle would simulate a pre-fractured condition.
Figure 24.
Casting parameters employed in this study [
13].
Gall
et al. [
14] reported Needelman’s postulation [
15,
16] in that the maximum hydrostatic stress would be the driving force for debonding the particles, and the maximum principal stress would be responsible for the fracture of the particles. The casting pore’s influence on these two stress components was carefully considered by Lu
et al. [
13] as discussed in below.
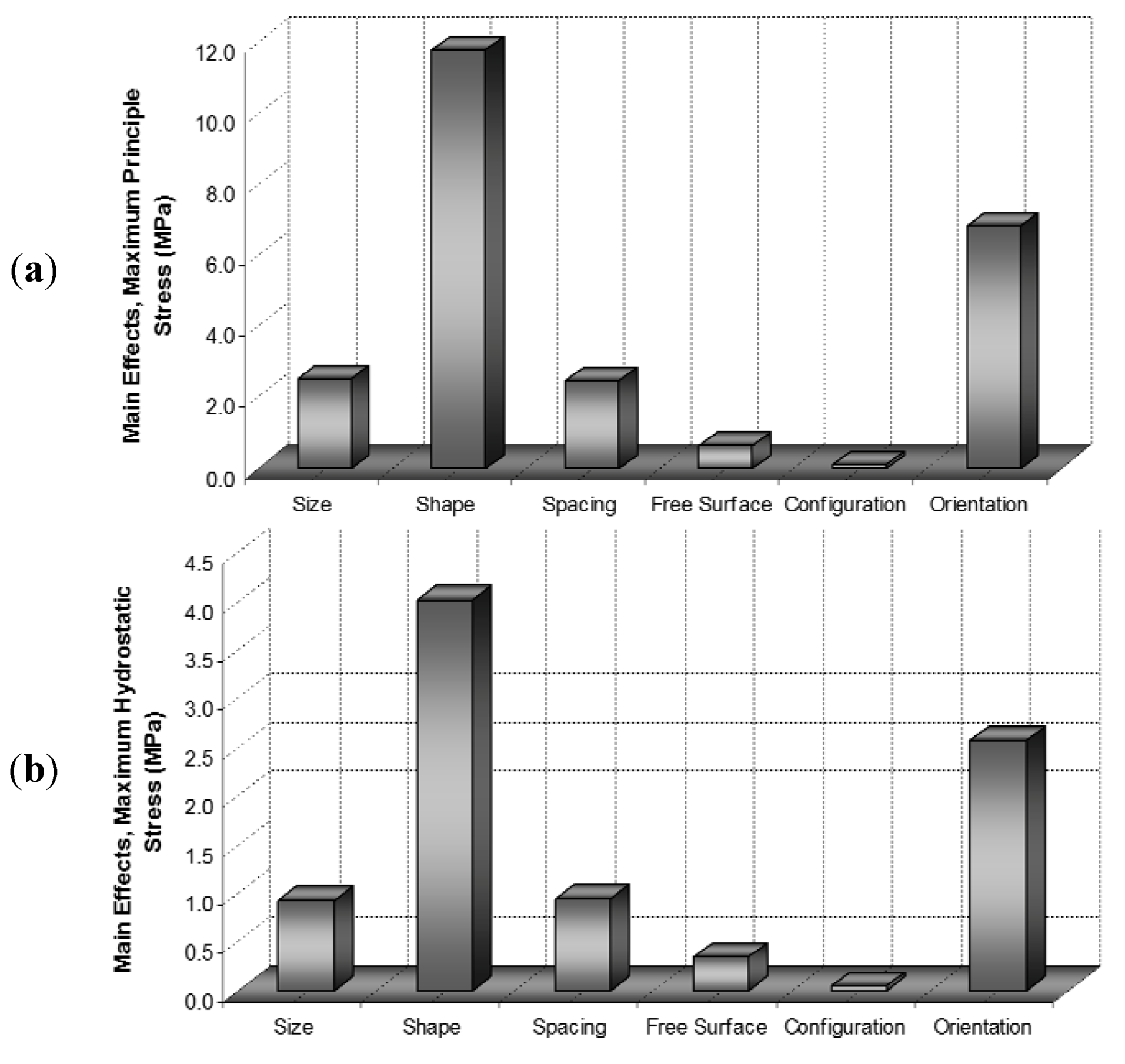
The numerical results of the case in which all of the particles were assumed to have been fully bonded to the α-Mg matrix are summarized in
Figure 25. The results reveal that when the particles have no damage, their shape and orientation are the dominant features that control the fracture and debonding of the particles.
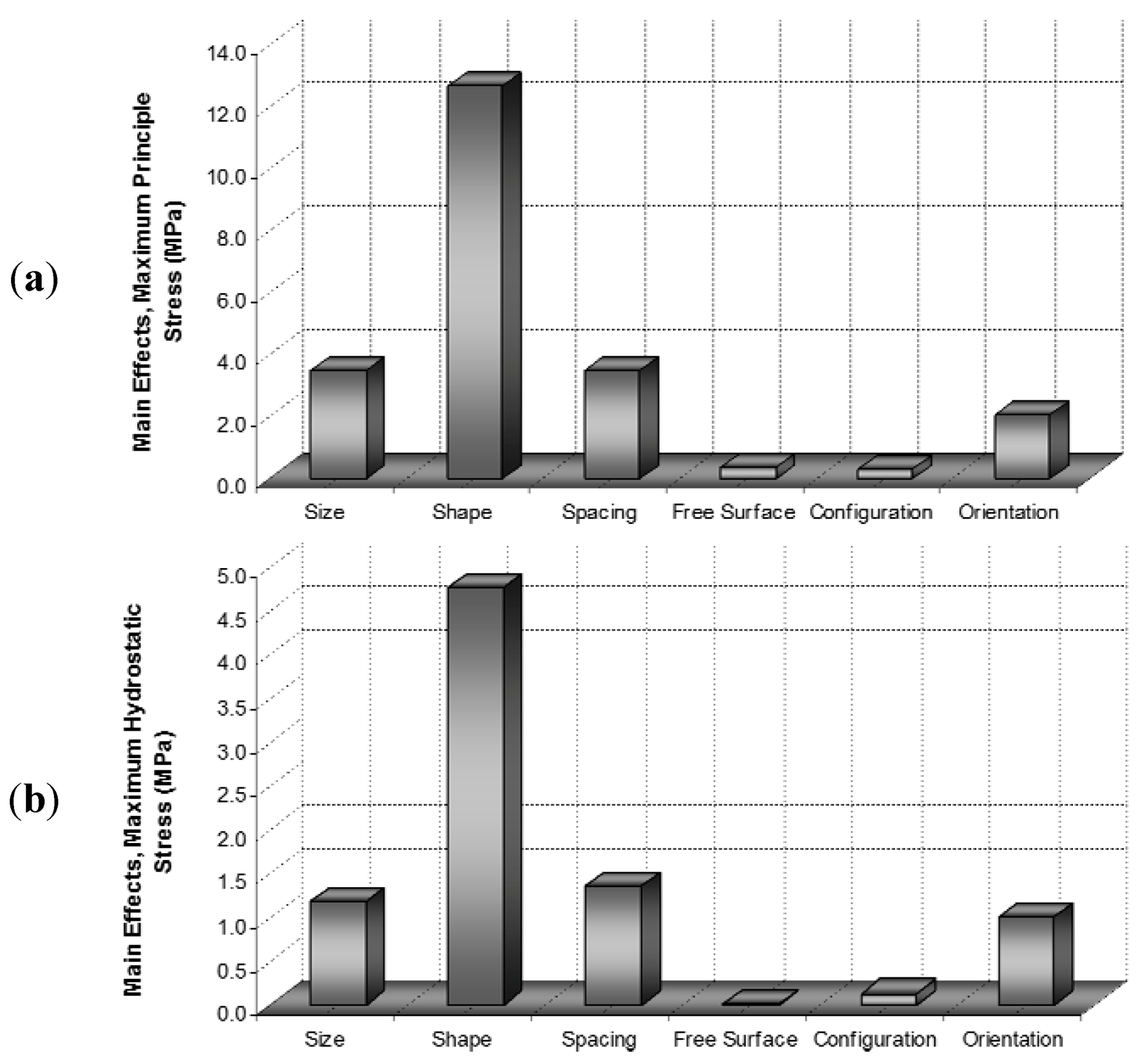
The influence of the casting defects on the stress component, when half of the particles were assumed to have been pre-fractured or pre-debonded, is shown in
Figure 26 and
Figure 27 respectively. In both cases, as seen, the effect of particles’ configuration is vanished, while the shape of the particles exhibits its own significant role. The results depicted in
Figure 27 show that the distance between the defects will produce a large effect on the maximum principal and hydrostatic stress when half of the particles were assumed to be pre-debonded.
Figure 25.
The influence of casting parameters on (
a) Maximum principal stress; (
b) Maximum hydrostatic stress (all the particles are fully bonded to the matrix) [
13].
Figure 26.
The influence of casting parameters on (
a) Maximum principal stress; (
b) Maximum hydrostatic stress (half of the particles are pre-fractured) [
13].
Figure 27.
The influence of casting parameters on (
a) Maximum principal stress; (
b) Maximum hydrostatic stress (half of the particles are pre-debonded) [
13].
3. The Influence of Environment (Temperature) on Fatigue Response of AM60B
The influence of temperature on the fatigue life of AM60B was studied by Nour Hossain and Taheri [
16,
17]. A series of fatigue tests were carried out in different scenarios,
i.e., room, elevated and cold temperatures.
The experimental investigation was initiated by conducting a monotonic tensile test to establish the material properties; yield strength of 145 MPa and a maximum elongation of 6.6% were observed.
3.1. Fatigue Behaviour at Elevated Temperature
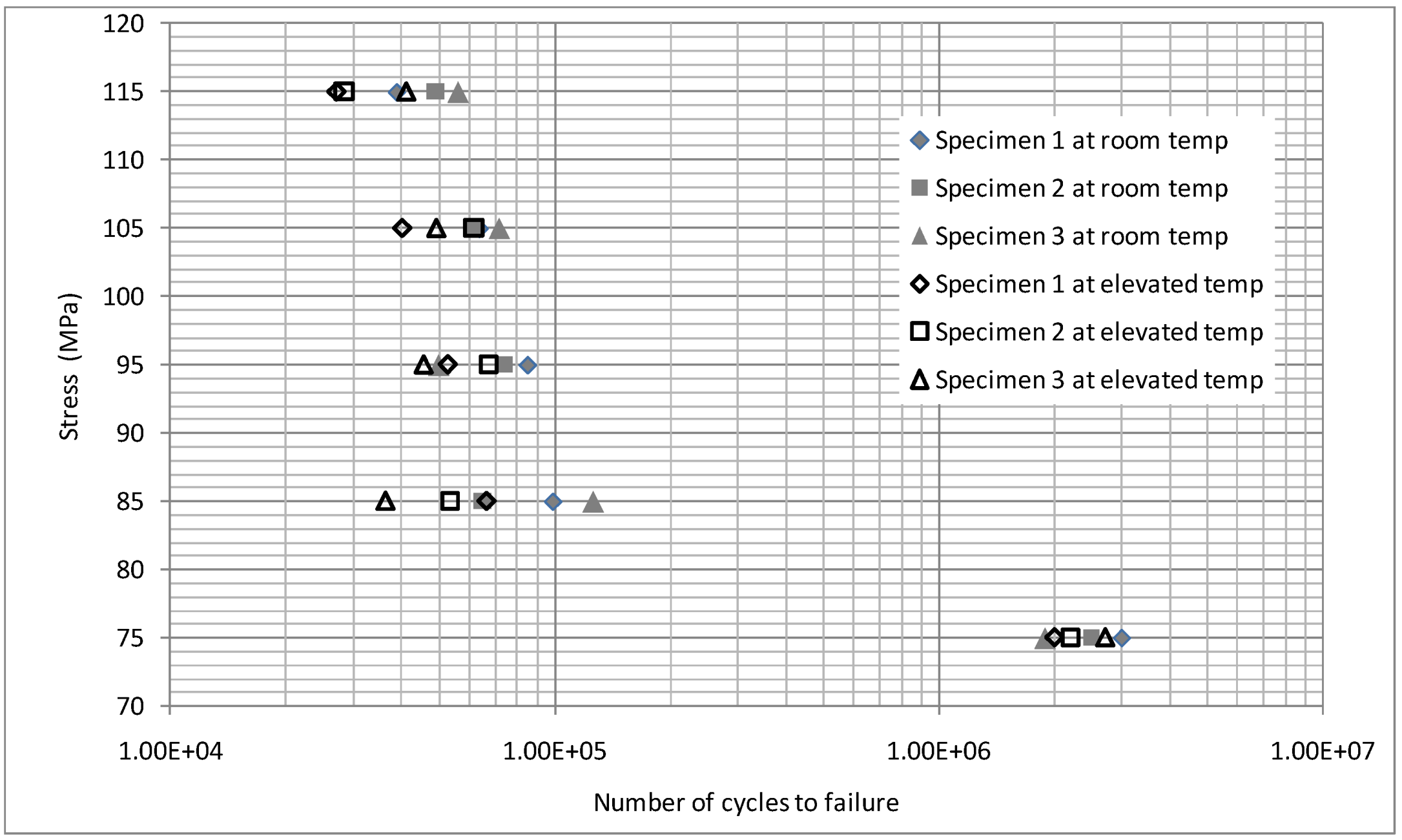
Dog-bone shaped specimens were subjected to cyclic loading at an elevated temperature of 80 °C and at room temperature, with the results shown in
Figure 28. The stress ratio was set constant at
R = 0.1, but with the consideration of various maximum stress amplitudes, ranging from 75 MPa to 115 MPa with 10 MPa increment. The results show that the run-out (fatigue life greater than 10
6 cycles) would happen at the maximum stress level of 75 MPa for both room and elevated temperatures. The graph in
Figure 28 shows that the influence of an elevated temperature on the fatigue life is not very significant; however, the alloy tends to have a shorter fatigue life at higher temperature in general. Moreover, these results indicate that there could be a threshold stress, above which, the elevated temperature would exert an insignificant influence of fatigue life of the alloy; however, below this stress level the effect would be significant.
Figure 28.
Fatigue life results at room and elevated temperature [
17].
3.2. Fatigue Behaviour at Cold Temperature
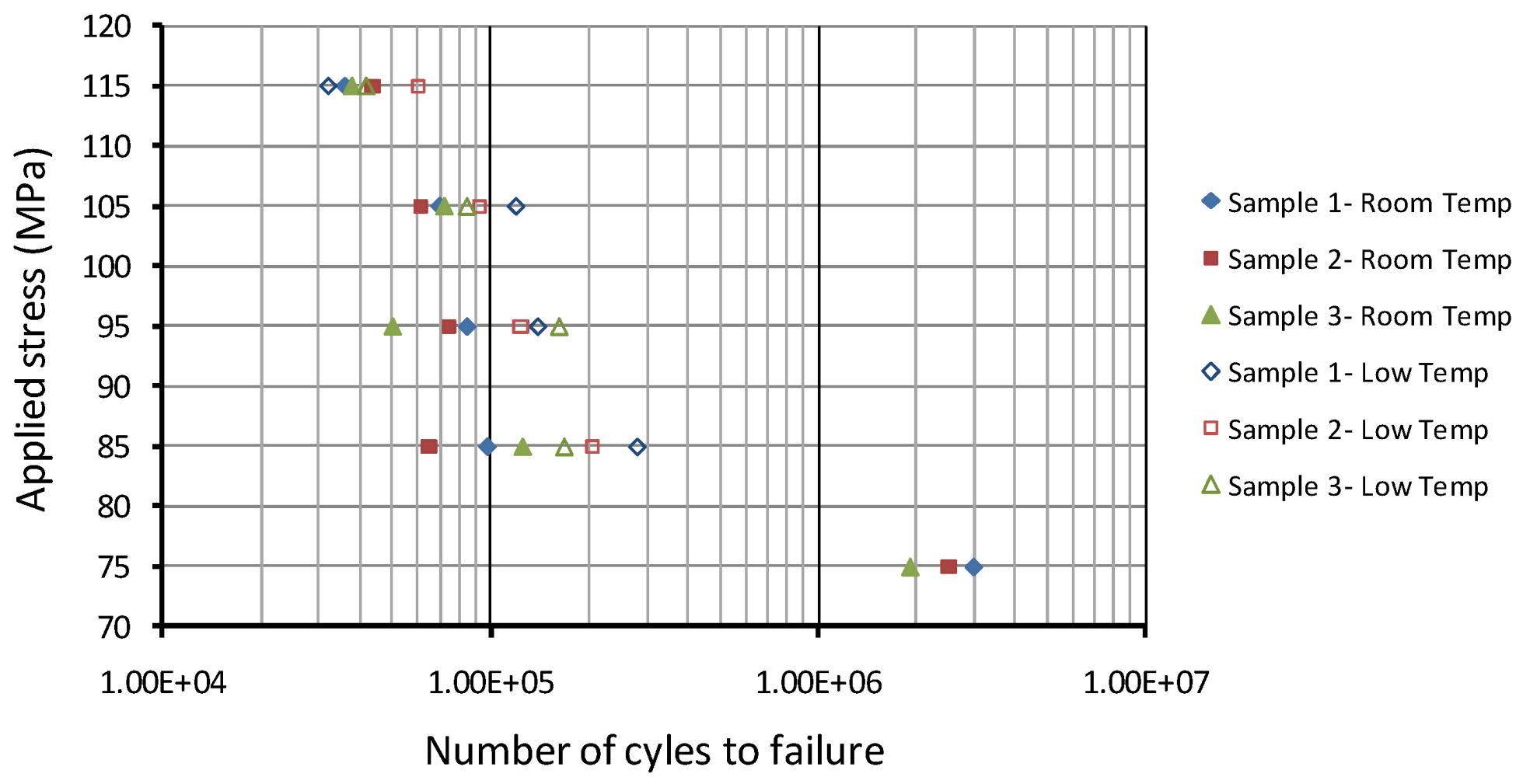
The experimental fatigue tests results at low (−40 °C) and room temperatures are summarized in
Figure 29. According to these results, low (subfreezing) temperature results in a longer fatigue life of the alloy. Again, the run-out fatigue life was observed at a stress level of 75 MPa and the threshold stress level has been observed similar to the results that obtained from an elevated temperature. On the other hand, a higher increase in fatigue life was observed at a stress level of 85 MPa and at other higher levels of stress lower and somewhat consistent influence was observed under cold temperature.
Figure 29.
Fatigue life results at room and cold temperature [
18].
4. Fatigue Crack Growth in AM60B
In general, crack propagation in a metal may be characterized by three regions. In the first region, the crack propagates very slowly and includes a threshold limit. In the second region, the FCGR follows a linear variation with respect to the stress intensity range in a logarithmic scale. The third region deals with fast crack propagation. Several models have been presented to describe the FCGR behavior of materials. Among them, the Paris [
19] model is the best known, and extensively utilized by researchers. The model predicts the FCGR with the following equation:
where d
a/d
N and ∆
K are the fatigue crack growth rate and stress intensity rang respectively;
Cp and
mp are the Paris model coefficient. It should be noted that the Paris model does not consider the stress ratio effect; therefore, its coefficients should be established for each stress ratio. Walker [
20] proposed a model for predicting the FCGR also capable of accounting for different stress ratios (R) by including a new parameter, γ
w.
The effect of stress ratio on FCGR has been investigated by other researchers (e.g., [
21,
22,
23,
24,
25]) and different driving forces have been identified for FCGR. As stated earlier, the study on FCGR of AM60B in our research group was initiated by Nur Hossain and Taheri [
17]. That study investigated the growth rate of an edge crack subjected to a cyclic loading with three different stress ratios of
R = 0, 0.1 and 0.2 and observed that the Walker model with the γ
w = 0.5 could result in good prediction of the experimentally observed FCGR. That work was continued in a separate study [
26], by considering a wider range of stress ratios. The influence of the negative and positive stress ratios was considered and an FCGR model was proposed for a wide range of stress ratios.
4.1. The Influence of Stress Ratio on FCGR of the Alloy
Plates containing a center crack were cyclically loaded under the stress ratios of
R = −1, −0.8, −0.6, −0.3, 0, 0.25, 0.5 and 0.75 and maximum stress of 55 MPa. The crack length was measured using a digital microscope and recorded after a certain number of cycles. The test setup and a typical image of the crack are shown in
Figure 30 and
Figure 31.
Figure 30.
Fatigue test setup [
26].
Figure 31.
A typical image of a sharp crack [
26].
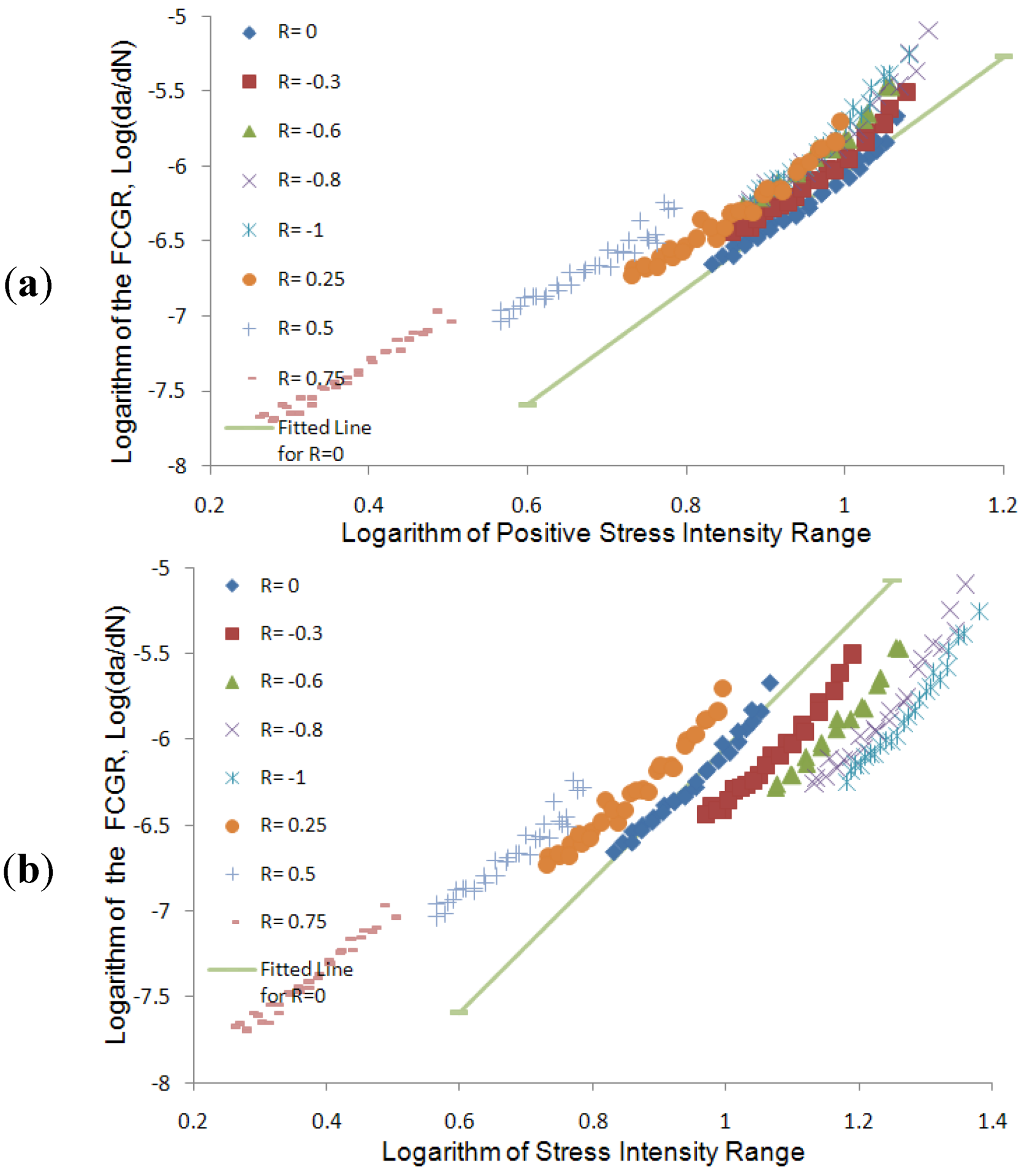
4.2. Experimental Results and Discussion
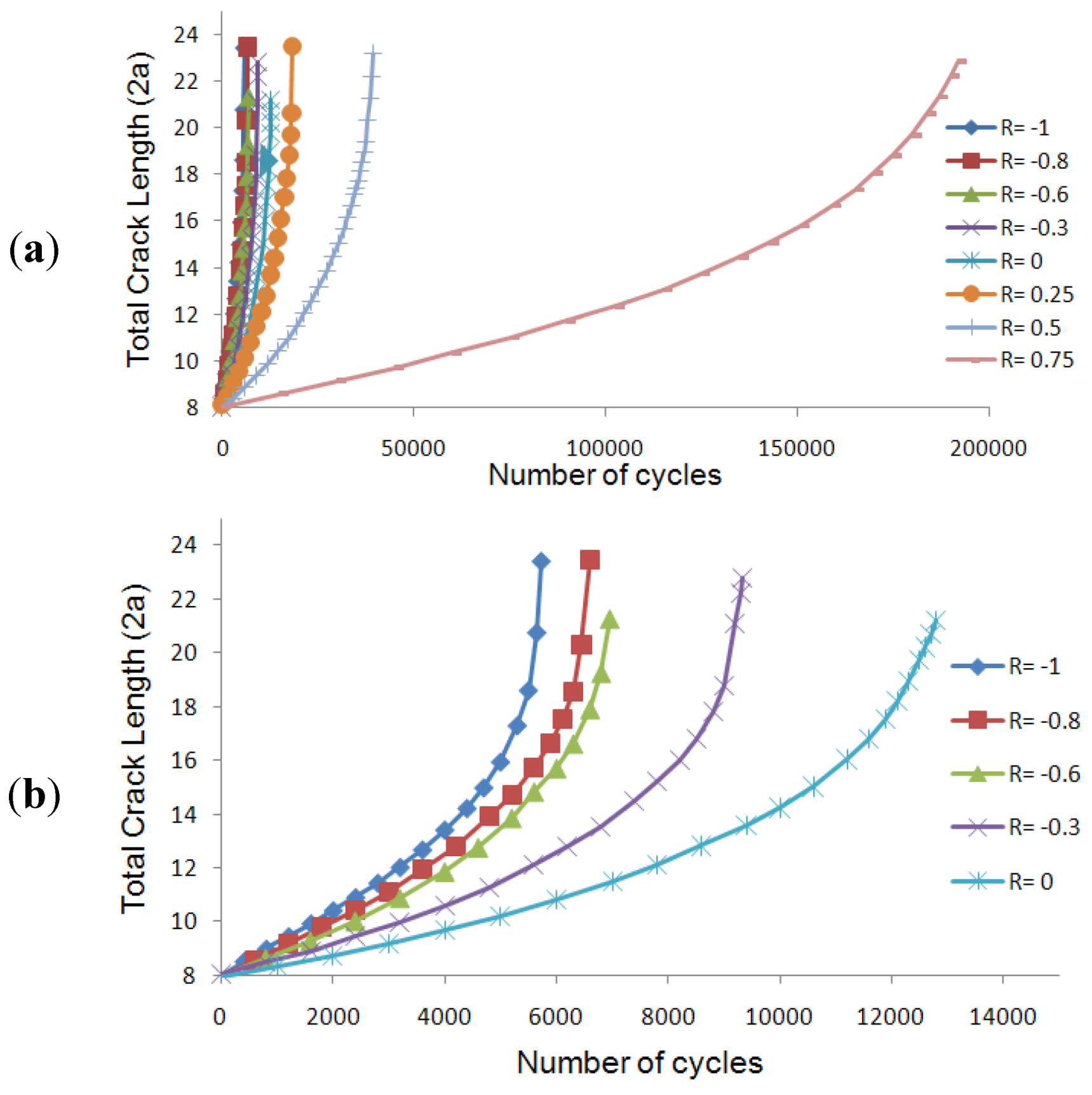
The crack length versus the number of cycles is shown in
Figure 32a for the whole range of stress ratios. The results for the negative part is magnified and depicted in a separate graph as shown in
Figure 32b.
The results illustrated in
Figure 32b indicate that the negative stress ratios or (compressive cycles) have a significant effect on crack propagation in AM60B. Ironically, some standards (e.g., [
27]) suggest the dismissal of the compressive stress cycles when calculating the FCGR.
Figure 32.
Crack length versus the number of cycles for (
a) the whole stress ratios; and (
b) negative stress ratios [
26].
4.3. A Verified FCGR Models
The experimental data is presented using the Paris and Walker models, as illustrated in
Figure 33 and
Figure 34.
Figure 33a presents the Paris model’s fit of the data considering only the positive stress intensity range (that is, the compressive portion is dismissed), while
Figure 33b shows the Paris model based on the consideration of the entire stress intensity range (
i.e., both tensile and compressive cycles), both presented in logarithmic scale. The results indicate that decreasing the stress ratio results in shift of the data points to the right. On the contrary, presenting the data versus the positive stress intensity range results in reverse behavior (shifting to the left) for the negative stress ratios. These results clearly indicate that, in order to represent the trend in FCGR with respect to the stress intensity range in a more consistent manner, one should consider the entire stress intensity range, instead of considering only the positive part of the stress intensity range.
Figure 33.
Experimental data presented by the Paris model versus (
a) positive stress intensity range; and (
b) the whole stress intensity range [
26].
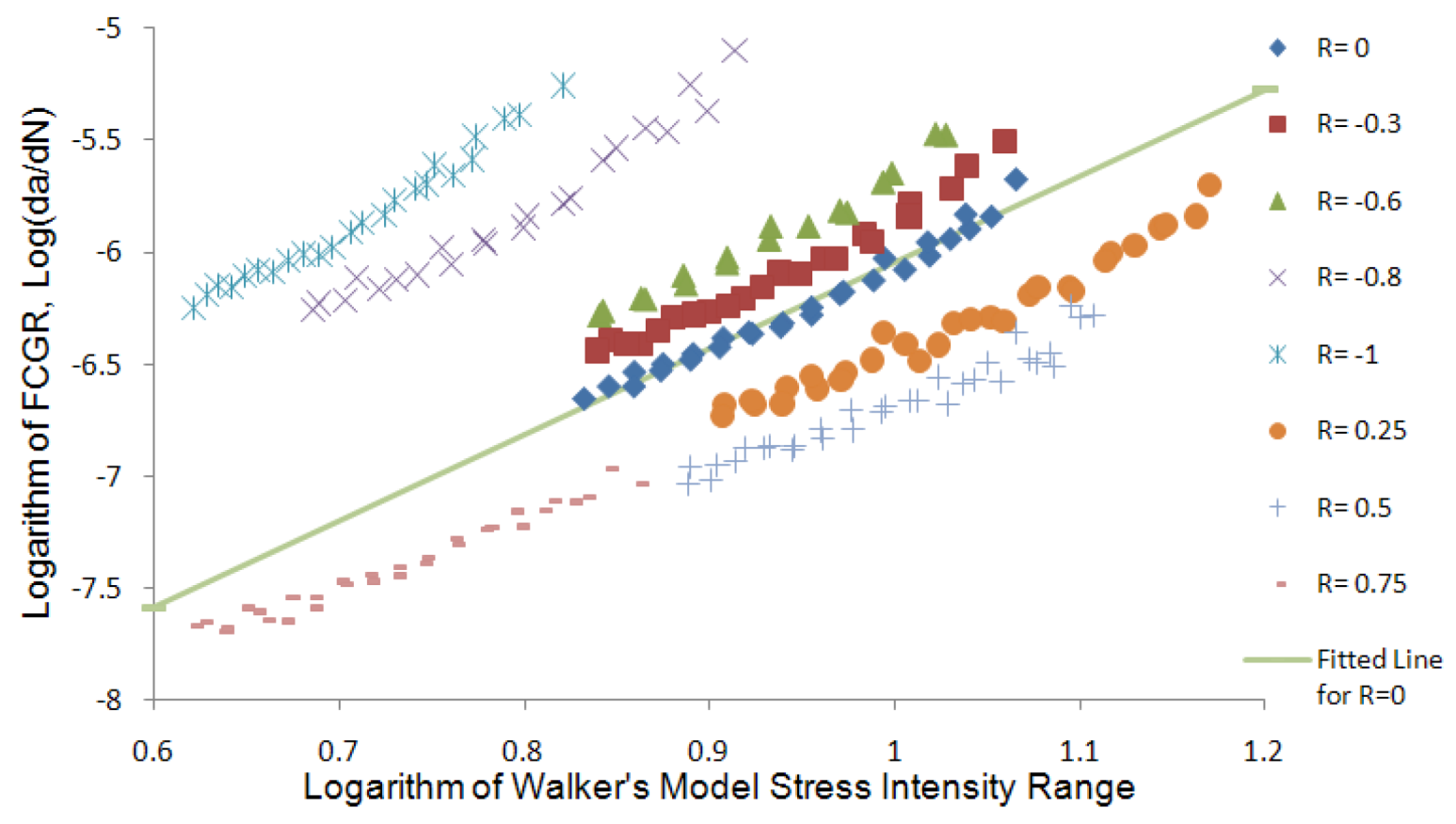
Figure 34.
Experimental data presented by the Walker model [
26].
As previously mentioned, it has been well accepted that the Walker model can effectively consider the influence of the stress ratio in a consistent manner. If that is true, it would be expected to see the plot of the FCGR data for different stress ratios on a straight line (or concentrated along a straight line). Unfortunately, the presentation of the data, as illustrated in
Figure 34, does not validate the accepted notion.
It should be noted that there are two methods for establishing the value of γ
w used in the Walker model; both methods are based on the fact that the slope (
mp), of the FCGR lines, when plotted in the logarithmic scale, would be constant for all stress ratio values, while the slopes of the FCGR of AM60B are found to be variable (
i.e., between 3 and 5), which is a relatively large band considering the fact that the values were plotted in the logarithmic scale. As seen in
Figure 34, the Walker model cannot condense the data on a single line; thus, it is not capable of accounting for the influence of stress ratios.
4.4. Proposed Model
Based on the above-mentioned observation and finding the shortfall of Walker model, the following FCGR relation is proposed to overcome the Walker model’s shortfall:
where
where
Cw and
mw are the Paris model coefficients for
R = 0 (calculated to be 1.22603 × 10
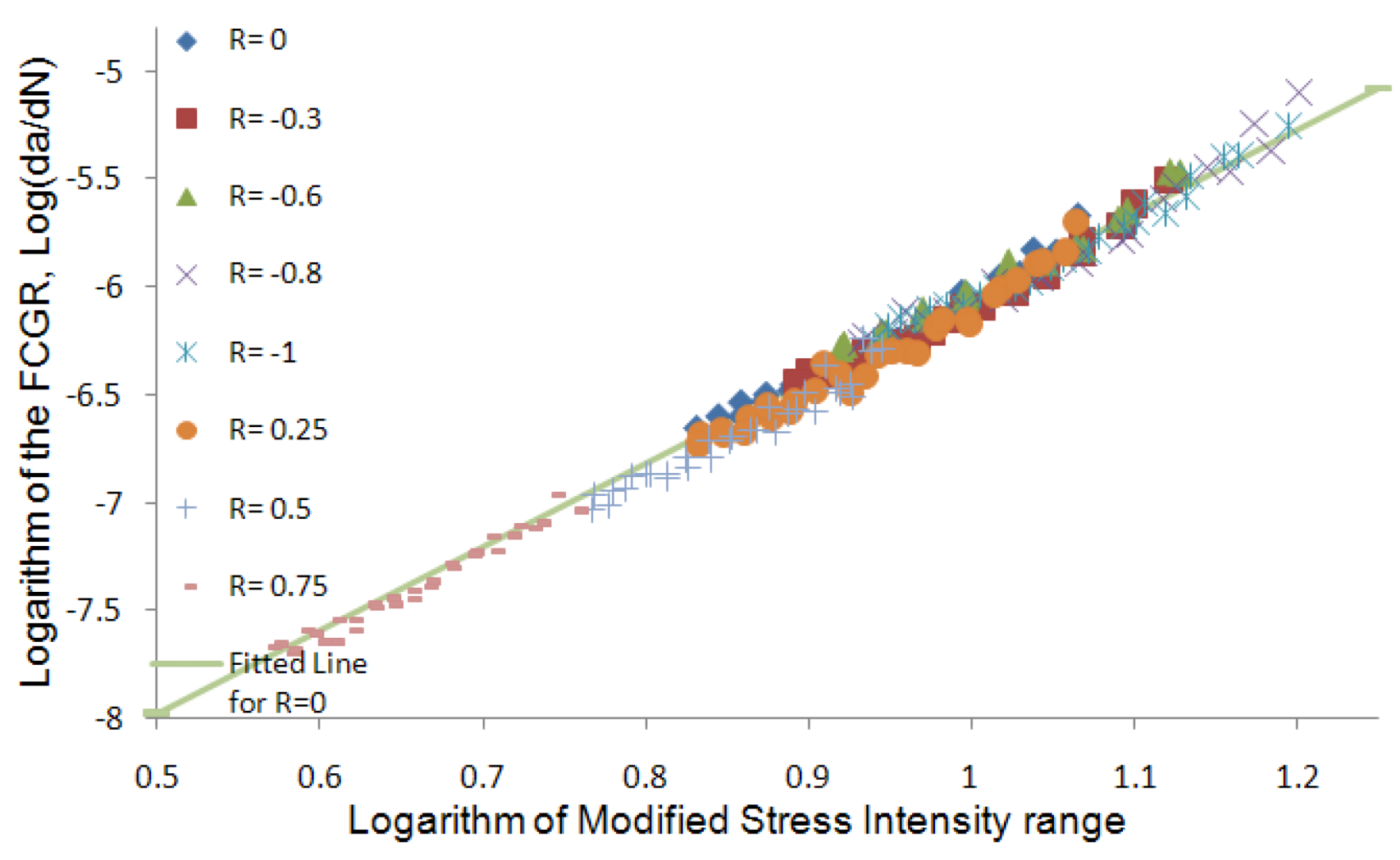
−10 and 3.8666, respectively, for this alloy). The fit of the experimental data based on the proposed model is presented in
Figure 35. As seen, the model is much more powerful than the Paris and Walker models in considering the stress ratios’ effect.
Figure 35.
Experimental data presented by the proposed model [
26].
4.5. Further Investigation of the Influence of Compressive Loading Cycles on FCG under Constant and Random Amplitude Loading
As stated in the last section, the influence of compressive stress cycles is customarily dismissed when estimating fatigue life of a material based on the suggestion noted in some standards and guidelines (e.g., [
27]). This suggestion has been made based on the notion that under the compressive portion of a loading cycle, the crack would be closed, and thus, it would not propagate. As shown in the experimental results presented in part 4.2, the compressive loading could have a significant effect on the fatigue life of the specimens. A similar investigation was conducted on center-cracked plate specimens subjected to random amplitude loading scenarios, hosting different contribution of the compressive portion of the loading. In other words, the amplitude of the compressive portion of the random loading was scaled with several scaling factor (Compressive loading contribution (CLC) = 30%, 60%, 80% and 100%). A typical graph of the random amplitude loading is shown in
Figure 36.
Figure 36.
Random amplitude loading.
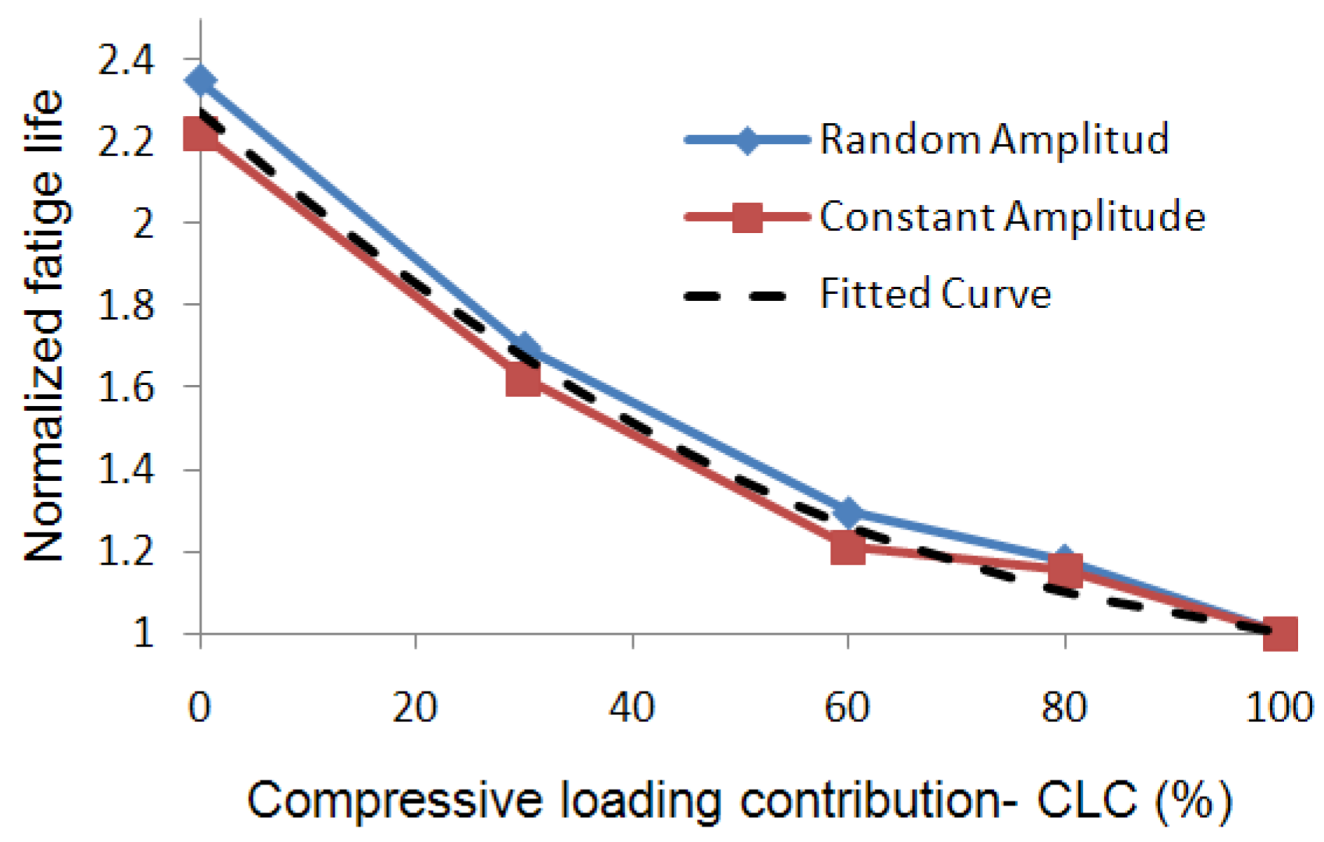
The fatigue life of the specimen under cyclic loadings with different CLCs were recorded and are presented in
Figure 37 for both random and constant amplitude loading. It should be mentioned that the results are normalized to the shortest fatigue life (
i.e., when CLC = 100%).
Figure 37.
Normalized fatigue life versus Compressive loading contribution (CLC).
The results shown in
Figure 37 confirm the considerable influence of compressive loading cycles on the material’s fatigue life reduction, and that has the same trend for both constant and random amplitude loading.
As briefly alluded earlier, some standards [
27] suggest to completely dismiss the compressive cycles when calculating the fatigue life of a material, while some others (e.g., [
28]) advise to consider only 60% of the magnitude of the compressive loading portion of cyclic loading scenarios.
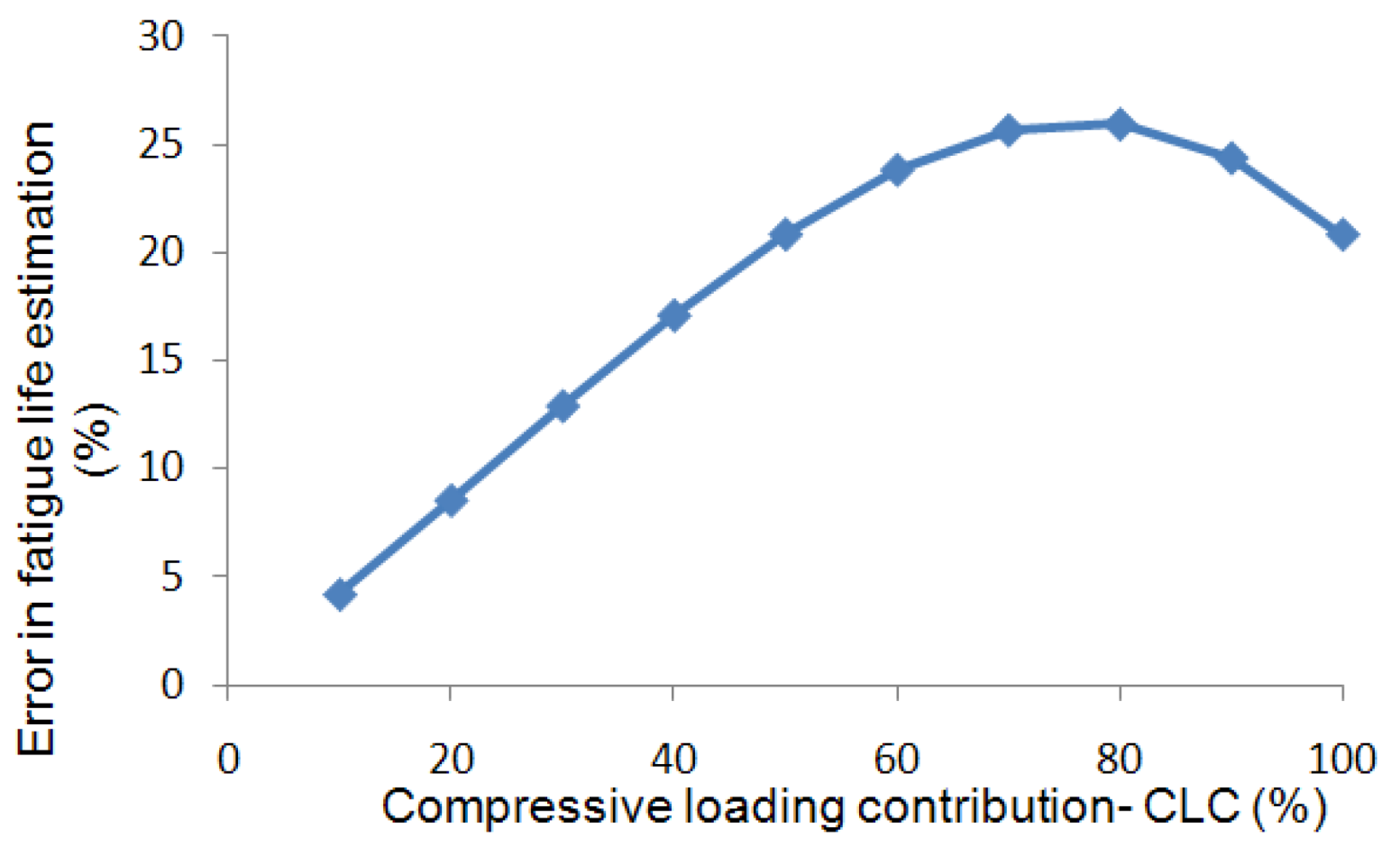
Figure 38 shows the margin of error in fatigue life calculation when one considers the API standard’s suggestion (which at least suggests the inclusion of the 60% of the compressive load cycles).
Figure 38.
Fatigue life calculation’s error as a function of CLC.
As can be seen in
Figure 38, dismissing the 40% margin of the compressive portion of the cyclic loading would result in a maximum error of 25% in the estimated fatigue life and the margin of error would vary as a function of the compressive loading contribution.
5. Conclusions
The microstructure of the casting AM60B alloy is shown to have a significant effect on the material’s monotonic and cyclic behavior. As a result of the casting process, the porosity is non-uniformly distributed in the alloy, and as such the alloy’s stress-strain behavior is considerably different from one region of a cast body to the next. Moreover, the yield strength of the AM60B changes when the loading direction is reversed (from tension to compression or vice versa). It is therefore postulated that the alloy develops a marked kinematic hardening when subjected to a cyclic loading.
Non-uniform solidification also causes variation in the mechanical properties of different layers of the alloy. The microstructure of the skin layer was shown to be significantly different from that of the core layer. Because of the difference in microstructure, these layers also showed different yield and ultimate strengths.
Fatigue testing conducted at a constant stress level on the specimens taken from different regions of the cast body exhibited wide and scatter range of response, thereby confirming the variability in material’s microstructures. SEM observation showed that the pore size, spacing and location are the main parameters that affect the fatigue life of the alloy. In addition, Weilbull’s linear distribution confirmed that the porosity is the most effective parameter affecting the performance of the alloy; this parameter overrides the other casting defects’ influence.
The influence of the β-phase particles was analyzed using the cell element in a finite element framework. Shape and orientation of these particles produced the largest influence on material’s failure when the particles were not pre-fractured or pre-debonded. When half of the particles were assumed to be pre-fractured, the shape of the particles became the main parameter that controlled alloy’s failure; on the other hand, when half of the particles were assumed to be pre-debonded, the shape and the spacing of the particles were observed to be the governing parameters.
Environmental changes affect the AM60B’s fatigue life. It has been shown that elevated temperatures degrade alloy’s fatigue life, while cold temperatures enhance alloy’s fatigue life. Additionally it is shown that, at certain stress levels, temperature exercises the greatest effect.
The fatigue crack growth rate of the alloy is highly dependent on the stress ratio of the applied cyclic loading. The conventional models (e.g., Paris and Walker models) could not predict the FCGR behavior of the material under different ratios with; therefore, a new model was proposed to overcome this shortfall. The compressive portion of a cyclic loading also has a significant effect on shortening the fatigue life of the alloy.