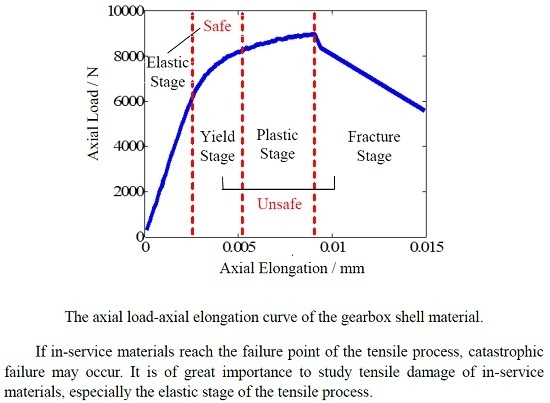
Study of the Tensile Damage of High-Strength Aluminum Alloy by Acoustic Emission
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Tensile Test
| Composition | Si | Mg | Ti | Sr |
|---|---|---|---|---|
| wt. % | 6.5~7.5 | 0.20~0.35 | 0.08~0.2 | 0.005~0.015 |
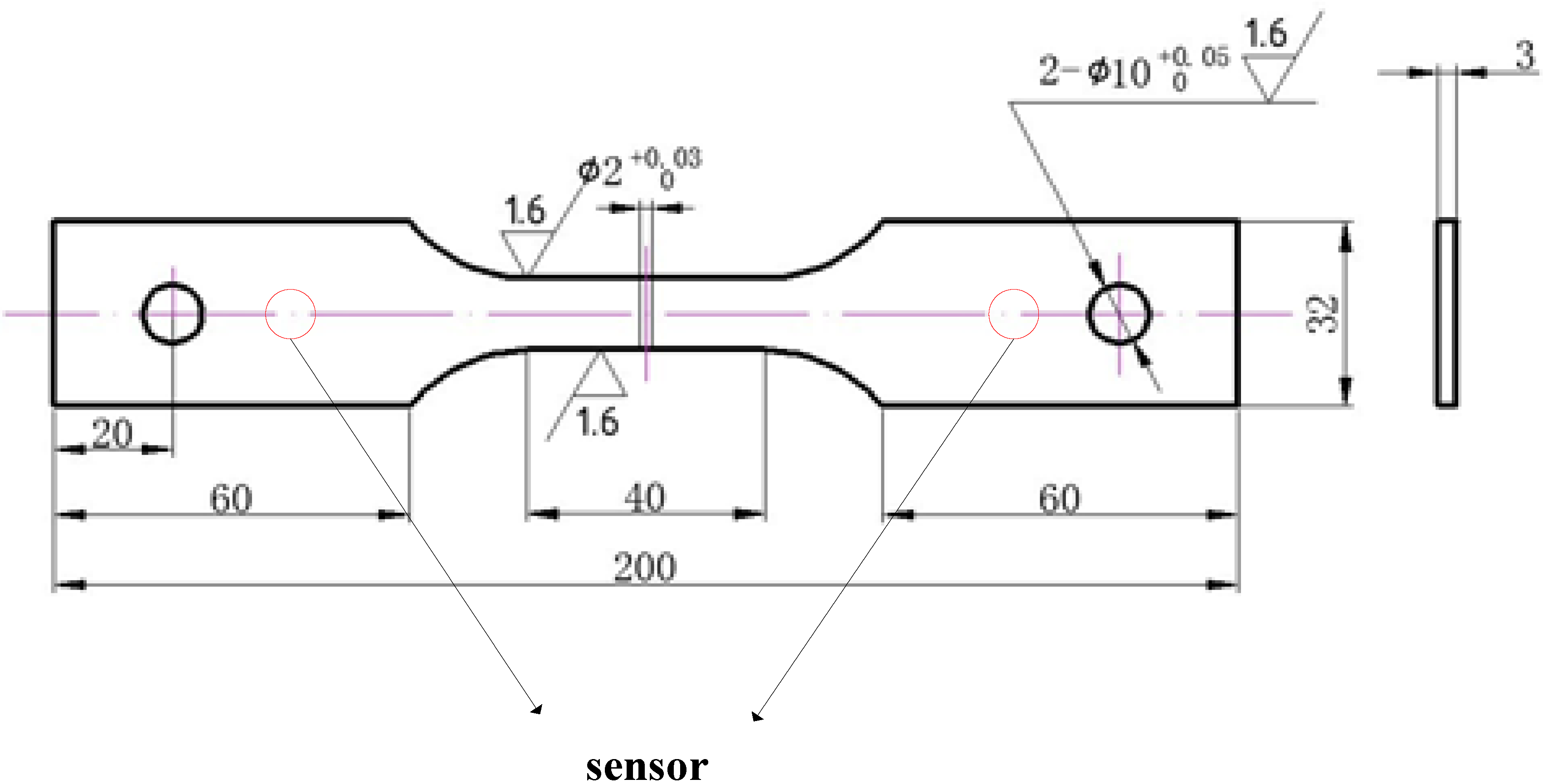
2.2. Acoustic Emission Technology

3. Results and Discussion
3.1. Material Tensile Damage

3.2. Characteristic of AE Signal for the Tensile Damage

| Sample | tf/s | ACf(t) |
|---|---|---|
| S1 | 88.6 | 0.000780 |
| S2 | 73.0 | 0.000769 |
| S3 | 88.9 | 0.000779 |
| S4 | 95.8 | 0.000782 |
| S5 | 122.0 | 0.000773 |
| S6 | 129.0 | 0.000781 |
| S7 | 111.8 | 0.000777 |
| S8 | 159.0 | 0.000775 |
| S9 | 92.6 | 0.000776 |
3.3. Tensile Damage Quantification Model
3.4. Model Parameters Estimation

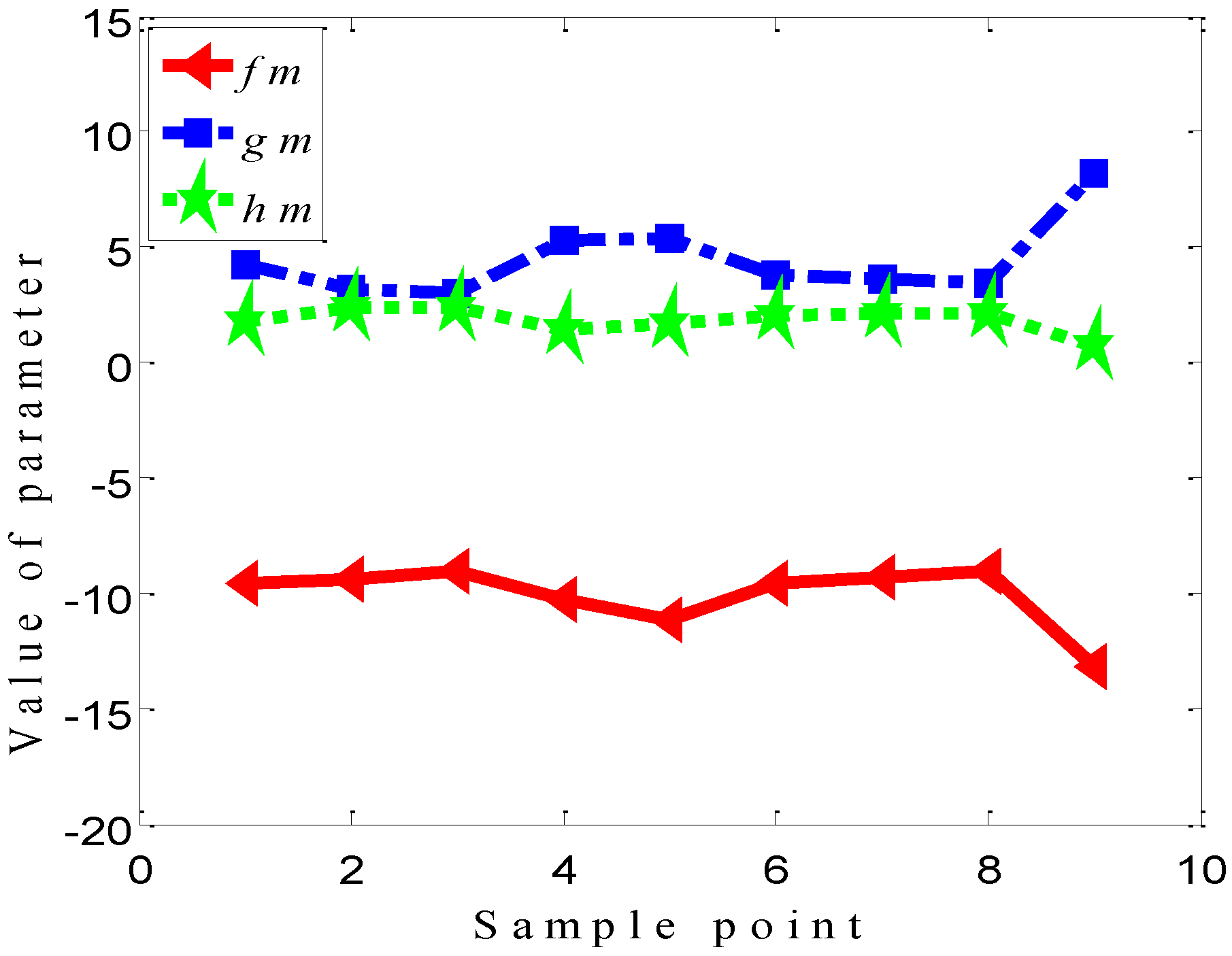
3.5. Results and Verification of the Model


| Sample | Maximum Error/s | Minimum Error/s | Average Error/s |
|---|---|---|---|
| S1 | 5.7 | 0.001 | 2.0 |
| S2 | 7.9 | 0.003 | 2.6 |
| S3 | 4.6 | 0.003 | 1.0 |
| S4 | 14.5 | 0.001 | 3.3 |
| S5 | 25.0 | 0.144 | 3.4 |
| S6 | 36.5 | 0.001 | 4.1 |
| S7 | 14.8 | 0.002 | 3.8 |
| S8 | 59.9 | 2.046 | 11.0 |
| S9 | 10.8 | 0.224 | 3.2 |
4. Conclusions
- (1)
- The correlation between tensile damage and AE signals was established by characteristic parameter AC(t), which can be used to monitor material elastic deformation of tensile damage.
- (2)
- The proposed model is effective to quantify elastic deformation of tensile damage of high-strength aluminum alloy A356 of high-speed train gearbox shells.
- (3)
- Cumulative counts, as one of the most commonly-used AE parameters, can be performed in combination with the proposed model to provide warning signs for gearbox of high-speed trains when tensile damage comes to the failure point, where the final fracture will be attained quickly, and catastrophic failure may occur.
- (4)
- The method presented in this paper was a prognostic method only if data obtained from tensile tests is applied. In other words, the proposed elastic stage remaining time quantification model in this paper is offline. Hence, building an online elastic stage remaining time prediction model is work that needs to be done in the future.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, B.M. Overall System and Bogie of High-Speed Motor Train Units; Southwest Jiaotong University Press: Chengdu, China, 2008. [Google Scholar]
- Li, X.J. CRH bullet trains overview. Railw. Tech. Superv. 2007, 9, 26–28. [Google Scholar]
- Yang, M.W. Acoustic Emission Testing; Machinery Industry Press: Beijing, China, 2005. [Google Scholar]
- Haneef, T.; Lahiri, B.B.; Bagavathiappan, S.; Mukhopadhyay, C.K.; Philip, J.; Rao, B.P.C.; Jayakumar, T. Study of the tensile behavior of AISI type 316 stainless steel using acoustic emission andinfrared thermography techniques. J. Mater. Res. Technol. 2015, 137, 1–13. [Google Scholar]
- Jalaj, K.; Sony, P.; Mukhopadhyay, C.K.; Jayakumar, T.; Vikas, K. Acoustic emission during tensile deformation of smooth and notched specimens of near alpha titanium alloy. Res. Nondestruct. Eval. 2012, 23, 17–31. [Google Scholar]
- Luo, X.; Haya, H.; Inaba, T.; Shiotani, T.; Nakanishi, Y. Damage evaluation of railway structures by using train-induced AE. Constr. Build Mater. 2004, 18, 215–223. [Google Scholar] [CrossRef]
- Re, V.D. Acoustic emission applications for defect detection in steels and GFRP. Int. J. Mater. Prod. Technol. 1988, 3, 38–53. [Google Scholar]
- Chen, H.L.; Choi, J.H. Acoustic emission study of fatigue cracks in materials used for AVLB. J. Nondestruct. Eval. 2004, 23, 133–151. [Google Scholar] [CrossRef]
- Johnson, M. Waveform based clustering and classification of AE transients in composite laminates using principal component analysis. NDT E Int. 2002, 35, 367–376. [Google Scholar] [CrossRef]
- Lugo, M.; Jordon, J.B.; Horstemeyer, M.F.; Tschopp, M.A.; Harris, J.; Gokhale, A.M. Quantification of damage evolution in a 7075 aluminum alloy using an acoustic emission technique. Mater. Sci. Eng. A 2011, 528, 6708–6714. [Google Scholar] [CrossRef]
- Patrik, D.; Jan, B.; Frantisek, C.; Pavel, L.; Dietmar, L.; Karl, U.K. Acoustic emission during stress relaxation of pure magnesium and AZ magnesium alloys. Mater. Sci. Eng. A 2007, 462, 307–310. [Google Scholar]
- Godin, N.; Huguet, S.; Gaertner, R.; Salmo, L. Clustering of acoustic emission signals collected during tensile tests on unidirectional glass/polyester composite using supervised and unsupervised classifiers. NDT E Int. 2004, 37, 253–264. [Google Scholar] [CrossRef]
- Cousland, S.M.; Scala, C.M. Acoustic emission during the plastic deformation of aluminum alloys 2024 and 2124. Mater. Sci. Eng. 1983, 57, 23–29. [Google Scholar] [CrossRef]
- Wen, W.; Morris, J.G. An investigation of serrated yielding in 5000 series aluminum alloys. Mater. Sci. Eng. A 2003, 354, 279–285. [Google Scholar] [CrossRef]
- Bohlen, J.; Chmelı́k, F.; Dobrŏn, P.; Kaiser, F.; Letzig, D.; Lukáč, P.; Kainer, K.U. Orientation effects on acoustic emission during tensile deformation of hot rolled magnesium alloy AZ31. J. Alloys Compd. 2004, 378, 207–213. [Google Scholar] [CrossRef]
- Máthis, K.; Chmelík, F.; Janeček, M.; Hadzima, B.; Trojanová, Z.; Luká, P. Investigating deformation processes in AM60 magnesium alloy using the acoustic emission technique. Acta Mater. 2006, 54, 5361–5366. [Google Scholar] [CrossRef]
- Cakir, A.; Tuncell, S.; Aydin, A. AE response of 205L SS during SSR test under potentiostatic control. Corros. Sci. 1999, 41, 1175–1183. [Google Scholar] [CrossRef]
- Vinogradov, A.; Lazarev, A.; Linderov, M.; Weidner, A.; Biermann, H. Kinetics of deformation processes in high-alloyed cast transformation-induced plasticity/twinning-induced plasticity steels determined by acoustic emission and scanning electron microscopy: Influence of austenite stability on deformation mechanisms. Acta Mater. 2013, 61, 2434–2449. [Google Scholar] [CrossRef]
- Kocich, R.; Cagala, M.; Crha, J.; Kozelsky, P. Character of acoustic emission signal generated during plastic deformation. In Proceedings of the 30th European Conference on Acoustic Emission Testing & 7th International Conference on Acoustic Emission, Granada, Spain, 12–15 September 2012; pp. 1–8.
- Zhang, W.D.; Zhang, X.W.; Yang, B.; Ai, Y.B. Damage characterization and recognition of aluminum alloys based on acoustic emission signal. J. Univ. Sci. Technol. Beijing 2013, 35, 626–633. [Google Scholar]
- Ai, Y.B.; Sun, C.; Que, H.B.; Zhang, W.D. Investigation of material performance degradation for high-strength aluminum alloy using acoustic emission. Metals 2015, 5, 228–238. [Google Scholar] [CrossRef]
- Okafor, A.C.; Natarajan, S. Acoustic emission monitoring of tensile testing of corroded and un-corroded clad aluminum 2024-T3 and characterization of effects of corrosion on AE source events and material tensile properties. AIP Conf. Proc. 2014, 1581, 492–500. [Google Scholar]
- Keshtgar, A.; Modarres, M. Acoustic emission-based fatigue crack growth prediction. In Proceedings of the Reliability and Maintainability Symposium: Product Quality & Integrity, Orlando, FL, USA, 28–31 January 2013; pp. 1–5.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Zhang, W.; Ai, Y.; Que, H. Study of the Tensile Damage of High-Strength Aluminum Alloy by Acoustic Emission. Metals 2015, 5, 2186-2199. https://doi.org/10.3390/met5042186
Sun C, Zhang W, Ai Y, Que H. Study of the Tensile Damage of High-Strength Aluminum Alloy by Acoustic Emission. Metals. 2015; 5(4):2186-2199. https://doi.org/10.3390/met5042186
Chicago/Turabian StyleSun, Chang, Weidong Zhang, Yibo Ai, and Hongbo Que. 2015. "Study of the Tensile Damage of High-Strength Aluminum Alloy by Acoustic Emission" Metals 5, no. 4: 2186-2199. https://doi.org/10.3390/met5042186
APA StyleSun, C., Zhang, W., Ai, Y., & Que, H. (2015). Study of the Tensile Damage of High-Strength Aluminum Alloy by Acoustic Emission. Metals, 5(4), 2186-2199. https://doi.org/10.3390/met5042186