Tensile Strength Reliability Analysis of Cu₄₈Zr₄₈Al₄ Amorphous Microwires

Abstract

Uniform Cu₄₈Zr₄₈Al₄ amorphous microwires with a high surface quality are fabricated by a melt extraction technique. The mechanical property of microwires is evaluated via tensile tests. To estimate the strength scattering, statistical analysis of fracture strengths is conducted using logarithmic normal distribution, and two- and three-parameter Weibull analysis, severally. The results show that the tensile strengths of Cu₄₈Zr₄₈Al₄ amorphous microwires range from 1724 to 1937 MPa with the arithmetical average value of 1836 MPa, and the arithmetical standard deviation of 56.4 MPa. The geometric mean of fracture strength is 1840 MPa using logarithmic normal distribution statistical analysis. Using two- and three-parameter Weibull analysis, the Weibull modulus and fracture threshold value are respectively calculated for 34.8 and 1483 MPa, which shows the excellent tensile mechanical properties with a high predictability of Cu₄₈Zr₄₈Al₄ amorphous microwires and further indicates the great potential of application.

1. Introduction

Compared to traditional metallic materials, amorphous alloys exhibit unique mechanical properties, such as high strength and hardness, great corrosion resistance, and fatigue durability. [1,2,3]. The amorphous microwires fabricated by a higher cooling rate have drawn much attention to their application in the last two decades due to their unique size effect [4]. In all fields of research on amorphous microwires, such as magnetic bistability [5], the giant magneto impedance (GMI) effect [6,7], electromagnetic shielding (EMS) [8], soft magnetic properties [9], and the magnetocaloric effect (MCE) [10], the mechanical properties are always taken seriously. Cu–Zr amorphous alloy has been investigated on the plasticity and toughness by introducing the B2 phases to form composites structure [11,12,13,14,15]. The tensile and damping tests of small-sized Cu–Zr–Al metallic glass wires exhibited that the Young’s modulus of the Cu–Zr–Al metallic glass wires was smaller than that of the bulk one [16], which indicates the size of specimens affecting the mechanical property. As a kind of brittle material, BMG materials usually fail by one dominant shear band with highly localized strain deformation without any warning, which is generally believed to be a sign that BMGs are mechanically less reliable [17,18]. What is more, the experimentally measured mechanical properties of metallic glasses are usually inhomogeneous, i.e., the values are scattering. Therefore, the distribution and reliability of the mechanical properties, such as the strength, need to be characterized, which is of importance for the application of metallic glass wires in the field of structural materials. To date, the mechanical properties, especially the fracture strength of Cu–Zr–Al-based amorphous microwires, have not been adequately investigated. In the present study, the distribution of the fracture strength of a Cu–Zr–Al amorphous wire is statistically analyzed. The purpose is to provide a fundamental basis for the evaluation of service reliability of this alloy.

2. Experimental Details

For alloy preparation, the melt-extracted microwires with a nominal composition of Cu₄₈Zr₄₈Al₄ (at. %) was firstly fabricated to an ingot with the raw materials Cu (99.99%), Zr (99.99%), and Al (99.99%) using a vacuum arc melting method. Then, an alloy rod with a diameter of 10 mm was obtained using suction casting. The microwires were extracted by a copper wheel with a diameter of 320 mm and a 60° knife-edge in melt-extracted equipment, in which the rod was fixed in a boron nitride crucible and re-melted by high frequency electromagnetic induction. The surface tension contributed to the forming of wires. The parameter of constant linear velocity of the wheel rim was 30 m·s⁻¹. The feeding rate of the molten rod was 10–15 m·s⁻¹ [19]. Macro and micro morphologies of melt-extracted wires with uniform, smooth, and rounding surfaces were shown in Figure 1.

The structural characteristics of the microwires were represented using X-ray diffraction with Cu K_α radiation (XRD, D/max-rB, Rigaku, Japan) and a differential scanning calorimeter (Pyris 1 DSC, PerkinElmer, Waltham, UK) at a heating rate of 20 K·min⁻¹. Energy dispersive spectroscopy (EDS) was conducted under a scanning electron microscope (HITSCHI SU-1500, Hitachi, Ltd. Chiyoda, Tokyo, Japan). The tensile mechanical tests were taken on an Instron-5500R11185 machine (Instron, Grove City, PA, USA) with a mini-force sensor ranging from 0 to 50 N. The morphologies and fracture surfaces of microwires were observed using a field emission scanning electron microscope (SEM-Helios Nanolab 600i, FEI, Hillsboro, OR, USA) at 20 kV.

3. Results and Discussion

The melt extraction process achieves a cooling rate as high as 10⁶ K·s⁻¹, which can guarantee the wires to be an amorphous structure. In XRD spectra, shown in the inset of Figure 2, a broad halo near the diffraction angle of 38° without any keen-edged lattice peaks is observed, which demonstrates that the structure of the wires are fully amorphous. The DSC curve in Figure 2 shows that, with increasing temperature, an endothermic reaction appears owing to the glass transition, and an exothermic reaction corresponding to the crystallization process then occurs following the glass transition. The glass transition temperature (T_g), and the crystallization temperature (T_x) are measured to be 700 K and 760 K, respectively.

To further characterize the structure of the microwire, SEM and EDS observations were carried out. Figure 3 shows the morphology of a microwire and its corresponding EDS mapping result and energy spectrum. The surface of the microwire is relatively smooth, as shown in Figure 3a. Figure 3b–d shows the element distribution of Zr, Cu, and Al in the area corresponding to the region marked by the rectangle in Figure 3a, respectively, which suggests that the microwire is homogeneous. The concentrations of the three elements were analyzed and are shown in

Table 1. Composition analysis by EDS.

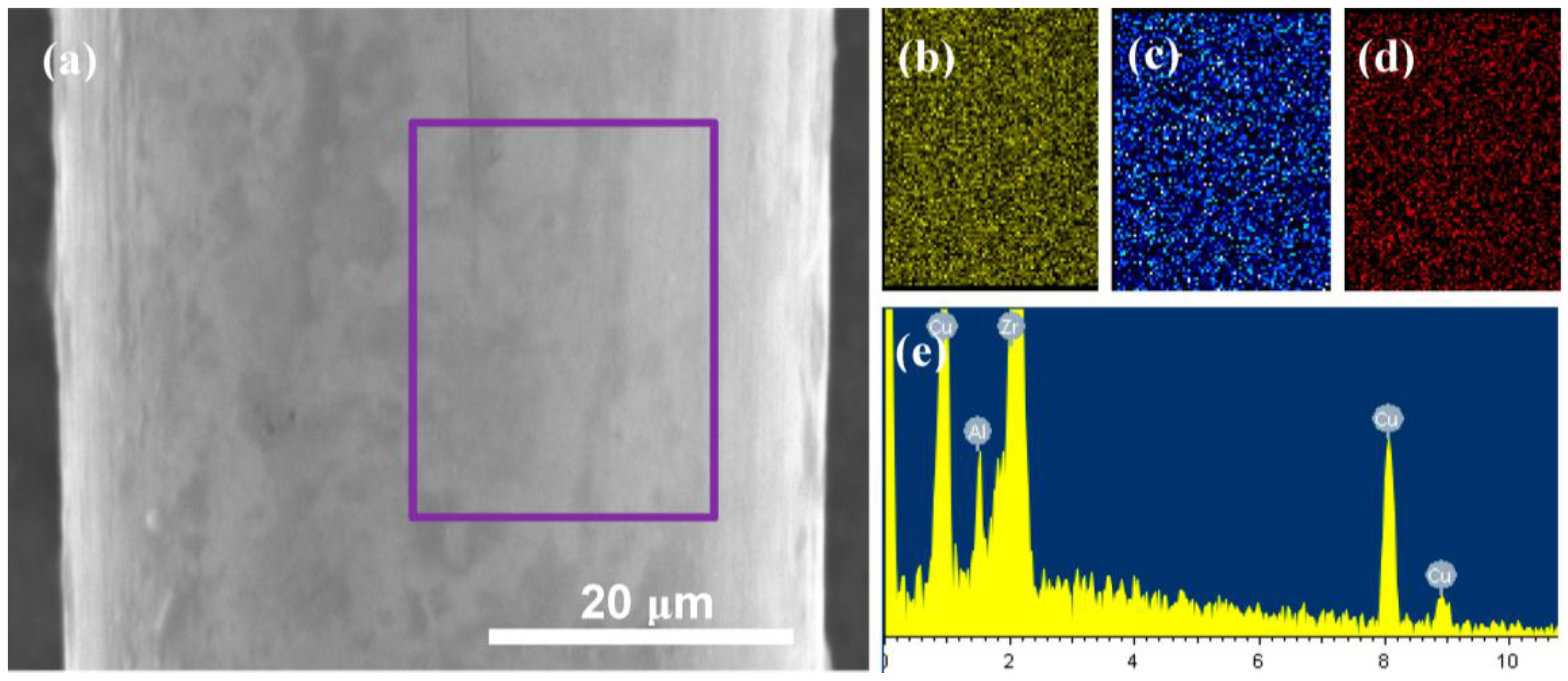
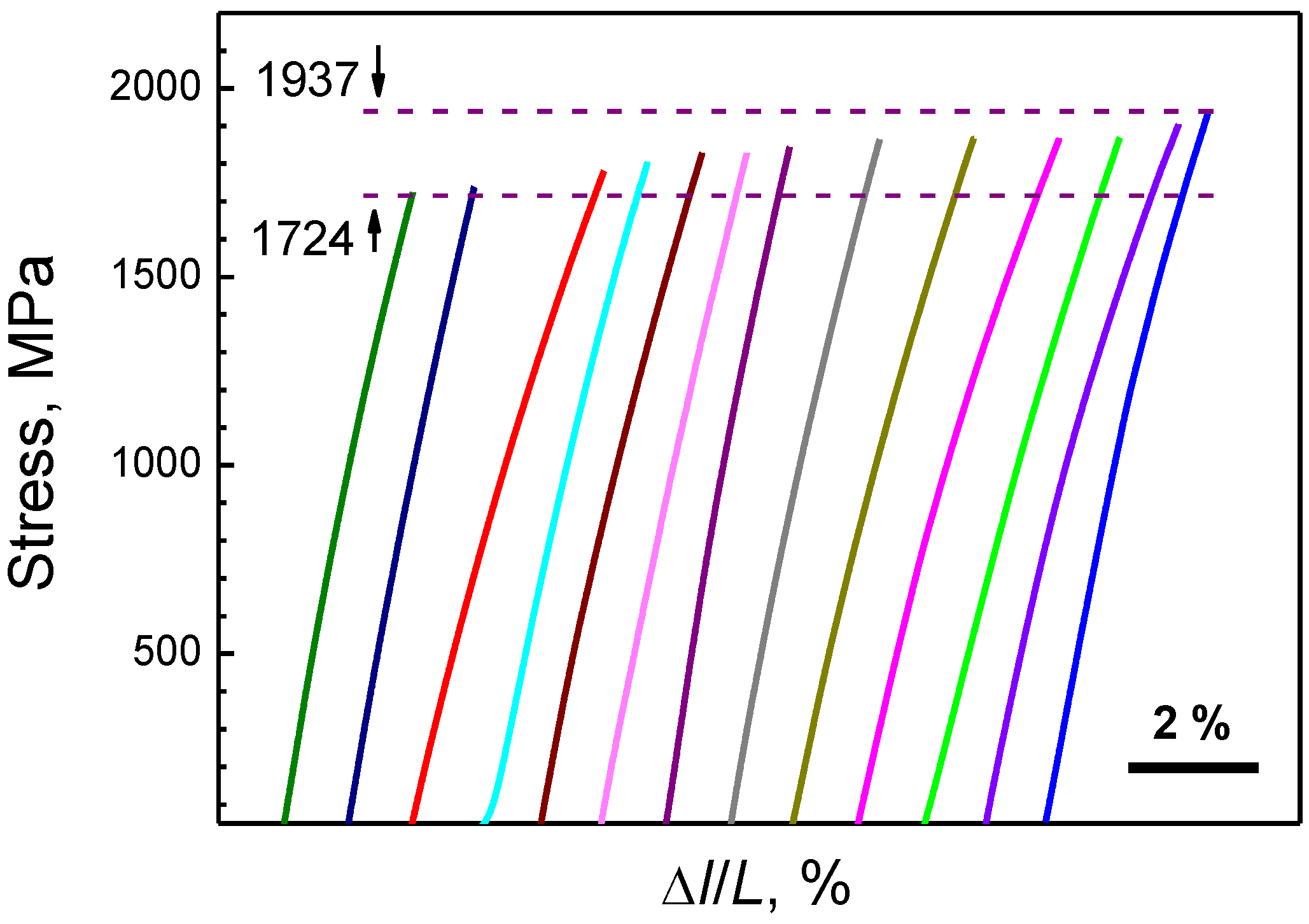
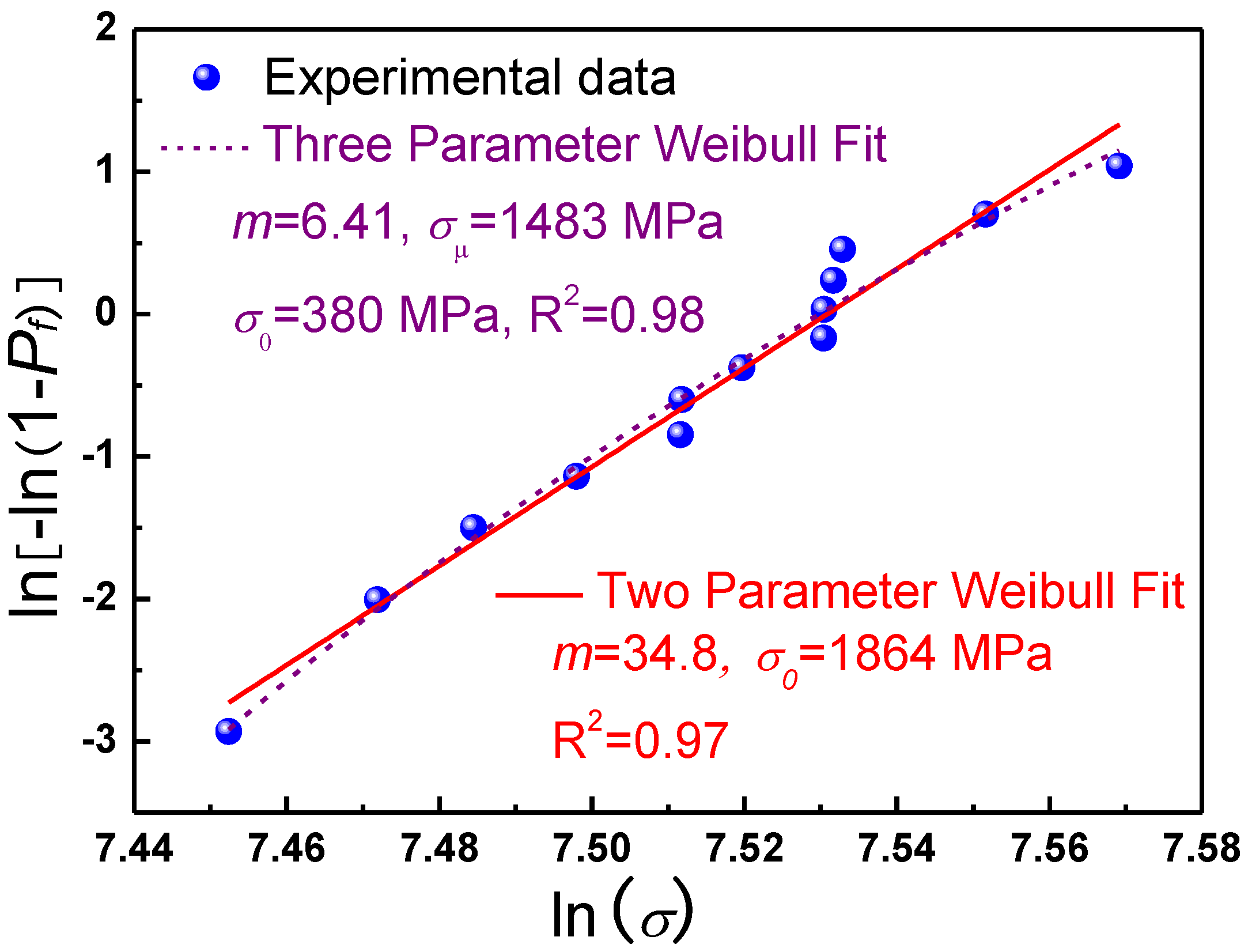
No.	Zr, at. %	Cu, at. %	Al, at. %
1	46.72	48.76	4.52
2	49.75	47.02	3.22
3	47.47	48.63	3.90
4	46.06	48.55	5.39
5	48.65	47.32	4.03
Average	47.73	48.057	4.213

. One typical energy spectrum is shown in Figure 3e. It can be seen that the actual concentrations of the chemical composition is close to the nominal composition, which means that the melt extraction method is suitable for fabricating the microwire.

Figure 4 shows the room temperature engineering stress-strain curves of all specimens. ΔI/L represents the tension strain value, in which ΔI is the elongation, and L is the gauge length of the specimen. There is no plasticity in the tensile tests, which suggests that the amorphous microwire shows the brittle nature. In these 13 tests, the fracture strengths (σ_f) ranged from 1724 MPa to 1937 MPa with a variation of ±7%; the arithmetic average value is 1836 MPa with the standard deviation of 56 MPa. The elastic modulus evaluated directly from the stress-strain curve is ~88.5 GPa, which is comparable to similar BMGs Zr₄₈Cu₄₈Al₄ [20] and Zr₄₈Cu₄₅Al₇ [17].

Regarding the scattering fracture strength value (Figure 4), the logarithmic normal distribution method is introduced to describe brittle materials, and the cumulative probability function is shown as [21]

$$P_f^{LN}=\frac{1}{2}[1+erf\left(\frac{\ln \left(\mathsf{\sigma }\right)-\mathsf{\kappa }}{s\sqrt{2}}\right)]$$

(1)

where σ is a given uniaxial stress, κ is the mean, and s is the standard deviation of the natural logarithms of the fracture strength. $P_f^{LN}$ represents the probability of failure behavior under the given stress. The mean of κ is a parameter, which is equal to ln(σ₀), where σ₀ is the geometric mean of fracture strengths.

The probability of failure ($P_f^{LN}$) at a uniaxial stress σ_i, can be calculated using the following expression (median rank value), and the data obtained from Figure 4:

$$P_i^{LN}=\frac{i-0.3}{N+0.4}\times 100\%$$

(2)

where i is for the ith sample, and N is the total number of sample tested.

The values of κ and σ₀ can be calculated by fitting the experimental data of ln(σ) vs. (2 $P_f^{LN}$ − 1) shown in Figure 5. According to the fitting results, the geometric average strength at κ = 7.52 is calculated to be 1840 MPa, which is extremely close to the arithmetic average stress value of 1836 MPa.

Compared with a logarithmic normal distribution, a Weibull distribution is more commonly used to evaluate the service reliability of brittle materials. The cumulative probability function is expressed as follows [22,23]:

$$P_f^{WB}=1-\exp [-V{\left(\frac{\mathsf{\sigma }-{\mathsf{\sigma }}_{\mathsf{\mu }}}{{\mathsf{\sigma }}_p}\right)}^m]$$

(3)

where $P_f^{WB}$ describes the Weibull cumulative distribution, V indicates the volume of the wire specimen, σ_μ is the threshold value of fracture strength, σ_p is the Weibull scale parameter that is the stress when $P_f^{WB}$ equals to 63.2%, and m is the parameter known as Weibull modulus, which displays the variability of the fracture strength, where a larger value of m yields a narrower distribution. Usually, Equation (3) can be translated into a three-parameter Weibull model (TrPWM):

$$\ln \left[\ln \left(\frac{1}{1-P_f^{WB}}\right)\right]=m\ln \left(\mathsf{\sigma }-{\mathsf{\sigma }}_{\mathsf{\mu }}\right)-m{\ln \mathsf{\sigma }}_0$$

(4)

The parameter of σ_μ denotes the stress at which there is no failure possibility and is usually taken to be σ_μ = 0 [24]. Thus, Equation (3) is rearranged to be a two-parameter Weibull model (TPWM):

$$\ln \left[\ln \left(\frac{1}{1-P_f^{WB}}\right)\right]=m\ln \left(\mathsf{\sigma }\right)-m{\ln \mathsf{\sigma }}_0$$

(5)

Through non-line fitting experimental data of ln(σ) vs. ln[−(1 − ln $P_f^{WB}$)], the parameters of TPWM and TrPWM are obtained. The fitting curves are shown in Figure 6, which suggests that the three-parameter Weibull model is better than the two-parameter Weibull model for the prediction of the distribution of the fracture strength of the Cu₄₈Zr₄₈Al₄ metallic glass wire. For the TrPWM, the values of m, σ_μ, and σ₀ are 6.4, 1483 MPa, and 365 MPa, respectively. For the TPWM, the values of m and σ₀ are 34.8 and 1864 MPa, respectively, a relatively higher R² than the logarithmic normal distribution.

The Weibull modulus, m, describes the service reliability of wires. A large m-value represents a narrow distribution of the strength, which indicates a high reliability of materials. The narrow distribution of the strength in compression indicating the fracture mode of BMGs is evidently very different even though the tensile and compressive strength are similar [17,25]. Undoubtedly, the tensile testing is more critical for evaluating a material in its application, and

Table 2. Summary of fracture strength and the Weibull modulus of BMGs based on two-parameter Weibull model.

Material	Test Method	Sample Sizes	No. of Test Samples	Fracture Strength	Weibull Modulus	Ref.
Mg66Zn30Ca4	Compression	Φ5 mm	25	716–854	26	[23]
Mg71Zn25Ca4	Compression	Φ2 mm	25	672–752	44	[23]
Mg67Zn28Ca5 microwires	Tension	~Φ100 μm	23	675–894	20.6	[21]
Gd55Al25Co20	Tension	~Φ30 μm	11	1067–1286	19.9	[30]
Zr55Ti2Co28Al15	Compression	Φ6 mm	31	1840–2080	36.2	[22]
(Zr48Cu45Al7)98Y2	Compression	Φ1.5 mm	47	1430–1780	25.5	[22]
(Zr48Cu45Al7)99Y1	Compression	Φ1.5 mm	30	1636–1883	34.9	[22]
(Zr48Cu45Al7)99.5Y0.5	Compression	Φ1.5 mm	27	1667–1838	55.9	[22]
Zr48Cu45Al7	Compression	Φ1.5 mm	28	1791–1898	73.7	[17]
Zr48Cu45Al7	Tension	1 × 0.7 mm2	22	1790–1890	36.5	[12]
Cu48Zr48Al4 microwires	Tension	~Φ30 μm	13	1724–1937	34.8	This work

summarizes the fracture strength and Weibull parameters of BMGs based on the two-parameter Weibull model [10,17,23,26,27,28,29]. According to a comparation of the results given in Table 1, the m-value is sensitive to the composition of Mg-based and Zr-based BMGs; in tension tests, the microwires of this work are comparable to the Zr₄₈Cu₄₅Al₇ BMGs in terms of fracture strength and Weibull modulus. Meanwhile, the maximum fracture strength of microwires investigated is higher than the Zr₄₈Cu₄₅Al₇ bulk one, which might be attributed to the relatively uniform structures of the wires. The tested results of Cu₄₈Zr₄₈Al₄ amorphous microwires show a higher value of Weibull modulus and a relatively high threshold value of 1483 MPa than others wires, which shows an excellent potential engineering application of the wires.

Typical fracture morphologies of amorphous microwires were shown in Figure 7. The angles between the stress axis and the fracture surface are about 57° as displayed in Figure 7a. The fracture surface of specimens consists of two regions: the relatively smooth “featureless” zone and the vein-pattern zone shown in Figure 7b, which indicates that the fracture process was triggered by the extension of shear bands under stress. The shear slip then induced the initial shear displacement and the remaining part finally ruptured, producing the vein pattern [31,32,33].

Compared with the fracture morphology of bulk metallic glasses (BMGs), the fracture features of amorphous microwires are roughly similar to the BMGs, which shows some vein-like patterns (Figure 7). This is attributed to the formation of viscous layer on the fracture surface due to the shear dilatation and adiabatic heating [34]. The angle between the fracture surface and the loading direction is slightly changed from 54° (for the BMG) [17,35,36] to 57°. The fracture surface does not show fracture cores that are obvious in the BMG. These differences may be attribute to the higher cooling rates as well as the size effect of microwires.

4. Summary

In summary, the tension tests of the melt-extracted Cu₄₈Zr₄₈Al₄ amorphous microwires were carried out, indicating that the fracture strength ranged from 1724 MPa to 1937 MPa, and the average strength and standard deviation were 1836 MPa and 56 MPa, respectively. Brittle failure occurred in the fracture sections of the microwires, and the fracture strength was 1840 MPa, obtained via logarithmic normal fitting. The Weibull modulus and the fracture threshold value were 34.8 and 1483 MPa, respectively, calculated by two-parameter and three-parameter Weibull non-line fitting method, which indicates a relatively high damage tolerance and service reliability of the melt-extracted Cu₄₈Zr₄₈Al₄ amorphous microwires. Thus, these microwires have good potential for engineering applications.