First-Principles Investigation of Structural, Electronic and Elastic Properties of HfX (X = Os, Ir and Pt) Compounds

Abstract

The structural, electronic and elastic properties of B2 structure Hafnium compounds were investigated by means of first-principles calculations based on the density functional theory within generalized gradient approximation (GGA) and local density approximation (LDA) methods. Both GGA and LDA methods can make acceptable optimized lattice parameters in comparison with experimental parameters. Therefore, both GGA and LDA methods are used to predict the electronic and elastic properties of B2 HfX (X = Os, Ir and Pt) compounds. Initially, the calculated formation enthalpies have confirmed the order of thermodynamic stability as HfPt > HfIr > HfOs. Secondly, the electronic structures are analyzed to explain the bonding characters and stabilities in these compounds. Furthermore, the calculated elastic properties and elastic anisotropic behaviors are ordered and analyzed in these compounds. The calculated bulk moduli are in the reduced order of HfOs > HfIr > HfPt, which has exhibited the linear relationship with electron densities. Finally, the anisotropy of acoustic velocities, Debye temperatures and thermal conductivities are obtained and discussed.

1. Introduction

Hafnium and Hafnium compounds can be used as the tools and parts in the nuclear power plants due to their high neutron cross sections [1], and medical implants and other medical industry applications owing to their excellent mechanical properties, high corrosive resistant ability and biocompatibility [2]. With the growing importance of Hafnium compounds, the studies on the theoretical and experimental aspects of these compounds have increased [3,4,5,6,7,8,9]. Levy et al. [3] performed a comprehensive study in the structural and thermodynamic properties of binary Hf compounds using ab initio calculations. Among them, the B2 structure is one of the most typical crystal structures for HfX compounds. For example, Novakovic et al. [4] studied the electronic structures, cohesive energies and formation enthalpies of B2 structure HfT_M (T_M = Co, Rh, Ru and Fe) compounds using ab initio full-potential linearized augmented plane waves calculations. Iyigör et al. [5] reported the structural, electronic, elastic and vibrational properties of HfX (X = Rh, Ru and Tc) using the plane-wave pseudopotential density functional theory via VASP codes. Xing et al. [6] investigated the structural phase stabilities of B2 phases and formation enthalpies of HfM (M = Ir, Os, Pd, Pt, Ru, Rh) using VASP codes. Wu et al. [7] studied the structural, elastic and electronic properties of HfRu compound theoretically. Although the structural features of B2 HfX (X = Os, Ir and Pt) compounds have been achieved discussed experimentally [10,11,12] and theoretically [6,13,14], the elastic and electronic properties of HfX (X = Os, Ir and Pt) compounds are rarely reported and assessed to our knowledge.

Therefore, this work has been organized as the following description. In Section 2, the computational methods of binary HfX (X = Os, Ir and Pt) compounds are presented. In Section 3, the results and discussions are exhibited and analyzed, including structural properties, electronic structures, elastic constants, elastic properties, elastic anisotropy, anisotropic sound velocities, Debye temperatures and thermal conductivities. In Section 4, the conclusions are made in detail.

2. Computational Information

The first-principles calculations based on the pseudopotential plane-wave within density functional theory (DFT) were performed using CASTEP (Cambridge Sequential Total Energy Package) codes [15,16]. The ultrasoft pseudopotential was adopted to simulate the ion-electron interaction [17]. Both generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE) functional [18,19] and the local density approximation (LDA) functional with the form of Ceperley-Adler parameterized by Perdew and Zunger [20] were utilized to model the exchange-correlation. The basis sets have included atom states of Hf5d²6s², Os5s²5p⁶5d⁶6s², Ir5d⁷6s² and Pt5d⁹6s¹. With respect to cutoff energies and k-points, a series of convergence studies were performed. Afterwards, the cutoff energies were set at 400 eV. Besides, the special points sampling integration over the Brillouin zone was employed using Monkhorst-Pack method [21] with determined k-point separation of 0.02/Å in three lattice directions for each compound. Furthermore, the minimization scheme proposed by Brodyden-Fletcher-Goldfarb-Shanno (BFGS) was used during geometric optimization [22]. The tolerances of the geometrical optimization has to meet conditions, including the maximum ionic displacement ≤ 5.0 × 10⁻⁴ Å, maximum ionic force ≤ 0.01 eV/Å, maximum stress ≤ 0.02 GPa, and the difference of total energy ≤ 5.0 × 10⁻⁶ eV/atom. Followed by geometric optimization, the total energy and electronic structure were computed using self-consistent field tolerance of 5.0 × 10⁻⁷ eV/atom. Correspondingly, the lattice constants and atom coordinates were optimized via minimizing the total energy. At equilibrium structures, the corrected tetrahedron Blöchl method was utilized to derive the total energies [23].

3. Results and Discussion

3.1. Structural Properties

HfX (X = Os, Ir and Pt) compounds are in the (CsCl type) Pm3m space group, correspondingly. In an HfX unit cell, an Hf atom locates at 1a (0, 0, 0) and an X atom stays at 1b (0.5, 0.5, 0.5). In order to obtain structural properties of HfX compounds, the geometric optimizations are made firstly. The equilibrium lattice constants using both GGA and LDA methods are tabulated in

Table 1. The optimized (a_theo) and experimental (a_exp) lattice constants, calculated deviations, bulk moduli (B₀) and its pressure derivatives (B₀’), and formation enthalpies (H_f) for HfX (X = Os, Ir and Pt).

Compounds	atheo (Å)	aexp (Å)	Calculated Deviation (%)	B0 (GPa)	B0‘	Hf (eV/atom)
HfOs	3.291 a	3.239 c	1.600 a	234.3 a	4.43 a	−0.474 a
	3.236 b	-	−0.083 b	266.2 b	4.47 b	−0.451 b
	3.294 d	-	-	-	-	−0.495 d
	3.257 e	-	-	-	-	−0.707 f
	-	-	-	-	-	−0.793 g
	-	-		-	-	−0.484 ± −0.052 h
HfIr	3.311 a	3.21 i	3.143 a	220.9 a	4.66 a	0.807 a
	3.253 b	-	1.331 b	255.6 b	4.69 b	−0.769 b
	3.275 g	-	-	-	-	−0.977 g
	-	-	-	-	-	−1.016 ± −0.016 j
HfPt	3.359 a	3.3623 k	−0.096 a	191.6 a	4.64 a	−0.903 a
	3.298 b	-	−1.907 b	221.7 b	4.66 b	−0.900 b
	-		-	-	-	−1.063 g
	-	-	-	-	-	−1.175 ± −0.062 j

^a Theoretical values from GGA method in current work; ^b Theoretical values from LDA method in current work; ^c Experimental values from reference [10]; ^d Theoretical values from reference [14]; ^e Theoretical values from reference [13]; ^f Theoretical values from reference [3]; ^g Theoretical values from reference [6]; ^h Experimental values from reference [24]; ⁱ Experimental values from reference [11]; ^j Experimental values from reference [25]; ^k Experimental values from reference [12].

, along with the available experimental [10,11,12] and theoretical [6,13,14] values for reference. Generally, the qualities for structural optimizations in HfX compounds using both GGA and LDA methods are comparable and acceptable. In detail, the optimized lattice constants for HfOs and HfIr are in good agreement with theoretical values [6,13,14], respectively. For HfOs and HfIr, the LDA computed values are more approaching to the experimental value. On the other aspect, the GGA method can give better optimized values than the LDA method in HfPt. Therefore, either method shows obvious superiority in the structural optimization of HfX compounds. Resultantly, both GGA and LDA methods are used in the following theoretical studies for HfX compounds.

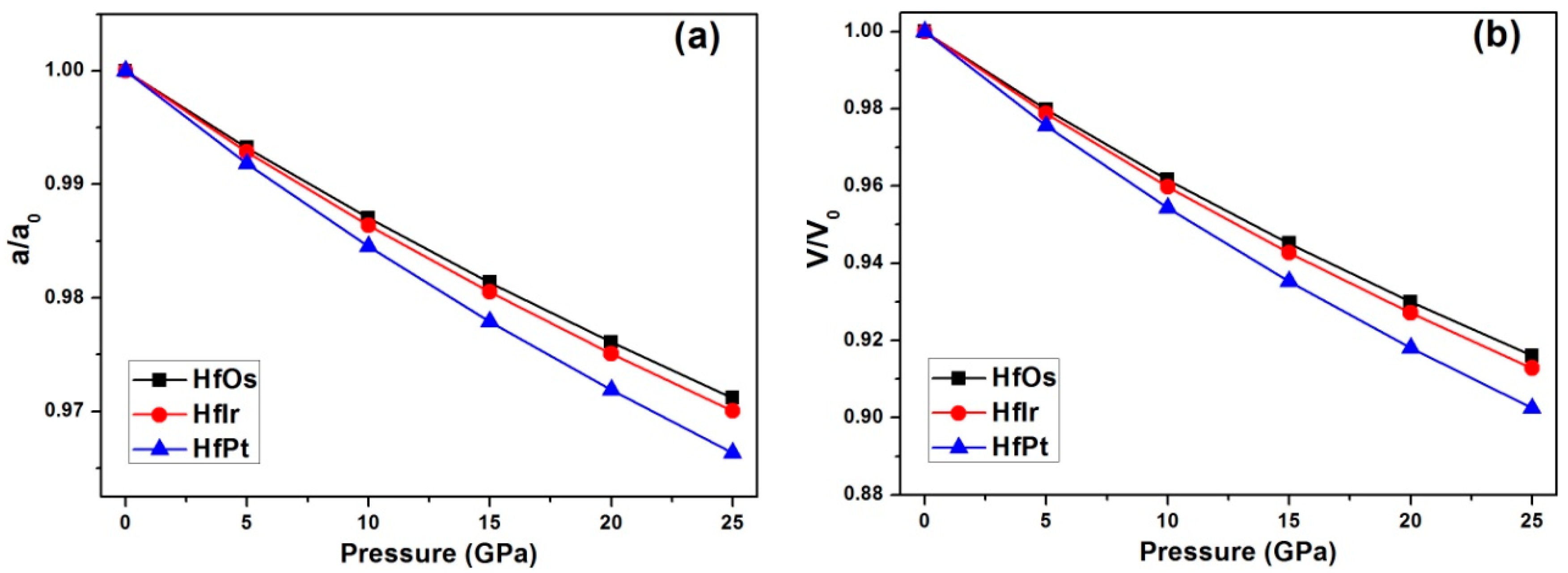
Under increasing pressures from 0 to 25 GPa with per step of 5 GPa, the relative changes of (a) lattice constant and (b) unit cell volume for HfX compounds using GGA method are exhibited in Figure 1. In Figure 1a, the relative change of lattice constant (a) for HfPt is alternated larger than HfIr and HfOs under growing pressures. Similarly, the unit cell volume (V) changes larger in HfPt than HfIr and HfOs under pressures (Figure 1b). Therefore, the obtained pressure volume curve for each compound is formulated to a third-order Birch-Murnaghan equation of state (EOS) [26]:

$$P=\frac{3}{2}{B}_0[{(\frac{V}{V_0})}^{-\frac{7}{3}}-{(\frac{V}{V_0})}^{-\frac{5}{3}}]\{1+\frac{3}{4}(B_0^{\prime }-4)[{(\frac{V}{V_0})}^{-\frac{2}{3}}-1]\}.$$

(1)

For HfOs, HfIr and HfPt, the fitted bulk moduli (B₀) are 234.3 GPa, 220.9 GPa and 191.9 GPa, and their pressure derivatives (B₀’) are 4.43, 4.66 and 4.64, accordingly. As a result, the bulk moduli are in the sequence of HfOs > HfIr > HfPt. Using LDA method, the bulk moduli are still in the order of HfOs > HfIr > HfPt, as exhibited in Table 1.

The thermodynamic stability is closely associated with formation enthalpy in binary compounds. To evaluate the thermodynamic stability of a compound, the formation enthalpy (H_f) is expressed by the following equation [27,28]:

$$H_{\mathrm{f}}^{\mathrm{HfX}}=\frac{E_{\mathrm{f}}^{\mathrm{HfX}}-E_{\mathrm{Hf}}-E_{\mathrm{X}}}{2},$$

(2)

where $E_{\mathrm{f}}^{\mathrm{HfX}}$ is the total energy of an HfX unit cell including an Hf atom and an X atom with equilibrium lattice parameters (X = Os, Ir and Pt); E_Hf and E_X are the total energy per atom of pure element solids at their ground states. Hf and Os are HCP metals, and Ir and Pt are FCC metals at ground state.

The negative formation enthalpy has denoted that the chemical process is exothermic, indicating the stability of resulted compounds. Moreover, the larger negative formation enthalpy has signified better stability of a compound [29]. In Table 1, the formation enthalpies of HfX compounds are tabulated. Generally, HfX compounds should be stable owing to their negative formation enthalpies derived from GGA and LDA methods. Furthermore, their thermodynamic stabilities are both in the order of HfPt > HfIr > HfOs. This conclusion is the same with Xing’s work [6]. In detail, the H_f values calculated by GGA method are typically more negative than LDA method. For HfOs, the calculated H_f value by GGA method is in good consistency with experimental value [24] and theoretical value from Liu’s work [14], but smaller than Xing’s [6] and Levy’s [3] reports. For HfIr and HfPt, our calculated H_f values are both smaller than theoretical values from Xing’s work [6] and experimental values from Gachon’s report [25]. Nevertheless, the crystal structures for HfIr and HfPt are not mentioned in this experimental work [25], which has degraded the reference value of this experimental work.

3.2. Density of States

The analyses on the total and partial density of states (DOS) are performed to further study the bonding characteristics and underlying mechanism of the structural stability of HfX compounds. Therefore, the total DOS (TDOS) and partial DOS (PDOS) computed by GGA method are presented and discussed herein. In Figure 2a, the Fermi level (E_F) is plotted at zero energy in all TDOS and PDOS spectra. Typically, there is not any energy gap identified near Fermi level for HfOs (Figure 2a), HfIr (Figure 2b) and HfPt (Figure 2c) in the TDOS, suggesting their essence of metallicity.

In the TDOS for HfOs (Figure 2a), the bonding interactions are dominated by the hybridization of Hfs and Oss states at −10 to −6 eV at the bonding states. Around the bonding states, the Osd states as the major role have intensively hybridized with the Hfd states as the minor role below the Fermi level. The two states have changed their roles in the hybridizations of above the Fermi level at the antibonding states. Around the Fermi level, a valley referring as a pseudogap, which is symbolized as the presence of covalent bonds [30,31], is considered to be the most observable feature in the TDOS. The pseudogaps have existed in the TDOS for HfOs (Figure 2a), HfIr (Figure 2b) and HfPt (Figure 2c), although their locations are different on energy scales. The pseudogap is located at the antibonding states for HfOs (Figure 2a), at the bonding states for HfIr (Figure 2b), and at the bonding states with the more negative energy states for HfPt (Figure 2c). Such differences should suggest HfOs has the least bonding stability.

For the sake of judging the structural stability of HfX compounds, the number of bonding electrons per atom is calculated based on the TDOS spectra. Since the charge interaction among bonding atoms is the critical factor to material’s stability, the compound possessing higher number of bonding electrons should be more structurally stable [32,33,34,35]. For HfOs, HfIr and HfPt phases, the number of bonding electrons per atom are 6.013, 6.493 and 6.995, accordingly. Conclusively, the HfX phases have the stability order of HfPt > HfIr > HfOs. This conclusion is in good accordance with the thermodynamic analysis shown in Table 1.

3.3. Elastic Properties

The elastic constants and elastic moduli are the critical information to study the mechanical properties of compounds. A full set of elastic constant for cubic crystal, including C₁₁, C₁₂ and C₄₄, can be achieved using the stress-train method [36] (

Table 2. The elastic constants (C_ij) for HfX (X = Os, Ir and Pt).

Compounds	C11 (GPa)	C12 (GPa)	C13 (GPa)	C33 (GPa)	C44 (GPa)
HfOs	402.1 a	149.7 a	-	-	121.0 a
	436.5 b	179.3 b	-	-	130.5 b
	393.7 c	139.8 c	-	-	110.1 c
	366.1 d	152.6 d	-	-	105.6 d
HfIr	285.7 a	239.5 a	-	-	103.2 a
	255.7 b	202.9 b	-	-	90.7 b
HfPt	244.3 a	209.2 a	-	-	67.8 a
	217.7 b	179.3 b	-	-	61.7 b
Hf	214.0 a	90.6 a	92.2 a	235.8 a	54.6 a
	193.6 b	82.7 b	77.4 b	205.1 b	56.3 b
	181.0 e	77.0 e	66.0 e	197.0 e	55.7 e

^a Theoretical values from GGA method in current work; ^b Theoretical values from LDA method in current work; ^c Theoretical values from reference [13]; ^d Theoretical values from reference [14]; ^e Experimental values from reference [37].

). Observably, the elastic constants obtained by LDA method are larger than GGA method in HfX compounds. In HfOs, the elastic constants derived from GGA method has agreed well with theoretical values from Arıkan’s [13] and Liu’s work [14]. Meanwhile, the elastic constants for pure Hf metal are calculated and presented with the published experimental values [37] for comparison, where the GGA computed elastic constants are in better agreement with experimental values [37].

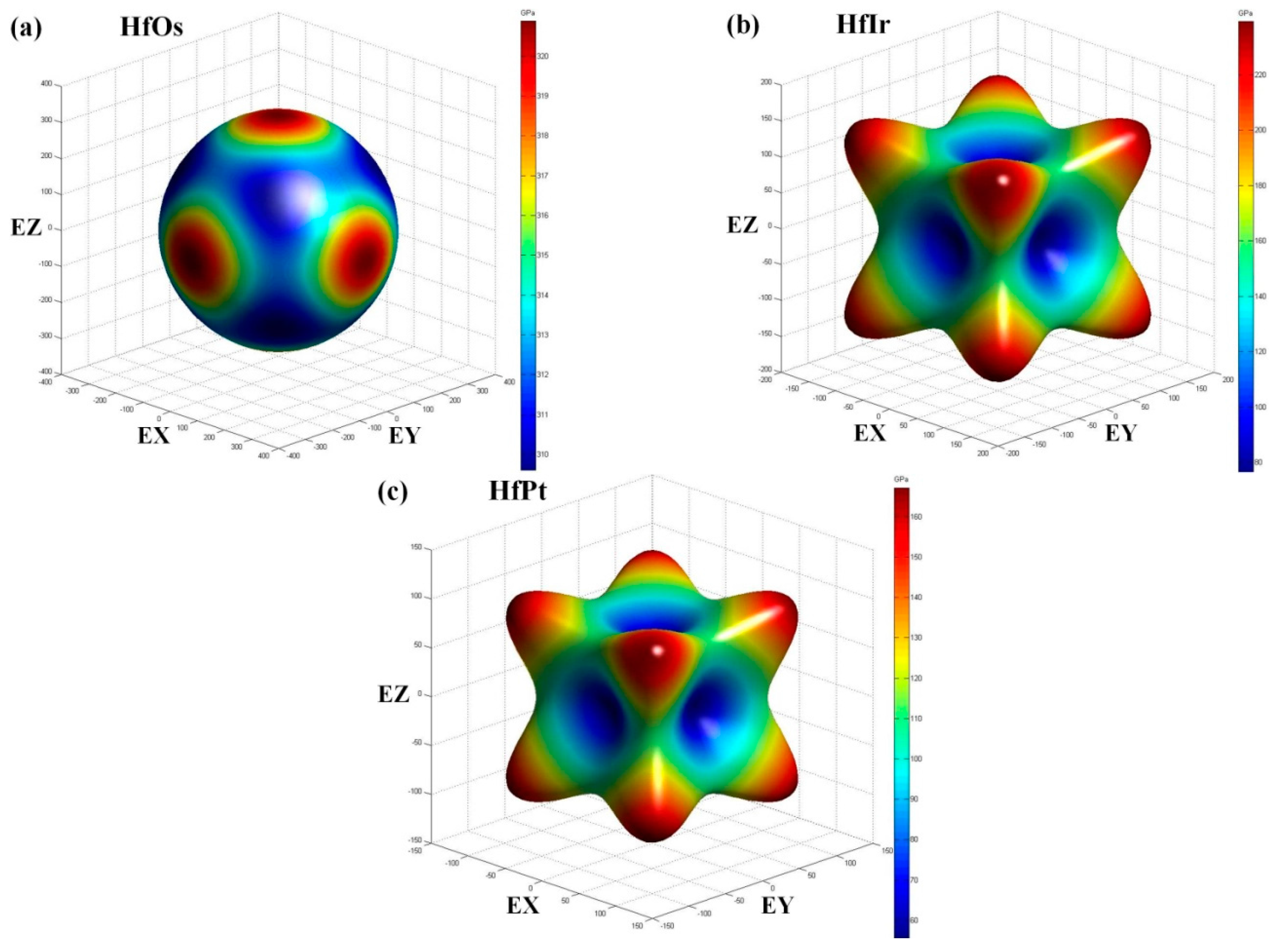
In order to analyze the elastic properties of HfX compounds, the elastic constants generated using GGA method are used as the example. C₁₁ is the symbol of compressive resistance along x axis. In each compound, the calculated C₁₁ has the largest value, indicating the incompressible essence of the compound under the x direction uniaxial stress [38]. HfOs has the most incompressible ability owing to the largest C₁₁ (402.1 GPa). Moreover, a larger C₄₄ (121.0 GPa) can reflect a stronger resistance to monoclinic shear in (100) plane, suggesting HfOs also has the strongest ability to resist shear distortion in (100) plane.

Furthermore, the mechanical stability is evaluated by Born’s criteria [39] for cubic crystals:

C₁₁ > 0; C₄₄ > 0; C₁₁ − C₁₂ > 0; C₁₁ + 2C₁₂ > 0.

(3)

HfX (X = Os, Ir and Pt) compounds are all found mechanically stable at the ground state by the successful validation of Born’s criteria.

In the engineering application, the elastic properties, i.e., bulk modulus (B), shear modulus (G), and Young’s modulus (E), are demanded in practice. Generally, the elastic properties can be derived from Voigt-Reuss-Hill (VRH) methods using elastic constants [40]. For cubic crystals, the equations are expressed as following [27,41,42]:

$$B_{\mathrm{V}}=B_{\mathrm{R}}=\frac{1}{3}(C_{11}+2C_{12}),$$

(4)

$$G_{\mathrm{V}}=\frac{1}{5}(C_{11}-C_{12}+3C_{44}),$$

(5)

$$G_{\mathrm{R}}=\frac{5(C_{11}-C_{12})C_{44}}{4C_{44}+3(C_{11}-C_{12})},$$

(6)

$$B=\frac{B_{\mathrm{V}}+B_{\mathrm{G}}}{2},$$

(7)

$$G=\frac{G_{\mathrm{V}}+G_{\mathrm{G}}}{2},$$

(8)

As soon as the bulk and shear moduli are achieved, Young’s modulus (E) and Poisson’s ratio (ν) can be predicted:

$$E=\frac{9BG}{3B+G},$$

(9)

$$\mathsf{\nu }=\frac{3B-2G}{2(3B+G)},$$

(10)

The calculated elastic moduli, Poisson’s ratio and B/G ratio using the VRH method at the ground state are tabulated for HfX compounds in

Table 3. The bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν), B/G ratio and hardness (H_V) for HfX (X = Os, Ir and Pt) and pure Hf deduced from the VRH method.

Compounds	B (GPa)	G (GPa)	E (GPa)	ν	HV (GPa)	B/G
HfOs	233.8 a	123.1 a	314.1 a	0.276 a	13.4a	1.900 a
	265.1 b	129.7 b	334.6 b	0.290 b	12.8b	2.043 b
	224.4 c	116.5 c	298.0 c	0.279 c	12.7c	1.926 c
	223.8 c	106.1 c	274.8 c	0.295 c	10.7c	2.110 c
HfIr	220.5 a	55.5 a	153.5 a	0.384 a	3.3a	3.977 a
	254.9 b	57.2 b	159.6 b	0.396 b	3.0b	4.458 b
HfPt	192.1 a	38.7 a	108.8 a	0.406 a	2.0a	4.962 a
	220.9 b	39.6 b	112.2 b	0.415 b	1.8b	5.572 b
Hf	118.6 a	57.2 a	147.8 a	0.292 a	-	2.074 a
	134.8 b	59.9 b	156.5 b	0.306 b	-	2.251 b
	108.5 e	55.8 e	142.9 e	0.28 e	-	1.944 e

^a Theoretical values from GGA method in current work; ^b Theoretical values from LDA method in current work; ^c Theoretical values from reference [13]; ^d Theoretical values from reference [14]; ^e Experimental values from reference [37].

, including the elastic moduli for pure Hf results for comparison. Overall, the elastic moduli obtained using GGA method are smaller than those provided by LDA method. Comparably, the calculated elastic moduli generated by the GGA method are in good agreement with theoretical values for HfOs. In detail, the elastic moduli are all larger than pure Hf in HfOs. However, HfIr has the similar shear and Young’s modulus over pure Hf, and HfPt owns the smaller values correspondingly. Therefore, HfOs should be a credible hardening phase in pure Hf.

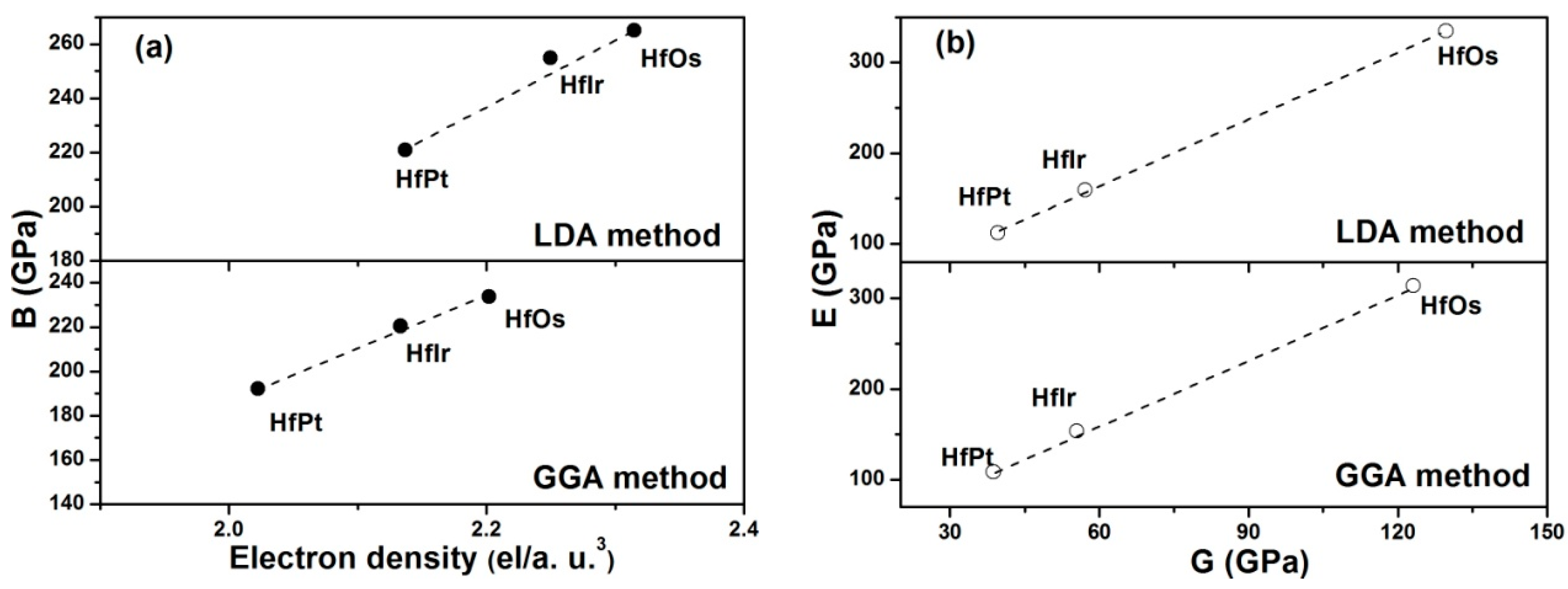
Typically, the bulk modulus (B) suggests the resistant ability against volume change under pressure of materials. In addition, the bulk moduli calculated by both methods using VRH principles are in good agreement with those provided by the EOS equations (Table 1), confirming good self-consistency of this work. From Table 3, it is seen that HfOs possesses the largest resistance to volume change by applied pressure, while HfPt has the smallest. In order to illustrate the fundamental factor on bulk moduli of HfX compounds, the relationship between electron densities and bulk moduli are constructed in Figure 3a. Herein, the electron density (n) is the quotient of the bonding valence (Z_B) and the volume per atom (V_M) in metal [43]. For example, the electron density (n) is evaluated using the following equation in HfX compounds:

$$n(\mathrm{HfX})=Z_{\mathrm{B}}(\mathrm{HfX})/V_{\mathrm{M}}(\mathrm{HfX}),$$

(11)

where V_M(HfX) is the volume (cm³/mol) of each HfX compound; Z_B(HfX) is the bonding valence in (el/atom) rationalized from Vegard’s law [44]:

$$Z_{\mathrm{B}}(\mathrm{HfX})=(Z_{\mathrm{B}}(\mathrm{Hf})+Z_{\mathrm{B}}(\mathrm{X}))/2,$$

(12)

where the bonding valence of pure element can be found in the reference [45].

In Figure 3a, the correlation between the electron density and bulk modulus can be constructed using the computed values either by LDA or GGA method. In detail, the linear relationships between the electron density and bulk modulus are clearly seen in HfX compounds.

The shear modulus has reflected the resistance to reversible deformations under the shear stress [27]. A larger shear modulus for HfOs suggests its higher resistance to reversible deformations. Young’s modulus is a symbol of the stiffness of a solid [46]. The material with a larger Young’s modulus is stiffer. Therefore, HfOs is much stiffer than any other considered HfX compounds due to its higher Young’s modulus. Overall, Young’s modulus has linearly improved with the shear modulus in the order of HfOs > HfIr > HfPt for both LDA and GGA methods (Figure 3b).

The B/G value [47] and Poisson’s ratio (ν) [32,48] have determined the brittleness and ductility of the solid. A solid with B/G < 1.75 or ν < 0.26 is usually brittle. Otherwise, it is ductile. In Table 3, it is found the HfPt is the most ductile compound with the largest B/G value and Poisson’s ratio, and HfOs is the least ductile compound owing to the smallest B/G value and Poisson’s ratio. Notably, the HfX compounds have similar ductile essence due to the small variations of B/G values and Poisson’s ratios using both GGA and LDA methods.

The hardness (H_V) is associated with the plastic and elastic properties of an intermetallic compound. The hardness can be calculated by a semi-empirical equation [49]:

$$H_{\mathrm{V}}=0.92{(G/B)}^{1.137}{G}^{0.708},$$

(13)

where B and G are the bulk modulus and shear modulus, respectively.

The hardness values (H_V) of HfX (X = Os, Ir and Pt) compounds are tabulated in Table 3. Generally, the hardness is related with the values of G/B and G that the high values of G/B and G correspond to the high hardness. It is seen that the hardness value computed by GGA method is a bit larger than LDA method. Overall, the hardness values (H_V) have followed the order of HfPt < HfIr < HfOs in both GGA and LDA methods.

3.4. Elastic Anisotropy

The degree of elastic anisotropy is a critical property related to the engineering application. The universal anisotropic index (A^U) [50] is a universal measure to quantify the single crystalline elastic anisotropy in consideration of the contributions from both the bulk and the shear modulus, i.e., [51],

$$A^{\mathrm{U}}=5\frac{G_{\mathrm{V}}}{G_{\mathrm{R}}}+\frac{B_{\mathrm{V}}}{B_{\mathrm{R}}}-6,$$

(14)

where B_V and G_V are the symbols of the Voigt bounds for bulk and shear modulus, respectively. B_R and G_R are the symbols of the Reuss bounds for bulk and shear modulus, respectively.

If A^U = 0 for a crystal, the crystal should be isotropic. A larger deviation of A^U from zero has indicated a severer degree of anisotropy. In cubic crystals, B_V/B_R is always equal to 1. Therefore, the universal anisotropic index is governed by G_V/G_R. Therefore, the calculated universal anisotropies by both LDA and GGA methods (

Table 4. The calculated Voigt and Reuss bounds for bulk (shear) modulus, and universal anisotropic index (A^U) for HfX (X = Os, Ir and Pt).

Compounds	BV	BR	GV	GR	BV/BR	GV/GR	AU
GGA method
HfOs	233.8	233.8	123.1	123.0	1	1.000	0.0022
HfIr	220.5	220.5	65.0	45.9	1	1.415	2.077
HfPt	192.1	192.1	44.7	32.7	1	1.367	1.830
LDA method
HfOs	265.1	265.1	129.7	129.7	1	1.000	0.00026
HfIr	254.9	254.9	71.1	43.2	1	1.646	3.229
HfPt	220.9	220.9	47.7	31.6	1	1.494	2.470

) are reduced in the sequence of HfIr > HfPt > HfOs. In detail, HfIr and HfOs have the largest and smallest universal anisotropies, respectively.

In order to describe the elastic anisotropic behavior more directly and effectively, the three-dimensional (3D) surface constructions of the directional dependence of reciprocal of Young’s modulus have also been studied by following equations [52]:

$$\frac{1}{E}=S_{11}-2(S_{11}-S_{12}-\frac{S_{44}}{2})(l_1^2{l}_2^2+l_2^2{l}_2^3+l_1^2{l}_3^2),$$

(15)

where S_ij is the usual elastic compliance constant, which can be obtained from the inverse of the matrix of elastic constants; l₁, l₂ and l₃ are the direction cosines in the sphere coordination.

If the 3D directional dependence of Young’s modulus exhibits a spherical shape, the crystal is ideal isotropic. Practically, the deviation extent from the spherical shape has reflected the degree of anisotropy. In Figure 4a, HfOs shows a quite spherical shape, signifying its near isotropic behavior. Furthermore, HfIr exhibits the largest deviation from the sphere shape with the strongest deviation along the <111> directions, confirming its intensive anisotropic behavior. Generally, the degree of the elastic anisotropy for HfX has followed the increasing order of HfOs < HfPt < HfIr. This conclusion is in good compliance with the result generated from the universal anisotropic index.

3.5. Anisotropy of Acoustic Velocities and Debye Temperature

In the crystalline material, the sound velocities are related to the crystal symmetry and the propagation direction. In cubic crystals, the pure transverse and longitudinal modes can be found in [111], [110] and [001] directions. With respect to other directions, the sound propagating modes have included the quasi-transverse or quasi-longitudinal waves. Therefore, the sound velocities can be derived from elastic constants using following expressions [53]:

$$[100]v_{\mathrm{l}}=\sqrt{C_{11}/\rho };[010]v_{\mathrm{t}1}=[001]v_{\mathrm{t}2}=\sqrt{C_{44}/\rho },$$

(16)

$$[110]v_{\mathrm{l}}=\sqrt{(C_{11}+C_{12}+C_{44})/(2\rho )},$$

(17)

$$[1\overline{1}0]v_{\mathrm{t}1}=\sqrt{(C_{11}-C_{12})/\rho },[001]v_{\mathrm{t}2}=\sqrt{C_{44}/\rho },$$

(18)

$${[111]}_{v1}=\sqrt{(C_{11}+2C_{12}+4C_{44})/(3\rho )},$$

(19)

$$[11\overline{2}]v_{\mathrm{t}1}=[11\overline{2}]v_{\mathrm{t}2}=\sqrt{(C_{11}-C_{12}+C_{44})/(3\rho )},$$

(20)

where ρ is the density; v_l is the longitudinal sound velocity; v_t1 and v_t2 refer to the first and the second transverse mode of sound velocity, respectively.

Generally, C₁₁ has determined the longitudinal sound velocity along [100] direction. C₄₄ is related to the transverse modes along [010] and [001] directions. C₁₁, C₁₂ and C₄₄ can influence the longitudinal sound velocities along [110] and [111] directions in combination.

The longitudinal and the transverse sound velocities by both LDA and GGA methods along [100], [110] and [111] directions for HfX compounds are exhibited in

Table 5. The calculated anisotropic sound velocities (m/s) for HfX (X = Os, Ir and Pt).

	[111]		[110]			[100]
Crystal orientations	[111]vl	[$11\overline{2}$]vt1,2	[110]vl	[$1\overline{1}0$]vt1	[001]vt2	[100]vl	[010]vt1	[001]vt2
GGA method
HfOs	4796.0	2691.9	4425.2	3833.6	2653.8	4838.3	2653.8	2653.8
HfIr	4487.1	1679.3	4024.3	1763.5	2313.0	3882.6	2313.0	2313.0
HfPt	4094.4	1427.9	3743.5	1531.8	1941.7	3647.2	1941.7	1941.7
LDA method
HfOs	4930.2	2674.7	4545.3	3773.4	2687.7	4916.0	2687.7	2687.7
HfIr	4684.4	1668.4	4191.3	1607.1	2401.7	3996.8	2401.7	2401.7
HfPt	4243.2	1408.4	3882.7	1424.5	1980.3	3758.8	1980.3	1980.3

. For the sound velocities obtained from LDA method, the longitudinal sound velocity v_l of each compound is reduced in the order of [111] > [110] > [100]. The anisotropic properties of sound velocities have also confirmed the elastic anisotropies in these cubic crystals. Meanwhile, the sound velocities derived from GGA method have shown the similar tendencies with those from LDA method.

The theoretically calculated structural properties (i.e., density) and elastic properties (i.e., Bulk modulus, shear modulus and Poisson’s ratio) can be used to deduce Debye temperature (Θ), as shown in the following equation [26,54]:

$$\mathsf{\Theta }=\frac{h}{k}{[\frac{3n}{4\pi }(\frac{N_A\rho }{M})]}^{\frac{1}{3}}{v}_D,$$

(21)

where h is Planck’s constant (h = 6.626 × 10⁻³⁴ J/s); N_A is Avogadro’s number (N_A = 6.023 × 10⁻²³/mol); k is Boltzmann’s constant (k = 1.381 × 10⁻²³ J/K); M is the molecular weight; n is the number of atoms per formula unit.

v_D is the average sound velocity in polycrystalline materials, as exhibited using the equation:

$$v_{\mathrm{D}}={[\frac{1}{3}(\frac{1}{v_{\mathrm{L}}^3}+\frac{2}{v_{\mathrm{T}}^3})]}^{-\frac{1}{3}},$$

(22)

where v_T and v_L are the transverse and longitudinal sound velocities, including:

$$v_{\mathrm{T}}=\sqrt{\frac{G}{\rho }},$$

(23)

$$v_{\mathrm{L}}=\sqrt{\frac{B+\frac{4}{3}G}{\rho }},$$

(24)

Table 6. Sound velocity (m/s) and Debye temperature (K) for HfX (X = Os, Ir and Pt).

Compounds	vL (m/s)	vT (m/s)	vD (m/s)	Θ (K)
GGA method
HfOs	4812.7	2676.5	2978.3	339.5
HfIr	4166.6	1808.2	2040.8	231.2
HfPt	3859.0	1538.0	1741.1	194.4
LDA method
HfOs	4924.5	2679.9	2987.0	346.2
HfIr	4303.0	1788.1	2021.4	233.1
HfPt	3979.1	1514.3	1716.5	195.2

shows the sound velocity (m/s) and Debye temperature (K) for HfX (X = Os, Ir and Pt) calculated by GGA and LDA methods. Generally, these values calculated by LDA method have the larger values than those computed by GGA method. Specifically, the following reduced orders have shown as HfOs > HfIr > HfPt in Debye temperatures.

3.6. Thermal Conductivity

The thermal conductivities (k) is a useful physical parameter for practical applications. The thermal conductivity is reduced with elevating temperature to a limiting value known as the minimum thermal conductivity (k_min), which can be evaluated according to Cahill’s model [55]:

$$k_{\min }=\frac{k}{2.48}{n}^{\frac{2}{3}}(v_l+v_{t1}+v_{t2}),$$

(25)

where k is Boltzmann constant; n is the number of density of atoms per volume. v_l and v_t are the longitudinal and transverse sound velocities, respectively (

Table 7. Calculated minimum thermal conductivities k_min (W/m/K) for HfX (X = Os, Ir and Pt).

Compounds	n (10303)	[100] kmin	[110] kmin	[111] kmin	kmin
GGA method
HfOs	0.0561	0.828	0.890	0.391	0.829
HfIr	0.0551	0.686	0.653	0.362	0.627
HfPt	0.0528	0.590	0.565	0.321	0.543
LDA method
HfOs	0.0590	0.868	0.929	0.416	0.868
HfIr	0.0581	0.735	0.685	0.391	0.658
HfPt	0.0558	0.627	0.592	0.345	0.569

).

Table 7 exhibits the calculated k_min values using Cahill’s model. Generally, the lattice thermal conductivity and the electronic thermal conductivity are the main compositions to the total thermal conductivity. At lower temperature, the effect from electron-phonon scattering is considered limited. Therefore, the thermal conductivities of HfX (X = Os, Ir and Pt) are ascribed to the lattice thermal conductivities at the ground state. The derived thermal conductivities are found small thereby. Based on Callaway-Debye theory [56], the lattice thermal conductivity is proportional to Debye temperature. It means a higher Debye temperature should correspond to a larger lattice thermal conductivity. Therefore, HfOs has the larger thermal conductivity than HfIr and HfPt in order. It is seen that the values offered by the GGA method are always smaller, but own the similar tendency with the LDA method. These HfX compounds show the relatively lower thermal conductivities, indicating that they are poor thermal conductors at the ground state.

Cahill’s model is suitable to discuss the anisotropic behavior of compounds on the thermal conductivity, since it has involved with treating the total thermal conductivity in association with each acoustic branch. For instance, it is seen that the calculated thermal conductivities have exhibited anisotropic behaviors owing to the differences of v_l, v_t1 and vt2 along [100], [110] and [111] directions. In detail, k_min[111] is always smaller than k_min[100] and k_min[110], suggesting that the dependence of thermal conductivities along [111] direction is less prominent than those along [100] and [110] directions. Although there is lacking experimental values for comparison, our theoretical results should prove the guidance for future studies.

4. Conclusions

The structural, electronic and elastic properties of B2 HfX (X = Os, Ir and Pt) compounds have been studied using first-principles calculations. Initially, the structural optimizations are comparable and acceptable for HfX compounds using both GGA and LDA methods. The calculated formation enthalpies by GGA and LDA methods have confirmed that the thermodynamic stability is in the order of HfPt > HfIr > HfOs. Secondly, the calculated electronic structures are derived, and similar features are identified in DOS spectra for HfX. The results show the sequence of structural stability should be HfPt > HfIr > HfOs, which is in good agreement with thermodynamic analyses. Mechanically, the elastic moduli obtained by GGA method are typically smaller than LDA method. In detail, the calculated bulk moduli using VRH method are in good agreement with those provided by EOS equation. Besides, the calculated bulk moduli are in the order of HfOs > HfIr > HfPt, where the bulk moduli can be correlated with electron densities in compounds. Additionally, Young’s modulus has augmented linearly with the shear modulus. HfOs has the Young’s modulus of 314.1 GPa and hardness of 13.4 GPa by GGA method, which should be a credible hardening phase in pure Hf. Then, the ductile essence is in the sequence of HfPt > HfIr > HfOs according to the analyses on Poisson’s ratio and B/G ratio. Based the universal anisotropic indexes and 3D surface constructions, the elastic anisotropy has followed the increasing order of HfIr > HfPt > HfOs. Finally, the anisotropy of acoustic velocities, Debye temperatures and thermal conductivities are obtained and discussed. Our results are hoped to inspire future experimental and theoretical investigations on these Hf-based compounds.