A Unified Physical Model for Creep and Hot Working of Al-Mg Solid Solution Alloys
Abstract
:1. Introduction
2. The Model
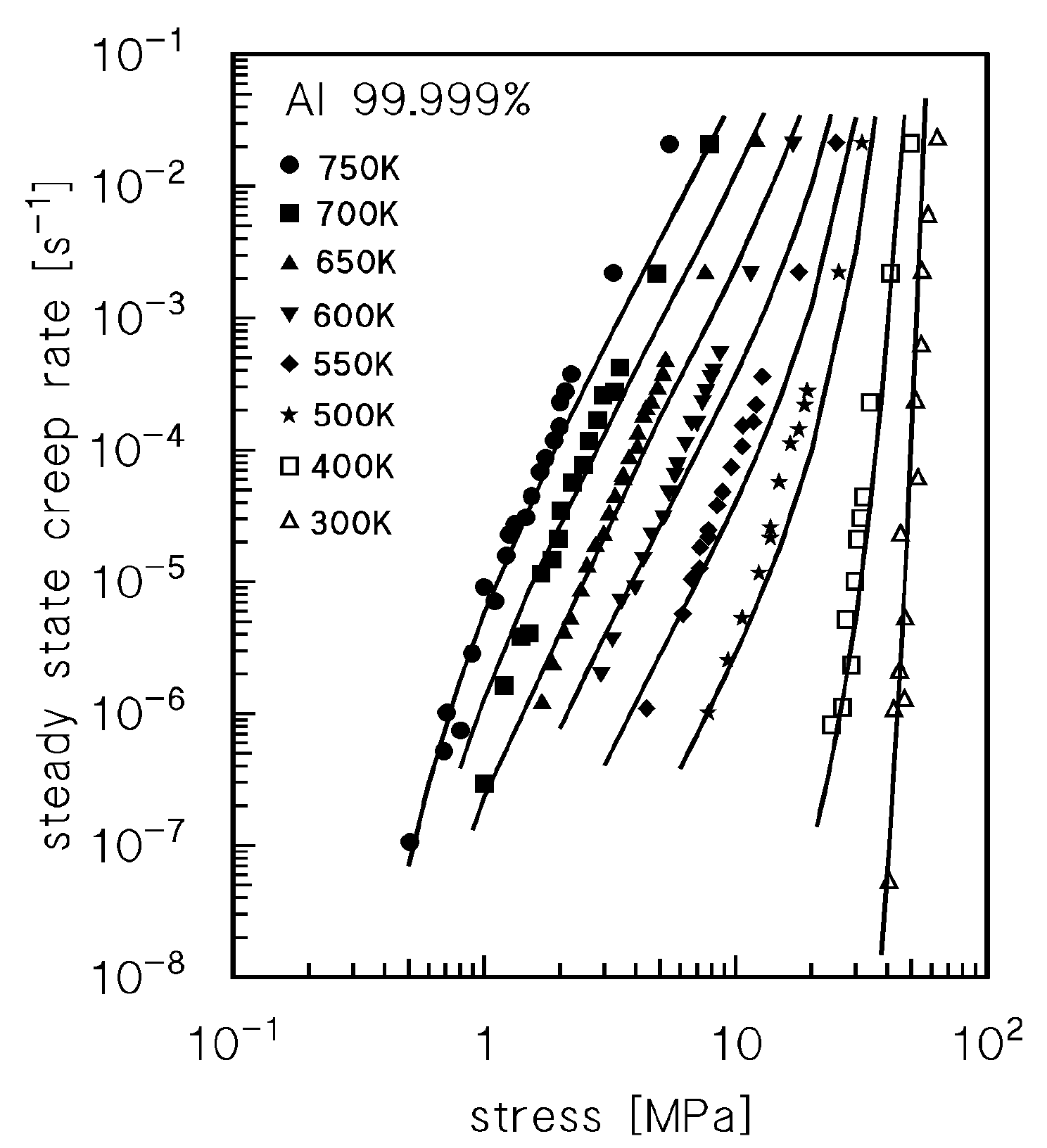
3. Description of High Purity Aluminium
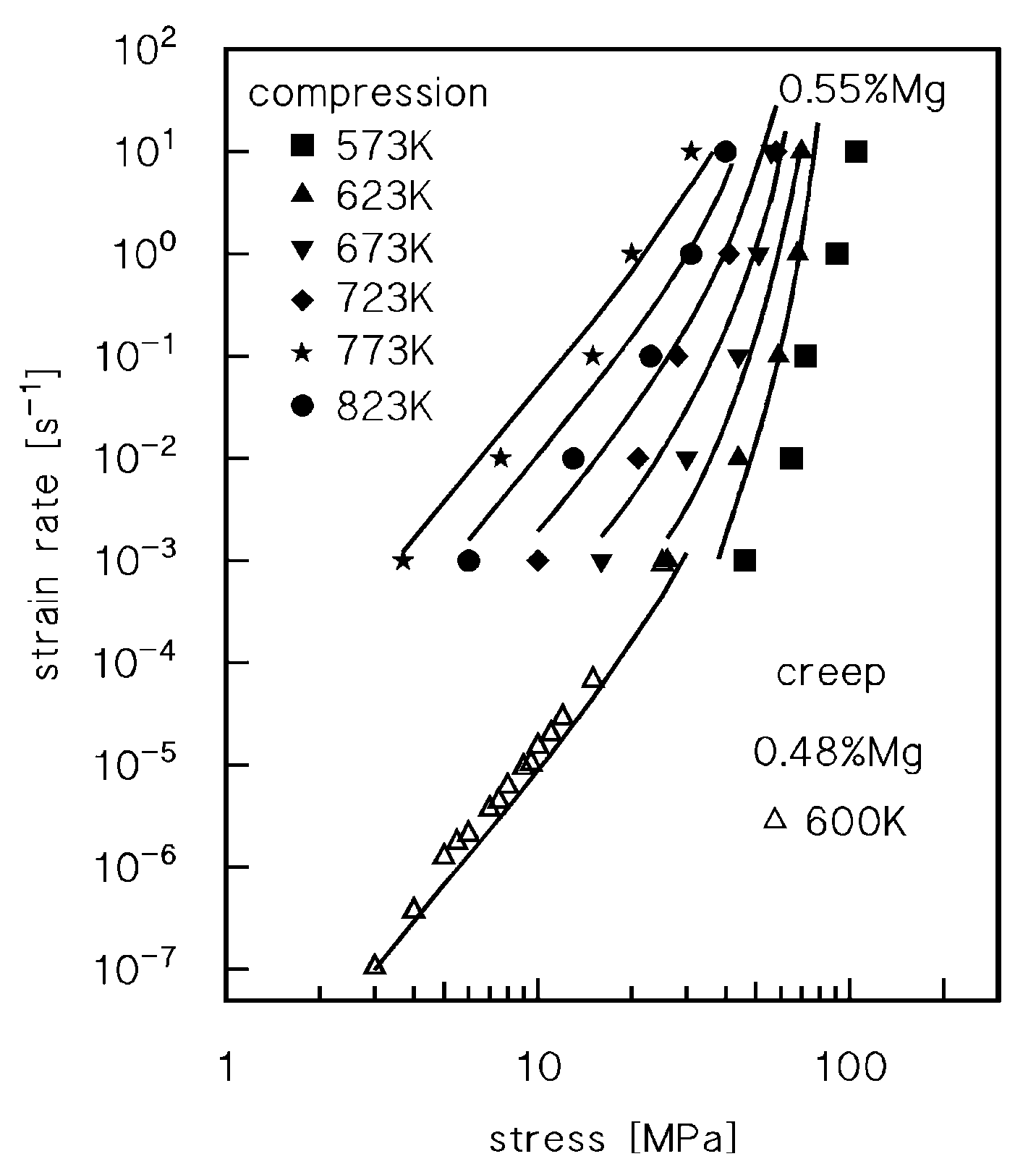
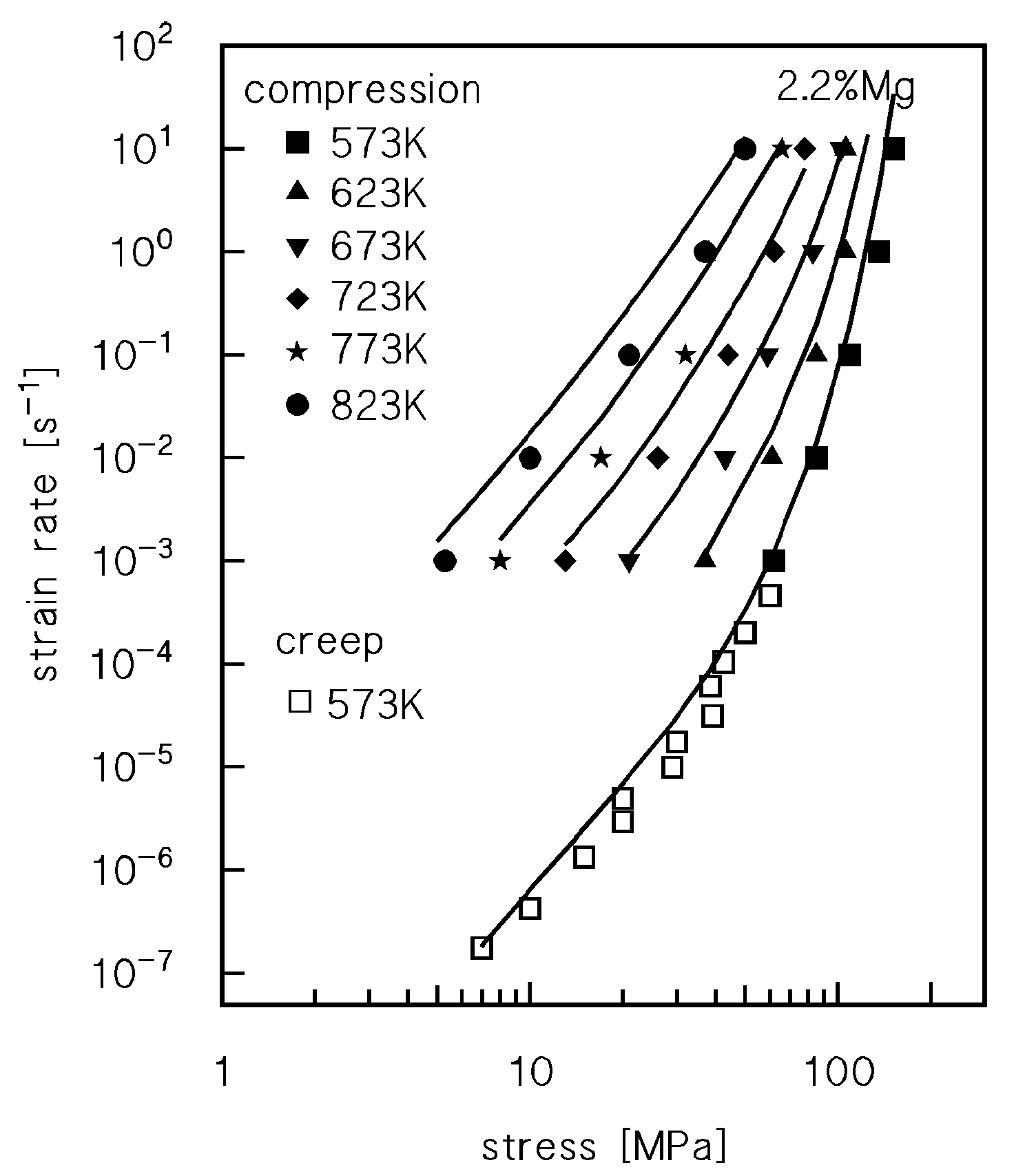
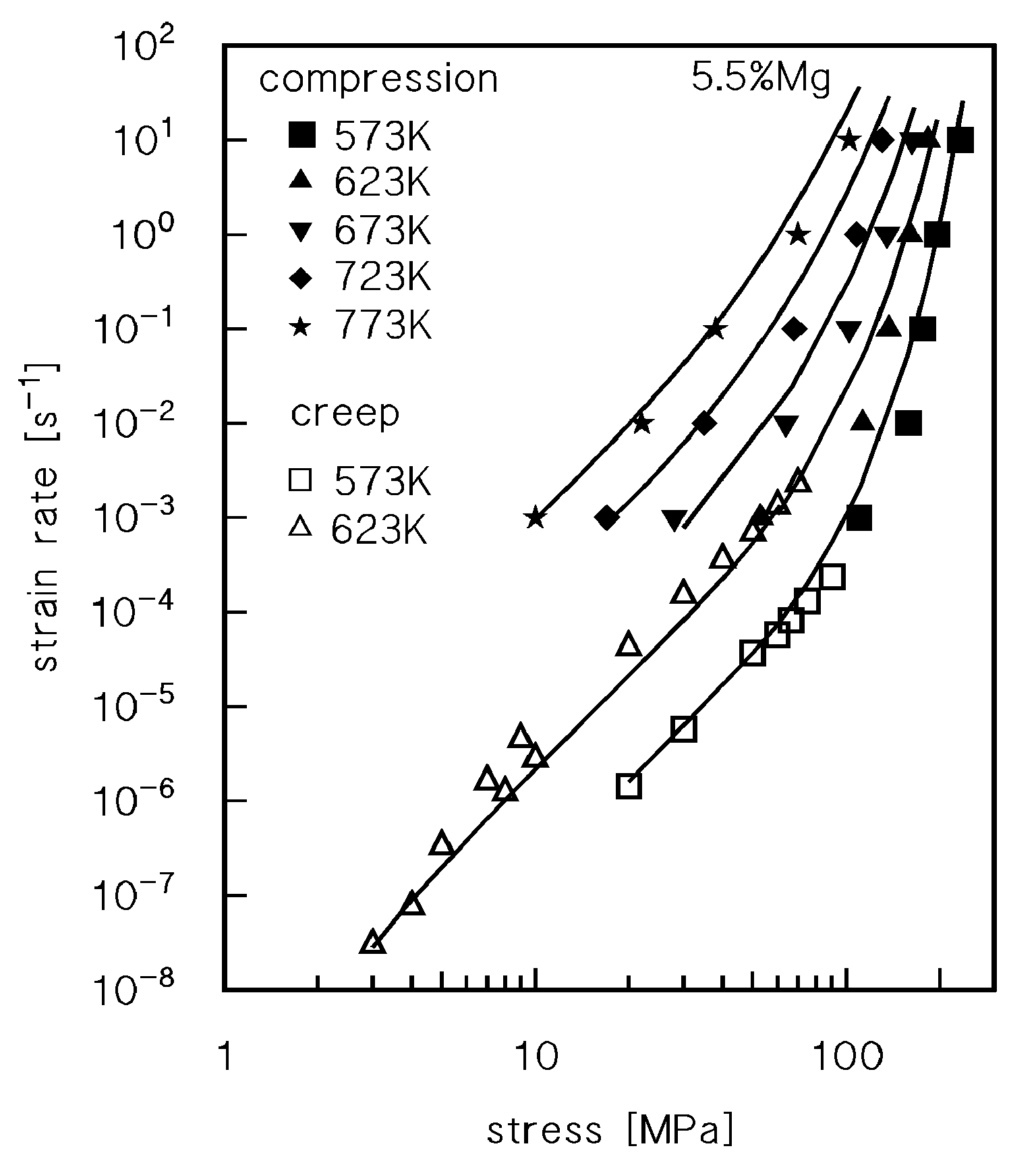
4. Description of High Purity Aluminium-Magnesium Single Phase Alloys
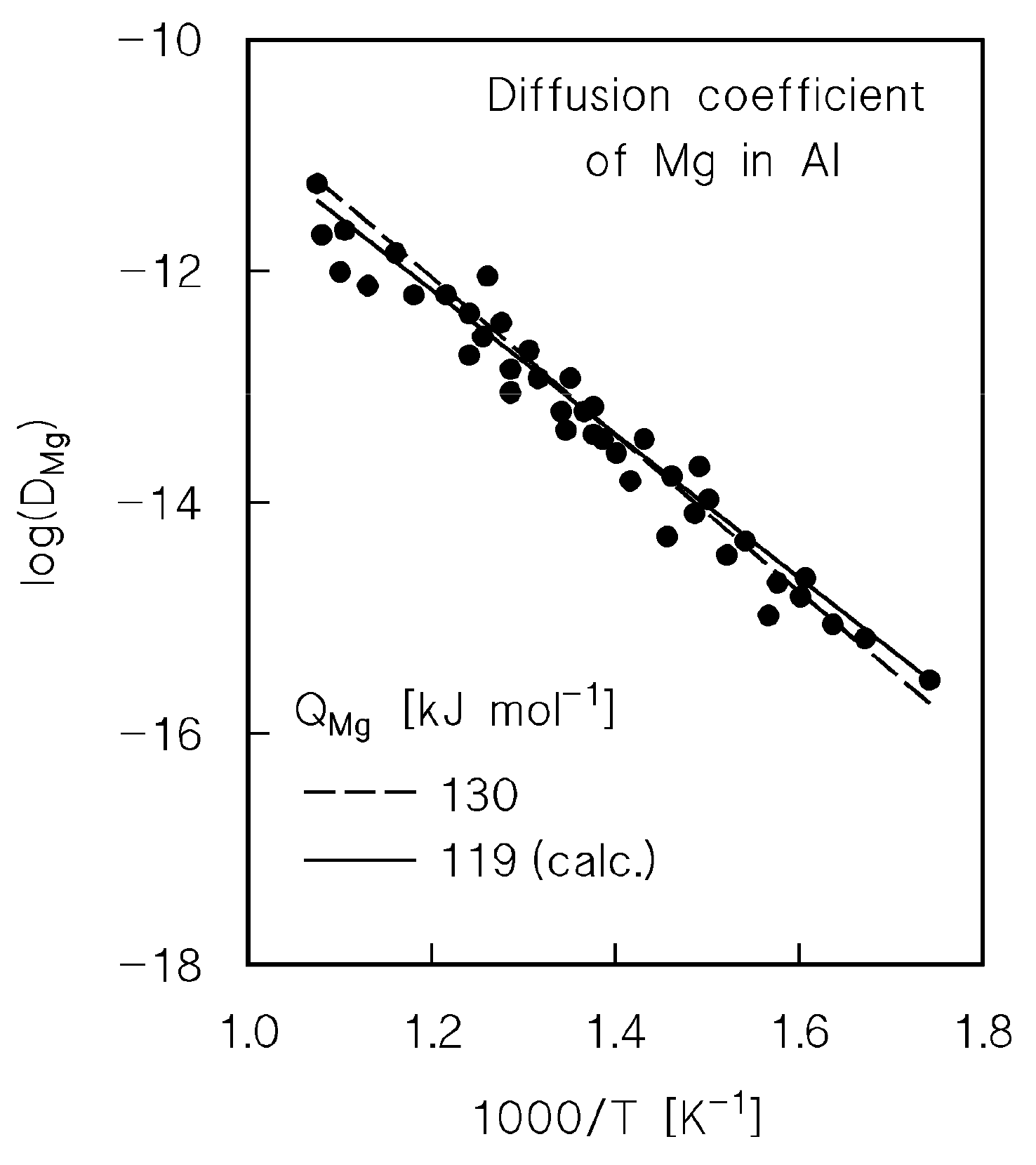
4.1. Diffusion Coefficient
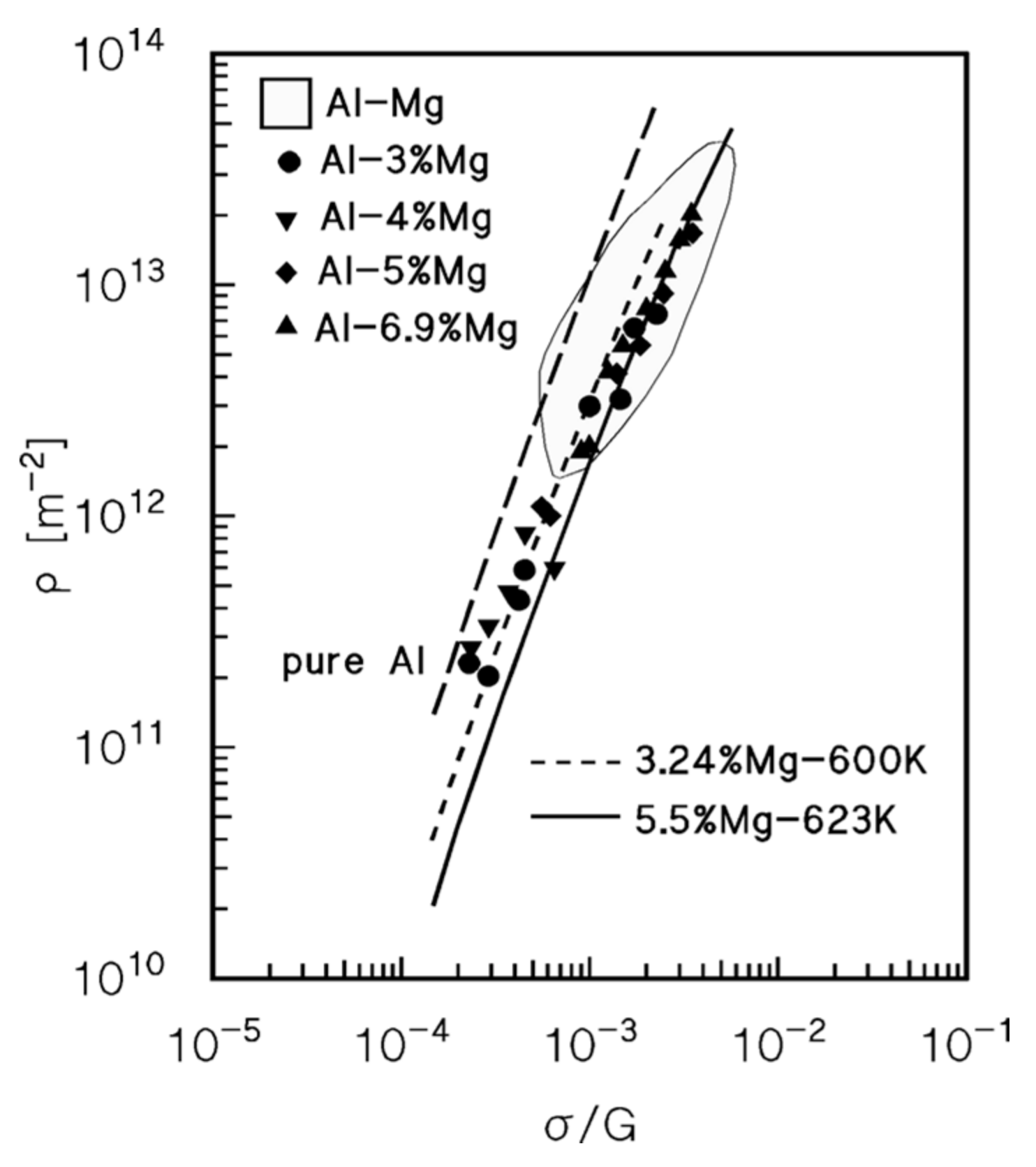
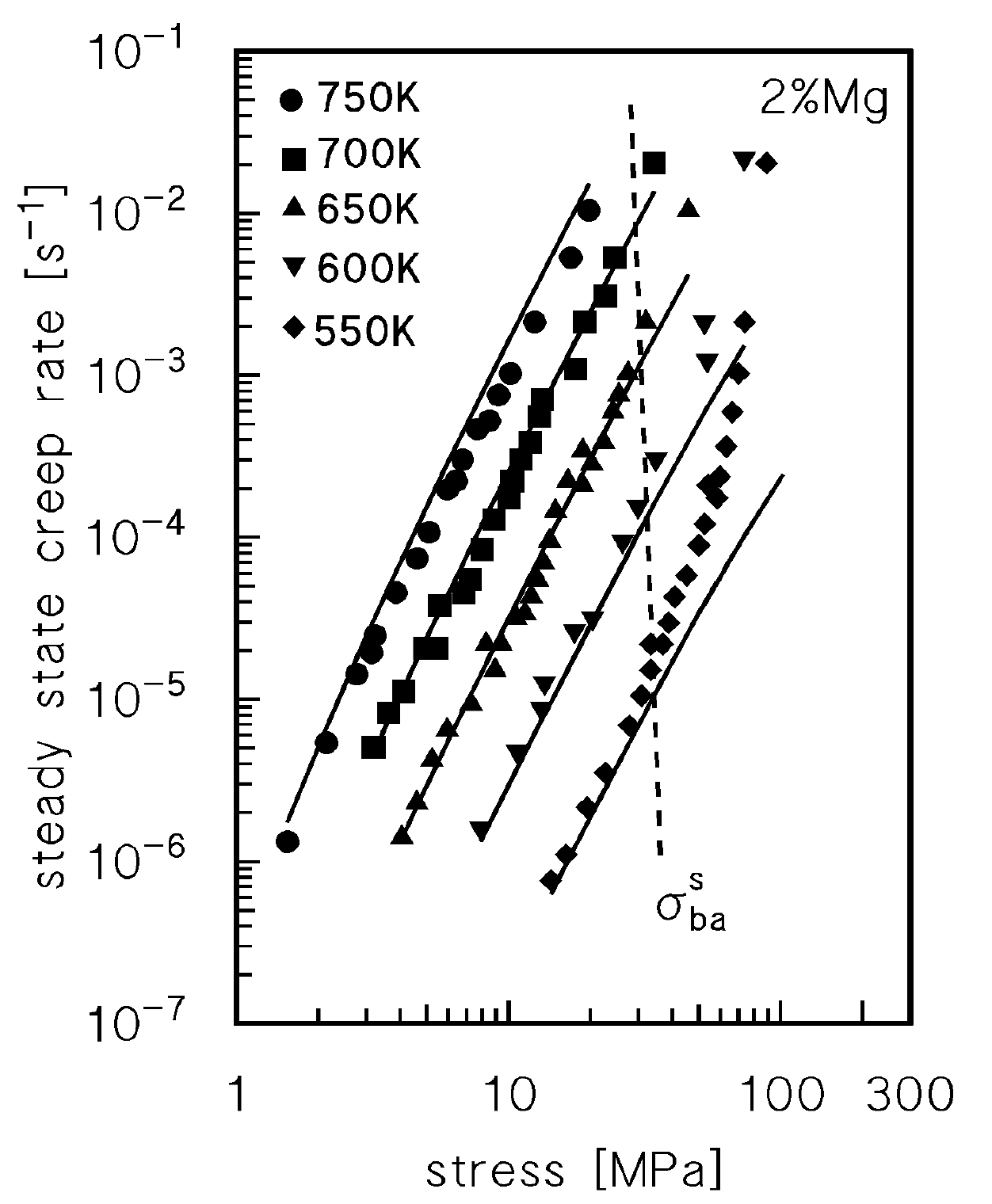
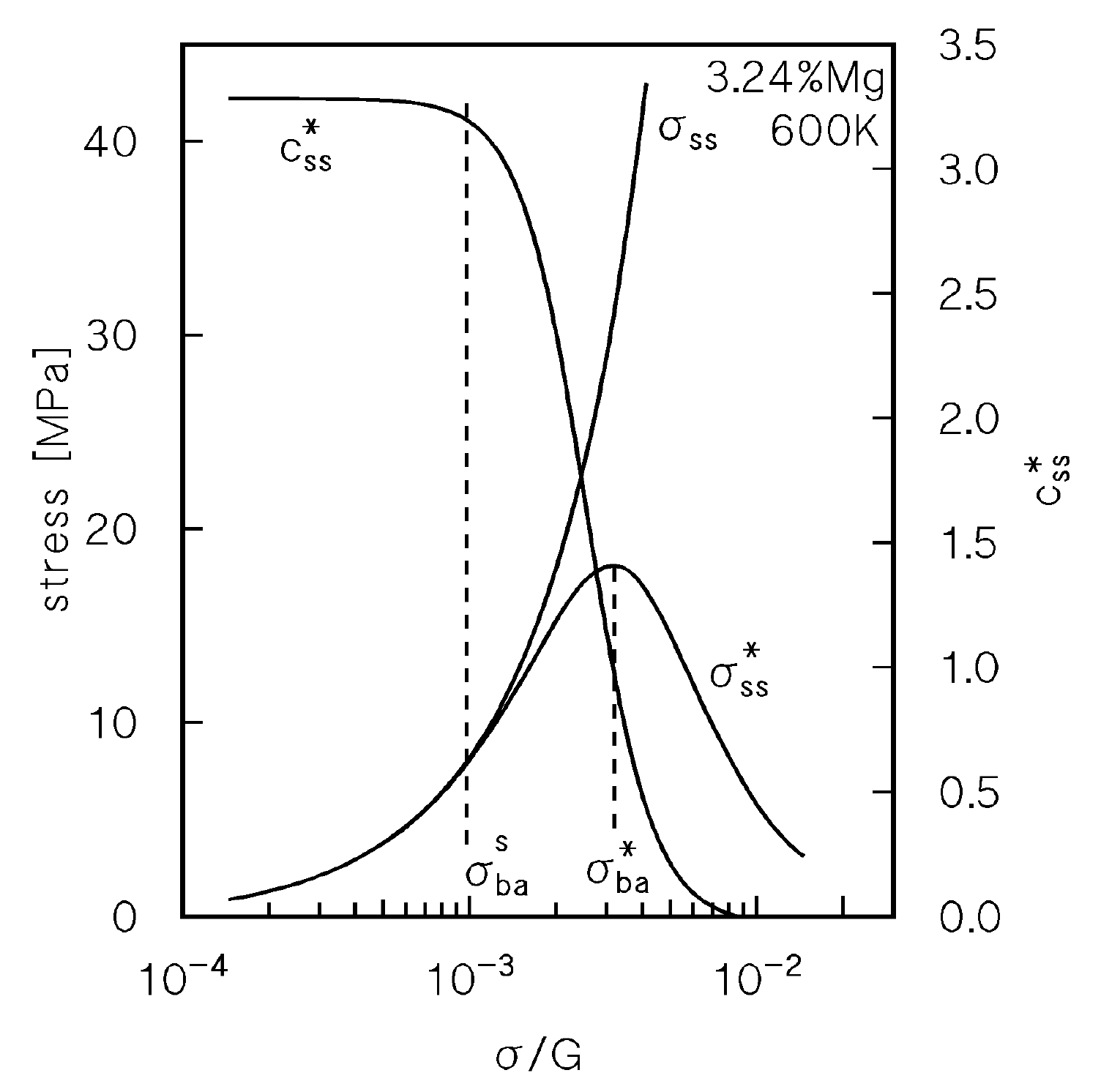
4.2. Drag Stress Calculation and Experimental Datasets on Dislocation Density and Strain Rate
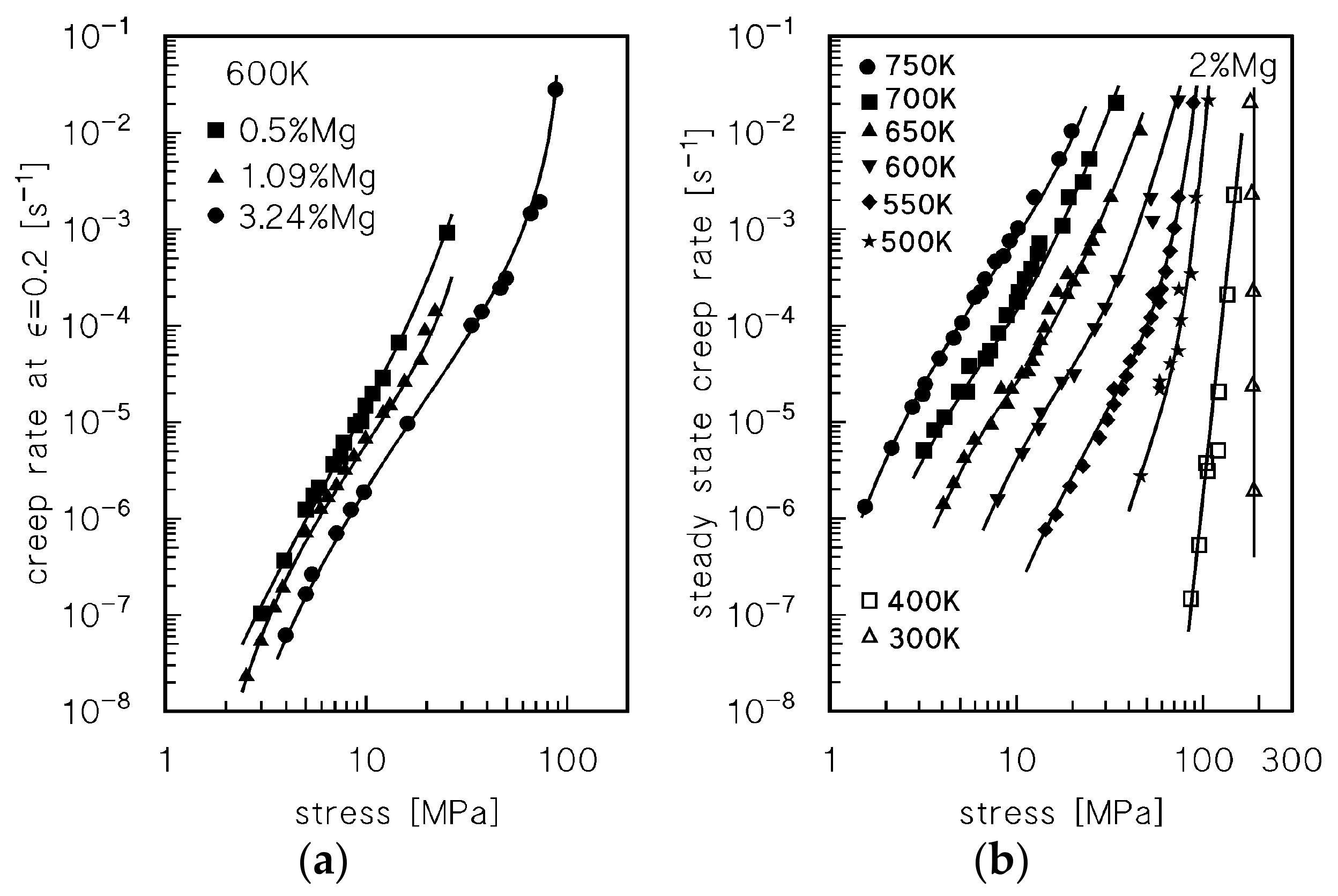
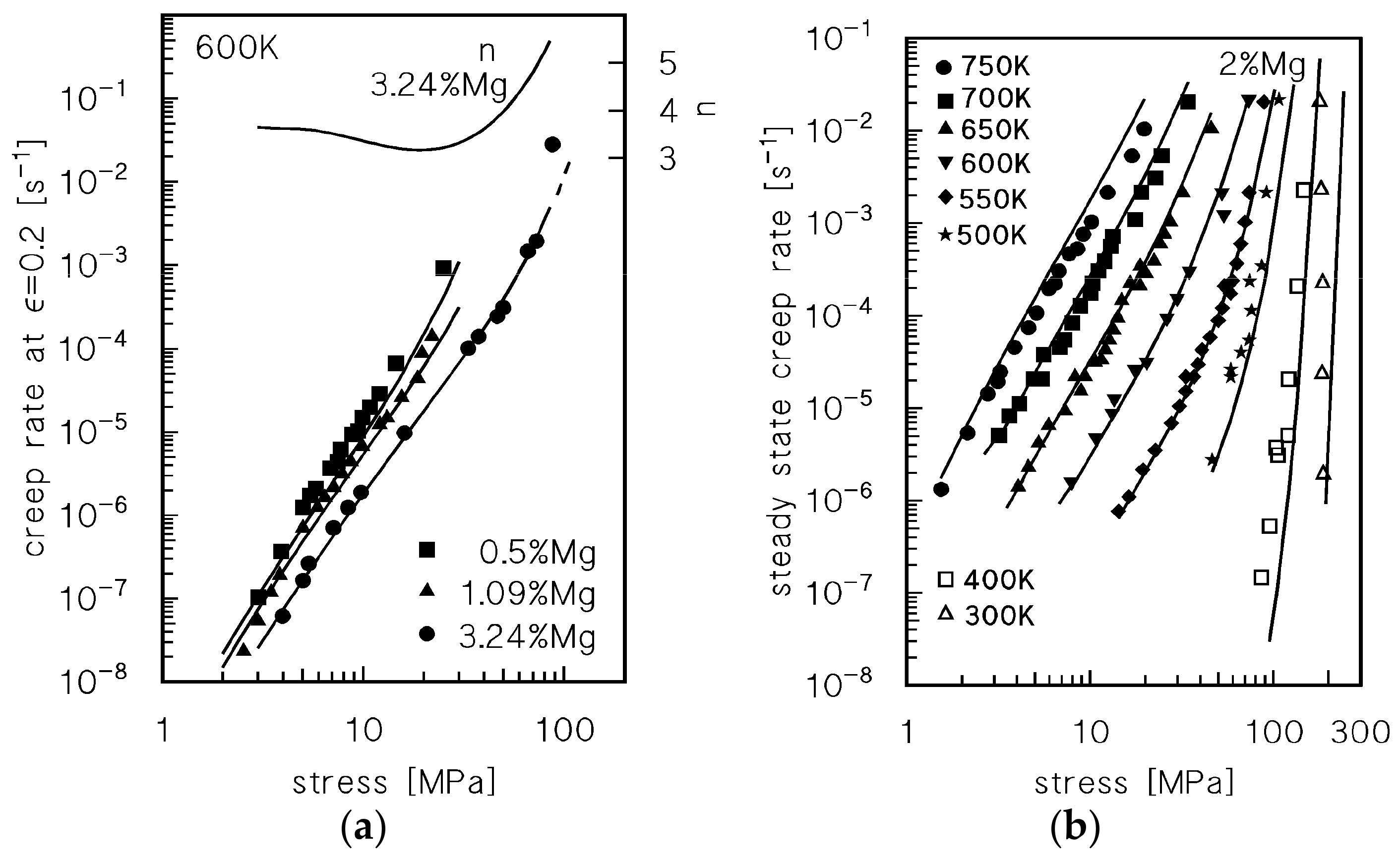
4.3. Viscous-Glide Controlled Creep: Strain Rate Dependence on Stress and Temperature at T ≥ 523 K
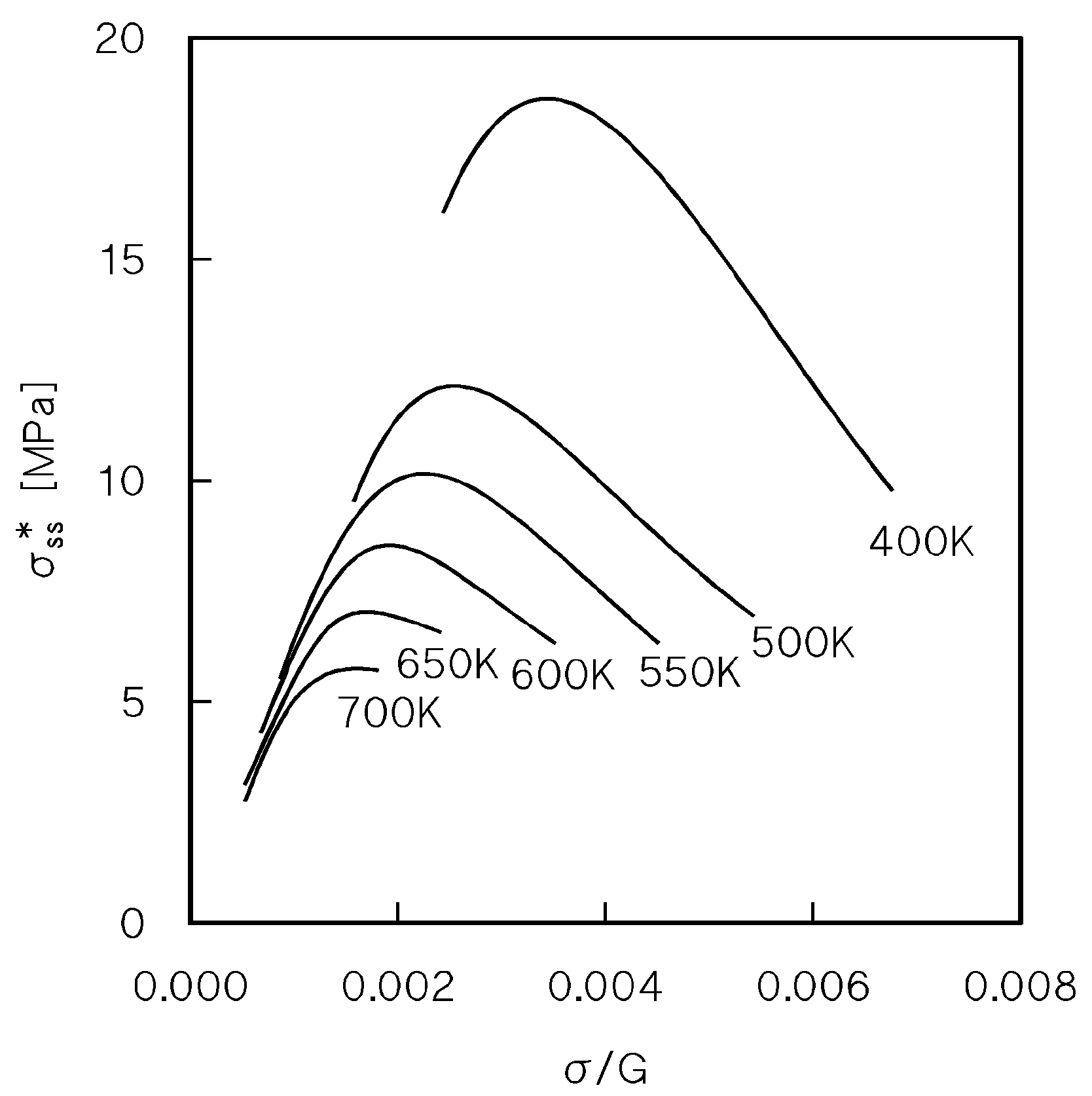
4.4. Creep Above the Transition for Break-Away of Dislocations from Solute Atom Atmospheres
4.5. Hot Working as an Extension of Creep: The Model in the High Strain Rate Plasticity Regime
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oikawa, H.; Langdon, T.G. The creep characteristics of pure metals and metallic solid solution alloys. In Creep Behaviour of Crystalline Solids; Wilshire, R., Evans, R.W., Eds.; Pineridge Press: Swansea, UK, 1985; pp. 33–82. ISBN 9780906674420. [Google Scholar]
- Čadek, J. Creep in Metallic Materials; Elsevier: Amsterdam, The Netherlands, 1988; pp. 160–175. ISBN 9780444989161. [Google Scholar]
- Kassner, M.E.; Pérez-Prado, M.T. Fundamentals of Creep in Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2004; pp. 11–120. ISBN 9780080436371. [Google Scholar]
- Oikawa, H.; Honda, K.; Ito, S. Experimental study on the stress range of class I behaviour in the creep of Al-Mg alloys. Mater. Sci. Eng. 1984, 64, 237–245. [Google Scholar] [CrossRef]
- Sato, H.; Maruyama, K.; Oikawa, H. Effects of the third element on creep behaviour of Al-Mg and α-Fe-Be sold solution alloys. Mater. Sci. Eng. A 1997, 234–236, 1067–1070. [Google Scholar] [CrossRef]
- Horita, Z.; Langdon, T.G. High temperature creep of Al-Mg alloys. In Strength of Metals and Alloys, Proc. ICSMA7; McQueen, H.J., Bailon, J.P., Dickson, J.I., Jonas, J.J., Akben, M.G., Eds.; Pergamon Press: Oxford, UK, 1986; pp. 797–802. ISBN 0080316409. [Google Scholar]
- Fernández, R.; González-Doncel, G. A unified description of solid solution creep strengthening in Al-Mg alloys. Mater. Sci. Eng. A 2012, 550, 320–324. [Google Scholar] [CrossRef] [Green Version]
- Sandström, R. Influence of phosphorus on the tensile stress strain curves in copper. J. Nucl. Mater. 2016, 470, 290–296. [Google Scholar] [CrossRef]
- Sandström, R.; Andersson, H.C.M. Creep in phosphorus alloyed copper during power-law breakdown. J. Nucl. Mater. 2008, 372, 76–88. [Google Scholar] [CrossRef]
- Orlová, A.; Čadek, J. Dislocation structure in the high temperature creep of metals and solid solution alloys: A review. Mater. Sci. Eng. 1986, 77, 1–18. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodinamics and kinetics of slip. Prog. Mater. Sci. 1979, 15, 1–291. [Google Scholar]
- Spigarelli, S.; Sandström, R. Basic creep modelling of Aluminium. Mater. Sci. Eng. A 2018, 711, 343–349. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Sandström, R. First-principles evaluation of the effect of alloying elements on the lattice parameter of a 23Cr25NiWCuCo austenitic stainless steel to model solid solution hardening contribution to the creep strength. Mater. Sci. Eng. A 2015, 626, 213–219. [Google Scholar] [CrossRef]
- Kassner, M.E. Taylor hardening in five-power-law creep of metals and Class-M alloys. Acta Mater. 2004, 52, 1–9. [Google Scholar] [CrossRef]
- Mecking, H.; Styczynski, A.; Estrin, Y. Steady state and transient plastic flow of Aluminum and Aluminum alloys. In Strength of Metals and Alloys-ICSMA8; Kettunen, P.O., Lepistö, T.K., Lehtonen, M.E., Eds.; Pergamon Press: Oxford, UK, 1988; pp. 989–994. ISBN 9781483294155. [Google Scholar]
- Zhang, L.; Du, Y.; Chen, O.; Steinbach, I.; Huang, B. Atomic mobilities and diffusivities in the fcc, L12 and B2 phases of the Ni-Al system. Int. J. Mater. Res. 2010, 101, 1461–1475. [Google Scholar] [CrossRef]
- Rothman, S.J.; Peterson, N.L.; Nowicki, L.J.; Robinson, L.C. Tracer Diffusion of Magnesium in Aluminum Single Crystals. Phys. Status Solidi (b) 1974, 63, K29–K33. [Google Scholar] [CrossRef]
- Zhang, W.; Du, Y.; Zhao, D.; Zhang, L.; Xu, H.; Liu, S.; Li, Y.; Liang, S. Assessment of the atomic mobility in FCC Al-Cu-Mg alloys. Calphad 2010, 34, 286–293. [Google Scholar] [CrossRef]
- Horiuchi, R.; Otsuka, M. Mechanism of high temperature creep of Aluminum-magnesium solid solution alloys. Trans. Jpn. Inst. Met. 1972, 13, 284–293. [Google Scholar] [CrossRef]
- Hayakawa, H.; Nakashima, H.; Yoshinaga, H. Dislocation density and Interaction between dislocations in Al-Mg solution hardened alloys deformed at high temperature. J. Jpn. Inst. Met. 1989, 53, 1113–1122. [Google Scholar] [CrossRef]
- Blum, W.; Zhu, Q.; Merkel, R.; McQueen, H.J. Geometric dynamic recrystallization in hot torsion of Al-5 Mg-0.6 Mn (AA5083). Mater. Sci. Eng. A 1996, 205, 23–30. [Google Scholar] [CrossRef]
- Friedel, J. Dislocations; Pergamon Press: Oxford, UK, 1964; ISBN 9781483135922. [Google Scholar]
- Yavari, P.; Langdon, T.G. An examination of the breakdown in creep by viscous glide in solid solution alloys at high stress level. Acta Metall. 1982, 30, 2181–2196. [Google Scholar] [CrossRef]
- Endo, T.; Shimada, T.; Langdon, T.G. The deviation from creep by viscous glide in solid solution alloys at high stresses-characteristics of the dragging stress. Acta Metall. 1984, 32, 1991–1999. [Google Scholar] [CrossRef]
- Northwood, D.O.; Moerner, L.; Smith, I.O. The Breakdown in Creep by Viscous Glide in Al-Mg Solid Solution Alloys at High Stress Levels. Phys. Status Solidi (a) 1984, 84, 509–515. [Google Scholar] [CrossRef]
- Kim, H.K. Low-temperature creep behavior of ultrafine-grained 5083 Al alloy processed by equal-channel angular pressing. J. Mech. Sci. Technol. 2010, 24, 2075–2081. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Sasidhara, S. Hot Working Guide—A Compendium of Processing Maps; ASM International: Almere, The Netherlands, 1997; pp. 98–100. ISBN 9781627080910. [Google Scholar]
- Oikawa, H.; Sugawara, K.; Karashima, S. Creep Behavior of Al-2.2 at% Mg Alloy at 573 K. Trans. Jpn. Inst. Met. 1978, 19, 611–616. [Google Scholar] [CrossRef]
- Pahutová, M.; Čadek, J. On Two Types of Creep Behaviour of F.C.C. Solid Solution Alloys. Phys. Status Solidi (a) 1979, 56, 305–313. [Google Scholar]
| b | Burgers vector | 2.86 × 10−10 m |
| c | concentration of Mg in solid solution | [at %] |
| CL | work hardening constant | 86 |
| D0sd | pre-exponential factor in equation for self-diffusion | 8.34 × 10−6 m2·s−1 |
| D0Mg | pre-exponential factor in equation for diffusion of Mg in Al | 1.9 × 10−5 m2·s−1 |
| G | shear modulus at the testing temperature | (3.022 × 1010–1.6 × 107 T) Pa |
| k | Boltzmann constant | 1.38 × 10−23 J·K−1 |
| L | mean dislocation free path | [m] |
| m | Taylor factor | 3.06 |
| Mc | climb mobility of dislocations | [m2·N−1·s−1] |
| Mcg | climb and glide mobility of dislocations | [m2·N−1·s−1] |
| n | stress exponent in power-law equation | |
| Qsd | activation energy for vacancy diffusion (self-diffusion) | 122 × 103 J·mol−1 |
| QdMg | activation energy for diffusion of Mg in Al | 119 × 103 J·mol−1 |
| R | universal gas constant | [J·mol−1·K−1] |
| Rmax | maximum back stress | [Pa] |
| RUTS | ultimate tensile strength | [Pa] |
| T | absolute temperature | [K] |
| vd | velocity of dislocations | [m·s−1] |
| α | material constant in Taylor equations | 0.3 |
| δMg | volume atomic misfit | |
| strain | ||
| strain rate | [s−1] | |
| ν | Poisson’s ratio | 0.3 |
| ρ | free dislocation density | [m−2] |
| ρa | free dislocation density in annealed state | [m−2] |
| σ | stress (creep or constant strain rate experiments) | [Pa] |
| σba | break-away stress | [Pa] |
| σi | internal stress | [Pa] |
| σss | solid solution strengthening stress | [Pa] |
| σ*ss | reduced solid solution strengthening stress | [Pa] |
| σy | yield strength | [Pa] |
| dislocation line tension | [N] | |
| ω | recovery constant | [Pa] |
| Ω | atomic volume of the host atom (Al) | 1.66 × 10−29 m3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spigarelli, S.; Paoletti, C. A Unified Physical Model for Creep and Hot Working of Al-Mg Solid Solution Alloys. Metals 2018, 8, 9. https://doi.org/10.3390/met8010009
Spigarelli S, Paoletti C. A Unified Physical Model for Creep and Hot Working of Al-Mg Solid Solution Alloys. Metals. 2018; 8(1):9. https://doi.org/10.3390/met8010009
Chicago/Turabian StyleSpigarelli, Stefano, and Chiara Paoletti. 2018. "A Unified Physical Model for Creep and Hot Working of Al-Mg Solid Solution Alloys" Metals 8, no. 1: 9. https://doi.org/10.3390/met8010009




