Next Article in Journal
Time Evolution Characterization of Atmospheric-Pressure Plasma Jet (APPJ)-Synthesized Pt-SnOx Catalysts
Next Article in Special Issue
Measuring Structural Heterogeneities in Metallic Glasses Using Transmission Electron Microscopy
Previous Article in Journal
Selection of Parameters and Strategies to Reduce Energy Consumption and Improve Surface Quality in EN-AW 7075 Molds Machining
Previous Article in Special Issue
The Effects of Metalloid Elements on the Nanocrystallization Behavior and Soft Magnetic Properties of FeCBSiPCu Amorphous Alloys
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 8
Issue 9
10.3390/met8090689
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Metallic Glass Structures for Mechanical-Energy-Dissipation Purpose: A Review

by
S. H. Chen
1,*,
H. Y. Cheng
1,
K. C. Chan
2,* and
G. Wang
3
1
School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China
2
Advanced Manufacturing Technology Research Centre, Department of Industrial and Systems Engineering, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, China
3
Laboratory for Microstructures, Shanghai University, Shanghai 200444, China
*
Authors to whom correspondence should be addressed.
Metals 2018, 8(9), 689; https://doi.org/10.3390/met8090689
Submission received: 24 July 2018 / Revised: 28 August 2018 / Accepted: 31 August 2018 / Published: 31 August 2018
(This article belongs to the Special Issue Metallic Glasses: Pathways to Viable Applications)
Browse Figures
Versions Notes

Abstract

:
Metallic glasses (MGs), a new class of advanced structural materials with extraordinary mechanical properties, such as high strength approaching the theoretical value and an elastic limit several times larger than the conventional metals, are being used to develop cellular structures with excellent mechanical-energy-dissipation performance. In this paper, the research progress on the development of MG structures for energy-dissipation applications is reviewed, including MG foams, MG honeycombs, cellular MGs with macroscopic cellular structures, microscopic MG lattice structures and kirigami MG structures. MG structures not only have high plastic energy absorption capacity superior to conventional cellular metals, but also demonstrate great potential for storing the elastic energy during cyclic loading. The deformation behavior as well as the mechanisms for the excellent energy-dissipation performance of varying kinds MG structures is compared and discussed. Suggestions on the future development/optimization of MG structures for enhanced energy-dissipation performance are proposed, which can be helpful for exploring the widespread structural-application of MGs.

1. Introduction

Since being synthesized in the 1960s, metallic glasses (MGs) are known to have attractive mechanical properties, superior to their crystalline counterparts, and are considered ready for widespread practical applications as structural materials [1]. A great deal of effort has been devoted to design alloy systems, to uncover the physical and mechanical properties, and to develop MG structures for practical applications [2,3,4,5,6]. With unique properties, some MGs were employed to develop MG structures which have demonstrated different mechanisms for the dissipation of the mechanical energy, resulting in attractive energy-dissipation performance. On the one hand, with relatively-higher strength, MGs are considered an ideal replacement of conventional crystalline metals for synthesizing cellular structures with enhanced energy-absorption performance, such as MG foams [7,8], MG honeycombs [9,10,11] and cellular MGs with macroscopic cellular structures [12,13]. For example, Brothers and Dunand have fabricated some open-cell Zr-based MG foams using a salt replication technique, which exhibited higher energy absorption capacity than conventional Al foams [7,14]. To better control the microstructures, Sarac et al. have then developed some MG honeycombs with accurately-controlled strut thicknesses [9,10]. The corresponding energy-dissipation mechanisms of the MG honeycombs have been found to result from the large plasticity of the struts at relatively-smaller scales [9,10]. On the other hand, inspired by the development of metamaterials, a class of artificial materials having intriguing properties which do not exist in nature [15,16], some specially-designed MG structures have been fabricated to achieve large elastic energy storability, such as microscopic hollow-tube MG lattice structures [17,18] and kirigami MG structures [19]. Although many studies have been devoted to develop MG structures that can achieve better mechanical energy-dissipation performance, and many articles have summarized the development, physical and mechanical properties, and potential applications of MGs [20,21,22,23,24,25,26,27,28,29], a summary of the development of MG structures for energy-dissipation purpose has not been made. The aim of this paper is to review the recent research progress on the development of MG structures having excellent mechanical-energy-dissipation performance, including high plastic energy absorption capacity and large elastic energy storability, and to discuss the challenges and possible research directions for the practical application of MG structures.

2. MG Foams

Cellular materials are able to dissipate mechanical energy by forming a wide range of plastic-flow-plateau stages, demonstrating a high plastic energy absorption capacity. It is a common route to use parent materials with higher strength to improve the plastic energy absorption capacity of cellular structures, for instance, the replacement of polymers by using Al alloys to fabricate Al foams [30]. With relatively-higher strength as compared with conventional crystalline alloys, MGs are powerful candidates to replace the parent metals in achieving higher plastic energy absorption capacity, and have been used extensively to develop foam structures. One critical issue for the development of conventional metallic foams, such as Al, Ti and Mg foams, is the low foamability of the molten metals [31,32,33,34]. However, apart from attractive mechanical properties, MGs demonstrated excellent foamability at high temperature. In the supercooled liquid region (SLR), MGs can relax into metastable liquid state with dramatically-decreased viscosity, resulting in high formability of MGs which can be formed like plastics [35]. Many attempts have been devoted to fabricate MG foams from varying MG communities, for example, the Pd-based MG foams [36,37,38,39,40,41], Zr-based MG foams [14,42,43,44], Ni-based MG foams [45,46], and Fe-based MG foams [47]. The engineering applications of MGs are significantly restricted by the limited sample sizes and the room-temperature brittleness. Fortunately, the MG foams can have both larger sample dimensions and better room-temperature plasticity. As compared with the solid MG samples, MG foams can exhibit greatly-enhanced nominal plasticity, where wide plastic-flow-plateau stages can be achieved for achieving a higher plastic energy absorption capacity [37,38,39,40,41,42,48,49,50,51,52]. Moreover, the glass transition nature endows MGs with a relatively-lower processing temperature as compared with conventional metals [14]. Brothers and Dunand [7] examined the plastic energy absorption capacity of some Vit106 MG (Zr57Nb5Cu15.4Ni12.6Al10, at.%) foams with pore sizes ranging from 150–355 µm. As shown in Figure 1, the relatively-larger nominal stress of the MG foams is preferred in the plastic-energy-absorption applications of cellular metals, which could be promising in replacing conventional metallic foams. The attractive plastic-energy-absorption performance of MG foams is attributed to the extensive plastic bending of the struts as well as the high strength of MGs. Wei et al. [8] developed some Vit1 (Zr41.25Ti13.75Cu12.5Ni10Be22.5, at.%) MG foams, which have shown higher plastic energy absorption capacity than Al foams, as shown in Figure 2. The enhanced plastic energy absorption capacity of the Vit1 MG foams results from the bending of the struts, the formation of multiple shear bands and the ductile cracking. Although MG foams have attractive plastic-energy-absorption potential, the fabrication of MG foams is limited to certain MG communities and foaming agents, restricting their engineering applications. For example, the expansion of the foams is based on the thermal stability of the foamed melts, and the corresponding thermal conductivity is also affected by the cellular structure, resulting in limited foam dimensions.
The introducing of composite microstructures to MGs can enhance their plasticity, and at the same time, can partially-relax the limitations of the glass forming ability [53,54,55]. Some MG matrix composite foams have also been developed to achieve higher plastic-energy-absorption performance. For example, Brothers et al. have developed some Mg-based MG foams with reinforced hollow iron spheres, which have demonstrated a higher plastic energy absorption capacity than their crystalline counterparts (crystalline foams) [56]. Thereafter, in collaboration with other research groups, Brothers et al. developed some W-particle reinforced Vit106 MG foams, exhibiting higher compressive strains than the Vit106 foams [57]. However, MG foams also face a similar challenge with conventional metallic foams, i.e., how to control the cellular structures accurately, including the porosity, pore sizes and morphologies [33,34]. The non-uniform/stochastic microstructures of these MG foams/MG matrix composite foams make it difficult to predict and achieve desired plastic-energy-absorption performance. How to resolve this issue has attracted a lot of research attention, for example, to develop MG structures with accurately-tailored microstructures, which is reviewed in the following sections. It is worth mentioning that some nano-porous structures were also developed by dealloying MGs [58,59,60], similar to some nano-foams produced from conventional crystalline metals [61,62], which were mainly designed for potentially functional applications, such as oxidative degradation and development of electrical/chemical devices. Since the present work mainly focused on the development of MG structures for mechanical-energy-dissipation purpose, the development of nano-porous structures from MGs is not discussed in detail here.

3. MG Honeycombs

Honeycomb structures are widely used to develop cellular materials with high plastic-energy-absorption performance. With relatively-high strength and elasticity, it expected that honeycomb structures making use of MGs could also have high plastic energy absorption capacity. Jayakumar et al. developed some teardrop-shaped MG honeycomb structures using Fe45Ni45Mo7B3 MG ribbons [63]. The analytical modeling studies of the teardrop-shaped MG honeycomb structures have shown a three-fold improvement in the strength of the cellular structures as compared with the Al honeycomb structures, having great potential in achieving a higher plastic energy absorption capacity. Inheriting from amorphous atomic structures, MGs relax at high temperatures (SLRs), where low viscosities are achieved, resulting in a high forming ability, like plastics [64,65,66]. This enables MGs be formed into complex geometries through high-temperature forming techniques, such as superplastic forming, thermoplastic forming and hot-forming. By combining lithography and thermoplastic forming, Sarac et al. developed some in-plane MG honeycombs with accurately-controlled microstructures [9]. Figure 3a shows the nominal stress strain curve of a Zr35Ti30Cu7.5Be27.5 MG honeycomb with a wide plastic-flow-plateau stage till densification. The plastic energy absorption capacity of the MG honeycombs represents the upper bound of the MG foams (Figure 3b). They demonstrate better energy-absorption performance than honeycomb structures made using zinc, polyethylene (PE) and polyether ether ketone (PEEK), and are comparable to 2004Al honeycombs. The variation of the plastic energy absorption capacity of the MG honeycombs on the change of the ligament thickness has also been studied. Further studies have shown that the deformation mode of the MG honeycombs, from brittle to ductile, can be tailored by tuning the relative densities, where an optimal density of about 25% was identified for the purpose of plastic-energy-absorption applications. MG honeycombs with such relative density offer the best compromises between strength and plasticity, where local failure and shear band-like cracks play an important role during the plastic flow stages [10].
Chen et al. have studied the deformation behavior as well as the plastic energy absorption performance of some MG honeycombs with stochastic cellular structures [11]. They have shown that MG honeycombs with stochastic cellular structures have decreased plastic energy absorption capacity than those with periodic cellular structures. However, they demonstrated higher flaw tolerance, which also plays a significant role in achieving desirable properties in engineering materials. Based on the two-dimensional MG honeycombs, Liu et al. have developed some 3D MG honeycomb structures using a parallel joining technique [67]. Theoretical analyses have shown that with a good combination of both high strength and elastic limit, these 3D MG honeycomb structures can demonstrate a high plastic energy absorption capacity, superior to those cellular structures made of conventional metals and ceramics. The development of MG honeycombs provides a new window to develop cellular MG structures with both high plastic energy absorption capacity and accurately-controlled microstructures, which are useful in developing energy-absorption structures or devices. However, MG honeycomb structures made from the thermoplastic forming technique have relatively-smaller dimensions as compared with MG foams, where in wide-spread structural applications of cellular materials, larger sample dimensions are usually expected.

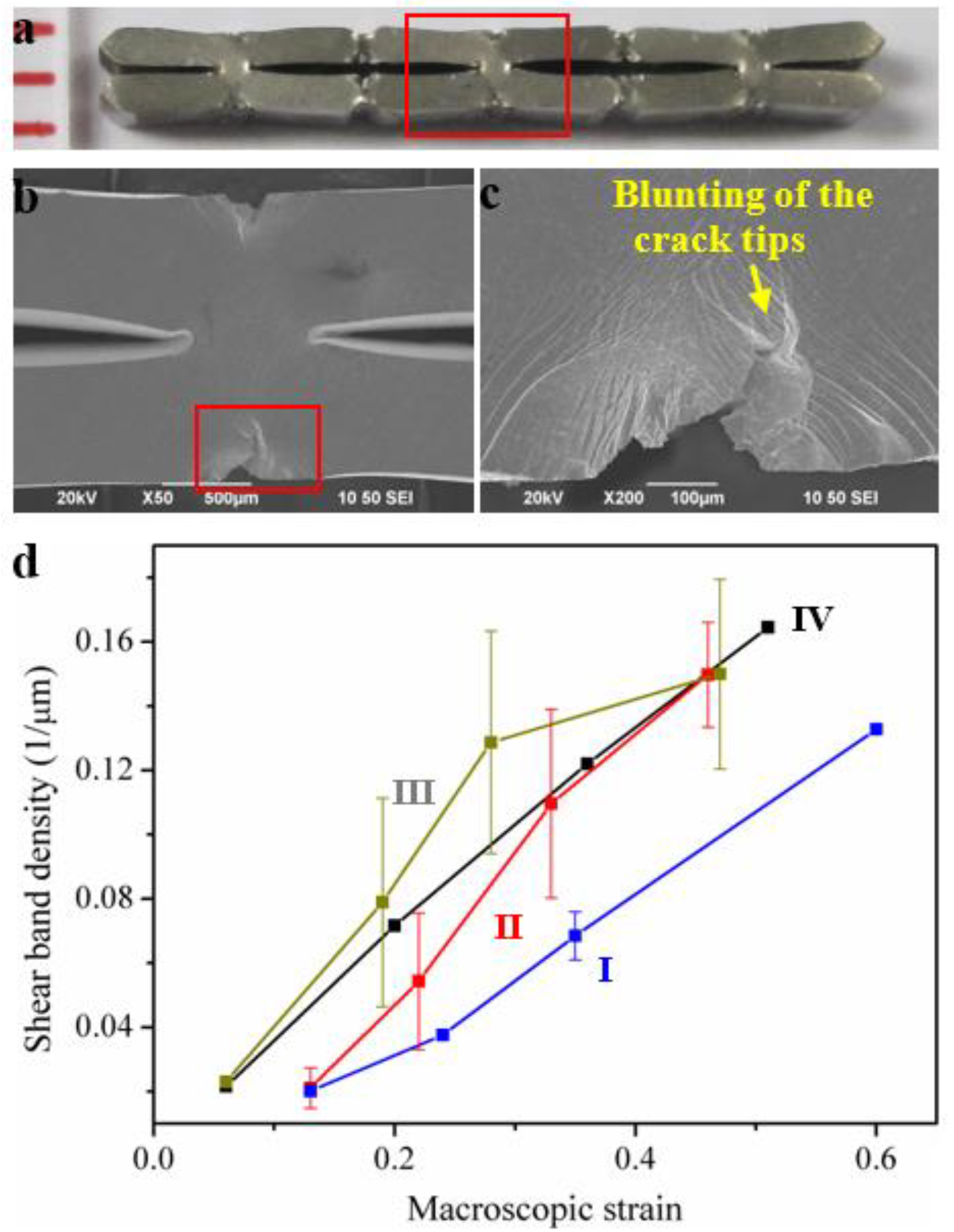
4. Cellular MGs with Macroscopic Cellular Structures

The improvement of the plastic energy absorption capacity of cellular materials is usually achieved in two ways: one is to use the parent materials with higher strength, and the other is to optimize the deformation behavior of the cellular structures [8,30]. Similar to the development of metal foams as compared with the polymer foams, the improvement of the plastic energy absorption capacity of the MG foams/honeycombs as compared with conventional metal foams/honeycombs is readily understood to result from the relatively-higher strength. How about the effect of the change of cellular structures on the plastic-energy-absorption performance of the MG structures? Based on the enhanced deformation behavior of MGs under complex stress states [68,69,70], Chen et al. have developed some cellular MGs using macroscopic cellular structures instead of microscopic pores, as shown in Figure 4 [12]. Although the parent MG materials used have strength no larger than other MG materials for MG foams/honeycombs, these cellular MGs have demonstrated a greatly-enhanced plastic energy absorption capacity than MG foams/honeycombs, and the improved plastic-energy-absorption performance is mainly attributed to the deformation behavior of the macroscopic cellular structures.
Differing from the bending, buckling and the collapse of the struts in MG foams/honeycombs, the mechanical-energy-dissipation of cellular MGs with macroscopic cellular structures is mainly due to the plastic bending of the struts, the blunting of the crack tips at the nodes and the large plastic deformation of the nodes [12]. During the densification process, the tilted struts are compressed to be perpendicular to the loading direction, and the square-shaped pores are nearly eliminated after densification (Figure 5a) [13]. The original square-shaped node has also been changed to a diamond shape with a larger shearing angle (Figure 5b) [13]. Due to the intrinsic high toughness of the parent Zr57Cu20Al10Ni8Ti5 MG, with a plastic zone radius of about 0.6 mm, the crack propagation was stopped by a blunting effect (Figure 5c), where the global large plasticity of the cellular MGs can be achieved [13]. At the nodes of the cellular MGs, the evolution of the shear and densities of four specimens are given in Figure 5d [71]. After densification, the smallest shear band density at the nodes of the cellular MGs was larger than 0.13 μm−1, and the largest average value even reached 0.16 μm−1, corresponding to an average shear band spacing of 6.15 μm. Although some of the results have relatively-large error bars which may affect the certainty of the findings, the shear band densities are larger than the density in a Zr-based MG specimen with a compressive strain of about 80% (0.11 μm−1) [72]. Such large shear band densities have rarely been reported in the standard testing of MGs. Bei et al. [72] demonstrated that, under compression tests, the shear band density is proportional to the macroscopic plastic strain. While in these cellular MGs with macroscopic cellular structures, the large shear band densities indicate that a significant amount of plastic strain has been localized in this region, resulting in the large plastic bending of the struts and the densification of the cellular structures.
As shown in Figure 4b, the nominal stress–strain curves of the cellular MGs have relatively-high peak stresses and wide plastic-flow-plateau stages. The analytical modeling of the peak stress has shown that the peak stress of cellular MGs with macroscopic cellular structures is dependent on not only the relative density, but also the number of unit cells. The peak stress to yield strength ratio (σpeak/σy) is proportional to the ratio of the yield volume to the volume of the cellular MGs [13]. The cellular MGs with larger yield volume when peaking occurs have higher peak stresses and higher plastic energy absorption capacity. On the other hand, clear decay of the stresses during the plastic-flow plateau stages has been observed, resulting from the work-softening nature of the parent MGs, the formation of shear bands in the middle of the struts and the change of the macroscopic cellular structures during the densification processes [13]. Therefore, for certain parent MGs, the design strategies which can increase the yield volume at the peak stress and reduce the decay of stress during the densification process can definitely increase the plastic-energy-absorption performance of cellular MGs. Chen et al. have developed some saw-tooth-like MG structures with an increasing stress trend during the densification processes, demonstrating a greatly-enhanced plastic energy absorption capacity than the cellular MGs with macroscopic cellular structures [73]. By the use of MG composites [53,55,74] or MGs with atomic inhomogeneities with a work-hardening effect [75] may also be helpful for achieving higher plastic-energy-absorption performance in cellular MGs. As a case in point, Schramm et al. developed some MG-matrix-composite-based egg-box structures, which exhibited a high plastic energy absorption capacity superior to Al-based structures [76]. The MG-matrix-composites can have good combinations of high strength, high toughness, better processing capability and larger sample dimensions, which are beneficial for developing MG structures with larger sample dimensions and better mechanical performance.

5. Microscopic MG Lattice Structures

The use of cellular structures for mechanical-energy-dissipation purposes is usually twofold: one is to absorb the mechanical energy through plastic deformation, and the other one is to store the elastic energy by achieving large elastic recovery after deformation. The relatively-large elastic limit of about 2%, superior to conventional crystalline metals and ceramics, enables MGs to be a good candidate for developing structures with large elastic energy storability. For example, 3D MG honeycomb structures have a higher recoverable strain (about 40%) than honeycomb structures making use of conventional metals [67]. The large elasticity of 3D MG honeycomb structures is mainly attributed to the large elastic limit of the parent MGs, and can be further optimized by tuning the aspect ratio and the tilt angle between the side wall and the loading direction [67]. The development of some hollow-tube metallic and ceramic lattice structures has shown the characteristics of ultra-light, ultra-strong and recovery of large strains exceeding 50%, having wide application potential for catalyst supports, storage of elastic energy, shock-energy damping, damage-tolerance, and acoustic and electronic devices [77,78,79]. It is known that MGs have a significant size effect, where MG specimens have larger elasticity and plastic deformation when the sample size decreases to the nanoscale [80,81,82,83]. Even the plastic deformation mode of MGs also transits from inhomogeneous deformation localized into shear bands to homogeneous deformation [80,81,82]. Therefore, it may also be possible to develop some microscopic MG lattice structures with attractive large elastic energy storability.
Rys et al. developed some microscopic hollow-tube NiP MG lattice structures using electroless deposition [84]. They showed that the deformation behavior of microscopic hollow MG lattice structures demonstrates two different regimes for varying wall thickness, where the maximum stress was achieved when the wall thickness decreased to below a threshold value of about 150 nm [84]. Thereafter, Lee et al. fabricated some hollow-tube Cu60Zr40 MG lattice structures and examined the corresponding deformation mechanisms, including brittle-to-ductile transitions and elastic instability [17]. However, how to achieve large elastic energy storability comparable to the metallic and ceramic lattice structures is still somewhat a mystery. Liontas et al. developed some hollow Zr-Ni-Al MG lattice structures with wall thicknesses ranging from 88 nm to 10 nm [18]. As shown in Figure 6, the compressive testing results suggest that an obvious brittle-to-ductile transition occurs in these MG lattice structures, resulting from the size effect of the MGs where MG specimens with smaller sample size are more deformable. The Zr-Ni-Al MG lattice structures have elastic recovery of about 33% nominal strain, and the value is proportional to the wall thickness [18]. The elastic recovery of the microscopic MG lattice structures was smaller than that of ceramic and crystalline metallic lattice structures [77,78], however, the microstructures of these lattice structures have not been optimized for achieving better mechanical performance, and the effect of the relatively-larger elastic limit of the parent MGs has not been fully explored. Additionally, the fabrication of some thin-walled MG hollow tubes at the macroscopic scale, with outstanding plastic energy absorption capacity [85], has suggested that with the decrease of the sample size, a high plastic energy absorption capacity may also be achieved in the microscopic MG lattice structures, for instance, in MG lattice structures with thicker walls. The development of architectured microscopic MG lattice structures is still an unexplored area, where better mechanical performance may be achieved in the future by optimizing the processing parameters and lattice structures as well as the wall thickness.

6. Kirigami MG Structures

Kirigami structures are mechanical meta-materials based on the ancient art of paper cutting, demonstrating attractive mechanical properties which do not exist in nature [86,87,88]. Inspired by the large elastic recovery of microscopic MG lattice structures, Sha et al. investigated the mechanical properties of some CuZr MG-based chiral nanolattice structures using molecular dynamics (MD) simulations [89]. As shown in Figure 7, the MG-based chiral nanolattice structures have in-plane chiral kirigami patterns, and are able to demonstrate good combinations of large elasticity, large ductility and negative Poisson’s ratio. The excellent performance results from the deformation of the chiral structures, such as the bending of the ligaments and rotation of the nodes. The deformation behavior also depends on the physical properties of the MGs as well as the corresponding geometrical parameters. Therefore, it is a reasonable expectation to achieve desirable large elastic storability in the in-plane MG structures by appropriate experimental design and processing technologies.
More recently, Chen et al. developed some Fe-based kirigami MG structures using photochemical machining (PCM), as shown in the example in Figure 8a [19]. The kirigami MG structures have shown programmable stretchability with elastic strain larger than 198% [19]. The large stretchability is attributed to the out-of-plane bending of the elements, coexisting with the rotation, where the large elasticity of the MGs is able to maintain the elastic states of the nodes at large nominal strains. With a much smaller elastic limit, the stainless steel kirigami structures only exhibited elastic strains less than 59%. Finite Element Modelling (FEM) results have shown that after buckling, the stress-concentration regions in the stainless steel-based kirigami structures tend to yield while the kirigami MG structures are still in elastic states. Additionally, stemming from the relatively-high strength and large elastic limit, the kirigami MG structures have demonstrated ultra-small elastic strain energy loss after 1000 loading cycles (Figure 8c). An elastic strain energy loss less than 3% was observed, which is much smaller than the kirigami structures that made use of Kapton/GaAs [90] or nanocomposites [86]. The stretchable kirigami MG structures are useful for developing mechanical meta-materials and optoelectronic devices with extended cycle life. For example, Xian et al. have reported some MG film skins with a piezoresistance effect, large strain range and good conductivity [91]. The use of kirigami structures to develop electronic skins may further enhance the stretchability for wearable devices.

7. Summary and Outlook

MGs have unique mechanical properties superior to conventional metals, such as the high strength approaching the theoretical values and a relatively-large elastic limit of about 2%. The excellent mechanical properties enable MGs to be powerful parent materials for developing structures/devices for mechanical-energy-dissipation purposes. On the one hand, MG foams, MG honeycombs, cellular MGs with macroscopic cellular structures and saw-tooth-like MG structures have demonstrated greatly-enhanced energy-absorption capacity compared to conventional metal foams/honeycombs. On the other hand, 3D MG honeycombs, microscopic MG lattice structures and kirigami MG structures have demonstrated excellent elastic energy storability than structures making use of conventional metals. The kirigami MG structures have also demonstrated an ultra-small strain-energy-loss after 1000 cycles of loading, which can be employed to develop stretchable optoelectronic devices with extended life cycles. However, the following problems for the developing of MG structures are still unresolved, and may be worthy of further effort to expand the structural application of MG structures:
(1)
The development of 3D MG honeycomb structures is based on the thermoplastic forming and joining technique, where only thin sheet materials are used [67]. It is still challenging to develop honeycomb structures with more complex geometries and a wide range of relative densities.
(2)
Due to the limited sample dimensions, cellular MGs with macroscopic cellular structures and saw-tooth-like MG structures have only one layer of structure [12,73]. However, more layers of cellular structures are usually required for practical applications. The use of additive manufacturing (3D printing) may be helpful for developing cellular MGs with larger sample dimensions [92,93,94]. The 3D printing technique also has the advantage of fabricating cellular structures with complex geometries, which could further be used to optimize macroscopic cellular structures for better energy-absorption performance.
(3)
Although up-to-date hollow microscopic MG lattice structures have relatively-smaller elastic strain energy recovery than lattice structures that make use of ceramic and crystalline metals [18,84], the high strength and large elastic limit of MGs at the nanoscale make micro MG lattice structures have good potential for high elastic performance. Further efforts need to be devoted to optimize the processing parameters or lattice structures to achieve better elastic energy storability.
(4)
Kirigami MG structures have demonstrated large elastic energy storability and ultra-small strain energy loss for a longer cycle life. However, how to use the kirigami structures to develop optoelectronic devices or wearing devices is still challenging. Because of the unique properties, it is expected more functional devices using MGs will be developed in future, such as large elasticity, light weight, wearable sensors and optoelectronic devices [19,89,91].

Author Contributions

S.H.C. prepared the manuscript. S.H.C. and H.Y.C. collected the data. S.H.C, K.C.C. and G.W. designed the scope of the paper. All authors discussed the conclusions and reviewed the manuscript.

Funding

National Natural Science Foundation of China: 51801049, Faculty of Engineering of the Hong Kong Polytechnic University: 1-45-37-99QP.

Acknowledgments

The work described in this paper was supported by a grant from the National Natural Science Foundation of China under research project No. 51801049. K.C.C. would like to acknowledge the financial support from the Faculty of Engineering of the Hong Kong Polytechnic University under research project No. 1-45-37-99QP.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Plummer, J.; Johnson, W.L. Is metallic glass poised to come of age? Nat. Mater. 2015, 14, 553–555. [Google Scholar] [CrossRef] [PubMed]
  2. Wang, W.H.; Dong, C.; Shek, C.H. Bulk metallic glasses. Mater. Sci. Eng. Rep. 2004, 44, 45–89. [Google Scholar] [CrossRef]
  3. Yavari, A.R.; Lewandowski, J.J.; Eckert, J. Mechanical properties of bulk metallic glasses. MRS Bull. 2007, 32, 635–638. [Google Scholar] [CrossRef]
  4. Chen, M.W. Mechanical behavior of metallic glasses: Microscopic understanding of strength and ductility. Annu. Rev. Mater. Res. 2008, 38, 445–469. [Google Scholar] [CrossRef]
  5. Trexler, M.M.; Thadhani, N.N. Mechanical properties of bulk metallic glasses. Prog. Mater. Sci. 2010, 55, 759–839. [Google Scholar] [CrossRef]
  6. Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
  7. Brothers, A.H.; Dunand, D.C. Plasticity and damage in cellular amorphous metals. Acta Mater. 2005, 53, 4427–4440. [Google Scholar] [CrossRef]
  8. Wei, X.; Chen, J.H.; Dai, L.H. Energy absorption mechanism of open-cell Zr-based bulk metallic glass foam. Scr. Mater. 2012, 66, 721–724. [Google Scholar] [CrossRef]
  9. Sarac, B.; Ketkaew, J.; Popnoe, D.O.; Schroers, J. Honeycomb structures of bulk metallic glasses. Adv. Funct. Mater. 2012, 22, 3161–3169. [Google Scholar] [CrossRef]
  10. Sarac, B.; Schroers, J. From brittle to ductile: Density optimization for Zr-BMG cellular structures. Scr. Mater. 2013, 68, 921–924. [Google Scholar] [CrossRef]
  11. Chen, W.; Liu, Z.; Robinson, H.M.; Schroers, J. Flaw tolerance vs. performance: A tradeoff in metallic glass cellular structures. Acta Mater. 2014, 73, 259–274. [Google Scholar] [CrossRef]
  12. Chen, S.H.; Chan, K.C.; Wu, F.F.; Xia, L. Pronounced energy absorption capacity of cellular bulk metallic glasses. Appl. Phys. Lett. 2014, 104, 111907. [Google Scholar] [CrossRef]
  13. Chen, S.H.; Chan, K.C.; Wu, F.F.; Xia, L. Achieving high energy absorption capacity in cellular bulk metallic glasses. Sci. Rep. 2015, 5, 10302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Brothers, A.H.; Scheunemann, R.; DeFouw, J.D.; Dunand, D.C. Processing and structure of open-celled amorphous metal foams. Scr. Mater. 2005, 52, 335–339. [Google Scholar] [CrossRef]
  15. O’Brien, K.; Suchowski, H.; Rho, J.; Salandrino, A.; Kante, B.; Yin, X.B.; Zhang, X. Predicting nonlinear properties of metamaterials from the linear response. Nat. Mater. 2015, 14, 379–383. [Google Scholar] [CrossRef]
  16. Paulose, J.; Chen, B.G.G.; Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 2015, 11, 153–156. [Google Scholar] [CrossRef] [Green Version]
  17. Lee, S.W.; Jafary-Zadeh, M.; Chen, D.Z.; Zhang, Y.W.; Greer, J.R. Size Effect Suppresses brittle failure in hollow Cu60Zr40 metallic glass nanolattices deformed at cryogenic temperatures. Nano Lett. 2015, 15, 5673–5681. [Google Scholar] [CrossRef] [PubMed]
  18. Liontas, R.; Greer, J.R. 3D nano-architected metallic glass: Size effect suppresses catastrophic failure. Acta Mater. 2017, 133, 393–407. [Google Scholar] [CrossRef] [Green Version]
  19. Chen, S.H.; Chan, K.C.; Yue, T.M.; Wu, F.F. Highly stretchable kirigami metallic glass structures with ultra-small strain energy loss. Scr. Mater. 2018, 142, 83–87. [Google Scholar] [CrossRef]
  20. Greer, A.L.; Cheng, Y.Q.; Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. Rep. 2013, 74, 71–132. [Google Scholar] [CrossRef]
  21. Louzguine-Luzgin, D.V.; Louzguina-Luzgina, L.V.; Churyumov, A.Y. Mechanical properties and deformation behavior of bulk metallic glasses. Metals 2013, 3, 1–22. [Google Scholar] [CrossRef]
  22. Maaß, R.; Löffler, J.F. Shear-band dynamics in metallic glasses. Adv. Funct. Mater. 2015, 25, 2353–2368. [Google Scholar] [CrossRef]
  23. Sun, B.A.; Wang, W.H. The fracture of bulk metallic glasses. Prog. Mater. Sci. 2015, 74, 211–307. [Google Scholar] [CrossRef]
  24. Hufnagel, T.C.; Schuh, C.A.; Falk, M.L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater. 2016, 109, 375–393. [Google Scholar] [CrossRef] [Green Version]
  25. Madge, S.V. Toughness of bulk metallic glasses. Metals 2015, 5, 1279–1305. [Google Scholar] [CrossRef]
  26. Ma, E.; Cheng, Y.Q. Atomic-level structure and structure-property relationship in metallic glasses. Prog. Mater. Sci. 2011, 56, 379–473. [Google Scholar] [CrossRef]
  27. Gong, P.; Deng, L.; Jin, J.S.; Wang, S.B.; Wang, X.Y.; Yao, K.F. Review on the research and development of Ti-based bulk metallic glasses. Metals 2016, 6, 264. [Google Scholar] [CrossRef]
  28. Khan, M.M.; Nemati, A.; Rahman, Z.U.; Shah, U.H.; Asgar, H.; Haider, W. Recent advancements in bulk metallic glasses and their applications: A review. Crit. Rev. Solid State Mater. Sci. 2018, 43, 233–268. [Google Scholar] [CrossRef]
  29. Jafary-Zadeh, M.; Kumar, G.P.; Branicio, P.S.; Seifi, M.; Lewandowski, J.J.; Cui, F. A critical review on metallic glasses as structural materials for cardiovascular stent applications. J. Funct. Biomater. 2018, 9, 19. [Google Scholar] [CrossRef] [PubMed]
  30. Evans, A.G.; Hutchinson, J.W.; Ashby, M.F. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef] [Green Version]
  31. Miyoshi, T.; Itoh, M.; Akiyama, S.; Kitahara, A. ALPORAS aluminum foam: Production process, properties, and applications. Adv. Eng. Mater. 2000, 2, 179–183. [Google Scholar] [CrossRef]
  32. Wen, C.E.; Mabuchi, M.; Yamada, Y.; Shimojima, K.; Chino, Y.; Asahina, T. Processing of biocompatible porous Ti and Mg. Scr. Mater. 2001, 45, 1147–1153. [Google Scholar] [CrossRef]
  33. Lefebvre, L.P.; Banhart, J.; Dunand, D.C. Porous metals and metallic foams: Current status and recent developments. Adv. Eng. Mater. 2008, 10, 775–787. [Google Scholar] [CrossRef] [Green Version]
  34. Garcia-Moreno, F. Commercial applications of metal foams: Their properties and production. Materials 2016, 9, 85. [Google Scholar] [CrossRef] [PubMed]
  35. Schroers, J. Processing of bulk metallic glass. Adv. Mater. 2010, 22, 1566–1597. [Google Scholar] [CrossRef] [PubMed]
  36. Schroers, J.; Veazey, C.; Johnson, W.L. Amorphous metallic foam. Appl. Phys. Lett. 2003, 82, 370–372. [Google Scholar] [CrossRef]
  37. Demetriou, M.D.; Schramm, J.P.; Veazey, C.; Johnson, W.L.; Hanan, J.C.; Phelps, N.B. High porosity metallic glass foam: A powder metallurgy route. Appl. Phys. Lett. 2007, 91, 161903. [Google Scholar] [CrossRef] [Green Version]
  38. Wada, T.; Inoue, A. Fabrication, thermal stability and mechanical properties of porous bulk glassy Pd-Cu-Ni-P alloys. Mater. Trans. 2003, 44, 2228–2231. [Google Scholar] [CrossRef]
  39. Wada, T.; Inoue, A. Formation of porous Pd-based bulk glassy alloys by a high hydrogen pressure melting-water quenching method and their mechanical properties. Mater. Trans. 2004, 45, 2761–2765. [Google Scholar] [CrossRef]
  40. Wada, T.; Kinaka, M.; Inoue, A. Effect of volume fraction and geometry of pores on mechanical properties of porous bulk glassy Pd42.5Cu30Ni7.5P20 alloys. J. Mater. Res. 2006, 21, 1041–1047. [Google Scholar] [CrossRef]
  41. Wada, T.; Inoue, A.; Greer, A.L. Enhancement of room-temperature plasticity in a bulk metallic glass by finely dispersed porosity. Appl. Phys. Lett. 2005, 86, 251907. [Google Scholar] [CrossRef]
  42. Cox, M.E.; Dunand, D.C. Anisotropic mechanical properties of amorphous Zr-based foams with aligned, elongated pores. Acta Mater. 2013, 61, 5937–5948. [Google Scholar] [CrossRef]
  43. Brothers, A.H.; Dunand, D.C. Syntactic bulk metallic glass foam. Appl. Phys. Lett. 2004, 84, 1108–1110. [Google Scholar] [CrossRef]
  44. Wada, T.; Wang, X.M.; Kimura, H.; Inoue, A. Supercooled liquid foaming of a Zr-Al-Cu-Ag bulk metallic glass containing pressurized helium pores. Mater. Lett. 2009, 63, 858–860. [Google Scholar] [CrossRef]
  45. Lee, M.H.; Sordelet, D.J. Synthesis of bulk metallic glass foam by powder extrusion with a fugitive second phase. Appl. Phys. Lett. 2006, 89, 021921. [Google Scholar] [CrossRef]
  46. Scudino, S.; Kim, J.Y.; Prashanth, K.G.; Lee, M.H.; Kim, B.S.; Kuhn, U.; Eckert, J. Production of customized hybrid porous structures by powder metallurgy of Ni59Zr20Ti16Si2Sn3 glassy powders. J. Mater. Res. 2013, 28, 2490–2498. [Google Scholar] [CrossRef]
  47. Demetriou, M.D.; Duan, G.; Veazey, C.; De Blauwe, K.; Johnson, W.L. Amorphous Fe-based metal foam. Scr. Mater. 2007, 57, 9–12. [Google Scholar] [CrossRef]
  48. Wada, T.; Takenaka, K.; Nishiyama, N.; Inoue, A. Formation and mechanical properties of porous Pd-Pt-Cu-P bulk glassy alloys. Mater. Trans. 2005, 46, 2777–2780. [Google Scholar] [CrossRef]
  49. Demetriou, M.D.; Veazey, C.; Harmon, J.S.; Schramm, J.P.; Johnson, W.L. Stochastic metallic-glass cellular structures exhibiting benchmark strength. Phys. Rev. Lett. 2008, 101, 145702. [Google Scholar] [CrossRef] [PubMed]
  50. Brothers, A.H.; Dunand, D.C. Ductile bulk metallic glass foams. Adv. Mater. 2005, 17, 484–486. [Google Scholar] [CrossRef]
  51. Schramm, J.P.; Demetriou, M.D.; Johnson, W.L.; Poon, B.; Ravichandran, G.; Rittel, D. Effect of strain rate on the yielding mechanism of amorphous metal foam. Appl. Phys. Lett. 2010, 96, 021906. [Google Scholar] [CrossRef] [Green Version]
  52. Demetriou, M.D.; Hanan, J.C.; Veazey, C.; Di Michiel, M.; Lenoir, N.; Ustundag, E.; Johnson, W.L. Yielding of metallic glass foam by percolation of an elastic buckling instability. Adv. Mater. 2007, 19, 1957–1962. [Google Scholar] [CrossRef]
  53. Hofmann, D.C. Shape memory bulk metallic glass composites. Science 2010, 329, 1294–1295. [Google Scholar] [CrossRef] [PubMed]
  54. Hofmann, D.C.; Suh, J.Y.; Wiest, A.; Duan, G.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 2008, 451, 1085–1089. [Google Scholar] [CrossRef] [PubMed]
  55. Wu, Y.; Xiao, Y.H.; Chen, G.L.; Liu, C.T.; Lu, Z.P. Bulk metallic glass composites with transformation-mediated work-hardening and ductility. Adv. Mater. 2010, 22, 2770–2773. [Google Scholar] [CrossRef] [PubMed]
  56. Brothers, A.H.; Dunand, D.C.; Zheng, Q.; Xu, J. Amorphous Mg-based metal foams with ductile hollow spheres. J. Appl. Phys. 2007, 102, 023508. [Google Scholar] [CrossRef]
  57. Brothers, A.H.; Mangrich, B.; Cox, M.; Dunand, D.C. Effect of crystalline metallic particles on the compressive behavior of a cellular amorphous metal. Scr. Mater. 2011, 64, 1031–1034. [Google Scholar] [CrossRef]
  58. Li, R.; Liu, X.J.; Wang, H.; Zhou, D.Q.; Wu, Y.; Lu, Z.P. Formation mechanism and characterization of nanoporous silver with tunable porosity and promising capacitive performance by chemical dealloying of glassy precursor. Acta Mater. 2016, 105, 367–377. [Google Scholar] [CrossRef]
  59. Yu, J.S.; Ding, Y.; Xu, C.X.; Inoue, A.; Sakurai, T.; Chen, M.W. Nanoporous metals by dealloying multicomponent metallic glasses. Chem. Mater. 2008, 20, 4548–4550. [Google Scholar] [CrossRef]
  60. Li, R.; Chan, K.C.; Liu, X.J.; Zhang, X.H.; Liu, L.; Li, T.; Lu, Z.P. Synthesis of well-aligned CuO nanowire array integrated with nanoporous CuO network for oxidative degradation of methylene blue. Corros. Sci. 2017, 126, 37–43. [Google Scholar] [CrossRef]
  61. Romano, L.; Impellizzeri, G.; Bosco, L.; Ruffino, F.; Miritello, M.; Grimaldi, M.G. Nanoporosity induced by ion implantation in deposited amorphous Ge thin films. J. Appl. Phys. 2012, 111, 113515. [Google Scholar] [CrossRef]
  62. Grillo, R.; Torrisi, V.; Ruffino, F. Nanoporous Au: An experimental study on the porosity of dealloyed AuAg leafs. Superlattices Microstruct. 2016, 100, 780–791. [Google Scholar] [CrossRef]
  63. Jayakumar, B.; Hanan, J.C. Modeling the axial mechanical response of amorphous Fe45Ni45Mo7B3 honeycombs. Metall. Mater. Trans. A 2012, 43, 2669–2675. [Google Scholar] [CrossRef]
  64. Schroers, J.; Pham, Q.; Peker, A.; Paton, N.; Curtis, R.V. Blow molding of bulk metallic glass. Scr. Mater. 2007, 57, 341–344. [Google Scholar] [CrossRef]
  65. Duan, G.; Wiest, A.; Lind, M.L.; Li, J.; Rhim, W.K.; Johnson, W.L. Bulk metallic glass with benchmark thermoplastic processability. Adv. Mater. 2007, 19, 4272–4275. [Google Scholar] [CrossRef]
  66. Ma, J.; Zhang, X.; Wang, W.H. Metallic glass mold insert for hot embossing of polymers. J. Appl. Phys. 2012, 112, 024506. [Google Scholar] [CrossRef]
  67. Liu, Z.; Chen, W.; Carstensen, J.; Ketkaew, J.; Mota, R.M.O.; Guest, J.K.; Schroers, J. 3D metallic glass cellular structures. Acta Mater. 2016, 105, 35–43. [Google Scholar] [CrossRef] [Green Version]
  68. Chen, S.H.; Chan, K.C.; Xia, L. Deformation behavior of bulk metallic glass structural elements. Mater. Sci. Eng. A 2014, 606, 196–204. [Google Scholar] [CrossRef]
  69. Chen, S.H.; Chan, K.C.; Xia, L. Deformation behavior of a Zr-based bulk metallic glass under a complex stress state. Intermetallics 2013, 43, 38–44. [Google Scholar] [CrossRef]
  70. Chen, S.H.; Chan, K.C.; Xia, L. Fracture morphologies of Zr-based bulk metallic glasses under different stress states. Adv. Eng. Mater. 2015, 17, 366–373. [Google Scholar] [CrossRef]
  71. Chen, S.H. Deformation Behaviour of Bulk Metallic Glasses under Complex Stress States. Ph.D. Thesis, The Hong Kong Polytechnic University, Hong Kong, China, September 2014. [Google Scholar]
  72. Bei, H.; Xie, S.; George, E.P. Softening caused by profuse shear banding in a bulk metallic glass. Phys. Rev. Lett. 2006, 96, 105503. [Google Scholar] [CrossRef] [PubMed]
  73. Chen, S.H.; Chan, K.C.; Wang, G.; Yi, J. Saw-tooth-like bulk metallic glass structures with greatly enhanced energy-absorption performance. J. Alloy. Compd. 2016, 661, 49–54. [Google Scholar] [CrossRef]
  74. Wu, F.F.; Chan, K.C.; Jiang, S.S.; Chen, S.H.; Wang, G. Bulk metallic glass composite with good tensile ductility, high strength and large elastic strain limit. Sci. Rep. 2014, 4, 5302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  75. Das, J.; Tang, M.B.; Kim, K.B.; Theissmann, R.; Baier, F.; Wang, W.H.; Eckert, J. “Work-hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 2005, 94, 205501. [Google Scholar] [CrossRef] [PubMed]
  76. Schramm, J.P.; Hofmann, D.C.; Demetriou, M.D.; Johnson, W.L. Metallic-glass-matrix composite structures with benchmark mechanical performance. Appl. Phys. Lett. 2010, 97, 241910. [Google Scholar] [CrossRef] [Green Version]
  77. Schaedler, T.A.; Jacobsen, A.J.; Torrents, A.; Sorensen, A.E.; Lian, J.; Greer, J.R.; Valdevit, L.; Carter, W.B. Ultralight metallic microlattices. Science 2011, 334, 962–965. [Google Scholar] [CrossRef] [PubMed]
  78. Meza, L.R.; Das, S.; Greer, J.R. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 2014, 345, 1322–1326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  79. Jang, D.C.; Meza, L.R.; Greer, F.; Greer, J.R. Fabrication and deformation of three-dimensional hollow ceramic nanostructures. Nat. Mater. 2013, 12, 893–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  80. Guo, H.; Yan, P.F.; Wang, Y.B.; Tan, J.; Zhang, Z.F.; Sui, M.L.; Ma, E. Tensile ductility and necking of metallic glass. Nat. Mater. 2007, 6, 735–739. [Google Scholar] [CrossRef] [PubMed]
  81. Jang, D.C.; Greer, J.R. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat. Mater. 2010, 9, 215–219. [Google Scholar] [CrossRef] [PubMed]
  82. Deng, Q.S.; Cheng, Y.Q.; Yue, Y.H.; Zhang, L.; Zhang, Z.; Han, X.D.; Ma, E. Uniform tensile elongation in framed submicron metallic glass specimen in the limit of suppressed shear banding. Acta Mater. 2011, 59, 6511–6518. [Google Scholar] [CrossRef]
  83. Liontas, R.; Jafary-Zadeh, M.; Zeng, Q.S.; Zhang, Y.W.; Mao, W.L.; Greer, J.R. Substantial tensile ductility in sputtered Zr-Ni-Al nano-sized metallic glass. Acta Mater. 2016, 118, 270–285. [Google Scholar] [CrossRef] [Green Version]
  84. Rys, J.; Valdevit, L.; Schaedler, T.A.; Jacobsen, A.J.; Carter, W.B.; Greer, J.R. Fabrication and Deformation of Metallic Glass Micro-Lattices. Adv. Eng. Mater. 2014, 16, 889–896. [Google Scholar] [CrossRef]
  85. Hu, Q.; Fu, M.W.; Zeng, X.R.; Ma, C.L. Thin-walled Ti41.5Zr2.5Hf5Cu42.5Ni7.5Si1 bulk metallic glass tubes: Promising energy absorbers and lightweight structures. J. Alloy. Compd. 2013, 546, 180–184. [Google Scholar] [CrossRef]
  86. Shyu, T.C.; Damasceno, P.F.; Dodd, P.M.; Lamoureux, A.; Xu, L.Z.; Shlian, M.; Shtein, M.; Glotzer, S.C.; Kotov, N.A. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat. Mater. 2015, 14, 785–789. [Google Scholar] [CrossRef] [PubMed]
  87. Isobe, M.; Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 2016, 6, 24758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef] [Green Version]
  89. Sha, Z.D.; She, C.M.; Xu, G.K.; Pei, Q.X.; Liu, Z.S.; Wang, T.J.; Gao, H.J. Metallic glass-based chiral nanolattice: Light weight, auxeticity, and superior mechanical properties. Mater. Today 2017, 20, 569–576. [Google Scholar] [CrossRef]
  90. Lamoureux, A.; Lee, K.; Shlian, M.; Forrest, S.R.; Shtein, M. Dynamic kirigami structures for integrated solar tracking. Nat. Commun. 2015, 6, 8092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  91. Xian, H.J.; Cao, C.R.; Shi, J.A.; Zhu, X.S.; Hu, Y.C.; Huang, Y.F.; Meng, S.; Gu, L.; Liu, Y.H.; Bai, H.Y.; et al. Flexible strain sensors with high performance based on metallic glass thin film. Appl. Phys. Lett. 2017, 111, 121906. [Google Scholar] [CrossRef]
  92. Pauly, S.; Lober, L.; Petters, R.; Stoica, M.; Scudino, S.; Kuhn, U.; Eckert, J. Processing metallic glasses by selective laser melting. Mater. Today 2013, 16, 37–41. [Google Scholar] [CrossRef]
  93. Shen, Y.Y.; Li, Y.Q.; Chen, C.; Tsai, H.L. 3D printing of large, complex metallic glass structures. Mater. Des. 2017, 117, 213–222. [Google Scholar] [CrossRef]
  94. Li, N.; Zhang, J.J.; Xing, W.; Ouyang, D.; Liu, L. 3D printing of Fe-based bulk metallic glass composites with combined high strength and fracture toughness. Mater. Des. 2018, 143, 285–296. [Google Scholar] [CrossRef]
Metals 08 00689 g001 550
Figure 1. The comparison of the plastic energy absorption capacity between the conventional Al foams and the Vit106 metallic glass (MG) foams with pore sizes of 180 µm, 230 µm and 330 µm, where the inset shows an MG foam (pore size 230 µm) at a nominal strain of 4%. Adapted from [7] with copyright permission from Elsevier, 2005.
Figure 1. The comparison of the plastic energy absorption capacity between the conventional Al foams and the Vit106 metallic glass (MG) foams with pore sizes of 180 µm, 230 µm and 330 µm, where the inset shows an MG foam (pore size 230 µm) at a nominal strain of 4%. Adapted from [7] with copyright permission from Elsevier, 2005.
Metals 08 00689 g001
Metals 08 00689 g002 550
Figure 2. The comparison of the evolution the plastic energy absorption capacity between a Vit1 MG foam and a conventional Al foam, where the inset shows the morphology of the MG foam. Adapted from [8] with copyright permission from Elsevier, 2012.
Figure 2. The comparison of the evolution the plastic energy absorption capacity between a Vit1 MG foam and a conventional Al foam, where the inset shows the morphology of the MG foam. Adapted from [8] with copyright permission from Elsevier, 2012.
Metals 08 00689 g002
Metals 08 00689 g003 550
Figure 3. (a) The stress–strain curve of an MG honeycomb with ligament length/thickness ratio of 50, where the inset image shows an MG honeycomb with 39 cells. (b) The comparison of the plastic-energy-absorption performance of the Zr35Ti30Cu7.5Be27.5 MG honeycombs and other cellular MG structures. Adapted from [9] with copyright permission from Wiley, 2012.
Figure 3. (a) The stress–strain curve of an MG honeycomb with ligament length/thickness ratio of 50, where the inset image shows an MG honeycomb with 39 cells. (b) The comparison of the plastic-energy-absorption performance of the Zr35Ti30Cu7.5Be27.5 MG honeycombs and other cellular MG structures. Adapted from [9] with copyright permission from Wiley, 2012.
Metals 08 00689 g003
Metals 08 00689 g004 550
Figure 4. (a) Three cellular MGs with macroscopic cellular structures with varying strut thicknesses. (b) The nominal stress–strain curves of the three cellular MGs with macroscopic cellular structures. Adapted from [12] with copyright permission from AIP Publishing, 2014.
Figure 4. (a) Three cellular MGs with macroscopic cellular structures with varying strut thicknesses. (b) The nominal stress–strain curves of the three cellular MGs with macroscopic cellular structures. Adapted from [12] with copyright permission from AIP Publishing, 2014.
Metals 08 00689 g004
Metals 08 00689 g005 550
Figure 5. (a) The optical image of a cellular MG after densification, where the original square-shaped pores are nearly eliminated. (b) The SEM image of a deformed node indicated by the red rectangle in (a) at a higher magnification. (c) Blunting effect of the propagation of a crack as indicated by the red rectangle in (b). (d) The evolution of the shear band densities at the nodes of four specimens, I–IV [71].
Figure 5. (a) The optical image of a cellular MG after densification, where the original square-shaped pores are nearly eliminated. (b) The SEM image of a deformed node indicated by the red rectangle in (a) at a higher magnification. (c) Blunting effect of the propagation of a crack as indicated by the red rectangle in (b). (d) The evolution of the shear band densities at the nodes of four specimens, I–IV [71].
Metals 08 00689 g005
Metals 08 00689 g006 550
Figure 6. The engineering stress–strain curves of the hollow Zr-Ni-Al MG lattice structures, where the SEM images below were taken at the stages indicated by the circles in the curves. Reprinted from [18] with copyright permission from Elsevier, 2017.
Figure 6. The engineering stress–strain curves of the hollow Zr-Ni-Al MG lattice structures, where the SEM images below were taken at the stages indicated by the circles in the curves. Reprinted from [18] with copyright permission from Elsevier, 2017.
Metals 08 00689 g006
Metals 08 00689 g007 550
Figure 7. The molecular dynamics (MD) simulation results of an engineering stress–strain curve of the MG-based chiral nanolattice structures, showing a large elastic strain of about 9%, where the inset schematic diagram shows the design of the chiral lattice structure. Adapted from [89] with copyright permission from Elsevier, 2017.
Figure 7. The molecular dynamics (MD) simulation results of an engineering stress–strain curve of the MG-based chiral nanolattice structures, showing a large elastic strain of about 9%, where the inset schematic diagram shows the design of the chiral lattice structure. Adapted from [89] with copyright permission from Elsevier, 2017.
Metals 08 00689 g007
Metals 08 00689 g008 550
Figure 8. (a) The optical image of a kirigami MG structure. (b) The load-nominal strain curves of a kirigami MG structures, showing an elastic strain larger than 165%. For comparison, a stainless steel kirigami structure has an elastic limit smaller than 62%. (c) The elastic strain energy loss of the kirigami MG structures after 1000 cycles of loadings with four different kirigami patterns. Adapted from [19] with copyright permission from Elsevier, 2018.
Figure 8. (a) The optical image of a kirigami MG structure. (b) The load-nominal strain curves of a kirigami MG structures, showing an elastic strain larger than 165%. For comparison, a stainless steel kirigami structure has an elastic limit smaller than 62%. (c) The elastic strain energy loss of the kirigami MG structures after 1000 cycles of loadings with four different kirigami patterns. Adapted from [19] with copyright permission from Elsevier, 2018.
Metals 08 00689 g008

Share and Cite

MDPI and ACS Style

Chen, S.H.; Cheng, H.Y.; Chan, K.C.; Wang, G. Metallic Glass Structures for Mechanical-Energy-Dissipation Purpose: A Review. Metals 2018, 8, 689. https://doi.org/10.3390/met8090689

AMA Style

Chen SH, Cheng HY, Chan KC, Wang G. Metallic Glass Structures for Mechanical-Energy-Dissipation Purpose: A Review. Metals. 2018; 8(9):689. https://doi.org/10.3390/met8090689

Chicago/Turabian Style

Chen, S. H., H. Y. Cheng, K. C. Chan, and G. Wang. 2018. "Metallic Glass Structures for Mechanical-Energy-Dissipation Purpose: A Review" Metals 8, no. 9: 689. https://doi.org/10.3390/met8090689

APA Style

Chen, S. H., Cheng, H. Y., Chan, K. C., & Wang, G. (2018). Metallic Glass Structures for Mechanical-Energy-Dissipation Purpose: A Review. Metals, 8(9), 689. https://doi.org/10.3390/met8090689

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop