A Review on Heterogeneous Nanostructures: A Strategy for Superior Mechanical Properties in Metals
Abstract
:1. Introduction
2. Heterogeneous Grain/Lamella/Phase Structures
2.1. Hetero-Interfaces and Deformation Mechanisms
2.2. Heterogeneous Grain Structures
2.3. Heterogeneous Lamella Structures
2.4. Heterogeneous Phase Structures
3. Gradient Structure
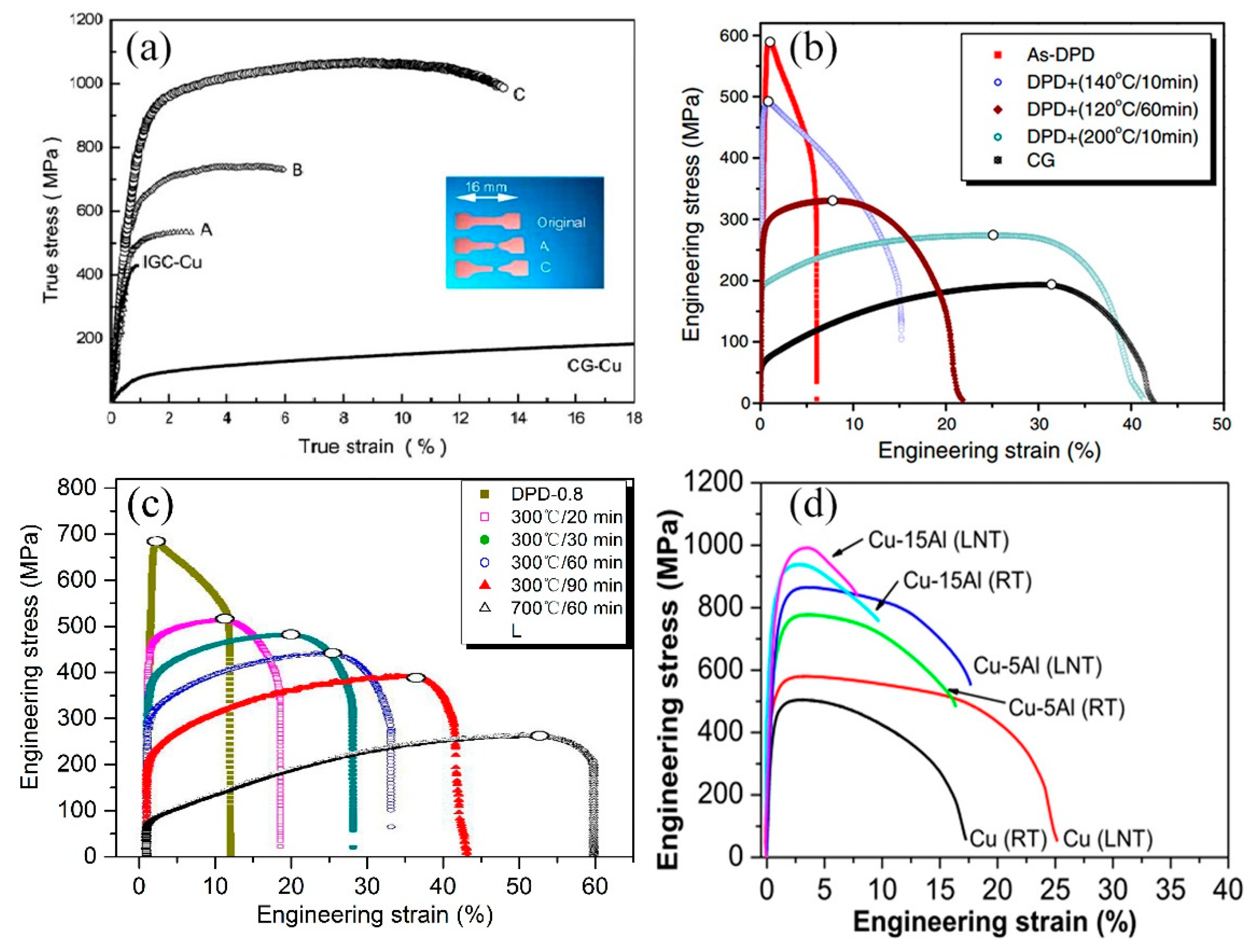
3.1. Fabrication Methods
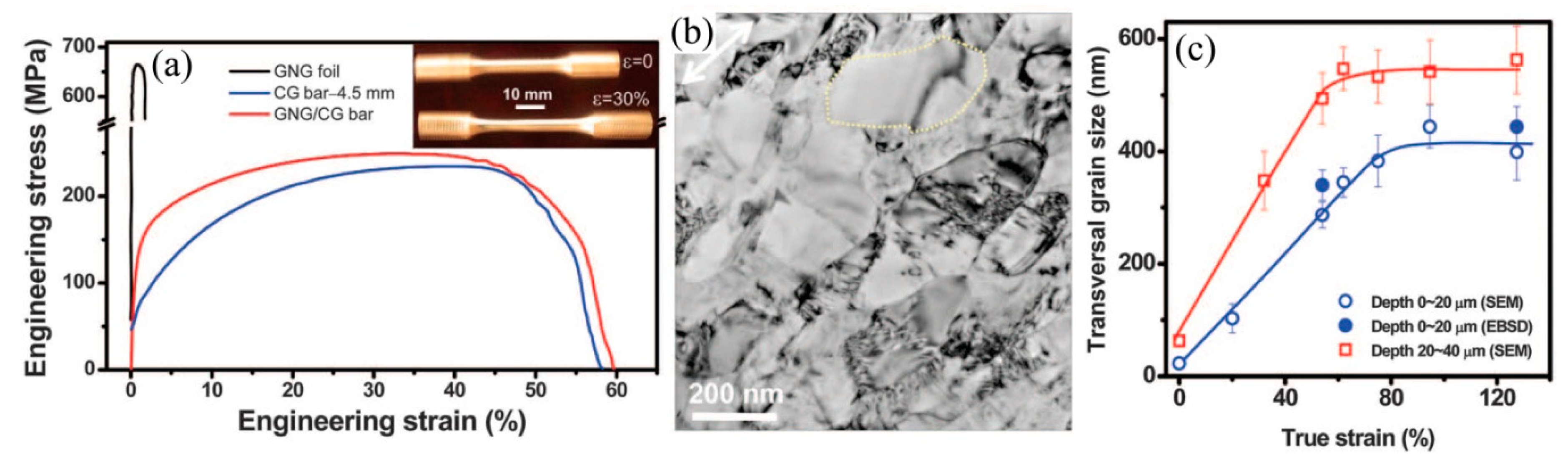
3.2. Tensile Behaviors of Gradient Grained Structures
3.3. Tensile Behaviors for Other Types of Gradient Structures
3.4. Dynamic Behaviors of Gradient Structures
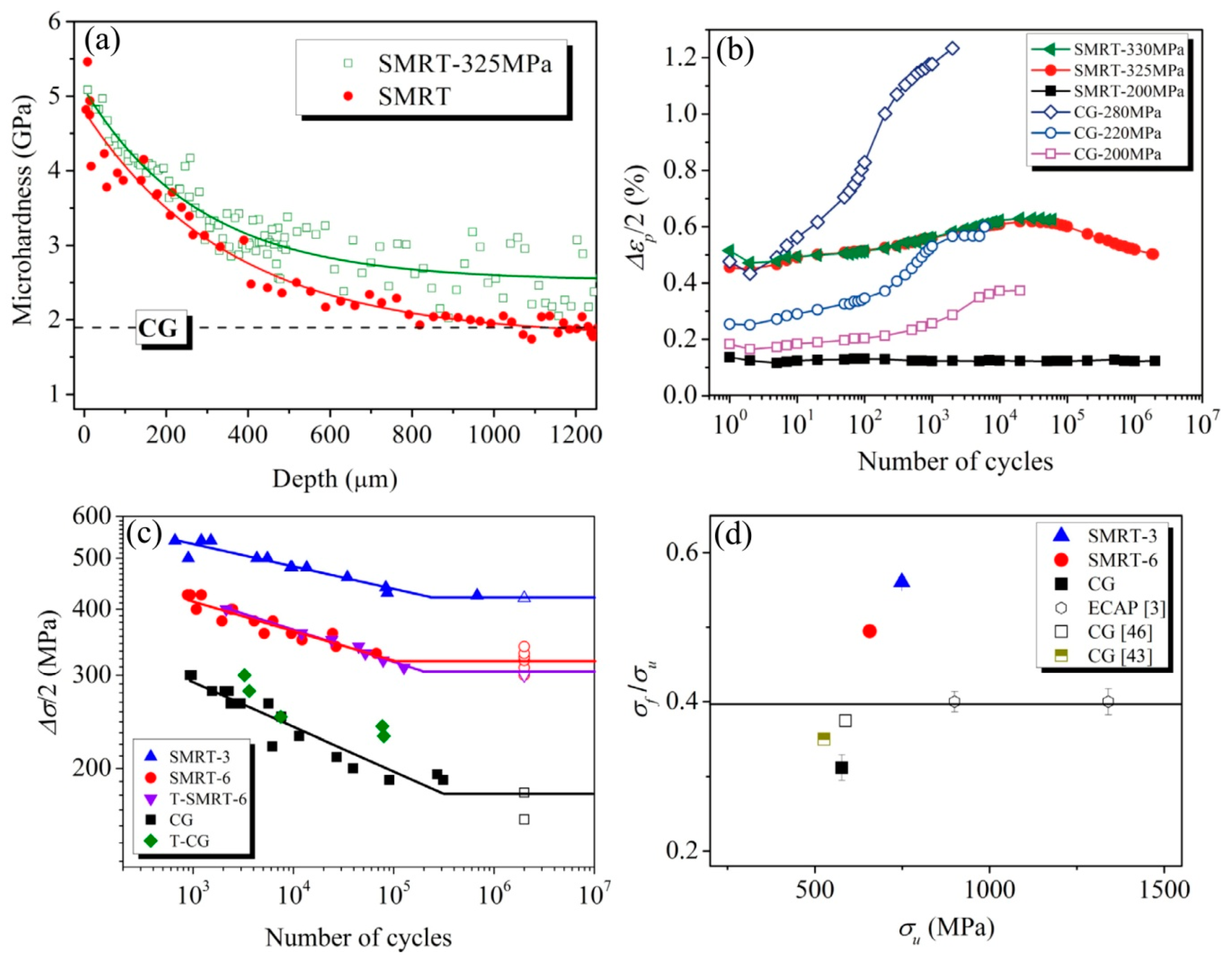
3.5. Fatigue Behaviors of Gradient Structures
3.6. Theoretical and Numerical Work for Gradient Structures
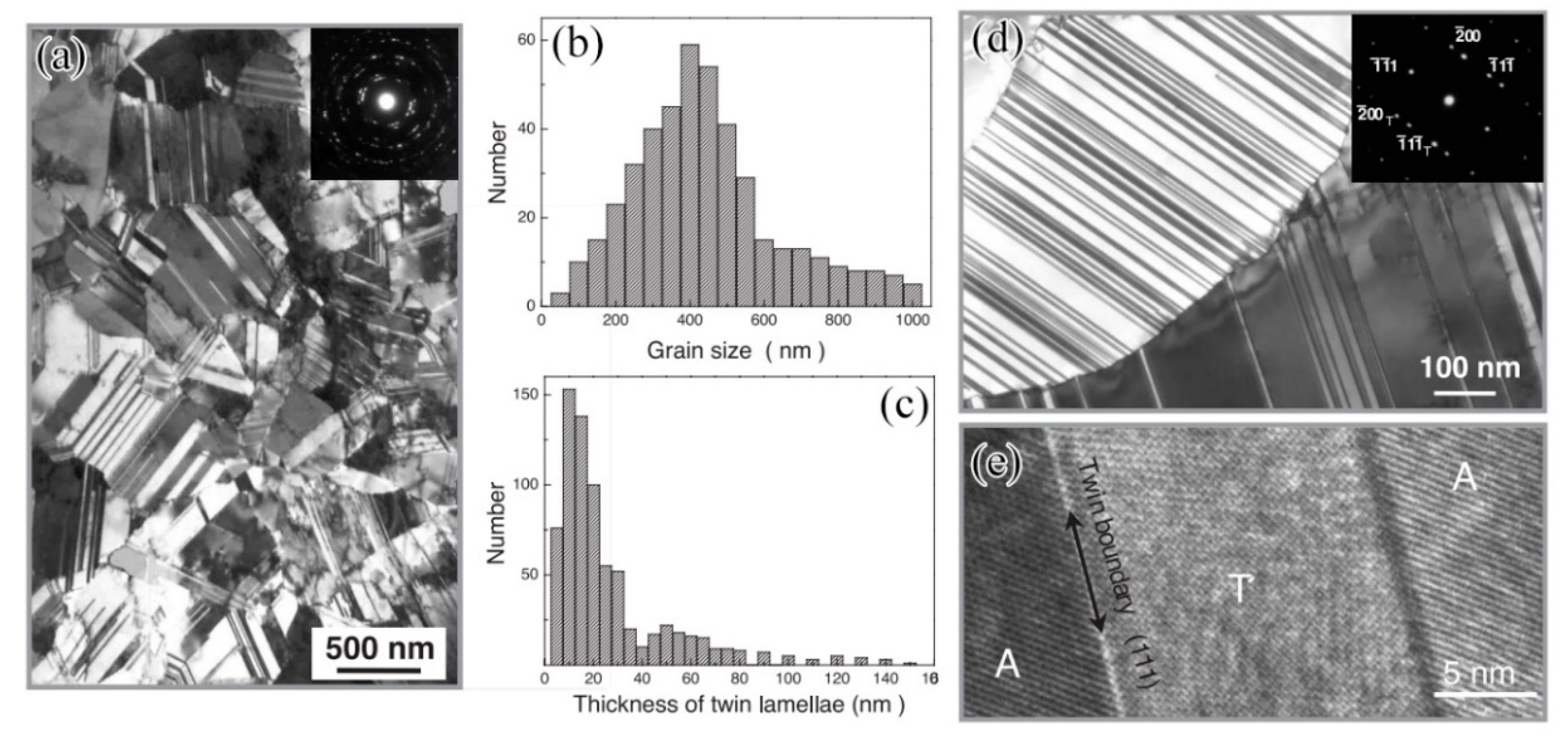
4. Nanotwinned Structure
4.1. Strength and Ductility
4.2. Strain Rate Effect and Activation Volume
4.3. Fatigue and Damage Tolerance
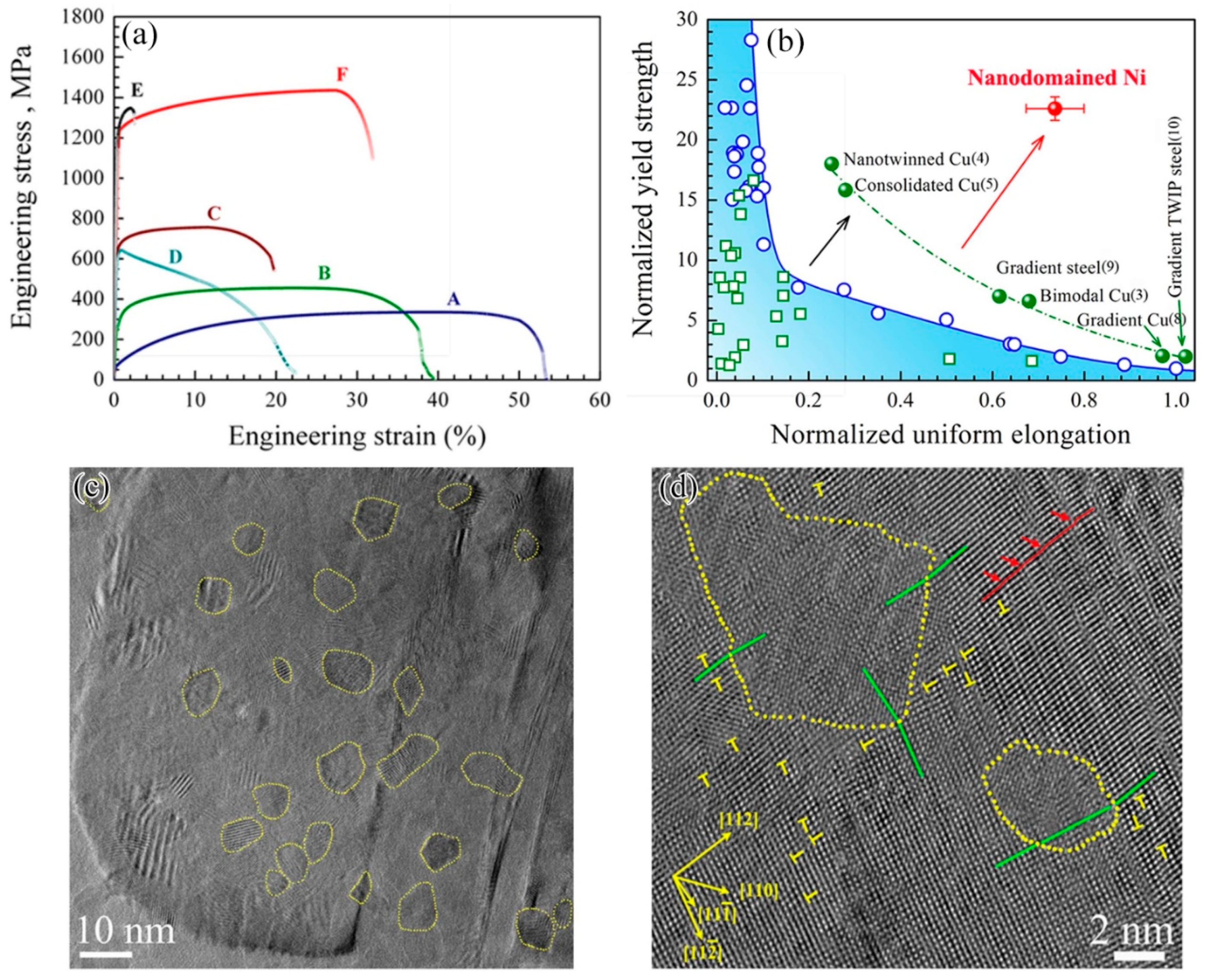
5. Nanoprecipitate
6. Conclusions, Future Perspective and Challenges
Author Contributions
Funding
Conflicts of Interest
References
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Ma, E.; Zhu, T. Towards strength–ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today 2017, 20, 323–331. [Google Scholar] [CrossRef]
- Wu, X.L.; Zhu, Y.T. Heterogeneous materials: A new class of materials with unprecedented mechanical properties. Mater. Res. Lett 2017, 5, 527–532. [Google Scholar] [CrossRef]
- Ovid’ko, I.A.; Valiev, R.Z.; Zhu, Y.T. Review on superior strength and enhanced ductility of metallic nanomaterials. Prog. Mater. Sci. 2018, 94, 462–540. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J.; Zhu, Y.T. Fundamentals of superior properties in bulk NanoSPD materials. Mater. Res. Lett 2016, 4, 1–21. [Google Scholar] [CrossRef]
- Cao, Y.; Ni, S.; Liao, X.Z.; Song, M.; Zhu, Y.T. Structural evolutions of metallic materials processed by severe plastic deformation. Mater. Sci. Eng. R. 2018, 133, 1–59. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Alexandrov, I.V.; Zhu, Y.T.; Lowe, T.C. Paradox of strength and ductility in metals processed by severe plastic deformation. J. Mater. Res. 2002, 17, 5–8. [Google Scholar] [CrossRef]
- Valiev, R. Nanostructuring of metals by severe plastic deformation for advanced properties. Nat. Mater. 2004, 3, 511–516. [Google Scholar] [CrossRef]
- Langdon, T.G. Twenty-five years of ultrafine-grained materials: Achieving exceptional properties through grain refinement. Acta Mater. 2013, 61, 7035–7059. [Google Scholar] [CrossRef]
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Lu, K. Stabilizing nanostructures in metals using grain and twin boundary architectures. Nat. Rev. Mater. 2016, 1, 13. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.F.; Lu, Q.H.; Gao, H.J.; Lu, L. Extra strengthening and work hardening in gradient nanotwinned metals. Science 2018, 362, 559–567. [Google Scholar] [CrossRef]
- Wu, X.L.; Jiang, P.; Chen, L.; Yuan, F.P.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.L.; Jiang, P.; Chen, L.; Zhang, J.F.; Yuan, F.P.; Zhu, Y.T. Synergetic Strengthening by Gradient Structure. Mater. Res. Lett. 2014, 2, 185–191. [Google Scholar] [CrossRef]
- Wu, X.L.; Yang, M.X.; Yuan, F.P.; Wu, G.L.; Wei, Y.J.; Huang, X.X.; Zhu, Y.T. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. USA 2015, 112, 14501–14505. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.X.; Yan, D.S.; Yuan, F.P.; Jiang, P.; Ma, E.; Wu, X.L. Dynamically reinforced heterogeneous grain structure prolongs ductility in a medium-entropy alloy with gigapascal yield strength. Proc. Natl. Acad. Sci. USA 2018, 115, 7224–7229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.M.; Chen, M.W.; Zhou, F.H.; Ma, E. High tensile ductility in a nanostructured metal. Nature 2002, 419, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.; Choudhuri, D.; Wang, T.; Liu, K.; Wheeler, R.; Williams, S.; Gwalani, B.; Mishra, R.S. Hierarchical features infused heterogeneous grain structure for extraordinary strength–ductility synergy. Mater. Res. Lett. 2018, 6, 676–682. [Google Scholar] [CrossRef]
- Wu, G.; Chan, K.C.; Zhu, L.L.; Sun, L.G.; Lu, J. Dual-phase nanostructuring as a route to high-strength magnesium alloys. Nature 2017, 545, 80–83. [Google Scholar] [CrossRef]
- Shi, P.J.; Ren, W.L.; Zheng, T.X.; Ren, Z.M.; Hou, X.L.; Peng, J.C.; Hu, P.F.; Gao, Y.F.; Zhong, Y.B.; Liaw, P.K. Enhanced strength–ductility synergy in ultrafine-grained eutectic high-entropy alloys by inheriting microstructural lamellae. Nat. Commun. 2019, 10, 489. [Google Scholar] [CrossRef] [PubMed]
- Koyama, M.; Zhang, Z.; Wang, M.M.; Ponge, D.; Raabe, D.; Tsuzaki, K.; Noguchi, H.; Tasan, C.C. Bone-like crack resistance in hierarchical metastable nanolaminate steels. Science 2017, 355, 1055–1057. [Google Scholar] [CrossRef] [PubMed]
- He, B.B.; Hu, B.; Yen, H.W.; Cheng, G.J.; Wang, Z.K.; Luo, H.W.; Huang, M.X. High dislocation density-induced large ductility in deformed and partitioned steels. Science 2017, 357, 1029–1032. [Google Scholar] [CrossRef]
- Liang, Y.J.; Wang, L.J.; Wen, Y.R.; Cheng, B.Y.; Wu, Q.L.; Cao, T.Q.; Xiao, Q.; Xue, Y.F.; Sha, G.; Wang, Y.D.; et al. High-content ductile coherent nanoprecipitates achieve ultrastrong high-entropy alloys. Nat. Commun. 2018, 9, 4063. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.X.; Wang, Y.F.; Ma, X.L.; Yin, S.; Hoeppel, H.W.; Goeken, M.; Wu, X.L.; Gao, H.J.; Zhu, Y.T. Interface affected zone for optimal strength and ductility in heterogeneous laminate. Mater. Today 2018, 21, 713–719. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Yuan, F.P.; Yang, M.X.; Jiang, P.; Ma, E.; Wu, X.L. Dynamic shear deformation of a CrCoNi medium-entropy alloy with heterogeneous grain structures. Acta Mater. 2018, 148, 407–418. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.L.; Yang, M.X.; Yuan, F.P.; Chen, L.; Zhu, Y.T. Combining gradient structure and TRIP effect to produce austenite stainless steel with high strength and ductility. Acta Mater. 2016, 112, 337–346. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.X.; Yuan, F.P.; Xie, Q.G.; Wang, Y.D.; Ma, E.; Wu, X.L. Strain hardening in Fe-16Mn-10Al-0.86C-5Ni high specific strength steel. Acta Mater. 2016, 109, 213–222. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, M.X.; Jiang, P.; Yuan, F.P.; Wu, X.L. Plastic deformation mechanisms in a severely deformed Fe-Ni-Al-C alloy with superior tensile properties. Sci. Rep. 2017, 7, 15619. [Google Scholar] [CrossRef]
- Miserez, A.; Schneberk, T.; Sun, C.; Zok, F.W.; Waite, J.H. The transition from stiff to compliant materials in squid beaks. Science 2008, 319, 1816–1819. [Google Scholar] [CrossRef]
- Gao, S.L.; Maeder, E.; Plonka, R. Nanostructured-coatings of glass fibers: Improvement of alkali resistance and mechanical properties. Acta Mater. 2007, 55, 1043–1052. [Google Scholar] [CrossRef]
- Edalati, K.; Matsuda, J.; Iwaoka, H.; Toh, S.; Akiba, E.; Horita, Z. High-pressure torsion of TiFe intermetallics for activation of hydrogen storage at room temperature with heterogeneous nanostructure. Int. J. Hydrog. Energy 2013, 38, 4622–4627. [Google Scholar] [CrossRef]
- Liu, R.; Duay, J.; Lee, S.B. Heterogeneous nanostructured electrode materials for electrochemical energy storage. Chem. Commun. 2011, 47, 1384–1404. [Google Scholar] [CrossRef]
- Tong, W.P.; Han, Z.; Wang, L.M.; Lu, J.; Lu, K. Low-temperature nitriding of 38CrMoAl steel with a nanostructured surface layer induced by surface mechanical attrition treatment. Surf. Coat. Tech. 2008, 202, 4957–4963. [Google Scholar] [CrossRef]
- Lu, K.; Lu, J. Surface nanocrystallization (SNC) of metallic materials-presentation of the concept behind a new approach. J. Mater. Sci. Technol. 1999, 15, 193–197. [Google Scholar]
- Suresh, S. Graded materials for resistance to contact deformation and damage. Science 2001, 292, 2447–2451. [Google Scholar] [CrossRef] [PubMed]
- Yuan, F.P.; Jiang, P.; Xie, J.J.; Wu, X.L. Analysis of spherical indentation of materials with plastically graded surface layer. Int. J. Solids. Struct. 2012, 49, 527–536. [Google Scholar] [CrossRef] [Green Version]
- Tong, W.P.; Tao, N.R.; Wang, Z.B.; Lu, J.; Lu, K. Nitriding iron at lower temperatures. Science 2003, 299, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Roland, T.; Retraint, D.; Lu, K.; Lu, J. Fatigue life improvement through surface nanostructuring of stainless steel by means of surface mechanical attrition treatment. Scr. Mater. 2006, 54, 1949–1954. [Google Scholar] [CrossRef]
- Chen, A.Y.; Li, D.F.; Zhang, J.B.; Song, H.W.; Lu, J. Make nanostructured metal exceptionally tough by introducing non-localized fracture behaviors. Scr. Mater. 2008, 59, 579–582. [Google Scholar] [CrossRef]
- Li, W.L.; Tao, N.R.; Lu, K. Fabrication of a gradient nano-micro-structured surface layer on bulk copper by means of a surface mechanical grinding treatment. Scr. Mater. 2008, 59, 546–549. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing Extraordinary Intrinsic Tensile Plasticity in Gradient Nano-Grained Copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [Green Version]
- Jerusalem, A.; Dickson, W.; Perez-Martin, M.J.; Dao, M.; Lu, J.; Galvez, F. Grain size gradient length scale in ballistic properties optimization of functionally graded nanocrystalline steel plates. Scr. Mater. 2013, 69, 773–776. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.C.; Zhang, H.W.; Lu, K. Strain-Induced Ultrahard and Ultrastable Nanolaminated Structure in Nickel. Science 2013, 342, 337–340. [Google Scholar] [CrossRef]
- Huang, H.W.; Wang, Z.B.; Yong, X.P.; Lu, K. Enhancing torsion fatigue behaviour of a martensitic stainless steel by generating gradient nanograined layer via surface mechanical grinding treatment. Mater. Sci. Technol. 2013, 29, 1200–1205. [Google Scholar] [CrossRef]
- Fang, T.H.; Tao, N.R.; Lu, K. Tension-induced softening and hardening in gradient nanograined surface layer in copper. Scr. Mater. 2014, 77, 17–20. [Google Scholar] [CrossRef]
- Wei, Y.J.; Li, Y.Q.; Zhu, L.C.; Liu, Y.; Lei, X.Q.; Wang, G.; Wu, Y.X.; Mi, Z.L.; Liu, J.B.; Wang, H.T.; et al. Evading the strength- ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 2014, 5, 3580. [Google Scholar] [CrossRef] [PubMed]
- Li, J.J.; Chen, S.H.; Wu, X.L.; Soh, A.K. A physical model revealing strong strain hardening in nano-grained metals induced by grain size gradient structure. Mater. Sci. Eng. A 2015, 620, 16–21. [Google Scholar] [CrossRef]
- Huang, H.W.; Wang, Z.B.; Lu, J.; Lu, K. Fatigue behaviors of AISI 316L stainless steel with a gradient nanostructured surface layer. Acta Mater. 2015, 87, 150–160. [Google Scholar] [CrossRef]
- Li, W.B.; Yuan, F.P.; Wu, X.L. Atomistic tensile deformation mechanisms of Fe with gradient nano-grained structure. AIP Adv. 2015, 5, 087120. [Google Scholar] [CrossRef]
- Ma, Z.W.; Liu, J.B.; Wang, G.; Wang, H.T.; Wei, Y.J.; Gao, H.J. Strength gradient enhances fatigue resistance of steels. Sci. Rep. 2016, 6, 22156. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.P.; Chen, P.; Feng, Y.P.; Jiang, P.; Wu, X.L. Strain hardening behaviors and strain rate sensitivity of gradient-grained Fe under compression over a wide range of strain rates. Mech. Mater. 2016, 95, 71–82. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.X.; Pan, Y.; Yuan, F.P.; Zhu, Y.T.; Wu, X.L. Back stress strengthening and strain hardening in gradient structure. Mater. Res. Lett. 2016, 4, 145–151. [Google Scholar] [CrossRef]
- Li, J.J.; Weng, G.J.; Chen, S.H.; Wu, X.L. On strain hardening mechanism in gradient nanostructures. Int. J. Plast. 2017, 88, 89–107. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.L.; Wen, C.S.; Gao, C.Y.; Guo, X.; Lu, J. A study of dynamic plasticity in austenite stainless steels with a gradient distribution of nanoscale twins. Scr. Mater. 2017, 133, 49–53. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.X.; Wang, W.J.; Wang, X.; Li, Q.; Wei, Y.J. Optimal stress and deformation partition in gradient materials for better strength and tensile ductility: A numerical investigation. Sci. Rep. 2017, 7, 10954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bian, X.D.; Yuan, F.P.; Wu, X.L.; Zhu, Y.T. The evolution of strain gradient and anisotropy in gradient-structured metal. Metall. Mater. Trans. A 2017, 48A, 3951–3960. [Google Scholar] [CrossRef]
- Bian, X.D.; Yuan, F.P.; Zhu, Y.T.; Wu, X.L. Gradient structure produces superior dynamic shear properties. Mater. Res. Lett. 2017, 5, 501–507. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Yuan, F.P.; Jiang, P.; Xie, J.J.; Wu, X.L. Mechanical properties and deformation mechanism of Mg-Al-Zn alloy with gradient microstructure in grain size and orientation. Mater. Sci. Eng. A 2017, 694, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Pan, J.; Zhou, H.F.; Gao, H.J.; Li, Y. Mechanical properties and optimal grain size distribution profile of gradient grained nickel. Acta Mater. 2018, 153, 279–289. [Google Scholar] [CrossRef]
- Long, J.Z.; Pan, Q.S.; Tao, N.R.; Lu, L. Abnormal grain coarsening in cyclically deformed gradient nanograined Cu. Scr. Mater. 2018, 145, 99–103. [Google Scholar] [CrossRef]
- Liu, X.L.; Yuan, F.P.; Zhu, Y.T.; Wu, X.L. Extraordinary Bauschinger effect in gradient structured copper. Scr. Mater. 2018, 150, 57–60. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.P.; Yan, D.S.; Sun, J.D.; Zhou, L.L.; Zhu, Y.T.; Wu, X.L. Ductility by shear band delocalization in the nano-layer of gradient structure. Mater. Res. Lett. 2019, 7, 12–17. [Google Scholar] [CrossRef]
- Lu, X.C.; Zhang, X.; Shi, M.X.; Roters, F.; Kang, G.Z.; Raabe, D. Dislocation mechanism based size-dependent crystal plasticity modeling and simulation of gradient nano-grained copper. Int. J. Plast. 2019, 113, 52–73. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.Y.; Xu, D.S.; Lu, L.; Gao, H.J.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extreme Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef]
- Lu, K.; Lu, L.; Suresh, S. Strengthening materials by engineering coherent internal boundaries at the nanoscale. Science 2009, 324, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Gu, P.; Dao, M.; Asaro, R.J.; Suresh, S. A unified mechanistic model for size-dependent deformation in nanocrystalline and nanotwinned metals. Acta Mater. 2011, 59, 6861–6868. [Google Scholar] [CrossRef]
- Lu, L.; Schwaiger, R.; Shan, Z.W.; Dao, M.; Lu, K.; Suresh, S. Nano-sized twins induce high rate sensitivity of flow stress in pure copper. Acta Mater. 2005, 53, 2169–2179. [Google Scholar] [CrossRef]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the maximum strength in nanotwinned copper. Science 2009, 323, 607–610. [Google Scholar] [CrossRef]
- Pan, Q.S.; Zhou, H.F.; Lu, Q.H.; Gao, H.J.; Lu, L. History-independent cyclic response of nanotwinned metals. Nature 2017, 551, 214–217. [Google Scholar] [CrossRef]
- Dao, M.; Lu, L.; Shen, Y.F.; Suresh, S. Strength, strain-rate sensitivity and ductility of copper with nanoscale twins. Acta Mater. 2006, 54, 5421–5432. [Google Scholar] [CrossRef]
- Wei, Q.; Cheng, S.; Ramesh, K.T.; Ma, E. Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume: fcc versus bcc metals. Mater. Sci. Eng. A 2004, 381, 71–79. [Google Scholar] [CrossRef]
- Li, X.Y.; Wei, Y.J.; Lu, L.; Lu, K.; Gao, H.J. Dislocation nucleation governed softening and maximum strength in nanotwinned metals. Nature 2010, 464, 877–880. [Google Scholar] [CrossRef]
- Lu, L.; Shen, Y.F.; Chen, X.H.; Qian, L.H.; Lu, K. Ultrahigh strength and high electrical conductivity in copper. Science 2004, 304, 422–426. [Google Scholar] [CrossRef]
- Shen, Y.F.; Lu, L.; Lu, Q.H.; Jin, Z.H.; Lu, K. Tensile properties of copper with nano-scale twins. Scr. Mater. 2005, 52, 989–994. [Google Scholar] [CrossRef]
- Sun, L.G.; He, X.Q.; Lu, J. Atomistic simulation study on twin orientation and spacing distribution effects on nanotwinned Cu films. Philos. Mag. 2015, 95, 3467–3485. [Google Scholar] [CrossRef]
- Sun, L.G.; He, X.Q.; Lu, J. Nanotwinned and hierarchical nanotwinned metals: a review of experimental, computational and theoretical efforts. npj Comput. Mater. 2018, 4, 6. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Chen, X.H.; Lu, L.; Lu, K.; Hoagland, R.G.; Misra, A. High-strength sputter-deposited Cu foils with preferred orientation of nanoscale growth twins. Appl. Phys. Lett. 2006, 88, 173116. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.B.; Wu, B.; Sui, M.L. Dynamical dislocation emission processes from twin boundaries. Appl. Phys. Lett. 2008, 93, 041906. [Google Scholar] [CrossRef]
- Xiao, G.H.; Tao, N.R.; Lu, K. Strength–ductility combination of nanostructured Cu–Zn alloy with nanotwin bundles. Scr. Mater. 2011, 65, 119–122. [Google Scholar] [CrossRef]
- Zhang, P.; Qu, S.; Yang, M.X.; Yang, G.; Wu, S.D.; Li, S.X.; Zhang, Z.F. Varying tensile fracture mechanisms of Cu and Cu–Zn alloys with reduced grain size: From necking to shearing instability. Mater. Sci. Eng. A 2014, 594, 309–320. [Google Scholar] [CrossRef]
- Zhang, Y.; Tao, N.R.; Lu, K. Effects of stacking fault energy, strain rate and temperature on microstructure and strength of nanostructured Cu–Al alloys subjected to plastic deformation. Acta Mater. 2011, 59, 6048–6058. [Google Scholar] [CrossRef]
- Qu, S.; An, X.H.; Yang, H.J.; Huang, C.X.; Yang, G.; Zang, Q.S.; Wang, Z.G.; Wu, S.D.; Zhang, Z.F. Microstructural evolution and mechanical properties of Cu–Al alloys subjected to equal channel angular pressing. Acta Mater. 2009, 57, 1586–1601. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Horst, O.M.; Eggeler, G.; George, E.P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 2016, 118, 152–163. [Google Scholar] [CrossRef] [Green Version]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S.; Bhattacharjee, T.; Bai, Y.; Tsuji, N. Friction stress and Hall–Petch relationship in CoCrNi equi-atomic medium entropy alloy processed by severe plastic deformation and subsequent annealing. Scr. Mater. 2017, 134, 33–36. [Google Scholar] [CrossRef]
- Slone, C.E.; Miao, J.; George, E.P.; Mills, M.J. Achieving ultra-high strength and ductility in equiatomic CrCoNi with partially recrystallized microstructures. Acta Mater. 2019, 165, 496–507. [Google Scholar] [CrossRef]
- Miao, J.; Slone, C.E.; Smith, T.M.; Niu, C.; Bei, H.; Ghazisaeidi, M.; Pharr, G.M.; Mills, M.J. The evolution of the deformation substructure in a Ni-Co-Cr equiatomic solid solution alloy. Acta Mater. 2017, 132, 35–48. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, S.; Diao, H.; Liaw, P.K.; Meyers, M.A. High-velocity deformation of Al0.3CoCrFeNi high-entropy alloy: Remarkable resistance to shear failure. Sci. Rep. 2017, 7, 42742. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, Y.; Tao, N.R.; Lu, K. Effect of thermal annealing on mechanical properties of a nanostructured copper prepared by means of dynamic plastic deformation. Scr. Mater. 2008, 59, 475–478. [Google Scholar] [CrossRef]
- Wei, K.X.; Horky, J.; Wei, W.; Zehetbauer, M.J.; Setman, D.; Schafler, E.; Hu, J. Enhancing tensile properties of Cu and Cu-Al alloys cryogenically processed by high pressure torsion. J. Alloys Compd. 2019, 771, 317–321. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, Y.; Tao, N.R.; Lu, K. Effect of the Zener-Hollomon parameter on the microstructures and mechanical properties of Cu subjected to plastic deformation. Acta Mater. 2009, 57, 761–772. [Google Scholar] [CrossRef]
- Yuan, F.P.; Wu, X.L. Formation sequences and roles of multiple deformation twins during the plastic deformation in nanocrystalline fcc metals. Mater. Sci. Eng. A 2013, 580, 58–65. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.P.; Wu, X.L. Size effects of primary/secondary twins on the atomistic deformation mechanisms in hierarchically nanotwinned metals. J. Appl. Phys. 2013, 113, 203516. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.W.; Sun, L.G.; Zhu, L.L.; Liu, J.B.; Lu, K.; Lu, J. High-order hierarchical nanotwins with superior strength and ductility. Acta Mater. 2018, 149, 397–406. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, F.P.; Jiang, P.; Wu, X.L. Size effects of lamellar twins on the strength and deformation mechanisms of nanocrystalline hcp cobalt. Sci. Rep. 2017, 7, 9550. [Google Scholar] [CrossRef]
- Wang, Y.; Hamza, A.; Ma, E. Temperature-dependent strain rate sensitivity and activation volume of nanocrystalline Ni. Acta Mater. 2006, 54, 2715–2726. [Google Scholar] [CrossRef]
- Shen, Y.F.; Lu, L.; Dao, M.; Suresh, S. Strain rate sensitivity of Cu with nanoscale twins. Scr. Mater. 2006, 55, 319–322. [Google Scholar] [CrossRef]
- Liang, Z.Y.; Wang, X.; Huang, W.; Huang, M.X. Strain rate sensitivity and evolution of dislocations and twins in a twinning-induced plasticity steel. Acta Mater. 2015, 88, 170–179. [Google Scholar] [CrossRef]
- Yuan, F.P.; Wu, X.L. Shock response of nanotwinned copper from large-scale molecular dynamics simulations. Phys. Rev. B 2012, 86, 134108. [Google Scholar] [CrossRef]
- You, Z.S.; Lu, L. Effect of strain rate on tensile ductility and fracture behavior of bulk nanotwinned copper. Adv. Eng. Mater. 2015, 17, 1754–1759. [Google Scholar] [CrossRef]
- Yuan, F.P.; Chen, L.; Jiang, P.; Wu, X.L. Twin boundary spacing effects on shock response and spall behaviors of hierarchically nanotwinned fcc metals. J. Appl. Phys. 2014, 115, 063509. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Zhu, T.; Shen, Y.F.; Dao, M.; Lu, K.; Suresh, S. Stress relaxation and the structure size-dependence of plastic deformation in nanotwinned copper. Acta Mater. 2009, 57, 5165–5173. [Google Scholar] [CrossRef]
- Schwaiger, R.; Moser, B.; Dao, M.; Chollacoop, N.; Suresh, S. Some critical experiments on the strain-rate sensitivity of nanocrystalline nickel. Acta Mater. 2003, 51, 5159–5172. [Google Scholar] [CrossRef]
- Pan, Q.S.; Lu, Q.H.; Lu, L. Fatigue behavior of columnar-grained Cu with preferentially oriented nanoscale twins. Acta Mater. 2013, 61, 1383–1393. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.Y.; Lu, L.; Zhu, T. Fracture in a thin film of nanotwinned copper. Acta Mater. 2015, 98, 313–317. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.G.; He, X.Q.; Wang, J.B.; Lu, J. Deformation and failure mechanisms of nanotwinned copper films with a pre-existing crack. Mater. Sci. Eng. A 2014, 606, 334–345. [Google Scholar] [CrossRef]
- Yuan, F.P.; Wu, X.L. Atomistic scale fracture behaviours in hierarchically nanotwinned metals. Philos. Mag. 2013, 93, 3248–3259. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.P.; Wu, X.L. Size effect and atomistic deformation mechanisms of hierarchically nanotwinned fcc metals under nanoindentation. J. Mater. Sci. 2015, 50, 7557–7567. [Google Scholar] [CrossRef]
- Luo, S.S.; You, Z.S.; Lu, L. Intrinsic fracture toughness of bulk nanostructured Cu with nanoscale deformation twins. Scr. Mater. 2017, 133, 1–4. [Google Scholar] [CrossRef]
- Kim, S.W.; Li, X.Y.; Gao, H.J.; Kumar, S. In situ observations of crack arrest and bridging by nanoscale twins in copper thin films. Acta Mater. 2012, 60, 2959–2972. [Google Scholar] [CrossRef]
- Xiong, L.; You, Z.S.; Qu, S.D.; Lu, L. Fracture behavior of heterogeneous nanostructured 316L austenitic stainless steel with nanotwin bundles. Acta Mater. 2018, 150, 130–138. [Google Scholar] [CrossRef]
- Xiong, L.; You, Z.S.; Lu, L. Fracture behavior of an austenitic stainless steel with nanoscale deformation twins. Scr. Mater. 2017, 127, 173–177. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.T.; Liao, X.Z.; Wu, X.L. Deformation twinning in nanocrystalline materials. Prog. Mater. Sci. 2012, 57, 1–62. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Zhang, G.J.; Jiang, F.; Ding, X.D.; Sun, Y.J.; Sun, J.; Ma, E. Nanostructured high-strength molybdenum alloys with unprecedented tensile ductility. Nat. Mater. 2013, 12, 344–350. [Google Scholar] [CrossRef]
- Raabe, D.; Ponge, D.; Dmitrieva, O.; Sander, B. Nanoprecipitate-hardened 1.5 GPa steels with unexpected high ductility. Scr. Mater. 2009, 60, 1141–1144. [Google Scholar] [CrossRef]
- Fu, Z.Q.; Jiang, L.; Wardini, J.L.; Macdonald, B.E.; Wen, H.M.; Xiong, W.; Zhang, D.L.; Zhou, Y.Z.; Rupert, T.J.; Chen, W.P.; et al. A high-entropy alloy with hierarchical nanoprecipitates and ultrahigh strength. Sci. Adv. 2018, 4, 8712. [Google Scholar] [CrossRef]
- Wu, X.L.; Yuan, F.P.; Yang, M.X.; Jiang, P.; Zhang, C.X.; Chen, L.; Wei, Y.G.; Ma, E. Nanodomained nickel unite nanocrystal strength with coarse-grain ductility. Sci. Rep. 2015, 5, 11728. [Google Scholar] [CrossRef]
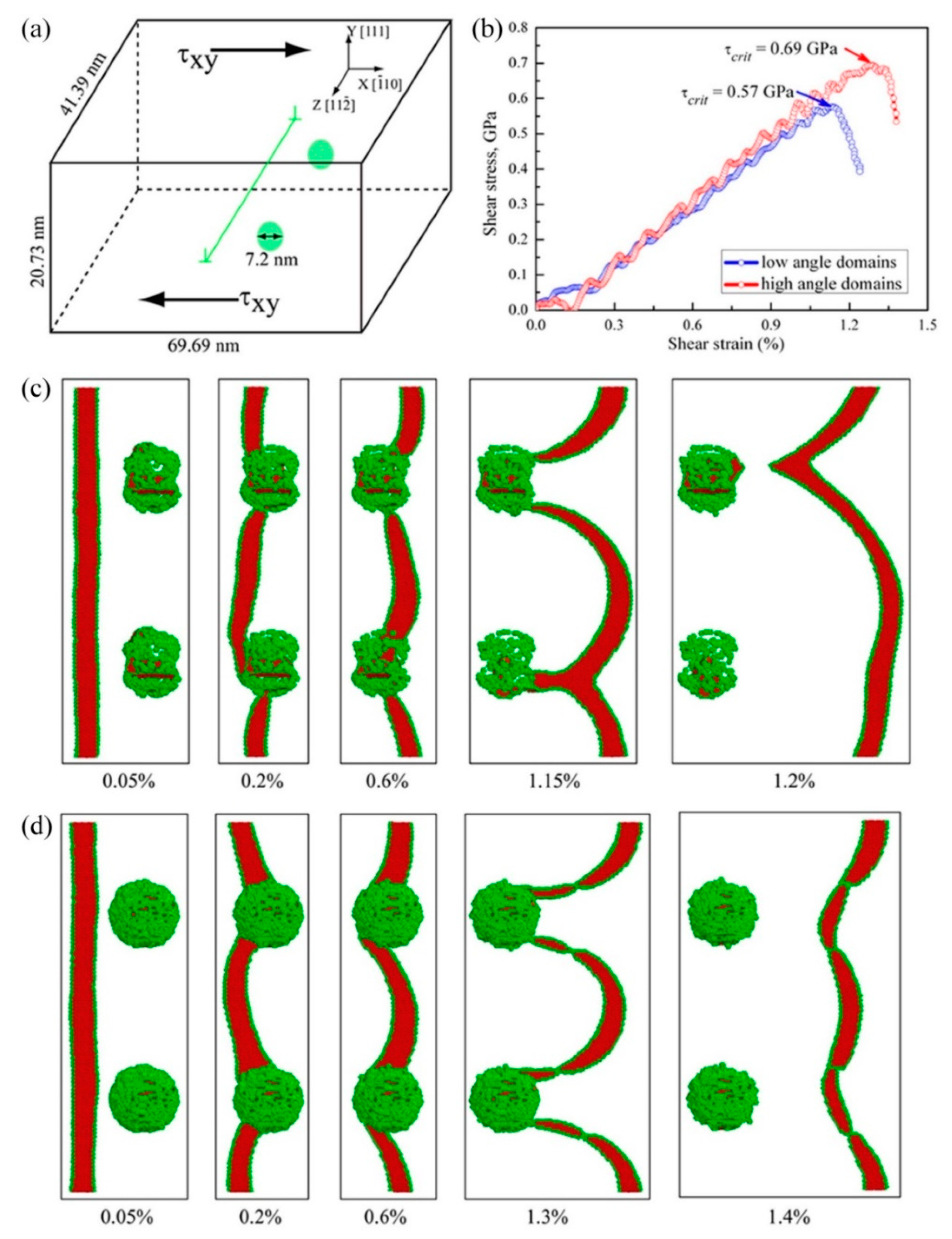
- Yuan, F.P.; Wu, X.L. Size effect and boundary type on the strengthening of nanoscale domains in pure nickel. Mater. Sci. Eng. A 2015, 648, 243–251. [Google Scholar] [CrossRef] [Green Version]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Thilly, L.; Van Petegem, S.; Renault, P.-O.; Lecouturier, F.; Vidal, V.; Schmitt, B.; Van Swygenhoven, H. A new criterion for elasto-plastic transition in nanomaterials: Application to size and composite effects on Cu-Nb nanocomposite wires. Acta Mater. 2009, 57, 3157–3169. [Google Scholar] [CrossRef]
- Calcagnotto, M.; Adachi, Y.; Ponge, D.; Raabe, D. Deformation and fracture mechanisms in fine- and ultrafine-grained ferrite/martensite dual-phase steels and the effect of aging. Acta Mater. 2011, 59, 658–670. [Google Scholar] [CrossRef]
- Wang, M.M.; Tasan, C.C.; Ponge, D.; Dippel, A.C.; Raabe, D. Nanolaminate transformation-induced plasticity-twinning-induced plasticity steel with dynamic strain partitioning and enhanced damage resistance. Acta Mater. 2015, 85, 216–228. [Google Scholar] [CrossRef]
- Park, K.; Nishiyama, M.; Nakada, N.; Tsuchiyama, T.; Takaki, S. Effect of the martensite distribution on the strain hardening and ductile fracture behaviors in dual-phase steel. Mater. Sci. Eng. A 2014, 604, 135–141. [Google Scholar] [CrossRef]
- Paul, S.K.; Mukherjee, M. Determination of bulk flow properties of a material from the flow properties of its constituent phases. Comp. Mater. Sci. 2014, 84, 1–12. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, W.R. Tensile properties of fibre-reinforced metals: copper/tungsten and copper/molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Ojima, M.; Adachi, Y.; Tomota, Y.; Ikeda, K.; Kamiyama, T.; Katada, Y. Work hardening mechanism in high nitrogen austenitic steel studied by in situ neutron diffraction and in situ electron backscattering diffraction. Mater. Sci. Eng. A 2009, 527, 16–24. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.N.; Wang, Y.Q.; Zhang, S.Y.; Van Petegem, S.; Cocks, A.C.F.; Smith, D.J.; Flewitt, P.E.J. Role of the misfit stress between grains in the Bauschinger effect for a polycrystalline material. Acta Mater. 2015, 85, 229–242. [Google Scholar] [CrossRef]
- Geng, J.; Nie, J.F. Unloading yield effect in a twin-roll-cast Mg-3Al-1Zn alloy. Scr. Mater. 2015, 100, 78–81. [Google Scholar] [CrossRef]
- Nieh, T.G.; Nix, W.D. Unloading yield effects in aluminum alloys. Metall. Trans. A 1986, 17, 121–126. [Google Scholar] [CrossRef]
- Hart, E.W. Theory of the tensile test. Acta Metall. 1967, 15, 351–355. [Google Scholar] [CrossRef]
- Wang, Y.M.; Ma, E. Three strategies to achieve uniform tensile deformation in a nanostructured metal. Acta Mater. 2004, 52, 1699–1709. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Topping, T.; Bingert, J.F.; Thornton, J.J.; Dangelewicz, A.M.; Li, Y.; Liu, W.; Zhu, Y.T.; Zhou, Y.Z.; Lavernia, E.L. High tensile ductility and strength in bulk nanostructured nickel. Adv. Mater. 2008, 20, 3028–3033. [Google Scholar] [CrossRef]
- Li, Y.S.; Tao, N.R.; Lu, K. Microstructural evolution and nanostructure formation in copper during dynamic plastic deformation at cryogenic temperatures. Acta Mater. 2008, 56, 230–241. [Google Scholar] [CrossRef]
- Fisher, J.C.; Hart, E.W.; Pry, R.H. The hardening of metal crystals by precipitate particles. Acta Metall. 1953, 1, 336–339. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A 1957, 241, 376–396. [Google Scholar]
- Brown, L.M.; Stobbs, W.M. The work-hardening of copper-silica. Philos. Mag. 1971, 23, 1201–1233. [Google Scholar] [CrossRef]
- Atkinson, J.D.; Brown, L.M.; Stobbs, W.M. The work-hardening of copper-silica: IV. The Bauschinger effect and plastic relaxation. Philos. Mag. 1974, 30, 1247–1280. [Google Scholar] [CrossRef]
- Asaro, R.J. Elastic-plastic memory and kinematic-type hardening. Acta Metall. 1975, 23, 1255–1265. [Google Scholar] [CrossRef]
- Monzen, M.; Kawaguchi, Y.; Mori, T. Back stress hardening and static and dynamic softening in a cu alloy with α-Fe particles. Acta Metall. 1982, 30, 965–972. [Google Scholar] [CrossRef]
- Feaugas, X. On the origin of the tensile flow stress in the stainless steel AISI 316L at 300 K: Back stress and effective stress. Acta Mater. 1999, 47, 3617–3632. [Google Scholar] [CrossRef]
- Cottrell, A.H.; Dexter, D.L. Dislocations and Plastic Flow in Crystals. Am. J. Phys. 1954, 22, 242–243. [Google Scholar] [CrossRef]
- Orowan, E. Discussion on internal stresses. In Symposium on Internal Stresses in Metals and Alloys; Institute of Metals: London, UK, 1948; pp. 451–453. [Google Scholar]
- Orowan, E. Causes and effects of internal stress. Int. Stress Fat. Met. 1959, 7, 59–80. [Google Scholar]
- Moan, G.D.; Embury, J.D. Study of the Bauschinger effect in Al-Cu alloys. Acta Metall. 1979, 27, 903–914. [Google Scholar] [CrossRef]
- Wilson, D.V. Reversible work hardening in alloys of cubic metals. Acta Metall. 1965, 13, 807–814. [Google Scholar] [CrossRef]
- Tomota, Y.; Lukas, P.; Harjo, S.; Park, J.H.; Tsuchida, N.; Neov, D. In situ neutron diffraction study of IF and ultra low carbon steels upon tensile deformation. Acta Mater. 2003, 51, 819–830. [Google Scholar] [CrossRef]
- Xu, Q.; Lavernia, E.J. Influence of nucleation and growth phenomena on microstructural evolution during droplet-based deposition. Acta Mater. 2001, 49, 3849–3861. [Google Scholar] [CrossRef]
- Xu, Q.; Lavernia, E.J. Microstructural evolution during the initial stages of spray atomization and deposition. Scr. Mater. 1999, 41, 535–540. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhuang, Y.; Hu, A.; Kai, J.J.; Liu, C.T. The origin of negative stacking fault energies and nanotwin formation in face-centered cubic high entropy alloys. Scr. Mater. 2017, 130, 96–99. [Google Scholar] [CrossRef]
- An, X.H.; Wu, S.D.; Wang, Z.G.; Zhang, Z.F. Significance of stacking fault energy in bulk nanostructured materials: Insights from Cu and its binary alloys as model systems. Prog. Mater. Sci. 2019, 101, 1–45. [Google Scholar] [CrossRef]
- Fischer, F.D.; Reisner, G.; Werner, E.; Tanaka, K.; Cailletaud, G.; Antretter, T. A new view on transformation induced plasticity (TRIP). Int. J. Plast. 2000, 16, 723–748. [Google Scholar] [CrossRef]
- Bouaziz, O.; Guelton, N. Modelling of TWIP effect on work-hardening. Mater. Sci. Eng. A 2001, 319, 246–249. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yang, M.X.; Ma, X.L.; Wang, M.S.; Yin, K.; Huang, A.H.; Huang, C.X. Improved back stress and synergetic strain hardening in coarse-grain/nanostructure laminates. Mater. Sci. Eng. A 2018, 727, 113–118. [Google Scholar] [CrossRef] [Green Version]
- Mughrabi, H. On the current understanding of strain gradient plasticity. Mater. Sci. Eng. A 2004, 387, 209–213. [Google Scholar] [CrossRef]
- Meyers, M.A.; Ashworth, E. A model for the effect of grain size on the yield stress of metals. Philos. Mag. A 1982, 46, 737–759. [Google Scholar] [CrossRef]
- Wang, W.; Yang, M.X.; Yan, D.S.; Jiang, P.; Yuan, F.P.; Wu, X.L. Deformation mechanisms for superplastic behaviors in a dual-phase high specific strength steel with ultrafine grains. Mater. Sci. Eng. A 2017, 702, 133–141. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Zhang, H.S.; Yang, M.X.; Jiang, P.; Yuan, F.P.; Wu, X.L. Shock and spall behaviors of a high specific strength steel: Effects of impact stress and microstructure. J. Appl. Phys. 2017, 121, 135901. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Wei, Q. Strain rate effects in the ultrafine grain and nanocrystalline regimes-influence on some constitutive responses. J. Mater. Sci. 2007, 42, 1709–1727. [Google Scholar] [CrossRef]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Yang, M.; Yuan, F.; Wu, X. A Review on Heterogeneous Nanostructures: A Strategy for Superior Mechanical Properties in Metals. Metals 2019, 9, 598. https://doi.org/10.3390/met9050598
Ma Y, Yang M, Yuan F, Wu X. A Review on Heterogeneous Nanostructures: A Strategy for Superior Mechanical Properties in Metals. Metals. 2019; 9(5):598. https://doi.org/10.3390/met9050598
Chicago/Turabian StyleMa, Yan, Muxin Yang, Fuping Yuan, and Xiaolei Wu. 2019. "A Review on Heterogeneous Nanostructures: A Strategy for Superior Mechanical Properties in Metals" Metals 9, no. 5: 598. https://doi.org/10.3390/met9050598





