Numerical Simulation of Macrosegregation with Solid Deformation During the Solidification of Steel Ingots Using a Single-Phase/Two-Phase Integrated Model
Abstract
:1. Introduction
2. Model Description and Numerical Approach
2.1. Volume-Averaged Two-Phase Model
- The volume-averaging method is utilized to derive the conservation equations for the solid and liquid phases during the solidification of steel ingots;
- For the conservation of mass, energy, and species, the governing equations are derived for the solid-liquid mixture, while for momentum conservation, the solid and liquid phases are considered separately;
- The Boussinesq approximation is utilized to calculate the thermal-solutal buoyancy force. The mushy zone is modeled as an isotropic porous medium saturated with liquid, and the momentum interaction between the solid and liquid phases is described by Darcy law. The permeability is calculated by the Carman-Kozeny formula;
- The densities of the solid and liquid phases are equal, thus solidification shrinkage is omitted;
- The microscopic solidification phenomenon is described by the lever rule;
- The thermophysical properties of the solid and liquid phases are equal and constant;
- The liquid phase is considered as Newtonian. The solid deformation behavior of the mushy zone with a high solid fraction (gs > 0.5) is considered as compressible viscoplastic. For the mushy zone with a low solid fraction, the grain sedimentation is neglected.
2.2. Extension to the Single-Phase/Two-Phase Integrated Model
- Initialize the variables of the current time step with those of the previous time step;
- Determine whether it is in the deformation stage based on the current time t, the deformation start time ts, and the deformation duration ∆td. If ts + ∆td > t > ts, the deformation flag is true. Otherwise, it is false;
- If the deformation flag is true, the stabilized multi-phase pressure correction method is utilized to solve Equations (1)–(6) and (9)–(15). Otherwise, the stabilized pressure correction method is used to solve Equations (1)–(5), where the solid velocity is zero;
- Solve the non-linear energy conservation equation (Equation (7)) with the Newton–Raphson method;
- Solve the non-linear species conservation equation (Equation (8)) with the Newton–Raphson method;
- Calculate the difference in liquid velocity, temperature, and solute concentration between two adjacent iterations. If they are not converged, return to step 3;
- If the deformation is true, update the mesh according to the solid velocity;
- Advance the time to the next time step.
3. Results
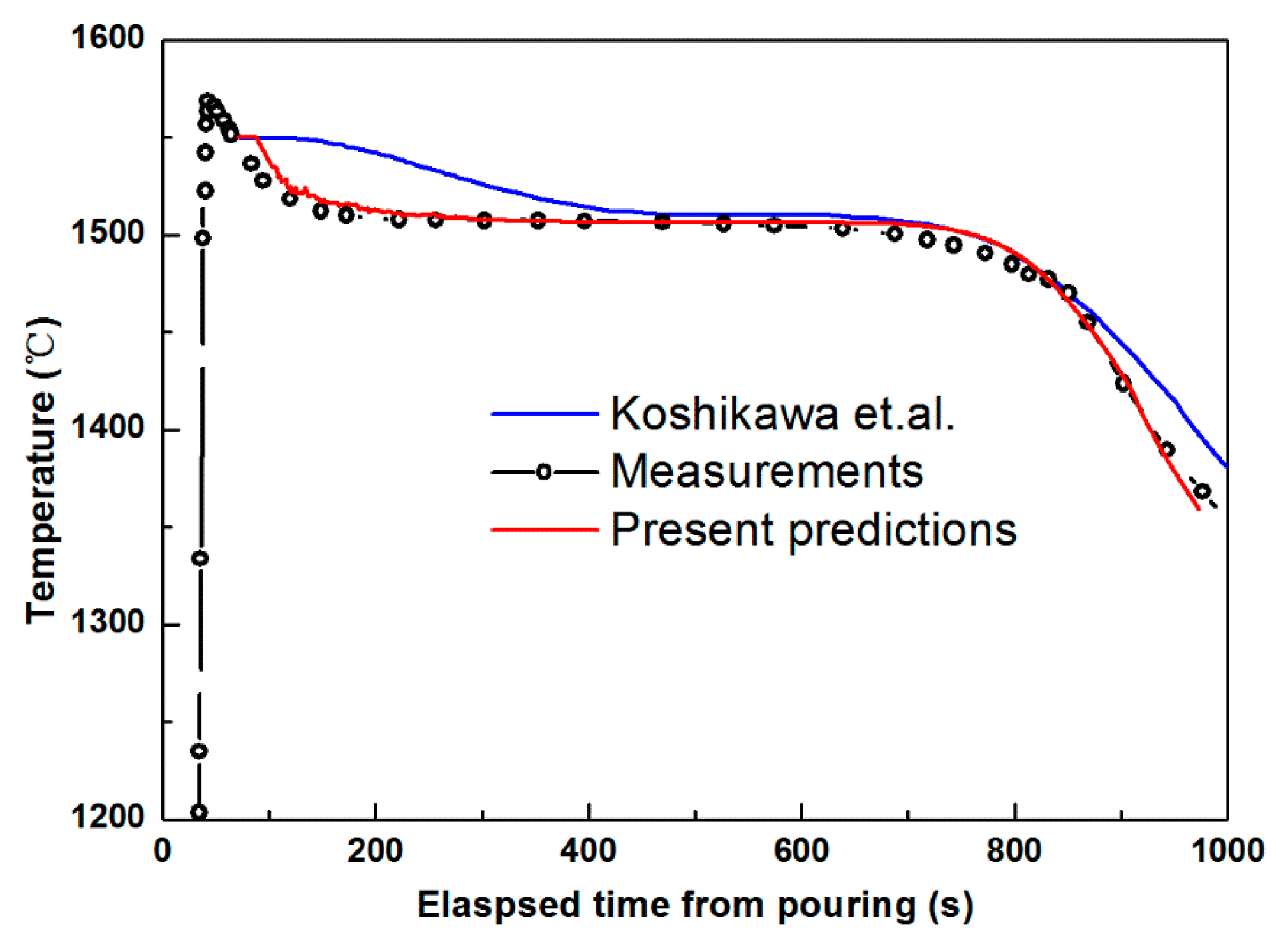
3.1. 450 kg Steel Ingot Punching Test and Simulation Setup
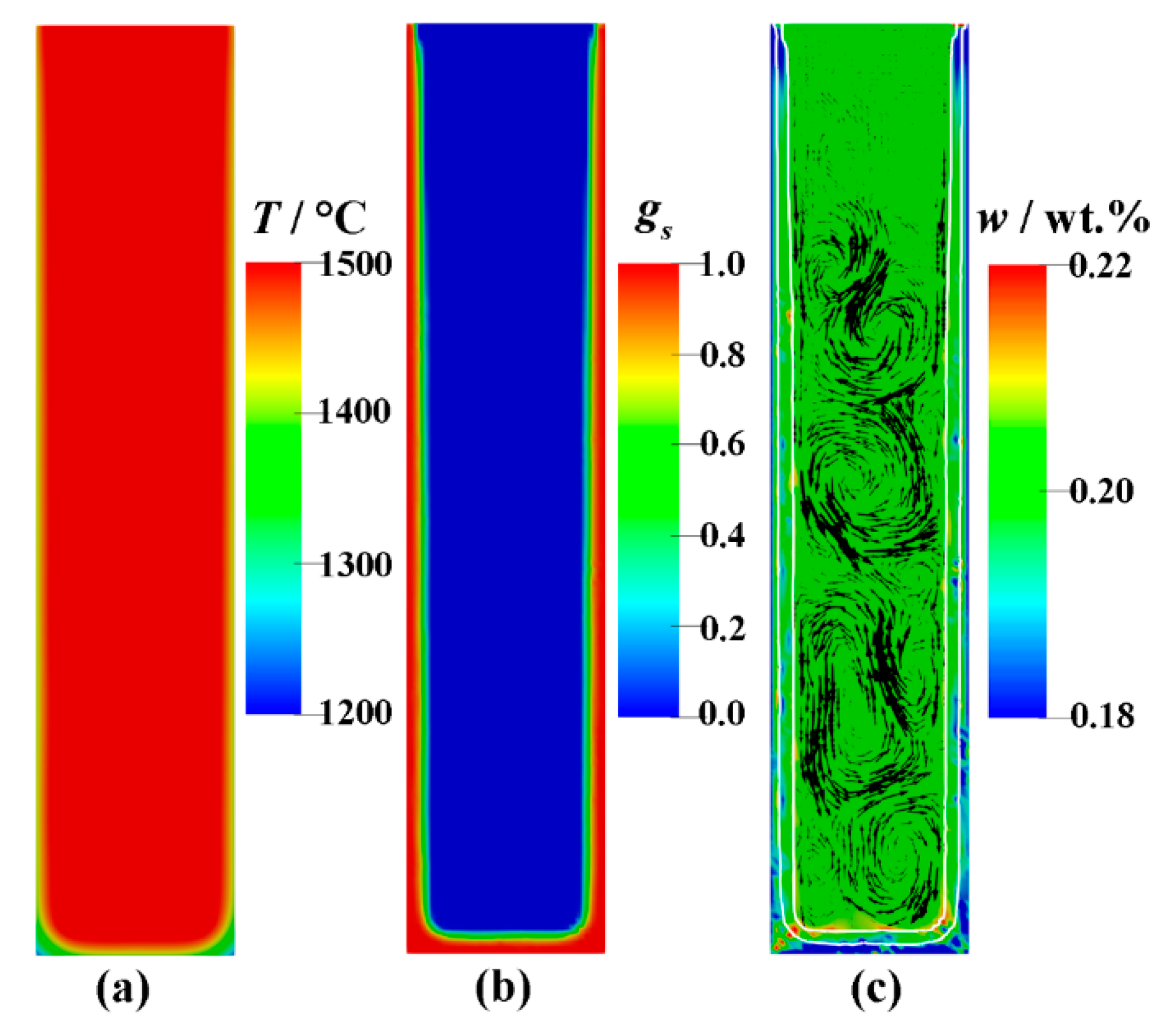
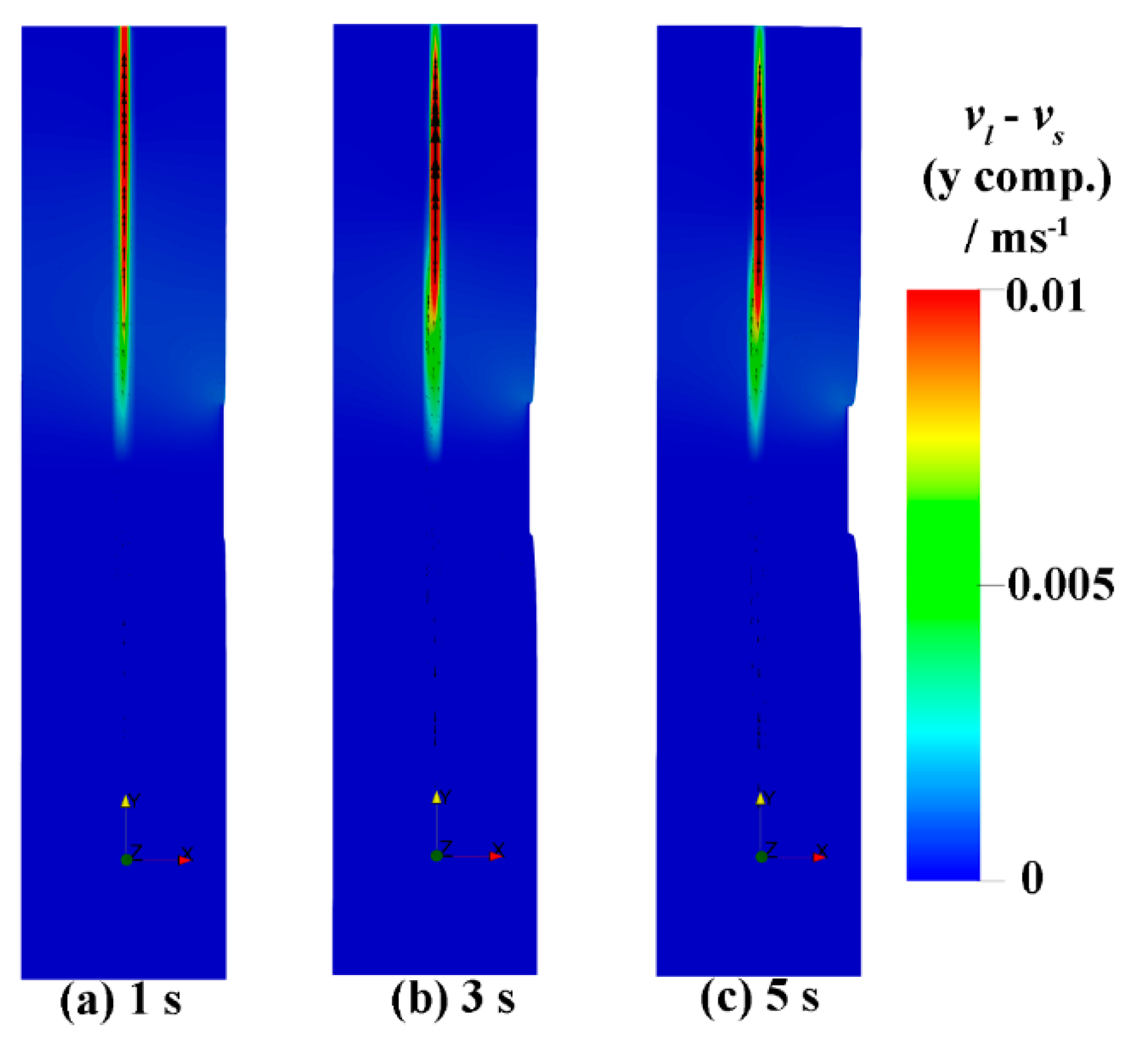
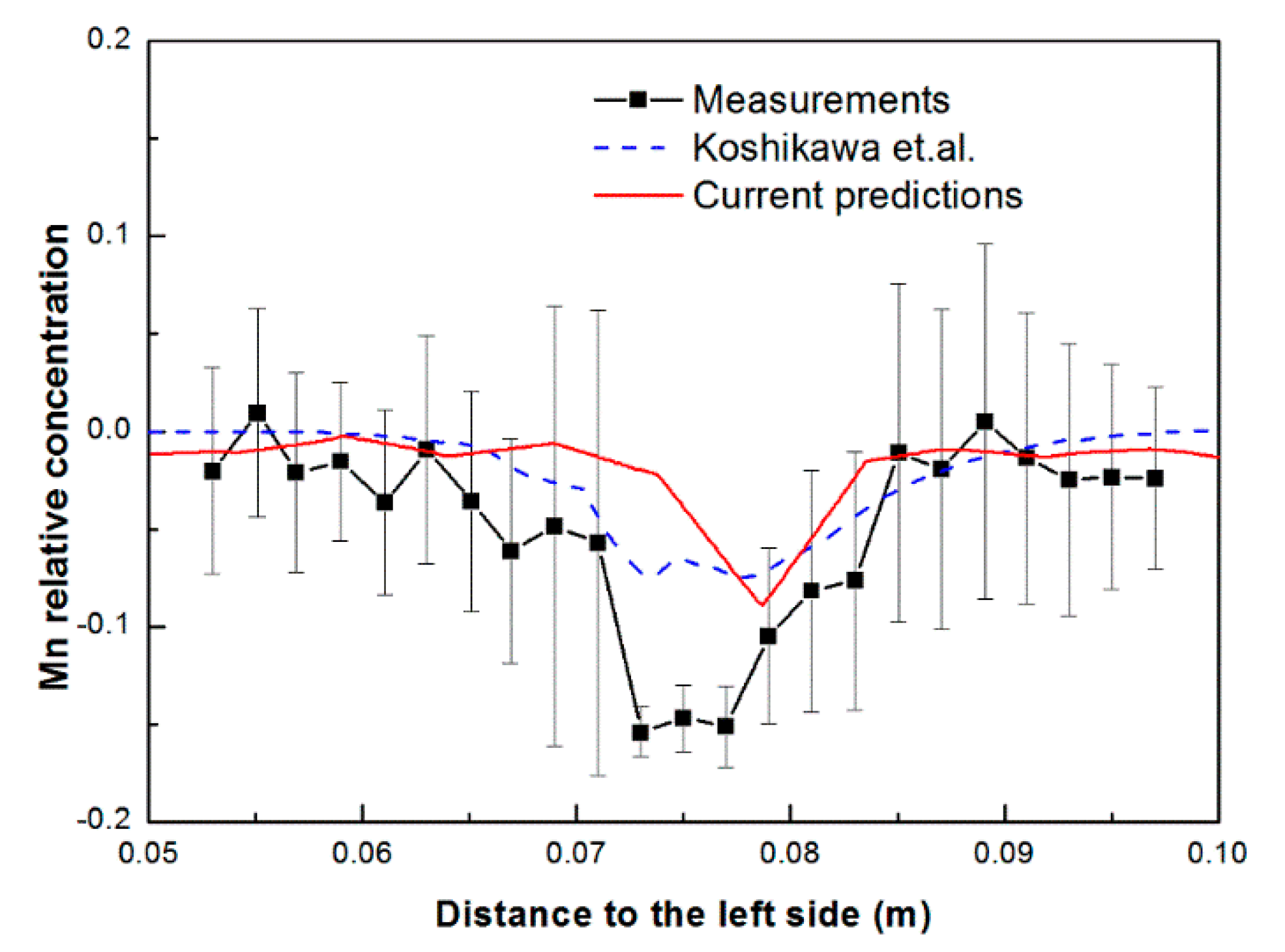
3.2. Initial Soldification Stage Before Punching Starts
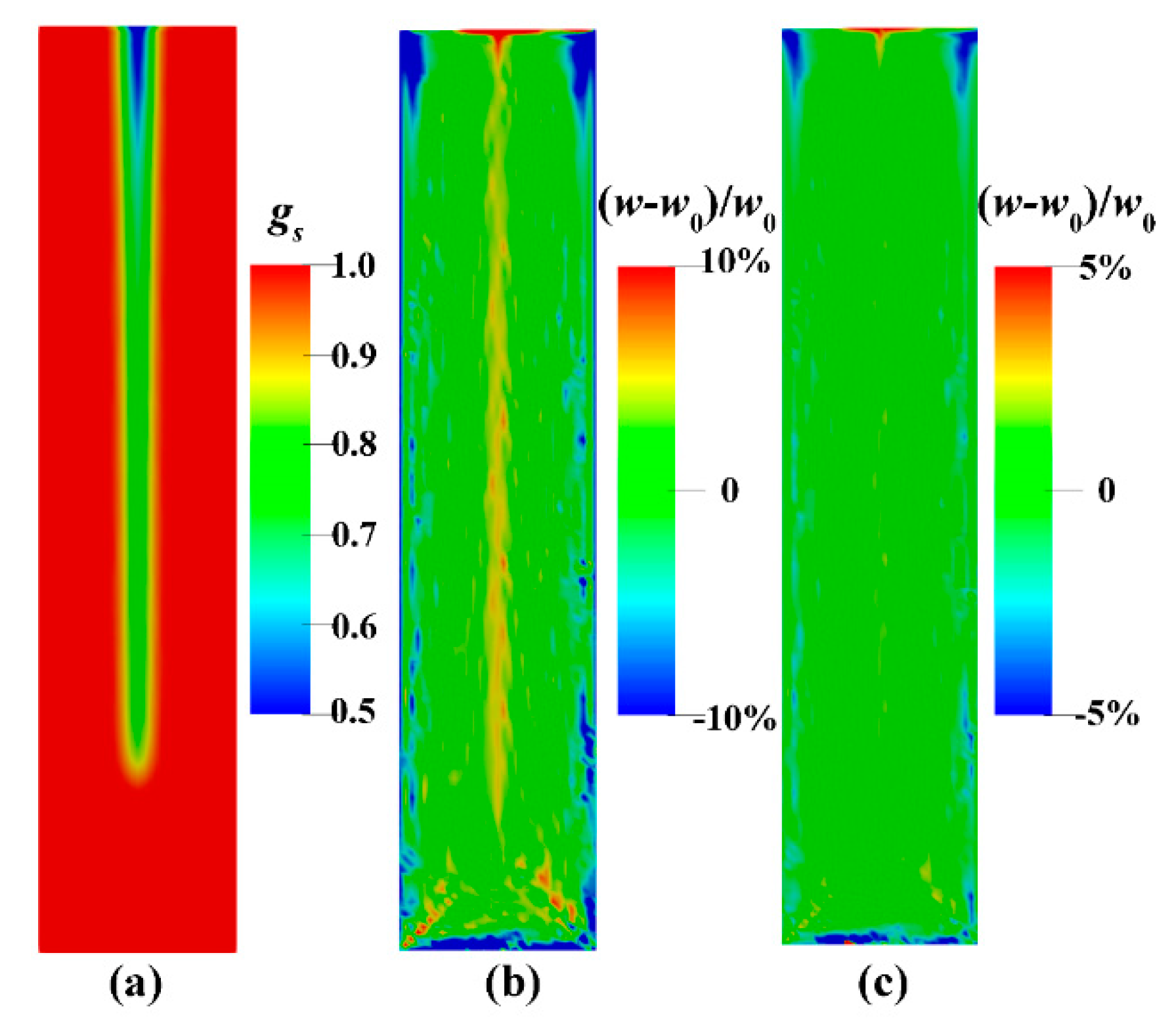
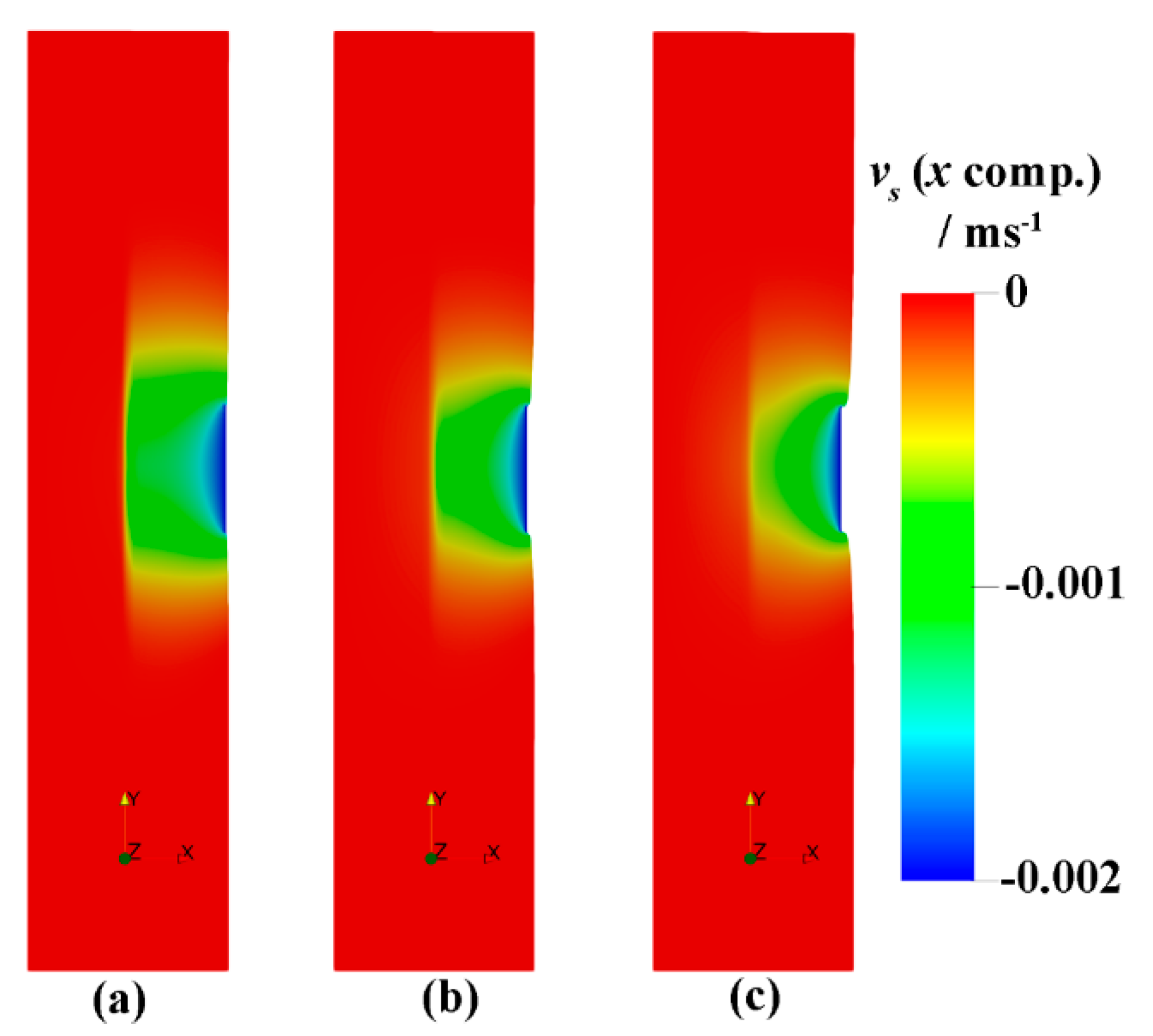
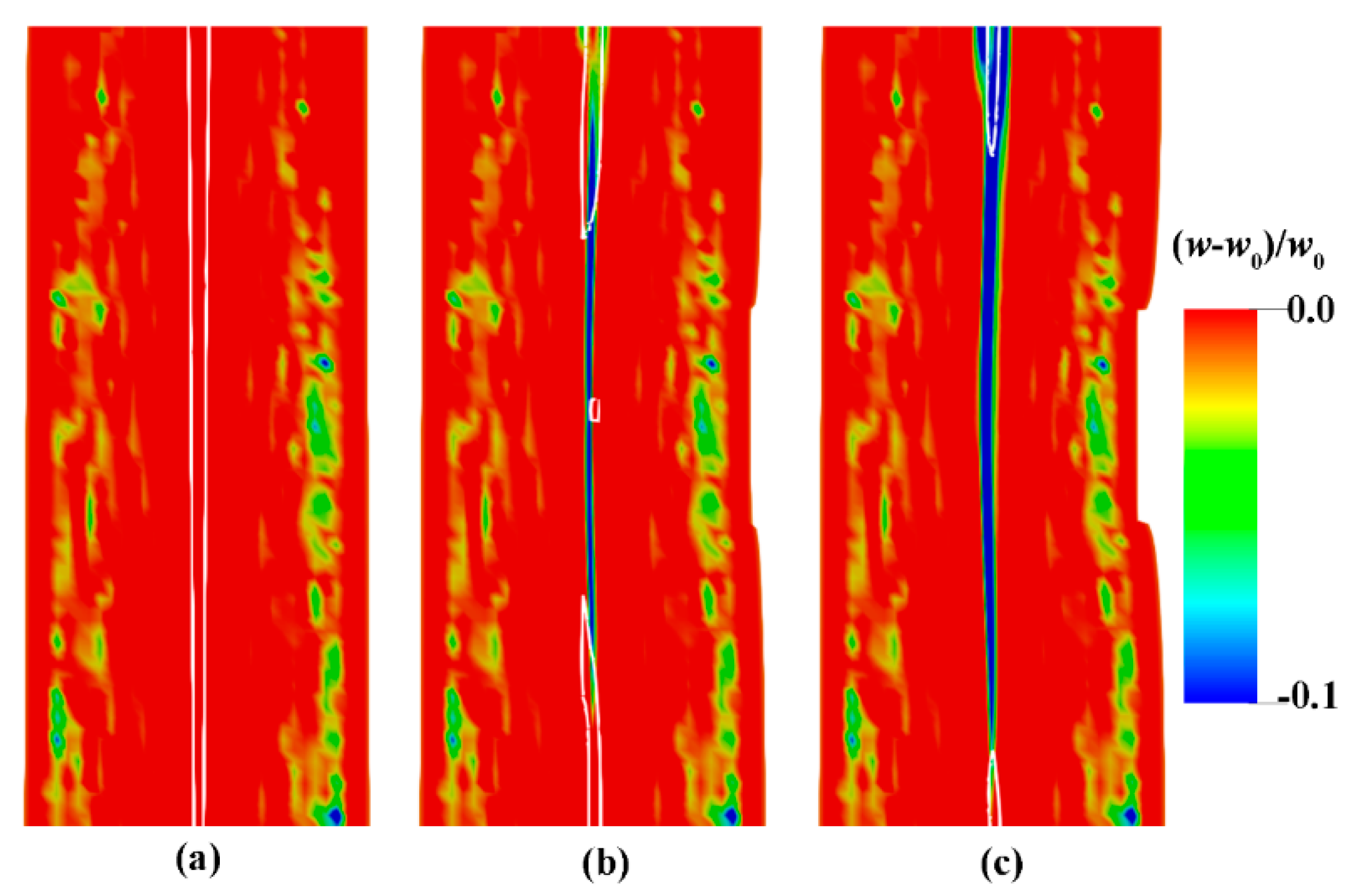
3.3. Punching Stage
4. Discussion
4.1. Formation Mechanism of Macrosegregation With Deformation
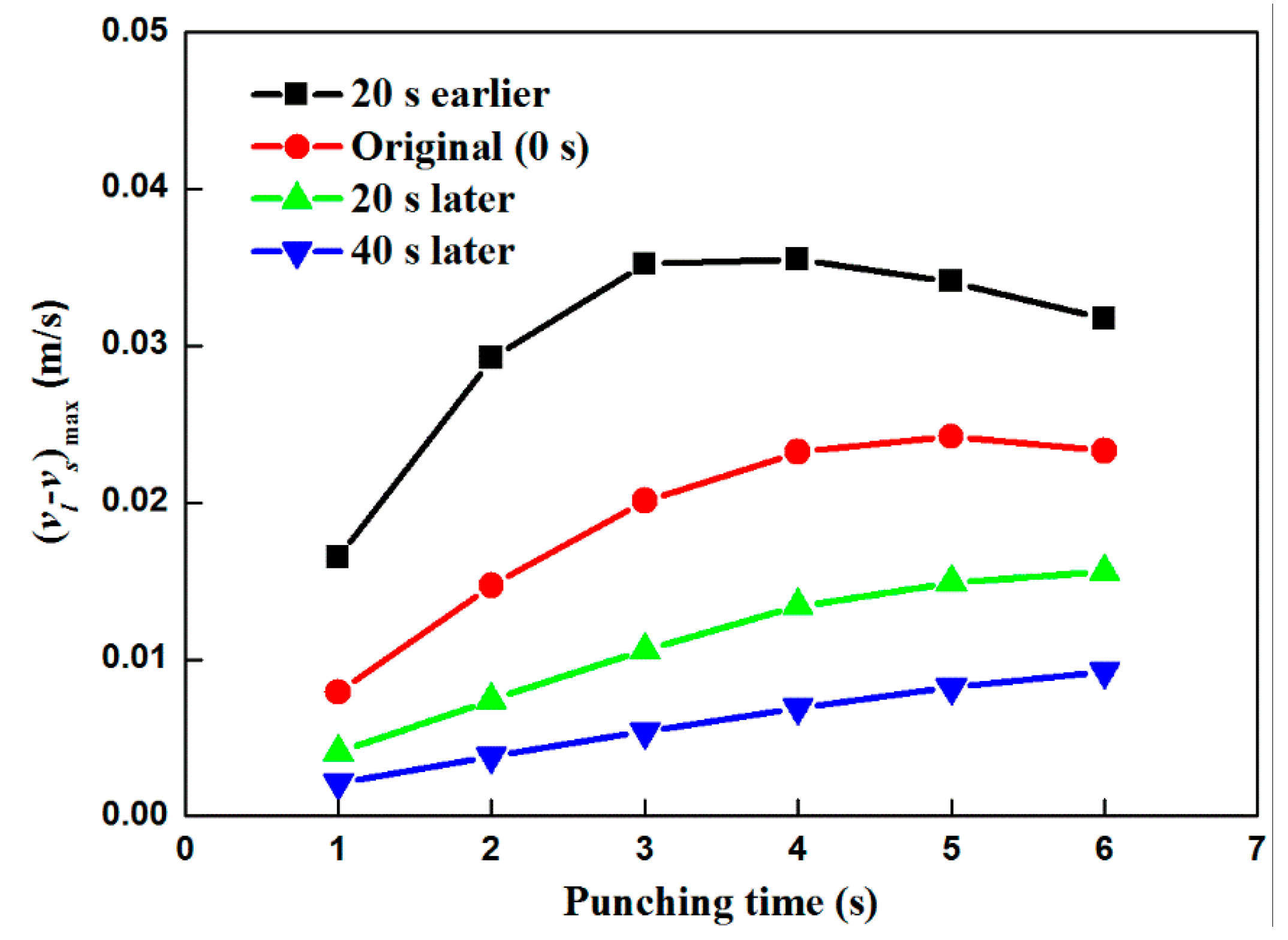
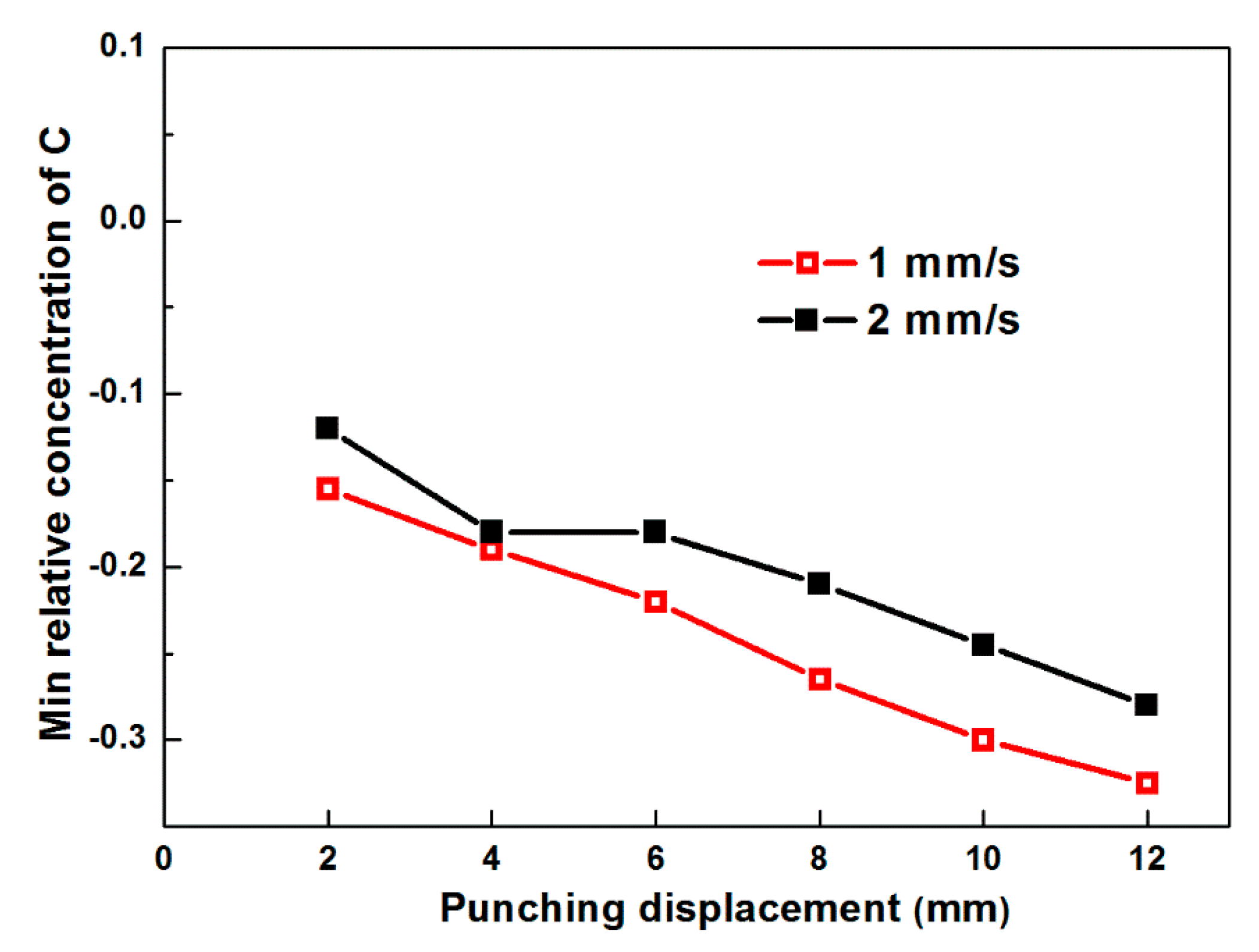
4.2. Influence of the Punching Parameters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Flemings, M.C. Our understanding of macrosegregation: past and present. ISIJ Int. 2000, 40, 833–841. [Google Scholar] [CrossRef]
- Beckermann, C. Modelling of macrosegregation: applications and future needs. Int. Mater. Rev. 2002, 47, 243–261. [Google Scholar] [CrossRef]
- Ludwig, A.; Wu, M.; Kharicha, A. On macrosegregation. Metall. Mater. Trans. A 2015, 46, 4854–4867. [Google Scholar] [CrossRef]
- Bennon, W.D.; Incropera, F.P. A continuum model for momentum, heat and species transport in binary solid-liquid phase change systems—I. Model formulation. Int. J. Heat Mass Tran. 1987, 30, 2161–2170. [Google Scholar] [CrossRef]
- Beckermann, C.; Viskanta, R. Double-diffusive convection during dendritic solidification of a binary mixture. PhysicoChem. Hydrodyn. 1988, 10, 195–213. [Google Scholar]
- Zhang, S.; Yanke, J.R.; Johnson, D.; JM Krane, M. Modeling defects in castings using a volume of fluid method. Int. J. Numer. Method H 2014, 24, 468–482. [Google Scholar] [CrossRef]
- Chen, K.; Shen, H. Numerical simulation of macrosegregation caused by thermal-solutal convection and solidification shrinkage Using ALE Model. Acta Metall. Sin. (Engl. Lett.). (accepted). [CrossRef]
- Wu, M.; Ludwig, A. Modeling equiaxed solidification with melt convection and grain sedimentation—I: Model description. Acta Mater. 2009, 57, 5621–5631. [Google Scholar] [CrossRef]
- Wu, M.; Fjeld, A.; Ludwig, A. Modelling mixed columnar-equiaxed solidification with melt convection and grain sedimentation—Part I: Model description. Comp. Mater. Sci. 2010, 50, 32–42. [Google Scholar] [CrossRef]
- Tu, W.; Duan, Z.; Shen, B.; Shen, H.; Liu, B. Three-dimensional simulation of macrosegregation in a 36-ton steel ingot using a multicomponent multiphase model. JOM-US 2016, 68, 3116–3125. [Google Scholar] [CrossRef]
- Ge, H.; Ren, F.; Li, J.; Han, X.; Xia, M.; Li, J. Four-phase dendritic model for the prediction of macrosegregation, shrinkage cavity, and porosity in a 55-ton ingot. Metall. Mater. Trans. A 2017, 48, 1–12. [Google Scholar] [CrossRef]
- Wu, M.; Ludwig, A.; Kharicha, A. A four phase model for the macrosegregation and shrinkage cavity during solidification of steel ingot. Appl. Math. Model. 2017, 41, 102–120. [Google Scholar] [CrossRef]
- Nguyen, T.T.M.; Gandin, C.A.; Combeau, H.; Založnik, M.; Bellet, M. Finite element multi-scale modeling of chemical segregation in steel solidification taking into account the transport of equiaxed grains. Metall. Mater. Trans. A 2018, 49, 1725–1748. [Google Scholar] [CrossRef]
- Lesoult, G.; Gandin, C.; Niane, N.T. Segregation during solidification with spongy deformation of the mushy zone. Acta Mater. 2003, 51, 5263–5283. [Google Scholar] [CrossRef]
- Fachinotti, V.D.; Le Corre, S.; Triolet, N.; Bobadilla, M.; Bellet, M. Two-phase thermo-mechanical and macrosegregation modelling of binary alloys solidification with emphasis on the secondary cooling stage of steel slab continuous casting processes. Int. J. Numer. Meth. Eng. 2006, 67, 1341–1384. [Google Scholar] [CrossRef] [Green Version]
- Koshikawa, T.; Bellet, M.; Gandin, C.; Yamamura, H.; Bobadilla, M. Study of hot tearing during steel solidification through ingot punching test and its numerical simulation. Metall. Mater. Trans. A 2016, 47, 4053–4067. [Google Scholar] [CrossRef]
- Koshikawa, T.; Bellet, M.; Gandin, C.A.; Yamamura, H.; Bobadilla, M. Experimental study and two-phase numerical modeling of macrosegregation induced by solid deformation during punch pressing of solidifying steel ingots. Acta Mater. 2017, 124, 513–527. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, W.; Sun, M.; Xu, B.; Li, D. A method based on semi-solid forming for eliminating coarse dendrites and shrinkage porosity of H13 tool steel. Metals-Basel 2018, 8, 277. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, Y.; Sun, M.; Xu, B.; Li, D. Effects of liquid fraction on the microstructure and mechanical properties in forge solidifying 12Cr1MoV steel. J. Mater. Process. Tech. 2018, 256, 25–35. [Google Scholar] [CrossRef]
- Nguyen, T.G.; Favier, D.; Suery, M. Theoretical and experimental study of the isothermal mechanical behaviour of alloys in the semi-solid state. Int. J. Plasticity 1994, 10, 663–693. [Google Scholar] [CrossRef]





| Parameters | Units | Value |
|---|---|---|
| Density, ρ | kg⋅m−3 | 6990 |
| Specific heat, cp | J⋅kg−1⋅K-1 | 815 |
| Thermal conductivity, k | W⋅m−1⋅K-1 | 39.3 |
| Latent heat, L | J⋅kg−1 | 2.6 × 105 |
| Liquid dynamic viscosity, μl | kg⋅m−1⋅s−1 | 4.2 × 10−3 |
| Thermal expansion coefficient, βT | K−1 | 1.07 × 10−4 |
| Secondary dendrite arm spacing, λ2 | m | 3 × 10−4 |
| Initial temperature, T0 | °C | 1550 |
| Diffusion coefficient in liquid, Dl | m2⋅s−1 | 2.0 × 10−8 |
| Convective heat transfer coefficient, h | W·m−2·K−1 | 250 |
| External temperature, Text | °C | 20 |
| Melting point of pure Fe, Tf | °C | 1538 |
| Liquidus slope for C, m[C] | °C(wt.%)−1 | 81 |
| Liquidus slope for Mn, m[Mn] | °C(wt.%)−1 | 5 |
| Partition coefficient for C, kp[C] | wt.%/wt.% | 0.162 |
| Partition coefficient for Mn, kp[Mn] | wt.%/wt.% | 0.703 |
| Solutal expansion coefficient for C, βw[C] | wt.%−1 | 1.10 × 10−2 |
| Solutal expansion coefficient for Mn, βw[Mn] | wt.%−1 | 1.92 × 10−3 |
| Viscoplastic consistency, Kν | Pa⋅sm | 1 × 107 |
| Strain rate sensitivity, m | 1 | 0.225 |
| Punching velocity | m⋅s−1 | 2 × 10−3 |
| Total punching distance | m | 1.3 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Shen, H. Numerical Simulation of Macrosegregation with Solid Deformation During the Solidification of Steel Ingots Using a Single-Phase/Two-Phase Integrated Model. Metals 2019, 9, 669. https://doi.org/10.3390/met9060669
Chen K, Shen H. Numerical Simulation of Macrosegregation with Solid Deformation During the Solidification of Steel Ingots Using a Single-Phase/Two-Phase Integrated Model. Metals. 2019; 9(6):669. https://doi.org/10.3390/met9060669
Chicago/Turabian StyleChen, Kangxin, and Houfa Shen. 2019. "Numerical Simulation of Macrosegregation with Solid Deformation During the Solidification of Steel Ingots Using a Single-Phase/Two-Phase Integrated Model" Metals 9, no. 6: 669. https://doi.org/10.3390/met9060669





