Nonlinear Numerical Assessment of Exterior Beam-Column Connections with Low-Strength Concrete
Abstract
:1. Introduction
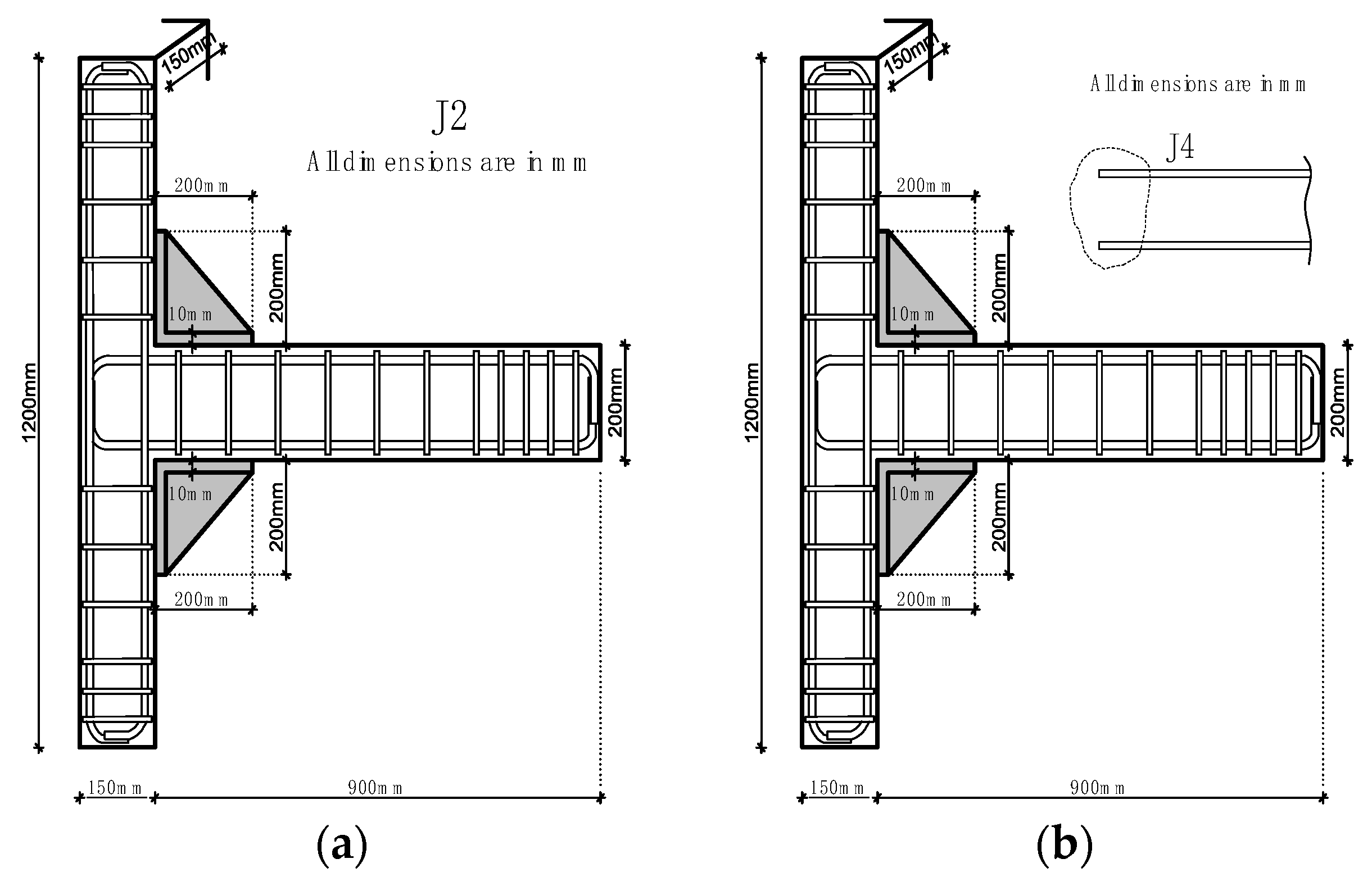
2. Details of Reference Joints
3. Proposed Numerical Models
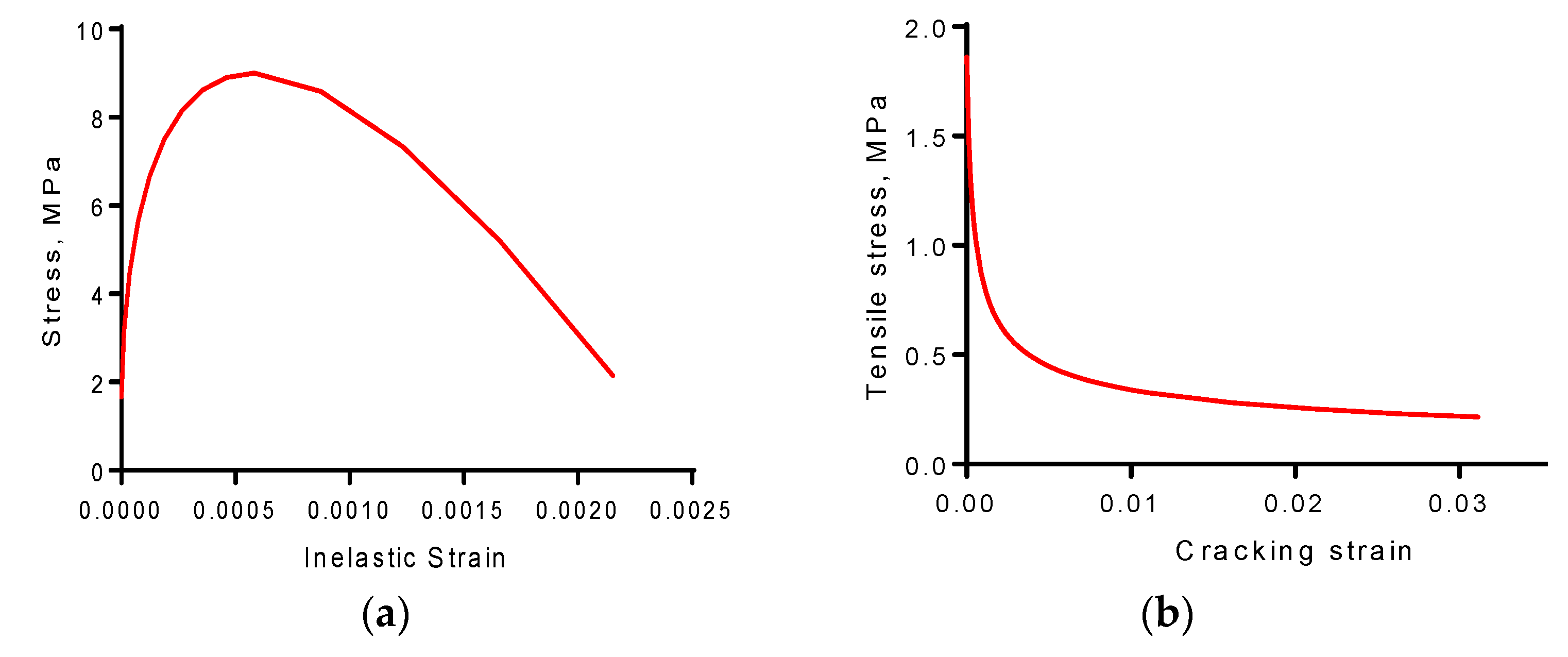
3.1. Concrete Material Model
3.2. Reinforcing Steel Material Model
3.3. Boundary Condition and Loading
4. Results and Discussion
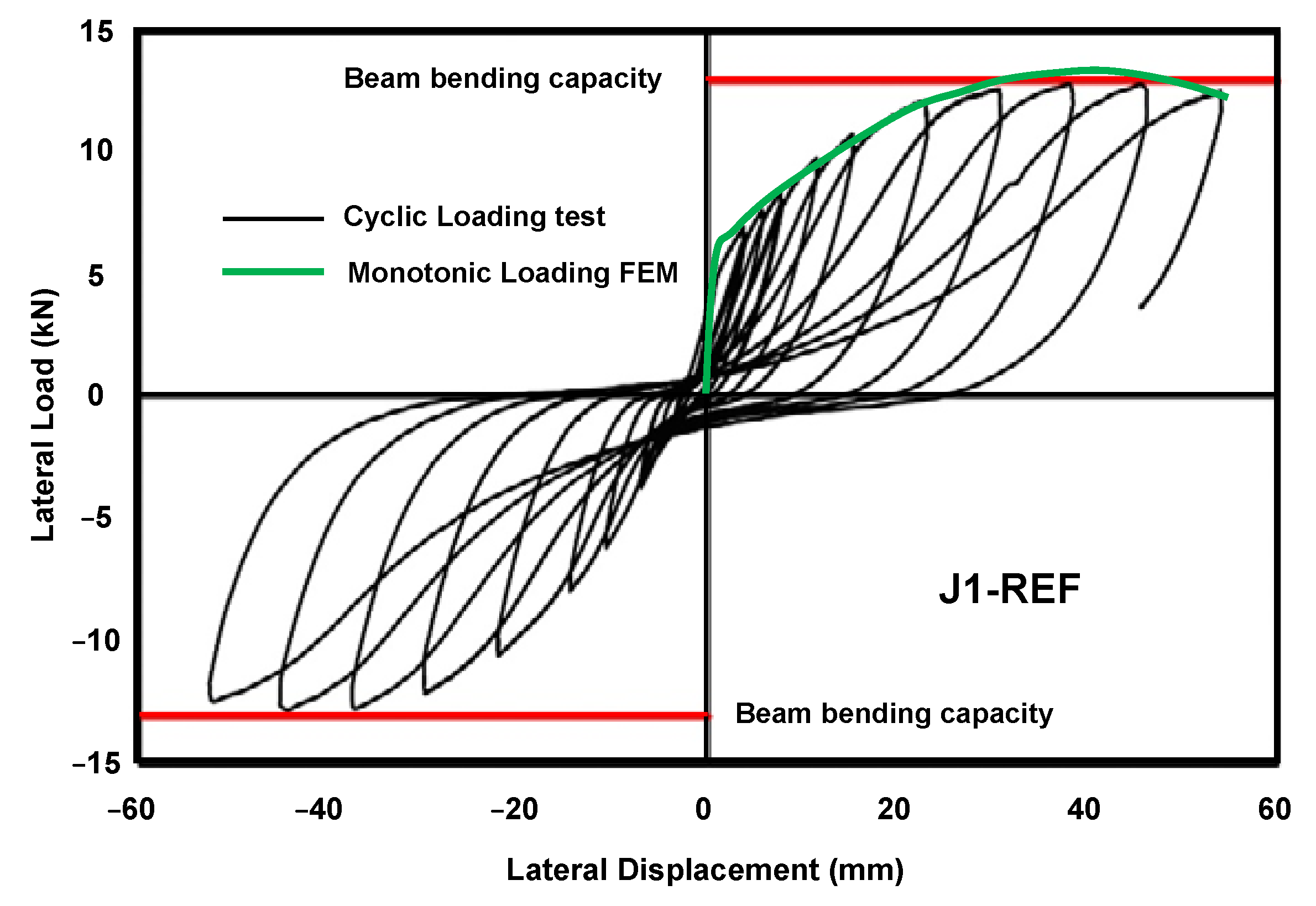
4.1. Standard Joint
4.2. Sub-Standard Joints
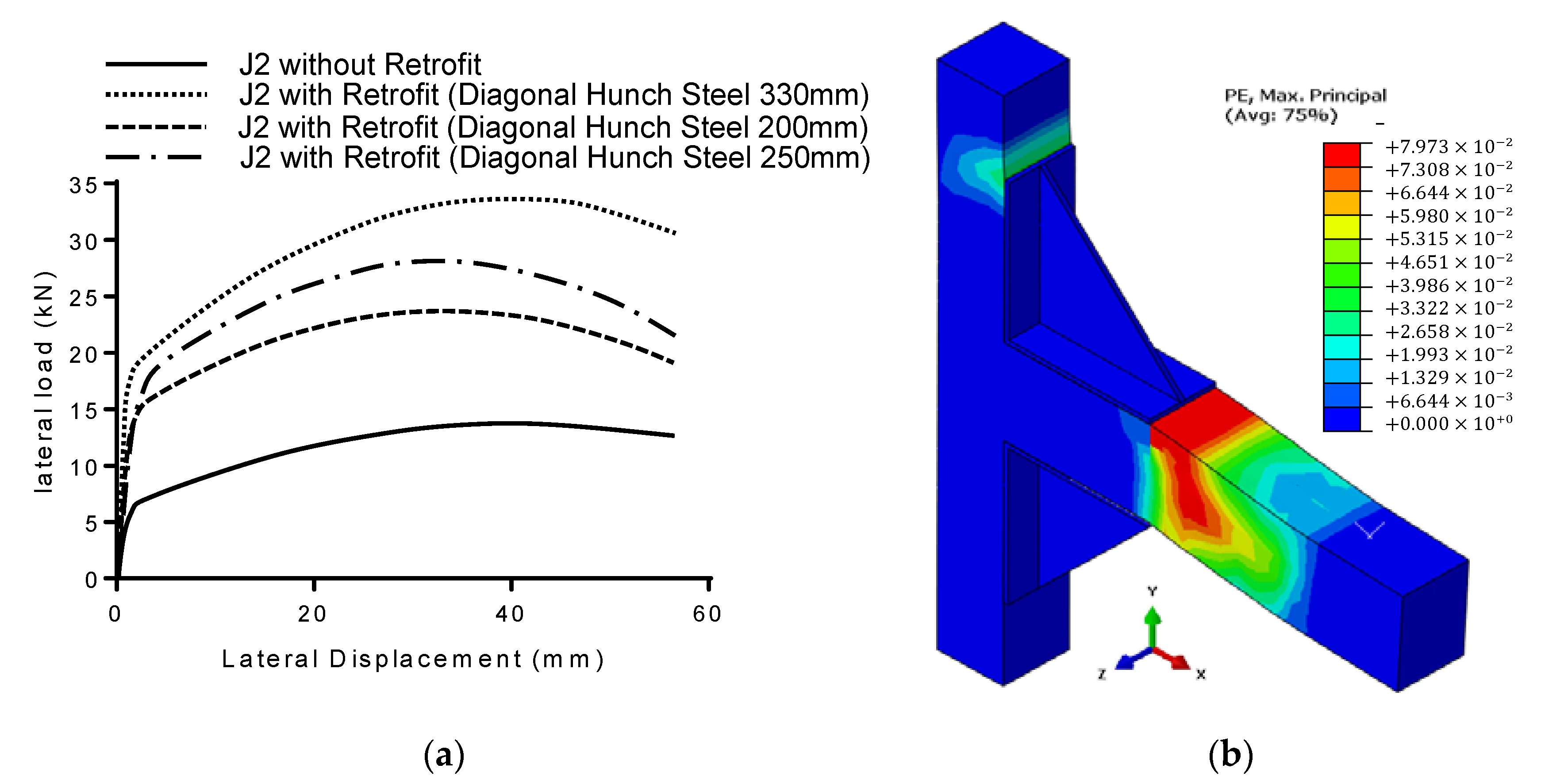
4.3. Retrofitted Joints
5. Conclusions
- The material model of CDP in ABAQUS showed effectiveness in representing concrete response in numerical simulation of the considered reference joints, as the simulation results were found to be closer to the experimental observed joint capacities.
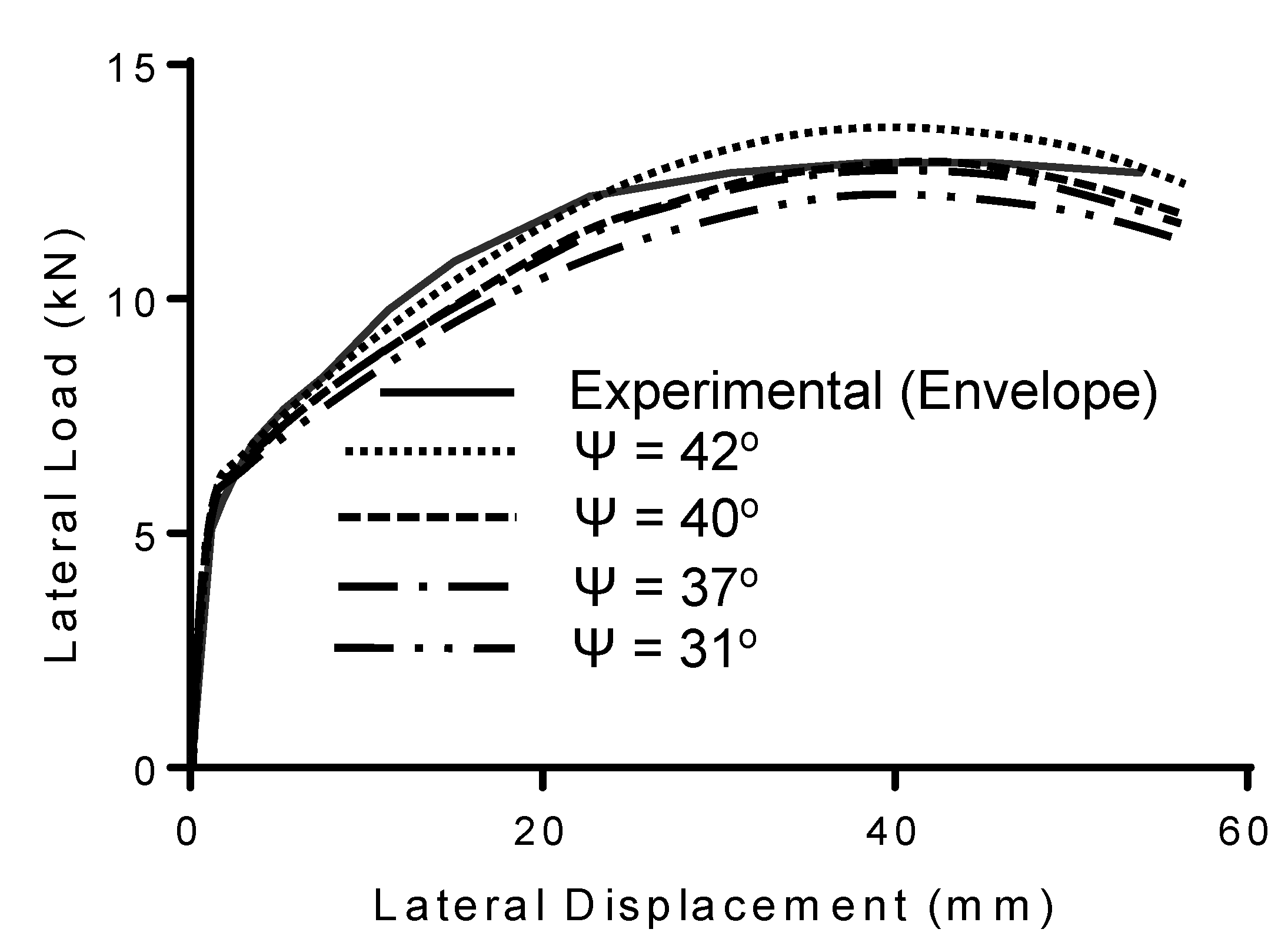
- Within the ABAQUS manual recommended range for the concrete material dilation angle, these numerical simulations recommended a value of 40° for standard joints and 30° and 10° for substandard joints with shear or shear and anchorage deficiencies, respectively.
- Empirical models that explicitly consider the stirrups’ contribution overestimated the shear strength, and models with implicit assumption estimated the strength accurately.
- The applicability of numerical, empirical, and analytical models for joints using low-strength concrete is demonstrated even with some discrepancies in the case of joints with anchorage problems.
- Without any separation problems and conflict with the building floors or beams, diagonal steel haunch usage can relocate the formed plastic hinge outside the joint panel and enable both the column and beam to reach their flexural ultimate capacity, albiet with no increase in the joint displacement capacity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adam, J.M.; Parisi, F.; Sagaseta, J.; Lu, X. Research and practice on progressive collapse and robustness of building structures in the 21st century. Eng. Struct. 2018, 173, 122–149. [Google Scholar] [CrossRef]
- El-Demerdash, W.; El-Metwally, S.; El-Zoughiby, M. Survival of reinforced concrete flat plate system against column loss. Electron. J. Struct. Eng. 2020, 20, 33–34. [Google Scholar]
- Basem, A. A review on building progressive collapse, survey and discussion. Case Stud. Constr. Mater. 2019, 11, e00264. [Google Scholar] [CrossRef]
- Vollum, R. Design and analysis of exterior beam column connections. Ph.D. Thesis, Imperial College of Science Technology and Medicine-University of London, London, UK, 1998. [Google Scholar]
- Bakir, P.; Boduroğlu, H. A new design equation for predicting the joint shear strength of monotonically loaded exterior beam-column joints. Eng. Struct. 2002, 24, 1105–1117. [Google Scholar] [CrossRef]
- Hegger, J.; Sherif, A.; Roeser, W. Nonseismic design of beam-column joints. ACI Struct. J. 2003, 100, 654–664. [Google Scholar]
- Hwang, S.; Lee, H. Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance. ACI Struct. J. 1999, 96, 846–858. [Google Scholar]
- Orton, S.; Jirsa, J.; Bayrak, O. Carbon fiber-reinforced polymer for continuity in existing reinforced concrete buildings vulnerable to collapse. ACI Struct. J. 2009, 106, 608–616. [Google Scholar]
- Basem, A.; Bachir, B.; John, V. Reinforced concrete beam-column inverted knee joint behavior after ground corner column loss-numerical analysis. Lat. Am. J. Solids Struct. 2018, 15, e122. [Google Scholar] [CrossRef]
- Shin, M.; LaFave, J. Modeling of cyclic joint shear deformation contributions in RC beam-column connections to overall frame behavior. Struct. Eng. Mech. J. 2004, 18, 645–669. [Google Scholar] [CrossRef]
- Qian, K.; Li, B.; Ma, J.X. Load carrying mechanism to resist progressive collapse of RC buildings. J. Struct. Eng. 2015, 141, 04014107. [Google Scholar] [CrossRef]
- Yap, S.; Li, B. Experimental investigation of RC exterior beam-column sub-assemblages for progressive collapse. ACI Struct. J. 2011, 108, 542–552. [Google Scholar]
- ACI committee 318. Building Code Requirements for Structural Concrete and Commentary ACI 318,14; ACI committee 318: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Peng, Z.; Wang, Z. ABAQUS FEM analysis on knee joints in reinforced concrete frames. J. Chongqing Jiaotong Univ. Nat. Sci. 2010, 29, 677–790. [Google Scholar]
- Danesh, F.; Esmaeeli, E.; Alam, M. Shear strengthening of 3D RC beam-column connection using GFRP: FEM Study. Asian J. Appl. Sci. 2008, 1, 217–227. [Google Scholar] [CrossRef] [Green Version]
- Architectural Institute of Japan. Guidelines for RC structures; Architectural Institute of Japan: Tokyo, Japan, 2004. [Google Scholar]
- Khan, U.; Al-Osta, M.; Ibrahim, A. Modeling shear behavior of reinforced concrete beams strengthened with externally bonded CFRP sheets. Struct. Eng. Mech.J. 2017, 1, 125–142. [Google Scholar] [CrossRef]
- Cumhur, C.; Ahmet, M.; Atakan, M.; Turgay, C.; Guven, K. Experimental behavior and failure of beam-column joints with plain bars, low-strength concrete and different anchorage details. Eng. Fail. Anal. 2020, 109, 104247. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Simulia. ABAQUS Analysis user’s manual 6.17-EF; Dassault Systems Simulia Corp: Providence, RI, USA, 2017. [Google Scholar]
- Sohaib, A.; Kypros, P.; Qaiser, K.; Kyriacos, N. Stress-strain model for low-strength concrete in uni-axial compression. Arab. J. Sci. Eng. 2015, 40, 313–328. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998. [Google Scholar]
- Giovacchino, G. Seismic assessment of RC exterior beam column joints and retrofit with haunches using post-installed anchors. Ph.D. Thesis, Stuttgart University, Stuttgart, Germany, 2012. [Google Scholar]









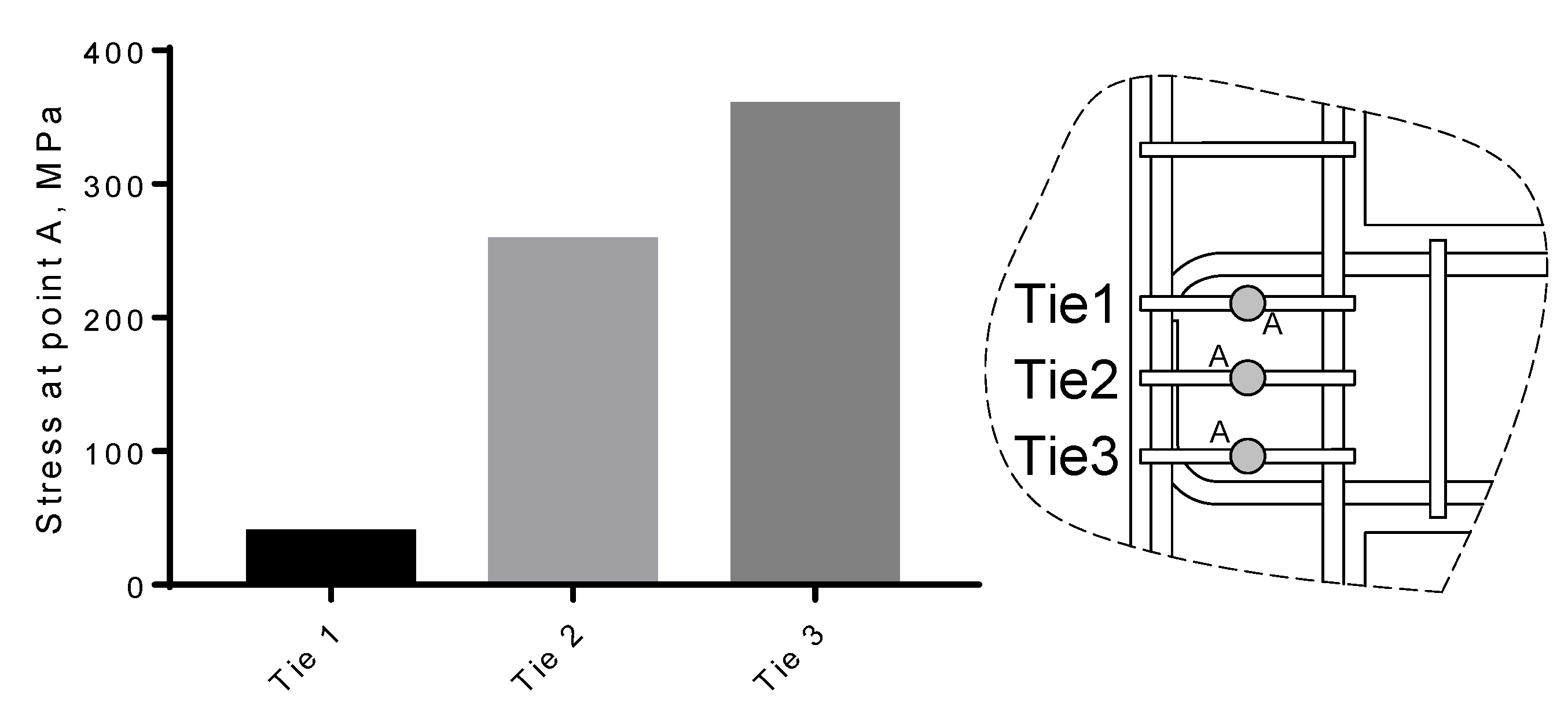


| CPD Parameter | Symbol | Recommended Value |
|---|---|---|
| Dilation angle | Ψ | 30°–45° |
| Shape factor | Kc | 0.667–1 |
| Biaxial stress ratio | 1–1.16 | |
| Eccentricity | 0.1 | |
| Viscosity parameter | 0.0001–0.008 |
| Set No. | Element Size (mm) | Model Capacity (kN) | Convergence Order P | GCI12% | GCI23% | GCI23/r p GCI12 |
|---|---|---|---|---|---|---|
| 1st set | 35, 40, 45 | 13.2, 13.3, 13.8 | 12.28 | 0.002366 | 0.0142 | 1.041 |
| 2nd set | 40, 45, 50 | 13.3, 13.8, 13.6 | 7.779 | 0.01166 | 0.03 | 1.03 |
| Results | Joint J1 | Joint J2 | Joint J4 | |||
|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Displacement (mm) | Ultimate Load (kN) | Displacement (mm) | Ultimate Load (kN) | Displacement (mm) | |
| Numerical findings | 13.3 | 56.27 | 9.5 | 56.27 | 5.22 | 9.6 |
| Experimental records | 12.97 | 57.6 | 8.77 | 57.6 | 5.06 | 14.6 |
| Numerical/Experimental | 1.02 | 0.97 | 1.08 | 0.97 | 1.03 | 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelwahed, B.S.; Kaloop, M.R.; El-Demerdash, W.E. Nonlinear Numerical Assessment of Exterior Beam-Column Connections with Low-Strength Concrete. Buildings 2021, 11, 562. https://doi.org/10.3390/buildings11110562
Abdelwahed BS, Kaloop MR, El-Demerdash WE. Nonlinear Numerical Assessment of Exterior Beam-Column Connections with Low-Strength Concrete. Buildings. 2021; 11(11):562. https://doi.org/10.3390/buildings11110562
Chicago/Turabian StyleAbdelwahed, Basem S., Mosbeh R. Kaloop, and Waleed E. El-Demerdash. 2021. "Nonlinear Numerical Assessment of Exterior Beam-Column Connections with Low-Strength Concrete" Buildings 11, no. 11: 562. https://doi.org/10.3390/buildings11110562







