Risk Response Strategies Selection over the Life Cycle of Project Portfolio
Abstract
:1. Introduction
2. Literature Review
2.1. Risk Interdependence in Project Risk Response
2.2. Risk Response Approaches in Project Risk Management
3. Model Construction
3.1. Construction of the Index System
3.2. Construction of the Dynamic Bayesian Network
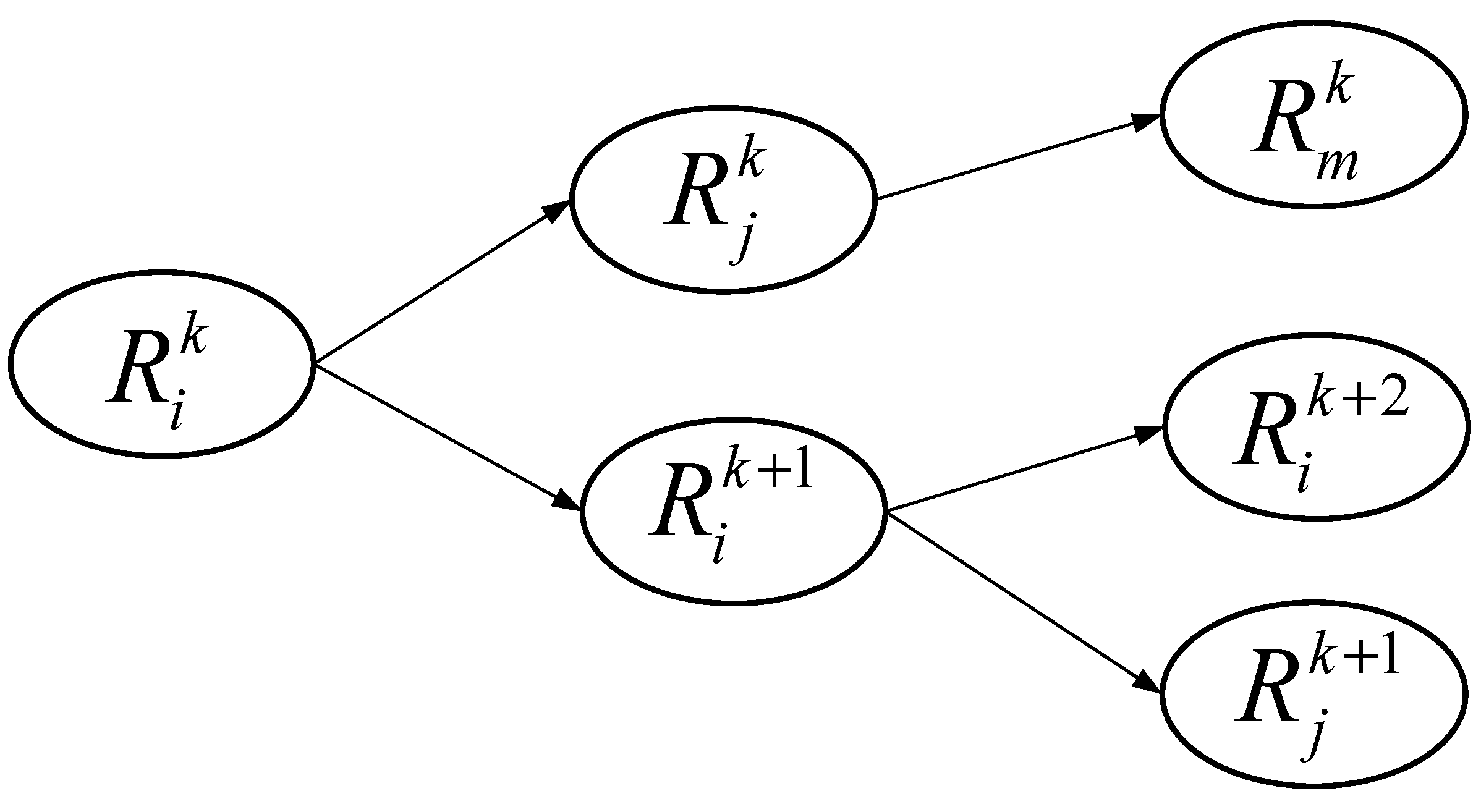
3.2.1. Structure of the Dynamic Bayesian Network
3.2.2. Parameterization of the Dynamic Bayesian Network
3.3. Construction of the Risk Response Optimization Model
3.3.1. Determining the Objective Function
3.3.2. Identifying the Constraints
3.3.3. Solving the Model
4. Illustrative Example
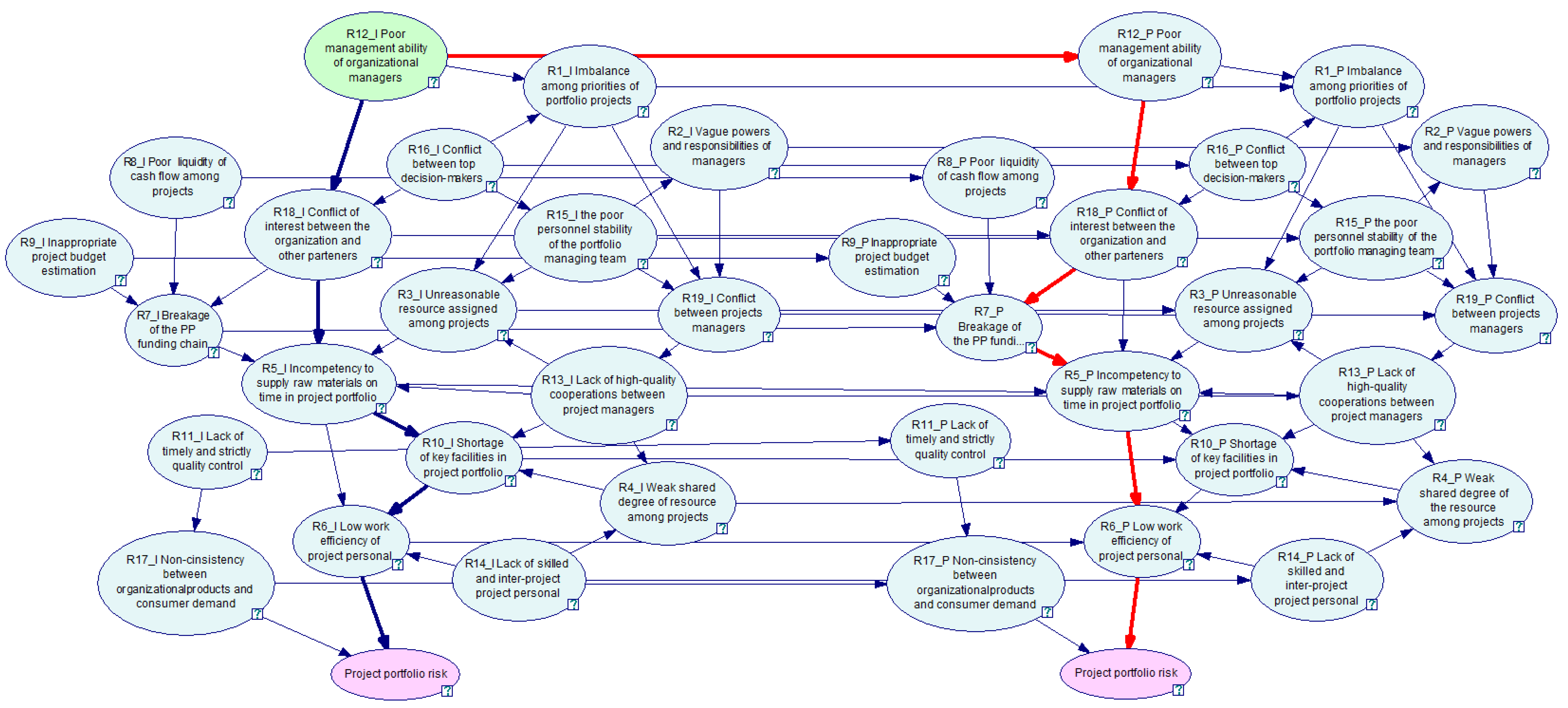
4.1. Problem Description
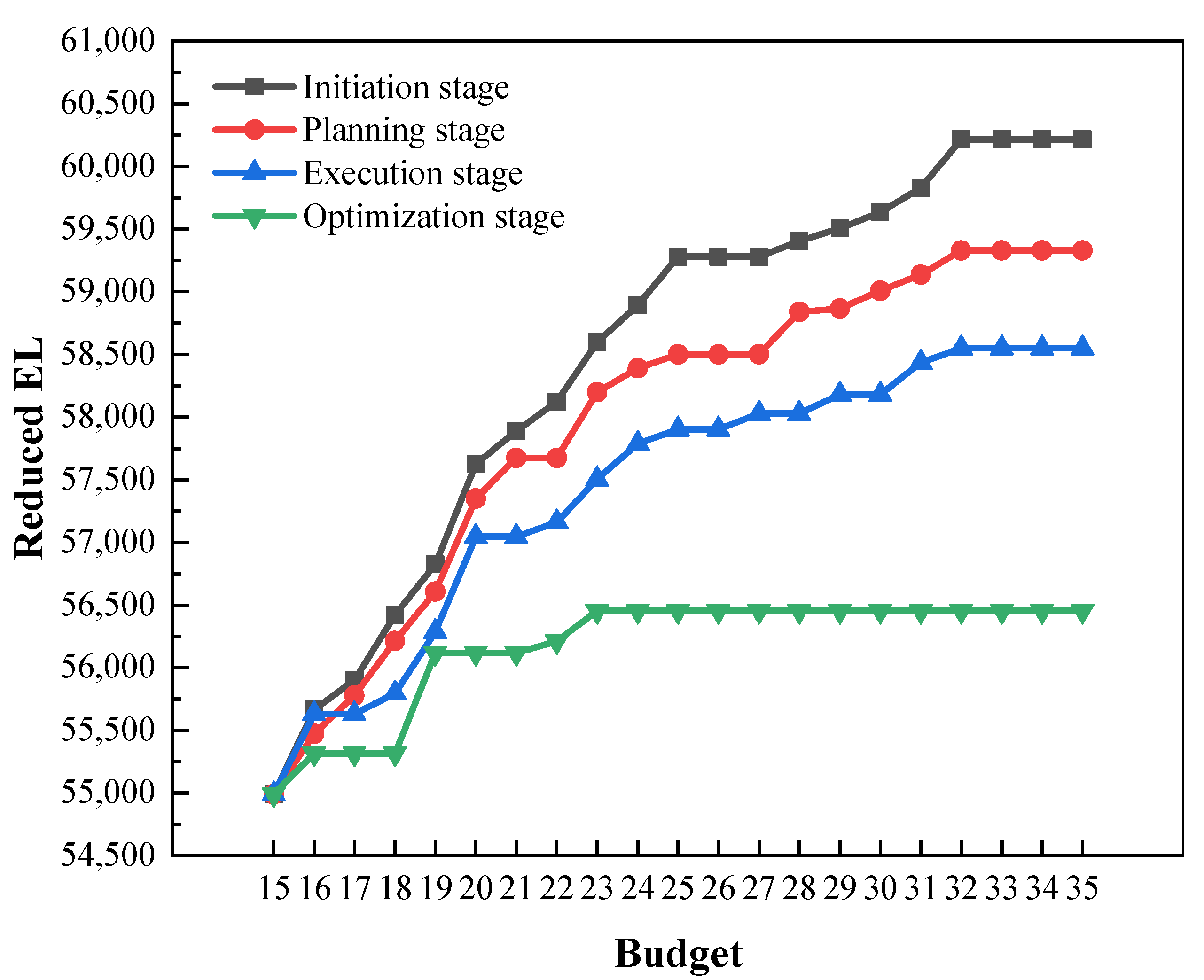
4.2. Results and Analysis
5. Discussion
5.1. Theoretical Implication
5.2. Managerial Implication
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. F-DBN Model of the PPRs
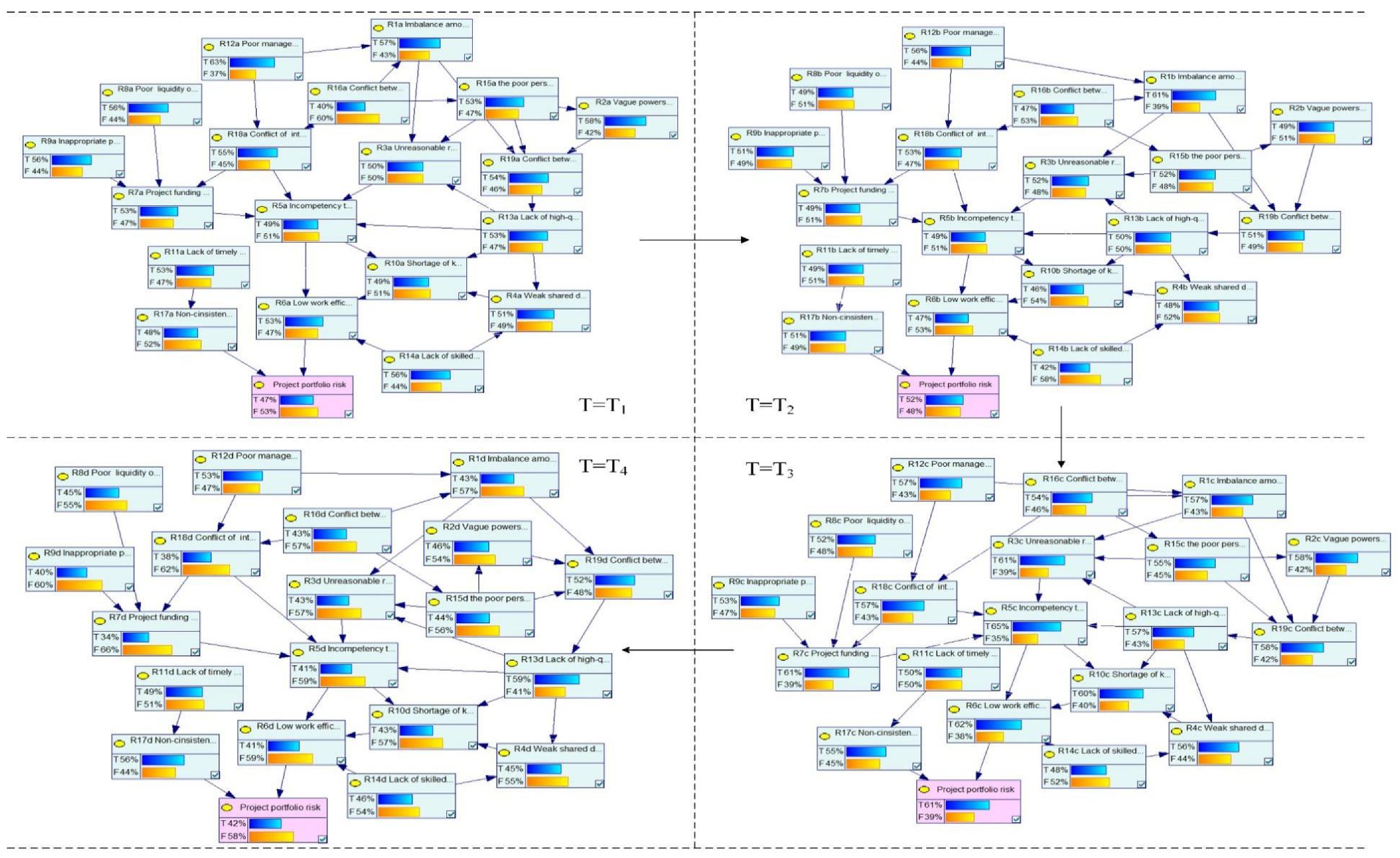
Appendix B. Expected Losses of the Risks at Each Stage
| Ri | Initiation Stage | Planning Stage | Execution Stage | Optimization Stage |
| R1 | 1240.32 | 1327.36 | 1240.32 | 935.68 |
| R2 | 675.7 | 570.85 | 675.7 | 535.9 |
| R3 | 835 | 868.4 | 1018.7 | 718.1 |
| R4 | 239.7 | 225.6 | 263.2 | 211.5 |
| R5 | 938.35 | 938.35 | 1244.75 | 785.15 |
| R6 | 431.95 | 383.05 | 505.3 | 334.15 |
| R7 | 991.1 | 916.3 | 1140.7 | 635.8 |
| R8 | 344.4 | 301.35 | 319.8 | 276.75 |
| R9 | 1103.2 | 1004.7 | 1044.1 | 788 |
| R10 | 735 | 690 | 900 | 645 |
| R11 | 749.95 | 693.35 | 707.5 | 693.35 |
| R12 | 1307.88 | 1162.56 | 1183.32 | 1100.28 |
| R13 | 973.61 | 918.5 | 1047.09 | 1083.83 |
| R14 | 588 | 441 | 504 | 483 |
| R15 | 776.45 | 761.8 | 805.75 | 644.6 |
| R16 | 606 | 712.05 | 818.1 | 651.45 |
| R17 | 1050.24 | 1115.88 | 1203.4 | 1225.28 |
| R18 | 255.75 | 246.45 | 265.05 | 176.7 |
| R19 | 626.4 | 591.6 | 672.8 | 603.2 |
Appendix C. Proposed Risk Response Actions and Estimated Costs
| Proposed Risk Response Actions | (Million Yuan) | |
| Implementing decentralized management and improving the policy-making procedure | 5 | |
| Hiring management experts for online instruction | 4 | |
| Providing training for project manager | 7 | |
| Development of a database | 2 | |
| Review the procurement schedule of major equipment according to the plan | 3.55 | |
| Introduce professional technical talent | 3.5 | |
| Application of contingency reserves (unallocated funds) | 2.8 | |
| Developing funding sources, such as fixed-rate loan contracts with lending banks | 6.7 | |
| Hire experts or outsourcing modules to third parties | 2 | |
| Replace imported equipment with analogous domestic equipment | 3.1 | |
| Planning and holding training courses for contractors and employees | 2.4 | |
| Developing and implementing a management screening system | 3.6 | |
| Improve communication networks and enhance the ability to communicate | 1 | |
| Prepare backup persons | 1.5 | |
| Training personnel and gaining the loyalty of key personnel | 3.5 | |
| Hiring a professional management team | 1 | |
| Perform market research and connect with users | 1.5 | |
| Hiring a local agent | 7.2 | |
| Building the prestige of the critical members and establishing proper values in the team | 5 |
References
- Project Management Institute. A Guide to the Project Management Body of Knowledge (PMBOK® Guide), 7th ed.; Project Management Institute: Newtown Square, PA, USA, 2021. [Google Scholar]
- Bai, L.; Sun, Y.; Shi, H.; Shi, C.; Bai, J.; Han, X. Dynamic assessment modelling for project portfolio benefits. J. Oper. Res. Soc. 2021, 73, 1596–1619. [Google Scholar] [CrossRef]
- Teller, J. Portfolio Risk Management and Its Contribution to Project Portfolio Success: An Investigation of Organization, Process, and Culture. Proj. Manag. J. 2013, 44, 36–51. [Google Scholar] [CrossRef]
- Bai, L.B.; Shi, H.J.; Kang, S.Y.; Zhang, B.B. Project portfolio risk analysis with the consideration of project interdependencies. Eng. Constr. Archit. Manag. 2021. [Google Scholar] [CrossRef]
- Sanchez, H.; Robert, B.; Bourgault, M.; Pellerin, R. Risk management applied to projects, programs, and portfolios. Int. J. Manag. Proj. Bus. 2009, 2, 14–35. [Google Scholar] [CrossRef]
- Reyck, B.D.; Grushka-Cockayne, Y.; Lockett, M.; Calderini, S.R.; Moura, M.; Sloper, A. The impact of project portfolio management on information technology projects. Int. J. Proj. Manag. 2005, 23, 524–537. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Z. An optimization method for selecting project risk response strategies. Int. J. Proj. Manag. 2014, 32, 412–422. [Google Scholar] [CrossRef]
- Mokhtari, G.; Aghagoli, F. Project Portfolio Risk Response Selection Using Bayesian Belief Networks. Iran. J. Basic Manag. Stud. 2020, 13, 197–219. [Google Scholar] [CrossRef]
- Ebrahimnejad, S.; Mousavi, S.M.; Seyrafianpour, H. Risk identification and assessment for build–operate–transfer projects: A fuzzy multi attribute decision making model. Expert Syst. Appl. 2010, 37, 575–586. [Google Scholar] [CrossRef]
- Teller, J.; Kock, A. An empirical investigation on how portfolio risk management influences project portfolio success. Int. J. Proj. Manag. 2013, 31, 817–829. [Google Scholar] [CrossRef]
- Miller, R.; Lessard, D. Understanding and managing risks in large engineering projects. Int. J. Proj. Manag. 2001, 19, 437–443. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, X. Selecting Project Risk Preventive and Protective Strategies Based on Bow-Tie Analysis. J. Manag. Eng. 2018, 34, 04018009. [Google Scholar] [CrossRef]
- Guan, D.; Guo, P. Assessment of Project Portfolio Risk Based on Bayesian Network. J. Industr. Eng. 2015, 18, 31–35. [Google Scholar] [CrossRef]
- Zhang, Y. Selecting risk response strategies considering project risk interdependence. Int. J. Proj. Manag. 2016, 34, 819–830. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Marle, F.; Xie, M.; Zio, E. An Integrated Framework for Risk Response Planning Under Resource Constraints in Large Engineering Projects. IEEE Trans. Eng. Manag. 2013, 60, 627–639. [Google Scholar] [CrossRef] [Green Version]
- Qin, Z.; Ji, C.; Su, X.; Nawaz, A. Probability Analysis of Construction Risk based on Noisy-or Gate Bayesian Networks. Reliab. Eng. Syst. Saf. 2022, 217, 107974. [Google Scholar] [CrossRef]
- Mancuso, A.; Compare, M.; Salo, A.; Zio, E. Portfolio optimization of safety measures for the prevention of time-dependent accident scenarios. Reliab. Eng. Syst. Saf. 2019, 190, 106500. [Google Scholar] [CrossRef]
- Cai, B.; Zhang, Y.; Yuan, X.; Gao, C.; Liu, Y.; Chen, G.; Liu, Z.; Ji, R. A Dynamic-Bayesian-Networks-Based Resilience Assessment Approach of Structure Systems: Subsea Oil and Gas Pipelines as A Case Study. China Ocean Eng. 2020, 34, 597–607. [Google Scholar] [CrossRef]
- Cagliano, A.C.; Grimaldi, S.; Rafele, C. Choosing project risk management techniques. A theoretical framework. J. Risk Res. 2014, 18, 232–248. [Google Scholar] [CrossRef] [Green Version]
- Fan, M.; Lin, N.-P.; Sheu, C. Choosing a project risk-handling strategy: An analytical model. Int. J. Prod. Econ. 2008, 112, 700–713. [Google Scholar] [CrossRef]
- Yang, L.; Li, N. Interval model and its algorithm for optimal selecting of software project risk response actions. J. Control. Decis. 2011, 26, 530–534. [Google Scholar] [CrossRef]
- Parsaei Motamed, M.; Bamdad, S. A multi-objective optimization approach for selecting risk response actions: Considering environmental and secondary risks. Opsearch 2021, 59, 266–303. [Google Scholar] [CrossRef]
- Soofifard, R.; Bafruei, M.K. An optimal model for Project Risk Response Portfolio Selection (P2RPS) (Case study: Research institute of petroleum industry). Iran. J. Basic Manag. Stud. 2016, 9, 741–765. [Google Scholar]
- Ahmadi-Javid, A.; Fateminia, S.H.; Gemünden, H.G. A Method for Risk Response Planning in Project Portfolio Management. Proj. Manag. J. 2019, 51, 77–95. [Google Scholar] [CrossRef]
- Wu, D.; Li, J.; Xia, T.; Bao, C.; Zhao, Y.; Dai, Q. A multiobjective optimization method considering process risk correlation for project risk response planning. Inf. Sci. 2018, 467, 282–295. [Google Scholar] [CrossRef]
- Bao, C.; Wan, J.; Wu, D.; Li, J. Aggregating risk matrices under a normative framework. J. Risk Res. 2019, 24, 999–1015. [Google Scholar] [CrossRef]
- Haimes, Y.Y. Risk Modeling, Assessment, and Management, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Cerezo-Narváez, A.; Pastor-Fernández, A.; Otero-Mateo, M.; Ballesteros-Pérez, P. Integration of Cost and Work Breakdown Structures in the Management of Construction Projects. Appl. Sci. 2020, 10, 1386. [Google Scholar] [CrossRef] [Green Version]
- Sharon, A.; Dori, D. A Project–Product Model–Based Approach to Planning Work Breakdown Structures of Complex System Projects. IEEE Syst. J. 2015, 9, 366–376. [Google Scholar] [CrossRef]
- Zhong, X.; Zhou, S. Risk analysis method of bank microfinance based on multiple genetic artificial neural networks. Neural. Comput. Appl. 2020, 32, 5367–5377. [Google Scholar] [CrossRef]
- Yang, R.J.; Zou, P.X.W. Stakeholder-associated risks and their interactions in complex green building projects: A social network model. Build Environ. 2014, 73, 208–222. [Google Scholar] [CrossRef]
- Ghasemi, F.; Sari, M.; Yousefi, V.; Falsafi, R.; Tamošaitienė, J. Project Portfolio Risk Identification and Analysis, Considering Project Risk Interactions and Using Bayesian Networks. Sustainability 2018, 10, 1609. [Google Scholar] [CrossRef] [Green Version]
- Fam, M.L.; He, X.; Konovessis, D.; Ong, L.S. Using Dynamic Bayesian Belief Network for analysing well decommissioning failures and long-term monitoring of decommissioned wells. Reliab. Eng. Syst. Saf. 2020, 197, 106855. [Google Scholar] [CrossRef]
- Khan, B.; Khan, F.; Veitch, B. A Dynamic Bayesian Network model for ship-ice collision risk in the Arctic waters. Saf. Sci. 2020, 130, 104858. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Ge, W.; Wei, D.; Li, H. Risk Analysis of Earth-Rock Dam Breach Based on Dynamic Bayesian Network. Water 2019, 11, 2305. [Google Scholar] [CrossRef] [Green Version]
- Umar, T. Key factors influencing the implementation of three-dimensional printing in construction. Proc. Inst. Civ. Eng. 2021, 174, 104–117. [Google Scholar] [CrossRef]
- Umar, T. Challenges of BIM implementation in GCC construction industry. Eng. Constr. Archit. Manag. 2021, 29, 1139–1168. [Google Scholar] [CrossRef]
- Eybpoosh, M.; Dikmen, I.; Talat Birgonul, M. Identification of Risk Paths in International Construction Projects Using Structural Equation Modeling. J. Constr. Eng. Manag. 2011, 137, 1164–1175. [Google Scholar] [CrossRef]
- Costa, H.R.; Barros, M.d.O.; Travassos, G.H. Evaluating software project portfolio risks. J. Syst. Softw. 2007, 80, 16–31. [Google Scholar] [CrossRef]
- Hadjinicolaou, N.; Dumrak, J. Investigating Association of Benefits and Barriers in Project Portfolio Management to Project Success. Procedia Eng. 2017, 182, 274–281. [Google Scholar] [CrossRef]
- Hofman, M.; Spalek, S.; Grela, G. Shedding New Light on Project Portfolio Risk Management. Sustainability 2017, 9, 1798. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Marle, F. A simulation-based risk network model for decision support in project risk management. Decis. Support Syst. 2012, 52, 635–644. [Google Scholar] [CrossRef]
- Browning, T.R.; Yassine, A.A. Resource-constrained multi-project scheduling: Priority rule performance revisited. Int. J. Prod. Econ. 2010, 126, 212–228. [Google Scholar] [CrossRef]
- Zou, P.X.W.; Zhang, G.; Wang, J. Understanding the key risks in construction projects in China. Int. J. Proj. Manag. 2007, 25, 601–614. [Google Scholar] [CrossRef]
- Keshk, A.M.; Maarouf, I.; Annany, Y. Special studies in management of construction project risks, risk concept, plan building, risk quantitative and qualitative analysis, risk response strategies. Alex. Eng. J. 2018, 57, 3179–3187. [Google Scholar] [CrossRef]
- Nieto, M.A.; Ruz, V.F. A fuzzy approach to construction project risk assessment. Int. J. Proj. Manag. 2011, 29, 220–231. [Google Scholar] [CrossRef] [Green Version]
- Palomo, J.; Rios Insua, D.; Ruggeri, F. Modeling external risks in project management. Risk Anal. 2007, 27, 961–978. [Google Scholar] [CrossRef]
- Park, J.; Park, B.; Cha, Y.; Hyun, C. Risk Factors Assessment Considering Change Degree for Mega-projects. Procedia Soc. Behav. Sci. 2016, 218, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Namazian, A.; Haji Yakhchali, S. Modified Bayesian Network–Based Risk Analysis of Construction Projects: Case Study of South Pars Gas Field Development Projects. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A 2018, 4, 05018003. [Google Scholar] [CrossRef]
- Micán, C.; Fernandes, G.; Araújo, M.; Araújo, E.A.A. Operational risk categorization in project-based organizations: A theoretical perspective from a project portfolio risk lens. In Proceedings of the 8th Manufacturing Engineering Society International Conference, Madrid, Spain, 19–21 June 2019. [Google Scholar]
- Abd El-Karim, M.S.B.A.; Mosa El Nawawy, O.A.; Abdel-Alim, A.M. Identification and assessment of risk factors affecting construction projects. HBRC J. 2019, 13, 202–216. [Google Scholar] [CrossRef] [Green Version]
- Yim, R.; Castaneda, J.; Doolen, T.; Tumer, I.; Malak, R. A study of the impact of project classification on project risk indicators. Int. J. Proj. Manag. 2015, 33, 863–876. [Google Scholar] [CrossRef]
- Vidal, L.A.; Marle, F. Understanding project complexity: Implications on project management. Kybernetes 2008, 37, 1094–1110. [Google Scholar] [CrossRef]
- Qiao, W.; Liu, Y.; Ma, X.; Liu, Y. Human Factors Analysis for Maritime Accidents Based on a Dynamic Fuzzy Bayesian Network. Risk Anal. 2020, 40, 957–980. [Google Scholar] [CrossRef]
- Zarei, E.; Yazdi, M.; Abbassi, R.; Khan, F. A hybrid model for human factor analysis in process accidents: FBN-HFACS. J Loss Prev. Process. Ind. 2019, 57, 142–155. [Google Scholar] [CrossRef]
- Ghasemi, F.; Ghasemi, A.; Kalatpour, O. Prediction of human error probability during the hydrocarbon road tanker loading operation using a hybrid technique of fuzzy sets, Bayesian network and CREAM. Int. J. Occup. Saf. Ergon. 2022, 28, 1342–1352. [Google Scholar] [CrossRef] [PubMed]
- Lyu, H.; Sun, W.; Shen, S.; Zhou, A. Risk Assessment Using a New Consulting Process in Fuzzy AHP. J. Constr. Eng. Manag. 2020, 146, 04019112. [Google Scholar] [CrossRef]
- Yang, X.; Ding, J.; Hou, H. Application of a triangular fuzzy AHP approach for flood risk evaluation and response measures analysis. Nat. Hazards 2013, 68, 657–674. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Qin, Y.; Skibniewski, M.J.; Liu, W. Towards a Fuzzy Bayesian Network Based Approach for Safety Risk Analysis of Tunnel-Induced Pipeline Damage. Risk Anal. 2016, 36, 278–301. [Google Scholar] [CrossRef]
- Chin, K.; Tang, D.; Yang, J.; Wong, S.; Wang, H. Assessing new product development project risk by Bayesian network with a systematic probability generation methodology. Expert Syst. Appl. 2009, 36, 9879–9890. [Google Scholar] [CrossRef]
- Kwan, T.W.; Leung, H.K.N. A Risk Management Methodology for Project Risk Dependencies. IEEE Trans. Softw. Eng. 2011, 37, 635–648. [Google Scholar] [CrossRef]
- He, Q.; Yang, D.; Luo, L.; Ma, L.; Li, L. Research of large scale and complex construction programs’ schedule risk based on Bayesian network. Soft Sci. 2016, 30, 120–126+139. [Google Scholar] [CrossRef]

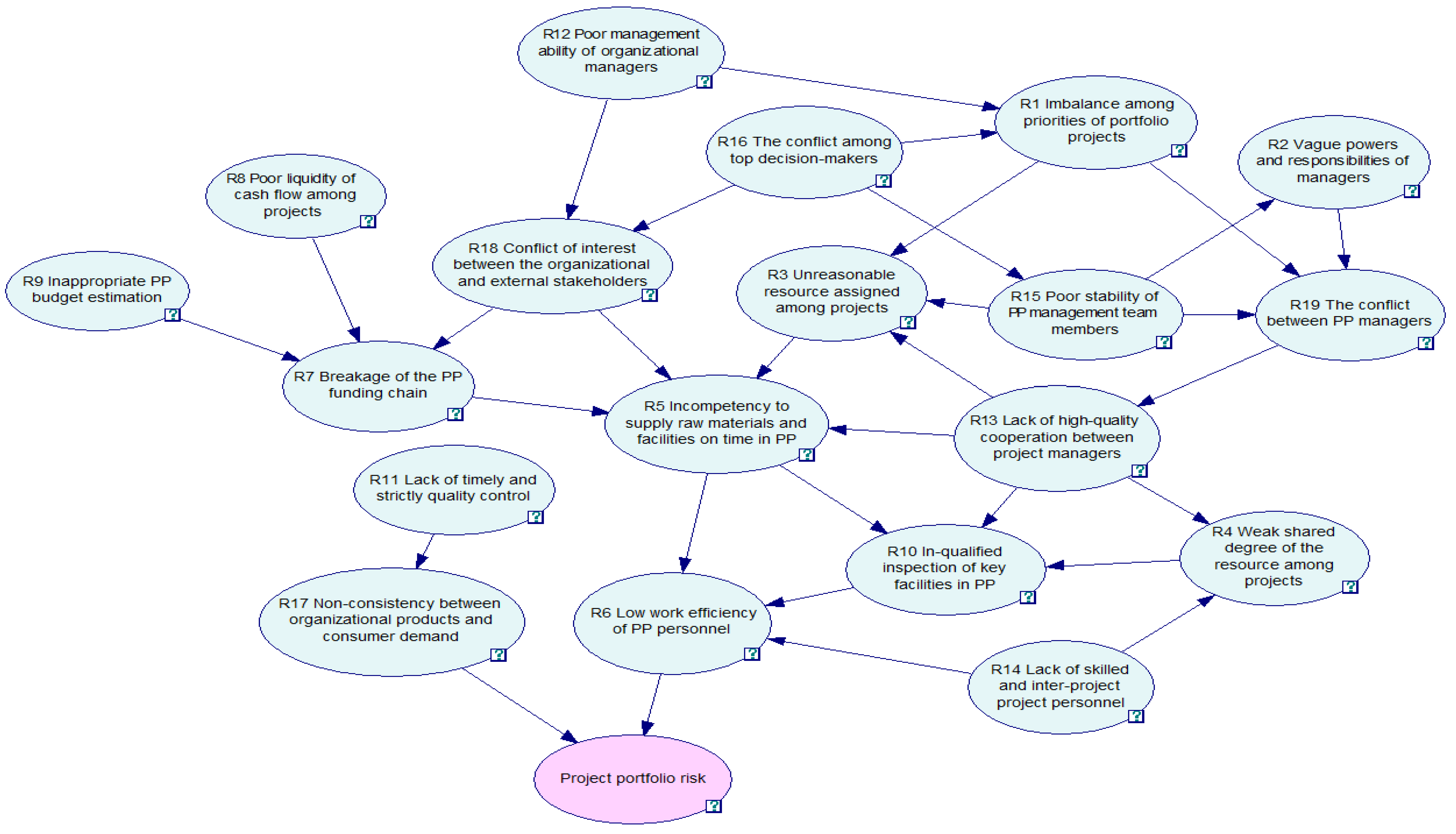

| Category | No. | Risk Factor | Description | Source |
|---|---|---|---|---|
| Organization Management | R1 | Imbalance among priorities of portfolio projects | Projects are inaccurately prioritized in the project portfolio (PP), including the sequence of project implementation or material distribution. | [40,41] |
| R2 | Vague powers and responsibilities of managers | The scope of the rights that the organization manager can exercise is not clear, and the responsibility goal to be undertaken is also not clear. | [32,42] | |
| R3 | Unreasonable resource assignment among projects | The limited resources for allocation cannot be reasonably allocated to important projects to achieve maximum benefits. | [14,43] | |
| R4 | Weak shared degree of the resource among projects | The coordination and sharing degree of critical materials in the PP is low, resulting in a low material utilization rate. | [32,44] | |
| Time Management | R5 | Incompetency to supply raw materials and facilities on time in the PP | The materials needed for project execution could not be delivered on time during the implementation, resulting in delays in PP progress. | [45,46] |
| R6 | Low work efficiency of PP personnel | Project workers are work-inefficient due to a lack of technical skills or conflicts with organizational culture, which affects the progress of the PP. | [14,44] | |
| Cost Management | R7 | Breakage of the PP funding chain | Financial problems or capital chain disruptions cannot provide adequate funding support for the smooth implementation of the PP. | [47] |
| R8 | Poor liquidity of cash flow among projects | The assets cannot be recovered in full as scheduled, and the repayment of due liabilities and new reasonable loans, and other financing needs cannot be met. | [48] | |
| R9 | Inappropriate PP budget estimation | Evaluation of the PP economic benefits is improper, and feasibility study results are inaccurate, thus affecting the subsequent management of the portfolio cost. | [44,49] | |
| Quality Management | R10 | In-qualified inspection of key facilities in the PP | Key large equipment entrance inspection, site installation, operation specifications, and other processes are unqualified. | [50] |
| R11 | Lack of timely and strict quality control | The production links of various projects in the PP lack strict control, and the quality of the project products do not meet the standards. | [14,49] | |
| Human Resource Management | R12 | Poor management ability of organizational managers | The manager is unable to manage and monitor the portfolio effectively. | [38,51] |
| R13 | Lack of high-quality cooperation between project managers | Project managers do not provide timely share information and resources to facilitate PP team collaboration. | [41,42] | |
| R14 | Lack of skilled and inter-project project personnel | Shortage of professional staff who can easily switch between projects to save time and improve project coordination. | [32] | |
| R15 | Poor stability of PP management team members | The management team is unstable: management personnel will constantly change, leading to blind or stagnant work handover. | [41] | |
| Stakeholder Management | R16 | The conflict among top decision-makers | Conflict among top decision-makers caused by their different interests will affect the correctness of organizational management decisions. | [32,41] |
| R17 | Non-consistency between organizational products and consumer demand | Organizational production cannot meet the needs of the market and users, affecting corporate performance and benefits. | [52] | |
| R18 | Conflict of interest between the organizational and external stakeholders | Conflicts between organization managers and external stakeholders such as suppliers, regulators, environmentalists, financial organizations, and the media affect the realization of strategic goals. | [32,48] | |
| R19 | The conflict between PP managers | PP managers have conflicts due to differences in interest distribution, management concepts, etc. | [41] |
| Indicator | Classification | Score | Indicator | Classification | Score |
|---|---|---|---|---|---|
| Experience time (years) | ≥30 | 5 | Professional position | Senior academic | 5 |
| 20–29 | 4 | Junior academic | 4 | ||
| 10-–19 | 3 | Engineer | 3 | ||
| 6–9 | 2 | Technician | 2 | ||
| 2–5 | 1 | Worker | 1 | ||
| Educational level | PhD | 5 | Age (years) | ≥50 | 5 |
| Master | 4 | 40–49 | 4 | ||
| Bachelor | 3 | 30–39 | 3 | ||
| Higher national diploma | 2 | 25–29 | 2 | ||
| School-level | 1 | <25 | 1 |
| Experts | Experience Time (Years) | Professional Position | Educational Level | Age | Weight Score | Weight |
|---|---|---|---|---|---|---|
| Expert 1 | 2–5 | Junior academic | PhD | 25–29 | 1 + 4 + 5 + 2 = 12 | 0.152 |
| Expert 2 | 6–9 | Engineer | Master | 25–29 | 2 + 3 + 4 + 2 = 11 | 0.139 |
| Expert 3 | 10–19 | Senior academic | PhD | 30–39 | 3 + 5 + 5 + 3 = 16 | 0.203 |
| Expert 4 | 10–19 | Engineer | Bachelor | 40-49 | 3 + 3 + 3 + 4 = 13 | 0.165 |
| Expert 5 | 6–9 | Junior academic | Master | 30–39 | 2 + 4 + 4 + 3 = 13 | 0.165 |
| Expert 6 | ≥30 | Technician | Bachelor | 40–49 | 5 + 2 +3 + 4 = 14 | 0.176 |
| Notation | Definition |
|---|---|
| z | The risk response effect. |
| The set of risk response strategies, . | |
| The cost of implementing a risk response strategy . | |
| The direct risk response effect on risk after implementing a risk response strategy in stage k. | |
| The indirect risk response effect to other risks in the subsequent stages (m = k + 1, …. t) after implementing the response strategy deal with in stage k. | |
| The indirect risk response effect to other risks in stage k after implementing the risk response strategy deal with in stage k. | |
| The budget for implementing risk response strategies at each stage. | |
| The expected loss in stage k before implementing the risk response strategy . | |
| The risk response effect after implementing a risk response strategy in stage k. | |
| The upper bound for expected losses that can be accepted in stage k. | |
| The set of all mutually exclusive pairs of strategies. | |
| Binary integer decision variables. equals 1 if the is selected in stage k; otherwise, is equal to 0. |
| Initiation | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 23.2 |
| Planning | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 17.5 |
| Execution | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11.4 |
| Optimization | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 3 |
| Z | 60,458.98 | |||||||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Bai, L.; Kang, S. Risk Response Strategies Selection over the Life Cycle of Project Portfolio. Buildings 2022, 12, 2191. https://doi.org/10.3390/buildings12122191
Zhang B, Bai L, Kang S. Risk Response Strategies Selection over the Life Cycle of Project Portfolio. Buildings. 2022; 12(12):2191. https://doi.org/10.3390/buildings12122191
Chicago/Turabian StyleZhang, Bingbing, Libiao Bai, and Shuyun Kang. 2022. "Risk Response Strategies Selection over the Life Cycle of Project Portfolio" Buildings 12, no. 12: 2191. https://doi.org/10.3390/buildings12122191






