Probabilistic Moment Bearing Capacity Model and Fragility of Beam-Column Joints with Cast Steel Stiffeners
Abstract
:1. Introduction
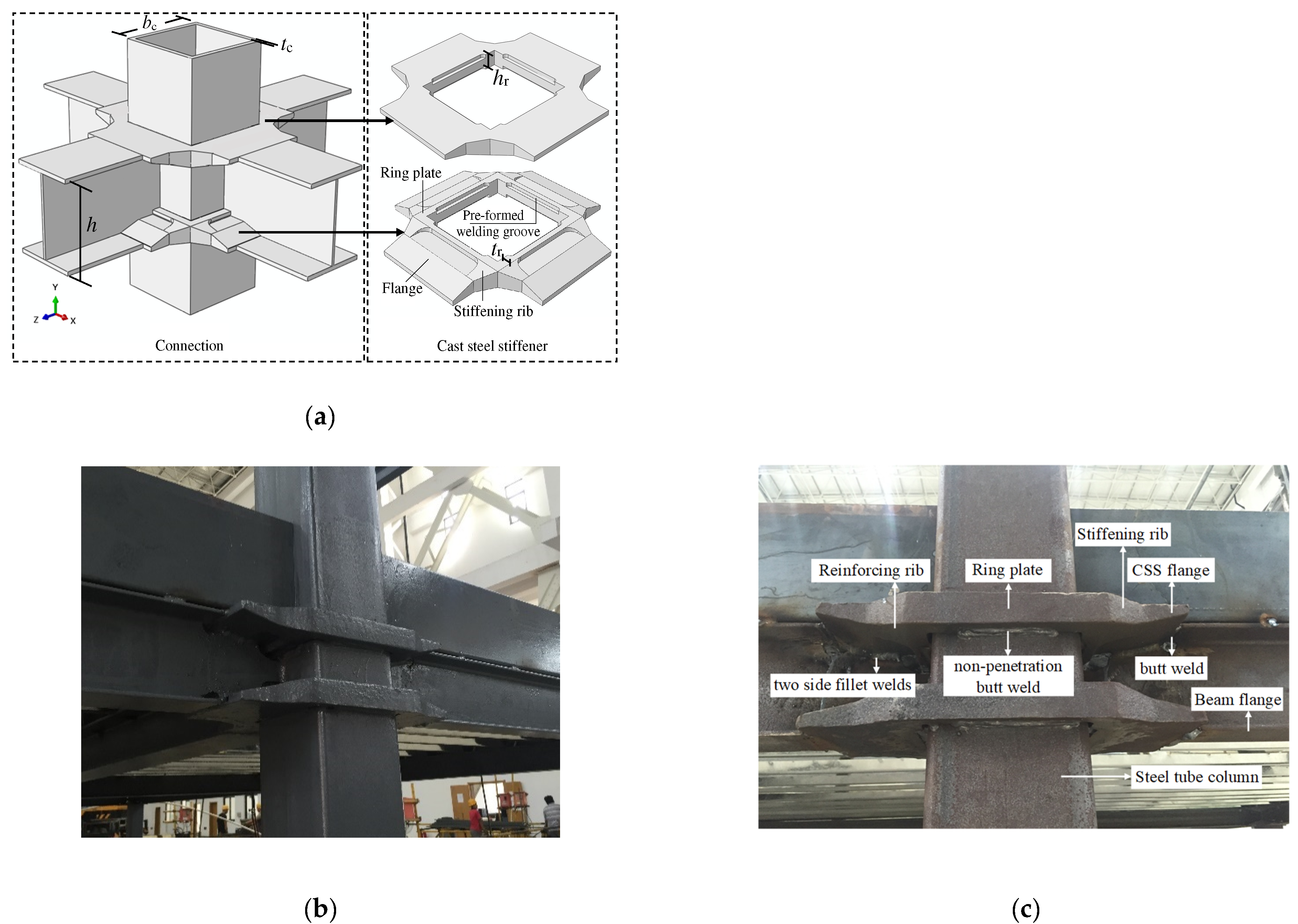
2. Data Preparation
3. Simplified Theoretical Model
4. General Formulations of the Probabilistic Model and Fragility
4.1. Probabilistic Capacity Model
4.2. Model Training Using a Bayesian Approach
4.3. Feature Importance Analysis
4.4. Fragility Analysis
5. Probabilistic Modeling and Fragility Analysis of the Joints with CSS in the Database
5.1. Probabilistic Capacity Model of the Joints with CSS
= θ0 + θ1 ln(tc) + θ2 ln(h) + θ3 ln(tr) +θ4 ln(hr) + θ5 ln(fyr) + θ6 bc/tc + θ7 fc/fyr + σe
5.2. Feature Importance Analysis of the Developed Capacity Model
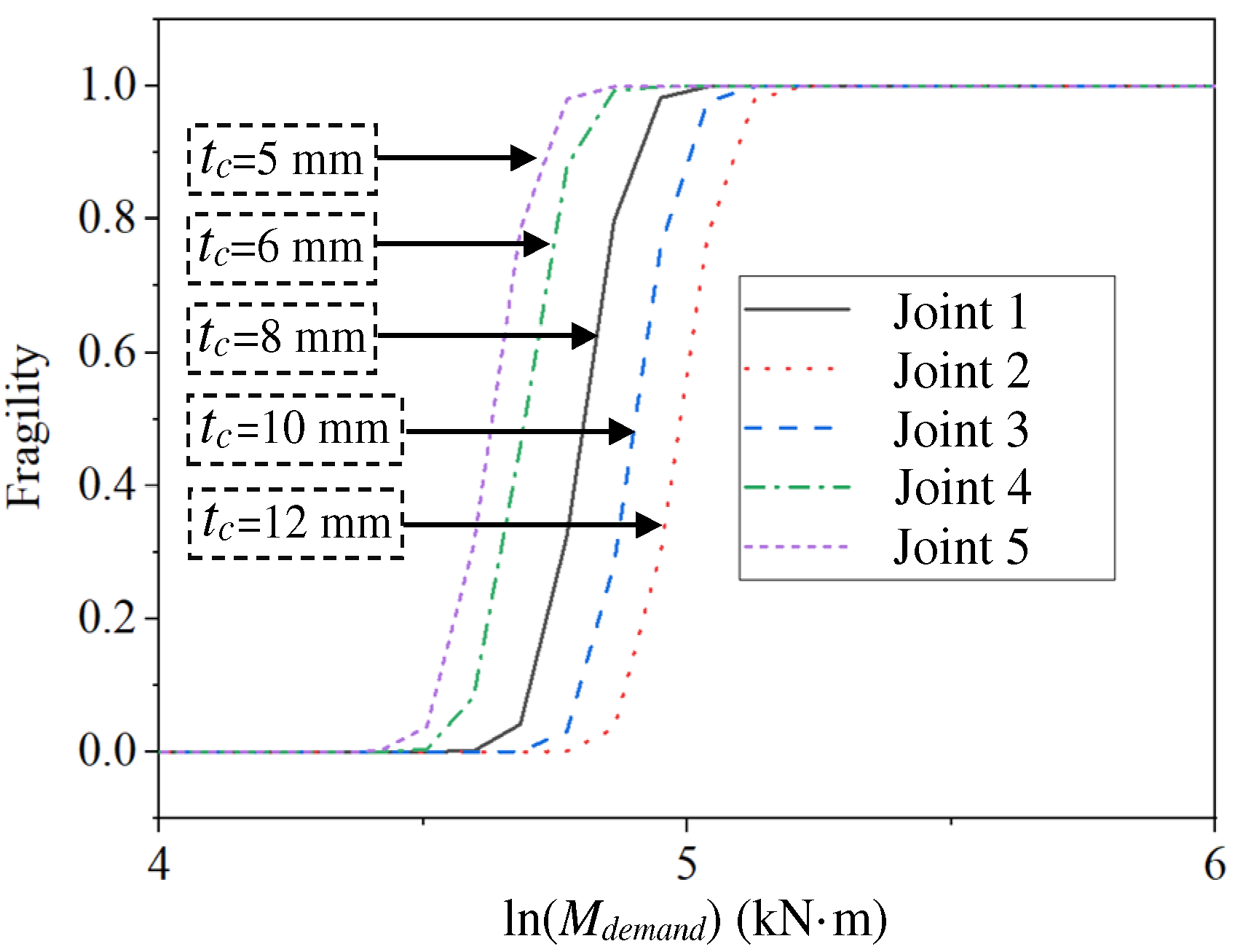
5.3. Fragility Analysis of Example Joints in the Database
6. Summary and Conclusions
- (1)
- The paper proposed a probabilistic model for the moment bearing capacity of joints with CSS. A Bayesian approach was developed for the training and updating of such a model. The proposed approach was implemented in the modeling of the moment bearing capacity of CSS joints at yielding points based on real observation data from the past study. Compared with the simplified theoretical model in the literature, the proposed model provides much higher prediction accuracy and captures the variability well. In addition, the model can be consistently updated over time when new experimental or simulation data become available. For the convenience of practice, the method to obtain the moment capacity estimate with an arbitrary exceeding probability p% by the proposed model was also demonstrated.
- (2)
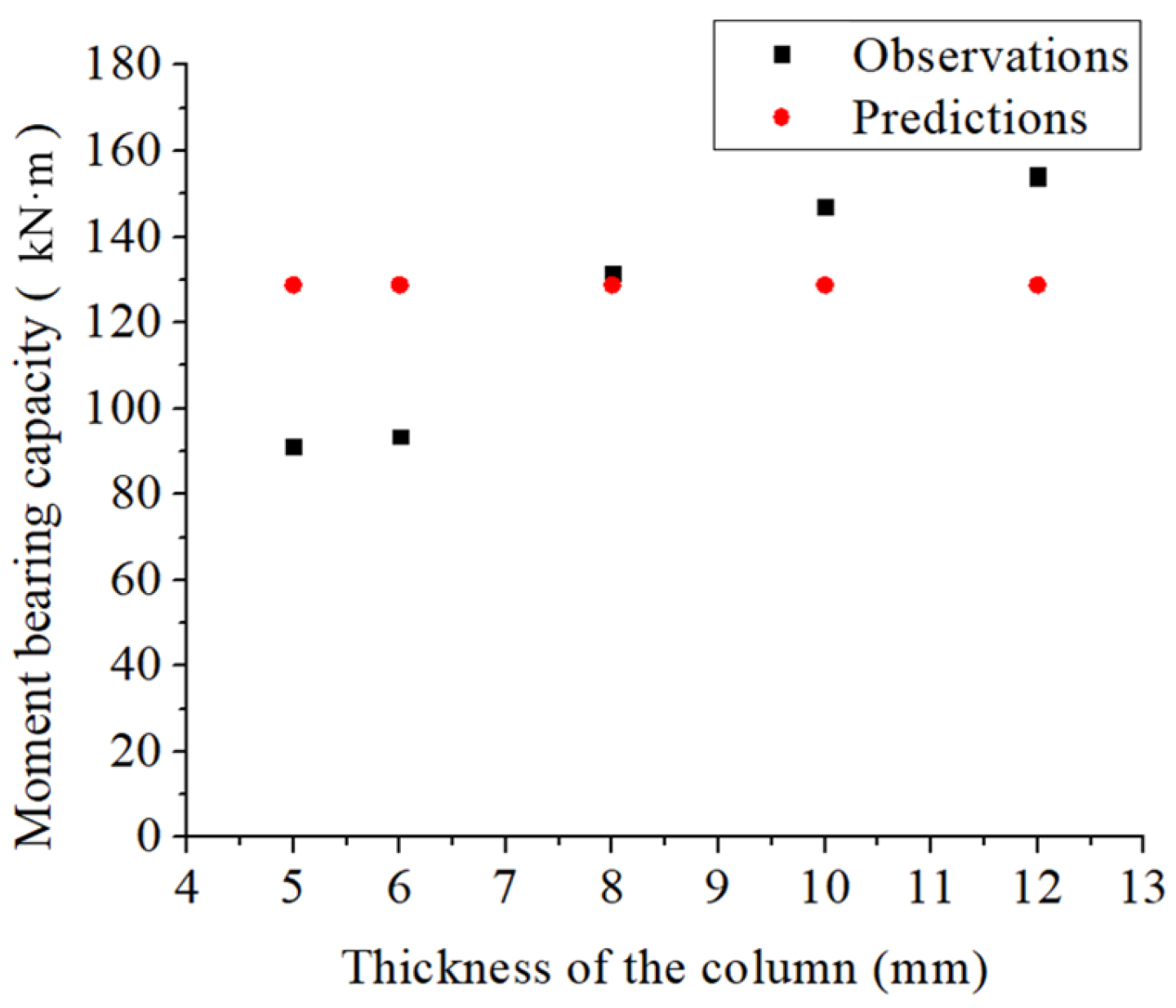
- The paper proposed a permutation-based method for the importance analysis of the variables in the capacity model. This proposed method is flexible and works for either linear or nonlinear/non-parametric capacity models. For the developed model based on data in the past study, the analysis showed that the height of the CSS ring hr is the most important variable impacting the moment capacity. The other variables that also significantly impact the capacity, in order from high importance to low importance, include: tr, h, tc, fyr, fc/fyr, and bc/tc, where tr is the width of the CSS ring, h is the distance between the outer surfaces of the upper and bottom flanges of the beam, tc is the thickness of the column, fyr is the yield strength of cast steel, fc is the axial compressive strength of concrete, and bc is the outer diameter of the column. Note that tc, which is more important than fyr, is not included in the simplified theoretical model. That is one of the reasons why the previous simplified theoretical model is biased and less accurate than the proposed model. This feature importance analysis can demonstrate the importance of the parameters in a quantitative way.
- (3)
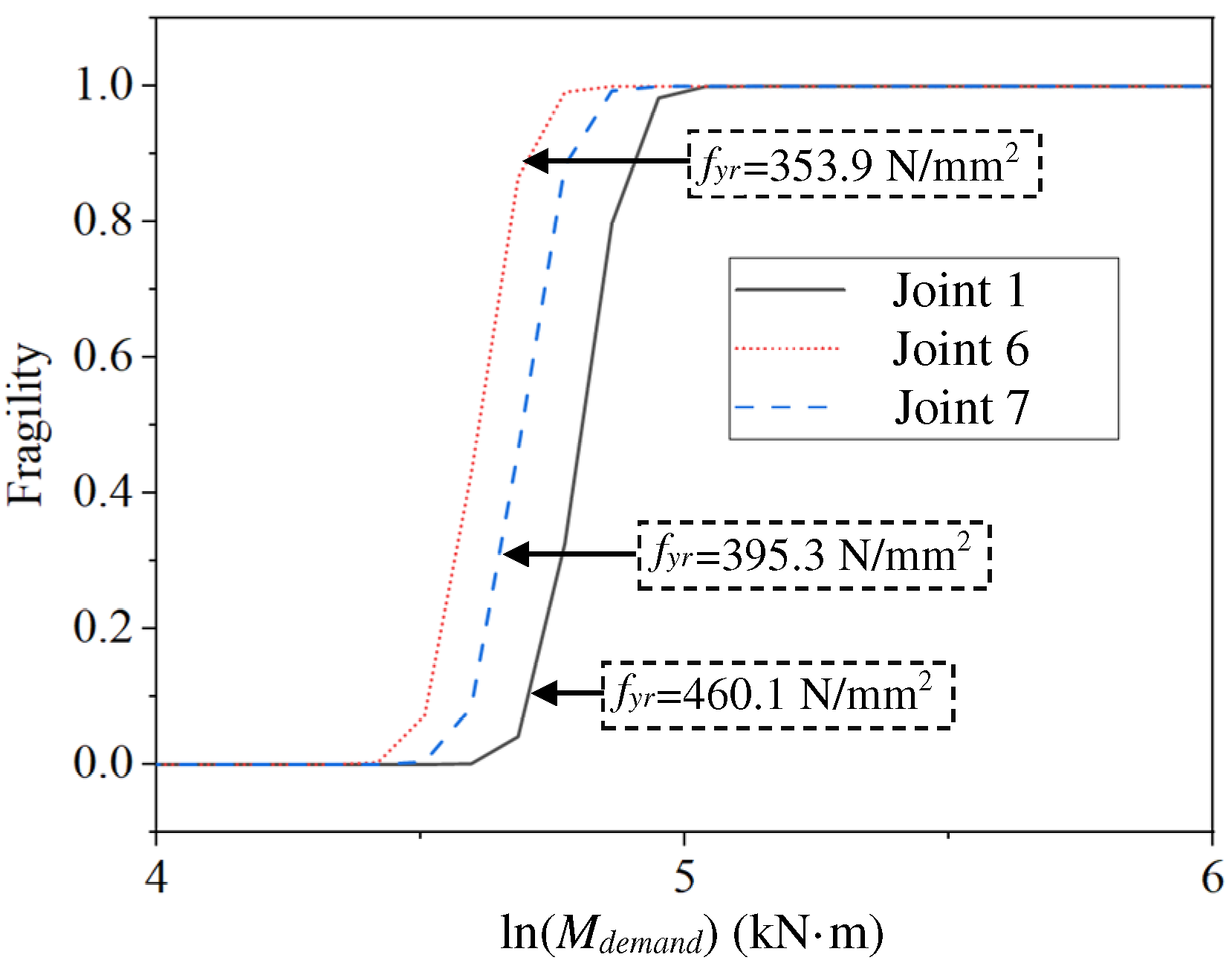
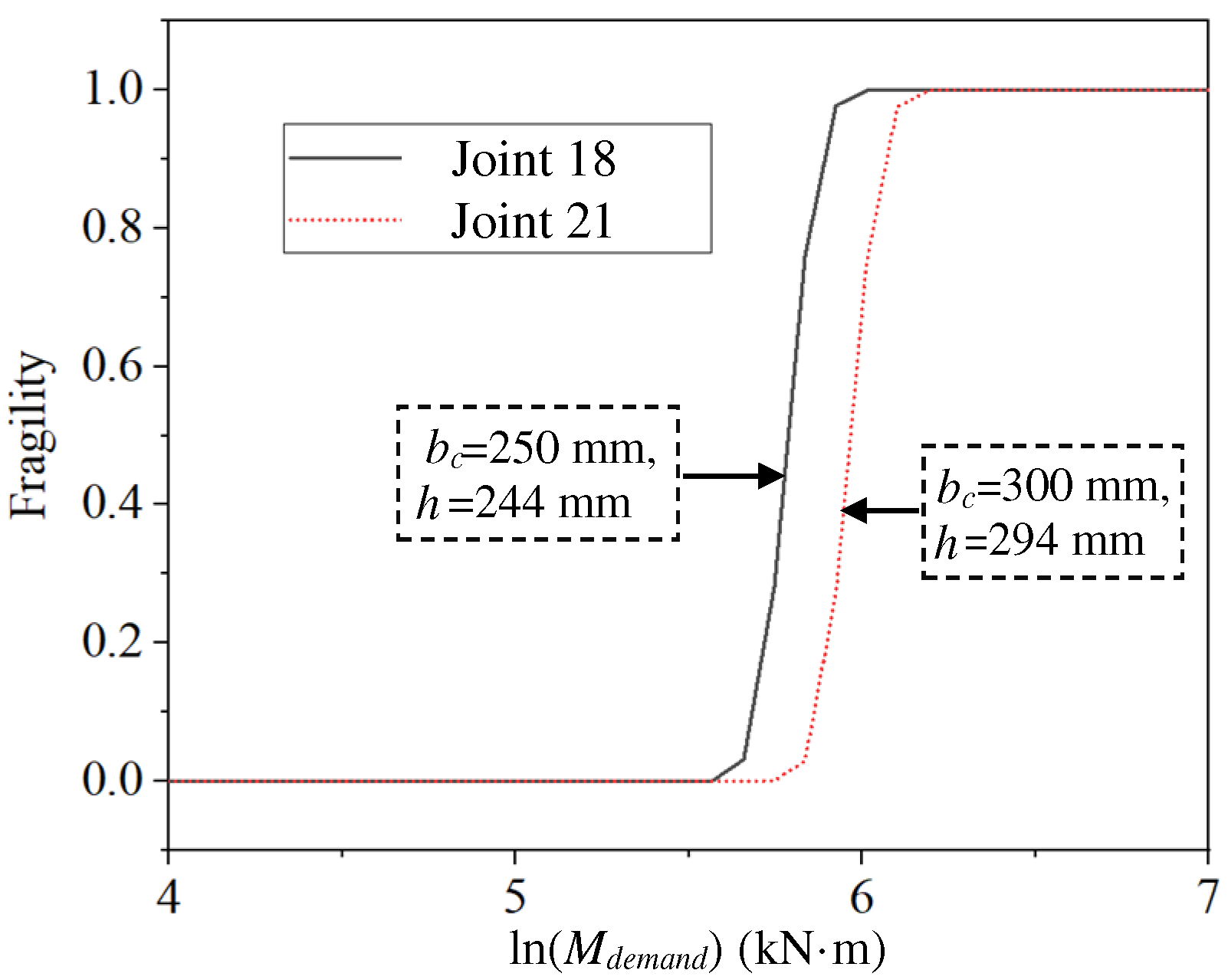
- The paper presented a method to estimate the fragility of joints with CSS using the proposed capacity model. Moreover, two practical values of fragility analysis of CSS joints were demonstrated by several joint examples. First, the fragility analysis can grasp how the fragilities vary by different characteristics of the joints. Based on the case study in this paper, the fragility decreases with an increase in tc, fyr, fc, hr, tr, bc, and h; namely, the joints with large tc, fyr, fc, hr, tr, bc, and h are not likely to be damaged. Second, fragility analysis can provide different designing or retrofitting plans with the same reliability, which can support engineers or researchers with decision-making. For instance, a joint with tc = 20 mm and fc = 0 kN/m2 roughly gives the same failure probability under different loads compared with a joint with tc = 8 mm and fc = 42.8 kN/m2. The designers can then make a choice between the two options based on their engineering judgment of cost and construction convenience.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
References
- Irvani, M.; Ezati, H.; Khafajeh, R.; Jaari, V.R.K. Numerically study on the seismic response of partially restrained moment connection with structural fuse T-stub for European sections. Structures 2022, 35, 82–105. [Google Scholar] [CrossRef]
- Rodriguez, D.; Brunesi, E.; Nascimbene, R. Fragility and sensitivity analysis of steel frames with bolted-angle connections under progressive collapse. Eng. Struct. 2021, 228, 111508. [Google Scholar] [CrossRef]
- De Domenico, D.; Falsone, G.; Laudani, R. Probability-based structural response of steel beams and frames with uncertain semi-rigid connections. Struct. Eng. Mech. 2018, 67, 439–455. [Google Scholar] [CrossRef]
- Gaxiola-Camacho, J.R.; Haldar, A.; Azizsoltani, H.; Valenzuela-Beltran, F.; Reyes-Salazar, A. Performance-based seismic design of steel buildings using rigidities of connections. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04017036. [Google Scholar] [CrossRef]
- Liu, M. Research on Mechanical Behavior of H-Shaped Beam to Square Tube Column Joint with Cast Steel Stiffener. Ph.D. Thesis, Tianjin University, Tianjin, China, 2016. (In Chinese). [Google Scholar]
- Feng, B.; Zhu, Y.H.; Xie, F.; Chen, J.; Liu, C.-B. Experimental Investigation and Design of Hollow Section, Centrifugal Concrete-Filled GFRP Tube Columns. Buildings 2021, 11, 598. [Google Scholar] [CrossRef]
- Xing, J.; Xu, P.; Yao, S.; Zhao, H.; Zhao, Z.; Wang, Z. Study on the layout strategy of diaphragms to enhance the energy absorption of thin-walled square tubes. Structures 2021, 29, 294–304. [Google Scholar] [CrossRef]
- Kenzo, N.; Takashi, K.; Katsunei, Y. Development of cast steel outer diaphragm high blade method. Hitachi Metals Tech. Rep. 2003, 19, 67–70. (In Japanese) [Google Scholar]
- Han, Q.; Li, X.; Liu, M.; Spencer, B.F. Experimental investigation of beam–column joints with cast steel stiffeners for progressive collapse prevention. J. Struct. Eng. 2019, 145, 04019020. [Google Scholar] [CrossRef]
- Kenzo, N.; Takeyuki, O.; Hiroaki, K.; Yuji, M.; Eijiro, U.; Takashi, K. Experimental study of beam-column joints using cast steel outer diaphragm: (Part 1) Experiment of shear type simple model. In Abstracts of Academic Lectures of the Japan Society for Architecture: C-1, Structure III, Wood Structure, Steel Structure, Steel Reinforced Concrete Structure; Architectural Institute of Japan: Tokyo, Japan, 1999; pp. 509–510. (In Japanese) [Google Scholar]
- Eijiro, U.; Takeyuki, O.; Hiroaki, K.; Yuji, M.; Kenzo, N.; Takashi, K. Experimental study of beam-column joints using cast steel outer diaphragm: (Part 2) Consideration of local deformation. In Abstracts of Academic Lectures at the Architectural Institute of Japan: C-1, Structure III, Wood Structure, Steel Structure, Steel Reinforced Concrete Structure; Architectural Institute of Japan: Tokyo, Japan, 1999; pp. 511–512. (In Japanese) [Google Scholar]
- Yuzo, S.; Takeyuki, O.; Yuji, M.; Hiroaki, K.; Kenzo, N.; Takashi, K. Experimental study of beam-column joints using cast steel outer diaphragm: (4) Additional experiment of shear type simple model. In Abstracts of Academic Lectures at the Architectural Institute of Japan: C-1, Structure III, Wood Structure, Steel Structure, Steel Reinforced Concrete Structure; Architectural Institute of Japan: Tokyo, Japan, 2000; pp. 629–630. (In Japanese) [Google Scholar]
- Masato, M.; Kenzo, N.; Takashi, K.; Takeyuki, O. Experimental study of beam-column joints using cast steel outer diaphragm: (Part 5) Cross-shaped frame experiment using concrete-filled steel pipe columns. In Abstracts of Academic Lectures at the Architectural Institute of Japan: C-1, Structure III, Wood Structure, Steel Structure, Steel Reinforced Concrete Structure; Architectural Institute of Japan: Tokyo, Japan, 2002; pp. 1125–1126. (In Japanese) [Google Scholar]
- Han, Q.; Liu, M.; Lu, Y. Mechanical Behavior Analysis of Cast Steel Joints Connecting H-Shaped Beam and Square Tube Column. J. Tianjin Univ. Sci. Tech. 2015, 48, 502–509. (In Chinese) [Google Scholar]
- Han, Q.; Liu, M.; Lu, Y.; Xu, Y.; Xu, J. Experimental research on static behavior of cast steel joints for H-shaped beam and square tube column. J. Build. Eng. 2015, 36, 101–109. (In Chinese) [Google Scholar]
- Han, Q.; Liu, M.; Lu, Y. Experimental research on load-bearing capacity of cast steel joints for beam-to-column. Struct. Eng. Mech. 2015, 56, 67–83. [Google Scholar] [CrossRef]
- Han, Q.; Liu, M.; Lu, Y.; Zhao, S. Experimental and simulation study on seismic behavior of beam-column joints with cast steel stiffener. J. Struct. Eng. 2016, 142, 04016030. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, Y. Probabilistic model of fatigue damage accumulation of materials based on the principle of failure probability equivalence. Structures 2020, 28, 659–667. [Google Scholar] [CrossRef]
- Gardoni, P.; Der, K.A.; Mosalam, K.M. Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations. J. Eng. Mech. 2002, 128, 1024–1038. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, H.; Zhao, Z.; Yan, R. Probability distribution model of the bending capacity for WHSJ with multiple randomly pitting corrosion. Structures 2020, 27, 1740–1751. [Google Scholar] [CrossRef]
- Kim, J.; LaFave, J.M. A simplified approach to joint shear behavior prediction of RC beam-column joints. Earthq. Spectra 2012, 28, 1071–1096. [Google Scholar] [CrossRef]
- Arshian, A.H.; Morgenthal, G. Probabilistic assessment of the ultimate load-bearing capacity in laterally restrained two-way reinforced concrete slabs. Eng. Struct. 2017, 150, 52–63. [Google Scholar] [CrossRef]
- Xu, H.; Gardoni, P. Probabilistic capacity and seismic demand models and fragility estimates for reinforced concrete buildings based on three-dimensional analyses. Eng. Struct. 2016, 112, 200–214. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, H.; Gardoni, P.; Lu, D.; Yu, X. Probabilistic demand models and fragilities for reinforced concrete frame structures subject to mainshock-aftershock sequences. Eng. Struct. 2021, 245, 112904. [Google Scholar] [CrossRef]
- Cui, S.; Chen, Y.; Lu, D. Probability assessment of structural response modification factor of RC frames by the demand-capacity-factor method. Structures 2021, 30, 628–637. [Google Scholar] [CrossRef]
- Lei, J.; Lu, Z.; He, L. The single-loop Kriging model combined with Bayes’ formula for time-dependent failure probability based global sensitivity. Structures 2021, 32, 987–996. [Google Scholar] [CrossRef]
- Sun, B.; Gardoni, P.; Xiao, R. Probabilistic aerostability capacity models and fragility estimates for cable-stayed bridge decks based on wind tunnel test data. Eng. Struct. 2016, 126, 106–120. [Google Scholar] [CrossRef]
- Xu, H.; Gardoni, P. Multi-level, multi-variate, non-stationary, random field modeling and fragility analysis of engineering systems. Struct. Safe. 2020, 87, 101999. [Google Scholar] [CrossRef]
- Contento, A.; Xu, H.; Gardoni, P. Probabilistic formulation for storm surge predictions. Struct. Infrastruct. Eng. 2020, 16, 547–566. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Der, K.A. Bayesian methods for seismic fragility assessment of lifeline components. In Acceptable Risk Processes–Lifelines and Natural Hazards; American Society of Civil Engineers: Reston, VA, USA, 2002; pp. 1–77. [Google Scholar]
- Anscombe, F.J. Normal likelihood functions. Ann. Inst. Stat. Math. 1964, 16, 1–19. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M.; Ibrahim, J.G. Monte Carlo Methods in Bayesian Computation; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 55, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Gardoni, P. Improved latent space approach for modelling non-stationary spatial–temporal random fields. Spat. Stat. 2018, 23, 160–181. [Google Scholar] [CrossRef]
- Xu, H.; Gardoni, P. Conditional formulation for the calibration of multi-level random fields with incomplete data. Reliab. Eng. Syst. Safe. 2020, 204, 107121. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Makridakis, S. Accuracy measures: Theoretical and practical concerns. Int. J. Forecast. 1993, 9, 527–529. [Google Scholar] [CrossRef]
- De, M.A.; Golden, B.; Le, G.B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Ellingwood, B.R.; Celik, O.C.; Kinali, K. Fragility assessment of building structural systems in Mid-America. Earthq. Eng. Struct. Dyn. 2007, 36, 1935–1952. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]









| Joint | bc (mm) | tc (mm) | h (mm) | tr (mm) | hr (mm) | fyr (N/mm2) | fc (N/mm2) | Ma (kN·m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 200 | 8 | 194 | 20 | 35 | 460.1 | - | 131.48 |
| 2 | 200 | 12 | 194 | 20 | 35 | 460.1 | - | 153.90 |
| 3 | 200 | 10 | 194 | 20 | 35 | 460.1 | - | 147.06 |
| 4 | 200 | 6 | 194 | 20 | 35 | 460.1 | - | 93.48 |
| 5 | 200 | 5 | 194 | 20 | 35 | 460.1 | - | 91.20 |
| 6 | 200 | 8 | 194 | 20 | 35 | 353.9 | - | 101.84 |
| 7 | 200 | 8 | 194 | 20 | 35 | 395.3 | - | 118.94 |
| 8 | 200 | 12 | 194 | 20 | 35 | 460.1 | - | 154.66 |
| 9 | 200 | 8 | 194 | 20 | 35 | 460.1 | 42.8 | 171.76 |
| 10 | 200 | 8 | 194 | 20 | 35 | 460.1 | 42.8 | 179.74 |
| 11 | 200 | 8 | 194 | 20 | 35 | 460.1 | 42.8 | 176.32 |
| 12 | 250 | 8 | 244 | 25 | 60 | 300.0 | - | 217.50 |
| 13 | 250 | 10 | 244 | 25 | 60 | 300.0 | - | 233.10 |
| 14 | 250 | 12 | 244 | 25 | 60 | 300.0 | - | 248.60 |
| 15 | 250 | 12 | 244 | 25 | 60 | 180.0 | - | 187.80 |
| 16 | 250 | 8 | 244 | 30 | 70 | 300.0 | - | 290.10 |
| 17 | 250 | 10 | 244 | 30 | 70 | 300.0 | - | 294.40 |
| 18 | 250 | 12 | 244 | 30 | 70 | 300.0 | - | 310.80 |
| 19 | 250 | 12 | 244 | 30 | 70 | 230.0 | - | 272.80 |
| 20 | 300 | 10 | 294 | 30 | 70 | 300.0 | - | 359.80 |
| 21 | 300 | 12 | 294 | 30 | 70 | 300.0 | - | 368.50 |
| 22 | 300 | 14 | 294 | 30 | 70 | 300.0 | - | 387.60 |
| 23 | 300 | 14 | 294 | 30 | 70 | 230.0 | - | 306.90 |
| 24 | 300 | 10 | 294 | 40 | 70 | 300.0 | - | 482.00 |
| 25 | 300 | 12 | 294 | 40 | 70 | 300.0 | - | 514.90 |
| 26 | 300 | 14 | 294 | 40 | 70 | 300.0 | - | 533.00 |
| 27 | 300 | 14 | 294 | 40 | 70 | 230.0 | - | 395.40 |
| 28 | 400 | 10 | 390 | 40 | 70 | 300.0 | - | 660.80 |
| 29 | 400 | 12 | 390 | 40 | 70 | 300.0 | - | 654.20 |
| 30 | 400 | 14 | 390 | 40 | 70 | 300.0 | - | 719.70 |
| 31 | 400 | 16 | 390 | 40 | 70 | 300.0 | - | 752.30 |
| 32 | 400 | 16 | 390 | 40 | 70 | 230.0 | - | 568.40 |
| 33 | 400 | 10 | 390 | 40 | 90 | 300.0 | - | 817.80 |
| 34 | 400 | 12 | 390 | 40 | 90 | 300.0 | - | 862.70 |
| 35 | 400 | 14 | 390 | 40 | 90 | 300.0 | - | 917.80 |
| 36 | 400 | 16 | 390 | 40 | 90 | 300.0 | - | 941.40 |
| 37 | 400 | 16 | 390 | 40 | 90 | 230.0 | - | 681.80 |
| 38 | 200 | 6 | 200 | 20 | 35 | 300.0 | 14.3 | 96.66 |
| 39 | 200 | 8 | 200 | 20 | 35 | 300.0 | 14.3 | 114.03 |
| 40 | 200 | 10 | 200 | 20 | 35 | 300.0 | 14.3 | 129.17 |
| 41 | 200 | 12 | 200 | 20 | 35 | 300.0 | 14.3 | 143.51 |
| 42 | 300 | 6 | 300 | 40 | 70 | 300.0 | 14.3 | 543.24 |
| 43 | 300 | 8 | 300 | 40 | 70 | 300.0 | 14.3 | 605.19 |
| 44 | 300 | 10 | 300 | 40 | 70 | 300.0 | 14.3 | 642.16 |
| 45 | 300 | 12 | 300 | 40 | 70 | 300.0 | 14.3 | 694.07 |
| 46 | 400 | 6 | 400 | 40 | 90 | 300.0 | 14.3 | 874.37 |
| 47 | 400 | 8 | 400 | 40 | 90 | 300.0 | 14.3 | 911.56 |
| 48 | 400 | 10 | 400 | 40 | 90 | 300.0 | 14.3 | 940.71 |
| 49 | 400 | 12 | 400 | 40 | 90 | 300.0 | 14.3 | 1025.83 |
| 50 | 500 | 6 | 500 | 50 | 100 | 300.0 | 14.3 | 1509.71 |
| 51 | 500 | 8 | 500 | 50 | 100 | 300.0 | 14.3 | 1566.02 |
| 52 | 500 | 10 | 500 | 50 | 100 | 300.0 | 14.3 | 1684.23 |
| 53 | 500 | 12 | 500 | 50 | 100 | 300.0 | 14.3 | 1704.18 |
| 54 | 600 | 6 | 600 | 50 | 100 | 300.0 | 14.3 | 1950.48 |
| 55 | 600 | 8 | 600 | 50 | 100 | 300.0 | 14.3 | 2175.25 |
| 56 | 600 | 10 | 600 | 50 | 100 | 300.0 | 14.3 | 2269.63 |
| 57 | 600 | 12 | 600 | 50 | 100 | 300.0 | 14.3 | 2332.84 |
| Joint | Ma (kN·m) | Mp1 (kN·m) | Absolute Prediction Error (%) | Joint | Ma (kN·m) | Mp1 (kN·m) | Absolute Prediction Error (%) |
|---|---|---|---|---|---|---|---|
| 1 | 131.48 | 128.83 | 2.02 | 30 | 719.70 | 655.20 | 8.96 |
| 2 | 153.90 | 128.83 | 16.29 | 31 | 752.30 | 655.20 | 12.91 |
| 3 | 147.06 | 128.83 | 12.40 | 32 | 568.40 | 502.30 | 11.63 |
| 4 | 93.48 | 128.83 | 37.82 | 33 | 817.80 | 842.40 | 3.01 |
| 5 | 91.20 | 128.83 | 41.26 | 34 | 862.70 | 842.40 | 2.35 |
| 6 | 101.84 | 99.09 | 2.70 | 35 | 917.80 | 842.40 | 8.22 |
| 7 | 118.94 | 110.68 | 6.94 | 36 | 941.40 | 842.40 | 10.52 |
| 8 | 154.66 | 128.83 | 16.70 | 37 | 681.80 | 645.80 | 5.28 |
| 9 | 171.76 | 128.83 | 24.99 | 38 | 96.66 | 84.00 | 13.10 |
| 10 | 179.74 | 128.83 | 28.32 | 39 | 114.03 | 84.00 | 26.34 |
| 11 | 176.32 | 128.83 | 26.93 | 40 | 129.17 | 84.00 | 34.97 |
| 12 | 217.50 | 219.60 | 0.97 | 41 | 143.51 | 84.00 | 41.47 |
| 13 | 233.10 | 219.60 | 5.79 | 42 | 543.24 | 504.00 | 7.22 |
| 14 | 248.60 | 219.60 | 11.67 | 43 | 605.19 | 504.00 | 16.72 |
| 15 | 187.80 | 168.40 | 10.33 | 44 | 642.16 | 504.00 | 21.51 |
| 16 | 290.10 | 307.40 | 5.96 | 45 | 694.07 | 504.00 | 27.38 |
| 17 | 294.40 | 307.40 | 4.42 | 46 | 874.37 | 864.00 | 1.19 |
| 18 | 310.80 | 307.40 | 1.09 | 47 | 911.56 | 864.00 | 5.22 |
| 19 | 272.80 | 235.70 | 13.60 | 48 | 940.71 | 864.00 | 8.15 |
| 20 | 359.80 | 370.40 | 2.95 | 49 | 1025.83 | 864.00 | 15.78 |
| 21 | 368.50 | 370.40 | 0.52 | 50 | 1509.71 | 1500.00 | 0.64 |
| 22 | 387.60 | 370.40 | 4.44 | 51 | 1566.02 | 1500.00 | 4.22 |
| 23 | 306.90 | 284.00 | 7.46 | 52 | 1684.23 | 1500.00 | 10.94 |
| 24 | 482.00 | 493.90 | 2.47 | 53 | 1704.18 | 1500.00 | 11.98 |
| 25 | 514.90 | 493.90 | 4.08 | 54 | 1950.48 | 1800.00 | 7.72 |
| 26 | 533.00 | 493.90 | 7.34 | 55 | 2175.25 | 1800.00 | 17.25 |
| 27 | 395.40 | 378.70 | 4.22 | 56 | 2269.63 | 1800.00 | 20.69 |
| 28 | 660.80 | 655.20 | 0.85 | 57 | 2332.84 | 1800.00 | 22.84 |
| 29 | 654.20 | 655.20 | 0.15 |
| Parameter | Mean | Standard Deviation | Correlation Coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| θ0 | θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | θ7 | σ | |||
| θ0 | −10.950 | 0.533 | 1.000 | ||||||||
| θ1 | 0.594 | 0.094 | 0.208 | 1.000 | |||||||
| θ2 | 0.806 | 0.133 | −0.393 | −0.727 | 1.000 | ||||||
| θ3 | 0.948 | 0.103 | 0.252 | 0.087 | −0.404 | 1.000 | |||||
| θ4 | 0.753 | 0.088 | −0.263 | 0.130 | −0.299 | −0.559 | 1.000 | ||||
| θ5 | 0.747 | 0.066 | −0.795 | 0.199 | −0.203 | −0.024 | 0.426 | 1.000 | |||
| θ6 | 0.007 | 0.002 | 0.387 | 0.915 | −0.796 | 0.139 | 0.111 | 0.093 | 1.000 | ||
| θ7 | 4.547 | 0.382 | 0.045 | 0.200 | −0.190 | −0.103 | 0.268 | 0.006 | 0.058 | 1.000 | |
| σ | 0.069 | 0.007 | 0.009 | 0.019 | −0.022 | 0.010 | 0.002 | 0.005 | 0.022 | −0.014 | 1.000 |
| Joint | Ma (kN·m) | Mp (kN·m) | Absolute Prediction Error (%) | Confidence Interval | Joint | Ma (kN·m) | Mp (kN·m) | Absolute Prediction Error (%) | Confidence Interval |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 131.48 | 121.92 | 7.27 | [122.71, 140.87] | 30 | 719.7 | 722.86 | 0.44 | [671.72, 771.11] |
| 2 | 153.9 | 146.34 | 4.91 | [143.64, 164.89] | 31 | 752.3 | 763.21 | 1.45 | [702.14, 806.04] |
| 3 | 147.06 | 134.42 | 8.60 | [137.26, 157.57] | 32 | 568.4 | 625.81 | 10.10 | [530.50, 609.00] |
| 4 | 93.48 | 108.95 | 16.55 | [87.25, 100.16] | 33 | 817.8 | 774.79 | 5.26 | [763.27, 876.22] |
| 5 | 91.2 | 102.43 | 12.31 | [85.12, 97.71] | 34 | 862.7 | 824.04 | 4.48 | [805.18, 924.33] |
| 6 | 101.84 | 100.22 | 1.59 | [95.05, 109.12] | 35 | 917.8 | 873.45 | 4.83 | [856.61, 983.36] |
| 7 | 118.94 | 108.85 | 8.48 | [111.01, 127.44] | 36 | 941.4 | 922.21 | 2.04 | [878.63, 1008.65] |
| 8 | 154.66 | 146.34 | 5.38 | [144.35, 165.71] | 37 | 681.8 | 756.19 | 10.91 | [636.34, 730.51] |
| 9 | 171.76 | 186.12 | 8.36 | [160.31, 184.03] | 38 | 96.66 | 100.75 | 4.23 | [90.22, 103.57] |
| 10 | 179.74 | 186.12 | 3.55 | [167.76, 192.58] | 39 | 114.03 | 112.76 | 1.11 | [106.43, 122.18] |
| 11 | 176.32 | 186.12 | 5.56 | [164.56, 188.92] | 40 | 129.17 | 124.31 | 3.76 | [120.56, 138.40] |
| 12 | 217.5 | 206.42 | 5.09 | [203.00, 233.04] | 41 | 143.51 | 135.33 | 5.70 | [133.94, 153.76] |
| 13 | 233.1 | 225.59 | 3.22 | [217.56, 249.75] | 42 | 543.24 | 510.40 | 6.05 | [507.02, 582.05] |
| 14 | 248.6 | 244.17 | 1.78 | [232.03, 266.36] | 43 | 605.19 | 554.78 | 8.33 | [564.84, 648.42] |
| 15 | 187.8 | 166.71 | 11.23 | [175.28, 201.22] | 44 | 642.16 | 601.02 | 6.41 | [599.35, 688.03] |
| 16 | 290.1 | 275.57 | 5.01 | [270.76, 310.82] | 45 | 694.07 | 646.73 | 6.82 | [647.79, 743.65] |
| 17 | 294.4 | 301.16 | 2.30 | [274.77, 315.43] | 46 | 874.37 | 873.91 | 0.05 | [816.07, 936.83] |
| 18 | 310.8 | 325.96 | 4.88 | [290.08, 333.00] | 47 | 911.56 | 922.59 | 1.21 | [850.78, 976.68] |
| 19 | 272.8 | 267.28 | 2.02 | [254.61, 292.29] | 48 | 940.71 | 982.14 | 4.40 | [877.99, 1007.91] |
| 20 | 359.8 | 362.45 | 0.74 | [335.81, 385.50] | 49 | 1025.83 | 1044.58 | 1.83 | [957.43, 1099.11] |
| 21 | 368.5 | 390.01 | 5.84 | [343.93, 394.82] | 50 | 1509.71 | 1572.42 | 4.15 | [1409.05, 1617.56] |
| 22 | 387.6 | 416.86 | 7.55 | [361.76, 415.29] | 51 | 1566.02 | 1612.30 | 2.96 | [1461.61, 1677.89] |
| 23 | 306.9 | 341.81 | 11.38 | [286.44, 328.82] | 52 | 1684.23 | 1686.59 | 0.14 | [1571.94, 1804.55] |
| 24 | 482 | 476.09 | 1.23 | [449.86, 516.43] | 53 | 1704.18 | 1773.01 | 4.04 | [1590.56, 1825.92] |
| 25 | 514.9 | 512.29 | 0.51 | [480.57, 551.68] | 54 | 1950.48 | 2046.71 | 4.93 | [1820.44, 2089.81] |
| 26 | 533 | 547.56 | 2.73 | [497.46, 571.08] | 55 | 2175.25 | 2038.30 | 6.30 | [2030.22, 2330.64] |
| 27 | 395.4 | 448.98 | 13.55 | [369.04, 423.65] | 56 | 2269.63 | 2095.23 | 7.68 | [2118.31, 2431.76] |
| 28 | 660.8 | 641.21 | 2.96 | [616.74, 708.01] | 57 | 2332.84 | 2177.03 | 6.68 | [2177.30, 2499.49] |
| 29 | 654.2 | 681.97 | 4.24 | [610.58, 700.93] |
| p% | Z | γ |
|---|---|---|
| 99 | 2.326 | 0.852 |
| 97.5 | 1.960 | 0.874 |
| 95 | 1.645 | 0.893 |
| 90 | 1.282 | 0.915 |
| 75 | 0.675 | 0.954 |
| 50 | 0 | 1 |
| Group ID | Joints in the Group | Logic |
|---|---|---|
| 1 | Joints 1 to 5 | Different column thicknesses (tc) |
| 2 | Joints 1, 6, and 7 | Different yield strengths of cast steel (fyr) |
| 3 | Joints 1 and 9 | Different axial compressive strengths of concrete (fc) |
| 4 | Joints 12 and 16 | Different heights and widths of the ring on the cast steel stiffener (hr and tr) |
| 5 | Joints 18 and 21 | Different outer diameters of the column and different distances between the outer surfaces of the upper and bottom flanges of the beam (bc and h) |
| Joint | ln(tc) | ln(h) | ln(tr) | ln(hr) | ln(fyr) | bc/tc | fc/fyr |
|---|---|---|---|---|---|---|---|
| 1 | 2.079 | 5.268 | 2.996 | 3.555 | 6.131 | 25.000 | 0.000 |
| 2 | 2.485 | 5.268 | 2.996 | 3.555 | 6.131 | 16.667 | 0.000 |
| 3 | 2.303 | 5.268 | 2.996 | 3.555 | 6.131 | 20.000 | 0.000 |
| 4 | 1.792 | 5.268 | 2.996 | 3.555 | 6.131 | 33.333 | 0.000 |
| 5 | 1.609 | 5.268 | 2.996 | 3.555 | 6.131 | 40.000 | 0.000 |
| 6 | 2.079 | 5.268 | 2.996 | 3.555 | 5.869 | 25.000 | 0.000 |
| 7 | 2.079 | 5.268 | 2.996 | 3.555 | 5.980 | 25.000 | 0.000 |
| 9 | 2.079 | 5.268 | 2.996 | 3.555 | 6.131 | 25.000 | 0.093 |
| 12 | 2.079 | 5.497 | 3.219 | 4.094 | 5.704 | 31.250 | 0.000 |
| 16 | 2.079 | 5.497 | 3.401 | 4.248 | 5.704 | 31.250 | 0.000 |
| 18 | 2.485 | 5.497 | 3.401 | 4.248 | 5.704 | 20.833 | 0.000 |
| 21 | 2.485 | 5.684 | 3.401 | 4.248 | 5.704 | 25.000 | 0.000 |
| Joint | ln(Mdemand) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.329 | 4.506 | 4.684 | 4.861 | 5.038 | 5.215 | 5.392 | 5.570 | 5.747 | 5.924 | 6.101 | 6.278 | |
| 1 | 0.000 | 0.000 | 0.041 | 0.797 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 2 | 0.000 | 0.000 | 0.000 | 0.035 | 0.775 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 3 | 0.000 | 0.000 | 0.001 | 0.281 | 0.977 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 4 | 0.000 | 0.004 | 0.458 | 0.993 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 5 | 0.000 | 0.038 | 0.785 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 6 | 0.000 | 0.072 | 0.866 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 7 | 0.000 | 0.004 | 0.463 | 0.993 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 9 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.436 | 0.992 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 12 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.048 | 0.818 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 16 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.238 | 0.968 | 1.000 | 1.000 | 1.000 |
| 18 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.282 | 0.977 | 1.000 | 1.000 |
| 21 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.271 | 0.975 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xu, H. Probabilistic Moment Bearing Capacity Model and Fragility of Beam-Column Joints with Cast Steel Stiffeners. Buildings 2022, 12, 577. https://doi.org/10.3390/buildings12050577
Li X, Xu H. Probabilistic Moment Bearing Capacity Model and Fragility of Beam-Column Joints with Cast Steel Stiffeners. Buildings. 2022; 12(5):577. https://doi.org/10.3390/buildings12050577
Chicago/Turabian StyleLi, Xinxia, and Hao Xu. 2022. "Probabilistic Moment Bearing Capacity Model and Fragility of Beam-Column Joints with Cast Steel Stiffeners" Buildings 12, no. 5: 577. https://doi.org/10.3390/buildings12050577





