Fatigue Behavior of M20 Torque Shear High-Strength Bolts under Constant-Amplitude Loading
Abstract
:1. Introduction
2. Experimental Study
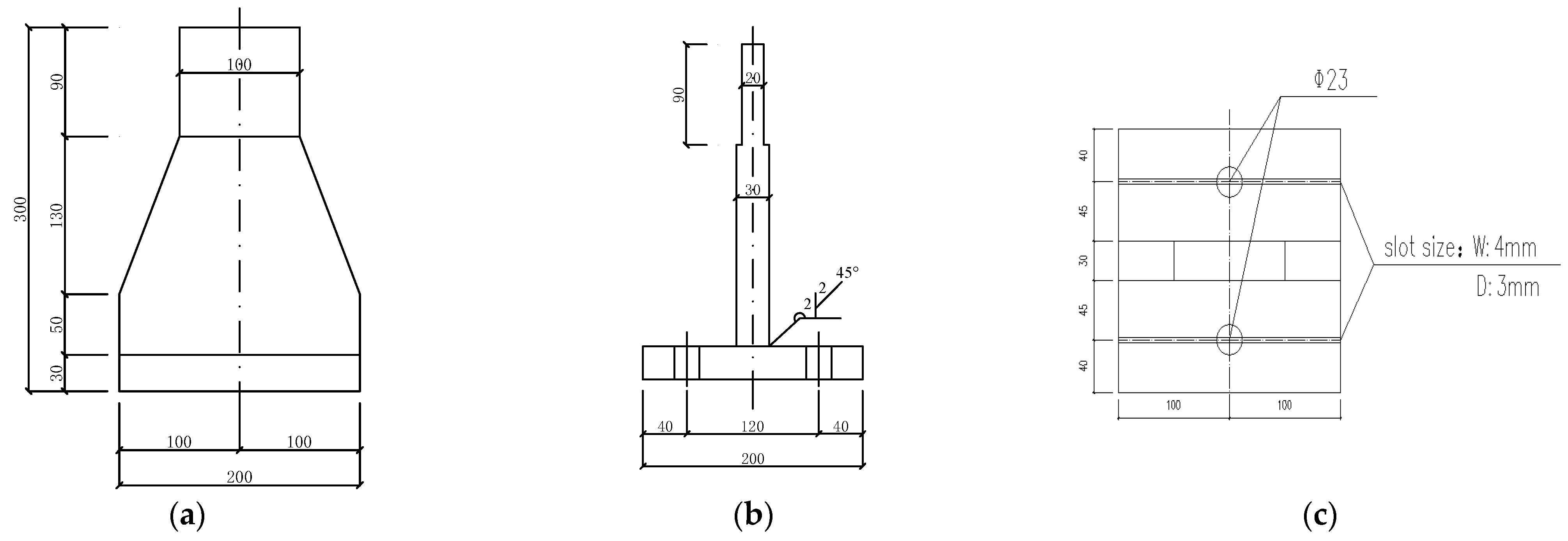
2.1. Specimen Design
2.1.1. M20 Torque Shear High-Strength Bolts
2.1.2. T-Shaped Connector
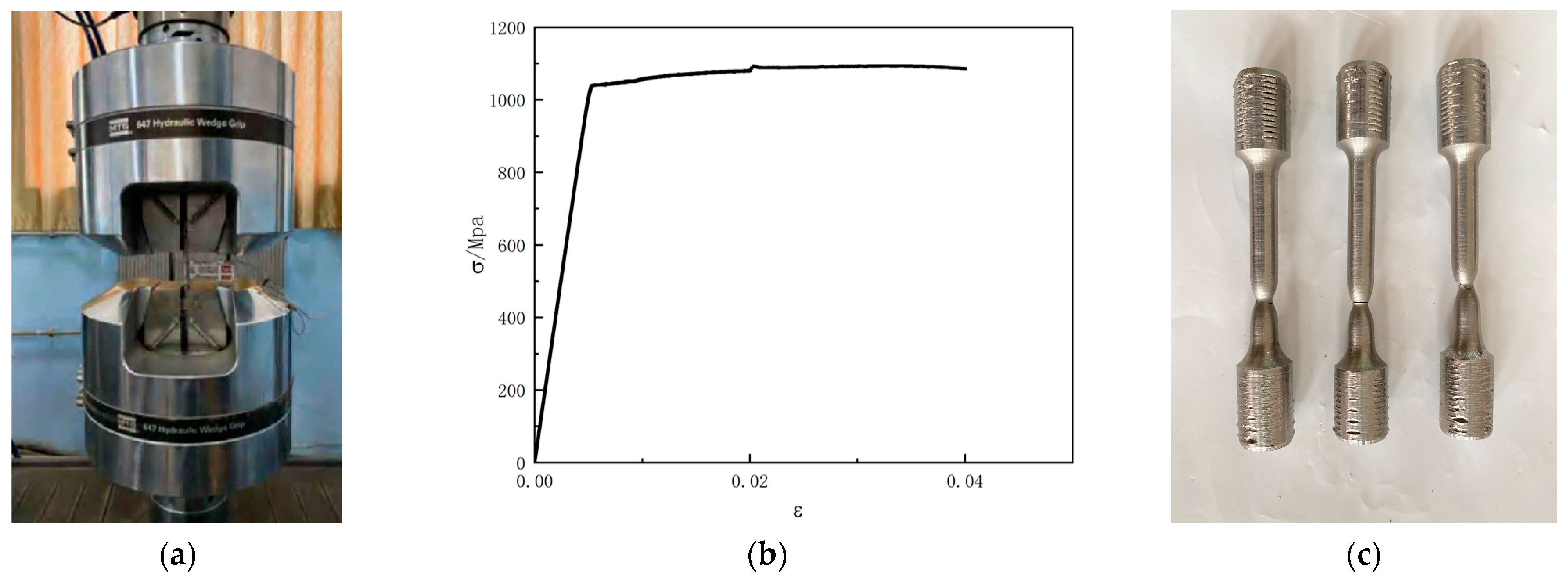
2.2. Material Testing
2.3. Testing-Rig and Loading Procedure
2.4. Experimental Results
3. Numerical Study
3.1. Development of Finite Element Model
3.2. Numerical Results
4. The Calculation Method for Constant-Amplitude Fatigue
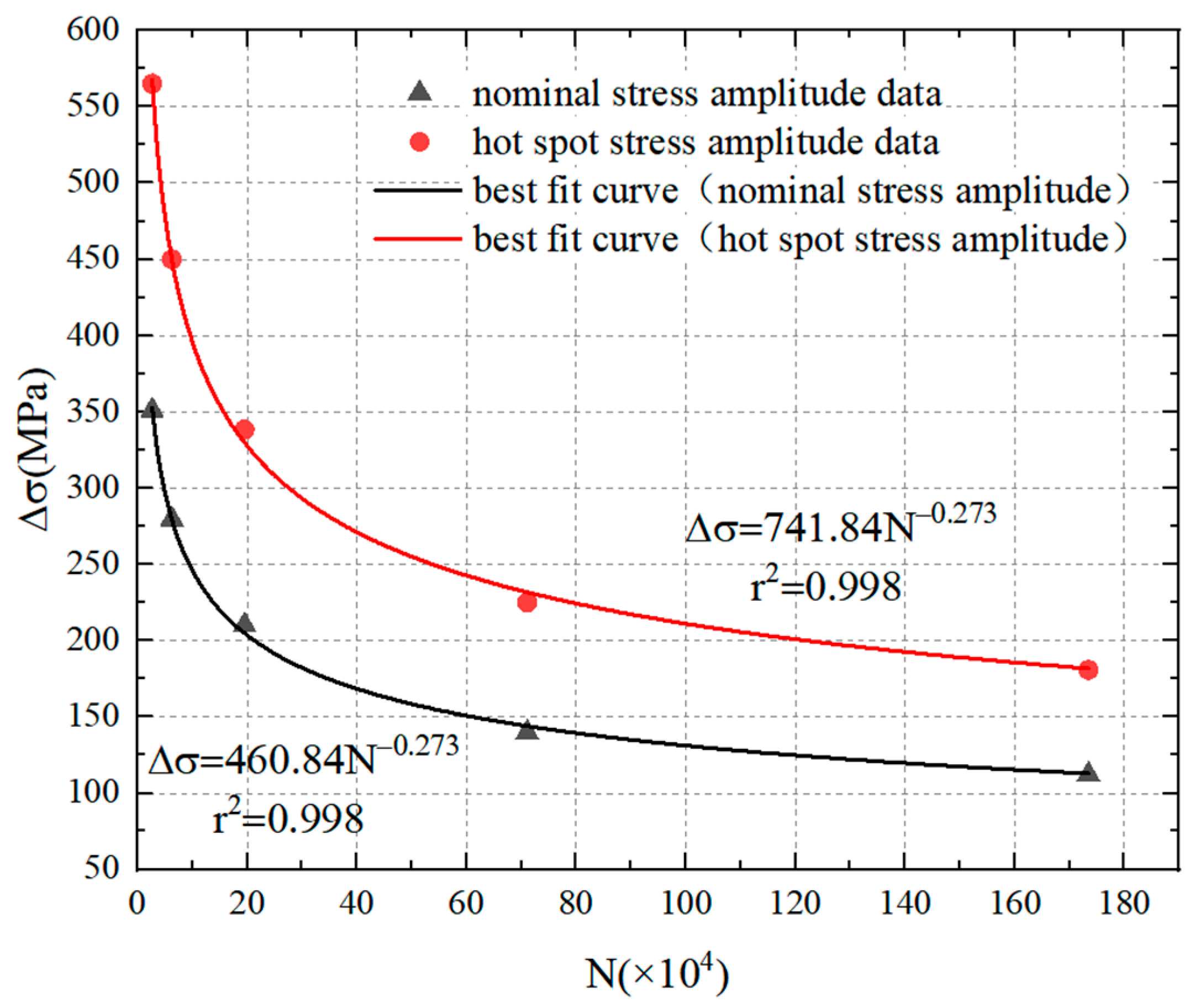
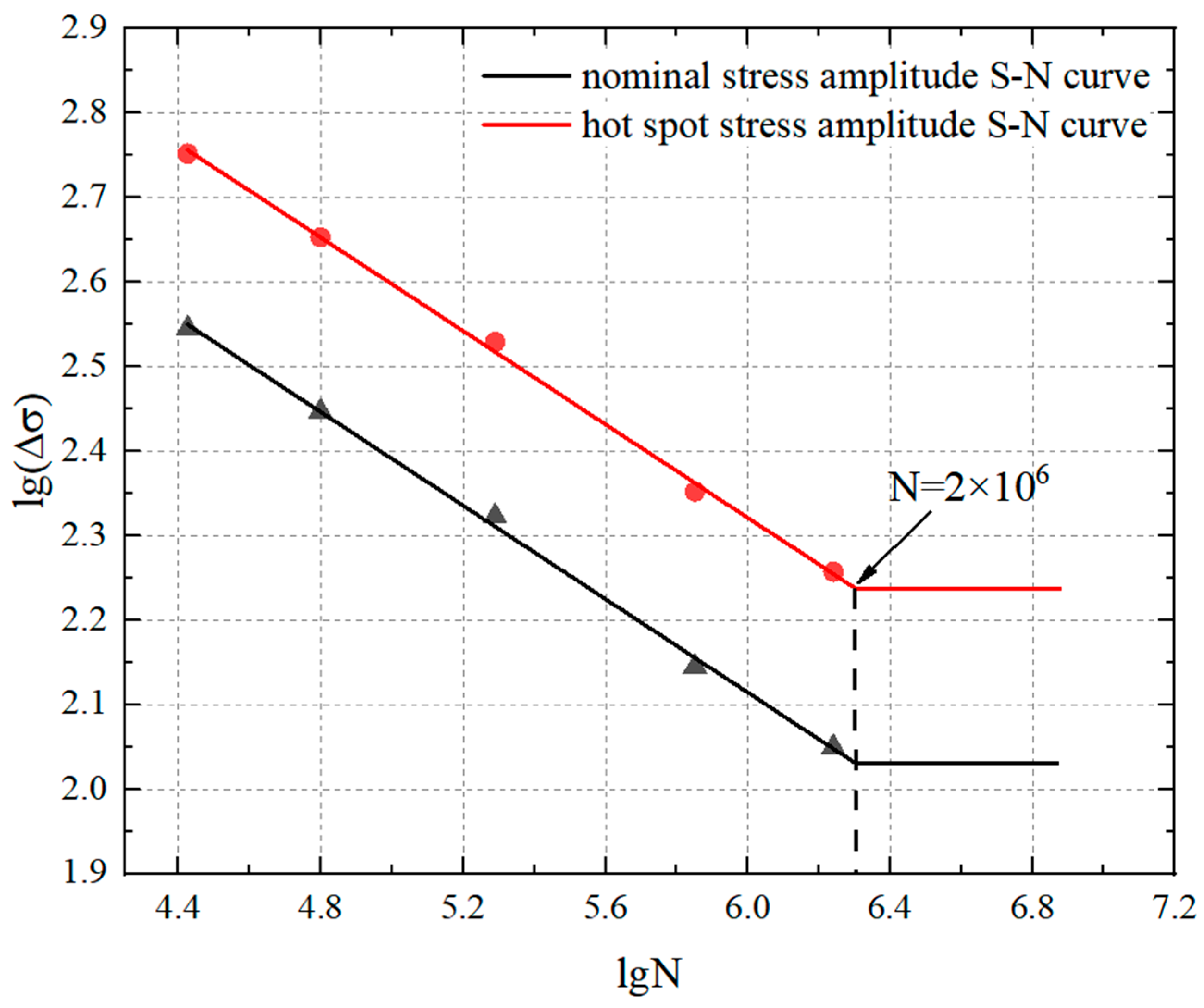
4.1. Allowable Nominal Stress Amplitude
4.2. Allowable Hot-Spot Stress Amplitude
4.3. Results and Discussion
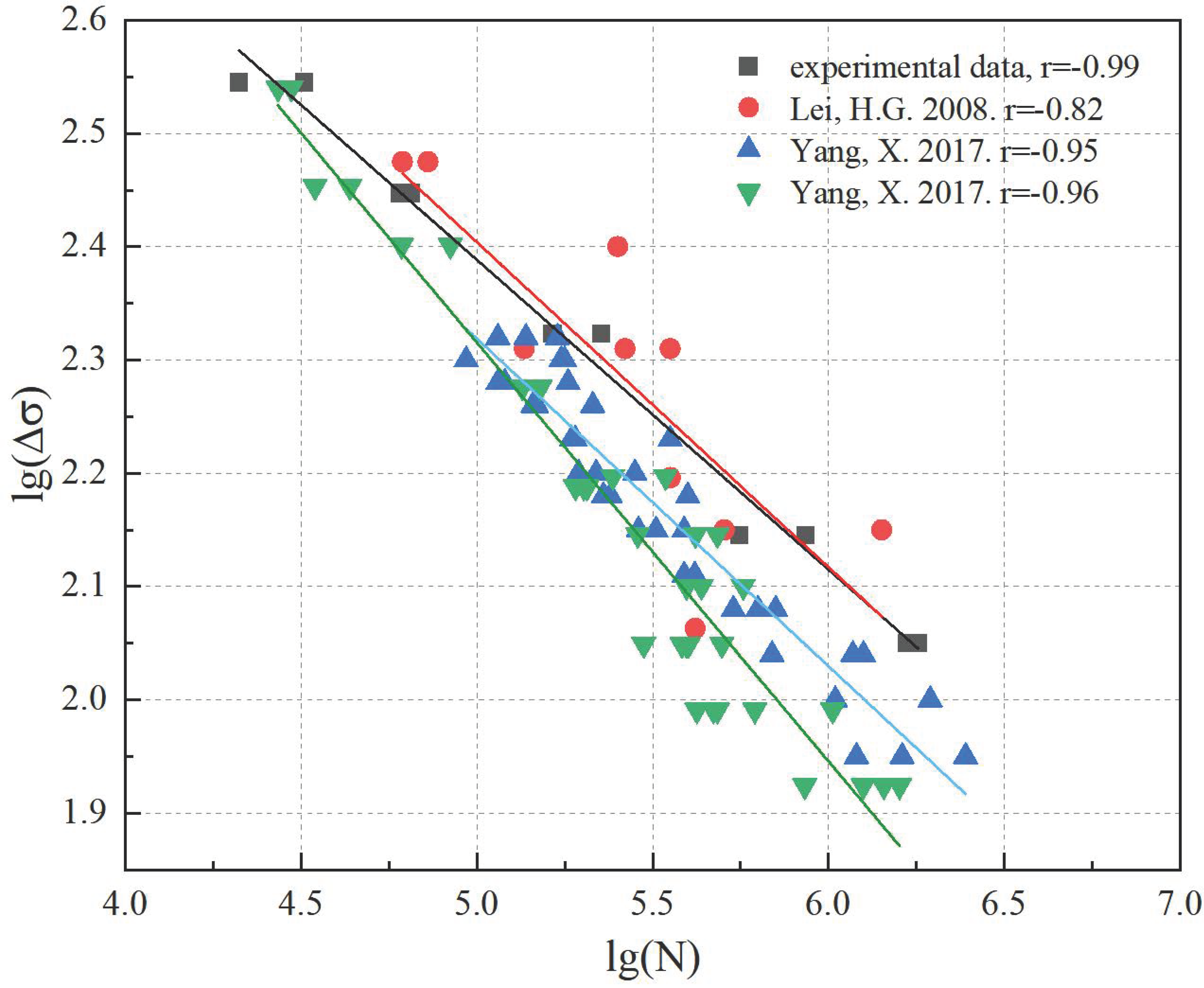
5. Comparison of Existing Design Specifications
6. Fatigue Fracture Analysis
7. Concluding Remarks
- (1)
- The fatigue performance, stress concentration and fracture analysis were analyzed. The allowable nominal stress amplitude of M20 torque-shear type high-strength bolts was 96.371 MPa, while the allowable hot-spot stress amplitude was 283.296 MPa.
- (2)
- Upon comparison, it was found that the allowable stress amplitude of M20 torque shear high-strength bolts is twice the design value obtained from ANSI/AISC 360-16 (2016), and 1.93 times the design value obtained from Eurocode 3 (2005) and GB 50017 (2017). These indicate that the existing design standards are relatively conservative for predicting the fatigue performance of such bolts.
- (3)
- A finite element model was established, and the corresponding hot-spot stress and the amplitude of such bolts were obtained. The numerical results suggested that the maximum stress for each bolt was located at the root of the first exposed thread according to the stress nephogram. The fracture positions of the bolts were the same as those of the experimental results.
- (4)
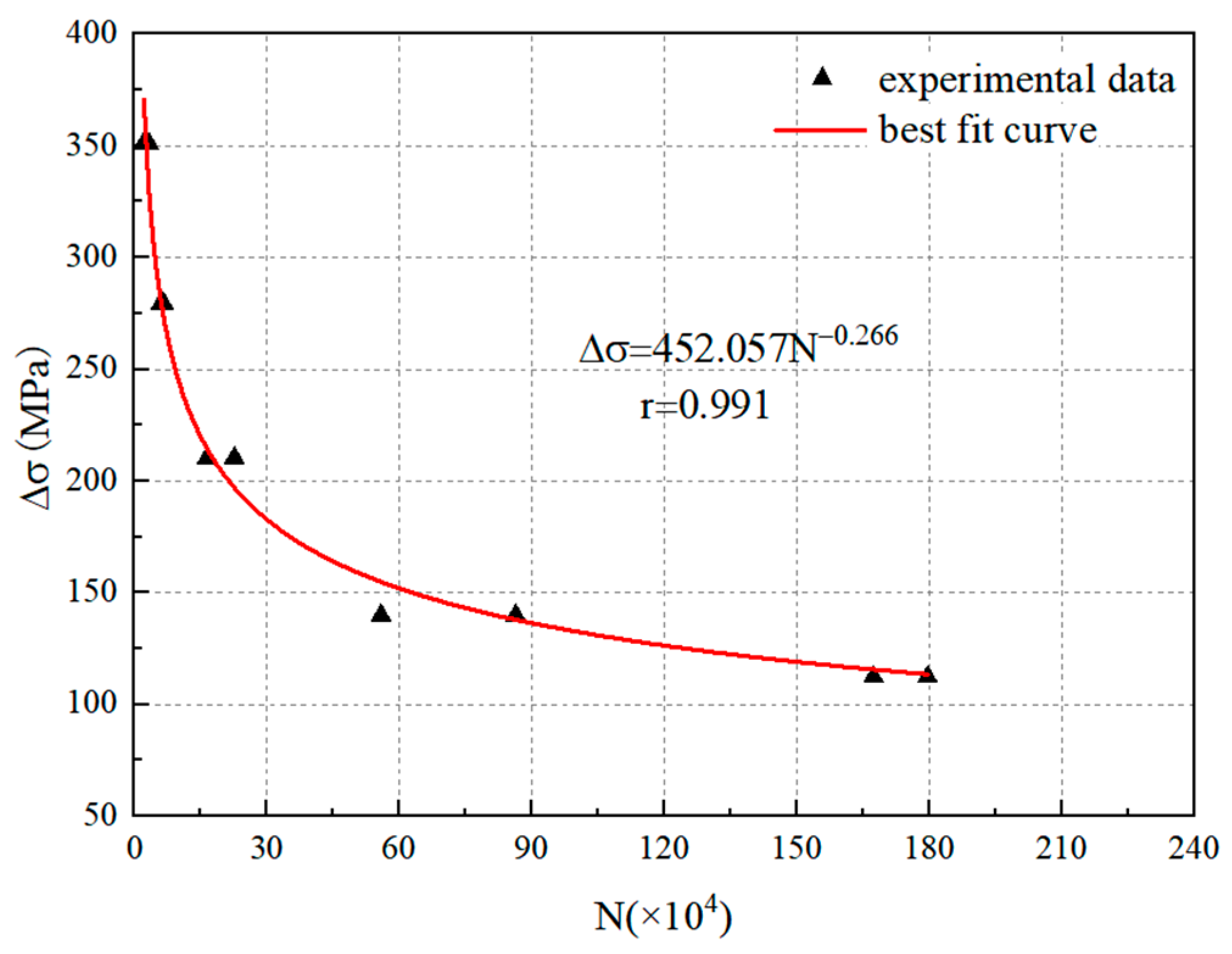
- Fatigue fracture analysis was conducted, and the influence of stress amplitude on the fatigue fracture of high-tensile bolts was evaluated by analyzing the fatigue fracture under different stress amplitudes. The results suggested that the stress amplitude of M20-1, M20-3 and M20-10 was 351.02 MPa, 279.59 MPa and 112.25 MPa, respectively.
- (5)
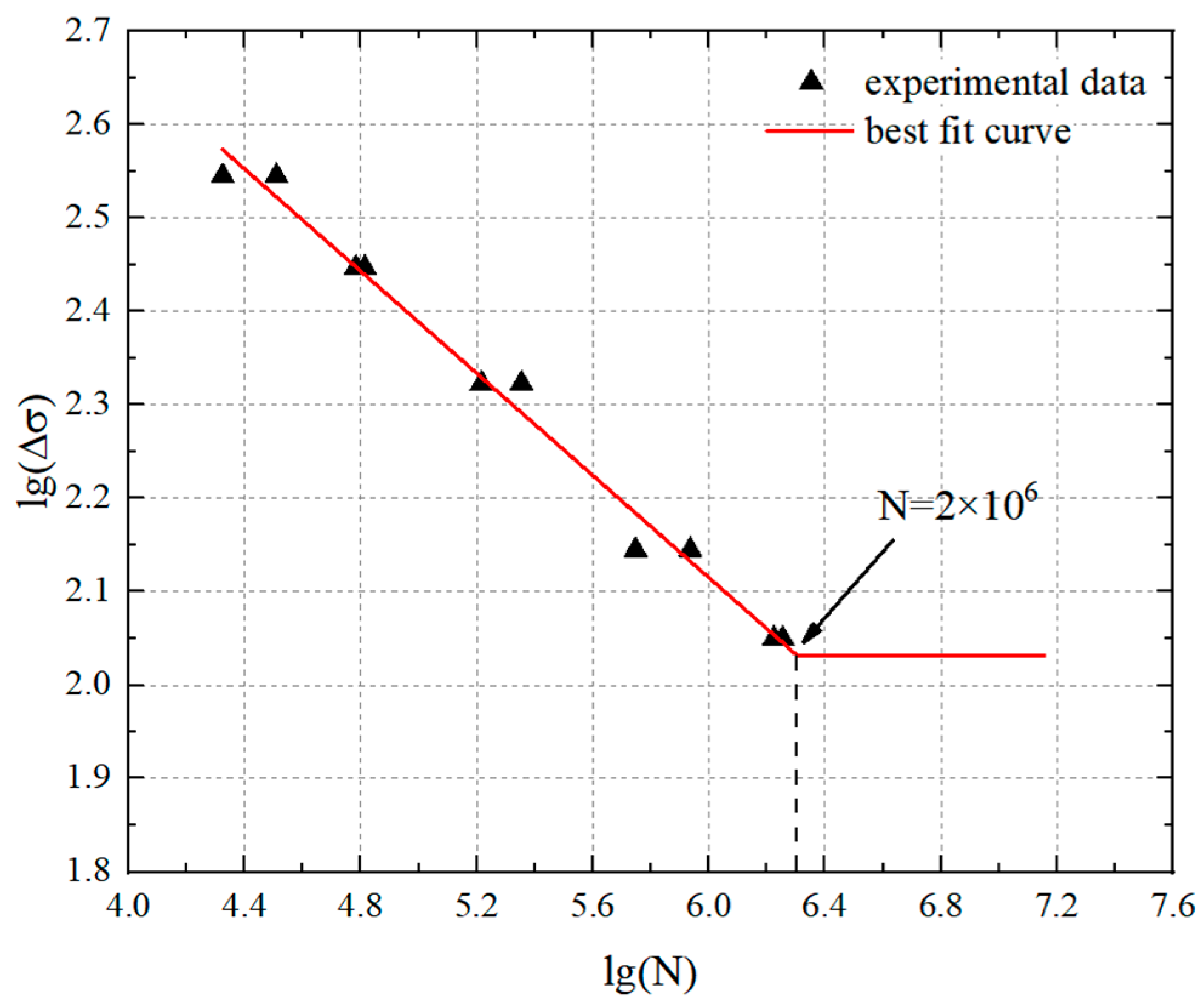
- The S-N curve of torque-shear high strength bolts under constant-amplitude loading was proposed using the hot-spot stress amplitudes.
8. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, H.G. The Theoretical and Experimental Research on Fatigue Performance of High Strength Bolt Connection in Grid Structure with Bolt Sphere Joint. Ph.D. Thesis, Taiyuan University of Technology, Taiyuan, China, 2008. [Google Scholar]
- Yang, X. The Theoretical and Experimental Research on Fatigue Performance of m30 and m39 High Strength Bolts in Grid Structures with Bolt Sphere Joints. Ph.D. Thesis, Taiyuan University of Technology, Taiyuan, China, 2017. [Google Scholar]
- Qiu, B.; Yang, X.; Zhou, Z.; Lei, H.G. Experimental study on fatigue performance of M30 high-strength bolts in bolted spherical joints of grid structures. Eng. Struct. 2020, 205, 110123. [Google Scholar] [CrossRef]
- Yang, X.; Lei, H.G.; Chen, Y.F. Constant amplitude fatigue test research on M20 high strength bolts in grid structure with bolt-sphere joints. Adv. Struct. Eng. 2016, 20, 1466–1475. [Google Scholar] [CrossRef]
- Yang, X.; Lei, H.G. Constant amplitude fatigue test of high strength bolts in grid structures with bolt-sphere joints. Steel Compos. Struct. Int. J. 2017, 25, 571–579. [Google Scholar] [CrossRef]
- Jiao, J.; Liu, Z.; Guo, Q.; Liu, Y.; Lei, H.G. Constant-amplitude fatigue behavior of m24 high-strength bolt of end-plate flange connection. Structures 2021, 34, 2041–2053. [Google Scholar] [CrossRef]
- Zhao, S.B. Fatigue-Resistant Design: A Handbook; Machinery Industry Press: South Norwalk, CT, USA, 2015. [Google Scholar]
- Lochan, S.; Mehmanparast, A.; Wintle, J. A review of fatigue performance of bolted connections in offshore wind turbines. Procedia Struct. Integr. 2019, 17, 276–283. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Lei, H.G.; Qiu, B.; Zhang, S.; Wang, G.Q. Experimental study on fatigue performance of m60 high-strength bolts with a huge diameter under constant amplitude applied in bolt–sphere joints of grid structures. Appl. Sci. 2022, 12, 8639. [Google Scholar] [CrossRef]
- Nam, J.; Kim, D.; Kim, K.; Choi, S.; Oh, J.H. Unified fatigue life prediction of bolts with different sizes and lengths under various axial loading conditions. Eng. Fail. Anal. 2022, 131, 105841. [Google Scholar] [CrossRef]
- Maljaars, J.; Euler, M. Fatigue S-N Curves of bolts and bolted connections for application in civil engineering structures. Int. J. Fatigue 2021, 151, 106355. [Google Scholar] [CrossRef]
- Lotsberg, I.; Sigurdsson, G. Hot spot stress SN curve for fatigue analysis of plated structures. J. Offshore Mech. Arct. Eng. 2006, 128, 330–336. [Google Scholar] [CrossRef]
- Redondo, R.; Mehmanparast, A. Numerical analysis of stress distribution in offshore wind turbine m72 bolted connections. Metals 2020, 10, 689. [Google Scholar] [CrossRef]
- Nah, H.S.; Choi, S.M. Evaluate the clamping force of torque-shear high strength bolts. Int. J. Steel Struct. 2018, 18, 935–946. [Google Scholar] [CrossRef]
- GB50017-2017; Code for Design of Steel Structures. China Architecture and Building Press: Beijing, China, 2017.
- ANSI/AISC 360–16; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2016.
- EN 1993-1-9; Eurocode 3: Design of Steel Structures-Part 1-9: Fatigue. European Union: Maastricht, The Netherlands, 2005.
- ISO 6892-1; Metallic Materials–Tensile Testing–Part 1: Method of Test at Room Temperature. International Standard: Geneva, Switzerland, 2019.
- ABAQUS. Analysis User’s Manual-Version 6.14-2; ABAQUS Inc.: Palo Alto, CA, USA, 2018. [Google Scholar]
- Gui, X.W.; Zhang, J.D.; Liao, R.D. Finite element simulation study of bolt preload process. Strength Environ. 2021, 48, 9–16. [Google Scholar]








| Specimen No. | Strength (MPa) | Elastic Modulus (GPa) | Elongation Rate | Shrinkage Rate | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| δ(%) | (%) | ψ(%) | (%) | |||||||
| M20-a | 1016.4 | 1022.4 | 1090.4 | 1097.1 | 209.6 | 208.6 | 10.0 | 10.8 | 42.2 | 42.3 |
| M20-b | 1028.1 | 1094.3 | 205.7 | 10.3 | 42.1 | |||||
| M20-c | 1022.6 | 1106.7 | 210.6 | 12.2 | 42.7 | |||||
| Serial No. | Tension (kN) | Nominal Stress (MPa) | Stress Amplitude (MPa) | Frequency (Hz) | Number of Cycles | ||||
|---|---|---|---|---|---|---|---|---|---|
| Fmax | Fmin | σmax | σmin | N (×104) | lg(N) | ||||
| 1 | 123 | 37 | 502.04 | 151.02 | 351.02 | 2.545 | 5 | 2.1068 | 4.324 |
| 2 | 123 | 37 | 502.04 | 151.02 | 351.02 | 2.545 | 5 | 3.2280 | 4.509 |
| 3 | 98 | 29.5 | 400.00 | 120.41 | 279.59 | 2.447 | 5 | 6.0624 | 4.783 |
| 4 | 98 | 29.5 | 400.00 | 120.41 | 279.59 | 2.447 | 5 | 6.5227 | 4.814 |
| 5 | 73.5 | 22 | 300.00 | 89.80 | 210.20 | 2.323 | 5 | 22.5973 | 5.354 |
| 6 | 73.5 | 22 | 300.00 | 89.80 | 210.20 | 2.323 | 5 | 16.4380 | 5.216 |
| 7 | 49 | 14.75 | 200.00 | 60.20 | 139.80 | 2.145 | 7 | 55.8406 | 5.747 |
| 8 | 49 | 14.75 | 200.00 | 60.20 | 139.80 | 2.145 | 7 | 86.3280 | 5.936 |
| 9 | 39.25 | 11.75 | 160.20 | 47.96 | 112.24 | 2.050 | 7 | 167.3545 | 6.224 |
| 10 | 39.25 | 11.75 | 160.20 | 47.96 | 112.24 | 2.050 | 7 | 179.5946 | 6.254 |
| Serial No. | Nominal Stress (MPa) | Hot-Spot Stress (MPa) | Nominal Stress Amplitude (MPa) | Hot-Spot Stress Amplitude (MPa) | Number of Cycles | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| σmax | σmin | max | min | N (×104) | lg(N) | |||||
| 1 | 502.04 | 151.02 | 808.39 | 243.33 | 351.02 | 2.54 | 565.05 | 2.75 | 2.66 | 4.42 |
| 2 | 400.00 | 120.41 | 644.04 | 194.03 | 279.59 | 2.44 | 450.00 | 2.65 | 6.29 | 4.79 |
| 3 | 300.00 | 89.80 | 482.97 | 144.73 | 210.20 | 2.32 | 338.24 | 2.52 | 19.51 | 5.29 |
| 4 | 200.00 | 60.20 | 322.07 | 97.10 | 139.80 | 2.14 | 224.97 | 2.35 | 71.08 | 5.85 |
| 5 | 160.20 | 47.96 | 258.10 | 77.39 | 112.24 | 2.05 | 180.71 | 2.25 | 173.47 | 6.24 |
| Type of Bolts | S-N Equation | 2×106 | 2×106 |
|---|---|---|---|
| M20 bolts used in this study | lg(N) = 13.633 − 3.613lg() ± 0.165 | 96.37 | 283.29 |
| M20 bolts [1] | lg(N) = 13.2414 − 3.4483lg() ± 0.578 | 70.04 | 304.69 |
| M30 bolts [2] | lg(N) = 12.2205 − 3.0872lg() ± 0.4554 | 58.91 | 256.26 |
| M39 bolts [2] | lg(N) = 10.8511 − 2.5131lg() ± 0.5028 | 40.82 | 177.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lei, H.; Shen, Y.; Zhang, S.; Zhou, Z. Fatigue Behavior of M20 Torque Shear High-Strength Bolts under Constant-Amplitude Loading. Buildings 2023, 13, 367. https://doi.org/10.3390/buildings13020367
Zhang L, Lei H, Shen Y, Zhang S, Zhou Z. Fatigue Behavior of M20 Torque Shear High-Strength Bolts under Constant-Amplitude Loading. Buildings. 2023; 13(2):367. https://doi.org/10.3390/buildings13020367
Chicago/Turabian StyleZhang, Liang, Honggang Lei, Yu Shen, Shujia Zhang, and Zichun Zhou. 2023. "Fatigue Behavior of M20 Torque Shear High-Strength Bolts under Constant-Amplitude Loading" Buildings 13, no. 2: 367. https://doi.org/10.3390/buildings13020367










