Influence of Underground Excavation Expansion on Surrounding Rock Characteristics at Intersection of Ventilation Shaft and Tunnel: A Case Study

Abstract

Existing railways can no longer meet transportation requirements, and it is an urgent need to expand old tunnels. However, the existence of ventilations shaft makes expansions face greater risks. This study analyzed the tangential stress change trend during the expansion process through field monitoring, and numerical simulation was used to analyze the changes in stress and displacement under different shaft depths and width–span ratios. The results show that as one approaches the tunnel face, the tangential stress in the arch foot and side wall of the J-2 and J-3 sections gradually increased, and the tangential stress in the arch foot and side wall of the J-1 section gradually decreased. The distance of the tunnel expansion’s influence on tangential stress is about 0.91 to 1.45 times the tunnel span. The largest value of vertical displacement had a linear relationship with shaft depth, and the largest value of horizontal displacement had a quadratic relationship with shaft depth. Changes in the width–span ratio only had a greater impact on the ventilation shaft section. These results can provide a reference for similar in situ expansion projects.

1. Introduction

With China’s economic construction in full swing, the flow of people and materials became more frequent, leading to a surge in traffic demand [1,2,3]. Relying only on new railways cannot effectively alleviate the problem of insufficient railway capacity. Therefore, it is urgent to rebuild and expand the original tunnels. In the actual tunnel expansion process, the situation of passing under the ventilation shaft is often encountered. The stress characteristics and deformation mechanisms of the surrounding rock caused by this are very complicated, and it is worthy of in-depth study.

At present, changes in laws caused by the reconstruction of tunnels without shafts are more in-depth, but research on the changes caused by the reconstruction of tunnels with shafts is relatively lacking. Liu et al. [4] studied the pressure of the vault caused by in situ expansion through numerical calculations. Lai et al. [5] studied the surrounding rock pressure distribution laws of different types of tunnel expansions based on model tests. Lin [6] studied the influence of expansion projects within existing tunnels on the tunnels’ structures and the surrounding rock. Taking the Tai Mo Shan Tunnel Reconstruction and Expansion Project as the background, Zhang [7] studied the impact of blasting and excavation within existing tunnels on adjacent tunnels. Sun et al. [8] analyzed the stress change law of the arch foot and vault during the construction of the Houci expansion tunnel. Jia et al. [9,10] developed an excavation model test system to study the reconstruction and expansion process for existing tunnels. The above literature studied the impact of the expansion process on surrounding rock and relevant issues and did not involve crossing shafts, but the research methods and conclusions have positive significance for reference.

In the tunnel expansion project, the ventilation shaft and the tunnel form a spatial cross structure. This kind of project is currently less researched. However, structures similar to this project are more common in underground engineering projects, such as the horse headgate at the junction of the shaft and the main tunnel, the intersection of the substation’s horizontal tunnel and the main tunnel, the intersection of the pedestrian crossing and the crosswalk with the main tunnel, etc. Deformations and stress distributions in tunnel intersection areas are more complicated than those in common tunnels [11]. Hsiao et al. [12] studied the mechanical properties of the rock mass in the tunnel intersection area with 75 three-dimensional numerical models. Huang et al. [13] proposed a construction method for the connection between the inclined shaft and the main tunnel in the presence of soft surrounding rock. Zhang et al. [14] used FEA to analyze the construction mechanics of the spatial cross structure composed of the expressway and the cross-passage, and they analyzed the stress change trends of the main tunnel and the cross-passage. Some scholars studied the influence of other factors such as the cross-sectional area of the shafts [15,16], the form and number of shafts [17,18], and the inclination angle of shafts [19] on tunnel ventilation and smoke exhaust.

The existing shaft not only destroys the original arching effect of the tunnel, but also causes stress concentration in the crossing section and faces greater construction risks during expansion. Based on the project of the Nanling tunnel in Beipiao city, Liaoning Province, China, this paper reports the results of a study on the influence of in situ expansion on stress and displacement in the presence of a shaft. The research results have certain engineering value and reference significance for similar projects.

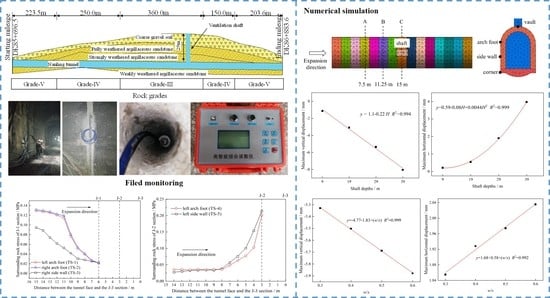
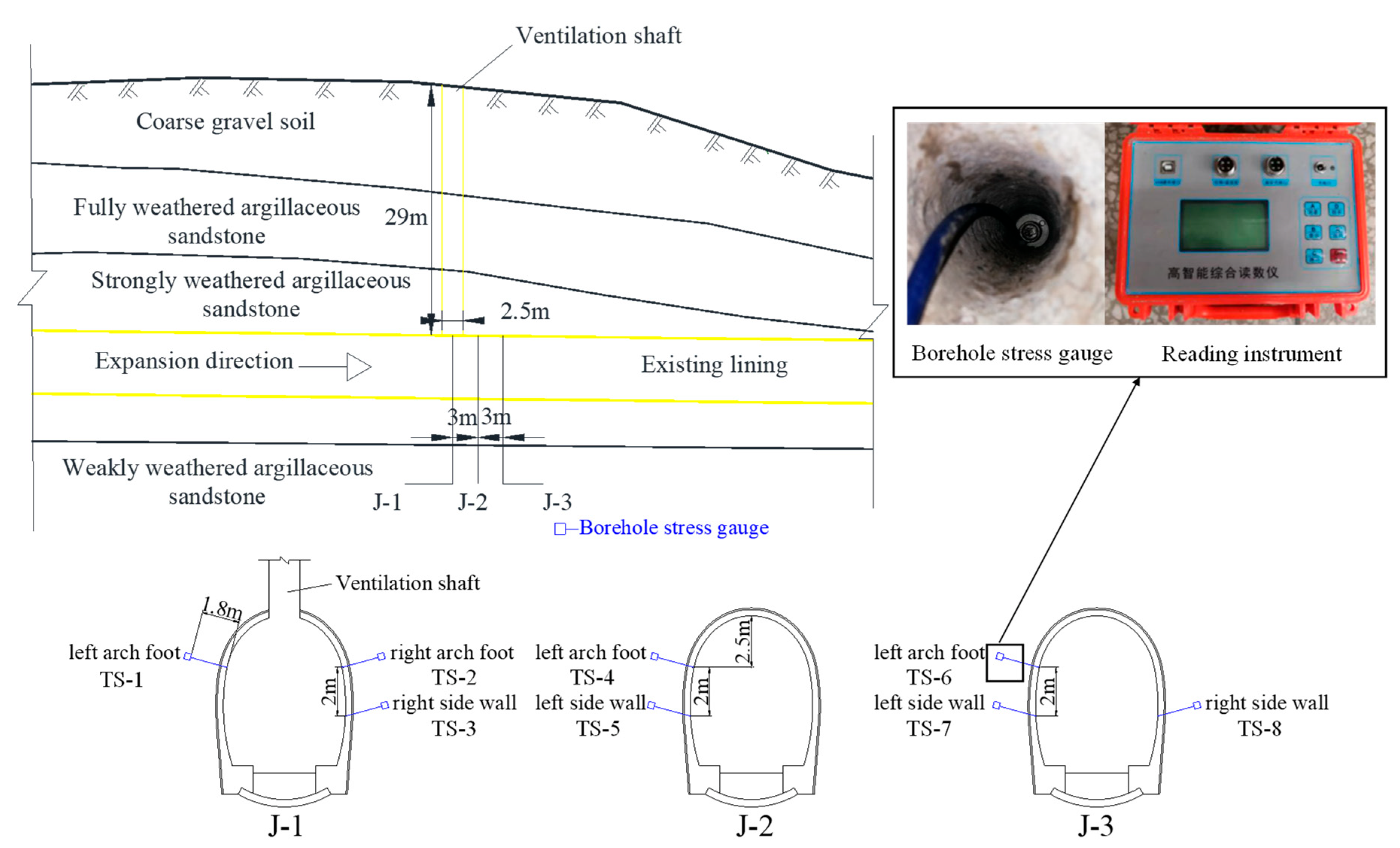
2. Project Overview

The Nanling tunnel was built in 1924 and is located in the city of Beipiao, Liaoning Province, China. The tunnel lining cracks, dislocation, and corrosion are serious. The starting and ending mileage of the tunnel are DK85+696.5 and DK86+883.6, respectively; the total length is 1187.10 m, and the buried depth is 9.56 m–37.75 m, making it a shallow-buried arched tunnel. According to the China railway tunnel standard, the surrounding rock grades are mainly Ⅲ and IV. The stratum is fully weathered argillaceous sandstone, strongly weathered argillaceous sandstone, and weakly weathered argillaceous sandstone, listed in order from top to bottom. The tunnel is located in the strongly weathered argillaceous sandstone formation, as shown in Figure 1. The tunnel originally had a span of 5.5 m, a height of 8.1 m, and a cross-sectional area of 41.3 m². After the expansion, the tunnel has a span of 7.15 m, a height of 9.25 m, and a cross-sectional area of 64.9 m². The existing lining of the tunnel was C20 concrete with a thickness of 400 mm. After the expansion, the initial lining is C25 concrete with a thickness of 200 mm. The tunnel has a ventilation shaft at DK86+520. The bottom of the shaft intersects and connects with the vault of the tunnel perpendicularly. The sectional dimension of the shaft is 1.5 m × 2.5 m, and the shaft depth is 29 m. Figure 2 is a schematic diagram of the Nanling tunnel.

The whole section method was used to enlarge the tunnel. Depending on the grade of the surrounding rock, each excavation step was 2.4 m~3 m. After excavation, a steel arch frame and lock anchor bolt were used for support.

3. Field Monitoring

3.1. Monitoring Points Layout

To understand changes in stress and reveal the disturbances’ characteristics during the expansion construction, a vibrating wire borehole stress gauge was used to monitor the tangential stress in the ventilation shaft interval on-site. A borehole stress gauge is a kind of vibration string sensor with a special structure. In the process of installation and use, it can be set to any position within 14 m in the borehole according to need, and one can choose the direction of force measurement. Three monitoring sections on DK86+520, DK86+523, and DK86+526 were set up, the section numbers were J-1, J-2, and J-3, respectively, and the spacing between each monitoring section was 3 m. The stress gauges were placed in the arch foot and side wall of each monitoring section. However, the stress gauges could not be placed in the right-side wall of the J-2 section due to the existence of vehicle-avoidance holes there. The locations of the monitoring points are shown in Figure 3; a total of eight stress gauges were arranged and numbered TS-1 to TS-8.

The scene installation process is shown in Figure 4. The monitoring points were arranged one month before tunnel expansion. The specific installation process is as follows: first, the steel bar was threaded into the tool tube, inserted into the central groove of the stress gauge tail, and the tool tube was then used to send the stress gauge to the specified depth in the borehole. The cable plug of the stress gauge was connected to the reading instrument, the deviation value was displayed, and zero adjustments were selected. The steel bar was pulled out, and the tool tube was left in the borehole as protection for the line during blasting for the expansion. When the frequency was stable, the frequency of the stress gauge was recorded as the initial frequency. After that, the stress value increased by the surrounding rock were directly read out by operating the reading instrument. By monitoring the development of the tangential stress in the shaft intervals during the forward advancement of the tunnel face, the influence of tunnel expansion on the surrounding rock in the shaft was analyzed.

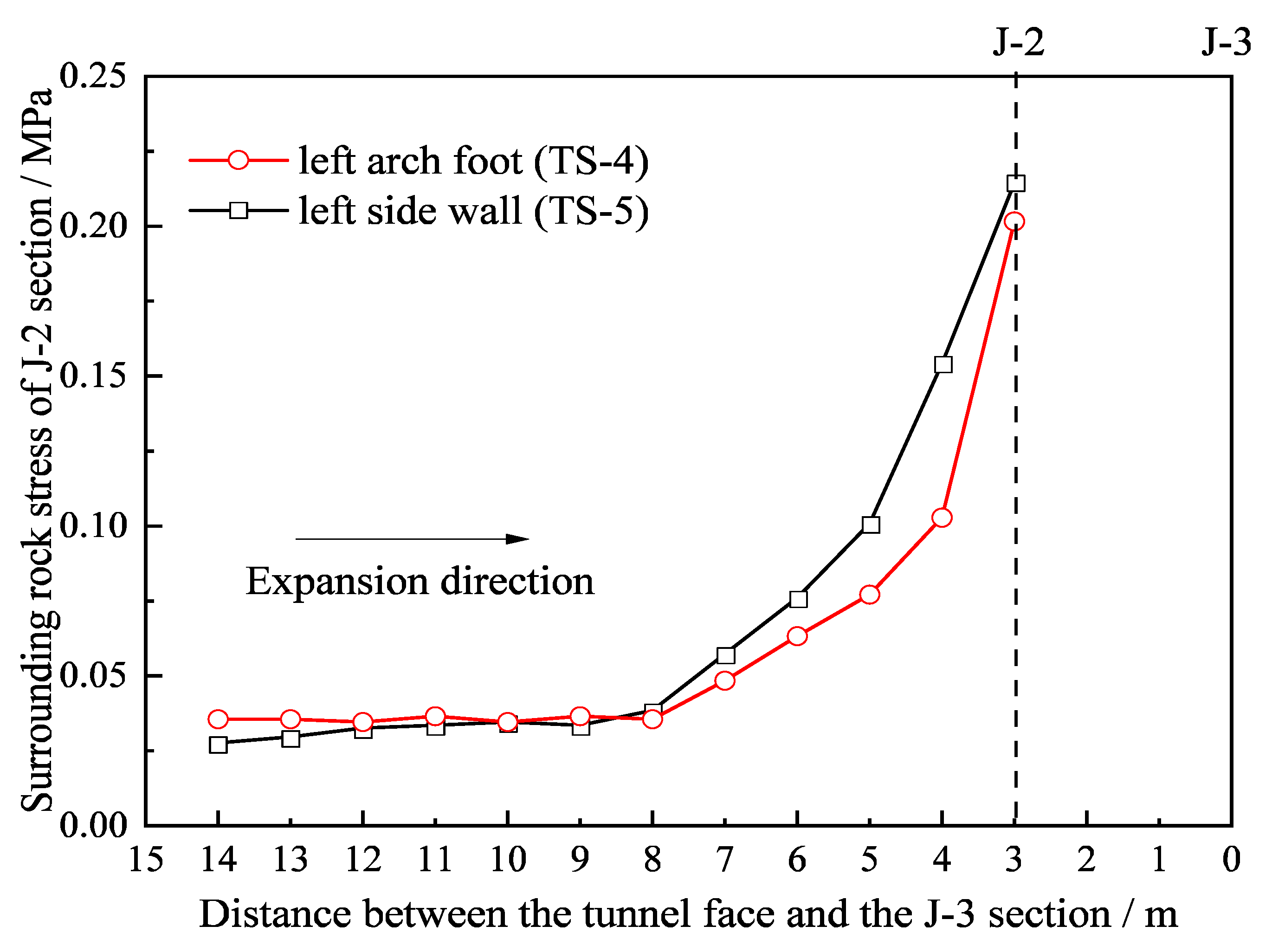
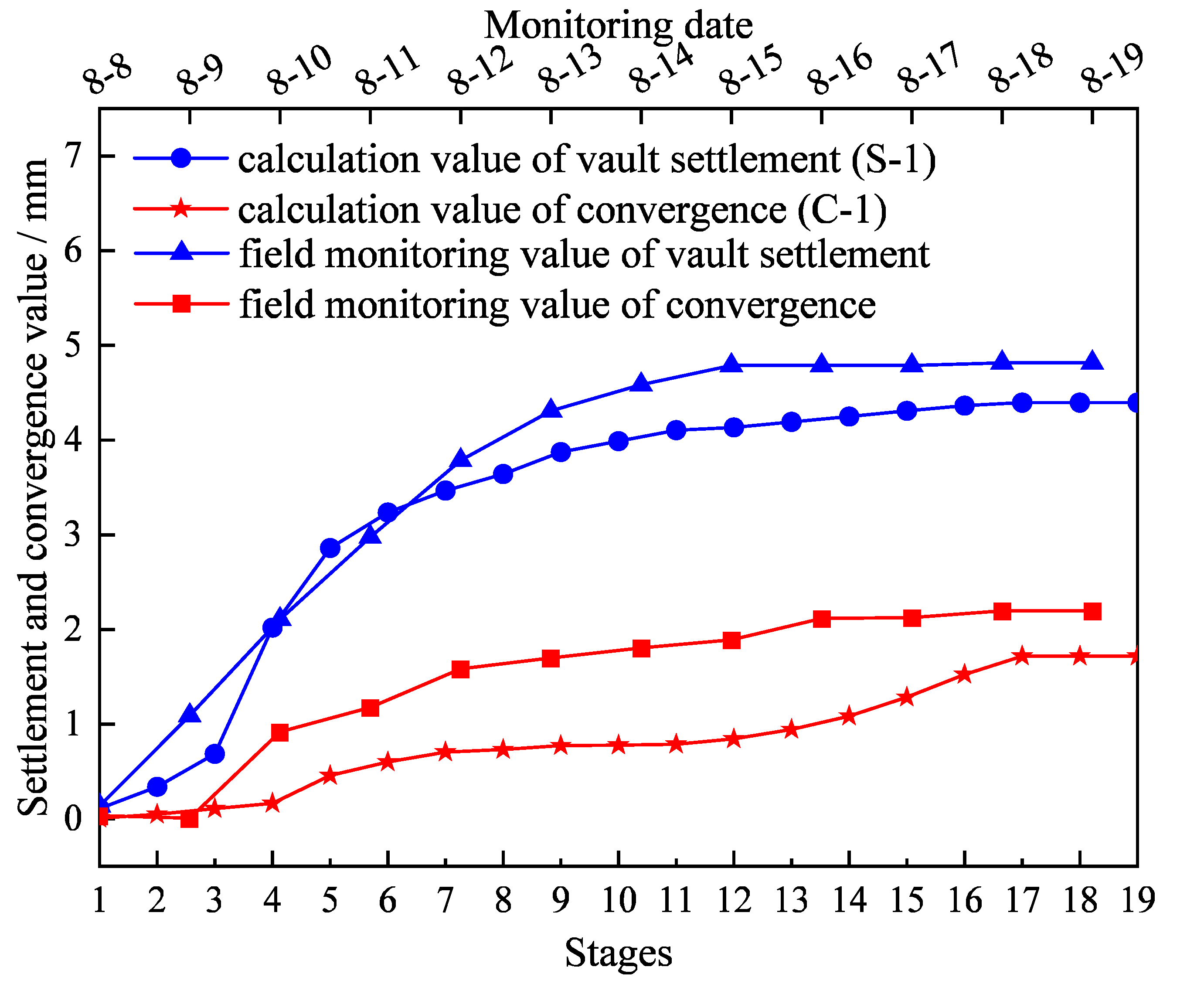
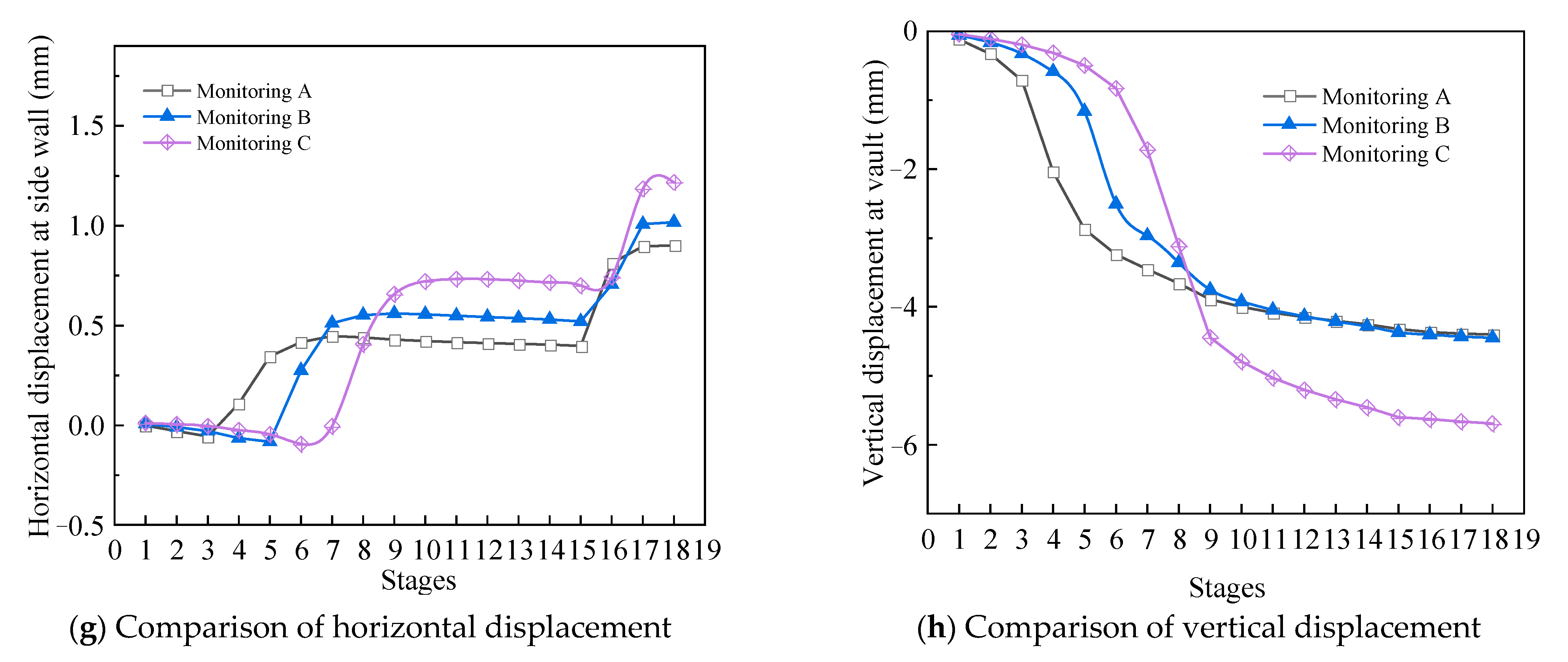
3.2. Analysis of Monitoring Results

The monitoring started at 15 m from the J-3 monitoring section and ended when the tunnel face was excavated to the J-3 monitoring section. Data were recorded every 1 m of excavation. The curve of the tangential stress with the distance between the tunnel face and the J-3 section is shown in Figure 5, Figure 6 and Figure 7, where the J-3 section is at 0 m on the x-axis.

Figure 5 shows that as the tunnel face approached J-1, the tangential stress in the arch foot and side wall of the J-1 section gradually decreased. During the entire expansion process, the tangential stress in the arch foot was always greater than that of the side wall, and the tangential stress distribution of the left and right arch feet were more symmetrical. In the first 4 m of expansion, the tangential stress in the arch foot decreased more gently, and then, as expansion continued, the tangential stress of the arch foot decreased more. At this time, the distance between the tunnel face and the J-1 section was 5 m, which was 0.91 times the existing tunnel’s span. After the expansion, the maximum tangential stress in the arch foot was 0.13 MPa, and the maximum tangential stress in the side wall was 0.09 MPa.

Figure 6 shows that as the tunnel face approached J-2, the tangential stresses in the arch foot and side wall of the J-2 section had the same changing trend, and both increased with excavation distance. In the first 6 m of expansion, the growth rate of the tangential stress in the arch foot and the side wall was relatively gentle. When the tunnel face was 5 m before the J-2 section, the tangential stress redistribution in the J-2 section intensified, and the stress’s growth rate significantly accelerated. At this time, the distance between the tunnel face and J-2 was 0.91 times the existing tunnel’s span. After the expansion, the maximum tangential stress in the arch foot was 0.20 MPa, and the maximum tangential stress in the side wall was 0.21 MPa.

Figure 7 shows that as the tunnel face approached J-3, the tangential stress change trend in the J-3 section was similar to that of the J-2 section, and the tangential stress in the arch foot and side wall gradually increased. In the first 5 m of expansion, the growth rate of the tangential stress in the arch foot and the side wall was relatively gentle. When the tunnel face was 8 m before the J-3 section, the stress’s growth rate significantly accelerated. At this time, the distance between the tunnel face and J-3 was 1.45 times the existing tunnel’s span. After the expansion, the maximum tangential stress in the arch foot was 0.22 MPa, and the maximum tangential stress in the side wall was 0.39 MPa.

The excavation of a new tunnel changed the geometry of the original rock mass, which caused radial excavation and unloading of the rock mass on the boundary of the excavation, resulting in tangential stress concentration [20]. As the tunnel face approached J-3, the tangential stress in the arch foot and side wall of the J-2 and J-3 sections gradually increased; the tangential stress in the arch foot and side wall of the J-1 section gradually decreased. This paper argues that this was due to the existence of the shaft, which prevented the pressure arch of the tunnel from closing. When the distance between the tunnel face and monitoring section was about 0.91 to 1.45 times of the existing tunnel’s span, the growth rate of tangential stress in the surrounding rock increased obviously.

4. Finite Element Analysis (FEA) of the Expansion Tunnel

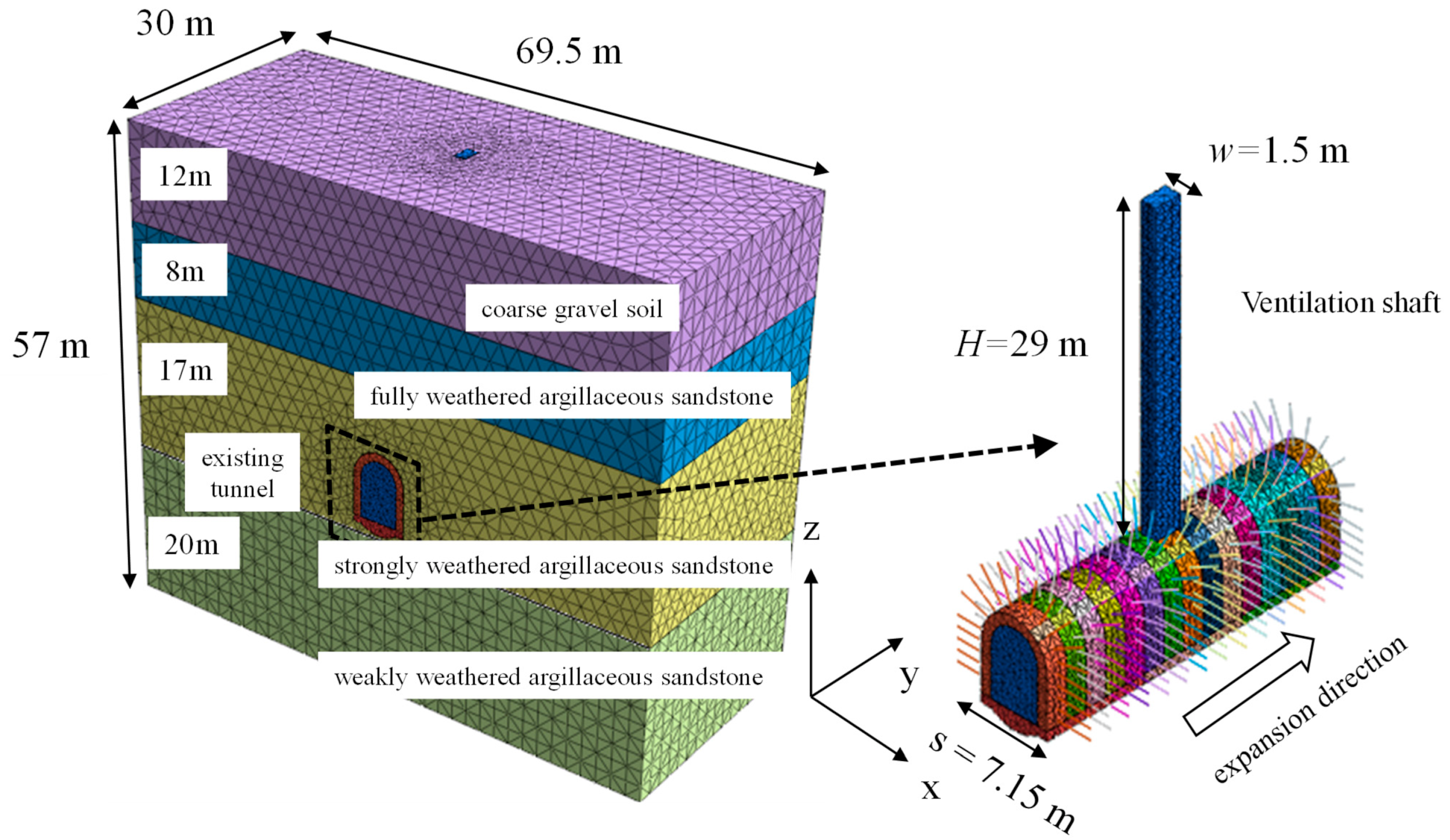
4.1. Finite Element Model

Given the limited field test conditions, to comprehensively analyze the influence of the shaft’s parameters on stress and displacement during the tunnel expansion process, a three-dimensional finite model was established in this study. The Midas GTS NX finite element software was used to establish the numerical model [21]. First, the changes in the stress and displacement during the expansion of the tunnel were studied, and then the influence of the shaft depths (H) and those of the width–span ratios (w/s) on the characteristics of the surrounding rock were also analyzed and studied. When taking into account factors such as displacement and stress in the surrounding rock, it is generally appropriate to select a calculation range that is not less than 3 w to 4 w along the tunnel diameter in all directions, where w is the span of the tunnel. Therefore, the horizontal length of the model was 69.5 m, the vertical length was 57 m, and the longitudinal length was 30 m. The dimensions of the tunnels and supporting structures were consistent with the actual project. The upper surface of the model was a free boundary without constraints, the lower surface was fixed, and the surroundings were normal displacement constraints. The calculation model is shown in Figure 8; the model had 121,206 units and 24,288 nodes.

4.2. Material Property

In this study, solid elements were used to build the rock mass, plate elements were used to build the existing tunnel’s lining and initial support for the expanded tunnel, and beam elements were used to build the anchor. The constitutive relationship of the rock mass adopted the Mohr–Coulomb strength criterion, and the original secondary lining of the tunnel, initial support of the expanded tunnel, and anchor adopted an elastic constitutive relationship. The initial stress field was simulated according to the gravity field. According to the on-site construction situation, the model was divided into 19 construction stages, where stage 1 represented the establishment of the initial stress field, stage 2 to stage 16 represented the expansion of the tunnel boundary, and stage 17 to stage 19 represented the excavation of the tunnel invert. In particular, the “element death” method was adopted to realize the expansion process.

Table 1. Physical and mechanical calculation parameters of surrounding rock.

Name	Elastic Modulus E/MPa	Poisson’s Ratio μ	Weight γ/(kN/m3)	Cohesion c/kPa	Friction Angle φ/º
coarse gravel soil	40	0.3	19	15	20
fully weathered argillaceous sandstone	400	0.3	19.9	50	21
strongly weathered argillaceous sandstone	520	0.28	21.2	60	26
weakly weathered argillaceous sandstone	1000	0.24	22.2	150	35

shows the calculation parameters for the surrounding rock.

Due to the long service time of the existing tunnel, the leakage was serious; the existing lining of the tunnel was corroded and rusted to different degrees. According to the on-site concrete lining strength test, the elastic modulus of the original existing lining was 15.6 MPa.

In the numerical simulation, the simulation of the mortar bolt was considered by using the method of equivalent elastic modulus [22], and the equivalent elastic modulus was calculated as follows:

$$E_1\times A_1+E_2\times A_2=E_{\mathrm{BE}}(A_1+A_2)$$

(1)

where E₁ and A₁ are the elastic modulus and cross-sectional area of the anchor, respectively; E₂ and A₂ are the elastic modulus and cross-sectional area of the mortar body, respectively; E_BE is the elastic modulus of equivalent anchor.

The simulation of the steel grid frame in the initial support of the expansion tunnel was also considered by using the equivalent method. According to the principle of equal compressive rigidity, the elastic modulus of the steel grid frame was converted into the elastic modulus of sprayed concrete, and the calculation formula is:

$$E_{\mathrm{SE}}=E_0+\frac{A_{\mathrm{g}}\times E_{\mathrm{g}}}{A_{\mathrm{c}}}$$

(2)

where E_SE is the elastic modulus of the converted sprayed concrete; E₀ is the elastic modulus of the sprayed concrete; E_g is the elastic modulus of the steel grid frame; A_g is the cross-sectional area of the steel grid frame; A_c is the cross-sectional area of the sprayed concrete.

To ensure construction safety during the expansion process, it was clear that the initial support of the expansion tunnel was the main bearing structure. The initial support and the surrounding rock shared all loads during the construction period, and the secondary lining served as a structural safety reserve, which was not simulated during the construction phase.

Table 2. Mechanical parameters of tunnel supporting structure.

Name	Elastic Modulus E/GPa	Poisson’s Ratio μ	Weight γ/(kN/m3)	Diameter d/mm	Thickness t/mm
original existing lining	15.6	0.27	25	-	400
shaft lining	20	0.27	22	-	300
initial lining	28	0.17	24.5	-	200
anchor of expanded tunnel	83.8	0.3	78	25	-

shows the tunnel supporting structure’s mechanical parameters.

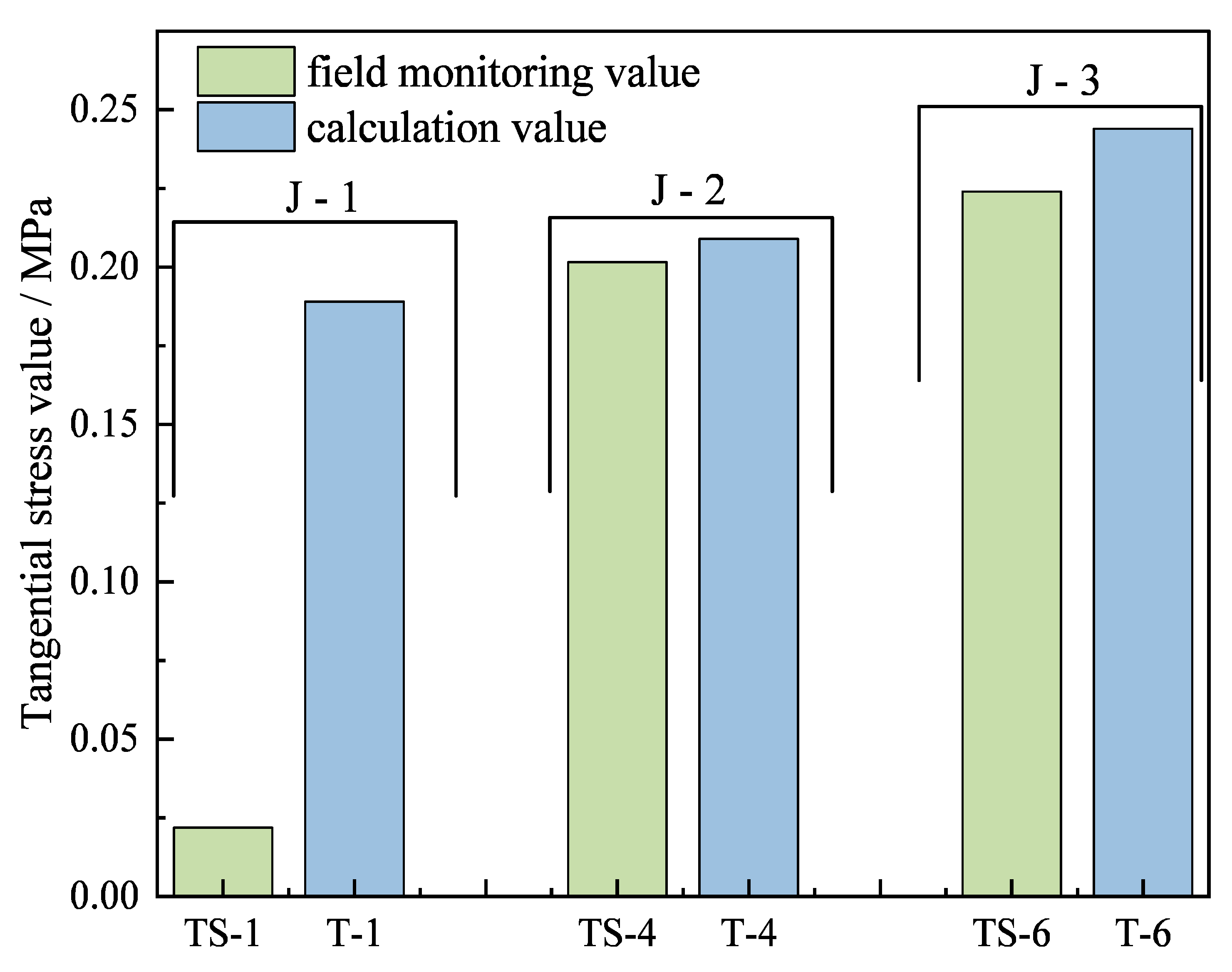
4.3. Validation of Model Accuracy

As shown in Figure 9, the feature points were selected at the same positions as the site monitoring sections. S-1 and C-1 represent the feature points of vault settlement and horizontal convergence, respectively. T1, T2, and T3 represent the tangential stresses of the arch foot.

To verify the rationality of the displacement results of FEA, the calculation values of the vault settlement (S-1) and horizontal convergence (C-1) were compared with the monitoring values from the field. The comparison results are shown in Figure 10. The calculated values of tunnel vault settlement and horizontal convergence were similar to the field monitoring values. The maximum calculated and monitoring values of vault settlement were 4.81 mm and 4.39 mm, respectively, with a difference of 0.42 mm. The maximum calculated and monitoring values of horizontal convergence were 2.19 mm and 1.72 mm, respectively, and the difference between the two was about 0.47 mm. The calculation value is consistent with the monitoring value, which shows that the FEA’s results are accurate.

To verify the rationality of the stress results of FEA, the calculated values of tangential stress (T-1, T-2, and T-3) were compared with the field monitoring values. Tangential stress cannot be generated directly from the post-processing results of FEA; it must be calculated according to the stress transformation formula to convert the data from cartesian coordinates to polar coordinates. The transformation formula is:

$$\begin{array}{c}{\sigma }_{\mathrm{r}}=\frac{{\sigma }_{\mathrm{x}}+{\sigma }_{\mathrm{z}}}{2}+\frac{{\sigma }_{\mathrm{x}}-{\sigma }_{\mathrm{z}}}{2}\cos 2\theta +{\tau }_{\mathrm{xz}}\cos 2\theta \\ {\sigma }_{\mathsf{\theta }}=\frac{{\sigma }_{\mathrm{x}}+{\sigma }_{\mathrm{z}}}{2}-\frac{{\sigma }_{\mathrm{x}}-{\sigma }_{\mathrm{z}}}{2}\cos 2\theta -{\tau }_{\mathrm{xz}}\cos 2\theta \end{array}$$

(3)

where σ_r is radial stress, σ_θ is tangential stress, σ_x is horizontal stress, σ_z is vertical stress, τ_xz is shear stress in the x–z plane, and θ is the angle between the horizon and the line which connects the arch foot to the center of the tunnel.

The comparison results are shown in Figure 11. The calculation values of tangential stress were greater than the field monitoring values. For the J-2 and J-3 sections, the calculation values were close to the field monitoring values, and the difference was within 9%. For the J-1 section, there was a great difference between the calculation value and the field monitoring value. As the calculation principle of FEA is based on continuum mechanics, it cannot simulate the phenomenon of a loose zone formed when the real surrounding rock exceeds its bearing limit. The surrounding rock in the loose zone no longer has bearing capacity; thus, tangential stress decreases.

5. Results and Discussion

The results were analyzed in three aspects. First, the variation trend of surrounding rock in the process of tunnel expansion was studied. Second, the influences of different shaft depths (H = 9 m, 19 m, 29 m, and 39 m) on surrounding rock displacement and stress were analyzed. Finally, the influences of different width span ratios (w/s = 0.3, 0.4, 0.5, and 0.6) on surrounding rock displacement and stress were analyzed.

5.1. Influences of Tunnel Expansion on Surrounding Rock

To explore the construction mechanical properties of the in situ expansion tunnel along the direction of tunnel expansion (Y direction), three monitoring sections (A, B, and C) were arranged at one quarter, three-eighths, and one-half of the whole length of the tunnel. Considering symmetry, four feature points (vault, arch foot, side wall, and corner) were set for each monitoring section; the layout of the monitoring sections and feature points are shown in Figure 12.

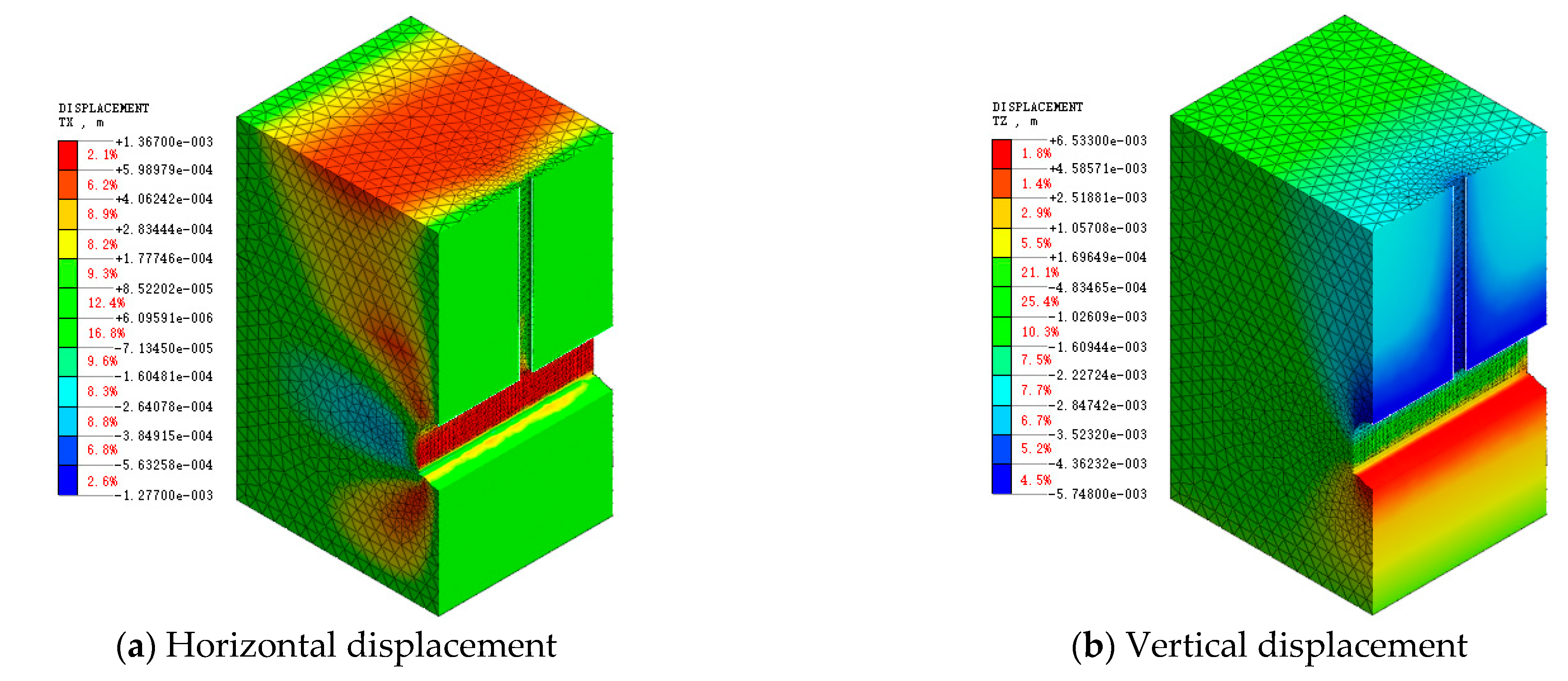
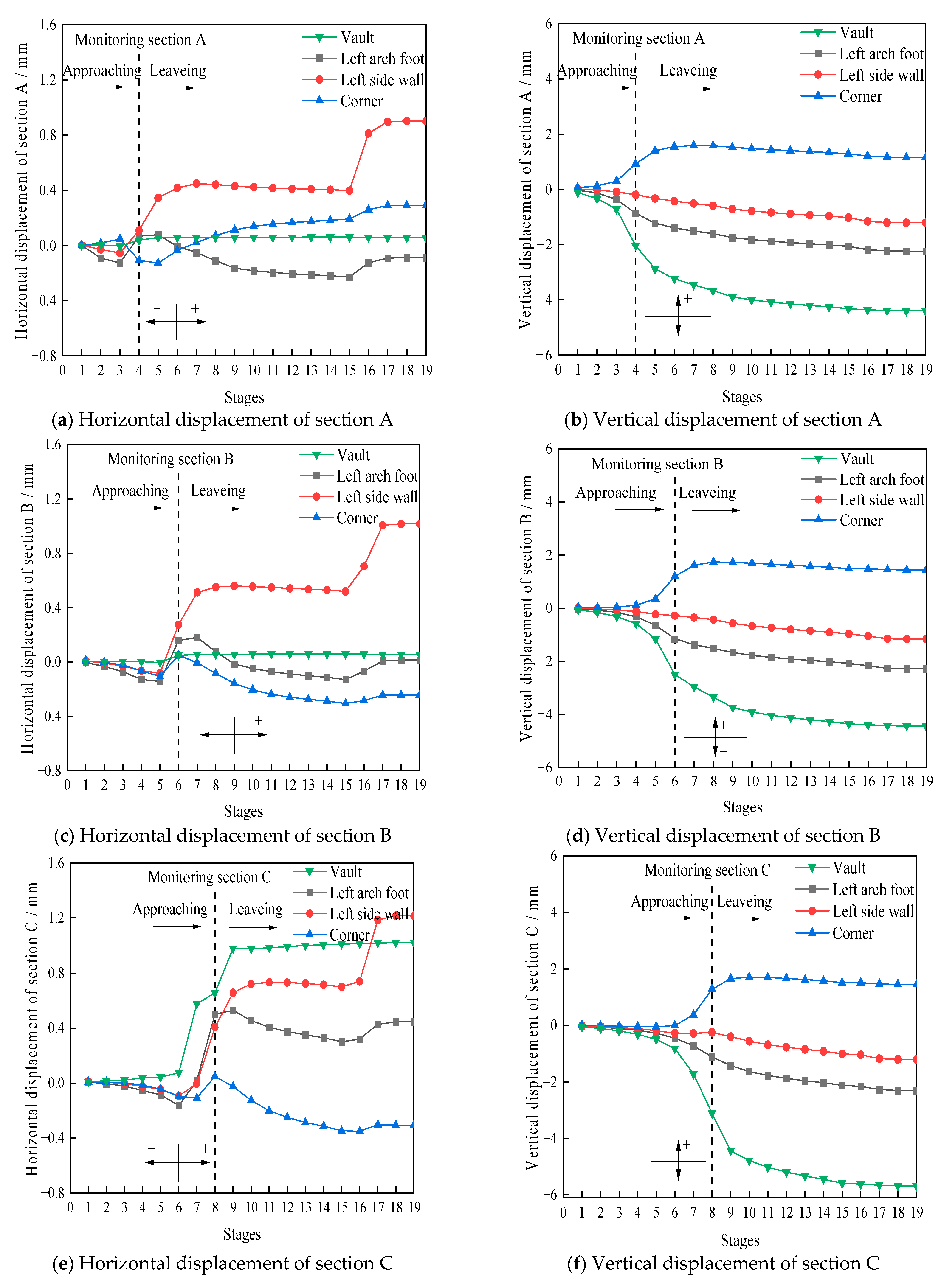
5.1.1. Deformation Analysis of Surrounding Rock

Figure 13 is the displacement cloud map after the tunnel expansion was completed. After the expansion of the tunnel, the surrounding rock as a whole showed intrusive deformation into the tunnel. The vertical displacement was greater than the horizontal displacement. The maximum horizontal displacement was 1.36 mm, and the maximum vertical displacement was −5.74 mm. Both the maximum horizontal displacement and the maximum vertical displacement were located in monitoring section C.

Figure 14 is the displacement curve of each feature point as the construction stage changed. At the same stage, the horizontal displacement at each feature point on the monitoring sections A and B was as follows: the side wall had the most displacement, the corner and the arch foot had similar degrees of deformation, and the vault had the least displacement. Due to the existence of the shaft in monitoring section C, the arch of the tunnel could not be closed into a ring, which caused the horizontal displacement of the vault to increase rapidly with the expansion and, finally, approach the horizontal displacement of the left side wall. The vertical displacement was manifested as the uplift in the corner, the settlement in the side wall, arch foot, and the vault, and the maximum settlement was in the vault. As the tunnel face approached the monitoring sections, the horizontal and vertical displacement of the surrounding rock gradually increased. When the tunnel face reached monitoring sections, due to the unloading effect of the rock mass, the vertical displacement rate increased rapidly and then stabilized as the tunnel face progressed further. Compared with section A, the maximum horizontal displacement of section C increased by 47.5%, the vault settlement increased by 29.3%, and the existence of a ventilation shaft weakened the stability of surrounding rock during the expansion process.

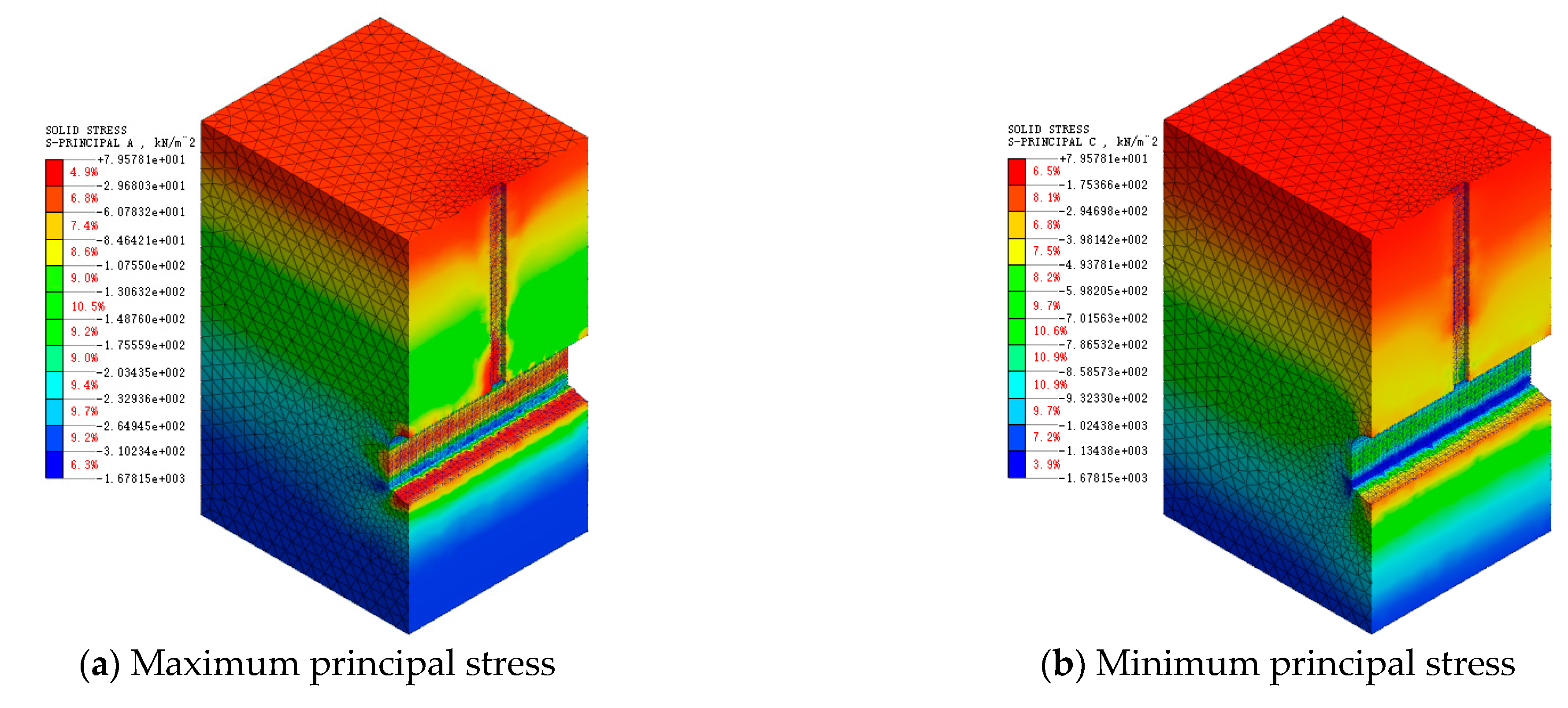
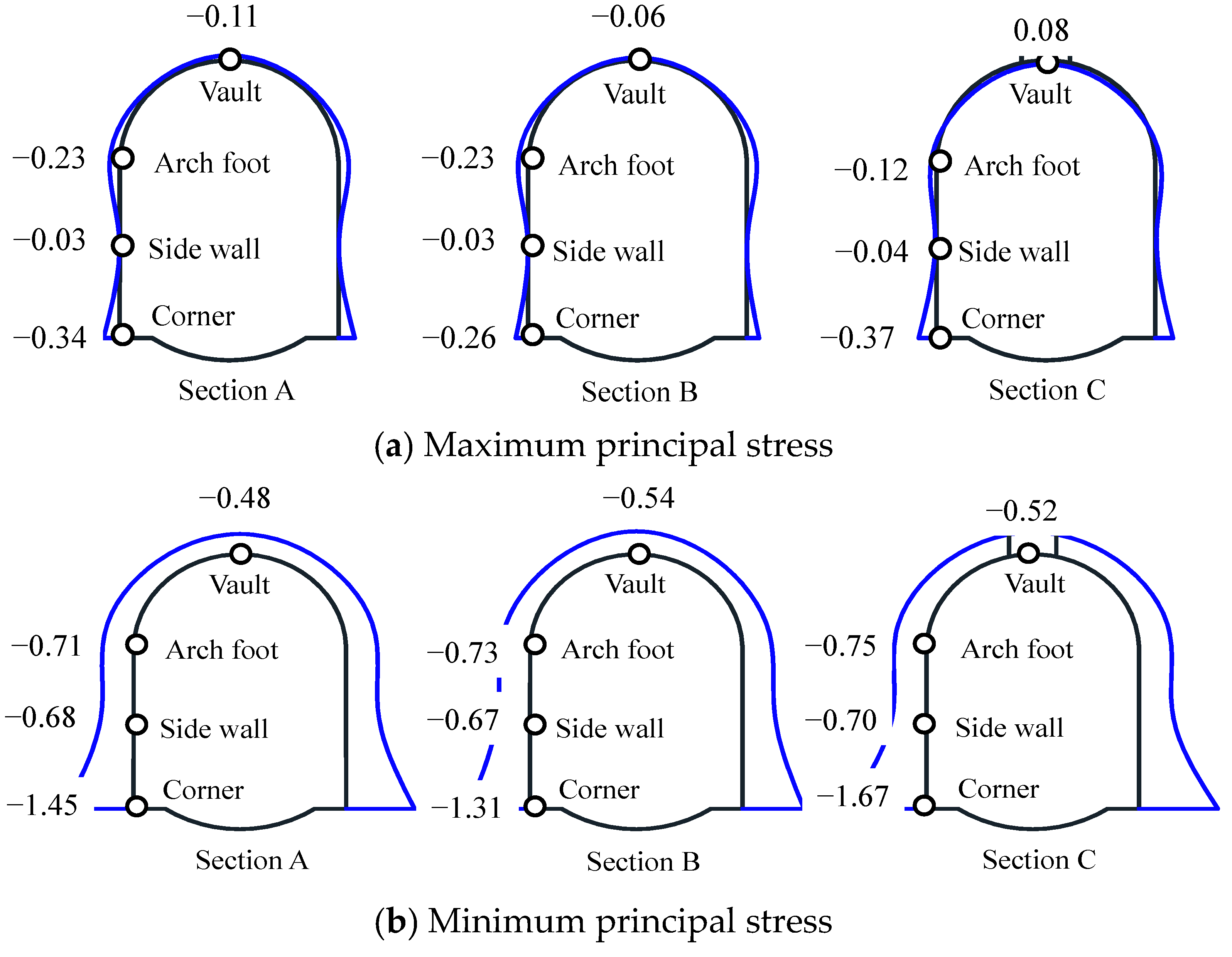
5.1.2. Stress Analysis of Surrounding Rock

Using the stress conversion formula, it takes many of calculations to convert all of the stress results of FEA into radial stress and tangential stress. Therefore, the calculation results of maximum and minimum principal stress in post-processing were selected for stress response analysis. Figure 15 is the cloud map of principal stress after the tunnel expansion was completed. The existence of the ventilation shaft caused the stress release of the surrounding rock of the vault, which changed the stress state of the surrounding rock from compression to tension. At the same time, the ventilation shaft destroyed the arching effect of the tunnel, and the self-supporting capacity of the surrounding rock could not be fully utilized, resulting in a greater concentration of compressive stress in the tunnel.

Figure 16 shows the principal stress distribution within the monitoring sections after tunnel expansion was completed. The maximum and minimum principal stresses in the vault, arch foot, side wall, and corner of monitoring sections A and B were all compressive stresses, and there were concentrations of compressive stress in the corners. The maximum principal stress values of the monitoring sections A and B are ordered as the corner > arch foot > vault > side wall, and the minimum principal stress values are ordered as the corner > arch foot > side wall > vault. Due to the existence of a ventilation shaft, tensile stress concentration existed in the maximum principal stress of the vault in monitoring section C. During the expansion of the tunnel, the maximum principal stress value was 0.08 MPa, which is tensile stress, located in the vault of monitoring section C, and the minimum principal stress value was −1.67 MPa, which is compressive stress, located in the corner of monitoring section C. As the tunnel face approached, the maximum principal stress of the vault in monitoring section C gradually decreased and changed from compressive stress to tensile stress.

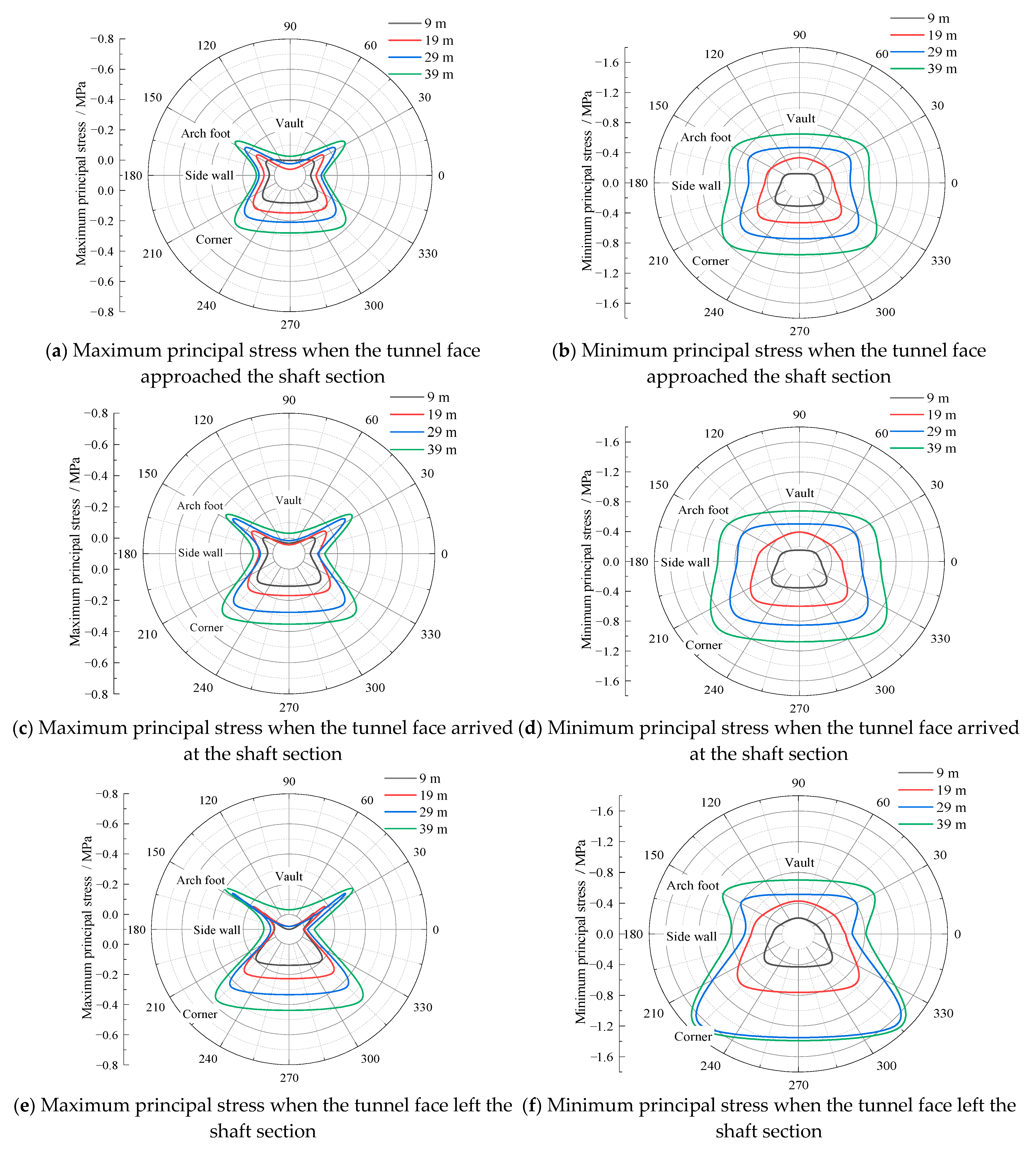
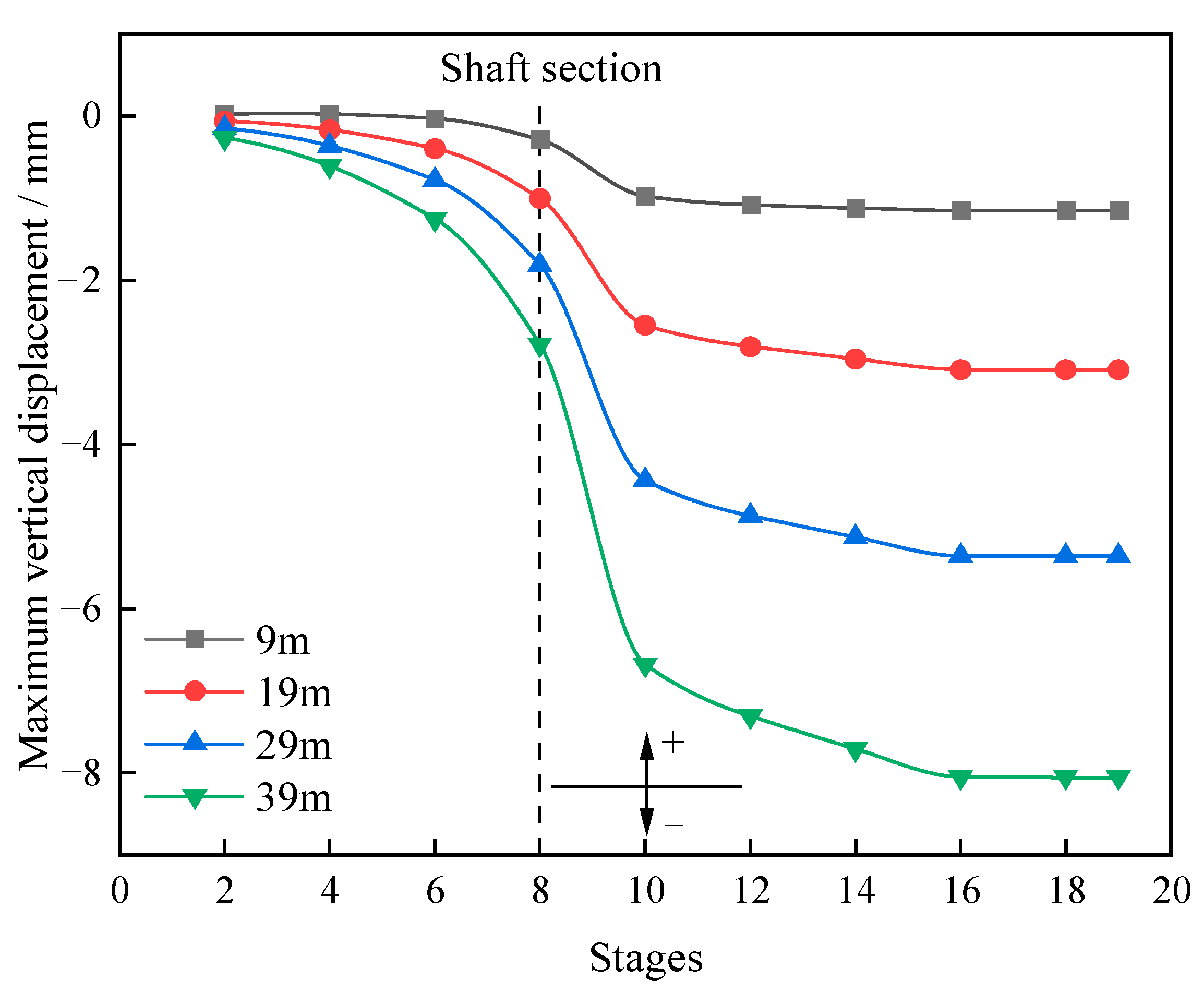
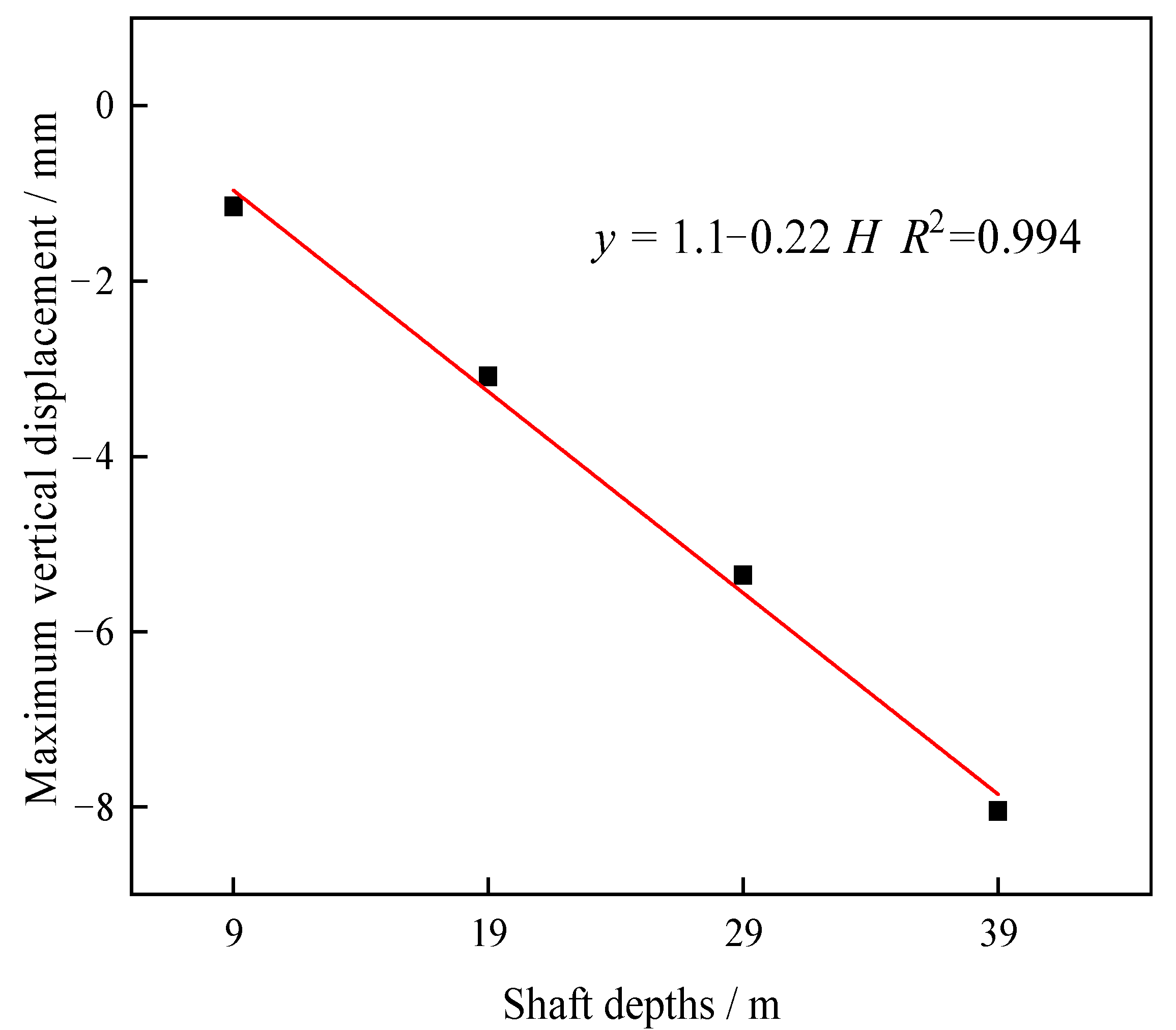
5.2. Influences of Shaft Depths

(1)

Principal stress distributions

The above analysis shows that the displacement and stress of monitoring section C were greatly affected by the expansion of the tunnel; thus, the follow-up analysis focused on the study of the surrounding rock characteristics in the shaft section. Figure 17 shows the variation trends of the principal stresses in the vault, arch foot, side wall, and corner with the excavation process at different shaft depths.

The stress variation trends of feature points at different positions varied at different shaft depths. At shaft depths between 9 m and 29 m, the maximum principal stress of the vault after tunnel expansion was tensile stress. The shallower the shaft depth, the greater the tensile stress was in the vault. At a shaft depth of 9 m, the tensile stress of the vault was five times higher than that of the stress at 29 m. The surrounding rock at the arch foot and corner were in a state of stress concentration, and the maximum and minimum principal stresses both increased as the tunnel face advanced. At shaft depths between 9 m and 19 m, the maximum principal stress of the side wall changed from compressive stress to tensile stress, and there was a risk of failure of the surrounding rock. At shaft depths between 29 m and 39 m, the maximum principal stress of the side wall was always compressive, and the minimum principal stress decreased with excavation.

Table 3. Greatest values of principal stresses at different depths (unit: MPa).

Shaft Depth	Maximum Principal Stress	Location	Minimum Principal Stress	Location
9 m	0.10	vault	−0.53	corner
19 m	0.08	vault	−0.94	corner
29 m	0.08	vault	−1.67	corner
39 m	−0.03	vault	−1.72	corner

shows the greatest values of principal stresses at different depths.

It can be seen from Table 3 that the greatest values of maximum principal stress were all located in the vault of the tunnel, and the greatest values of minimum principal stress were all located in the corners of the tunnel. The existence of the shaft prevented the surrounding rock of the tunnel vault from forming a closed arch. As the tunnel face passed under the shaft, a tensile stress zone was formed on the tunnel vault. As the shaft depth increased, the tensile stress of the vault gradually decreased and turned into compressive stress. At the same time, the initial ground stress of the existing tunnel increased with the increase of depth, the compressive stress of the corner increased accordingly, and there was a risk of compression failure to the surrounding rock around the corner.

In summary, under different shaft depth conditions, the redistribution of the surrounding rock’s stress caused by tunnel expansion was relatively similar. The overall performance was as follows: the surrounding rock at the corner and arch foot had stress concentration due to the change of curvature of the tunnel outline, and the surrounding rock at the corner had a higher degree of stress concentration; the greater the shaft depth, the greater the initial in situ stress of the existing tunnel was, and the greater the stress on the surrounding rock after expansion was; the smaller the shaft depth, the greater the tensile stress on the surrounding rock in the vault was.

(2)

Displacement distributions

Figure 18 shows the change in vertical displacement of the vault with the excavation process, and Figure 19 shows the relationship between the vault’s vertical displacement and shaft depth. The vertical displacement of the vault at different depths had the same change as the expansion process, and both gradually increased as the tunnel face approached. The maximum growth rate occurred just after the tunnel face passed under the shaft. The maximum vertical displacement increased linearly with the increase of the shaft depth. The relationship between the vault’s vertical displacement and the shaft’s depth was obtained as:

y = 1.1 − 0.22 H

(4)

Figure 20 shows the change law of the horizontal displacement of the side wall with the excavation process, and Figure 21 shows the relationship between the maximum horizontal displacement and shaft depth. Under different shaft depths, the horizontal displacement of the side wall varied with the expansion process in the same law. Before the tunnel face passed through the shaft section, the horizontal displacement did not change significantly. As the tunnel face approached, horizontal displacement gradually increased. At a shaft depth of 9 m, the maximum horizontal displacement was 0.22 mm. At a shaft depth of 39 m, the maximum horizontal displacement was 3.96 mm, which is 17 times larger than that of the 9 m depth. The maximum horizontal displacement increased nonlinearly with the increase of shaft depth, and the following relationship was obtained:

y = 0.59 − 0.08 H + 0.0044 H²

(5)

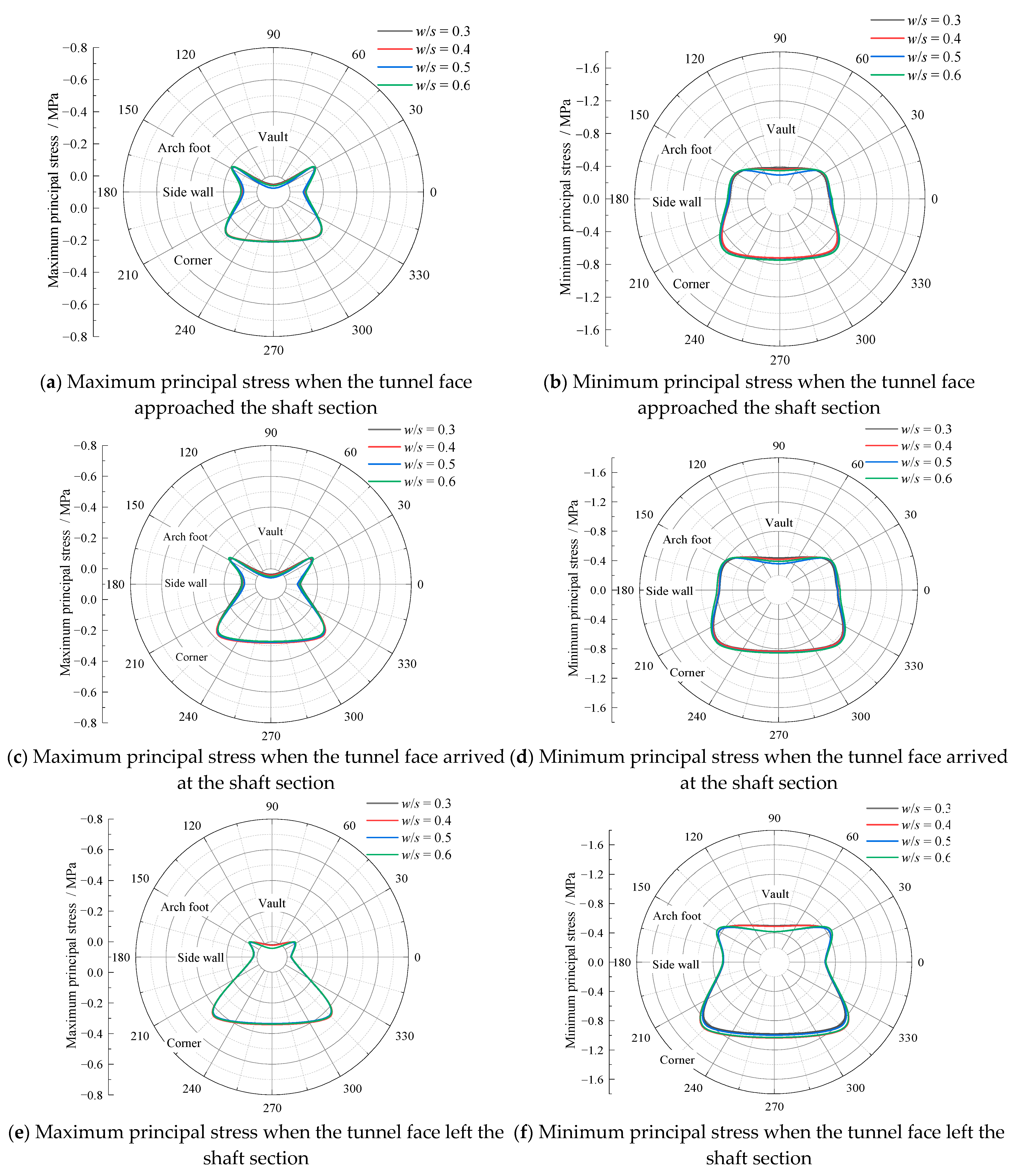
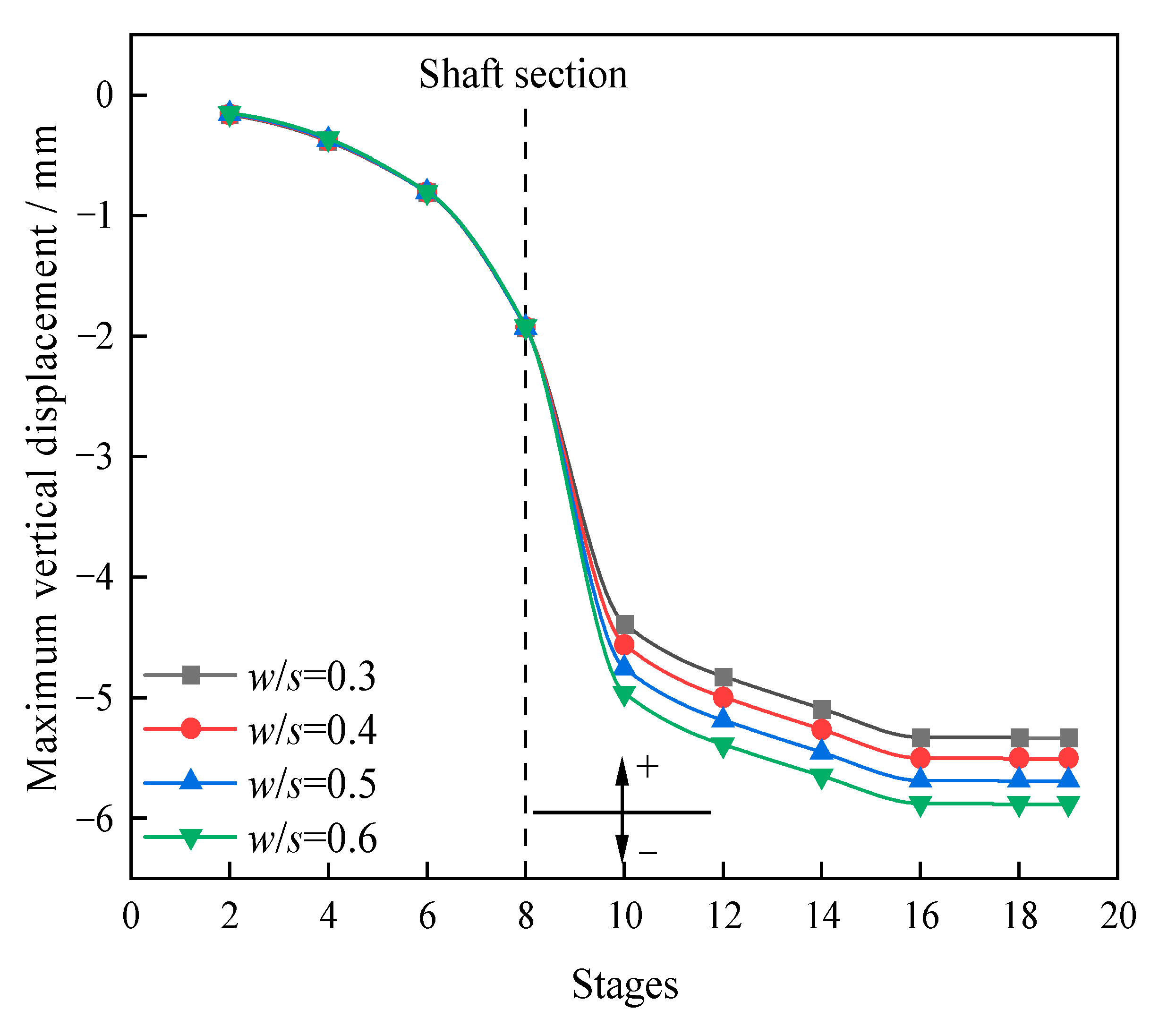
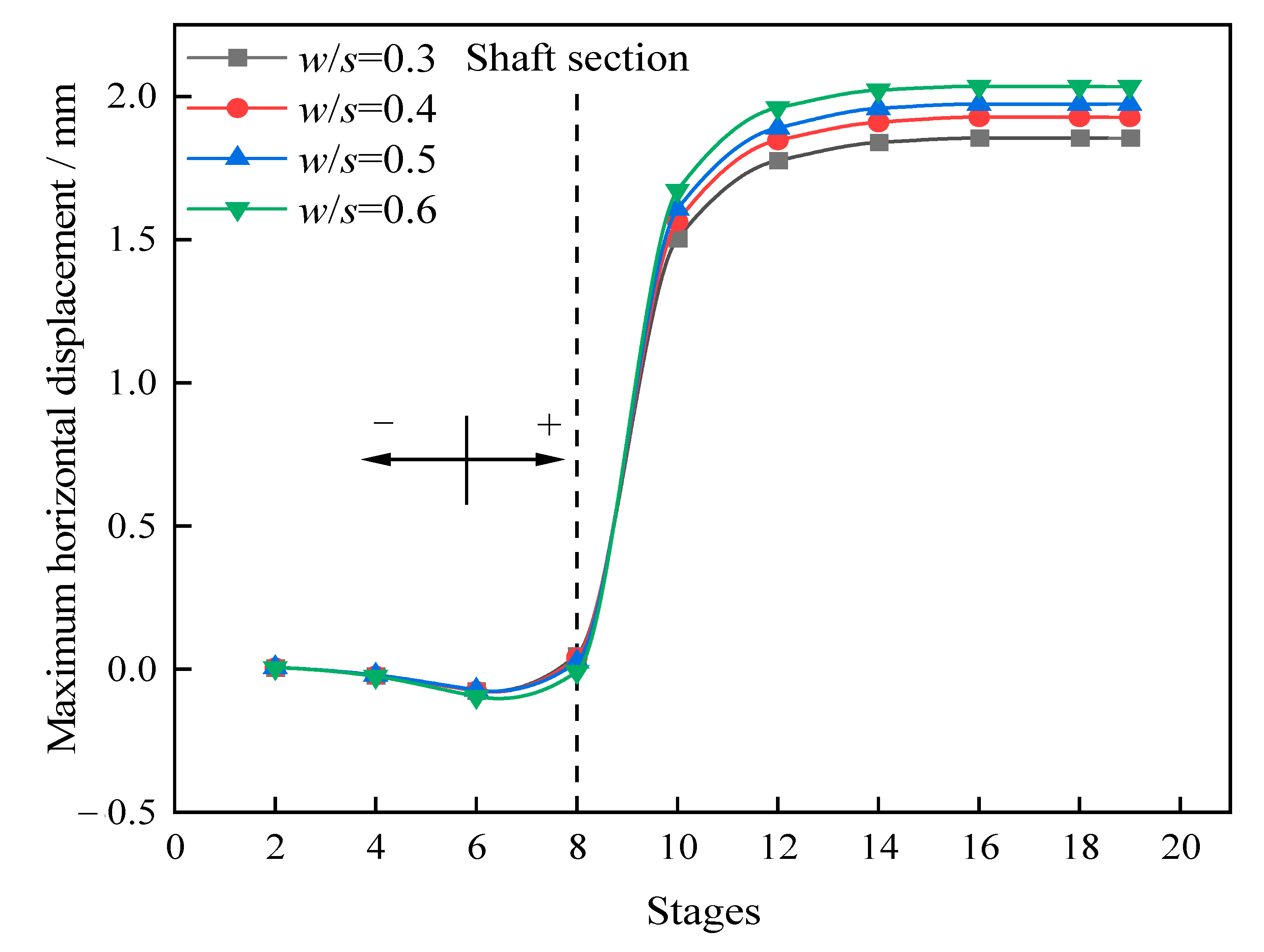
5.3. Influences of Width–Span Ratios

(1)

Principal stress distributions

Figure 22 shows the variation trends of the principal stresses in the vault, arch foot, side wall, and corner during the excavation process under different width–span ratios.

With increases in the width–span ratio, the tensile stress of the vault increased significantly, and compressive stress decreased significantly. When the width–span ratio was 0.3, the maximum principal stress of the vault was 0.021 MPa, and the minimum principal stress was −0.498 MPa. When the width–span ratio was 0.6, the maximum principal stress of the vault was 0.043 MPa, which is 105% larger than the 0.3 width–span ratio, and the minimum principal stress was −0.415 MPa, which is 16.7% smaller than the 0.3 width–span ratio. When the width–span ratio increased from 0.3 to 0.6, the maximum and minimum principal stresses of the arch foot increased by 9.8% and 3.4%, respectively. The maximum principal stress of the side wall decreased as the tunnel face approached, and the minimum principal stress underwent a complex stress path as the tunnel face advanced. When the tunnel face arrived at shaft section, the minimum principal stress increased rapidly. After the initial support was closed to form a bearing ring, the minimum principal stress gradually decreased and stabilized as the tunnel face progressed further. The maximum and minimum principal stresses at the corner were all compressive stresses, and the corner was in a state of stress concentration. The greatest values of principal stresses under different width–span ratios are shown in

Table 4. Greatest values of principal stresses with different w/s ratios (unit: MPa).

w/s	Maximum Principal Stress	Location	Minimum Principal Stress	Location
0.3	0.021	vault	−1.212	corner
0.4	0.024	vault	−1.212	corner
0.5	0.043	vault	−1.233	corner
0.6	0.043	vault	−1.272	corner

.

Table 4 shows that the greatest values of maximum principal stress were all located in the vault, and the greatest values of minimum principal stress were all located at the corner. As the tunnel face passed through the shaft section, a tensile stress zone formed at the vault. The greater the width–span ratio, the greater the tensile stress was in the vault. In summary, under different width–span ratios, the stress redistribution phenomenon caused by in situ expansion of the existing tunnel was relatively similar, and overall performance was as follows: the corner had stress concentration due to the change of the curvature of the tunnel outline; the increase in width–span ratio directly led to a significant increase in the tensile stress of the vault; variations of width–span ratio had a significant effect only on the stress state of the vault, but had a small impact on other parts of the tunnel.

(2)

Displacement distributions

Figure 23 shows the change in vertical displacement of the vault during the excavation process, and Figure 24 shows the relationship between the vault’s vertical displacement and width–span ratio. The vertical displacement of the vault at different width–span ratios changed in the same way as the excavation process, and the maximum growth rate occurred after the tunnel face passed through the shaft. When the width–span ratio was 0.3, the maximum vertical displacement was 5.32 mm. When the width–span ratio was 0.6, the maximum vertical displacement was 5.87 mm, which is 10.3% larger than the 0.3 width–span ratio. The maximum vertical displacement increased linearly with the width–span ratio. After fitting, the relationship between the maximum vertical displacement of the vault and the width–span ratio was obtained as:

y = −4.77 − 1.83 × (w/s)

(6)

Figure 25 shows the change law of the horizontal displacement at the side wall with tunnel expansion, and Figure 26 shows the relationship between the maximum horizontal displacement and width–span ratio. Under the conditions of different width–span ratios, the maximum horizontal displacement changed in the same way as the excavation process. They all increased gradually as the tunnel face approached, and the maximum growth rate occurred after the tunnel face passed under the shaft. When the width–span ratio was 0.3, the maximum horizontal displacement was 1.85 mm. When the width–span ratio was 0.6, the maximum horizontal displacement was 2.03 mm, which is 9.7% larger than the 0.3 width–span ratio. The maximum horizontal displacement of the side wall increased linearly with the width–span ratio, and the following relationship was obtained:

y = 1.68+0.58 (w/s)

(7)

6. Conclusions

In this study, the variation trends of surrounding rock stress and displacement during tunnel expansion were studied through field monitoring and numerical simulation. The main conclusions are summarized as follows:

(1)

The tangential stress at the J-1 section decreased with the approach of the tunnel face, and the tangential stress at the J-2 section and J-3 section increased. When the distance between the tunnel face and the monitoring section was about 0.91 to 1.45 times that of the existing tunnel’s span, the growth rate of tangential stress increased obviously.

(2)

The existence of the ventilation shaft weakened the stability of the surrounding rock during the expansion process. Compared with section A, the horizontal and vertical displacements in section C increased by 47.5% and 29.3%, respectively.

(3)

The maximum vertical displacement of the vault had a linear relationship with the shaft depth, and the maximum horizontal displacement of the side wall was in a quadratic relationship with the shaft depth. The smaller the shaft depth, the greater the tensile stress was on the surrounding rock in the vault.

(4)

The maximum vertical and horizontal displacements of the surrounding rock both had linear relationships with the width–span ratio. The greater the width–span ratio, the greater the tensile stress on the surrounding rock of the vault was, and the change in width–span ratio had less influence on other parts of the tunnel.