Multi-Role Collaborative Behavior in the Construction Industry through Training Strategies
Abstract
:1. Introduction
2. Related Work
2.1. Sustainable Development of the Individual
2.2. RBC Theory and the GRATP Model
3. The Proposed Model
3.1. Basic Assumptions
3.2. The Basic Definition of GRATP
| Algorithm 1: The algorithm for the GRATPC problem |
| Require: |
| , T, , H. |
| Ensure: |
| The training program matrix , the total benefit , the training start time , and the training duration . |
|
3.3. Description of the Experiments
4. Results
4.1. Preparation of the Experiments
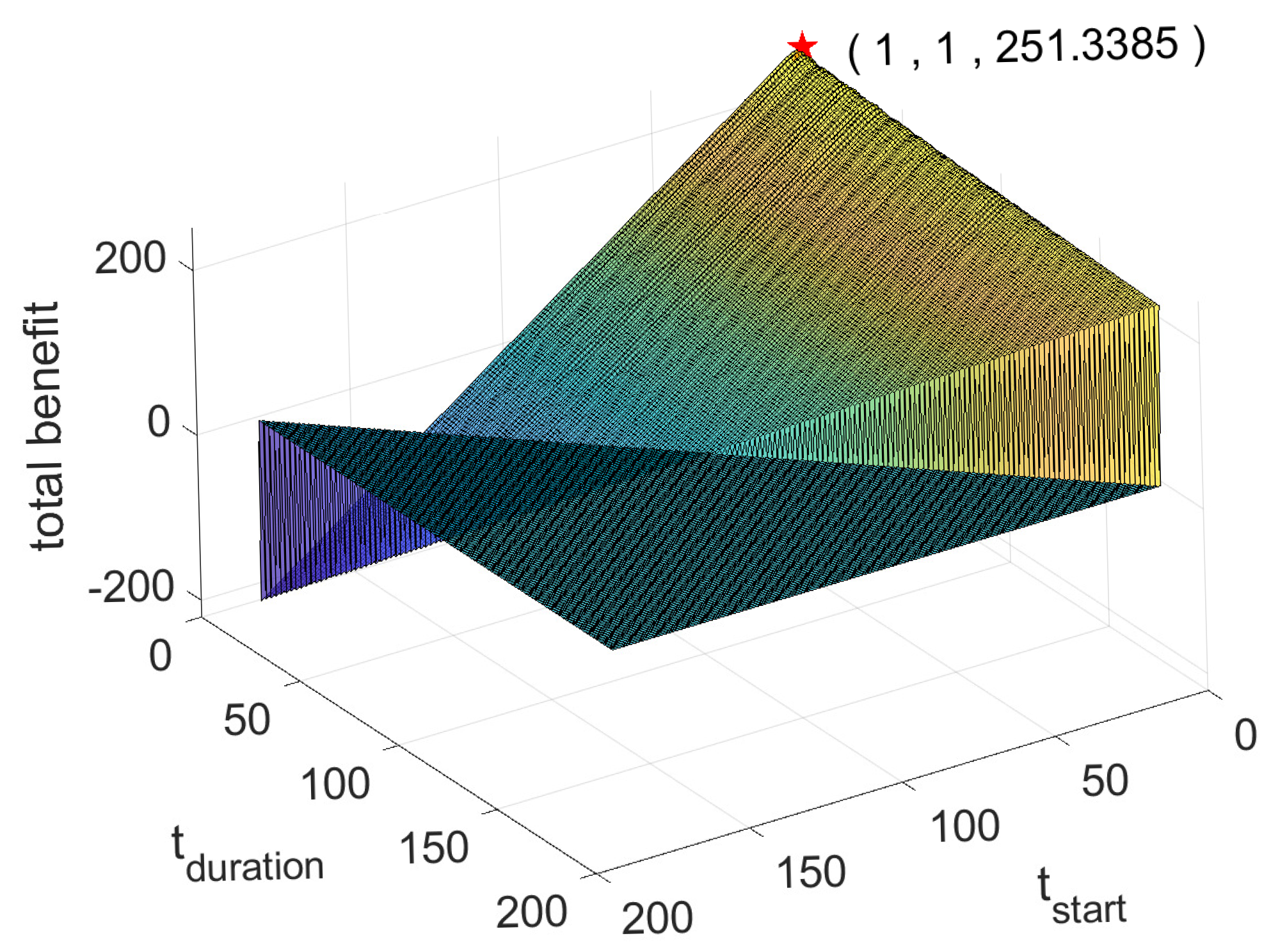
4.2. Experiment 1
4.3. Experiment 2
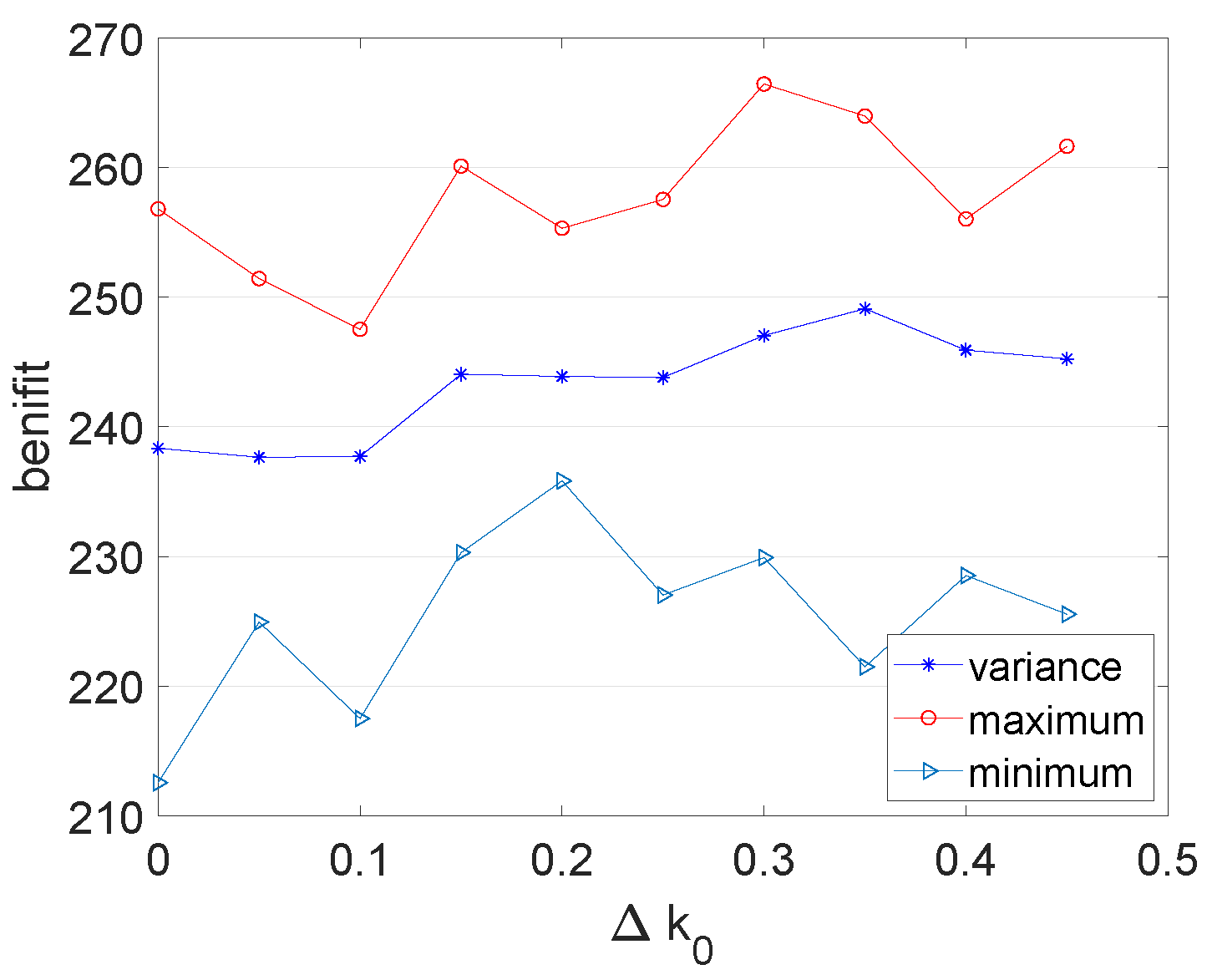
4.4. Experiment 3
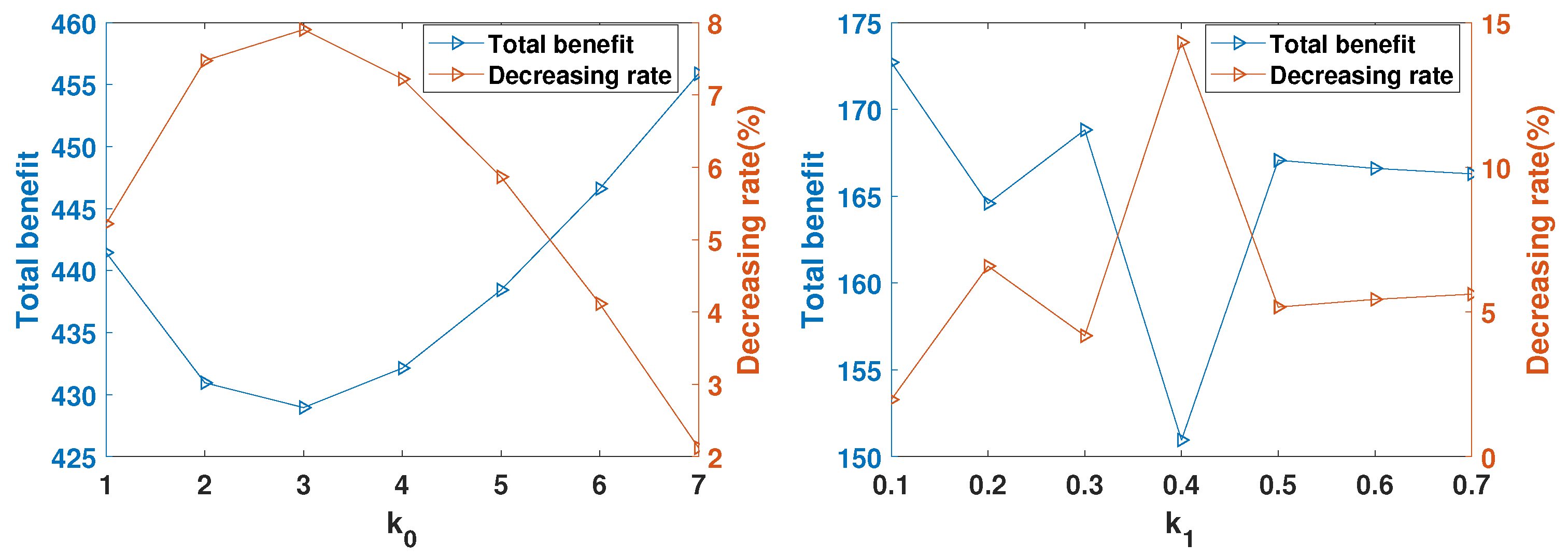
4.5. Experiment 4
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RBC | Role-based Collaboration |
| GRA | Group Role Assignment |
| GRATP | Group Role Assignment with a Training Plan |
| GRATPC | GRATP Problem with Training Cost |
| E-CARGO | Environment—Classes, Agents, Roles, Groups and Objects |
References
- Cao, X.; Qin, P.; Zhang, P. Knowledge Transfer Characteristics of Construction Workers Based on Social Network Analysis. Buildings 2022, 12, 1876. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, Z.; Zhu, H.; Sheng, Y. Group Role Assignment with a Training Plan. In Proceedings of the 2021 IEEE International Conference on Networking, Sensing and Control (ICNSC), Xiamen, China, 3–5 December 2021; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Guo, C.; Wu, S.; Zhu, H.; Sheng, Y.; Zhang, L. Adaptive Collaboration with a Training Plan. In Proceedings of the 2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Hangzhou, China, 4–6 May 2022; pp. 389–394. [Google Scholar]
- Zhang, W.; Li, W.; Teng, S.; Liu, D. A New Insight in Medical Resources Scheduling of Physical Examination with Adaptive Collaboration. In Proceedings of the 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 546–551. [Google Scholar] [CrossRef]
- Liu, Z.; Xue, J. Fuzzy Comprehensive Evaluation of Mixed Reality Seismic Retrofitting Training System. Buildings 2022, 12, 1598. [Google Scholar] [CrossRef]
- Rajabi, M.S.; Taghaddos, H.; Zahrai, S.M. Improving Emergency Training for Earthquakes through Immersive Virtual Environments and Anxiety Tests: A Case Study. Buildings 2022, 12, 1850. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, M. Role-based collaboration and its kernel mechanisms. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2006, 36, 578–589. [Google Scholar] [CrossRef]
- Ding, K.; Kong, X.; He, S.; Zong, D. Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels. Buildings 2022, 12, 2070. [Google Scholar] [CrossRef]
- Cabri, G.; Ferrari, L.; Leonardi, L. Agent role-based collaboration and coordination: A survey about existing approaches. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No.04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 6, pp. 5473–5478. [Google Scholar] [CrossRef]
- Hamadache, K.; Lancieri, L. Role-Based Collaboration Extended to Pervasive Computing. In Proceedings of the 2009 International Conference on Intelligent Networking and Collaborative Systems, Barcelona, Spain, 4–6 November 2009; pp. 9–15. [Google Scholar] [CrossRef]
- Zhu, H. Computational social simulation with E-CARGO: Comparison between collectivism and individualism. IEEE Trans. Comput. Soc. Syst. 2020, 7, 1345–1357. [Google Scholar] [CrossRef]
- Zhu, H. Some issues of role-based collaboration. In Proceedings of the CCECE 2003—Canadian Conference on Electrical and Computer Engineering, Toward a Caring and Humane Technology (Cat. No.03CH37436), Montréal, QC, Canada, 4–7 May 2003; Volume 2, pp. 687–690. [Google Scholar] [CrossRef]
- Zhu, H. E-CARGO and Role-Based Collaboration. In Proceedings of the 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; p. iii. [Google Scholar] [CrossRef]
- Chaimowicz, L.; Campos, M.F.; Kumar, V. Dynamic role assignment for cooperative robots. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 293–298. [Google Scholar]
- Zhu, H. Introduction to Special Session (R) on Role-Based Collaboration. In Proceedings of the IEEE Workshop on Distributed Intelligent Systems: Collective Intelligence and Its Applications (DIS’06), Prague, Czech Republic, 15–16 June 2006; pp. 335–336. [Google Scholar] [CrossRef]
- Xiang, S.; Liu, D.; Teng, S.; Zhu, H.; Zhang, W. Charging Pile Siting with Group Multirole Assignment. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 2822–2827. [Google Scholar] [CrossRef]
- Brownlee, E.; Zhu, H. Group Role Assignment with Busyness Degree and Cooperation and Conflict Factors. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1479–1484. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, Z. Team Performance due to Agent Conflicts: E-CARGO Simulations. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 2816–2821. [Google Scholar]
- Yu, Z.; Yang, R.; Liu, X.; Zhu, H.; Zhang, L. Multi-Group Role Assignment with Constraints in Adaptive Collaboration. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 748–754. [Google Scholar]
- Zhang, L.; Yu, Z.; Wu, S.; Zhu, H.; Sheng, Y. Adaptive Collaboration With Training Plan Considering Role Correlation. IEEE Trans. Comput. Soc. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Tsang, M.C. The cost of vocational training. Int. J. Manpow. 1997, 18, 63–89. [Google Scholar] [CrossRef]
- Patel, H.R.; Linares, A.; Joseph, J.V. Robotic and laparoscopic surgery: Cost and training. Surg. Oncol. 2009, 18, 242–246. [Google Scholar] [CrossRef]
- Jiang, H.; Sun, J.; Qiu, H.; Cao, D.; Ge, W.; Fang, Q.; Cui, H.; Chen, K. Cyclic Behavior of Multiple-Stiffness Hardening Precast Concrete Shear Walls. Buildings 2022, 12, 2069. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Liu, X.Y. Training cost-sensitive neural networks with methods addressing the class imbalance problem. IEEE Trans. Knowl. Data Eng. 2006, 18, 63–77. [Google Scholar] [CrossRef]
- Scott, D.J.; Bergen, P.C.; Rege, R.V.; Laycock, R.; Tesfay, S.T.; Valentine, R.J.; Euhus, D.M.; Jeyarajah, D.R.; Thompson, W.M.; Jones, D.B. Laparoscopic training on bench models: Better and more cost effective than operating room experience? J. Am. Coll. Surg. 2000, 191, 272–283. [Google Scholar] [CrossRef]
- Yang, J.; Yang, N.; Lin, X.; Wang, S.; Cosgrove, T.; Hughes, P. Design Method for Reinforced Concrete Based on Bond-Slip Energy Consumption. Buildings 2022, 12, 2065. [Google Scholar] [CrossRef]
- Kamranfar, S.; Azimi, Y.; Gheibi, M.; Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M. Analyzing green construction development barriers by a hybrid decision-making method based on DEMATEL and the ANP. Buildings 2022, 12, 1641. [Google Scholar] [CrossRef]
- Spence, R.; Mulligan, H. Sustainable development and the construction industry. Habitat Int. 1995, 19, 279–292. [Google Scholar] [CrossRef]
- Wang, T.K.; Wu, Z.; Luo, C. Multi-participant construction waste demolition and transportation decision-making system. Resour. Conserv. Recycl. 2021, 170, 105575. [Google Scholar] [CrossRef]
- Shurrab, J.; Hussain, M.; Khan, M. Green and sustainable practices in the construction industry: A confirmatory factor analysis approach. Eng. Constr. Archit. Manag. 2019, 26, 1063–1086. [Google Scholar] [CrossRef]
- Ingrao, C.; Messineo, A.; Beltramo, R.; Yigitcanlar, T.; Ioppolo, G. How can life cycle thinking support sustainability of buildings? Investigating life cycle assessment applications for energy efficiency and environmental performance. J. Clean. Prod. 2018, 201, 556–569. [Google Scholar] [CrossRef]
- Sharma, M.; Luthra, S.; Joshi, S.; Kumar, A. Analysing the impact of sustainable human resource management practices and industry 4.0 technologies adoption on employability skills. Int. J. Manpow. 2022, 43, 463–485. [Google Scholar] [CrossRef]
- Loosemore, M.; Malouf, N. Safety training and positive safety attitude formation in the Australian construction industry. Saf. Sci. 2019, 113, 233–243. [Google Scholar] [CrossRef]
- Demirkesen, S.; Arditi, D. Construction safety personnel’s perceptions of safety training practices. Int. J. Proj. Manag. 2015, 33, 1160–1169. [Google Scholar] [CrossRef]
- You, Z.; Feng, L. Integration of industry 4.0 related technologies in construction industry: A framework of cyber-physical system. IEEE Access 2020, 8, 122908–122922. [Google Scholar] [CrossRef]
- Dave, B.; Koskela, L. Collaborative knowledge management—A construction case study. Autom. Constr. 2009, 18, 894–902. [Google Scholar] [CrossRef]
- Zhu, H. Adaptive collaboration while agents’ performance changes periodically. In Proceedings of the 2015 International Conference on Collaboration Technologies and Systems (CTS), Atlanta, GA, USA, 1–5 June 2015; pp. 106–112. [Google Scholar] [CrossRef]
- Huang, B.; Zhu, H.; Liu, D.; Wu, N.; Qiao, Y.; Jiang, Q. Solving Last-Mile Logistics Problem in Spatiotemporal Crowdsourcing via Role Awareness With Adaptive Clustering. IEEE Trans. Comput. Soc. Syst. 2021, 8, 668–681. [Google Scholar] [CrossRef]
- Liu, D.; Yuan, Y.; Zhu, H.; Teng, S.; Huang, C. Balance Preferences with Performance in Group Role Assignment. IEEE Trans. Cybern. 2018, 48, 1800–1813. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, C.; Zhang, L.; Sheng, Y. A Three-Way Human-Robot Task Assignment Method under Intuitionistic Fuzzy Environment. In Proceedings of the 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 587–592. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, D.; Zhu, H.; Zhang, W.; Ye, Z. Solving the Task Allocation Problem under High-order Set via Group Role Assignment. In Proceedings of the 2022 IEEE 25th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Hangzhou, China, 4–6 May 2022; pp. 23–28. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, Q.; Zhu, H.; Huang, B. Distributing UAVs as wireless repeaters in disaster relief via group role assignment. Int. J. Coop. Inf. Syst. 2020, 29, 2040002. [Google Scholar] [CrossRef]
- Ma, H.; Chen, Y.; Zhu, H.; Zhang, H.; Tang, W. Optimization of Cloud Service Composition for Data-intensive Applications via E-CARGO. In Proceedings of the 2018 IEEE 22nd International Conference on Computer Supported Cooperative Work in Design (CSCWD), Nanjing, China, 9–11 May 2018; pp. 785–789. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhu, H.; Qiao, Y.; Liu, D.; Huang, B. Refugee Resettlement by Extending Group Multirole Assignment. IEEE Trans. Comput. Soc. Syst. 2021, 1–12. [Google Scholar] [CrossRef]
- Zhu, H. The Benefits of Dynamic Role Assignment in Collaboration. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Hong Kong, China, 9–12 October 2015; pp. 304–309. [Google Scholar] [CrossRef]
- Zhu, H. Avoiding Conflicts by Group Role Assignment. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 535–547. [Google Scholar] [CrossRef]
- Zhu, H. Group multi-role assignment with conflicting roles and agents. IEEE/CAA J. Autom. Sin. 2020, 7, 1498–1510. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, M.; Alkins, R. Group role assignment via a Kuhn–Munkres algorithm-based solution. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 42, 739–750. [Google Scholar] [CrossRef]
- Clements, C.J.; Josiam, B.M. Training: Quantifying the financial benefits. Int. J. Contemp. Hosp. Manag. 1995, 7, 10–15. [Google Scholar] [CrossRef]
- Wang, Y.; Goodrum, P.M.; Haas, C.; Glover, R.; Vazari, S. Analysis of the benefits and costs of construction craft training in the United States based on expert perceptions and industry data. Constr. Manag. Econ. 2010, 28, 1269–1285. [Google Scholar] [CrossRef]
- Lombardo, C.A. Do the benefits of training justify the costs? Train. Dev. J. 1989, 43, 60–65. [Google Scholar]
- Assaf, S.A.; Al-Hejji, S. Causes of delay in large construction projects. Int. J. Proj. Manag. 2006, 24, 349–357. [Google Scholar] [CrossRef]
- Ahmad Zaki, S.; Mohamed, S.; Mohd Yusof, Z. Construction skilled labour shortage–the challenges in Malaysian construction sector ontario international development agency (OIDA). Int. J. Sustain. Dev. 2012, 4, 99–108. [Google Scholar]
- Johari, S.; Jha, K. Development and implementation of on-the-job training system for construction workers. In Urbanization Challenges in Emerging Economies: Energy and Water Infrastructure; Transportation Infrastructure; and Planning and Financing; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 405–416. [Google Scholar]



| Paper Name | Innovation |
|---|---|
| Group role assignment with a training Plan [2] | GRA + training program (Redundant agent) |
| Adaptive collaboration with a training plan [3] | GRATP + training program + training start time |
| Adaptive collaboration with a training plan considering role correlation [20] | GRATP + role correlation |
| This paper | GRATP + training program + training start time + training cost |
| Positions | Decision Maker | Surveyor | Program Designer | Construction Worker | Acceptance Personnel | Operator | Maintainer |
|---|---|---|---|---|---|---|---|
| Required Number | 1 | 2 | 1 | 3 | 1 | 1 | 1 |
| Contribution Rate | 20% | 11% | 12% | 30% | 8% | 9% | 10% |
| Position | Decision Maker | Surveyor | Program Designer | Construction Worker | Acceptance Personnel | Operator | Maintainer |
|---|---|---|---|---|---|---|---|
| cost | 10 | 20 | 30 | 13 | 11 | 14 | 20 |
| Method | Reassignment | Noreassignment | Notraining | |
|---|---|---|---|---|
| Total Benefit | ||||
| Average | 260.15 | 238.71 | 212.55 | |
| Max | 271.44 | 259.25 | 231.99 | |
| Min | 246.66 | 215.84 | 189.44 | |
| ΔCost | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Benefit | |||||||||||
| time 1 | 219.45 | 219.34 | 219.23 | 219.12 | 219.01 | 218.90 | 218.79 | 218.68 | 218.57 | 218.46 | |
| time 2 | 230.99 | 230.89 | 230.79 | 230.69 | 230.59 | 230.49 | 230.39 | 230.29 | 230.19 | 230.09 | |
| time 3 | 243.77 | 243.68 | 243.59 | 243.50 | 243.41 | 243.31 | 243.22 | 243.13 | 243.04 | 242.96 | |
| Position | Decision Maker | Surveyor | Program Designer | Construction Worker | Acceptance Personnel | Operator | Maintainer | |
|---|---|---|---|---|---|---|---|---|
| k0 | total benefit | 552.33 | 541.84 | 539.836 | 543.01 | 549.32 | 557.49 | 566.75 |
| decreasing rate | 4.22% | 6.04% | 6.38% | 5.83% | 4.74% | 3.32% | 1.72% | |
| k1 | total benefit | 212.31 | 204.18 | 208.42 | 190.557 | 206.67 | 206.20 | 205.88 |
| decreasing rate | 1.61% | 5.38% | 3.41% | 11.69% | 4.22% | 4.44% | 4.59% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Yang, R.; Chong, H.-Y.; Feng, M. Multi-Role Collaborative Behavior in the Construction Industry through Training Strategies. Buildings 2023, 13, 482. https://doi.org/10.3390/buildings13020482
Yan X, Yang R, Chong H-Y, Feng M. Multi-Role Collaborative Behavior in the Construction Industry through Training Strategies. Buildings. 2023; 13(2):482. https://doi.org/10.3390/buildings13020482
Chicago/Turabian StyleYan, Xue, Ruisi Yang, Heap-Yih Chong, and Minyu Feng. 2023. "Multi-Role Collaborative Behavior in the Construction Industry through Training Strategies" Buildings 13, no. 2: 482. https://doi.org/10.3390/buildings13020482
APA StyleYan, X., Yang, R., Chong, H.-Y., & Feng, M. (2023). Multi-Role Collaborative Behavior in the Construction Industry through Training Strategies. Buildings, 13(2), 482. https://doi.org/10.3390/buildings13020482









