Soil–Structure Interaction Consideration for Base Isolated Structures under Earthquake Excitation
Abstract
:1. Introduction
2. Formulation of the Problem
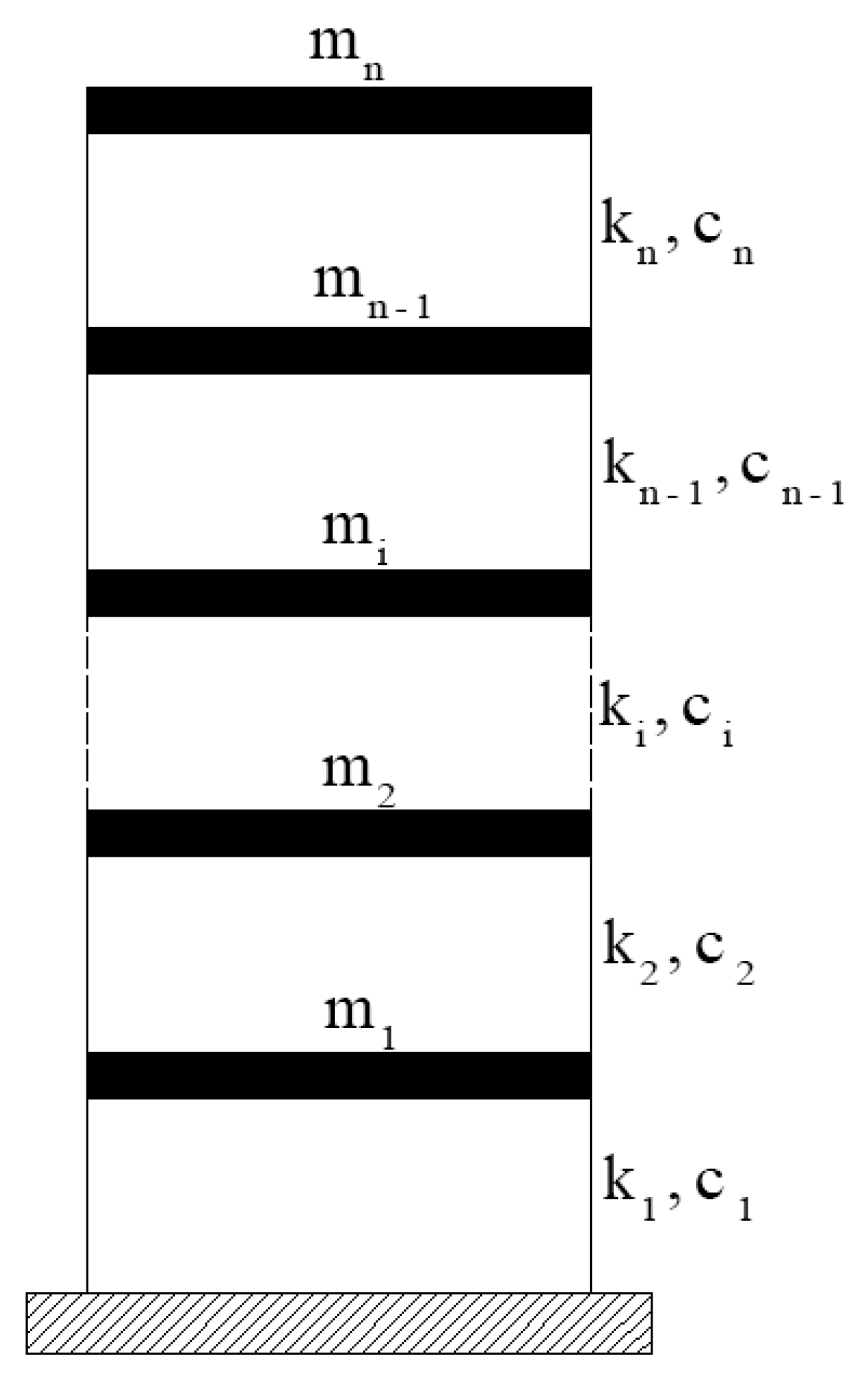
2.1. Representing Soil Structure
2.2. Matrix Formulation of the Structure
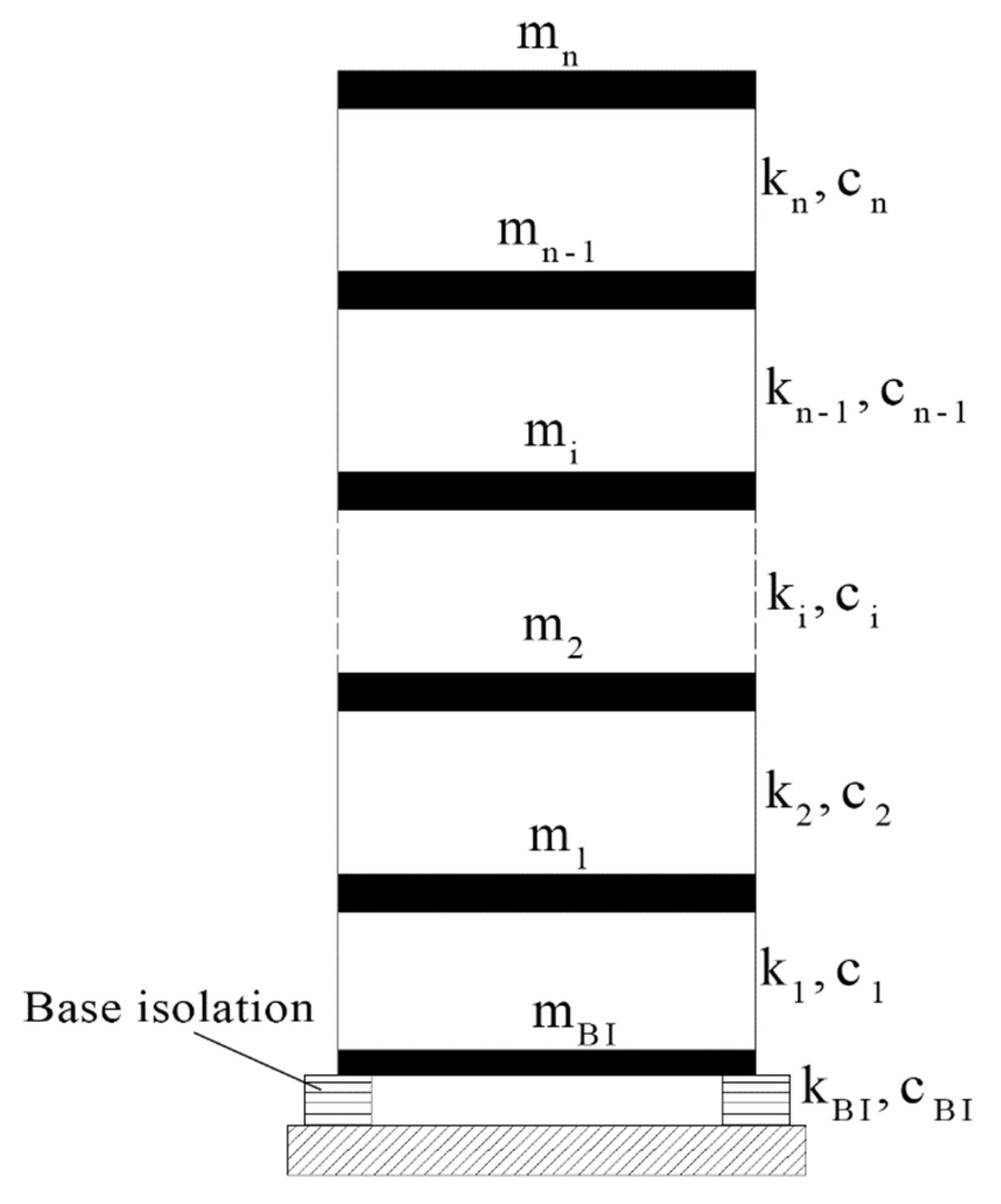
2.3. Base Isolated Structure
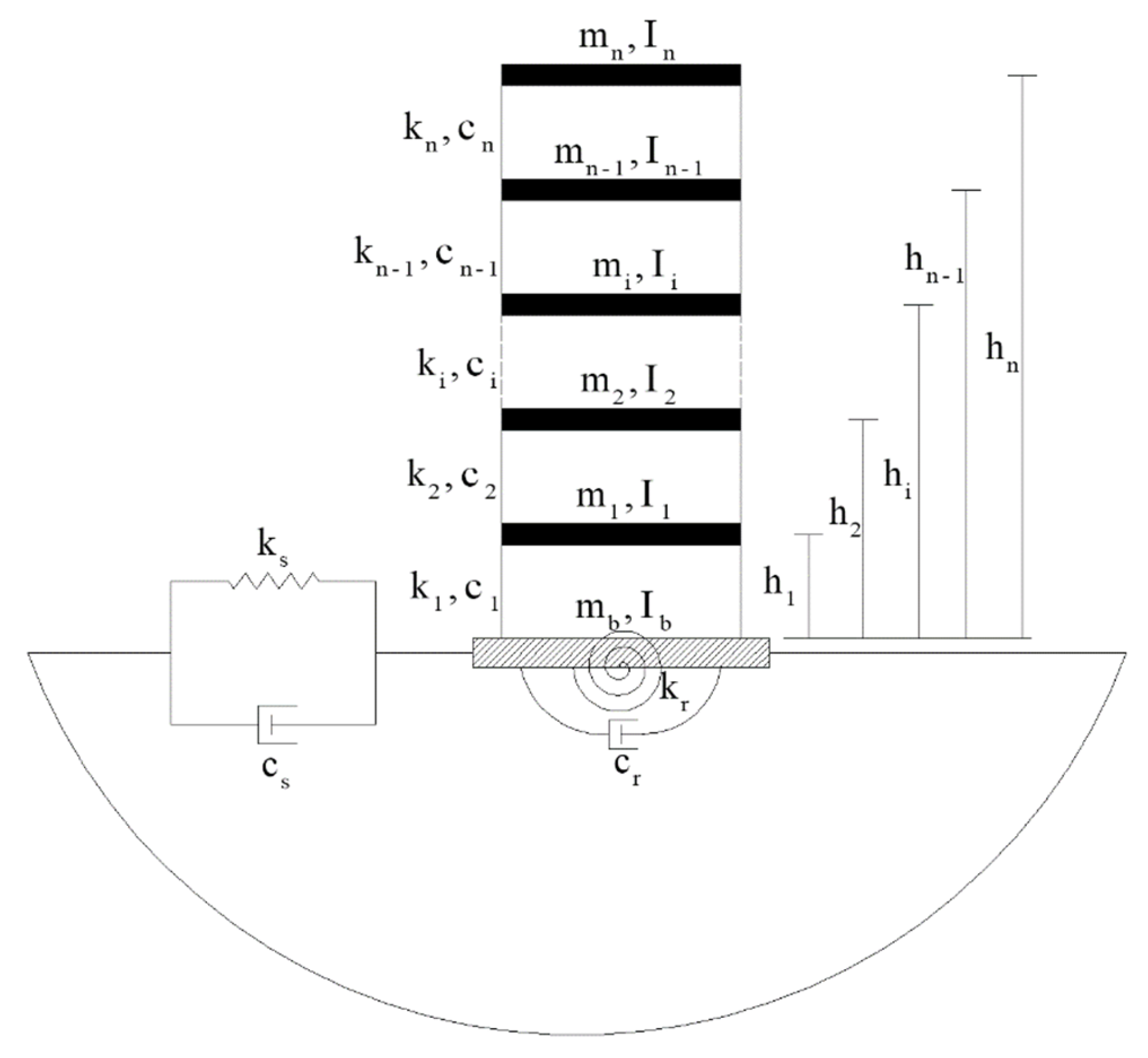
2.4. SSI Implementation
2.5. Proposed Simple Formulation for SSI with Base Isolation
2.6. Equations of the Motion of the Structure under Earthquake Excitation
3. Numerical Example
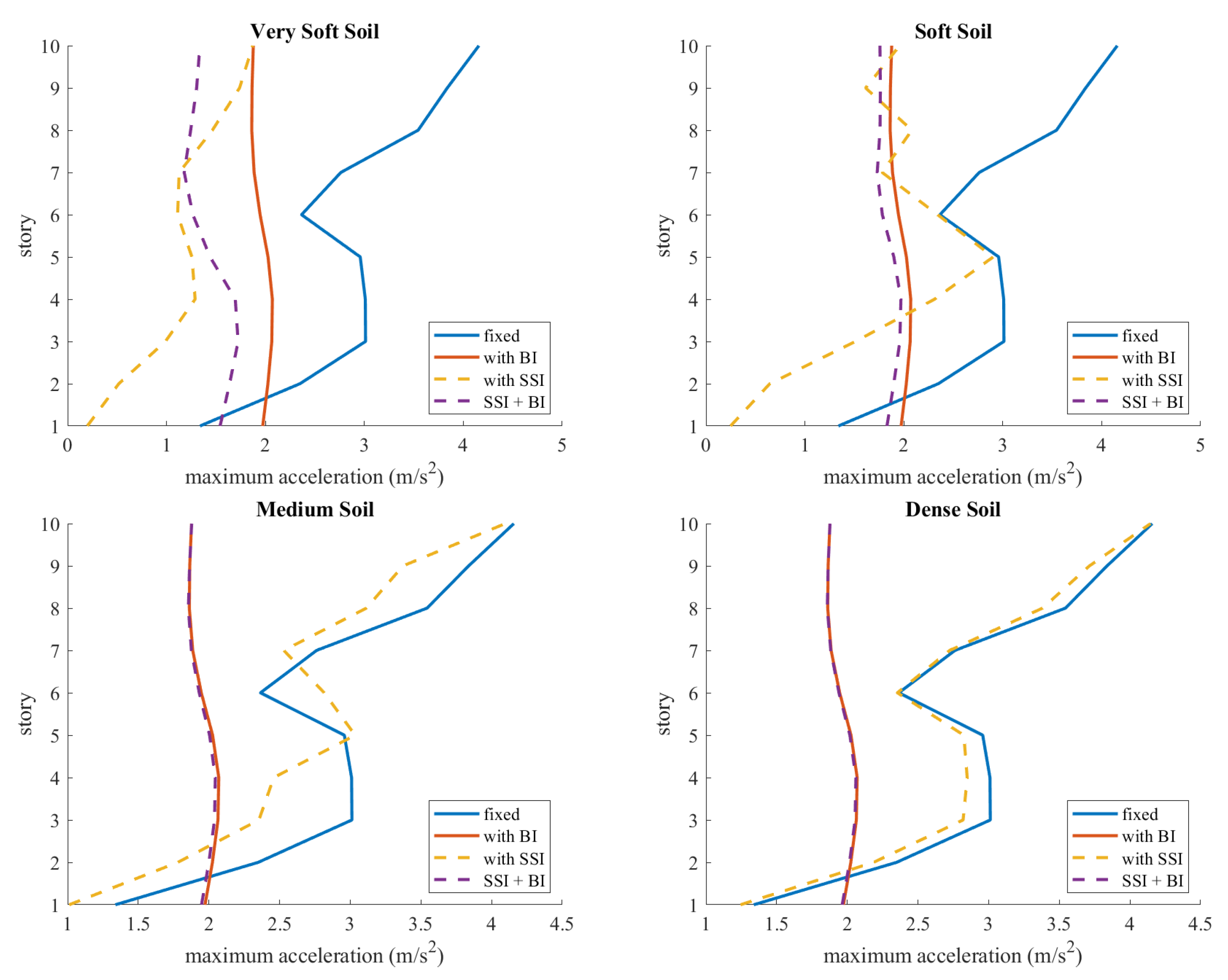
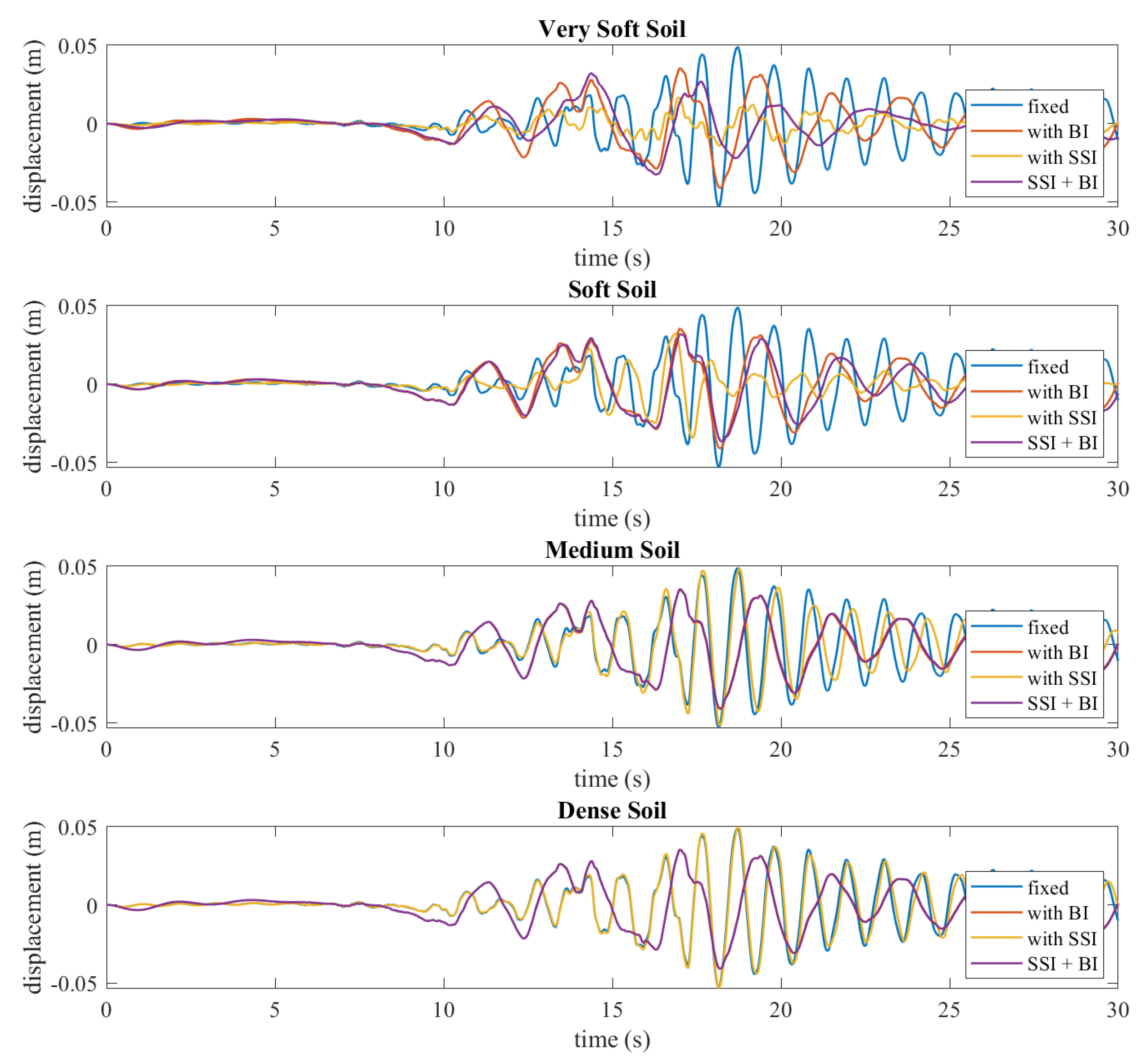
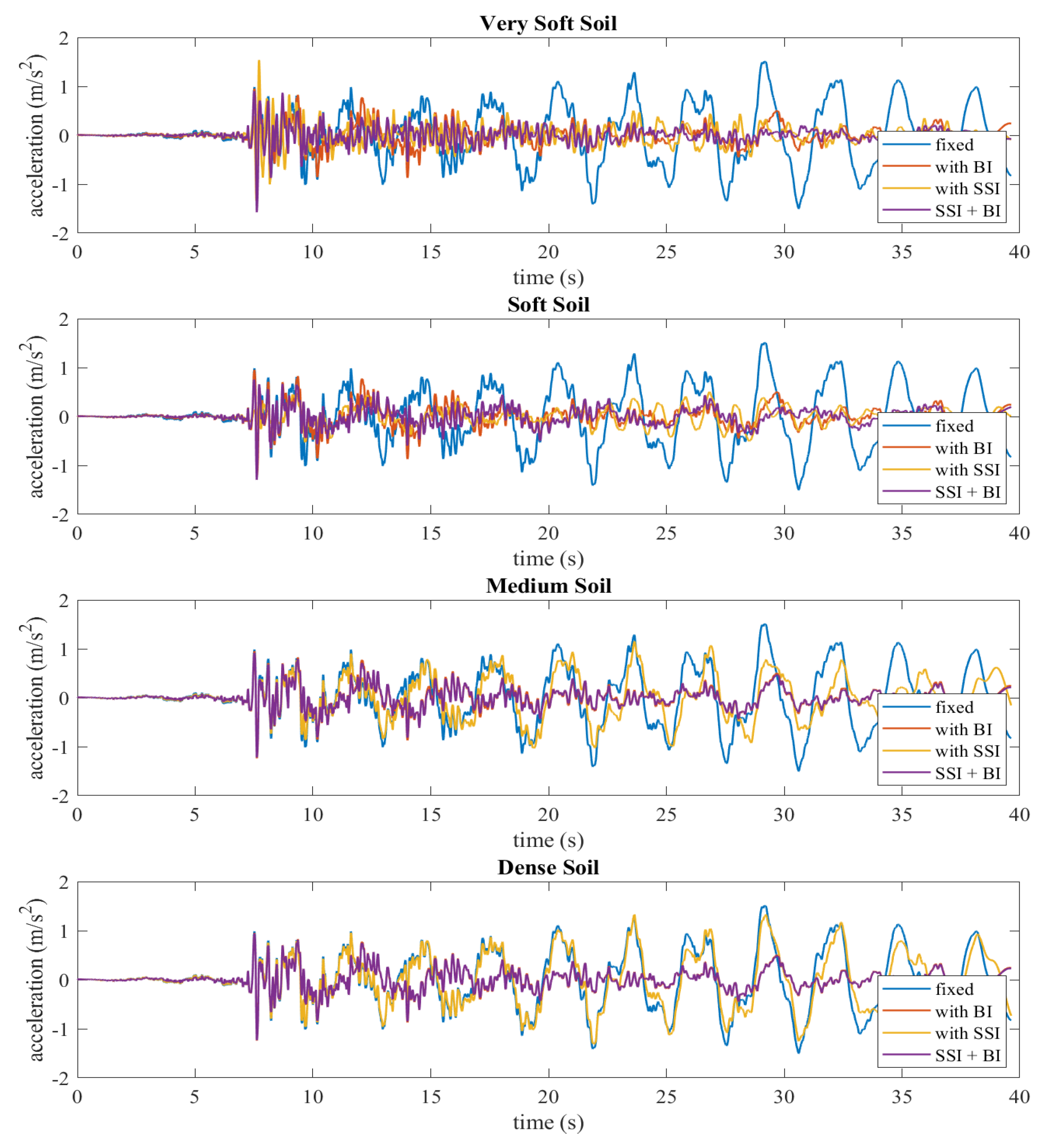
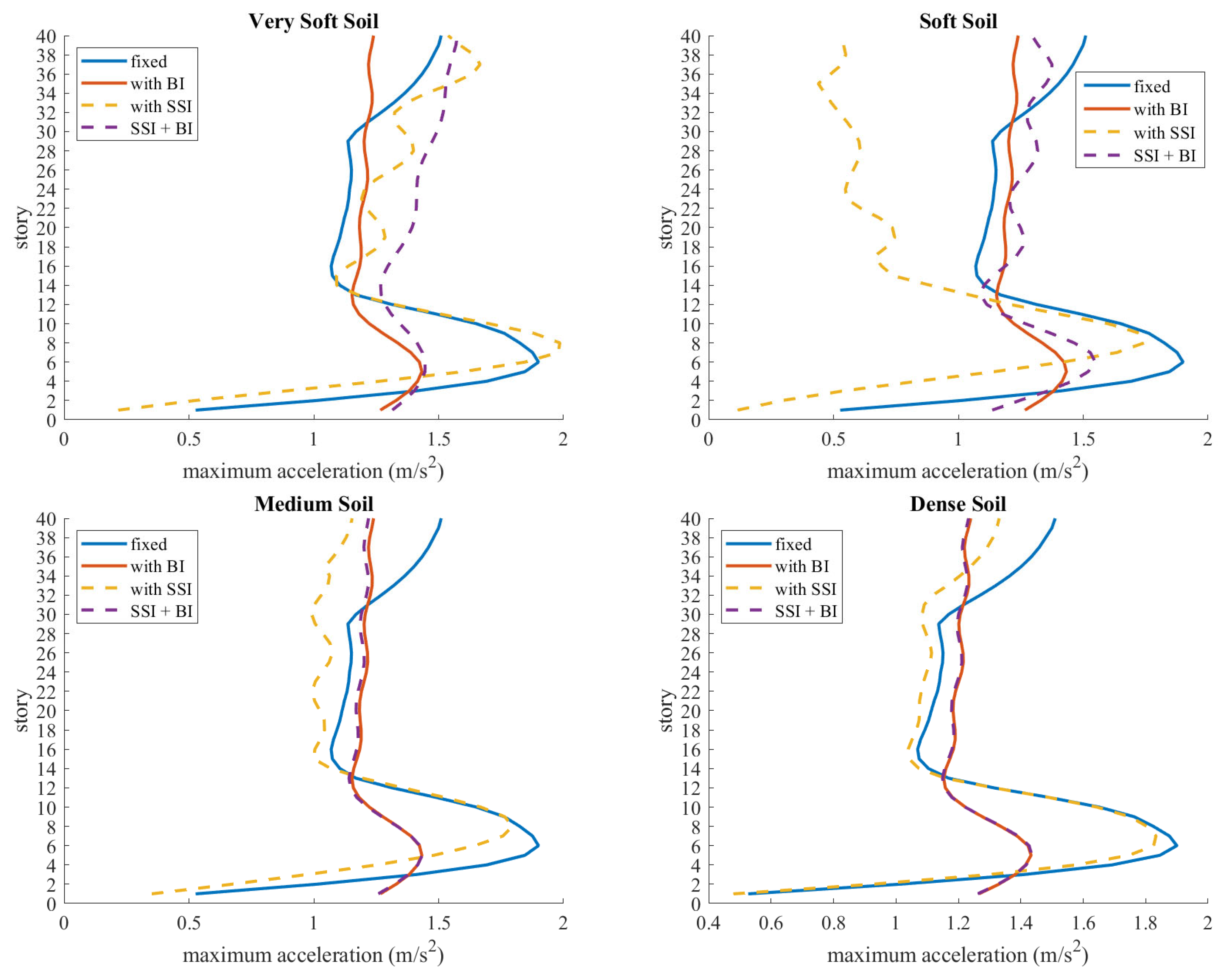
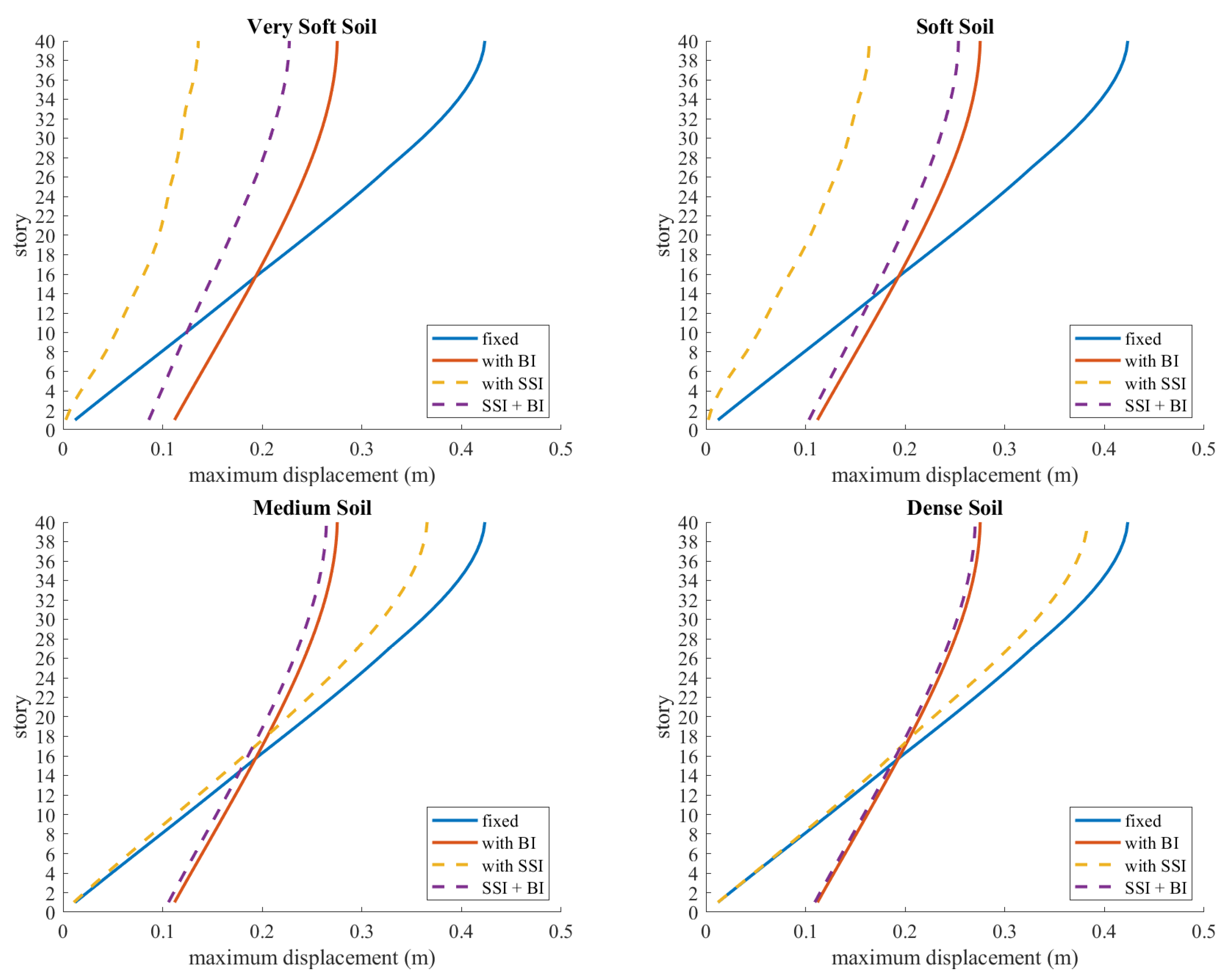
4. Numerical Results
Spectral Analysis
5. Conclusions
- BI may greatly reduce the acceleration, velocity and displacements of structures that are induced by earthquakes.
- Although the total displacement might be higher than in a fixed structure, most of it occurs on the isolation system, and the superstructure moves as a whole, resulting in much lower inter-story drift compared to the fixed base structure.
- SSI may modify the acceleration, velocity and displacement responses of structures.
- The results show that SSI mostly reduces the effects of earthquakes. In order to stay on the safer side, design codes do not specify SSI analysis procedures; they often briefly state that SSI can sometimes modify earthquake responses, and for those rare cases, it should be investigated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chopra, A.K. Dynamics of Structures, Theory and Applications to Earthquake Engineering, 4th ed.; Pearson Education Limited: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- American Society of Civil Engineers (ASCE). Fema 356 Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Constantinou, M.C.; Kneifati, M.C. Dynamics of Soil-Base-Isolated-Structure Systems. J. Struct. Eng. 1988, 114, 211–221. [Google Scholar] [CrossRef]
- Bycroft, G.N. Soil-structure interaction at higher frequency factors. Earthq. Eng. Struct. Dyn. 1977, 5, 235–248. [Google Scholar] [CrossRef]
- Novak, M.; Henderson, P. Base-isolated buildings with soil-structure interaction. Earthq. Eng. Struct. Dyn. 1989, 18, 751–765. [Google Scholar] [CrossRef]
- Pappin, J.W.; Lubkowski, Z.A.; King, R.A. The Significance of Site Response Effects on Performance Based Design. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Mylonakis, G.; Gazetas, G. Seismic Soil-Structure Interaction: Beneficial or Detrimental? J. Earthq. Eng. 2000, 4, 277–301. [Google Scholar] [CrossRef]
- Tongaonkar, N.; Jangid, R. Seismic response of isolated bridges with soil–structure interaction. Soil Dyn. Earthq. Eng. 2003, 23, 287–302. [Google Scholar] [CrossRef]
- Mylonakis, G.; Voyagaki, E.; Price, T. Damage Potential of the 1999 Athens, Greece, Accelerograms. Bull. Earthq. Eng. 2003, 1, 205–240. [Google Scholar] [CrossRef]
- Syngros, K. Seismic Response of Piles and Pile-Supported Bridge Piers Evaluated through Case Histories. Ph.D. Thesis, The City University of New York, New York, NY, USA, 2004. [Google Scholar]
- Deb, S. Seismic base isolation—An overview. Curr. Sci. 2004, 87, 1426–1430. Available online: http://www.jstor.org/stable/24109483 (accessed on 5 July 2019).
- Tsai, C.S.; Chen, C.-S.; Chen, B.-J. Effects of unbounded media on seismic responses of FPS-isolated structures. Struct. Control Health Monit. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Dicleli, M.; Albhaisi, S.; Mansour, M.Y. Static Soil–Structure Interaction Effects in Seismic-Isolated Bridges. Pract. Period. Struct. Des. Constr. 2005, 10, 22–33. [Google Scholar] [CrossRef]
- Liu, M.-Y.; Chiang, W.-L.; Hwang, J.-H.; Chu, C.-R. Wind-induced vibration of high-rise building with tuned mass damper including soil–structure interaction. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1092–1102. [Google Scholar] [CrossRef]
- Spyrakos, C.; Koutromanos, I.; Maniatakis, C. Seismic response of base-isolated buildings including soil–structure interaction. Soil Dyn. Earthq. Eng. 2009, 29, 658–668. [Google Scholar] [CrossRef]
- Jeremić, B.; Jie, G.; Preisig, M.; Tafazzoli, N. Time domain simulation of soil-foundation-structure interaction in non-uniform soils. Earthq. Eng. Struct. Dyn. 2009, 38, 699–718. [Google Scholar] [CrossRef]
- Karabörk, T.; Deneme, İ.Ö.; Bilgehan, R.P. Dynamic soil structure interaction analysis for base isolated structures. Erciyes Univ. J. Inst. Sci. Technol. 2010, 26, 77–87. [Google Scholar]
- Kausel, E. Early history of soil–structure interaction. Soil Dyn. Earthq. Eng. 2010, 30, 822–832. [Google Scholar] [CrossRef] [Green Version]
- Genes, M.; Doğanay, E.; Bikçe, M.; Kaçın, S. Soil-Structure Interaction in RC Frame Buildings from Strong-Motion Recordings. KSU J. Eng. Sci. 2011, 14, 1–7. Available online: http://jes.ksu.edu.tr/en/download/article-file/180955 (accessed on 9 August 2019).
- Matinmanesh, H.; Asheghabadi, M.S. Seismic Analysis on Soil-Structure Interaction of Buildings over Sandy Soil. Procedia Eng. 2011, 14, 1737–1743. [Google Scholar] [CrossRef] [Green Version]
- Manolis, G.D.; Markou, A. A distributed mass structural system for soil-structure-interaction and base isolation studies. Arch. Appl. Mech. 2012, 82, 1513–1529. [Google Scholar] [CrossRef]
- Giarlelis, C.; Mylonakis, G. The role of soil-structure interaction in the inelastic performance of multi-story buildings. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Li, C.P.; Liu, W.Q.; Wang, S.G.; Du, D.S. Analysis of Soil-Structure Interaction (SSI) Effects on Seismic Response of Base-Isolated Structures. Adv. Mater. Res. 2010, 163–167, 4199–4207. [Google Scholar] [CrossRef]
- Luco, J.E. Effects of soil–structure interaction on seismic base isolation. Soil Dyn. Earthq. Eng. 2014, 66, 167–177. [Google Scholar] [CrossRef]
- Tsai, C.S.; Hsueh, C.I.; Su, H.C. Roles of soil-structure interaction and damping in base-isolated structures built on numerous soil layers overlying a half-space. Earthq. Eng. Eng. Vib. 2016, 15, 387–400. [Google Scholar] [CrossRef]
- Yanik, A. Absolute Instantaneous Optimal Control Performance Index for Active Vibration Control of Structures under Seismic Excitation. Shock Vib. 2019, 2019, 4207427. [Google Scholar] [CrossRef] [Green Version]
- Ashiquzzaman; Hong, K.-J. Simplified Model of Soil-Structure Interaction for Seismically Isolated Containment Buildings in Nuclear Power Plant. Structures 2017, 10, 209–218. [Google Scholar] [CrossRef]
- Zhou, Z.; Wei, X. Seismic Soil-Structure Interaction Analysis of Isolated Nuclear Power Plants in Frequency Domain. Shock Vib. 2016, 2016, 6127895. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Wang, S.; Du, D.; Liu, W. Optimal Design of Viscoelastic Dampers in Frame Structures considering Soil-Structure Interaction Effect. Shock Vib. 2017, 2017, 9629083. [Google Scholar] [CrossRef] [Green Version]
- Forcellini, D. Seismic assessment of a benchmark based isolated ordinary building with soil structure interaction. Bull. Earthq. Eng. 2018, 16, 2021–2042. [Google Scholar] [CrossRef]
- McKenna, F. OpenSees: A Framework for Earthquake Engineering Simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]
- Dai, W.; Rojas, F.; Shi, C.; Tan, Y. Effect of soil structure interaction on the dynamic responses of base isolated bridges and comparison to experimental results. Soil Dyn. Earthq. Eng. 2018, 114, 242–252. [Google Scholar] [CrossRef]
- El-Sinawi, A.H.; AlHamaydeh, M.H.; Jhemi, A.A. Optimal Control of Magnetorheological Fluid Dampers for Seismic Isolation of Structures. Math. Probl. Eng. 2013, 2013, 251935. [Google Scholar] [CrossRef] [Green Version]
- Yanik, A. Seismic control performance indices for magneto-rheological dampers considering simple soil-structure interaction. Soil Dyn. Earthq. Eng. 2020, 129, 105964. [Google Scholar] [CrossRef]
- Zhenxia, S.; Haiping, D. The Analysis of Seismic Response for Base-isolated Structure by LS-DYNA. Indian Institute of Technology Kanpur. Available online: http://www.iitk.ac.in/nicee/wcee/artical/14_14-0204.pdf (accessed on 7 August 2019).
- Forcellini, D. Seismic fragility of tall buildings considering soil structure interaction (SSI) effects. Structures 2022, 45, 999–1011. [Google Scholar] [CrossRef]
- Jalali, H.H.; Farzam, M.F.; Gavgani, S.A.M.; Bekdaş, G. Semi-active control of buildings using different control algorithms considering SSI. J. Build. Eng. 2023, 67, 105956. [Google Scholar] [CrossRef]
- Maleska, T.; Beben, D. Behaviour of Soil–Steel Composite Bridges under Strong Seismic Excitation with Various Boundary Conditions. Materials 2023, 16, 650. [Google Scholar] [CrossRef]
- Wang, J.; Xie, Y.; Guo, T.; Du, Z. Predicting the Influence of Soil–Structure Interaction on Seismic Responses of Reinforced Concrete Frame Buildings Using Convolutional Neural Network. Buildings 2023, 13, 564. [Google Scholar] [CrossRef]
- Jin, L.; Li, B.; Lin, S.; Li, G. Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings 2022, 13, 17. [Google Scholar] [CrossRef]
- Deng, Y.; Ge, S.; Lei, F. Effects of Pounding and Abutment Behavior on Seismic Response of Multi-Span Bridge Considering Abutment-Soil-Foundation-Structure Interactions. Buildings 2023, 13, 260. [Google Scholar] [CrossRef]
- Datta, T.K. Seismic Analysis of Structures; John Wiley & Sons (Asia) Pte Ltd.: Singapore, 2010. [Google Scholar]
- Pioldi, F.; Salvi, J.; Rizzi, E. Refined FDD modal dynamic identification from earthquake responses with Soil-Structure Interaction. Int. J. Mech. Sci. 2017, 127, 47–61. [Google Scholar] [CrossRef]
- Bekdaş, G.; Nigdeli, S.M. Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil-structure interaction. Soil Dyn. Earthq. Eng. 2017, 92, 443–461. [Google Scholar] [CrossRef]
- Salvi, J.; Pioldi, F.; Rizzi, E. Optimum Tuned Mass Dampers under seismic Soil-Structure Interaction. Soil Dyn. Earthq. Eng. 2018, 114, 576–597. [Google Scholar] [CrossRef]
- Pacific Earthquake Engineering Research Center. PEER NGA-West2 Database. Available online: https://ngawest2.berkeley.edu/ (accessed on 2 July 2019).
- Cardone, D.; Viggiani, L.; Perrone, G.; Telesca, A.; Di Cesare, A.; Ponzo, F.; Ragni, L.; Micozzi, F.; Dall’Asta, A.; Furinghetti, M.; et al. Modelling and Seismic Response Analysis of Existing Italian Residential RC Buildings Retrofitted by Seismic Isolation. J. Earthq. Eng. 2023, 27, 1069–1093. [Google Scholar] [CrossRef]
- Cardone, D.; Conte, N.; Dall’Asta, A.; Di Cesare, A.; Flora, A.; Lamarucciola, N.; Micozzi, F.; Ponzo, F.C.; Ragni, L. RINTC-E project: The seismic risk of existing Italian RC buildings retrofitted with seismic isolation. In Proceedings of the 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, COMPDYN 2019, Crete, Greece, 24–26 June 2019. [Google Scholar]
- Iervolino, I.; Spillatura, A.; Bazzurro, P. Seismic Reliability of Code-Conforming Italian Buildings. J. Earthq. Eng. 2018, 22, 5–27. [Google Scholar] [CrossRef]
- Calvi, P.M.; Calvi, G.M. Historical development of friction-based seismic isolation systems. Soil Dyn. Earthq. Eng. 2018, 106, 14–30. [Google Scholar] [CrossRef]



| Soil | ν | ρ ton/m3 | VS m/s2 | G kN/m2 |
|---|---|---|---|---|
| Very Soft | 0.49 | 1.60 | 50 | 4000 |
| Soft | 0.49 | 1.80 | 100 | 18,000 |
| Medium | 0.48 | 1.90 | 300 | 171,000 |
| Dense | 0.33 | 2.40 | 500 | 600,000 |
| Soil | ks kN/m | kr kN/m | cs kNs/m | cr kNs/m |
|---|---|---|---|---|
| Very Soft | 2.39 × 105 | 3.00 × 107 | 3.49 × 105 | 1.01 × 106 |
| Soft | 1.07 × 106 | 1.35 × 108 | 7.87 × 105 | 2.28 × 106 |
| Medium | 1.02 × 107 | 1.26 × 109 | 2.47 × 106 | 7.09 × 106 |
| Dense | 3.24 × 107 | 3.43 × 109 | 4.74 × 106 | 1.16 × 107 |
| Soil | ks kN/m | kr kN/m | cs kNs/m | cr kNs/m |
|---|---|---|---|---|
| Very Soft | 4.78 × 105 | 2.40 × 108 | 2.79 × 106 | 1.62 × 107 |
| Soft | 2.15 × 106 | 1.08 × 109 | 6.30 × 106 | 3.66 × 107 |
| Medium | 2.03 × 107 | 1.01 × 1010 | 1.98 × 107 | 1.14 × 108 |
| Dense | 6.48 × 107 | 2.74 × 1010 | 3.79 × 107 | 1.86 × 108 |
| story height, hi (m) | 4 to 160 |
| story mass, mi (ton) | 980 |
| story stiffness, ki (kN/m) | 2.1 × 106 to 0.99 × 106 |
| story damping, ci (kNs/m) | 42.6 × 103 to 20 × 103 |
| story inertia, Ii (ton·m2) | 1.31 × 105 |
| foundation mass, m0 (ton) | 1960 |
| foundation inertia, I0 (ton·m2) | 1.96 × 105 |
| story height, hi (m) | 4 to 20 |
| story mass, mi (ton) | 300 |
| story stiffness, ki (kN/m) | 3.5 × 105 to 1.50 × 105 |
| story inertia, Ii (ton·m2) | 7.5 × 103 |
| foundation mass, m0 (ton) | 300 |
| foundation inertia, I0 (ton·m2) | 7.5 × 105 |
| story height, hi (m) | 4 to 40 |
| story mass, mi (ton) | 300 |
| story stiffness, ki (kN/m) | 7.0 × 105 to 3.00 × 105 |
| story inertia, Ii (ton·m2) | 7.5 × 103 |
| foundation mass, m0 (ton) | 300 |
| foundation inertia, I0 (ton·m2) | 7.5 × 105 |
| Event | Year | Magnitude (Mw) | Mechanism |
|---|---|---|---|
| Imperial Valley, US | 1940 | 6.95 | Strike Slip |
| Imperial Valley, US | 1979 | 6.53 | Strike Slip |
| Loma Prieta, US | 1989 | 6.93 | Reverse Oblique |
| Manjil, IR | 1990 | 7.37 | Strike Slip |
| Cape Mendocino, US | 1992 | 7.01 | Reverse |
| Erzincan, TR | 1992 | 6.69 | Strike Slip |
| Northridge, US | 1994 | 6.69 | Reverse |
| Dinar, TR | 1995 | 6.40 | Normal |
| Kobe, JP | 1995 | 6.90 | Strike Slip |
| Chi-Chi, TW | 1999 | 7.62 | Reverse Oblique |
| Düzce, TR | 1999 | 7.14 | Strike Slip |
| Hector Mine, US | 1999 | 7.13 | Strike Slip |
| Kocaeli, TR | 1999 | 7.51 | Strike Slip |
| Iwate, JP | 2008 | 6.90 | Reverse |
| Darfield, NZ | 2010 | 7.00 | Strike Slip |
| El Mayor Cucapah, MX | 2010 | 7.20 | Strike Slip |
| Christchurch, NZ | 2011 | 6.20 | Reverse Oblique |
| Earthquake | Station | Soil | Fixed (m) | BI (m) | BI Reduction (%) | SSI (m) | SSI_BI (m) | BI Reduction w/SSI (%) |
|---|---|---|---|---|---|---|---|---|
| Imperial Valley, 1940 | El Centro Array #9 | Very Soft | 0.185 | 0.078 | 57.86 | 0.075 | 0.053 | 29.29 |
| Imperial Valley, 1940 | El Centro Array #9 | Soft | 0.185 | 0.078 | 57.86 | 0.101 | 0.078 | 23.07 |
| Imperial Valley, 1940 | El Centro Array #9 | Medium | 0.185 | 0.078 | 57.86 | 0.163 | 0.078 | 52.06 |
| Imperial Valley, 1940 | El Centro Array #9 | Dense | 0.185 | 0.078 | 57.86 | 0.179 | 0.078 | 56.26 |
| Imperial Valley, 1979 | Calipatria Fire Station | Very Soft | 0.070 | 0.022 | 68.48 | 0.022 | 0.016 | 26.70 |
| Imperial Valley, 1979 | Calipatria Fire Station | Soft | 0.070 | 0.022 | 68.48 | 0.028 | 0.019 | 32.25 |
| Imperial Valley, 1979 | Calipatria Fire Station | Medium | 0.070 | 0.022 | 68.48 | 0.057 | 0.022 | 61.18 |
| Imperial Valley, 1979 | Calipatria Fire Station | Dense | 0.070 | 0.022 | 68.48 | 0.069 | 0.022 | 68.11 |
| Imperial Valley, 1979 | Delta | Very Soft | 0.103 | 0.051 | 50.32 | 0.053 | 0.046 | 12.30 |
| Imperial Valley, 1979 | Delta | Soft | 0.103 | 0.051 | 50.32 | 0.063 | 0.044 | 29.62 |
| Imperial Valley, 1979 | Delta | Medium | 0.103 | 0.051 | 50.32 | 0.084 | 0.051 | 39.14 |
| Imperial Valley, 1979 | Delta | Dense | 0.103 | 0.051 | 50.32 | 0.093 | 0.051 | 44.87 |
| Loma Prieta, 1989 | Alameda Naval Air Stn Hanger | Very Soft | 0.195 | 0.036 | 81.59 | 0.026 | 0.030 | −14.31 |
| Loma Prieta, 1989 | Alameda Naval Air Stn Hanger | Soft | 0.195 | 0.036 | 81.59 | 0.067 | 0.038 | 43.62 |
| Loma Prieta, 1989 | Alameda Naval Air Stn Hanger | Medium | 0.195 | 0.036 | 81.59 | 0.162 | 0.036 | 77.66 |
| Loma Prieta, 1989 | Alameda Naval Air Stn Hanger | Dense | 0.195 | 0.036 | 81.59 | 0.185 | 0.036 | 80.52 |
| Loma Prieta, 1989 | Capitola | Very Soft | 0.261 | 0.057 | 78.07 | 0.102 | 0.043 | 57.31 |
| Loma Prieta, 1989 | Capitola | Soft | 0.261 | 0.057 | 78.07 | 0.235 | 0.060 | 74.32 |
| Loma Prieta, 1989 | Capitola | Medium | 0.261 | 0.057 | 78.07 | 0.238 | 0.059 | 75.32 |
| Loma Prieta, 1989 | Capitola | Dense | 0.261 | 0.057 | 78.07 | 0.256 | 0.058 | 77.38 |
| Erzincan, 1992 (EW) | Erzincan | Very Soft | 0.516 | 0.250 | 51.55 | 0.232 | 0.197 | 15.14 |
| Erzincan, 1992 (EW) | Erzincan | Soft | 0.516 | 0.250 | 51.55 | 0.374 | 0.244 | 34.67 |
| Erzincan, 1992 (EW) | Erzincan | Medium | 0.516 | 0.250 | 51.55 | 0.481 | 0.250 | 47.90 |
| Erzincan, 1992 (EW) | Erzincan | Dense | 0.516 | 0.250 | 51.55 | 0.494 | 0.250 | 49.31 |
| Erzincan, 1992 (NS) | Erzincan | Very Soft | 0.571 | 0.249 | 56.40 | 0.231 | 0.196 | 15.26 |
| Erzincan, 1992 (NS) | Erzincan | Soft | 0.571 | 0.249 | 56.40 | 0.372 | 0.243 | 34.74 |
| Erzincan, 1992 (NS) | Erzincan | Medium | 0.571 | 0.249 | 56.40 | 0.479 | 0.249 | 47.95 |
| Erzincan, 1992 (NS) | Erzincan | Dense | 0.571 | 0.249 | 56.40 | 0.533 | 0.249 | 53.29 |
| Cape Mendocino, 1992 | Cape Mendocino | Very Soft | 0.285 | 0.106 | 62.85 | 0.126 | 0.111 | 12.50 |
| Cape Mendocino, 1992 | Cape Mendocino | Soft | 0.285 | 0.106 | 62.85 | 0.194 | 0.108 | 44.37 |
| Cape Mendocino, 1992 | Cape Mendocino | Medium | 0.285 | 0.106 | 62.85 | 0.256 | 0.106 | 58.53 |
| Cape Mendocino, 1992 | Cape Mendocino | Dense | 0.285 | 0.106 | 62.85 | 0.276 | 0.106 | 61.57 |
| Cape Mendocino, 1992 | Shelter Cove Airport | Very Soft | 0.009 | 0.004 | 52.19 | 0.006 | 0.003 | 50.17 |
| Cape Mendocino, 1992 | Shelter Cove Airport | Soft | 0.009 | 0.004 | 52.19 | 0.006 | 0.003 | 41.20 |
| Cape Mendocino, 1992 | Shelter Cove Airport | Medium | 0.009 | 0.004 | 52.19 | 0.008 | 0.004 | 44.65 |
| Cape Mendocino, 1992 | Shelter Cove Airport | Dense | 0.009 | 0.004 | 52.19 | 0.009 | 0.004 | 50.99 |
| Northridge, 1994 | Anacapa Island | Very Soft | 0.017 | 0.002 | 85.23 | 0.005 | 0.002 | 59.54 |
| Northridge, 1994 | Anacapa Island | Soft | 0.017 | 0.002 | 85.23 | 0.007 | 0.002 | 71.38 |
| Northridge, 1994 | Anacapa Island | Medium | 0.017 | 0.002 | 85.23 | 0.014 | 0.002 | 83.04 |
| Northridge, 1994 | Anacapa Island | Dense | 0.017 | 0.002 | 85.23 | 0.016 | 0.002 | 84.52 |
| Northridge, 1994 | Canoga Park | Very Soft | 0.637 | 0.320 | 49.77 | 0.297 | 0.252 | 15.26 |
| Northridge, 1994 | Canoga Park | Soft | 0.637 | 0.320 | 49.77 | 0.478 | 0.312 | 34.73 |
| Northridge, 1994 | Canoga Park | Medium | 0.637 | 0.320 | 49.77 | 0.614 | 0.320 | 47.87 |
| Northridge, 1994 | Canoga Park | Dense | 0.637 | 0.320 | 49.77 | 0.631 | 0.320 | 49.24 |
| Kobe, 1995 | Abeno | Very Soft | 0.107 | 0.025 | 76.62 | 0.034 | 0.016 | 53.33 |
| Kobe, 1995 | Abeno | Soft | 0.107 | 0.025 | 76.62 | 0.058 | 0.024 | 58.10 |
| Kobe, 1995 | Abeno | Medium | 0.107 | 0.025 | 76.62 | 0.080 | 0.025 | 68.67 |
| Kobe, 1995 | Abeno | Dense | 0.107 | 0.025 | 76.62 | 0.097 | 0.025 | 74.17 |
| Kobe, 1995 | HIK | Very Soft | 0.103 | 0.029 | 71.54 | 0.032 | 0.016 | 48.03 |
| Kobe, 1995 | HIK | Soft | 0.103 | 0.029 | 71.54 | 0.076 | 0.022 | 71.56 |
| Kobe, 1995 | HIK | Medium | 0.103 | 0.029 | 71.54 | 0.092 | 0.029 | 68.64 |
| Kobe, 1995 | HIK | Dense | 0.103 | 0.029 | 71.54 | 0.099 | 0.029 | 70.56 |
| Dinar, 1995 | Balikesir | Very Soft | 0.005 | 0.002 | 60.24 | 0.003 | 0.001 | 52.65 |
| Dinar, 1995 | Balikesir | Soft | 0.005 | 0.002 | 60.24 | 0.007 | 0.002 | 74.38 |
| Dinar, 1995 | Balikesir | Medium | 0.005 | 0.002 | 60.24 | 0.005 | 0.002 | 65.64 |
| Dinar, 1995 | Balikesir | Dense | 0.005 | 0.002 | 60.24 | 0.005 | 0.002 | 62.85 |
| Dinar, 1995 | Dinar | Very Soft | 0.309 | 0.110 | 64.31 | 0.156 | 0.061 | 61.02 |
| Dinar, 1995 | Dinar | Soft | 0.309 | 0.110 | 64.31 | 0.225 | 0.103 | 54.45 |
| Dinar, 1995 | Dinar | Medium | 0.309 | 0.110 | 64.31 | 0.269 | 0.110 | 59.31 |
| Dinar, 1995 | Dinar | Dense | 0.309 | 0.110 | 64.31 | 0.306 | 0.110 | 64.02 |
| Kocaeli, 1999 | Arcelik | Very Soft | 0.053 | 0.016 | 70.20 | 0.017 | 0.014 | 16.73 |
| Kocaeli, 1999 | Arcelik | Soft | 0.053 | 0.016 | 70.20 | 0.034 | 0.016 | 53.71 |
| Kocaeli, 1999 | Arcelik | Medium | 0.053 | 0.016 | 70.20 | 0.052 | 0.016 | 69.52 |
| Kocaeli, 1999 | Arcelik | Dense | 0.053 | 0.016 | 70.20 | 0.053 | 0.016 | 70.43 |
| Kocaeli, 1999 | Istanbul | Very Soft | 0.014 | 0.010 | 31.95 | 0.009 | 0.009 | 1.23 |
| Kocaeli, 1999 | Istanbul | Soft | 0.014 | 0.010 | 31.95 | 0.016 | 0.010 | 40.94 |
| Kocaeli, 1999 | Istanbul | Medium | 0.014 | 0.010 | 31.95 | 0.014 | 0.010 | 28.99 |
| Kocaeli, 1999 | Istanbul | Dense | 0.014 | 0.010 | 31.95 | 0.013 | 0.010 | 25.07 |
| Chi-Chi, 1999 | CHY006 | Very Soft | 0.362 | 0.073 | 79.85 | 0.087 | 0.060 | 31.67 |
| Chi-Chi, 1999 | CHY006 | Soft | 0.362 | 0.073 | 79.85 | 0.183 | 0.071 | 61.13 |
| Chi-Chi, 1999 | CHY006 | Medium | 0.362 | 0.073 | 79.85 | 0.344 | 0.073 | 78.76 |
| Chi-Chi, 1999 | CHY006 | Dense | 0.362 | 0.073 | 79.85 | 0.357 | 0.073 | 79.57 |
| Chi-Chi, 1999 | CHY101 | Very Soft | 0.216 | 0.080 | 62.68 | 0.092 | 0.103 | −11.95 |
| Chi-Chi, 1999 | CHY101 | Soft | 0.216 | 0.080 | 62.68 | 0.103 | 0.094 | 8.96 |
| Chi-Chi, 1999 | CHY101 | Medium | 0.216 | 0.080 | 62.68 | 0.173 | 0.082 | 52.78 |
| Chi-Chi, 1999 | CHY101 | Dense | 0.216 | 0.080 | 62.68 | 0.197 | 0.081 | 58.97 |
| Duzce, 1999 | Bursa | Very Soft | 0.848 | 0.433 | 48.95 | 0.401 | 0.341 | 15.03 |
| Duzce, 1999 | Bursa | Soft | 0.848 | 0.433 | 48.95 | 0.643 | 0.422 | 34.35 |
| Duzce, 1999 | Bursa | Medium | 0.848 | 0.433 | 48.95 | 0.820 | 0.433 | 47.22 |
| Duzce, 1999 | Bursa | Dense | 0.848 | 0.433 | 48.95 | 0.840 | 0.433 | 48.45 |
| Duzce, 1999 | Duzce | Very Soft | 0.632 | 0.316 | 49.95 | 0.295 | 0.249 | 15.42 |
| Duzce, 1999 | Duzce | Soft | 0.632 | 0.316 | 49.95 | 0.474 | 0.309 | 34.88 |
| Duzce, 1999 | Duzce | Medium | 0.632 | 0.316 | 49.95 | 0.610 | 0.317 | 48.03 |
| Duzce, 1999 | Duzce | Dense | 0.632 | 0.316 | 49.95 | 0.626 | 0.317 | 49.42 |
| Manjil, 1990 | Abbar | Very Soft | 0.110 | 0.079 | 28.09 | 0.061 | 0.060 | 1.50 |
| Manjil, 1990 | Abbar | Soft | 0.110 | 0.079 | 28.09 | 0.078 | 0.087 | −10.94 |
| Manjil, 1990 | Abbar | Medium | 0.110 | 0.079 | 28.09 | 0.092 | 0.082 | 10.35 |
| Manjil, 1990 | Abbar | Dense | 0.110 | 0.079 | 28.09 | 0.099 | 0.081 | 18.94 |
| Manjil, 1990 | Rudsar | Very Soft | 0.057 | 0.015 | 73.12 | 0.026 | 0.012 | 55.12 |
| Manjil, 1990 | Rudsar | Soft | 0.057 | 0.015 | 73.12 | 0.053 | 0.015 | 71.25 |
| Manjil, 1990 | Rudsar | Medium | 0.057 | 0.015 | 73.12 | 0.061 | 0.015 | 75.50 |
| Manjil, 1990 | Rudsar | Dense | 0.057 | 0.015 | 73.12 | 0.058 | 0.015 | 73.63 |
| Hector Mine, 1999 | Banning | Very Soft | 0.011 | 0.006 | 40.51 | 0.006 | 0.004 | 34.64 |
| Hector Mine, 1999 | Banning | Soft | 0.011 | 0.006 | 40.51 | 0.006 | 0.006 | 8.82 |
| Hector Mine, 1999 | Banning | Medium | 0.011 | 0.006 | 40.51 | 0.010 | 0.006 | 35.18 |
| Hector Mine, 1999 | Banning | Dense | 0.011 | 0.006 | 40.51 | 0.010 | 0.006 | 38.88 |
| Hector Mine, 1999 | Indio | Very Soft | 0.073 | 0.044 | 39.99 | 0.046 | 0.035 | 24.68 |
| Hector Mine, 1999 | Indio | Soft | 0.073 | 0.044 | 39.99 | 0.082 | 0.046 | 43.52 |
| Hector Mine, 1999 | Indio | Medium | 0.073 | 0.044 | 39.99 | 0.067 | 0.044 | 34.91 |
| Hector Mine, 1999 | Indio | Dense | 0.073 | 0.044 | 39.99 | 0.071 | 0.044 | 38.34 |
| Iwate, 2008 | AKT023 | Very Soft | 0.186 | 0.036 | 80.50 | 0.043 | 0.030 | 31.37 |
| Iwate, 2008 | AKT023 | Soft | 0.186 | 0.036 | 80.50 | 0.085 | 0.035 | 58.73 |
| Iwate, 2008 | AKT023 | Medium | 0.186 | 0.036 | 80.50 | 0.161 | 0.036 | 77.71 |
| Iwate, 2008 | AKT023 | Dense | 0.186 | 0.036 | 80.50 | 0.179 | 0.036 | 79.83 |
| Iwate, 2008 | IWT010 | Very Soft | 0.139 | 0.067 | 51.61 | 0.062 | 0.043 | 30.69 |
| Iwate, 2008 | IWT010 | Soft | 0.139 | 0.067 | 51.61 | 0.080 | 0.065 | 18.65 |
| Iwate, 2008 | IWT010 | Medium | 0.139 | 0.067 | 51.61 | 0.129 | 0.068 | 46.80 |
| Iwate, 2008 | IWT010 | Dense | 0.139 | 0.067 | 51.61 | 0.137 | 0.068 | 50.50 |
| El Mayor-Cucapah, 2010 | Chihuahua | Very Soft | 0.133 | 0.040 | 69.61 | 0.038 | 0.053 | −38.85 |
| El Mayor-Cucapah, 2010 | Chihuahua | Soft | 0.133 | 0.040 | 69.61 | 0.134 | 0.046 | 65.74 |
| El Mayor-Cucapah, 2010 | Chihuahua | Medium | 0.133 | 0.040 | 69.61 | 0.138 | 0.041 | 70.22 |
| El Mayor-Cucapah, 2010 | Chihuahua | Dense | 0.133 | 0.040 | 69.61 | 0.142 | 0.041 | 71.50 |
| El Mayor-Cucapah, 2010 | Michoacan de Ocampo | Very Soft | 0.332 | 0.113 | 65.99 | 0.107 | 0.095 | 11.68 |
| El Mayor-Cucapah, 2010 | Michoacan de Ocampo | Soft | 0.332 | 0.113 | 65.99 | 0.184 | 0.117 | 36.35 |
| El Mayor-Cucapah, 2010 | Michoacan de Ocampo | Medium | 0.332 | 0.113 | 65.99 | 0.276 | 0.114 | 58.63 |
| El Mayor-Cucapah, 2010 | Michoacan de Ocampo | Dense | 0.332 | 0.113 | 65.99 | 0.315 | 0.113 | 63.95 |
| Darfield, 2010 | Canterbury Aero Club | Very Soft | 0.056 | 0.037 | 35.09 | 0.045 | 0.029 | 34.56 |
| Darfield, 2010 | Canterbury Aero Club | Soft | 0.056 | 0.037 | 35.09 | 0.052 | 0.039 | 24.88 |
| Darfield, 2010 | Canterbury Aero Club | Medium | 0.056 | 0.037 | 35.09 | 0.050 | 0.037 | 25.14 |
| Darfield, 2010 | Canterbury Aero Club | Dense | 0.056 | 0.037 | 35.09 | 0.053 | 0.037 | 30.06 |
| Darfield, 2010 | DSLC | Very Soft | 0.218 | 0.064 | 70.61 | 0.053 | 0.046 | 12.41 |
| Darfield, 2010 | DSLC | Soft | 0.218 | 0.064 | 70.61 | 0.071 | 0.071 | 0.30 |
| Darfield, 2010 | DSLC | Medium | 0.218 | 0.064 | 70.61 | 0.196 | 0.066 | 66.20 |
| Darfield, 2010 | DSLC | Dense | 0.218 | 0.064 | 70.61 | 0.215 | 0.065 | 69.82 |
| Christchurch, 2011 | ADCS | Very Soft | 0.017 | 0.003 | 81.89 | 0.006 | 0.003 | 46.34 |
| Christchurch, 2011 | ADCS | Soft | 0.017 | 0.003 | 81.89 | 0.006 | 0.003 | 49.92 |
| Christchurch, 2011 | ADCS | Medium | 0.017 | 0.003 | 81.89 | 0.014 | 0.003 | 78.63 |
| Christchurch, 2011 | ADCS | Dense | 0.017 | 0.003 | 81.89 | 0.016 | 0.003 | 80.98 |
| Christchurch, 2011 | CECS | Very Soft | 0.009 | 0.006 | 38.67 | 0.009 | 0.003 | 64.57 |
| Christchurch, 2011 | CECS | Soft | 0.009 | 0.006 | 38.67 | 0.007 | 0.004 | 31.37 |
| Christchurch, 2011 | CECS | Medium | 0.009 | 0.006 | 38.67 | 0.008 | 0.006 | 30.16 |
| Christchurch, 2011 | CECS | Dense | 0.009 | 0.006 | 38.67 | 0.009 | 0.006 | 36.30 |
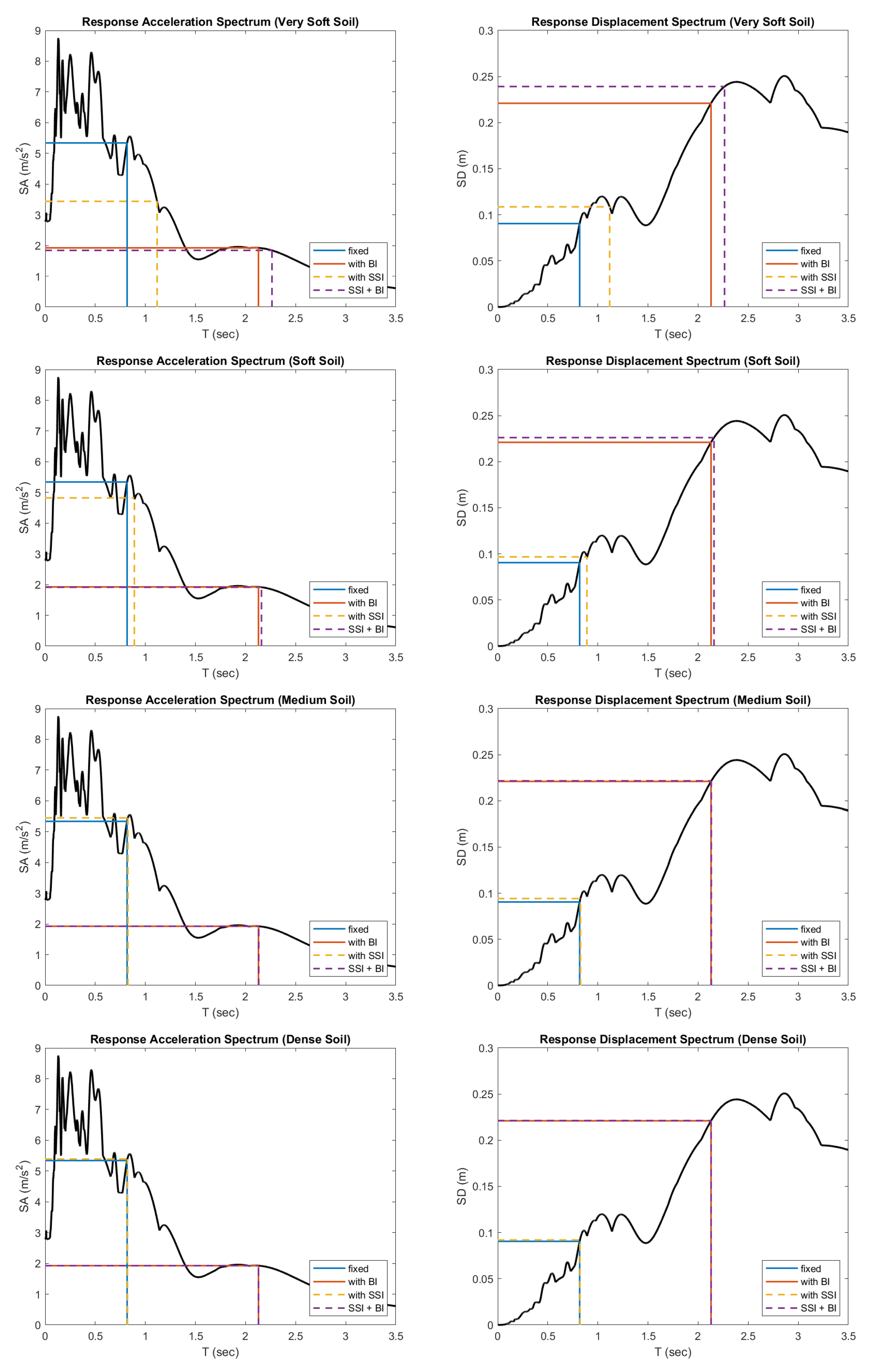
| Soil | Base | T (s) | SV (m/s) | SD (m) | |
|---|---|---|---|---|---|
| Very Soft Soil | fixed | 0.82 | 5.34 | 0.70 | 0.09 |
| Very Soft Soil | BI | 2.13 | 1.93 | 0.65 | 0.22 |
| Very Soft Soil | SSI | 1.12 | 3.44 | 0.61 | 0.11 |
| Very Soft Soil | SSI+BI | 2.26 | 1.84 | 0.66 | 0.24 |
| Soft Soil | fixed | 0.82 | 5.34 | 0.70 | 0.09 |
| Soft Soil | BI | 2.13 | 1.93 | 0.65 | 0.22 |
| Soft Soil | SSI | 0.89 | 4.82 | 0.68 | 0.10 |
| Soft Soil | SSI+BI | 2.16 | 1.92 | 0.66 | 0.23 |
| Medium Soil | fixed | 0.82 | 5.34 | 0.70 | 0.09 |
| Medium Soil | BI | 2.13 | 1.93 | 0.65 | 0.22 |
| Medium Soil | SSI | 0.83 | 5.45 | 0.72 | 0.09 |
| Medium Soil | SSI+BI | 2.13 | 1.92 | 0.65 | 0.22 |
| Dense Soil | fixed | 0.82 | 5.34 | 0.70 | 0.09 |
| Dense Soil | BI | 2.13 | 1.93 | 0.65 | 0.22 |
| Dense Soil | SSI | 0.82 | 5.39 | 0.70 | 0.09 |
| Dense Soil | SSI+BI | 2.13 | 1.92 | 0.65 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanik, A.; Ulus, Y. Soil–Structure Interaction Consideration for Base Isolated Structures under Earthquake Excitation. Buildings 2023, 13, 915. https://doi.org/10.3390/buildings13040915
Yanik A, Ulus Y. Soil–Structure Interaction Consideration for Base Isolated Structures under Earthquake Excitation. Buildings. 2023; 13(4):915. https://doi.org/10.3390/buildings13040915
Chicago/Turabian StyleYanik, Arcan, and Yalcincan Ulus. 2023. "Soil–Structure Interaction Consideration for Base Isolated Structures under Earthquake Excitation" Buildings 13, no. 4: 915. https://doi.org/10.3390/buildings13040915






