Safety Risk Analysis of Urban Viaduct Construction Based on Dynamic Weight
Abstract
:1. Introduction
- (1)
- The WBS-RBS matrix is utilized to identify and establish an evaluation index system for construction safety risks in urban elevated bridge projects, considering the perspectives of construction activities and risk sources. This index system effectively tackles the challenges of diverse construction activities and complex risk factors, thereby laying a solid foundation for systematic research in the related field;
- (2)
- A novel dynamic weighting calculation method is introduced, tailored to better suit engineering practices and management requirements. This method aptly elucidates the dynamic impact of various evaluation indicators on risk assessment outcomes, thereby facilitating a more scientific and effective calculation of construction risk weights;
- (3)
- A case study of the Longlingshan elevated bridge project in Wuhan, China, is undertaken, resulting in numerous novel and valuable research findings that offer practical guidance for engineering.
2. The Proposed Method for Safety Risk Analysis of Urban Viaduct Construction
2.1. Identification of Factors Influencing Construction Safety Risks in Urban Elevated Bridge Projects Based on WBS-RBS
2.1.1. WBS of Urban Elevated Bridge Projects
- (1)
- Deep foundation pit construction. The deep foundation pit project for elevated bridges mainly includes the following construction activities: dewatering (); earthwork excavation (); pile foundation construction (); and pit monitoring ();
- (2)
- Pier construction. The construction of piers for elevated bridges primarily involves various stages, such as construction preparation (), scaffold erection and removal (), steel reinforcement processing and installation (), formwork installation and removal (), and concrete pouring and curing ();
- (3)
- Component hoisting construction. The construction of component hoisting mainly emphasizes several stages, including construction preparation (), crane fixing (), vertical transportation (), and horizontal transportation ();
- (4)
- Construction of cast-in-situ formwork. The construction of cast-in-situ formwork regroups the preparation for construction (), foundation treatment (), formwork erection and prestressing (), formwork installation and removal (), and concrete pouring and curing ().
2.1.2. RBS of Urban Elevated Bridge Project
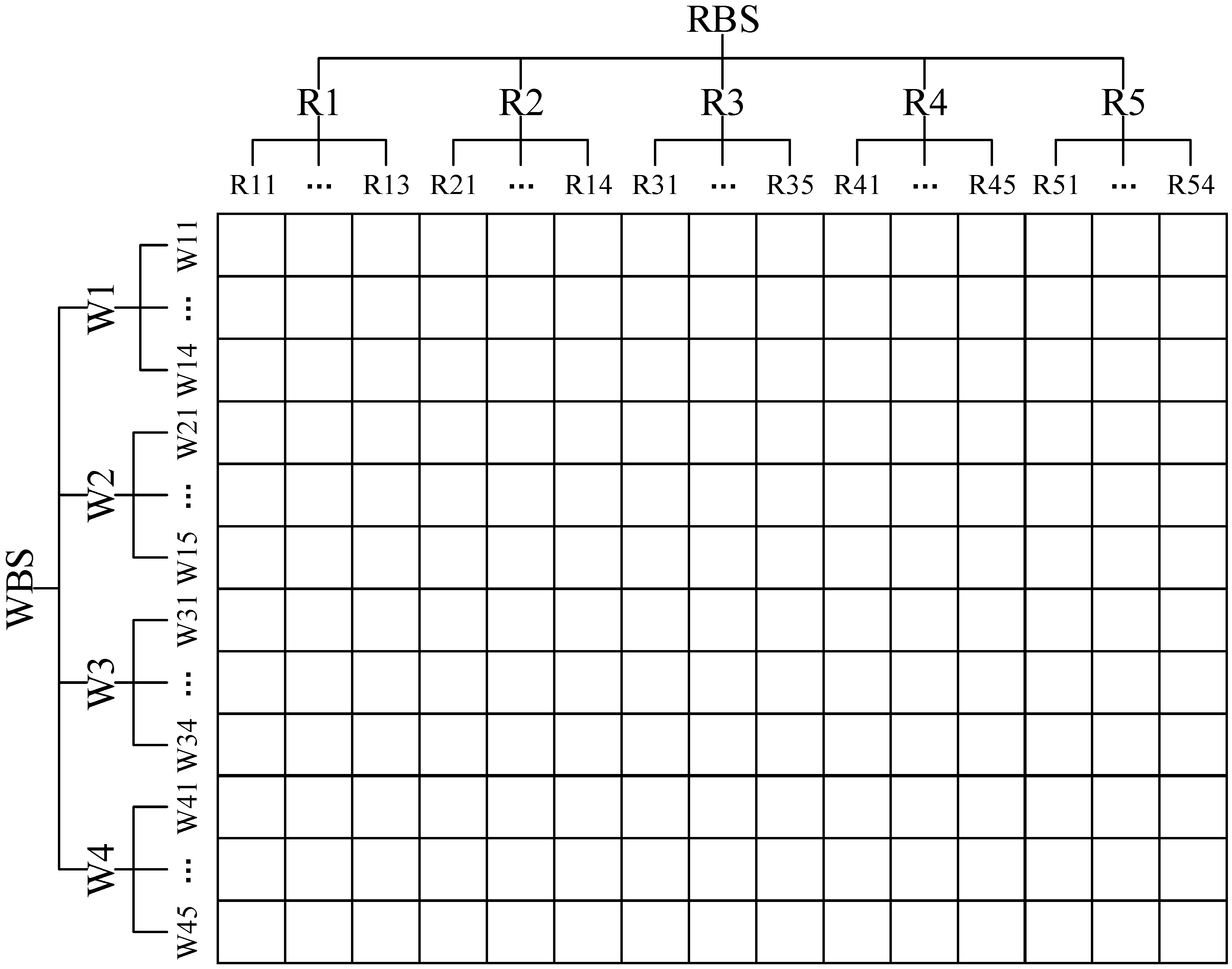
2.1.3. WBS-RBS Matrix for Construction Safety Risks of Urban Elevated Bridge Projects
2.2. Evaluation Indicator System Proposed in this Study
- (1)
- Determine the goals and objectives of the questionnaire survey. It is to obtain experts’ judgment on the importance of safety risk factors in urban viaduct construction using the questionnaire survey of many experts;
- (2)
- Select experts. According to the research needs, select experts with relevant knowledge and rich experience, including engineers, architects, construction managers, safety consultants, etc.;
- (3)
- Design a questionnaire. Design a questionnaire according to the research objectives to ensure that the questions cover all research topics. When formulating questions, we should not only cover closed questions (such as multiple-choice questions and true–false questions) for quantitative analysis but also include open questions to collect in-depth responses. Design concise and clear instructions and questions to prevent misunderstanding. A pretest was conducted before the official release to test the understandability and effectiveness of the questionnaire;
- (4)
- Determine the sample. According to the purpose and needs of this study, the survey object is determined by random sampling, stratified sampling, or convenient sampling. Set the sample size, considering the reliability and statistical power of the data;
- (5)
- Collect data. Determine the distribution method of the questionnaire, which can be online (e.g., via e-mail or online survey platform) or offline (paper questionnaire);
- (6)
- Data processing and analysis. After collection, data entry and cleaning are carried out, including eliminating invalid questionnaires and dealing with missing data. Descriptive statistical analysis (such as mean and standard deviation) and inferential analysis (such as correlation analysis and regression analysis) are carried out to answer the research questions.
2.3. Proposed Method for Dynamic Weight Calculation in This Article
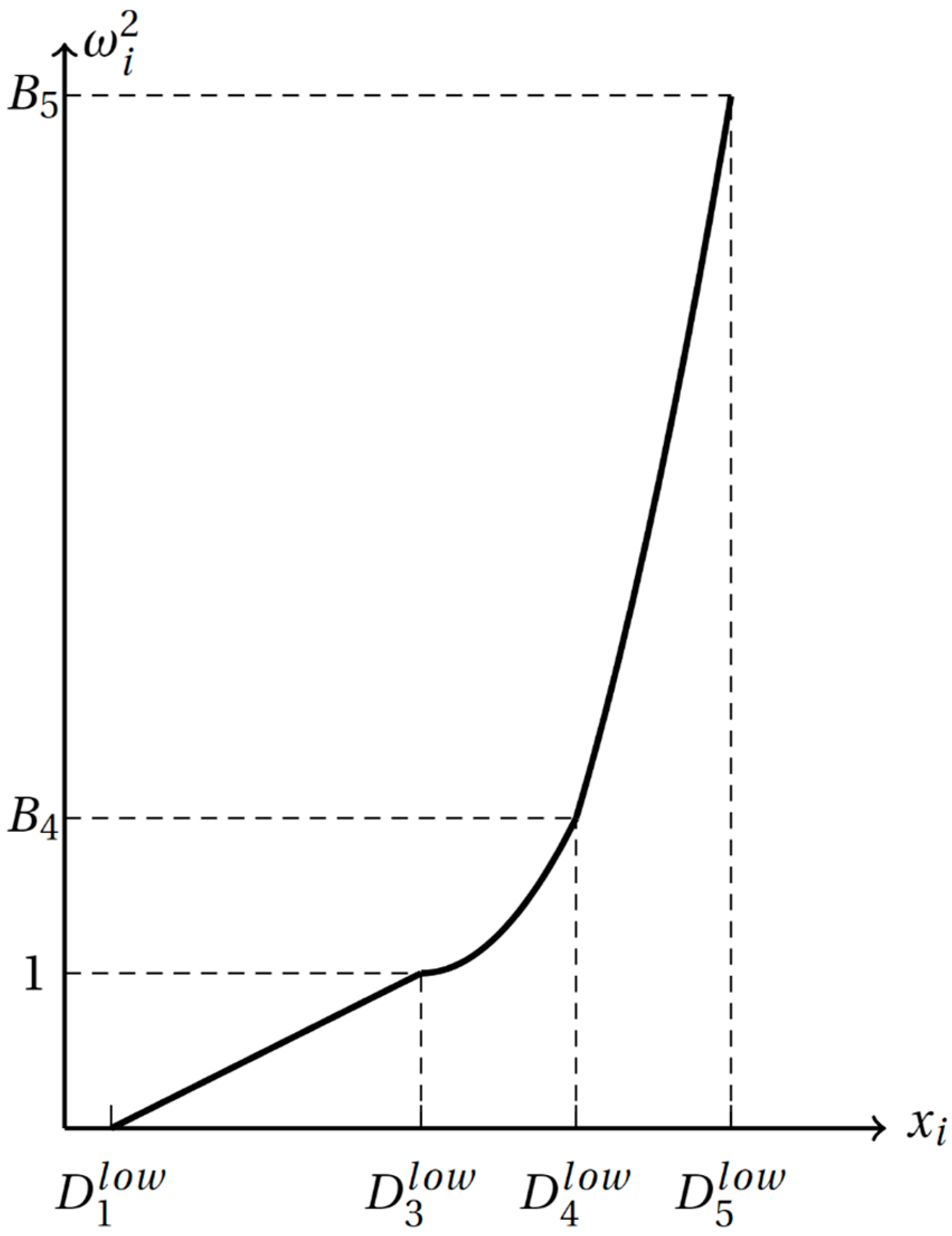
- (1)
- When the indicator score is within the safe risk levels I, II, and III, project managers have a relatively optimistic attitude toward risk. Therefore, the dynamic weight is small and shows a linear and slow growth trend. At this point, the indicator weight mainly relies on static weights;
- (2)
- When the indicator score is within the safe risk level IV, it shows that the indicator is within a more dangerous score range, leading project managers to adopt a relatively pessimistic attitude toward the risk. Therefore, the dynamic weight of the indicator should not be ignored, and it increases rapidly in a quadratic function form;
- (3)
- When the indicator score is within the safe risk level V, it indicates that the indicator is within a highly dangerous score range, prompting project managers to adopt an extremely pessimistic attitude toward risk. At this juncture, the dynamic weight of the indicator significantly impacts the risk evaluation results, leading to a rapid increase in an exponential function form. The mapping relationship between the dynamic score of the indicator and the dynamic weight is depicted in Figure 3. It is important to note that the reference to Figure 3 is based on the context provided by the user. The precise content and description of this figure may vary and should be provided by the user for accurate translation.
2.4. Implementation Method of the Proposed Model
- Step 1.
- Divide the evaluation levels of each secondary indicator according to project management needs. For quantitative indicators, divide them based on practical requirements and regulatory standards. The evaluation levels of qualitative indicators are more complex, including quantitative evaluation ranges and corresponding qualitative language descriptors. Different qualitative indicators correspond to the same quantitative range but have completely different qualitative language descriptors;
- Step 2.
- Data Collection and Preprocessing. Qualitative indicators are gathered using questionnaire surveys or expert interviews and then converted into quantitative data. Moreover, quantitative indicators are collected and calculated using on-site statistical methods. Depending on the type of indicator, data from different time points are normalized using Equations (1) or (2);
- Step 3.
- Calculate the static weights for all indicators. Before the implementation of the project, expert judgments on the relative importance of different indicators are collected using a questionnaire survey. This paper suggests the use of a scoring rule of 1–5 or 1–9 [11] to collect these static weights. The classic AHP is then employed to compute the static weights for all indicators;
- Step 4.
- Calculate the dynamic weights for all the indicators. In this step, Equation (4) is used to calculate the dynamic weights , using the scores of the secondary indicators collected in Step 2;
- Step 5.
- Calculate the combined weights of the indicators for subsequent analysis. By applying the static and dynamic weights to Equation (5), the final weights for each indicator can be generated.
3. Case Study
3.1. Engineering Background and Data Acquisition
3.2. Calculation of Indicator Weights
- (1)
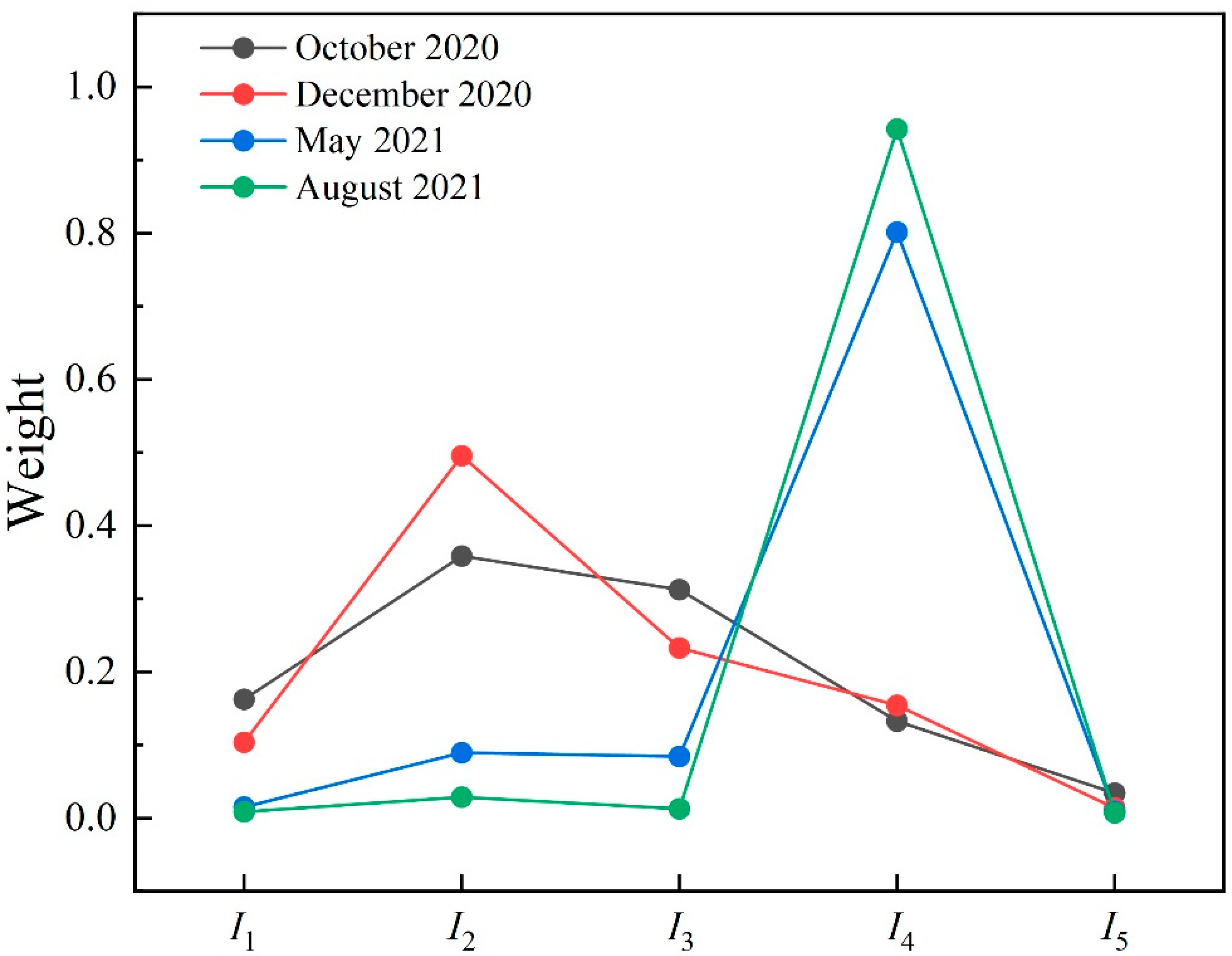
- The prevailing research suggests that man () or management () represent the most important primary indicators affecting construction safety. However, this study analyzed the weight variations in indicators during the construction stages and found that the most important primary indicators varied across different stages. Unlike typical construction projects, this case study involves an urban elevated bridge project that extensively applies construction machinery instead of relying heavily on construction workers. Therefore, it is reasonable to assign higher weights to machinery-related indicators;
- (2)
- Current research suggests that the uncertainty of construction risks appears to be evenly distributed among the five risk dimensions (e.g., man, machine, material, methods, and environment). However, the empirical results of this study highlight that the uncertainty of construction risks primarily stems from the construction environment (). This finding is attributed to the dynamic evaluation of this project. Wuhan is one of the hottest cities in China during the summer, and construction projects often experience work stoppages during high temperatures, while other factors are less likely to cause such disruptions. Hence, this unique condition in the present study is explainable.
- (1)
- Adjust the construction plan according to the climate forecast to avoid construction under extreme weather conditions. Use construction materials and technologies suitable for various weather conditions. Conduct a detailed geological survey before construction and take measures to reinforce or change the construction scheme if the risk of landslide or debris flow is found. Monitor the change in water level in real time, set up flood control measures, and reserve sufficient drainage facilities. Adopt environmental protection construction methods, such as using construction equipment with low vibration and noise and reasonably arranging construction time;
- (2)
- Conduct emergency drills to ensure that all personnel are familiar with the emergency plan and improve the ability to respond rapidly. Prepare emergency materials, such as flood control sandbags, emergency lighting, first aid kits, and emergency evacuation facilities. Establish a rapid response mechanism, including the establishment of effective communication channels, so as to respond quickly when sudden environmental incidents occur;
- (3)
- Implement continuous environmental monitoring, including weather monitoring, geological stability monitoring, and hydrological condition monitoring, to ensure that key environmental information can be obtained in time. Regularly review and update the environmental risk management plan and adjust the management measures according to the project progress and emerging risk information. Train all construction personnel in environmental risk management and emergency response to improve their awareness of environmental changes and their ability to deal with emergencies. Emphasize safety culture and encourage employees to report potential environmental risks and put forward suggestions for improvement.
4. Discussion
4.1. Discussion on Different Risk Identification Methods
4.2. Generalization of the Proposed Strategy in the Field of Weight Calculation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buyukozkan, G.; Feyzioglu, O.; Gocer, F. Selection of sustainable urban transportation alternatives using an integrated intuitionistic fuzzy Choquet integral approach. Transp. Res. Part D Transp. Environ. 2018, 58, 186–207. [Google Scholar] [CrossRef]
- Chen, F.Y.; Ji, H.C.; Wei, Y.C. Using Network Theory to Explore the Risk Characteristics of Bridge-Tunnel Hybrid Construction. IEEE Access 2019, 7, 116038–116046. [Google Scholar] [CrossRef]
- Okpala, I.; Nnaji, C.; Karakhan, A.A. Utilizing Emerging Technologies for Construction Safety Risk Mitigation. Pract. Period. Struct. Des. Constr. 2020, 25, 04020002. [Google Scholar] [CrossRef]
- Li, Q.F.; Zhou, J.P.; Feng, J.H. Safety Risk Assessment of Highway Bridge Construction Based on Cloud Entropy Power Method. Appl. Sci. 2022, 12, 8692. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Mortazavi, S. Risk Assessment in Bridge Construction Projects in Iran Using Monte Carlo Simulation Technique. Pract. Period. Struct. Des. Constr. 2019, 24, 04019026. [Google Scholar] [CrossRef]
- Lin, J.R.; Zhang, J.P.; Zhang, X.Y.; Hu, Z.Z. Automating closed-loop structural safety management for bridge construction through multisource data integration. Adv. Eng. Softw. 2019, 128, 152–168. [Google Scholar] [CrossRef]
- Wu, Y.; Lu, P.Z. Comparative Analysis and Evaluation of Bridge Construction Risk with Multiple Intelligent Algorithms. Math. Probl. Eng. 2022, 2022, 2638273. [Google Scholar] [CrossRef]
- Wu, H.; Liu, S.; Wang, J.W.; Yang, T.Y. Construction Safety Risk Assessment of Bridges in the Marine Environment Based on CRITIC and TOPSIS Models. J. Coast. Res. 2020, 108, 206–210. [Google Scholar] [CrossRef]
- Ji, T.; Liu, J.W.; Li, Q.F. Safety Risk Evaluation of Large and Complex Bridges during Construction Based on the Delphi-Improved FAHP-Factor Analysis Method. Adv. Civ. Eng. 2022, 2022, 5397032. [Google Scholar] [CrossRef]
- Khan, M.A.; Khan, A.A.; Anwar, G.A.; Usmani, A. Framework for fire risk assessment of bridges. Structures 2021, 33, 523–532. [Google Scholar] [CrossRef]
- Peng, K.K. Risk Evaluation for Bridge Engineering Based on Cloud-Clustering Group Decision Method. J. Perform. Constr. Facil. 2019, 33, 04018105. [Google Scholar] [CrossRef]
- Ju, W.Y.; Wu, J.; Kang, Q.C.; Jiang, J.C.; Xing, Z.X. A method based on the theories of game and extension cloud for risk assessment of construction safety: A case study considering disaster-inducing factors in the construction process. J. Build. Eng. 2022, 62, 105317. [Google Scholar] [CrossRef]
- Elmarzouky, M.; Hussainey, K.; Abdelfattah, T. The key audit matters and the audit cost: Does governance matter? Int. J. Account. Inf. Manag. 2023, 31, 195–217. [Google Scholar] [CrossRef]
- Ostenfeld, K.H.; Andersen, E.Y. Major bridge projects—A multi-disciplinary approach. Front. Struct. Civ. Eng. 2011, 5, 479–495. [Google Scholar] [CrossRef]
- Wang, J. Construction of Risk Evaluation Index System for Power Grid Engineering Cost by Applying WBS-RBS and Membership Degree Methods. Math. Probl. Eng. 2020, 2020, 6217872. [Google Scholar] [CrossRef]
- Chen, J.H.; Li, K.; Yang, S. Electric Vehicle Fire Risk Assessment Based on WBS-RBS and Fuzzy BN Coupling. Mathematics 2022, 10, 3799. [Google Scholar] [CrossRef]
- Bilal, M.; Ali, G.; Iqbal, M.W.; Anwar, M.; Malik, M.S.A.; Kadir, R.A. Auto-Prep: Efficient and Automated Data Preprocessing Pipeline. IEEE Access 2022, 10, 107764–107784. [Google Scholar] [CrossRef]
- Felix, E.A.; Lee, S.P. Systematic literature review of preprocessing techniques for imbalanced data. IET Softw. 2019, 13, 479–496. [Google Scholar] [CrossRef]
- Li, Y.K.; Hu, Y.; Xia, B.; Skitmore, M.; Li, H. Proactive behavior-based system for controlling safety risks in urban highway construction megaprojects. Autom. Constr. 2018, 95, 118–128. [Google Scholar] [CrossRef]
- Finan, J.S.; Hurley, W.J. Transitive calibration of the AHP verbal scale. Eur. J. Oper. Res. 1999, 112, 367–372. [Google Scholar] [CrossRef]
- Ji, B.; Ye, Y.; Xiao, Y. A Combination Weighting Algorithm Using Relative Entropy for Document Clustering. Int. J. Pattern Recognit. Artif. Intell. 2014, 28, 1453002. [Google Scholar] [CrossRef]
- Shohaieb, D.; Elmarzouky, M.; Albitar, K. Corporate governance and diversity management: Evidence from a disclosure perspective. Int. J. Account. Inf. Manag. 2022, 30, 502–525. [Google Scholar] [CrossRef]
- Cha, Y.J.; Lee, J.J.; Kim, D.H.; You, J.H. The validity and reliability of a dynamic neuromuscular stabilization-heel sliding test for core stability. Technol. Health Care 2017, 25, 981–988. [Google Scholar] [CrossRef] [PubMed]
- Dijksterhuis, M.G.K.; Jozwiak, I.; Braat, D.D.M.; Scheele, F. An exploratory study into the effect of time-restricted internet access on face-validity, construct validity and reliability of postgraduate knowledge progress testing. BMC Med. Educ. 2013, 13, 147. [Google Scholar] [CrossRef] [PubMed]
- Mu, E.; Pereyra-Rojas, M. Ratings Models Using Super Decisions v3. In Practical Decision Making Using Super Decisions V3: An Introduction to the Analytic Hierarchy Process; SpringerBriefs in Operations Research; Springer: Berlin/Heidelberg, Germany, 2018; pp. 61–70. [Google Scholar]
- Shirai, G.A.; Nematpour, L. Evaluation of resilience engineering using super decisions software. Health Promot. Perspect. 2019, 9, 191–197. [Google Scholar] [CrossRef] [PubMed]
- Jerie, S.; Shabani, T.; Mudyazhezha, O.C.; Shabani, T. A review towards developing a hierarchical model for sustainable hospital solid waste management in rural areas of Zimbabwe. Environ. Monit. Assess. 2024, 196, 308. [Google Scholar] [CrossRef] [PubMed]
- Lefort, A.; Bourdais, R.; Ansanay-Alex, G.; Guéguen, H. Hierarchical control method applied to energy management of a residential house. Energy Build. 2013, 64, 53–61. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, Y.H.; Shen, Q.; Yang, L.; Cai, H.B. Risk assessment and management via multi-source information fusion for undersea tunnel construction. Autom. Constr. 2020, 111, 103050. [Google Scholar] [CrossRef]
- You, Q.; Zhang, Z.W.; Wang, H.T.; Xu, M.Y. Risk identification of subway tunnel shield construction based on WBS-RBS method. Int. J. Crit. Infrastruct. 2023, 19, 261–273. [Google Scholar] [CrossRef]
- Chang, C.G.; Dai, B.B. Safety Risk Optimization of Prefabricated Building Construction based on Improved Bat Algorithm. In Proceedings of the 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 2059–2064. [Google Scholar]
- Dong, S.H.; Li, S.Q.; Yu, F.; Wang, K. Risk Assessment of Immersed Tube Tunnel Construction. Processes 2023, 11, 980. [Google Scholar] [CrossRef]
- He, Z.G.; Guo, J.N. Security Risk Assessment of Multimodal Transport Network Based on WBS-RBS and PFWA Operator. In Proceedings of the 4th International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 5–7 September 2019; pp. 203–206. [Google Scholar]
- Kim, K.N.; Kim, T.H.; Lee, M.J. Analysis of Building Construction Jobsite Accident Scenarios Based on Big Data Association Analysis. Buildings 2023, 13, 2120. [Google Scholar] [CrossRef]
- Liu, S.H.; Song, Z.P.; Zhang, Y.; Guo, D.S.; Sun, Y.H.; Zeng, T.; Xie, J.S. Risk assessment of deep excavation construction based on combined weighting and nonlinear FAHP. Front. Earth Sci. 2023, 11, 1204721. [Google Scholar] [CrossRef]
- Wang, X.; Lu, H.L.; Su, W.Y.; Zhu, X.H. Risk Analysis and Assessment of Shield Tunnel Construction in Karst Area. In Proceedings of the 8th International Conference on Hydraulic and Civil Engineering—Deep Space Intelligent Development and Utilization Forum (ICHCE), Xian, China, 25–27 November 2022; pp. 674–680. [Google Scholar]
- Kumar, R.; Singh, S.; Bilga, P.S.; Singh, J.; Singh, S.; Scutaru, M.L.; Pruncu, C.I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. JMRT 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Xu, G.X.; Liu, P.D. The Evaluation Study of Human Resource Based on Extended C-OWA Operators and TOPSIS Method. In Proceedings of the 3rd International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM 2007), Shanghai, China, 21–25 September 2007; pp. 4461–4465. [Google Scholar]
- Liu, X.H.; Yang, J.; Lu, J.; Yao, Z.C. Evaluation method for HRRP imaging quality based on intuitionistic interval fuzzy set. SN Appl. Sci. 2020, 2, 79. [Google Scholar] [CrossRef]
- Akhtar, N.; Ishak, M.I.S.; Ahmad, M.I.; Umar, K.; Yusuff, M.S.M.; Anees, M.T.; Qadir, A.; Almanasir, Y.K.A. Modification of the Water Quality Index (WQI) Process for Simple Calculation Using the Multi-Criteria Decision-Making (MCDM) Method: A Review. Water 2021, 13, 905. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Teruel-Solano, J.; Soto-Elvira, P.L.; García-Cascales, M.S. Geographical Information Systems (GIS) and Multi-Criteria Decision Making (MCDM) methods for the evaluation of solar farms locations: Case study in south-eastern Spain. Renew. Sustain. Energy Rev. 2013, 24, 544–556. [Google Scholar] [CrossRef]
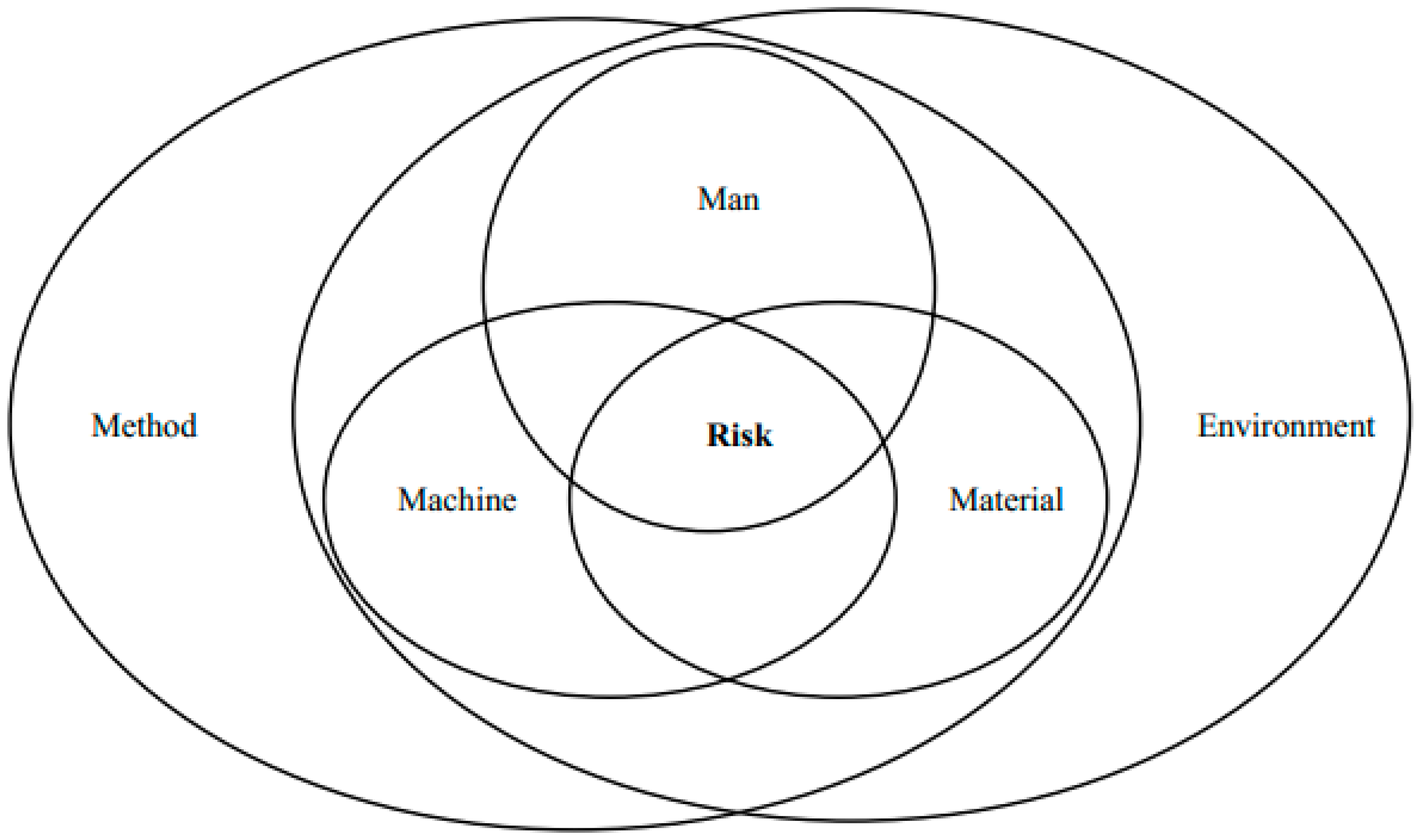
| Primary Index | Secondary Index | Position in the Matrix |
|---|---|---|
| : Man | : Safety protection capability of construction workers | |
| : Physical condition of construction workers | ||
| : Psychological state of construction workers | ||
| : Safety responsibility of management personnel | ||
| : Machine | : Mismatched types of lifting machinery equipment | |
| : Mismatched types of large-scale transportation equipment | ||
| : Power malfunction of rebar processing equipment | ||
| : Incorrect installation of rotary drilling rig machinery | ||
| : Improper machinery maintenance and repair | All elements except | |
| : Unstable machinery performance | ||
| : Material | : Quality defects of precast components | |
| : Concrete quality defects | ||
| : Quality defects of steel reinforcement | ||
| : Rough handling during material transportation | ||
| : Improper storage of materials | ||
| : Environment | : Poor geological conditions | |
| : Extreme high-temperature weather | ||
| : Unfavorable topography and geomorphological conditions | ||
| : Complicated bridge positioning | ||
| : Complex construction site | ||
| : Management | : Immature construction techniques | |
| : Non-compliant construction safety control | ||
| : Unreasonable construction plan | ||
| : Inadequate safety organizational structure | ||
| : Insufficient security measures |
| Secondary Index | October 2020 | December 2020 | May 2021 | August 2021 |
|---|---|---|---|---|
| 2.3% | 18.5% | 6.8% | 4.6% | |
| 13.2% | 9.7% | 6.0% | 11.8% | |
| 1.0% | 2.8% | 5.5% | 0.8% | |
| 15.9% | 2.5% | 0% | 0% | |
| 9.7% | 6.8% | 5.2% | 3.0% | |
| 19.3% | 26.8% | 13.3% | 35.9% | |
| 2.45% | 1.24% | 1.99% | 0.51% | |
| 1.94% | 1.36% | 1.38% | 1.86% | |
| 2.71% | 2.76% | 2.18% | 2.11% | |
| 0.44% | 0.58% | 1.13% | 0.62% | |
| 7.84% | 5.54% | 12.91% | 8.45% | |
| 36 | 12 | 35 | 41 | |
| 3.6% | 7.4% | 2.0% | 1.5% | |
| 16.3% | 34.9% | 21.2% | 19.4% | |
| 3.8% | 6.0% | 2.1% | 0.5% |
| Work Unit | Professional | Degree | Years of Work Experience |
|---|---|---|---|
| Scientific research institutions | No professional title | No degree | |
| 10 | 0 | 0 | 0 |
| Design institute | Junior professional title | Bachelor | |
| 3 | 0 | 16 | 3 |
| Construction company | Intermediate professional title | Master | |
| 13 | 12 | 6 | 6 |
| Regulatory authority | Senior professional title | Doctor | |
| 4 | 18 | 8 | 21 |
| Secondary Index | October 2020 | December 2020 | May 2021 | August 2021 |
|---|---|---|---|---|
| 85.33 | 67.00 | 76.67 | 89.33 | |
| 94.33 | 86.67 | 75.33 | 72.00 | |
| 86.33 | 75.67 | 67.00 | 89.67 | |
| 42.00 | 63.33 | 85.67 | 32.67 | |
| 84.67 | 83.33 | 72.67 | 67.67 | |
| 73.33 | 87.33 | 71.67 | 80.33 | |
| 62.67 | 83.67 | 71.33 | 72.00 | |
| 81.33 | 74.67 | 81.00 | 72.67 | |
| 83.67 | 81.33 | 82.33 | 61.00 | |
| 72.67 | 81.33 | 92.67 | 83.33 |
| Secondary Index | Static Weight | Dynamic Weights without Normalization | |||
|---|---|---|---|---|---|
| October 2020 | December 2020 | May 2021 | August 2021 | ||
| 0.0610 | 0.1333 | 0.3250 | 0.0833 | 0.2333 | |
| 0.0502 | 0.3583 | 0.1668 | 0.1168 | 0.2000 | |
| 0.0005 | 0.1583 | 0.1083 | 0.3250 | 0.2418 | |
| 0.0183 | 0.9500 | 0.4168 | 0.1418 | 1.1833 | |
| 0.0461 | 0.7700 | 0.8500 | 1.3200 | 0.5400 | |
| 0.0283 | 0.3400 | 0.5150 | 0.7000 | 0.4100 | |
| 0.0406 | 0.8000 | 0.4400 | 0.1000 | 0.8400 | |
| 0.0017 | 0.2050 | 0.8750 | 0 | 0 | |
| 0.0485 | 0.5150 | 0.6600 | 0.7400 | 0.8500 | |
| 0.0406 | 0.9300 | 1.6800 | 0.3300 | 2.5900 | |
| 0.0534 | 0.4900 | 0.2480 | 0.3984 | 0.1021 | |
| 0.0623 | 0.3880 | 0.2720 | 0.2761 | 0.3722 | |
| 0.0472 | 0.5422 | 0.5521 | 0.4361 | 0.4224 | |
| 0.0242 | 0.0880 | 0.1160 | 0.2262 | 0.1242 | |
| 0.0628 | 1.5681 | 1.1080 | 2.5822 | 1.6901 | |
| 0.0269 | 0.1168 | 0.0833 | 0.1833 | 0.3083 | |
| 0.0611 | 0.5000 | 1.0000 | 37.4159 | 206.4435 | |
| 0.0623 | 0.1668 | 0.1833 | 0.2083 | 0.0082 | |
| 0.0439 | 0.4333 | 0.0918 | 0.2168 | 0.2000 | |
| 0.0519 | 0.0333 | 0.1333 | 0.0250 | 0.1833 | |
| 0.0656 | 0.0002 | 0.0011 | 0.0003 | 0.0008 | |
| 0.0185 | 0.0009 | 0.0037 | 0.0003 | 0.0002 | |
| 0.0408 | 0.0041 | 0.0035 | 0.0045 | 0.0049 | |
| 0.0220 | 0.0918 | 0.0333 | 0.0583 | 1.4870 | |
| 0.0217 | 0.1833 | 0.0333 | 0.3168 | 0.0833 | |
| Secondary Index | I | II | III | IV | V |
|---|---|---|---|---|---|
| Secondary Index | October 2020 | December 2020 | May 2021 | August 2021 |
|---|---|---|---|---|
| 0.0155 | 0.0339 | 0.0022 | 0.0012 | |
| 0.0372 | 0.0181 | 0.0029 | 0.0010 | |
| 0.0156 | 0.0105 | 0.0078 | 0.0011 | |
| 0.0942 | 0.0412 | 0.0041 | 0.0054 | |
| 0.0776 | 0.0844 | 0.0281 | 0.0025 | |
| 0.0346 | 0.0511 | 0.0149 | 0.0019 | |
| 0.0803 | 0.0443 | 0.0120 | 0.0049 | |
| 0.0202 | 0.0851 | 0.0094 | 0.0036 | |
| 0.0526 | 0.0660 | 0.0159 | 0.0040 | |
| 0.0931 | 0.1648 | 0.0073 | 0.0118 | |
| 0.0503 | 0.0261 | 0.0088 | 0.0006 | |
| 0.0406 | 0.0288 | 0.0063 | 0.0018 | |
| 0.0552 | 0.0554 | 0.0095 | 0.0020 | |
| 0.0096 | 0.0122 | 0.0050 | 0.0006 | |
| 0.1568 | 0.1101 | 0.0548 | 0.0078 | |
| 0.0125 | 0.0091 | 0.0041 | 0.0014 | |
| 0.0516 | 0.0995 | 0.7866 | 0.9389 | |
| 0.0188 | 0.0202 | 0.0049 | 0.0001 | |
| 0.0443 | 0.0106 | 0.0049 | 0.0010 | |
| 0.0053 | 0.0149 | 0.0009 | 0.0009 | |
| 0.0025 | 0.0026 | 0.0005 | 0.0001 | |
| 0.0008 | 0.0011 | 0.0002 | 0.00003366 | |
| 0.0020 | 0.0019 | 0.0004 | 0.0001 | |
| 0.0099 | 0.0041 | 0.0014 | 0.0068 | |
| 0.0189 | 0.0041 | 0.0068 | 0.0004 |
| Secondary Index | October 2020 | December 2020 | May 2021 | August 2021 | Rate of Change |
|---|---|---|---|---|---|
| 31.39% | 15.80% | 42.27% | 20.73% | −194.30% | |
| 12.29% | 23.13% | 30.06% | 20.06% | 258.05% | |
| 0.31% | 0.46% | 0.15% | 0.21% | −190.18% | |
| 1.89% | 4.21% | 11.43% | 1.52% | −415.05% | |
| 5.65% | 5.14% | 3.37% | 7.87% | 354.83% | |
| 7.68% | 5.21% | 3.89% | 6.46% | −526.14% | |
| 4.83% | 8.45% | 28.88% | 4.61% | −2101.50% | |
| 0.82% | 0.19% | 0.17% | 0.17% | −26.00% | |
| 8.61% | 6.85% | 6.15% | 5.40% | −168.21% | |
| 4.18% | 2.36% | 10.96% | 1.54% | −58.47% | |
| 9.83% | 17.72% | 11.82% | 34.34% | 140.09% | |
| 13.84% | 18.64% | 18.41% | 14.34% | 2850.00% | |
| 8.01% | 7.88% | 9.77% | 10.05% | 491.99% | |
| 21.57% | 17.26% | 9.66% | 16.31% | −309.94% | |
| 3.85% | 5.36% | 2.37% | 3.58% | −1336.80% | |
| 18.72% | 24.41% | 12.80% | 8.03% | −75.04% | |
| 10.89% | 5.76% | 0.16% | 0.03% | −0.27% | |
| 27.19% | 25.37% | 23.02% | 88.37% | 144.45% | |
| 9.20% | 32.35% | 16.84% | 18.00% | 204.54% | |
| 60.92% | 28.02% | 67.49% | 22.07% | −56.80% | |
| 99.70% | 98.35% | 99.54% | 98.80% | 99.70% | |
| 95.36% | 83.33% | 98.40% | 98.93% | 95.36% | |
| 90.87% | 92.10% | 90.07% | 89.28% | 90.87% | |
| 19.33% | 39.78% | 27.40% | 1.46% | 19.33% | |
| 10.59% | 39.45% | 6.41% | 20.67% | 10.59% |
| Secondary Index | AHP-Dynamic Weight | EWM-Dynamic Weight | C-OWA–Dynamic Weight | IIFS-Dynamic Weight |
|---|---|---|---|---|
| −194.30% | −175.12% | −178.87% | −157.89% | |
| 258.05% | 272.87% | 264.31% | 285.12% | |
| −190.18% | −178.25% | −175.99% | −164.48% | |
| −415.05% | −404.83% | −407.30% | −386.86% | |
| 354.83% | 369.84% | 367.90% | 383.67% | |
| −526.14% | −518.49% | −517.52% | −524.12% | |
| −2101.50% | −2097.22% | −2096.32% | −2074.98% | |
| −26.00% | −24.29% | −19.45% | 10.24% | |
| −168.21% | −156.01% | −156.70% | −151.57% | |
| −58.47% | −53.76% | −47.86% | −43.68% | |
| 140.09% | 140.86% | 159.36% | 148.88% | |
| 2850.00% | 2865.93% | 2865.37% | 2860.48% | |
| 491.99% | 493.42% | 499.51% | 504.25% | |
| −309.94% | −299.40% | −302.72% | −298.18% | |
| −1336.80% | −1331.89% | −1331.31% | −1316.18% | |
| −75.04% | −71.36% | −69.38% | −62.27% | |
| −0.27% | 1.83% | 4.93% | 19.99% | |
| 144.45% | 145.74% | 152.33% | 182.38% | |
| 204.54% | 213.24% | 219.94% | 216.00% | |
| −56.80% | −47.53% | −43.18% | −49.57% | |
| 99.70% | 103.27% | 110.03% | 103.62% | |
| 95.36% | 112.77% | 97.22% | 100.40% | |
| 90.87% | 103.37% | 91.96% | 109.72% | |
| 19.33% | 37.69% | 28.09% | 53.41% | |
| 10.59% | 20.41% | 17.21% | 15.46% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, R.; Wang, S.; Fang, J.; Wang, Y. Safety Risk Analysis of Urban Viaduct Construction Based on Dynamic Weight. Buildings 2024, 14, 1014. https://doi.org/10.3390/buildings14041014
Ran R, Wang S, Fang J, Wang Y. Safety Risk Analysis of Urban Viaduct Construction Based on Dynamic Weight. Buildings. 2024; 14(4):1014. https://doi.org/10.3390/buildings14041014
Chicago/Turabian StyleRan, Ruijiang, Shengmin Wang, Jun Fang, and Yajie Wang. 2024. "Safety Risk Analysis of Urban Viaduct Construction Based on Dynamic Weight" Buildings 14, no. 4: 1014. https://doi.org/10.3390/buildings14041014
APA StyleRan, R., Wang, S., Fang, J., & Wang, Y. (2024). Safety Risk Analysis of Urban Viaduct Construction Based on Dynamic Weight. Buildings, 14(4), 1014. https://doi.org/10.3390/buildings14041014






