Experimental Study on the Effect of Steel Reinforcement Ration on the Cracking Behaviour of FRP-Strengthened RC Elements
Abstract
:1. Introduction
2. Experimental Program
2.1. Materials
2.1.1. Reinforced Concrete
2.1.2. CFRP Reinforcement Material
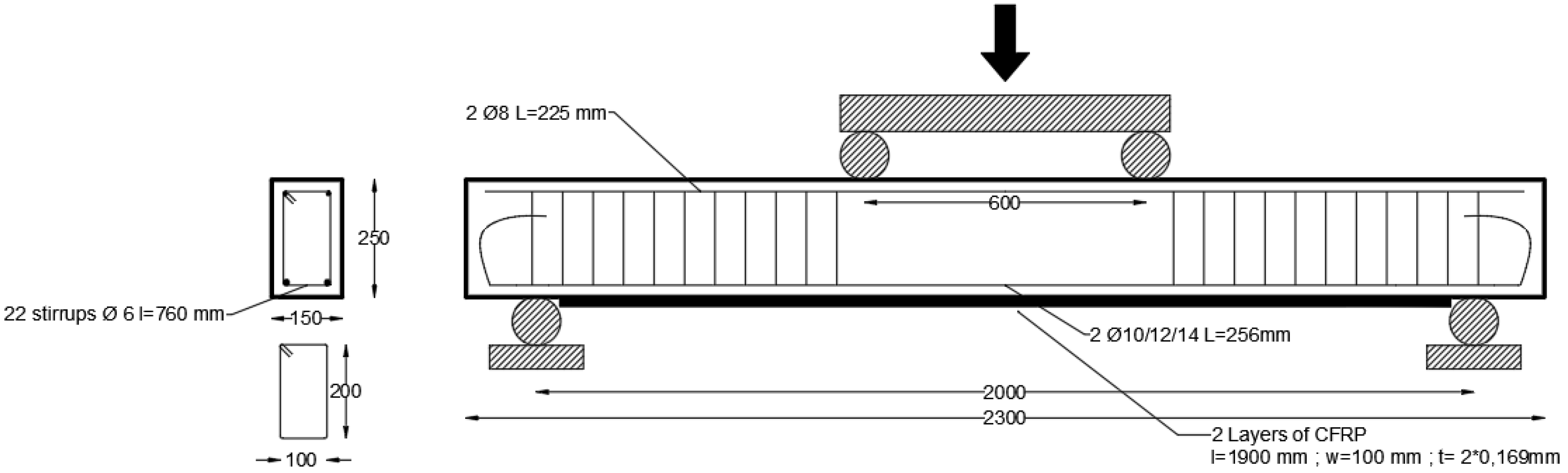
2.2. Specimen Preparation
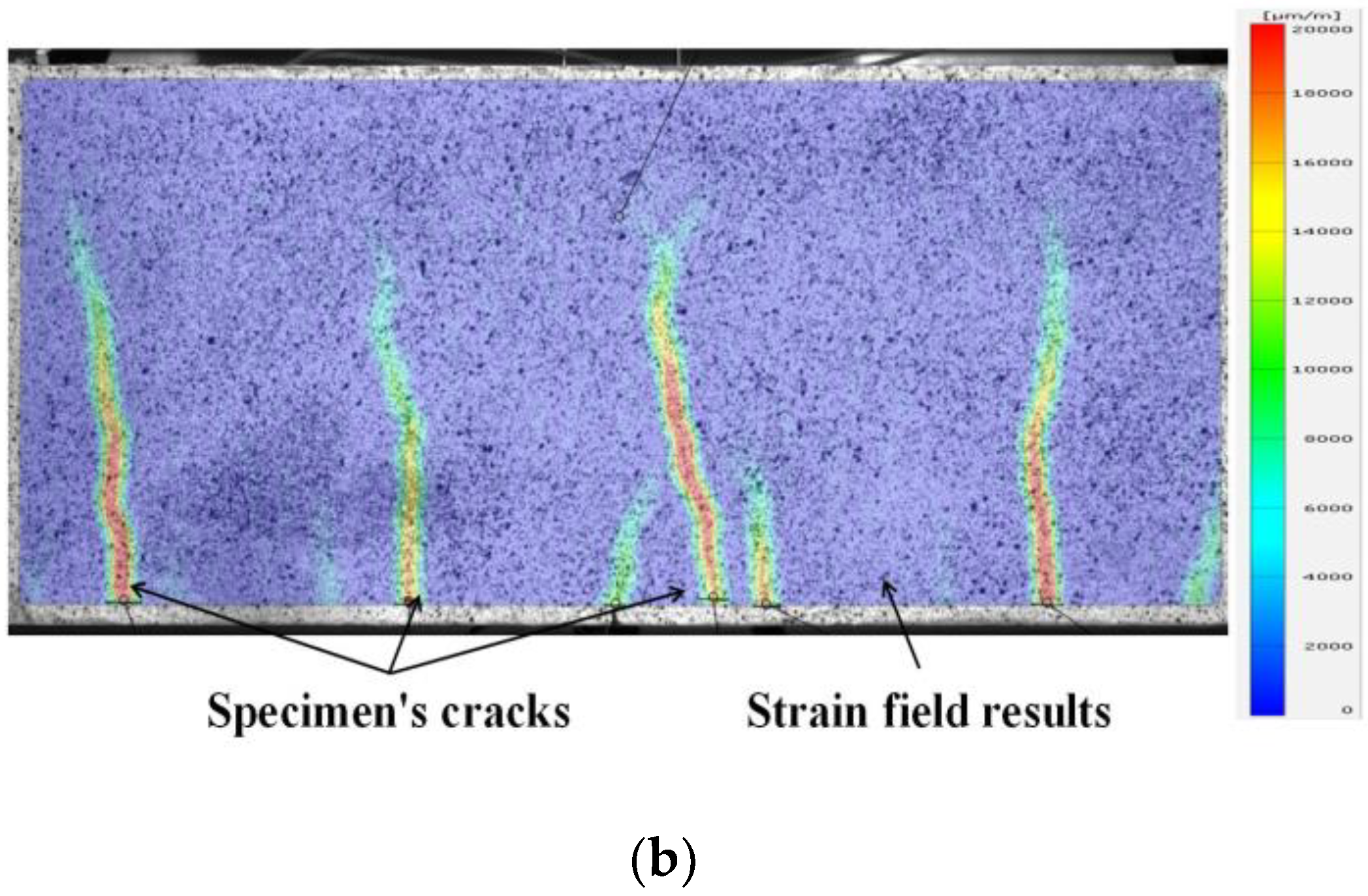
2.2.1. Two-Dimensional Digital Image Correlation (DIC 2D)
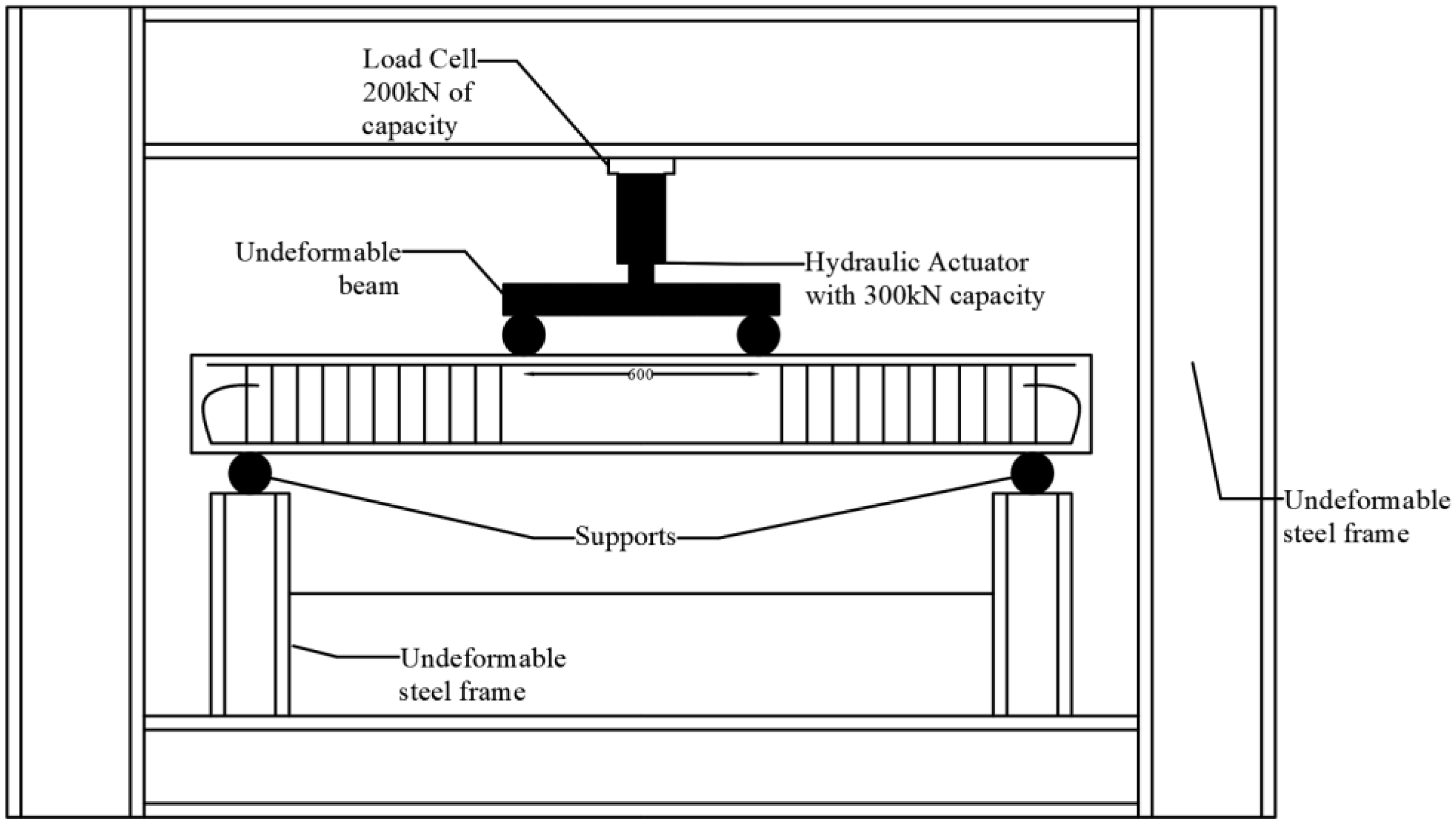
2.2.2. Loading Device
3. Results and Discussion
3.1. Ultimate Load
3.2. Mid-Span Displacement
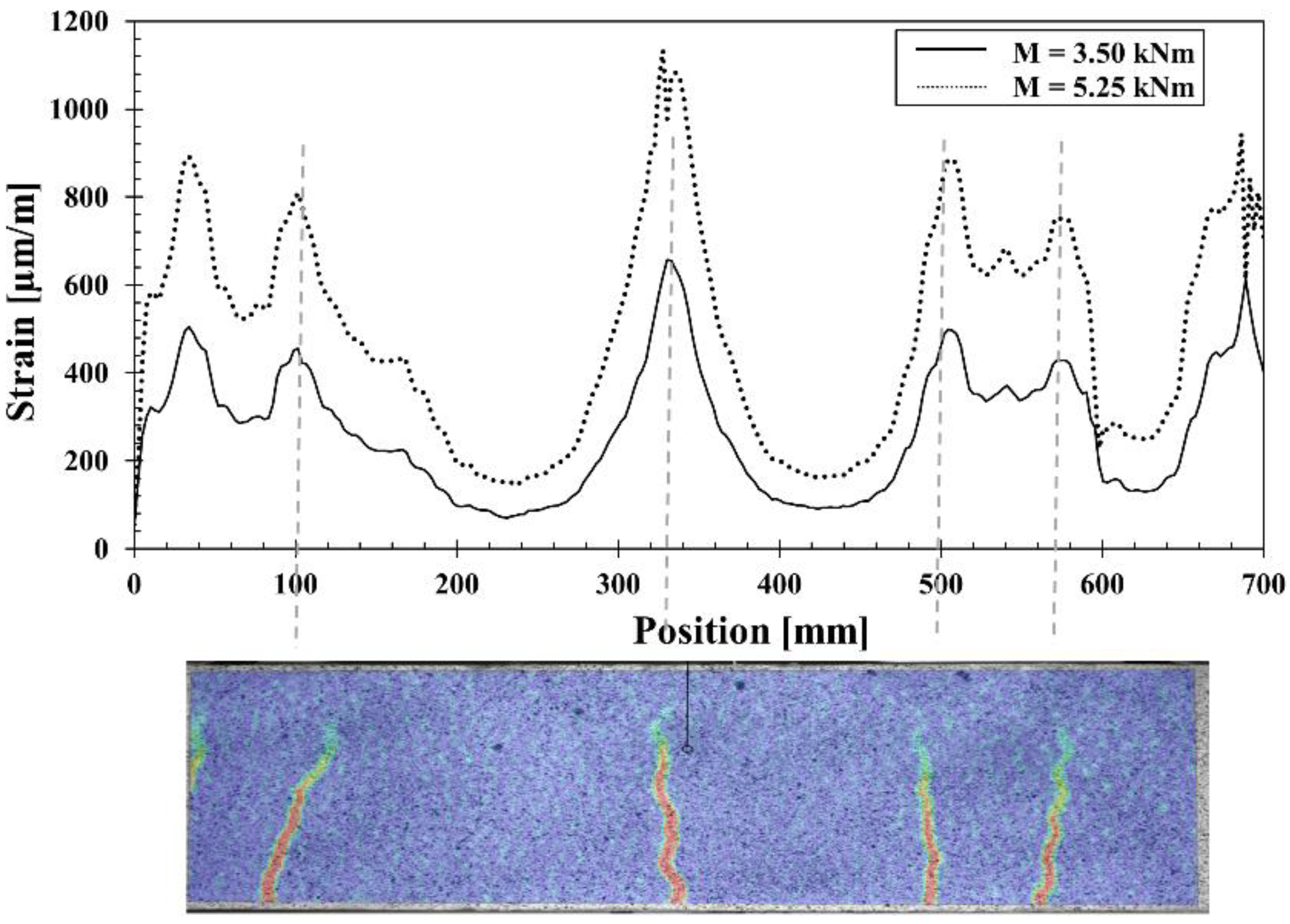
Composite Strain
3.3. Failure Modes
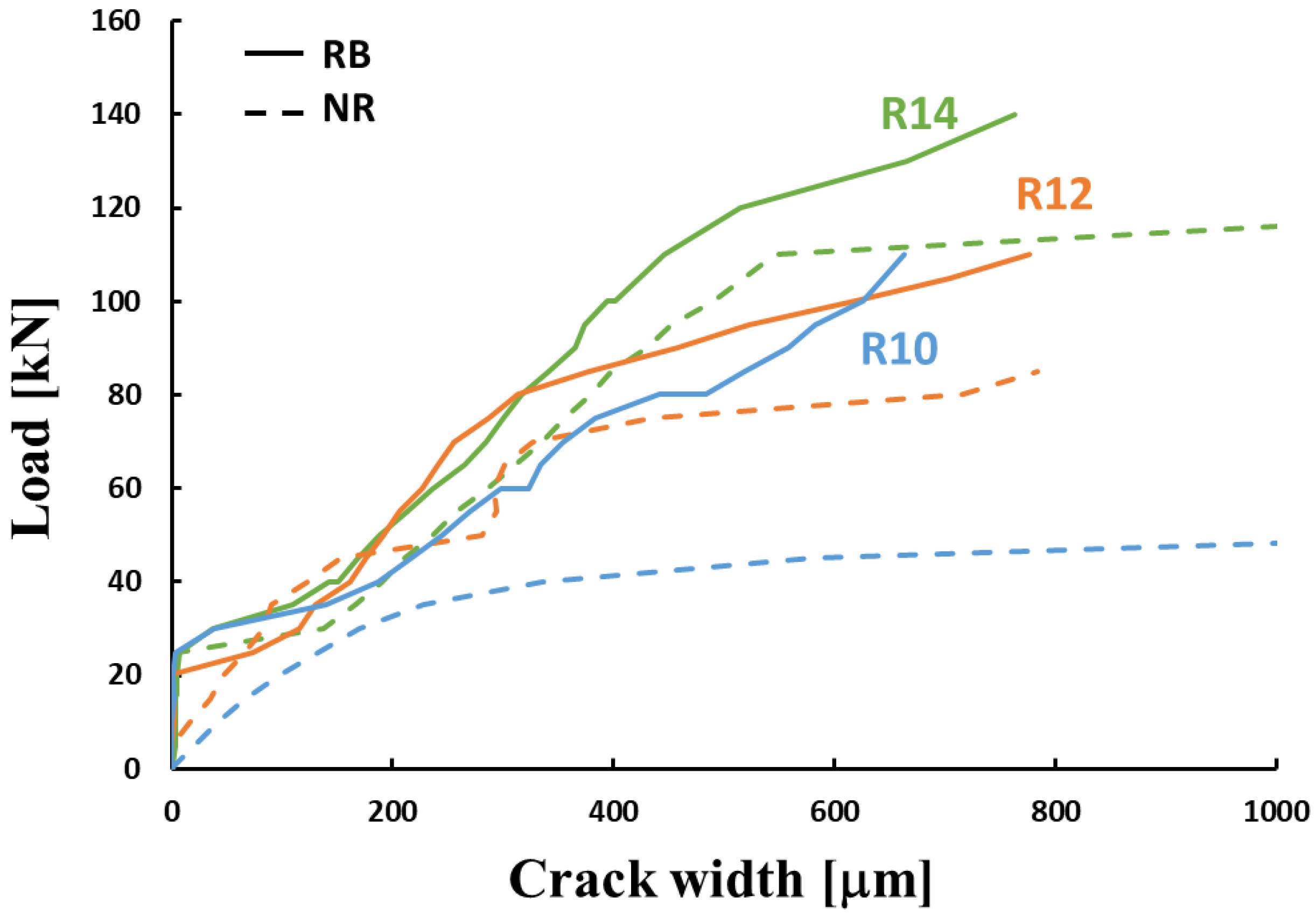
3.4. Cracking Behaviour
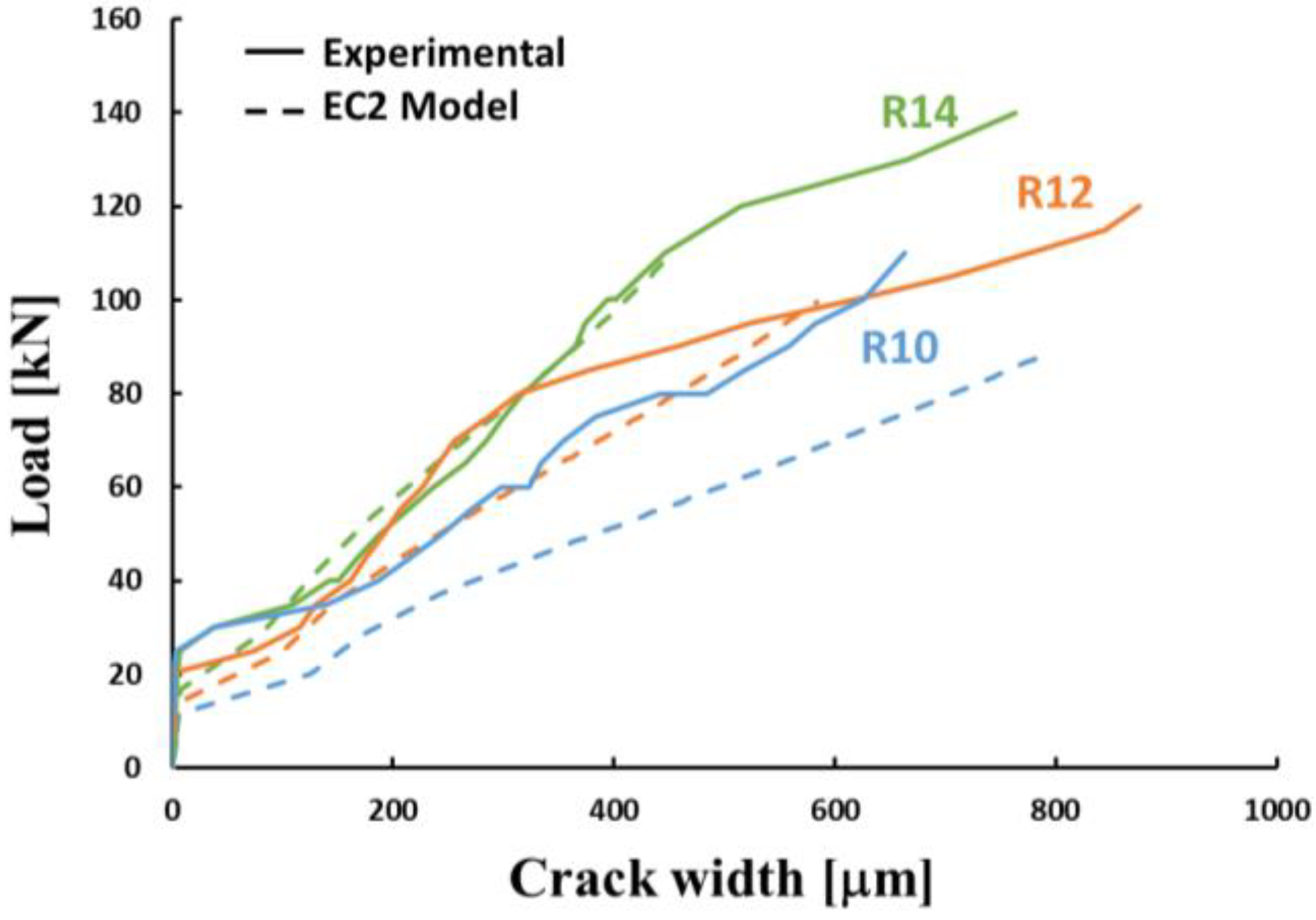
3.5. Model Proposal
3.5.1. Eurocode Model
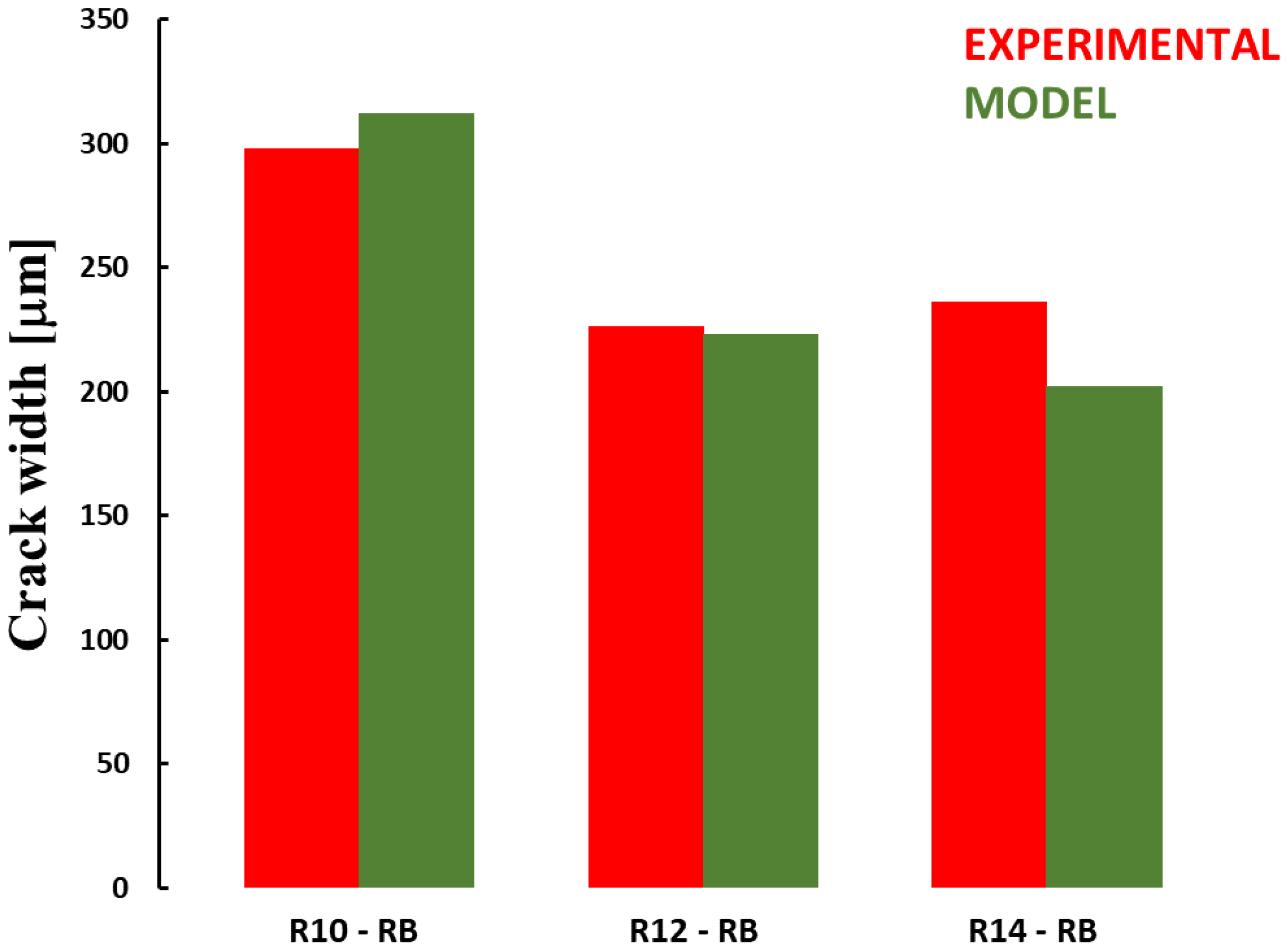
3.5.2. Modified Model
4. Conclusions
- ▪
- with a lower level of steel reinforcement, the contribution of the composite material was more significant.
- ▪
- the beams with a low steel ratio (0.4%) suffered less loss in ductility and cracking.
- ▪
- the crack opening calculation based on Eurocode 2 formula is too conservative compared with those measured.
- ▪
- an empirical model was proposed based on the formulation of the Eurocode with appropriate modifications, taking into account the geometric and mechanical aspects of a strengthened structure. The calculated values were compared with the measured values and showed good agreement.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maruyama, I.; Lura, P. Properties of early-age concrete relevant to cracking in massive concrete. Cem. Concr. Res. 2019, 123, 105770. [Google Scholar] [CrossRef]
- Adamo, N.; Al-Ansari, N.; Sissakian, V.; Laue, J.; Knutsson, S. Dam Safety: Technical Problems of Ageing Concrete Dams. J. Earth Sci. Geotech. Eng. 2020, 10, 241–279. [Google Scholar]
- Ahn, I.-S. Creep and Shrinkage of Early-Age Concrete at Cold Temperature. Adv. Civ. Eng. Mater. 2021, 10, 300–312. [Google Scholar] [CrossRef]
- Wan-Wendner, R. Aging concrete structures: A review of mechanics and concepts. Die Bodenkult. J. Land Manag. Food Environ. 2018, 69, 175–199. [Google Scholar] [CrossRef]
- Binda, L.; Tiraboschi, C.; Folli, R.T. On-site and Laboratory Investigation of Materials and Structure of a Belltower in Monza/Untersuchungen an den Werkstoffen und am Tragwerk im Labor und am Objekt am Beispiel eines Glockenturms in Monza. Restor. Build. Monum. 2000, 6, 41–62. [Google Scholar] [CrossRef]
- Issa, M.; Ismail, E.-S. Long-term deflections of FRP reinforced concrete beams. HBRC J. 2020, 16, 269–282. [Google Scholar] [CrossRef]
- Di Tommaso, A.; Neubauer, U.; Pantuso, A.; Rostasy, F. Behavior of Adhesively Bonded Concrete-CFRP Joints at Low and High Temperatures. Mech. Compos. Mater. 2001, 37, 327–338. [Google Scholar] [CrossRef]
- Hu, C.; Sang, L.; Jiang, K.; Xing, J.; Hou, W. Experimental and numerical characterization of flexural properties and failure behavior of CFRP/Al laminates. Compos. Struct. 2021, 281, 115036. [Google Scholar] [CrossRef]
- Bakis, C.E.; Bank, L.C.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber-reinforced polymer composites for construction—State-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Nayak, A.N.; Kumari, A.; Swain, R.B. Strengthening of RC Beams Using Externally Bonded Fibre Reinforced Polymer Composites. Structures 2018, 14, 137–152. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, J.; Shang, S.; Liu, Y.; Cai, C.S. Experimental study of flexural fatigue performance of reinforced concrete beams strengthened with prestressed CFRP plates. Eng. Struct. 2016, 127, 62–72. [Google Scholar] [CrossRef]
- Delle Ricerche, C.N. Guide for the Design and Construction of Fiber-Reinforced Concrete Structures; SN: CNR-DT; National Research Council-Advisory Committee on Technical Recommendations for Construction: Rome, Italy, 2006; Volume 204, p. 2006. [Google Scholar]
- Triantafillou, T.; International Federation for Structural Concrete (Eds.) Externally Bonded FRP Reinforcement for RC Structures: Technical Report on the Design and Use of Externally Bonded Fibre Reinforced Polymer Reinforcement (FRP EBR) for Reinforced Concrete Structures; International Federation for Structural Concrete: Lausanne, Switzerland, 2001. [Google Scholar]
- AFGC. Réparation et Renforcement des Structures en Béton au Moyen des Matériaux Composites. 2011. Available online: https://www.afgc.asso.fr/publication/reparation-et-renforcement-des-structures-en-beton-au-moyen-des-materiaux-composites/ (accessed on 1 February 2024).
- Darby, A.; Ibell, T.; Clarke, J. TR55 Design Guidance for Strengthening Concrete Structures Using Fibre Composite Materials; The Concrete Society: Sandhurst, United Kingdom, 2004. [Google Scholar]
- SIA166; Klebebewehrungen (Externally Bonded Reinforcements. Schweizer I. Architektenverein: Zürich, Switzerland, 2004.
- ACI Committee 440. 440.2R-17: Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar] [CrossRef]
- Gorbunov, I.; Kakusha, V. Behavior of concrete beams reinforced with FRP during bending. E3S Web Conf. 2021, 263, 02052. [Google Scholar] [CrossRef]
- del Rey Castillo, E.; Allen, T.; Henry, R.; Griffith, M.; Ingham, J. Digital image correlation (DIC) for measurement of strains and displacements in coarse, low volume-fraction FRP composites used in civil infrastructure. Compos. Struct. 2019, 212, 43–57. [Google Scholar] [CrossRef]
- Zhou, K.; Lei, D.; Chun, P.-j.; She, Z.; He, J.; Du, W.; Hong, M. Evaluation of BFRP strengthening and repairing effects on concrete beams using DIC and YOLO-v5 object detection algorithm. Constr. Build. Mater. 2024, 411, 134594. [Google Scholar] [CrossRef]
- Armonico, A.; Saidi, M.; Michel, L.; Bel, S.; Ferrier, E. Inverse analysis based on DFOS technology for the study of the bonding behaviour of FRP to concrete beams. Mater. Today Commun. 2023, 35, 105655. [Google Scholar] [CrossRef]
- Hoult, N.A.; Andy Take, W.; Lee, C.; Dutton, M. Experimental accuracy of two dimensional strain measurements using Digital Image Correlation. Eng. Struct. 2013, 46, 718–726. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Aravand, M.; Sabuncuoglu, B.; Callens, M.G.; Lomov, S.V.; Gorbatikh, L. Full-field strain measurements at the micro-scale in fiber-reinforced composites using digital image correlation. Compos. Struct. 2016, 140, 192–201. [Google Scholar] [CrossRef]
- Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Union: Brussels, Belgium, 2004; p. 230.
- BS EN 12390-3:2009; Testing Hardened Concrete. Compressive Strength of Test Specimens. British Standards Institution: London, UK, 2009.
- ISO 527-5:2021; Plastics—Determination of Tensile Properties—Part 5: Test Conditions for Unidirectional Fibre-Reinforced Plastic Composites. ISO: Geneva, Switzerland, 2021; Volume 5.
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- International Digital Image Correlation Society. A Good Practices Guide for Digital Image Correlation; International Digital Image Correlation Society (iDICs): Boston, MA, USA, 2018. [Google Scholar]
- Tehrani, A.D.; Kohankar Kouchesfehani, Z.; Najafi, M. Pipe profiling using digital image correlation. In Pipelines 2020; American Society of Civil Engineers Reston: Reston, VA, USA, 2020; pp. 36–45. [Google Scholar]
- Saidi, M.; Gabor, A. Use of distributed optical fibre as a strain sensor in textile reinforced cementitious matrix composites. Measurement 2019, 140, 323–333. [Google Scholar] [CrossRef]
- Bravo, M.; Sáenz, J.; Navas, M.; Lopez-Amo, M. Concrete Beam Bending Test Monitorization Using a High Strain Fiber Optic Sensor. J. Light. Technol. 2012, 30, 1085–1089. [Google Scholar] [CrossRef]
- Ferrier, E.; Caggegi, C.; Michel, L. Influence of EB-CFRP on Cracks for Reinforced Concrete Beams Strengthening. Spec. Publ. 2018, 237, 44.1–44.16. [Google Scholar]
- Yusra, A.; Opirina, L.; Triwulan, T.; Raka, G.; Safriani, M. Comparative Study of Steel Reinforced Concrete Beams with Bamboo Reinforced Concrete Beams. Solid State Technol. 2021, 63, 12857–12863. [Google Scholar]
- Banjara, N.K.; Ramanjaneyulu, K. Investigations on behaviour of flexural deficient and CFRP strengthened reinforced concrete beams under static and fatigue loading. Constr. Build. Mater. 2019, 201, 746–762. [Google Scholar] [CrossRef]
- Shamass, R.; Mahi, B.; Cashell, K.A.; Abarkan, I.; El-Khannoussi, F. Experimental investigation into the behaviour of continuous concrete beams reinforced with basalt FRP. Eng. Struct. 2022, 255, 113888. [Google Scholar] [CrossRef]
- Al-Khafaji, A.; Salim, H.; El-Sisi, A. Behavior of RC beams strengthened with CFRP sheets under sustained loads. Structures 2021, 33, 4690–4700. [Google Scholar] [CrossRef]
- Ali, H.; Assih, J.; Li, A. Flexural capacity of continuous reinforced concrete beams strengthened or repaired by CFRP/GFRP sheets. Int. J. Adhes. Adhes. 2020, 104, 102759. [Google Scholar] [CrossRef]
- Bocciarelli, M.; di Feo, C.; Nisticò, N.; Pisani, M.A.; Poggi, C. Failure of RC beams strengthened in bending with unconventionally arranged CFRP laminates. Compos. Part B Eng. 2013, 54, 246–254. [Google Scholar] [CrossRef]
- Pisani, M. Evaluation of Bending Strength of RC Beams Strengthened with FRP Sheets. J. Compos. Constr. 2006, 10, 313–320. [Google Scholar] [CrossRef]
- Chajes, M.J.; Thomson, T.A., Jr.; Januszka, T.F.; Finch, W.W., Jr. Flexural strengthening of concrete beams using externally bonded composite materials. Constr. Build. Mater. 1994, 8, 191–201. [Google Scholar] [CrossRef]
- Euro-International Committee for Concrete; Favre, R. CEB Design Manual on Cracking and Deformations; École Polytechnique Fédérale de Lausanne: Lausanne, Switzerland, 1985. [Google Scholar]
- Ng, P.L.; Kwan, A. A rigorous analytical model for shrinkage cracking of reinforced concrete. Mag. Concr. Res. 2017, 69, 120–133. [Google Scholar] [CrossRef]
- Hognestad, E. High-strength bars as concrete reinforcement, Part 2: Control of flexural cracking. J. PCA Res. Dev. Lab. 1962, 46–53. [Google Scholar]
- Watstein, D.; Parsons, D.E. Width and spacing of tensile cracks in axially reinforced concrete cylinders. J. Res. Natl. Bur. Stand. 1943, 31, 1–24. [Google Scholar] [CrossRef]
- Borosnyói, A.; Balázs, G.L. Models for flexural cracking in concrete: The state of the art. Struct. Concr. 2005, 6, 53–62. [Google Scholar] [CrossRef]
- ACI 318R-08; Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary: An ACI Standard. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2008.
- ECP 203-2007; Egyptian Code for Design and Construction of Reinforced Concrete Structures. Ministry of Housing, Utilities and Urban Communities: El Sayeda Zeinab, Egypt, 2007.
- BS 8110-2:1985; Structural Use of Concrete. Part 2: Code of Practice for Special Circumstances. British Standards Institution: Milton Keynes, UK, 1985.
- Ceroni, F.; Pecce, M. Design provisions for crack spacing and width in RC elements externally bonded with FRP. Compos. Part B Eng. 2009, 40, 17–28. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Vilanova, I.; Miàs, C.; Llorens, M. Experimental study on crack width and crack spacing for Glass-FRP reinforced concrete beams. Eng. Struct. 2017, 131, 231–242. [Google Scholar] [CrossRef]
- Leonhardt, F. Crack Control in Concrete Structures; PCI Journal: Chicago, IL, USA, 1977. [Google Scholar]







| Component | Cement CEM I 52.5 R | Sand | Gravel | Water |
|---|---|---|---|---|
| [kg/m3] | 420 | 890 | 890 | 200 |
| Specimen | 1 | 2 | 3 | 4 | 5 | 6 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|---|
| σ [MPa] at 28 days | 37.4 | 38.2 | 42.2 | 38.65 | 38.85 | 44.1 | 39.9→35 | 2.41 |
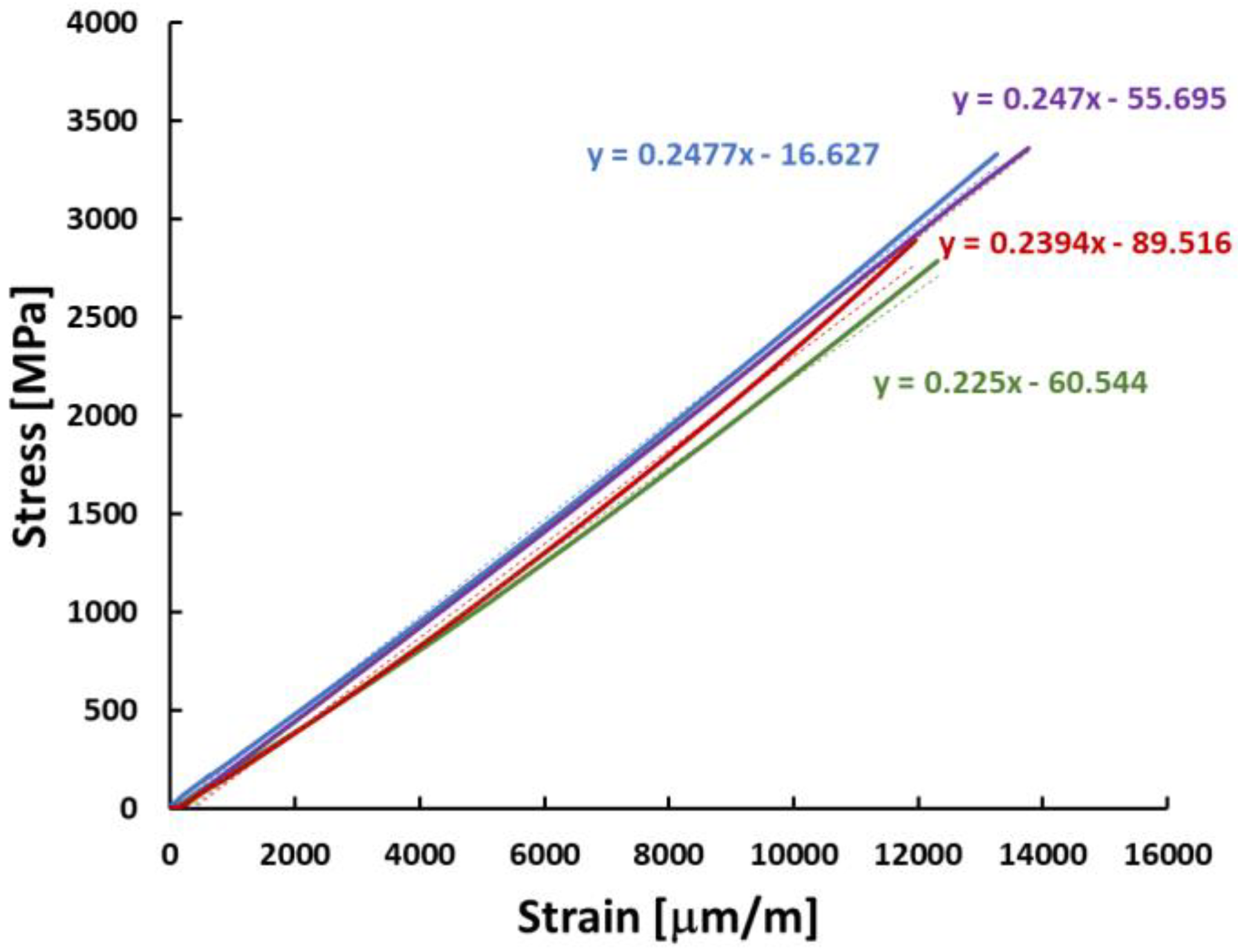
| Specimen | Young’s Modulus—Ef [MPa] | Maximal Strain—εu [%] | Ultimate Stress—ftk [MPa] |
|---|---|---|---|
| 1 | 225,000 | 1.23% | 2786.4 |
| 2 | 247,000 | 1.38% | 3363.4 |
| 3 | 242,200 | 0.88% | 2141.2 |
| 4 | 247,700 | 1.28% | 3329.5 |
| 5 | 239,400 | 1.20% | 2891.3 |
| Average | 240,260 | 1.19% | 2902.4 |
| Standard deviation | 9194.45 | 0.0018 | 496.99 |
| Coeff. of variation | 4% | 16% | 17% |
| Specimen Name | R10-NR * | R12-NR | R14-NR | R10-RB ** | R12-RB0 | R12-RB1 | R12-RB2 | R12-RB3 | R12-RB4 | R14-RB |
|---|---|---|---|---|---|---|---|---|---|---|
| Diameter of reinforcing bars | 10 | 12 | 14 | 10 | 12 | 12 | 12 | 12 | 12 | 14 |
| Presence of CFRP | No | No | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Name | First Crack | Steel Yielding | Failure | |||
|---|---|---|---|---|---|---|
| Load [kN] | Deflection [mm] | Load [kN] | Deflection [mm] | Load [kN] | Deflection [mm] | |
| R10-NR | 25 | 1.85 | 57.8 | 7.21 | 70.58 | 31.61 |
| R12-NR | 25 | 1.55 | 63.4 | 6.16 | 92.57 | 31.10 |
| R14-NR | 30 | 1.26 | 85.1 | 6.84 | 112.11 | 27.72 |
| R10-RB | 40 | 3.30 | 55.50 | 5.48 | 126.25 | 27.82 |
| R12-RB0 | 35 | 2.49 | 69.12 | 6.78 | 114.20 | 20.81 |
| R12-RB1 | 45 | 3.13 | 68.40 | 5.71 | 120.81 | 19.43 |
| R12-RB2 | 50 | 3.77 | 67.53 | 5.82 | 110.97 | 17.80 |
| R12-RB3 | 45 | 3.20 | 69.14 | 5.96 | 121.28 | 21.12 |
| R12-RB4 | 50 | 3.80 | 70.55 | 6.16 | 109.65 | 17.18 |
| R14-RB | 55 | 4.10 | 67.84 | 5.27 | 148.24 | 24.15 |
| Load [kN] | R10-RB | R12-RB | R14-RB | |||
|---|---|---|---|---|---|---|
| Composite Strain | Composite Strain | Composite Strain | ||||
| 10 | 19 | 22 | 58.19 | 70.46 | 63 | 68 |
| 35 | 1299 | 1696 | 1083 | 1350 | 1071 | 651 |
| 60 | 2730 | 2837 | 2112 | 2378 | 2132 | 1296 |
| 80 | 5433 | 4491 | 3314 | 3296 | 3020 | 1968 |
| 100 | 9798 | 7591 | 8257 | 6055 | 4398 | 2850 |
| 120 | 17,836 | 10,186 | - | - | 8379 | 4593 |
| 140 | - | - | - | - | 12,931 | 7161 |
| Load [kN] | Crack Width [μm] | |||||
|---|---|---|---|---|---|---|
| R10-NR | R12-NR | R14-NR | R10-RB | R12-RB1 | R14-RB | |
| 25 | 133 | 124 | 137 | 3 | 72 | 7 |
| 30 | 169 | 145 | 166 | 7 | 115 | 37 |
| 40 | 334 | 190 | 210 | 33 | 161 | 142 |
| 50 | 1221 | 237 | 258 | 122 | 191 | 188 |
| 60 | - | 278 | 311 | 200 | 226 | 236 |
| 70 | - | 335 | 355 | 244 | 255 | 284 |
| 80 | - | 877 | 398 | 313 | 312 | 316 |
| 90 | - | - | 451 | 444 | 458 | 364 |
| 100 | - | - | 545 | 516 | 618 | 394 |
| 110 | - | - | - | - | 776 | 446 |
| 120 | - | - | - | - | - | 514 |
| Group | R10 | R12 | R14 |
|---|---|---|---|
| 0.85 | 0.96 | 0.98 | |
| [μm] | 76.31 | 39.11 | 37.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armonico, A.; Michel, L.; Saidi, M.; Ferrier, E. Experimental Study on the Effect of Steel Reinforcement Ration on the Cracking Behaviour of FRP-Strengthened RC Elements. Buildings 2024, 14, 950. https://doi.org/10.3390/buildings14040950
Armonico A, Michel L, Saidi M, Ferrier E. Experimental Study on the Effect of Steel Reinforcement Ration on the Cracking Behaviour of FRP-Strengthened RC Elements. Buildings. 2024; 14(4):950. https://doi.org/10.3390/buildings14040950
Chicago/Turabian StyleArmonico, Andrea, Laurent Michel, Mohamed Saidi, and Emmanuel Ferrier. 2024. "Experimental Study on the Effect of Steel Reinforcement Ration on the Cracking Behaviour of FRP-Strengthened RC Elements" Buildings 14, no. 4: 950. https://doi.org/10.3390/buildings14040950
APA StyleArmonico, A., Michel, L., Saidi, M., & Ferrier, E. (2024). Experimental Study on the Effect of Steel Reinforcement Ration on the Cracking Behaviour of FRP-Strengthened RC Elements. Buildings, 14(4), 950. https://doi.org/10.3390/buildings14040950














