Impact of Wind Pressure Coefficients on the Natural Ventilation Effectiveness of Buildings through Simulations
Abstract
1. Introduction
Research Scope and Methodology
2. Review of Air Infiltration and Ventilation Studies
2.1. Ventilation Thresholds
2.2. Assessing Natural Ventilation Performance
Airflow Network Models
3. Natural Ventilation Effectiveness (NVE)—Building Performance Metric
3.1. Minimum Airflow Rate
3.2. Required Airflow Rate
3.3. Available Airflow Rate
4. Simulation Method
4.1. Reference Building and Measured Data
4.2. I-MA—Building Energy Simulation (BES) Model
| Cp Source | Primary or Direct | Secondary or Indirect | |
|---|---|---|---|
| i | E+ values (default values) Swami and Chandra [68] | x | |
iia iib iic | Cloud-based platform—simulator [86] Terrain type: Very flat (Vf) * Terrain type: Open country (Oc) * Terrain type: Suburban (Su) * | x x x | |
| iii | AIVC database [64] | x | |
| iv | TPU database [67] | x |
| Case | Considered Options | Z0 [m] | Zref [m] | Uref [m/s] |
|---|---|---|---|---|
| 1. Very flat terrain | iia | 0.0025 | 250 | 40 |
| 2. Open country | iib | 0.025 | 350 | 40 |
| 3. Suburban | iic | 0.25 | 450 | 40 |
| 4. Urban | - | 2.5 | 550 | 40 |
4.2.1. NVE—Required Airflow Rate (Cooling Loads—)
4.2.2. NVE—Available Airflow Rate ()
4.3. Cp Simulator
5. Values Considered in the E+ AFN Model
5.1. Primary Source—Cloud-Based Platform—Cp Simulator
5.2. Secondary Sources
5.3. Cp Impact over Predicted Temperatures and ACH
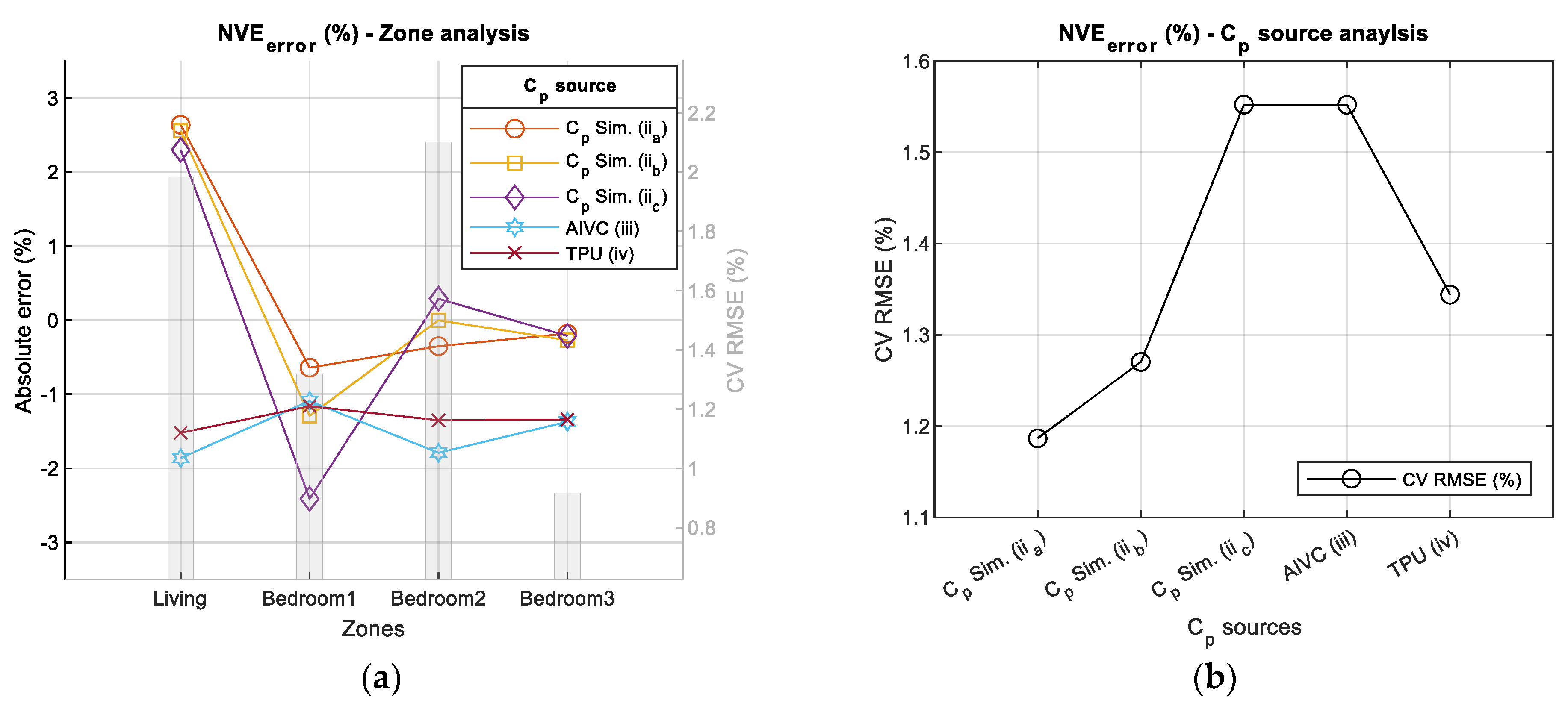
6. NVE Effectiveness
7. Research Constraints and Remarks
8. Conclusions
- The method of applying the Natural Ventilation Effectiveness (NVE) as a performance metric supports the design of naturally ventilated buildings. It provides quantitative data on NV performance and offers interactive feedback during project development based on BES airflow networks;
- The cloud-based platform (CpSimulator) appears to be a reliable source, representing a significant contribution to the BES community. It allows for the generation of primary wind pressure coefficient data for natural ventilation investigations (AFN E+) by employing external CFD resources. Thus, researchers and designers are better assisted when making preliminary design decisions for buildings with natural ventilation;
- The impact of different values on NVE performance was only 3% for the small building used in this study. In such cases, using secondary sources, such as the one implemented in E+ AFN, seems to be more convenient. Primary sources may be required for more complex buildings, which can be more easily obtained through the CpSimulator platform, for example.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- de Bortoli, K.C.R.; de Paula Resende, V.F.; Carlo, J.C.; Villa, S.B. Thermal comfort and air renewal in social housing: A case study in Uberlândia, Brazil. Eng. Sci. 2023, 12, 1–24. [Google Scholar] [CrossRef]
- Yoon, N.; Piette, M.A.; Han, J.M.; Wu, W.; Malkawi, A. Optimization of Window Positions for Wind-Driven Natural Ventilation Performance. Energies 2020, 13, 2464. [Google Scholar] [CrossRef]
- Martins, N.R.; da Graça, G.C. Validation of numerical simulation tools for wind-driven natural ventilation design. Build. Simul. 2016, 9, 75–87. [Google Scholar] [CrossRef]
- Brambilla, A.; Bonvin, J.; Flourentzou, F.; Jusselme, T. On the Influence of Thermal Mass and Natural Ventilation on Overheating Risk in Offices. Buildings 2018, 8, 47. [Google Scholar] [CrossRef]
- Nomura, M.; Hiyama, K. A review: Natural ventilation performance of office buildings in Japan. Renew. Sustain. Energy Rev. 2017, 74, 746–754. [Google Scholar] [CrossRef]
- Chen, Q. Ventilation performance prediction for buildings: A method overview and recent applications. Build. Environ. 2009, 44, 848–858. [Google Scholar] [CrossRef]
- Yoon, N.; Norford, L.; Malkawi, A.; Samuelson, H.; Piette, M.A. Dynamic metrics of natural ventilation cooling effectiveness for interactive modeling. Build. Environ. 2020, 180, 106994. [Google Scholar] [CrossRef]
- Karava, P.; Stathopoulos, T.; Athienitis, A.K. Airflow assessment in cross-ventilated buildings with operable façade elements. Build. Environ. 2011, 46, 266–279. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Comparison of different methods for estimating ventilation rates through wind driven ventilated buildings. Energy Build. 2012, 54, 297–306. [Google Scholar] [CrossRef]
- Tan, G.; Glicksman, L.R. Application of integrating multi-zone model with CFD simulation to natural ventilation prediction. Energy Build. 2005, 37, 1049–1057. [Google Scholar] [CrossRef]
- Asfour, O.S.; Gadi, M.B. A comparison between CFD and Network models for predicting wind-driven ventilation in buildings. Build. Environ. 2007, 42, 4079–4085. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Sakiyama, N.; Carlo, J.C.; Frick, J.; Garrecht, H. Perspectives of naturally ventilated buildings: A review. Renew. Sustain. Energy Rev. 2020, 130, 109933. [Google Scholar] [CrossRef]
- Zhai, Z. Application of Computational Fluid Dynamics in Building Design: Aspects and Trends. Indoor Built Environ. 2006, 15, 305–313. [Google Scholar] [CrossRef]
- Singh, M.; Sharston, R. A literature review of building energy simulation and computational fluid dynamics co-simulation strategies and its implications on the accuracy of energy predictions. Build. Serv. Eng. Res. Technol. 2022, 43, 113–138. [Google Scholar] [CrossRef]
- Coakley, D.; Raftery, P.; Keane, M. A review of methods to match building energy simulation models to measured data. Renew. Sustain. Energy Rev. 2014, 37, 123–141. [Google Scholar] [CrossRef]
- Wang, H.; Zhai, Z. Advances in Building Simulation and Computational Techniques: A Review between 1987 and 2014. Energy Build. 2016, 128, 319–335. [Google Scholar] [CrossRef]
- Lee, B. Building Energy Simulation and the Design of Sustainable and Resilient Buildings. In Sustainable Real Estate: Multidisciplinary Approaches to an Evolving System; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Cóstola, D.; Blocken, B.; Hensen, J. Overview of pressure coefficient data in building energy simulation and airflow network programs. Build. Environ. 2009, 44, 2027–2036. [Google Scholar] [CrossRef]
- Yoon, N.; Malkawi, A. Predicting the effectiveness of wind-driven natural ventilation strategy for interactive building design. In Proceedings of the 15th International Building Simulation Conference, San Francisco, CA, USA, 7–9 August 2017; pp. 2163–2170. [Google Scholar]
- Cóstola, D.; Blocken, B.; Ohba, M.; Hensen, J. Uncertainty in airflow rate calculations due to the use of surface-averaged pressure coefficients. Energy Build. 2010, 42, 881–888. [Google Scholar] [CrossRef]
- Ramponi, R.; Angelotti, A.; Blocken, B. Energy saving potential of night ventilation: Sensitivity to pressure coefficients for different European climates. Appl. Energy 2014, 123, 185–195. [Google Scholar] [CrossRef]
- Heijmans, N.; Wouters, P. Impact of the uncertainties on wind pressures on the prediction of thermal comfort performances. In Principles of Hybrid Ventilation (ed. P. Heiselberg); IEA ECBCS Annex: Paris, France, 2002. [Google Scholar]
- Clark, J.D.; Less, B.D.; Dutton, S.M.; Walker, I.S.; Sherman, M.H. Efficacy of occupancy-based smart ventilation control strategies in energy-efficient homes in the United States. Build. Environ. 2019, 156, 253–267. [Google Scholar] [CrossRef]
- Fernandes, M.S.; Rodrigues, E.; Gaspar, A.R.; Costa, J.J.; Gomes, Á. The contribution of ventilation on the energy performance of small residential buildings in the Mediterranean region. Energy 2020, 191, 116577. [Google Scholar] [CrossRef]
- Guillén-Lambea, S.; Rodríguez-Soria, B.; Marín, J.M. Review of European ventilation strategies to meet the cooling and heating demands of nearly zero energy buildings (nZEB)/Passivhaus. Comparison with the USA. Renew. Sustain. Energy Rev. 2016, 62, 561–574. [Google Scholar] [CrossRef]
- Clausen, G. Ventilation, Good Indoor Air Quality and Rational Use of Energy; European Collaborative Action Urban Air, Indoor Environment and Human Exposure EUR-20741-EN, Luxembourg, 2003. Available online: http://bookshop.europa.eu/en/-pbLBNA20741/ (accessed on 2 September 2024).
- ANVISA. Resolução RE/ANVISA nº 176 de 24 de Outubro de 2000 (176). Available online: https://www.saude.mg.gov.br/images/documentos/RES_176.pdf (accessed on 16 February 2021).
- DIN EN. 16798-1; Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings—Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics. Beuth Verlag GmbH: Berlin, Germany, 2019.
- D2 National Building Code of Finland Ministry of the Environment, Department of Built Environment. Indoor Climate and Ventilation for Buildings: Regulations and Guidelines 2012. Available online: http://www.puntofocal.gov.ar/notific_otros_miembros/fin41_t.pdf (accessed on 2 September 2024).
- Légifrance. Arrêté du 24 Mars 1982 Relatif à L’aération des Logements. Available online: https://www.legifrance.gouv.fr/loda/id/JORFTEXT000000862344/ (accessed on 16 February 2021).
- DIN. EN. 1946-6:2019-12; Ventilation and Air Conditioning—Part 6: Ventilation for Residential Buildings—General Requirements, Requirements for Design, Construction, Commissioning and Handover as well as Maintenance. Beuth Verlag GmbH: Berlin, Germany, 2019.
- Dimitroulopoulou, C. Ventilation in European dwellings: A review. Build. Environ. 2012, 47, 109–125. [Google Scholar] [CrossRef]
- Cook, M.; Shukla, Y.; Rawal, R.; Loveday, D.; Faria, L.C.; Angelopoulos, C. Low Energy Cooling and Ventilation for Indian Residences: Design Guide. 2020. Available online: https://carbse.org/low_energy_cooling_and_ventilation_for_indian_residences (accessed on 5 January 2021).
- Appolloni, L.; D’Amico, A.; Raffo, M.; Capasso, L. Hygienic and sanitary standards of housing in Europe: A comparative analysis of nine countries. Ann. Ig. 2020, 32, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Norwegian Building Authorities. Report NO. HO-2/93. Indoor Climate and Energy Consumption; Norwegian Building Authorities: Oslo, Norway, 1993. [Google Scholar]
- Feist, W.; Pfluger, R.; Kaufmann, B.; Schnieders, J.; Kah, O. Passivhaus Projektierungs Paket 2007. 2007. Available online: https://passiv.de/de/04_phpp/04_phpp.htm (accessed on 2 September 2024).
- Moreno-Rangel, A.; Sharpe, T.; McGill, G.; Musau, F. Indoor Air Quality in Passivhaus Dwellings: A Literature Review. Int. J. Environ. Res. Public Health 2020, 17, 4749. [Google Scholar] [CrossRef]
- IPQ. NP 1037-1; Ventilação e Evacuação dos Produtos da Combustão dos Locais com Aparelhos a Gás Parte 1: Edifícios de Habitação. Ventilação Natural; Instituto Português da Qualidade, 2002 (1037-1). Available online: https://protecaocivil.sintra.pt/images/servico-municipal-de-protecao-civil/legislacao/gaz/NP_1037-1_Ventilacao_produtos_combustao_aparelhos_gas-Ventilacao_natural.pdf (accessed on 16 February 2021).
- Boverket—Swedish National Board of Housing, Building and Planning. Boverket’s Building Regulations—Mandatory Provisions and General Recommendations, BBR: BFS 2011:6 with Amendments up to BFS 2018:4; Sweden. Available online: https://www.boverket.se/globalassets/publikationer/dokument/2019/bbr-2011-6-tom-2018-4-english-2.pdf (accessed on 17 February 2021).
- HM Government, Approved Document F—Ventilation. 2010. Available online: https://www.gov.uk/government/publications/ventilation-approved-document-f (accessed on 17 February 2021).
- ASHRAE. 62.1 Ventilation for Acceptable Indoor Air Quality; ASHRAE: Peachtree Corners, GA, USA, 2019. [Google Scholar]
- Buonanno, G.; Ricolfi, L.; Morawska, L.; Stabile, L. Increasing ventilation reduces SARS-CoV-2 airborne transmission in schools: A retrospective cohort study in Italy’s Marche region. Front. Public Health 2022, 10, 1087087. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Tang, J.W.; Bahnfleth, W.; Bluyssen, P.M.; Boerstra, A.; Buonanno, G.; Cao, J.; Dancer, S.; Floto, A.; Franchimon, F.; et al. How can airborne transmission of COVID-19 indoors be minimised? Environ. Int. 2020, 142, 105832. [Google Scholar] [CrossRef]
- Sundell, J.; Levin, H.; Nazaroff, W.W.; Cain, W.S.; Fisk, W.J.; Grimsrud, D.T.; Gyntelberg, F.; Li, Y.; Persily, A.K.; Pickering, A.C.; et al. Ventilation rates and health: Multidisciplinary review of the scientific literature. Indoor Air 2011, 21, 191–204. [Google Scholar] [CrossRef]
- Chenari, B.; Dias Carrilho, J.; Gameiro da Silva, M. Towards sustainable, energy-efficient and healthy ventilation strategies in buildings: A review. Renew. Sustain. Energy Rev. 2016, 59, 1426–1447. [Google Scholar] [CrossRef]
- Carrer, P.; Wargocki, P.; Fanetti, A.; Bischof, W.; Oliveira Fernandes, E.d.; Hartmann, T.; Kephalopoulos, S.; Palkonen, S.; Seppänen, O. What does the scientific literature tell us about the ventilation–health relationship in public and residential buildings? Build. Environ. 2015, 94, 273–286. [Google Scholar] [CrossRef]
- Aynsley, R.; Shiel, J.J. Ventilation strategies for a warming world. Archit. Sci. Rev. 2017, 60, 249–254. [Google Scholar] [CrossRef]
- Schoen, L.J. Guidance for Building Operations during the COVID-19 Pandemic. Available online: https://www.ashrae.org/file%20library/technical%20resources/ashrae%20journal/2020journaldocuments/72-74_ieq_schoen.pdf (accessed on 2 September 2024).
- Chitaru, G.-M.; Istrate, A.; Catalina, T. Numerical analysis of the impact of natural ventilation on the Indoor Air Quality and Thermal Comfort in a classroom. E3S Web Conf. 2019, 111, 1023. [Google Scholar] [CrossRef]
- Aviv, D.; Chen, K.W.; Teitelbaum, E.; Sheppard, D.; Pantelic, J.; Rysanek, A.; Meggers, F. A fresh (air) look at ventilation for COVID-19: Estimating the global energy savings potential of coupling natural ventilation with novel radiant cooling strategies. Appl. Energy 2021, 292, 116848. [Google Scholar] [CrossRef]
- Persily, A. Challenges in Developing Ventilation and Indoor Air Quality Standards: The Story of ASHRAE Standard 62. Build. Environ. 2015, 91, 61–69. [Google Scholar] [CrossRef]
- ASHRAE. 62.1—Ventilation and Acceptable Indoor Air Quality; ASHRAE: Peachtree Corners, GA, USA, 2022. [Google Scholar]
- Zhai, Z.; Mankibi, M.E.; Zoubir, A. Review of Natural Ventilation Models. Energy Procedia 2015, 78, 2700–2705. [Google Scholar] [CrossRef]
- Walton, G.N. NISTIR 89-4072; AIRNET—A Computer Program for Building Airflow Network Modeling. National Institute of Standards and Technology: Gaithersburg, MD, USA, 1989.
- Chu, C.R.; Chiu, Y.-H.; Chen, Y.-J.; Wang, Y.-W.; Chou, C.-P. Turbulence effects on the discharge coefficient and mean flow rate of wind-driven cross-ventilation. Build. Environ. 2009, 44, 2064–2072. [Google Scholar] [CrossRef]
- Chu, C.-R.; Wang, Y.-W. The loss factors of building openings for wind-driven ventilation. Build. Environ. 2010, 45, 2273–2279. [Google Scholar] [CrossRef]
- Flourentzou, F.; van der Maas, J.; Roulet, C.-A. Natural ventilation for passive cooling: Measurement of discharge coefficients. Energy Build. 1998, 27, 283–292. [Google Scholar] [CrossRef]
- Karava, P.; Stathopoulos, T.; Athienitis, A.K. Wind driven flow through openings—A review of discharge coefficients. Int. J. Vent. 2004, 3, 255–266. [Google Scholar] [CrossRef]
- Costola, D.; Etheridge, D.W. Unsteady natural ventilation at model scale—Flow reversal and discharge coefficients of a short stack and an orifice. Build. Environ. 2008, 43, 1491–1506. [Google Scholar] [CrossRef]
- Fernandes, L.; Friedrich, M.; Cóstola, D.; Matsumoto, E.; Labaki, L.; Wellershoff, F. Evaluation of discharge coefficients of large openable windows using full-scale samples in wind tunnel tests//Evaluación de los coeficientes de descarga de grandes ventanas que se pueden abrir utilizando muestras a escala real en ensayos en túneles de viento. Rev. Ing. Construcción 2020, 35, 203–2014. [Google Scholar] [CrossRef]
- Cruz, H.; Viegas, J.C. On-site assessment of the discharge coefficient of open windows. Energy Build. 2016, 126, 463–476. [Google Scholar] [CrossRef]
- Shirzadi, M.; Mirzaei, P.A.; Naghashzadegan, M. Development of an adaptive discharge coefficient to improve the accuracy of cross-ventilation airflow calculation in building energy simulation tools. Build. Environ. 2018, 127, 277–290. [Google Scholar] [CrossRef]
- Martin, W. Liddament. Air Infiltration Calculation Techniques—An Application Guide; The Air Infiltration and Ventilation Centre: Ghent, Belgium, 1986. [Google Scholar]
- Charisi, S.; Thiis, T.; Aurlien, T. Full-Scale Measurements of Wind-Pressure Coefficients in Twin Medium-Rise Buildings. Buildings 2019, 9, 63. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook—Fundamentals: Airflow around Buildings; ASHRAE: Peachtree Corners, GA, USA, 2005. [Google Scholar]
- Tokyo Polytechnic University. Aerodynamic Database for Low-Rise Buildings. Available online: http://www.wind.arch.t-kougei.ac.jp/info_center/windpressure/lowrise/g080627%7F%7F.html (accessed on 22 December 2020).
- Swami, M.V.; Chandra, S. Procedures for Calculating Natural Ventilation Airflow Rates in Buildings; University of Central Florida: Orlando, FL, USA, 1987. [Google Scholar]
- Grosso, M. Modelling wind pressure distribution on buildings for passive cooling. In Proceedings of the International Conference Solar Energy in Architecture and Urban Planning, Florence, Italy, 17–21 May 1993. [Google Scholar]
- Grosso, M.; Mariano, D.; Parisi, E. Wind pressure distribution on flat and tilted roofs: A parametrical model. In Proceedings of the European Conference on Energy Performance and Indoor Climate in Buildings, Lyon, France, 24–26 November 1994; pp. 167–172. [Google Scholar]
- Grosso, M. Wind pressure distribution around buildings: A parametrical model. Energy Build. 1992, 1992, 101–131. [Google Scholar] [CrossRef]
- Feustel, H.E. COMIS—An international multizone air-flow and contaminant transport model. Energy Build. 1999, 3–18. [Google Scholar] [CrossRef]
- Knoll, B.; Phaff, J.C.; de Gids, W.F. Pressure simulation program. In Implementing the results of ventilation research. In Proceedings of the 16th AIVC Conference, Palm Springs, CA, USA, 19–22 September 1995. [Google Scholar]
- Muehleisen, R.T.; Patrizi, S. A new parametric equation for the wind pressure coefficient for low-rise buildings. Energy Build. 2013, 57, 245–249. [Google Scholar] [CrossRef]
- Bre, F.; Gimenez, J.M.; Fachinotti, V.D. Prediction of wind pressure coefficients on building surfaces using artificial neural networks. Energy Build. 2018, 158, 1429–1441. [Google Scholar] [CrossRef]
- Belleri, A.; Lollini, R.; Dutton, S.M. Natural ventilation design: An analysis of predicted and measured performance. Build. Environ. 2014, 81, 123–138. [Google Scholar] [CrossRef]
- Charisi, S.; Waszczuk, M.; Thiis, T.K. Determining building-specific wind pressure coefficients to account for the microclimate in the calculation of air infiltration in buildings. Adv. Build. Energy Res. 2019, 111, 1–22. [Google Scholar] [CrossRef]
- Charisi, S.; Waszczuk, M.; Thiis, T.K. Investigation of the pressure coefficient impact on the air infiltration in buildings with respect to microclimate. Energy Procedia 2017, 122, 637–642. [Google Scholar] [CrossRef]
- Dogan, T.; Kastner, P. Streamlined CFD Simulation Framework to Generate Wind-Pressure Coefficients on Building Facades for Airflow Network Simulations. Build. Simul. 2021, 14, 1189–1200. [Google Scholar] [CrossRef]
- Gimenez, J.M.; Bre, F.; Nigro, N.M.; Fachinotti, V. Computational modeling of natural ventilation in low-rise non-rectangular floor-plan buildings. Build. Simul. 2018, 11, 1255–1271. [Google Scholar] [CrossRef]
- King, M.-F.; Gough, H.L.; Halios, C.; Barlow, J.F.; Robertson, A.; Hoxey, R.; Noakes, C.J. Investigating the influence of neighbouring structures on natural ventilation potential of a full-scale cubical building using time-dependent CFD. J. Wind Eng. Ind. Aerodyn. 2017, 169, 265–279. [Google Scholar] [CrossRef]
- Kastner, P.; Dogan, T. A cylindrical meshing methodology for annual urban computational fluid dynamics simulations. J. Build. Perform. Simul. 2020, 13, 59–68. [Google Scholar] [CrossRef]
- Kastner, P.; Dogan, T. Eddy3D: A toolkit for decoupled outdoor thermal comfort simulations in urban areas. Build. Environ. 2022, 212, 108639. [Google Scholar] [CrossRef]
- Robert McNeel \& Associates, Seattle, WA. Rhinoceros 3D. Available online: https://www.rhino3d.com/ (accessed on 2 September 2024).
- Davidson, S. Grasshopper. Available online: https://www.rhino3d.com/learn/?query=kind:%20grasshopper&modal=null (accessed on 2 September 2024).
- Bre, F.; Gimenez, J.M. A cloud-based platform to predict wind pressure coefficients on buildings. Build. Simul. 2022, 15, 1507–1525. [Google Scholar] [CrossRef] [PubMed]
- Sakiyama, N.R.M.; Carlo, J.C.; Frick, J.; Garrecht, H. CFD-based wind pressure coefficients on building facades with Butterfly/OpenFOAM for airflow network models. In Proceedings of the IBPSA LATAM 2023—VII Congresso Latino-Americano de Simulação de Edifícios, Florianópolis, Brazil, 9–10 March 2023; pp. 195–199, ISBN 978-65-992964-4-4. [Google Scholar]
- OpenCFD Ltd. OpenFOAM; OpenCFD: London, UK, 2024. [Google Scholar]
- ASHRAE. Thermal Environmental Conditions for Human Occupancy; ASHRAE: Peachtree Corners, GA, USA, 2013; p. 55. [Google Scholar]
- Sakiyama, N.; Mazzaferro, L.; Carlo, J.C.; Bejat, T.; Garrecht, H. Natural ventilation potential from weather analyses and building simulation. Energy Build. 2020, 231, 110596. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlus; U.S. Department of Energy: Washington, DC, USA, 2019.
- Gu, L. Airflow network modeling in energyplus. In Proceedings of the Building Simulation 2007, 10th IBPSA Conference, Beijing, China, 3–6 September 2007; pp. 964–971. [Google Scholar]
- Coakley, D. Calibration of Detailed Building Energy Simulation Models using an Analytical Optimisation Approach. Ph.D. Thesis, University of Galway Theses, Galway, Ireland, 2013. [Google Scholar]
- ASHRAE. Guideline 14-2002: Measurement of Energy and Demand Savings; ASHRAE: Peachtree Corners, GA, USA, 2002. [Google Scholar]
- Zhang, Y. “Parallel” EnergyPlus and development of a parametric analysis tool. In Proceedings of the Building Simulation 2009; Eleventh International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009; pp. 1382–1388. [Google Scholar]
- Zhang, Y.; Korolija, I. jEPlus—An EnergyPlus simulation manager for parametrics n.d. Available online: http://www.jeplus.org/wiki/doku.php (accessed on 2 September 2024).
- Loche, I.; Oliveira, K.d.; Oliveira, M.; Fracalanza, B.; Neves, L. Effects of balconies on the wind pressure coefficients of naturally ventilated high-rise office buildings. In Proceedings of the Symposium on Simulation for Architecture and Urban Design. SimAUD 2020: Symposum on Simulation in Architecture + Urban Design, online, 25–27 May 2020; pp. 365–372. [Google Scholar]
- Costanzo, V.; Yao, R.; Xu, T.; Xiong, J.; Zhang, Q.; Li, B. Natural ventilation potential for residential buildings in a densely built-up and highly polluted environment: A Case Study. Renew. Energy 2019, 138, 340–353. [Google Scholar] [CrossRef]
- Yang, F.; Kang, Y.; Gao, Y.; Zhong, K. Numerical simulations of the effect of outdoor pollutants on indoor air quality of buildings next to a street canyon. Build. Environ. 2015, 87, 10–22. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Adamkiewicz, G.; Spengler, J.D. Quantifying the impact of traffic-related air pollution on the indoor air quality of a naturally ventilated building. Environ. Int. 2016, 89–90, 138–146. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Liu, Z.; Freeman, R.B. Energy saving potential of natural ventilation in China: The impact of ambient air pollution. Appl. Energy 2016, 179, 660–668. [Google Scholar] [CrossRef]
- Nihar, K.; Nutkiewicz, A.; Jain, R.K. Natural ventilation versus air pollution: Assessing the impact of outdoor pollution on natural ventilation potential in informal settlements in India. Environ. Res. Infrastruct. Sustain. 2023, 3, 25002. [Google Scholar] [CrossRef]
- Chen, J.; Brager, G.S.; Augenbroe, G.; Song, X. Impact of outdoor air quality on the natural ventilation usage of commercial buildings in the US. Appl. Energy 2019, 235, 673–684. [Google Scholar] [CrossRef]
- Fudge, C.; Grant, M.; Wallbaum, H. Transforming cities and health: Policy, action, and meaning. Cities Health 2020, 4, 135–151. [Google Scholar] [CrossRef]


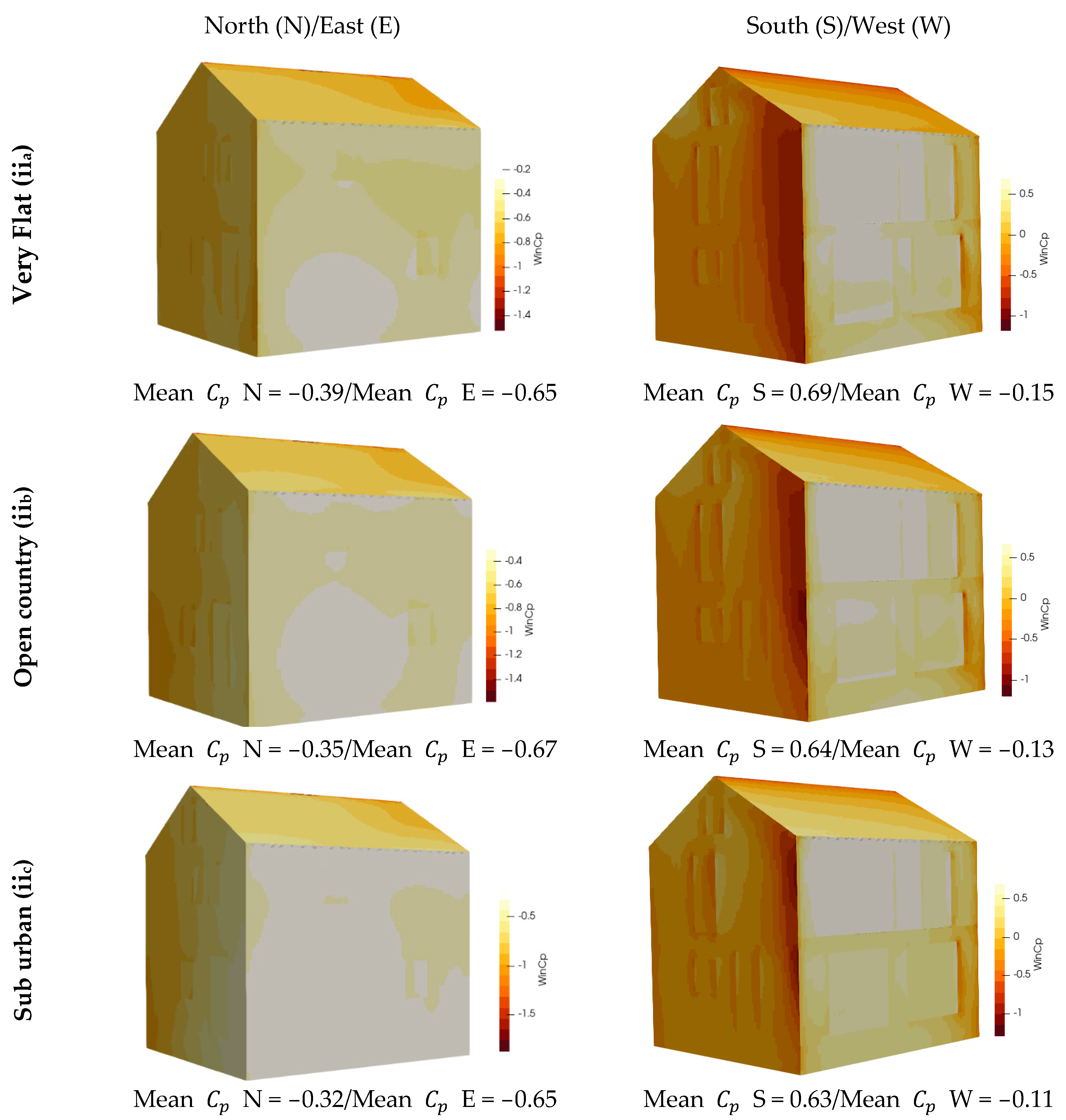
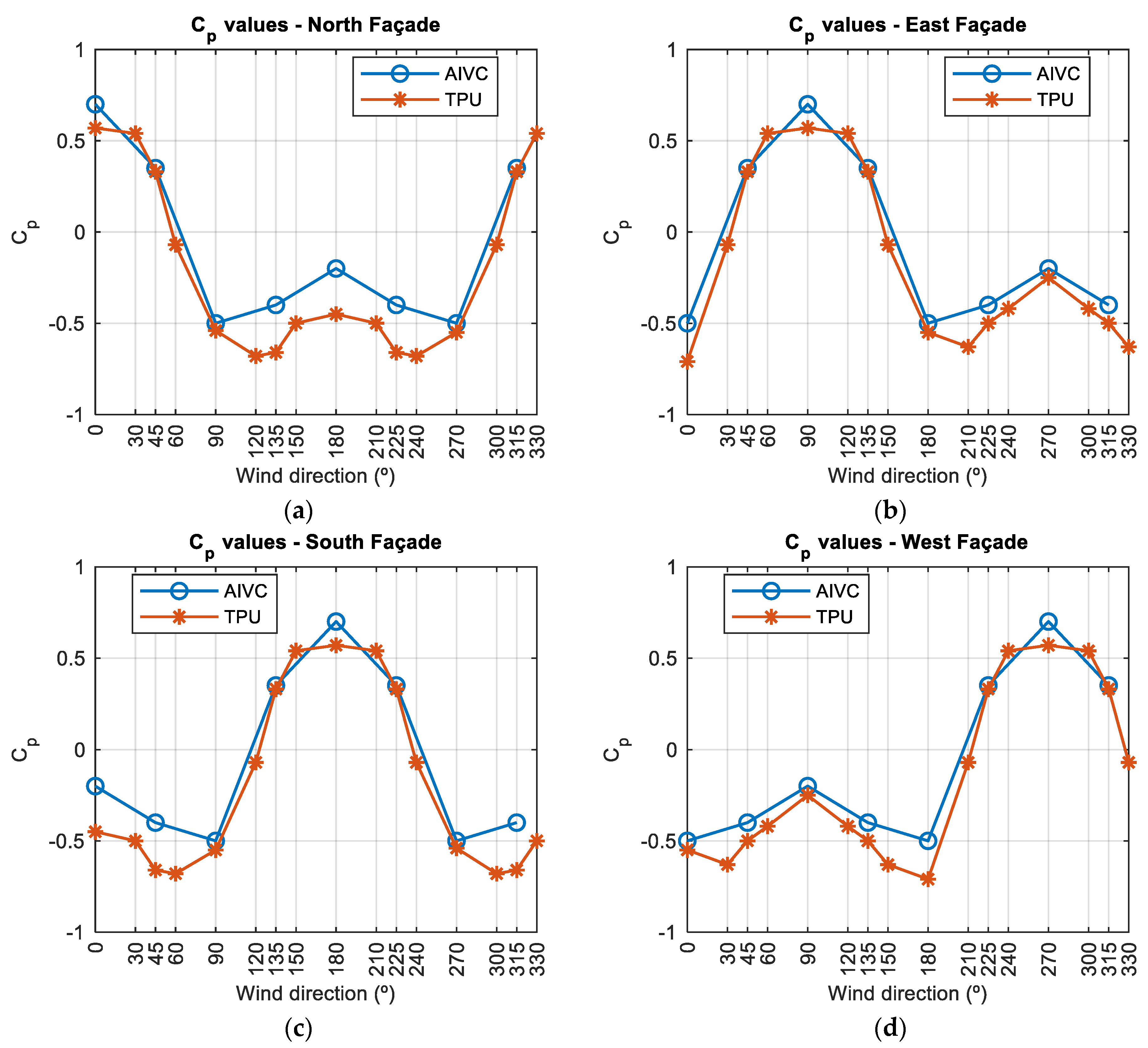
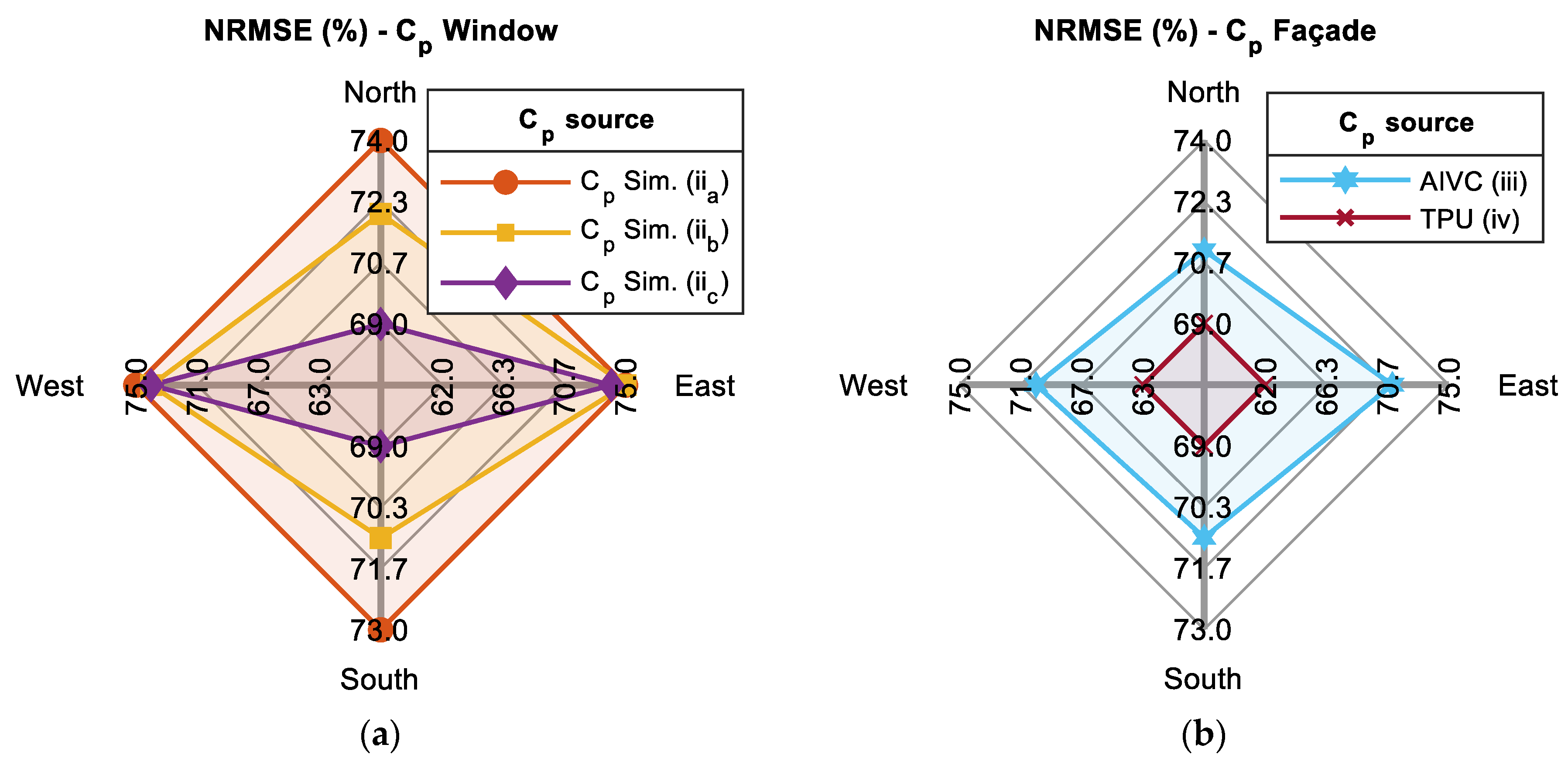


| Country/State | Standard | Whole Building Ventilation Rates |
|---|---|---|
| Brazil | ANVISA—RE n° 176, de 24 de outubro de 2000 [28] | The adequate air renewal rate for air conditioning environments (Workspaces): (1) 27 m3/h person; (2) 17 m3/h person for stores, shopping centers, and other places where the occupancy rate per m2 is critical. |
| Europe | EN 16798-1 [29] | Continuous flow rate with occupancy: (1) 0.42 L/s.m2; (2) 7 L/s person in living and bedroom; (3) 1 L/m2 for living and bedroom floor areas. Without occupancy: 0.05 L/s.m2–0.1 L/s.m2 |
| Finland | NBC—D2 [30] | >0.4 h−1 General rule: Outdoor airflow should be at least 0.35 L/s.m2 (1.26 m3/h.m2) |
| France | Arrêté du 24 Mars 1982. Modifié par arrêté du 28 octobre 1983 relatif à l’aération des logements [31] | Continuous ventilation must be assured during winter Total minimum flow assured for whole dwelling with regulation control device: 9.72 L/s (35 m3/h)–37.5 L/s (135 m3/h)—1- to 7-room house. Total minimum flow assured for whole dwelling with mechanical ventilation and control device: 2.77 L/s (10 m3/h)–9.72 L/s (35 m3/h)—1- to 7-room house |
| Germany | DIN 1946-6 [32] | Mechanical ventilation is required if the necessary air volume flow for moisture-proofing exceeds the infiltration air volume flow Demand-controlled ventilation specifies four levels for fan air flow: Pos 1, protection against humidity— 4.16 L/s (15 m3/h)–23.6 L/s (85 m3/h)—30 m2–210 m2; Pos 2, reduced ventilation— 11.11 L/s (40 m3/h)–41.66 L/s (150 m3/h)—30 m2–210 m2; Pos 3, nominal ventilation; 15.27 L/s (55 m3/h)–59.72 L/s (215 m3/h)—30 m2–210 m2; Pos 4, intensive ventilation— 19.44 L/s (70 m3/h)–79.16 L/s (285 m3/h)—30 m2–210 m2 |
| Greece | Greek Legislative Framework Document (as cited in [33]) | Detached houses, estimated five persons/100 m2 of floor area. Block of flats, estimated seven persons/100 m2 of floor area. |
| India | Low Energy Cooling and Ventilation [34] | Design charts that correlate airflow rates from 0 to 1.2 (m3/s) and free area of openings from 0 to 8 (m2) Application examples: desired ventilation rates (m3/s) for different room types (master bedroom—MB, small bedroom—SB, hall + open kitchen—HK) for eight cities (climates) and two case study apartments MB: 0.09–0.35 (case 1), 0.13–0.53 (case 2) SB: 0.08–0.32 (case 1), 0.09–0.36 (case 2) HK: 0.48–1.06 (case 1), 0.51–1.14 (case 2) |
| Italy | Ministerial Decree 05.07.75 [35] | Naturally ventilated dwelling 0.35–0.5 h−1 |
| Netherlands | Building Decree (as cited in [33]) | 300 m3/h |
| Norway | Norwegian Building Code [36] | Not less than 0.5 h−1 |
| Passivhaus | Standard Passivhaus [37,38] | 8.33 L/s–8.88 L/s (30–32 m3/h) per person Controlled ventilation depending on the occupancy |
| Portugal | NP 1037-1 Standard for natural ventilation [39] | 1.0–4.0 h−1: depending on the room type |
| Sweden | Swedish Building Regulations BBR94 [40] | Rooms shall have a continuous 0.35 L/s/m2 floor area (1.26 m3/h/m2) when in use. This corresponds to 0.5 h−1 in a room with a height of 2.5 m. |
| Switzerland | SIA 180, 2014 SIA 382/2, 1992 (as cited in [33]) | 12–15 m3/h/person (non-smoking, max CO2 1500 ppm) 30–70 m3/h/person (smoking) 25–30 m3/h/person (non-smoking, max CO2 1000 ppm). Air change rate in unoccupied rooms more than 0.3 h−1. |
| UK | Approved Doc. F Ventilation 2010 [41] | 13 L/s–29 L/s: 1- to 5-room house. The whole ventilation flow rate is always higher than 0.3 L/s m2. If dwelling permeability is 5 m3/(h m) to 50 Pa, it takes 0.15 ACH as the infiltration rate, which will be subtracted from the total ventilation rate. |
| US | ASHRAE Standard 62-1-2019 [42] | 2.5 L/s person, 0.3 L/s m2 |
| Database | Air Infiltration and Ventilation Centre (AIVC) [64] Data are presented for wind attack angles from 0° to 315° (45° range) for low-rise and high-rise buildings ASHRAE Handbook of fundamentals (Airflow around buildings) [66] Data are presented for wind attack angles from 0° to 180° (45° range) for low-rise/high-rise buildings Tokyo Polytechnic University (TPU) Aerodynamic database of low-rise buildings [67] Data are presented for wind attack angles from 0° to 90° (15° range) for different buildings examples (web-based application tool) |
| Analytical models | Swami and Chandra [68] One equation for low-rise buildings (from eight different investigators) and another for high-rise buildings (one source) CPCALC + [69,70] This is a program developed within the PASCOOL program as an upgrade of the CpCalc [71], an integrated module of the multizone airflow and contaminant transport model (COMIS) [72] Cp Generator [23,73] Web-based program developed by the Dutch institution TNO based on fits of measured data to mathematical expressions. New parametric equation [74] Developed through curve fits of the low-rise data from the TPU database, and it is easier to calculate by hand or with a spreadsheet than the Swami and Chandra equations. Artificial neural networks (ANN) [75] ANN is used to obtain analytical models to accurately predict the surface-averaged wind pressure coefficients in walls and roofs of low-rise buildings. |
| Database | North Façade | South Façade | West Façade | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| East Façade | ||||||||||
| Cellar ACH | Cellar Temp | LV ACH | LV Temp | BR2 ACH | BR2 Temp | BR3 ACH | BR3 Temp | BR1 ACH | BR1 Temp | |
| iia CpSimVf | 142.7% | 5.6% | 12.1% | 1.6% | 7.7% | 2.1% | 4.7% | 1.9% | 7.9% | 1.6% |
| iib CpSimOc | 129.7% | 5.4% | 20.2% | 1.6% | 7.4% | 2.1% | 5.3% | 1.9% | 10.3% | 1.8% |
| iic CpSimSb | 120.3% | 5.2% | 17.2% | 1.6% | 7.4% | 2.0% | 5.1% | 1.7% | 11.8% | 1.9% |
| iii AIVC | 14.2% | 2.8% | 7.2% | 2.0% | 6.7% | 2.7% | 10.2% | 2.9% | 11.6% | 3.2% |
| iv TPU | 15.3% | 3.0% | 9.5% | 2.2% | 7.2% | 2.7% | 10.3% | 2.2% | 11.6% | 3.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakiyama, N.R.M.; Carlo, J.C.; Sakiyama, F.I.H.; Abdessemed, N.; Frick, J.; Garrecht, H. Impact of Wind Pressure Coefficients on the Natural Ventilation Effectiveness of Buildings through Simulations. Buildings 2024, 14, 2803. https://doi.org/10.3390/buildings14092803
Sakiyama NRM, Carlo JC, Sakiyama FIH, Abdessemed N, Frick J, Garrecht H. Impact of Wind Pressure Coefficients on the Natural Ventilation Effectiveness of Buildings through Simulations. Buildings. 2024; 14(9):2803. https://doi.org/10.3390/buildings14092803
Chicago/Turabian StyleSakiyama, Nayara Rodrigues Marques, Joyce Correna Carlo, Felipe Isamu Harger Sakiyama, Nadir Abdessemed, Jürgen Frick, and Harald Garrecht. 2024. "Impact of Wind Pressure Coefficients on the Natural Ventilation Effectiveness of Buildings through Simulations" Buildings 14, no. 9: 2803. https://doi.org/10.3390/buildings14092803
APA StyleSakiyama, N. R. M., Carlo, J. C., Sakiyama, F. I. H., Abdessemed, N., Frick, J., & Garrecht, H. (2024). Impact of Wind Pressure Coefficients on the Natural Ventilation Effectiveness of Buildings through Simulations. Buildings, 14(9), 2803. https://doi.org/10.3390/buildings14092803








