Coupled Outdoor and Indoor Airflow Prediction for Buildings Using Computational Fluid Dynamics (CFD)
Abstract
:Nomenclature
 | Inlet opening area | (m2) |
 | Outlet opening area | (m2) |
 | Opening area | (m2) |
 | Opening area, refer to Equation (5) | (m2) |
 | Opening discharge coefficient | (-) |
 | Constant (windward/ parallel wind: 0.0012 and, leeward wind: 0.0026) | (-) |
 | Pressure coefficient | (-) |
 | Opening effectiveness | (-) |
 | Wind speed | (ms−1) |
 | Reference wind speed | (ms−1) |
 | Pressure | (Nm−2) |
 | Ventilation rate | (m3s−1) |
| Greek Letters or other Symbols | ||
 | Air density | (kgs−3) |
1. Introduction
2. Methodology
- Approach A: Fully empirical models;
- Approach B: Physical models (small or full scale) models;
- Approach C: Combination of physical and empirical models;
- Approach D: Combination of CFD and empirical models;
- Approach E: Fully CFD models (coupled or de-coupled).
3. Empirical Models





 is taken as total opening area for a single opening room or area of inlet opening for a room with two similar sized openings. According to ASHRAE [13], in a cross-ventilated room, the values of
is taken as total opening area for a single opening room or area of inlet opening for a room with two similar sized openings. According to ASHRAE [13], in a cross-ventilated room, the values of  are between 0.5 and 0.7 for perpendicular wind and 0.25 to 0.35 for diagonal wind. However, a study by Larsen [14] suggests that the value for diagonal wind is 0.48, but the opening area used in this study is only equal to 1% of the total area of the facade. In the case of a single-sided ventilation, the value is either 0.025 [15,16] or 0.02 [17].
are between 0.5 and 0.7 for perpendicular wind and 0.25 to 0.35 for diagonal wind. However, a study by Larsen [14] suggests that the value for diagonal wind is 0.48, but the opening area used in this study is only equal to 1% of the total area of the facade. In the case of a single-sided ventilation, the value is either 0.025 [15,16] or 0.02 [17]. , which is dependent on various factors, such as wind direction and opening configuration. For a single-cell room, the values for
, which is dependent on various factors, such as wind direction and opening configuration. For a single-cell room, the values for  range between 0.5 and 0.9 depending on the opening configuration [18]. For an opening area less than 10% of the facade, the values are between 0.5 and 0.65. While the first two equations can be applied to both single-sided and cross-ventilated rooms, Equation (3) [19] and Equation (4) [14] are limited to single-sided ventilation. In Equation (4), the
range between 0.5 and 0.9 depending on the opening configuration [18]. For an opening area less than 10% of the facade, the values are between 0.5 and 0.65. While the first two equations can be applied to both single-sided and cross-ventilated rooms, Equation (3) [19] and Equation (4) [14] are limited to single-sided ventilation. In Equation (4), the  values used are taken from Liddament [20].
values used are taken from Liddament [20].4. Building Configurations

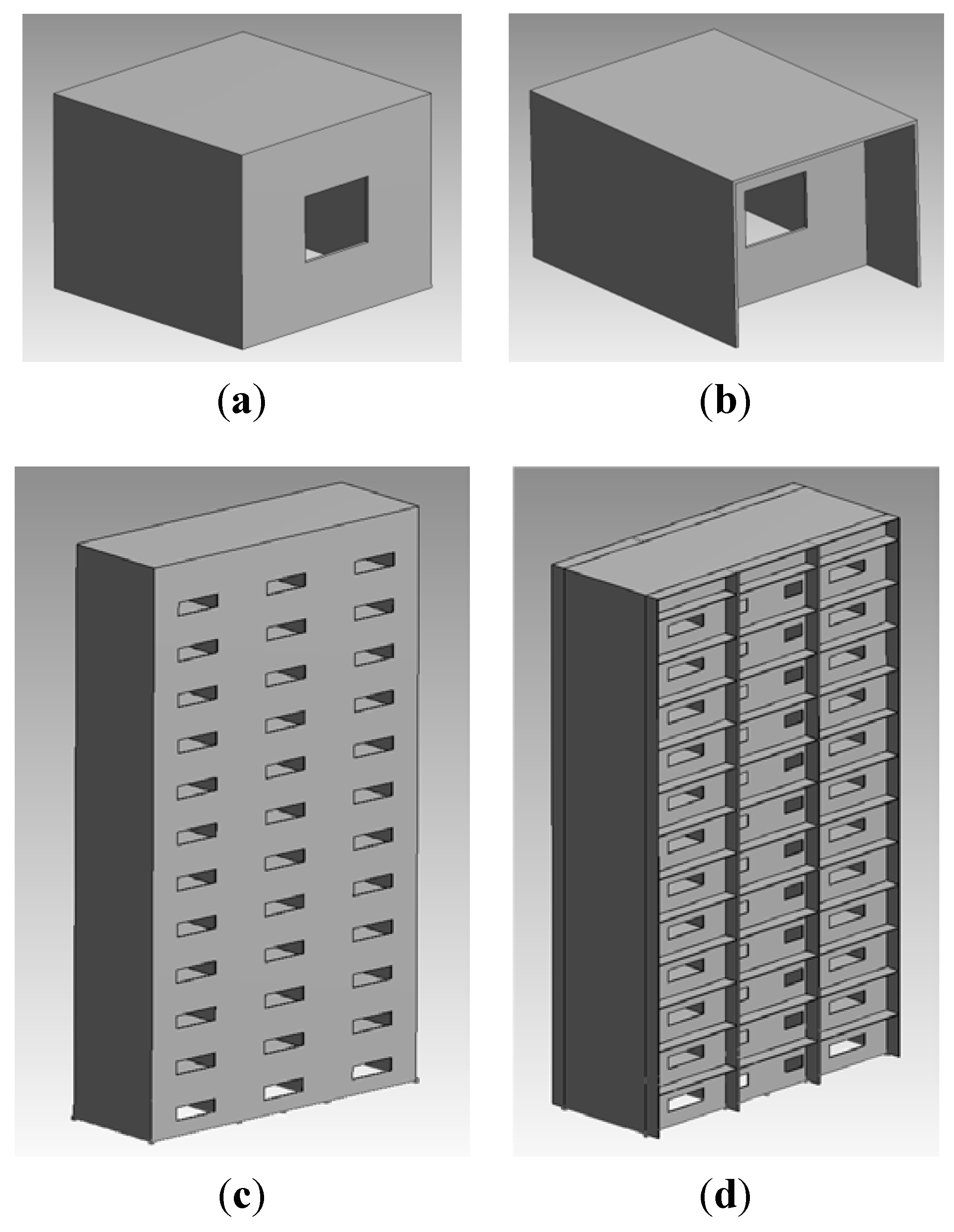
5. Computational Fluid Dynamics (CFD)
CFD Setup
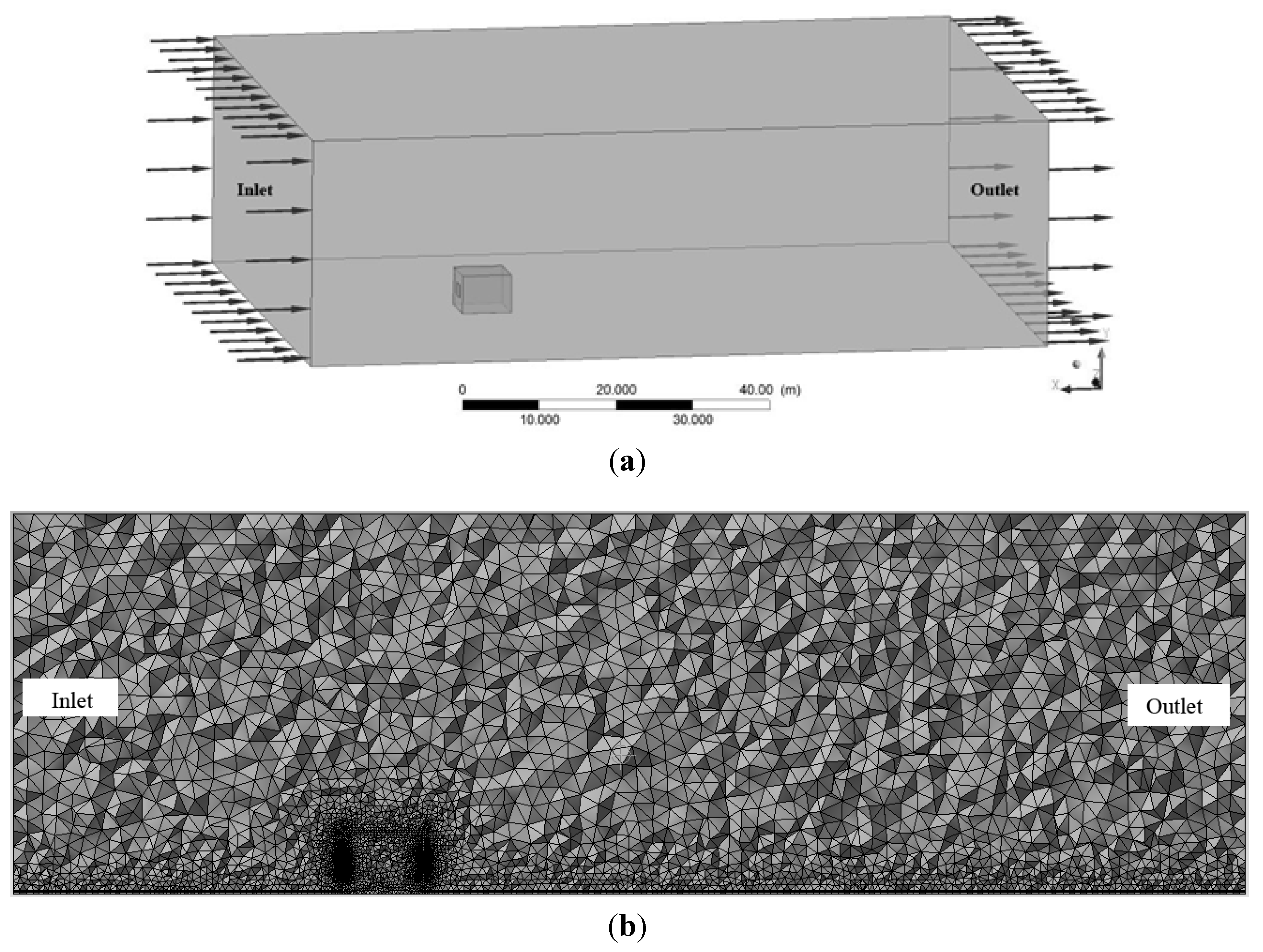
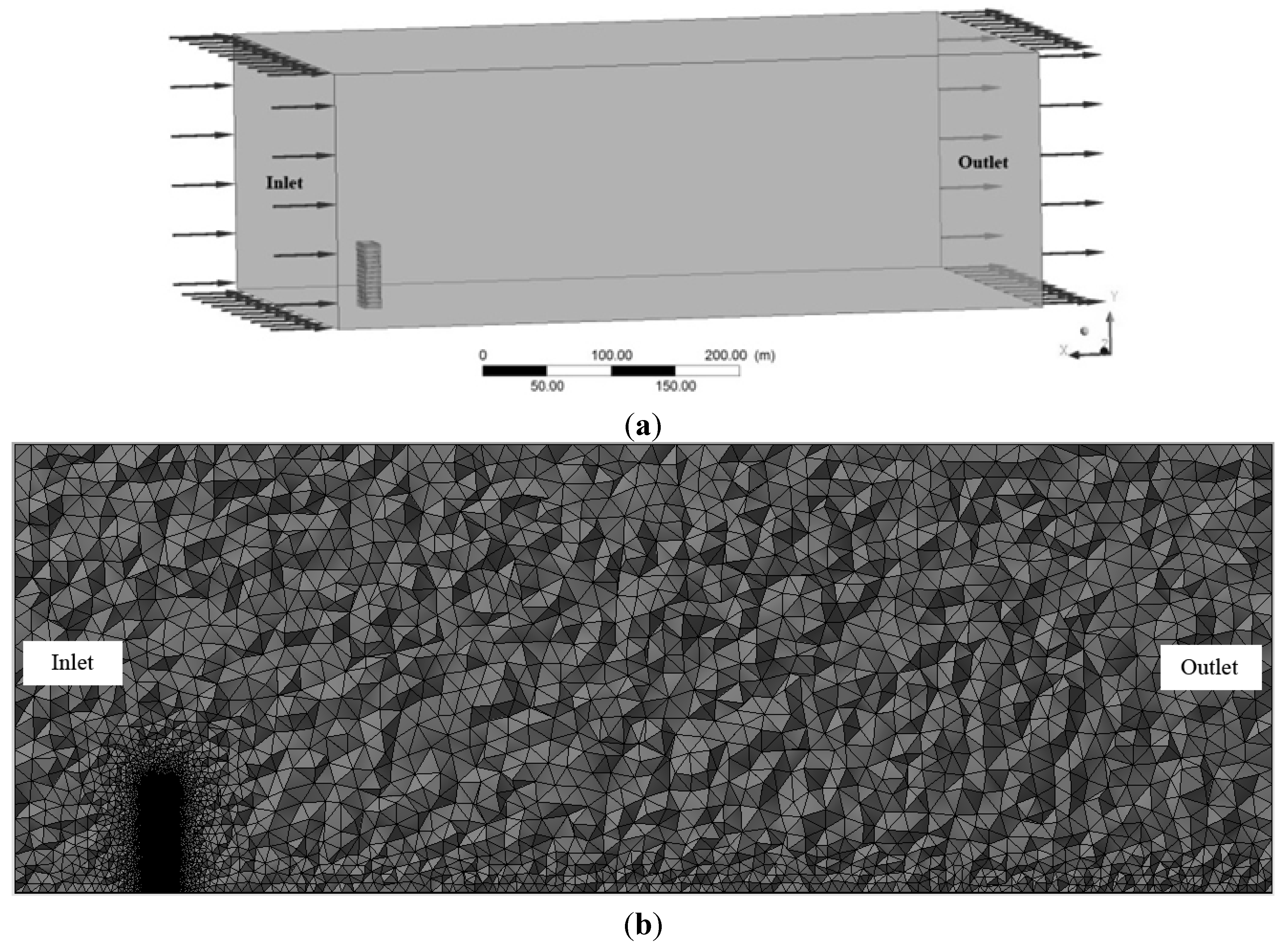
6. Results and Findings
6.1. Single-Cell Building
| Model | Wind angles | ||
|---|---|---|---|
| 0° | 45° | 135° | |
| G01 | A (Eqn. 4) | A (Eqn. 4) | A (Eqn. 4) |
| G02 | A (Eqn. 4) | D (Eqn. 2) | D (Eqn. 2) |
| G03 | D (Eqn. 2) | D (Eqn. 2) | D (Eqn. 2) |
| G04 | D (Eqn. 2) | D (Eqn. 2) | D (Eqn. 2) |
| G05 | D (Eqn. 2) | D (Eqn. 2) | D (Eqn. 2) |
| G06 | D (Eqn. 2) | D (Eqn. 2) | D (Eqn. 2) |
| G07 | D (Eqn. 2) | D (Eqn. 2) | D (Eqn. 2) |
| G08 | A (Eqn. 4) | A (Eqn. 4) | A (Eqn. 4) |
 in Equation (2) is between 0.5 and 0.65 for an opening area less than 10% of façade area, this study uses a value of 0.65 for direct cross ventilation at 0° wind angle and 0.5 for all other wind angles. The pressure values used in Equation (2) are measured at the centre of the openings.
in Equation (2) is between 0.5 and 0.65 for an opening area less than 10% of façade area, this study uses a value of 0.65 for direct cross ventilation at 0° wind angle and 0.5 for all other wind angles. The pressure values used in Equation (2) are measured at the centre of the openings.6.1.1. Modification of Facade Treatment
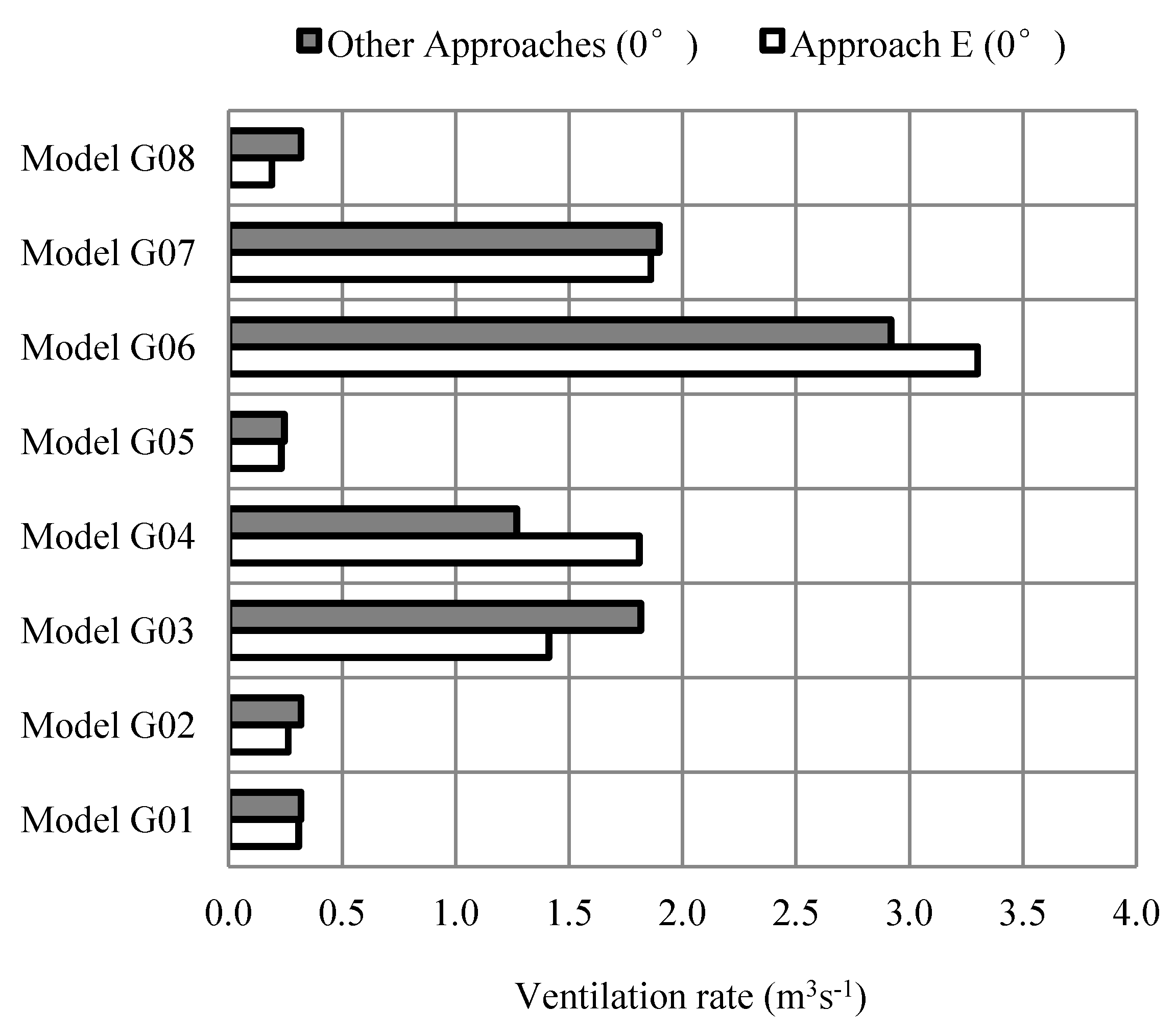
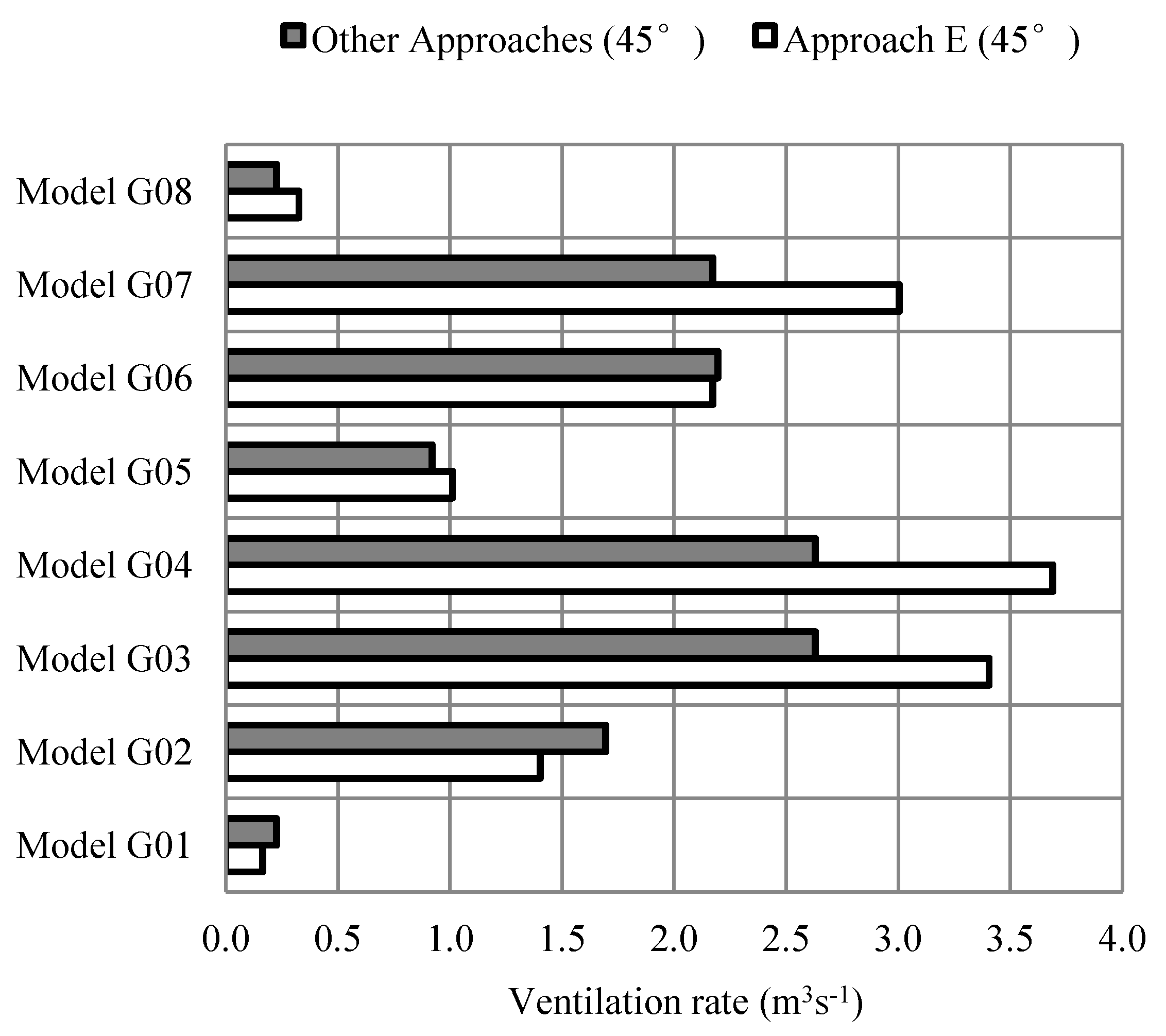
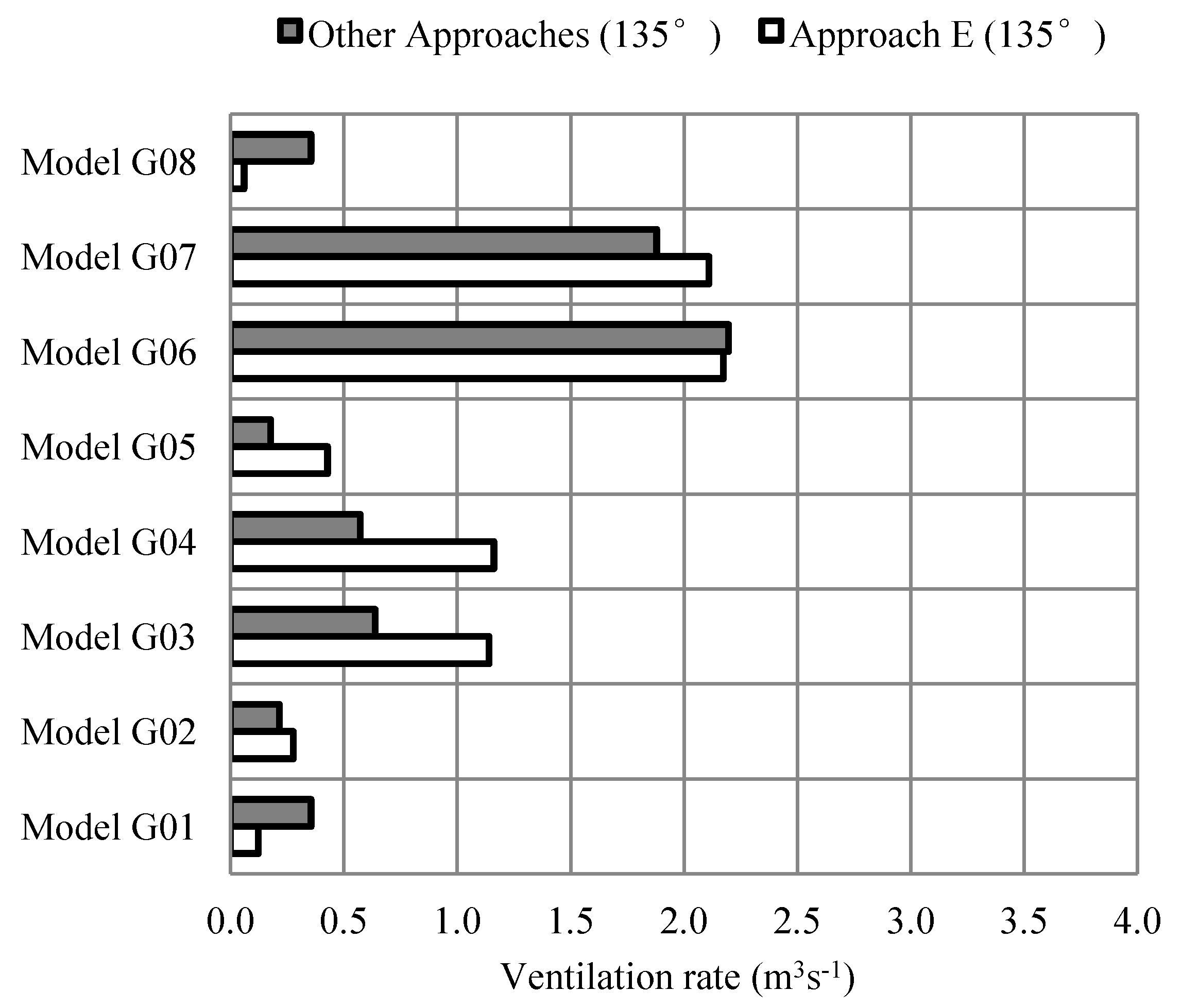
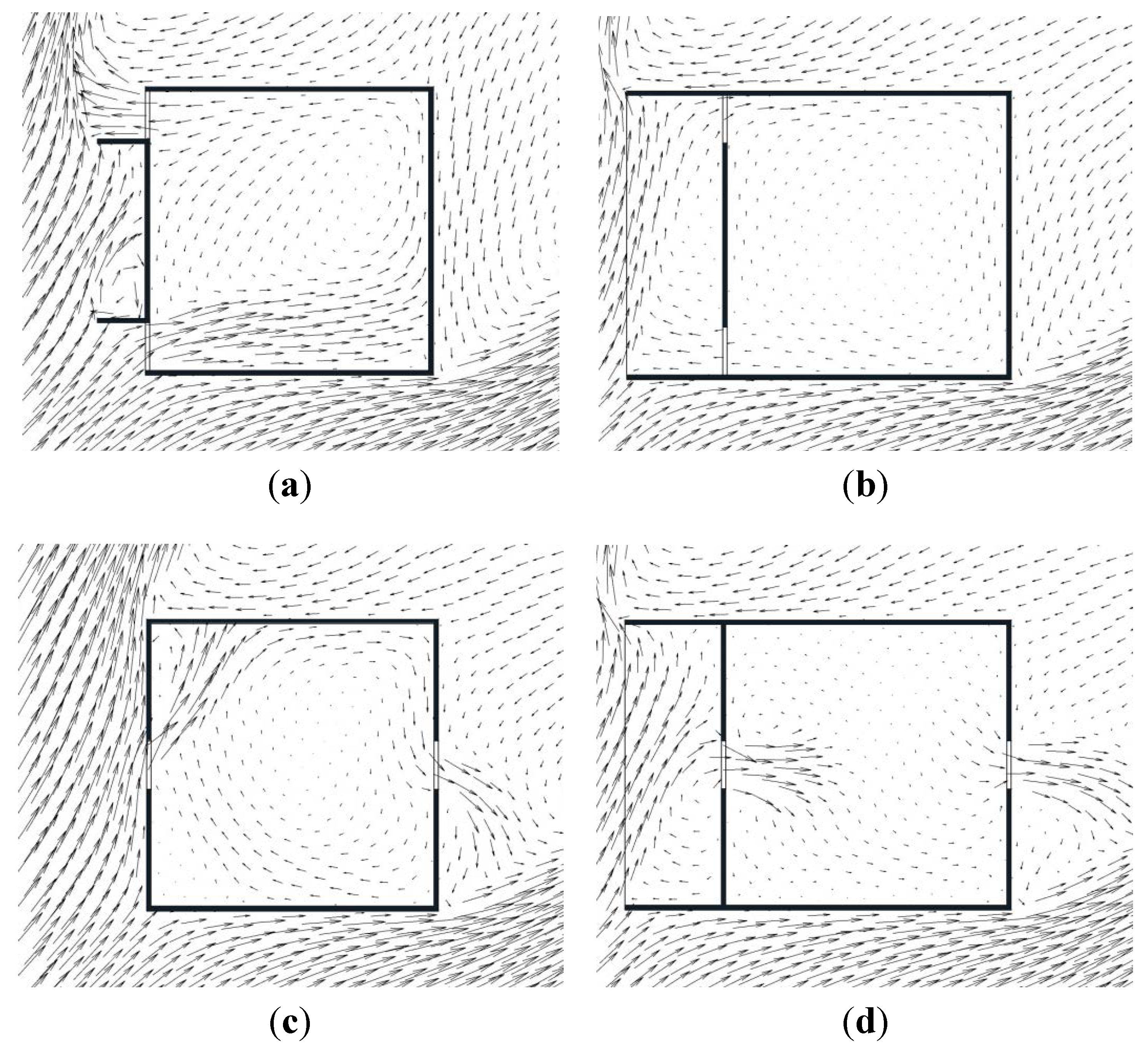
6.1.2. Wind Direction and Ventilation Strategy
| Model | Wind angles | ||
|---|---|---|---|
| 0° | 45° | 135° | |
| G01 | 3.2 | 37.8 | 191.0 |
| G02 | 21.3 | 20.8 | 22.4 |
| G03 | 28.6 | 22.8 | 44.0 |
| G04 | 29.8 | 28.2 | 50.7 |
| G05 | 6.0 | 9.0 | 58.6 |
| G06 | 11.5 | 1.1 | 1.1 |
| G07 | 2.0 | 27.7 | 10.9 |
| G08 | 67.9 | 30.7 | 491.7 |
6.1.3. Prediction Accuracy
6.2. 12-Storey Building
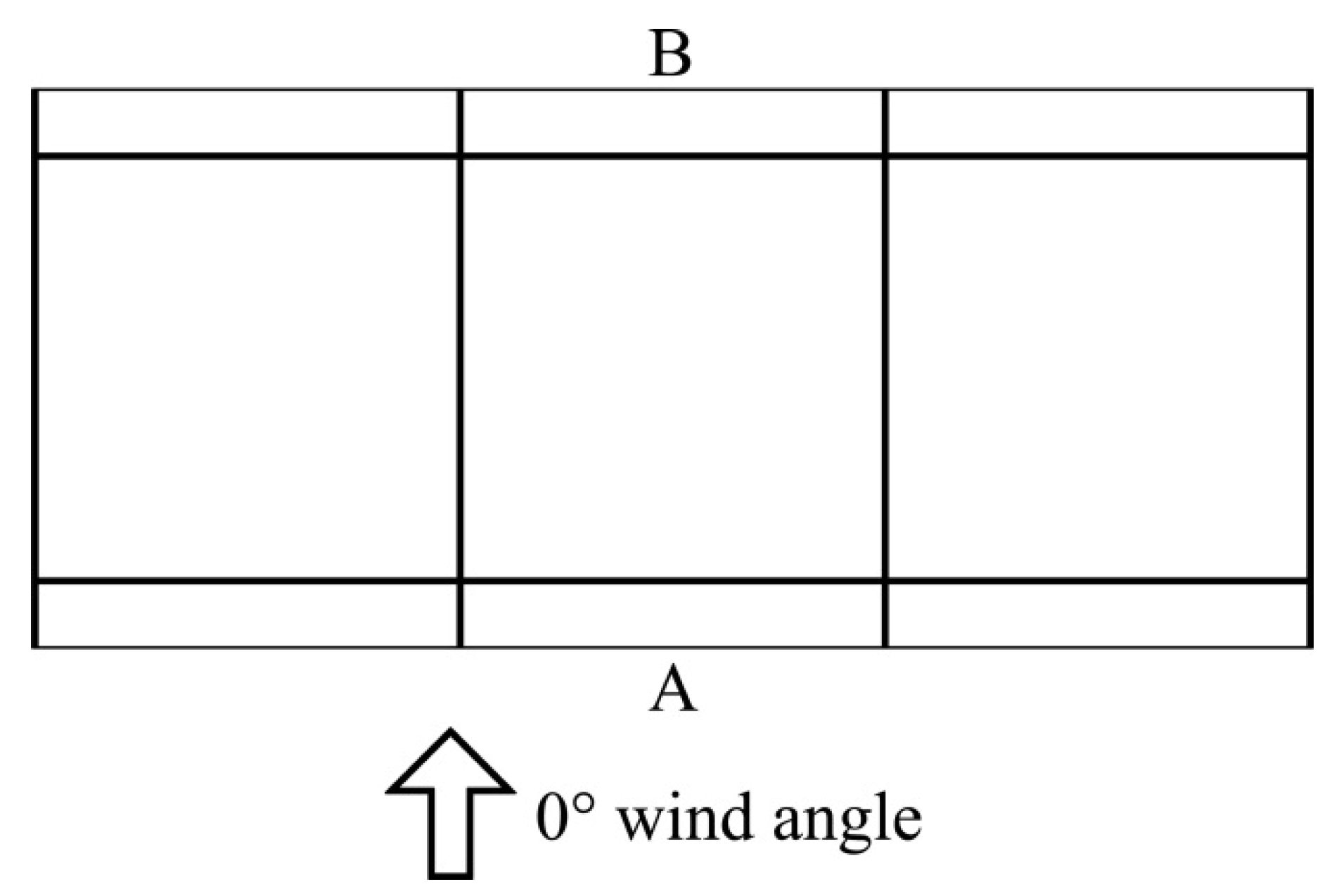

6.2.1. Validation of Wind Pressure Distribution
| Facade treatment | Percentage of differences (%) | |
|---|---|---|
| Line A | Line B | |
| Flat (0°) | 5.3* | 37.8* |
| Balcony (0°) | 6.6* | 27.2* |
| Flat 45°) | 12.9^ | 37.9* |
| Balcony (45°) | 30.8^ | 21.1* |
| Flat (90°) | 27.7* | 13.0* |
| Balcony (90°) | 14.1* | 15.5* |
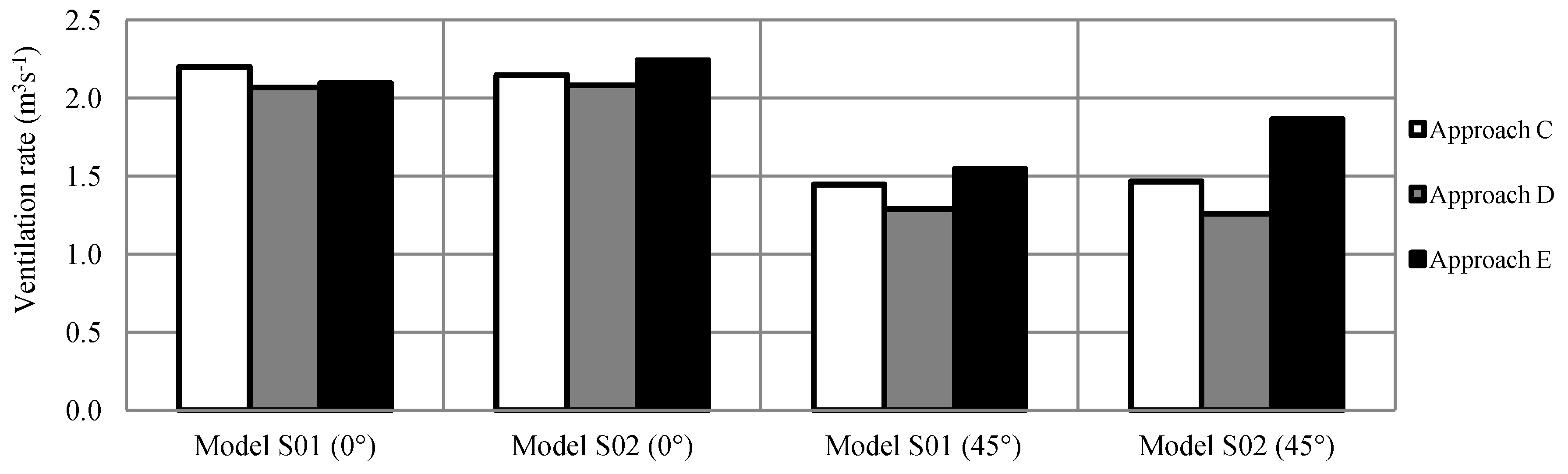
6.2.2. Validation for Cross Ventilation Strategies
 value of 0.65 for cross ventilation with 0° wind angle and 0.5 for all other wind angles. These values are selected because the porosity of the opening is less than 10%. Similar to the single-cell room, the pressure values to be applied in Equation (2) are measured at the centre of the openings.
value of 0.65 for cross ventilation with 0° wind angle and 0.5 for all other wind angles. These values are selected because the porosity of the opening is less than 10%. Similar to the single-cell room, the pressure values to be applied in Equation (2) are measured at the centre of the openings.| Model | Percentage of differences (%) | ||
|---|---|---|---|
| 0° | 45° | 90° | |
| S01 | C & D (Eqn. 2) | C & D (Eqn. 2) | - |
| S02 | C & D (Eqn. 2) | C & D (Eqn. 2) | - |
| S03 | - | A (Eqn. 1) | D (Eqn. 2) |
| S04 | - | D (Eqn. 2) | D (Eqn. 2) |
| S05 | - | D (Eqn. 2) | D (Eqn. 2) |
| S06 | - | D (Eqn. 2) | D (Eqn. 2) |
 is set at 0.025, which is a commonly used value. The wind speeds used for Equation (1) calculations are the ABL wind speeds at the same height of the midpoint of the openings.
is set at 0.025, which is a commonly used value. The wind speeds used for Equation (1) calculations are the ABL wind speeds at the same height of the midpoint of the openings.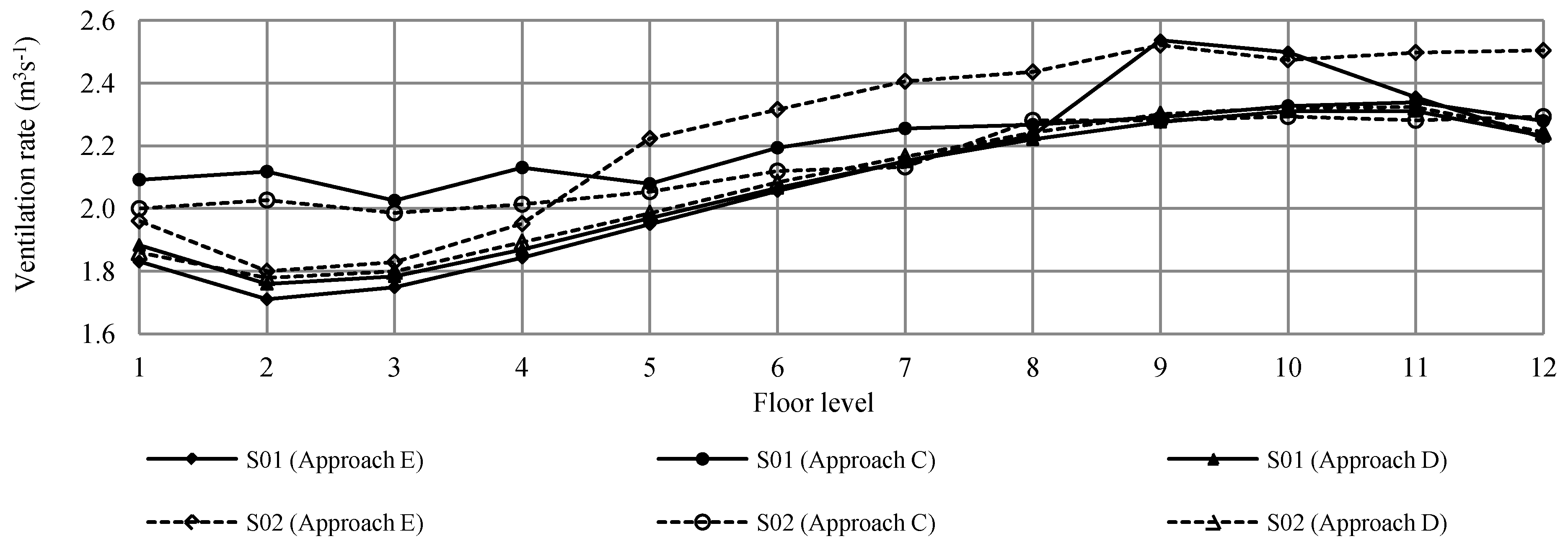

 , used in Approach C and D may not be accurate at levels 9 and 10 and should possibly have greater value due to the perpendicular wind angle. In the case of units located at level 7 and below, the reasons for-under prediction by Approach E are possibly a result of the limitations of CFD simulations. These limitations include inaccurate prediction at recirculation zones by the k-epsilon model. Another reason that may contribute to discrepancies for units located at level 7 and below between Approach E and others is inappropriate
, used in Approach C and D may not be accurate at levels 9 and 10 and should possibly have greater value due to the perpendicular wind angle. In the case of units located at level 7 and below, the reasons for-under prediction by Approach E are possibly a result of the limitations of CFD simulations. These limitations include inaccurate prediction at recirculation zones by the k-epsilon model. Another reason that may contribute to discrepancies for units located at level 7 and below between Approach E and others is inappropriate  values being applied to Approach C and D where the value should be lower than 0.65 because the wind changes its direction as it hits the building and travels almost parallel to the windward facade.
values being applied to Approach C and D where the value should be lower than 0.65 because the wind changes its direction as it hits the building and travels almost parallel to the windward facade. value for a flat facade and facade with balconies because the introduction of the balconies close to the openings could influence the effectiveness of the openings.
value for a flat facade and facade with balconies because the introduction of the balconies close to the openings could influence the effectiveness of the openings.6.2.3. Validation of Single-Sided Ventilation Strategies
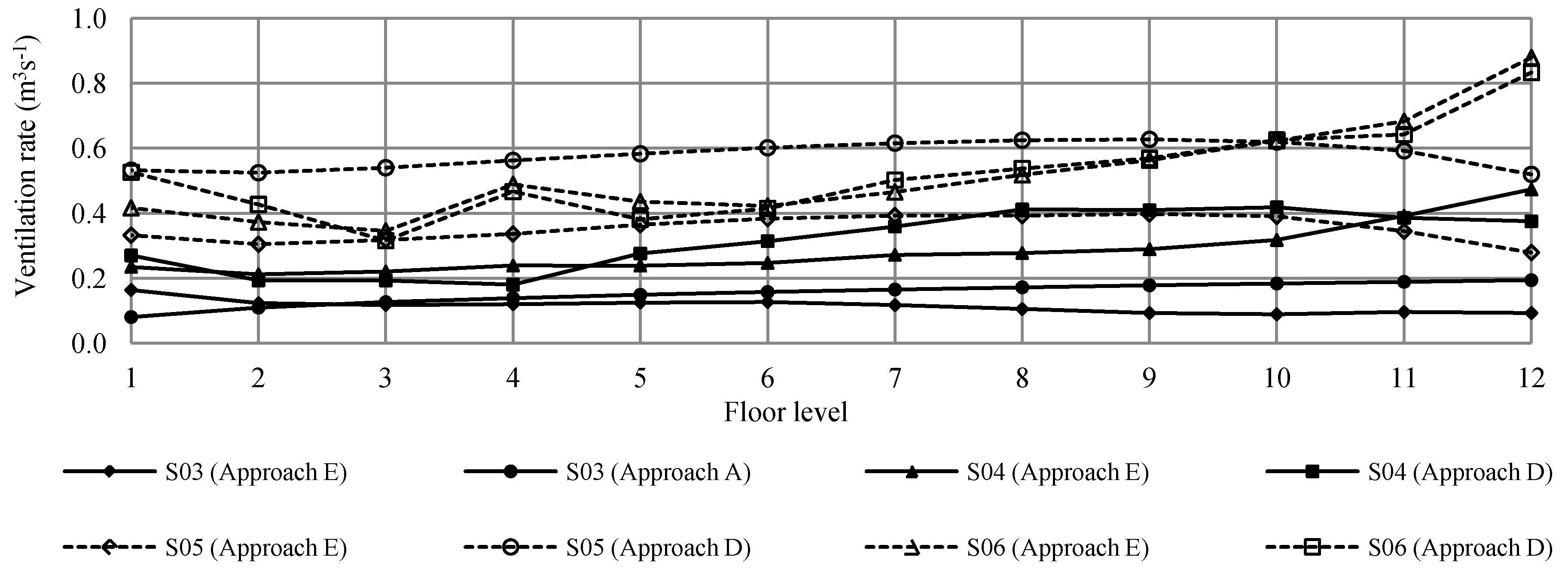
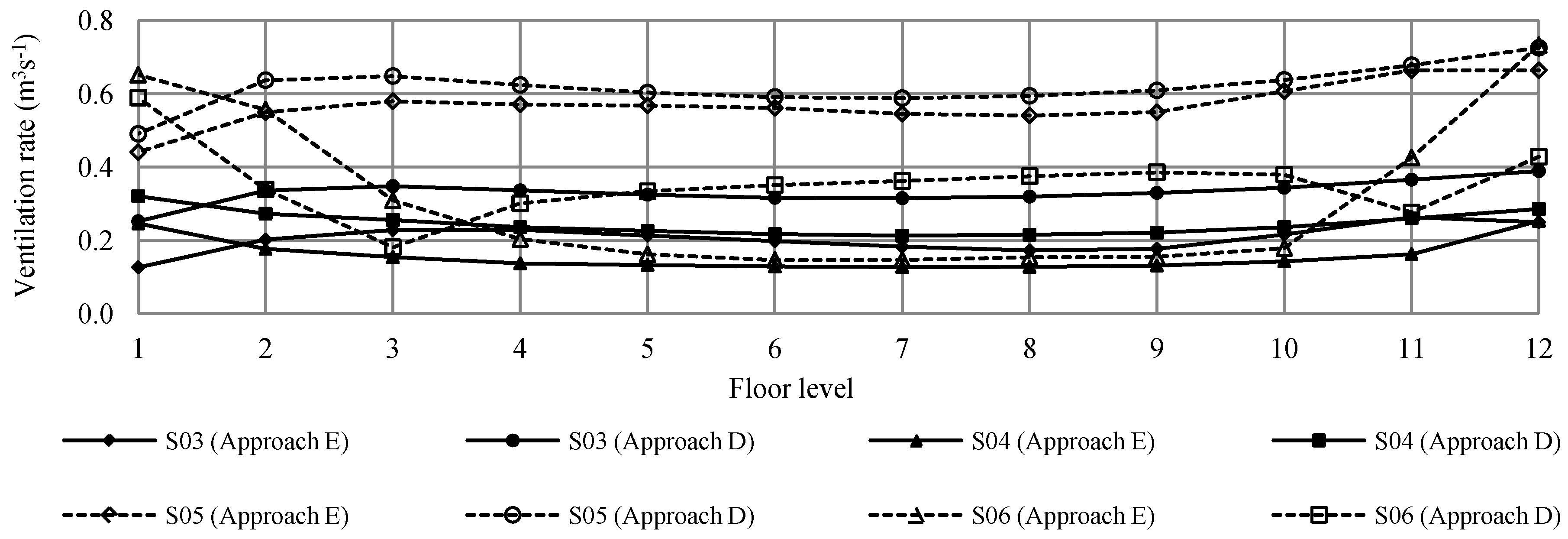

 which is used to accurately describe various wind directions for different facade treatments.
which is used to accurately describe various wind directions for different facade treatments.7. Conclusions
References
- Chen, Q. Ventilation performance prediction for buildings: A method overview and recent applications. Build. Environ. 2009, 44, 848–858. [Google Scholar] [CrossRef]
- Mohamed, M.F.; King, S.; Behnia, M.; Prasad, D. An investigation on ventilation potential as a result of the provision of series of balconies on high-rise residential buildings using Computational Fluid Dynamics (CFD). Int. J. Environ. Cult. Econ. Soc. Sustain. 2011, 7, 197–209. [Google Scholar]
- Jiru, T.E.; Bitsuamlak, T. Application of CFD in modelling wind-induced natural ventilation of buildings—A review. Int. J. Vent. 2010, 9, 131–147. [Google Scholar]
- Prianto, E.; Depecker, P. Characteristic of airflow as the effect of balcony, opening design and internal division on indoor velocity: A case study of traditional dwelling in urban living quarter in tropical humid region. Energy Build. 2002, 34, 401–409. [Google Scholar] [CrossRef]
- Chow, W.K. Wind-induced indoor-air flow in a high-rise building adjacent to a vertical wall. Appl. Energy 2004, 77, 225–234. [Google Scholar]
- Wang, L.L.; Dols, W.S.; Chen, Q. Using cfd capabilities of contam 3.0 for simulating airflow and contaminant transport in and around buildings. HVAC&R Res. 2010, 16, 749–764. [Google Scholar]
- Wang, L.; Chen, Q. Applications of a coupled multizone-cfd model to calculate airflow and contaminant dispersion in built environments for emergency management. HVAC&R Res. 2008, 14, 925–939. [Google Scholar]
- Allocca, C.; Chen, Q.; Glicksman, L.R. Design analysis of single-sided natural ventilation. Energy Build. 2003, 35, 785–795. [Google Scholar]
- Ai, Z.T.; Mak, C.M.; Niu, J.L.; Li, Z.R. Effect of balconies on thermal comfort in wind-induced, naturally-ventilated low-rise buildings. Build. Serv. Eng. Res. Technol. 2011, 32, 1–16. [Google Scholar]
- Van Hooff, T.; Blocken, B. Coupled urban wind flow and indoor natural ventilation modelling on a high-resolution grid: A case study for the amsterdam arena stadium. Environ. Model. Softw. 2010, 25, 51–65. [Google Scholar] [CrossRef]
- Givoni, B. Ventilation Problem in Hot Countries. Reserach Report to the Ford Foundation, Technion; Building Research Station, Israel Institute of Technology: Haifa, Israel, 1968. [Google Scholar]
- Ismail, A.M. Wind-Driven Natural Ventilation in High Rise Buildings with Special Reference to the Hot Humid Climate of Malaysia; University of Wales College of Cardiff: Cardiff, UK, 1996. [Google Scholar]
- ASHRAE (American Society of Heating, Refrigerating and Air-Conditioning Engineers), 1997 Ashrae Handbook: Fundamentals; ASHRAE: Atlanta, GA, USA, 1997.
- Larsen, T.S. Natural Ventilation Driven by Wind and Temperature Difference; Aalborg University: Aalborg, Denmark, 2006. [Google Scholar]
- Awbi, H.B. Ventilation of Buildings; E & FN Spon: London, UK, 1991. [Google Scholar]
- Warren, P.R.; Parkins, L.M. Single-Sided Ventilation through Open Windows. In Thermal Performance of the Exterior Envelopes of Buildings; ASHRAE: Clearwater Beach, FL, USA, 1985; pp. 209–228. [Google Scholar]
- Warren, P.R. Ventilation through openings on one wall only. In International Centre for Heat and Mass Transfer Conference: Energy Conservation in Heating, Cooling and Ventilating Buildings; Hoogendorn, C.J., Afgar, N.H., Eds.; Hemisphere Publishing Corporation: Dubrovnik, Yugoslavia, 1977; Volume 1, pp. 189–209. [Google Scholar]
- Aynsley, R.M.; Melbourne, W.; Vickery, B.J. Architectural Aerodynamics; Applied Science Publisher Ltd.: London, UK, 1977. [Google Scholar]
- De Gids, W.; Phaff, H. Ventilation rates and energy consumption due to open windows: A brief overview of research in the netherlands. Air Infiltration Rev. 1982, 4, 4–5. [Google Scholar]
- Liddament, M.W. A Guide to Energy Efficient Ventilation; Air Infiltration and Ventilation Centre: Conventry, UK, 1996. [Google Scholar]
- Yoshie, R.; Mochida, A.; Tominaga, Y.; Kataoka, H.; Harimoto, K.; Nozu, T.; Shirasawa, T. Cooperative project for cfd prediction of pedestrian wind environment in the architectural institute of Japan. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1551–1578. [Google Scholar] [CrossRef]
- Yim, S.H.L.; Fung, J.C.H.; Lau, A.K.H.; Kot, S.C. Air ventilation impacts of the “wall effect” resulting from the alignment of high-rise buildings. Atmos. Environ. 2009, 43, 4982–4994. [Google Scholar] [CrossRef]
- Cheng, C.C.K.; Lam, K.M.; Yuen, R.K.K.; Lo, S.M.; Liang, J. A study of natural ventilation in a refuge floor. Build. Environ. 2007, 42, 3322–3332. [Google Scholar] [CrossRef]
- Evola, G.; Popov, V. Computational analysis of wind driven natural ventilation in buildings. Energy Build. 2006, 38, 491–501. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Q. Buoyancy-driven single-sided natural ventilation in buildings with large openings. Int. J. Heat Mass Transf. 2003, 46, 973–988. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mohamed, M.F.; King, S.; Behnia, M.; Prasad, D. Coupled Outdoor and Indoor Airflow Prediction for Buildings Using Computational Fluid Dynamics (CFD). Buildings 2013, 3, 399-421. https://doi.org/10.3390/buildings3020399
Mohamed MF, King S, Behnia M, Prasad D. Coupled Outdoor and Indoor Airflow Prediction for Buildings Using Computational Fluid Dynamics (CFD). Buildings. 2013; 3(2):399-421. https://doi.org/10.3390/buildings3020399
Chicago/Turabian StyleMohamed, Mohd Farid, Steve King, Masud Behnia, and Deo Prasad. 2013. "Coupled Outdoor and Indoor Airflow Prediction for Buildings Using Computational Fluid Dynamics (CFD)" Buildings 3, no. 2: 399-421. https://doi.org/10.3390/buildings3020399
APA StyleMohamed, M. F., King, S., Behnia, M., & Prasad, D. (2013). Coupled Outdoor and Indoor Airflow Prediction for Buildings Using Computational Fluid Dynamics (CFD). Buildings, 3(2), 399-421. https://doi.org/10.3390/buildings3020399





