Assessing the Play Provisions for Children in Urban Neighborhoods of India: Case Study Nagpur, Maharashtra

Abstract

The creation of satisfying urban environments calls for the planners, designers and policy makers to understand the structures that cause residents to feel satisfied with their environments. The paper focuses on qualitative aspects of the childrens play spaces in the urban neighborhoods of Nagpur which were analysed with the background of their daily activity schedule survey, their assement of the existing play provisions and their aspirations from their neighborhood environment quality. Apart from these studies, the childrens and their parents perceptions of the quality of urban residential environments was also studied. The literature review gave an extract of relevant attributes of environmental quality (EQ) which became the theoritical basis for the work. The research generates an approach to assessing the child friendliness of our urban neighborhoods, which in certain ways is not even catering to the most fundamental right of the child to play; it also generates a matrix of children’s needs and parameters relevant to Indian context. A theoretical model of the residents satisfaction is also generated which forms the base for the qualitative questionnaire analysis in SPSS 20 with a set of dependent and independent variables which shows the correlation of the resident’s satisfaction with child friendliness of neighborhoods in the Indian context. The regression model and mathematical equation as an outcome of the qualitative analysis was also validated upon two other urban neighborhoods of the city of Nagpur. The research with all its tools used and the approach adopted can help in undertaking such child-centered researches in other cities of India which have their own unique issues and characteristics of urban growth.

1. Introduction

The research focuses on the relationship between the residents and their neighborhood of residence in an urban environment, which is a typical issue in environmental psychology on different levels of home, neighborhood and city with different levels of users, i.e., children, adolescents, adults and the elderly [1]. The perspective of the residents is extremely important in understanding the urban residential environment quality as some guidelines and standards can be established that can help in assessing the urban design and planning programs of intervention aimed at improving the urban residential environment. The approach based on what public seeks in the environment, how it trades one set of values with another and how it can be motivated to make choices about environmental changes before a crisis occurs is more practical and worthwhile [2,3].

The quality of the urban environment directly influences the social and economic development of the city. Good residential environments can bring socio-economic benefits to the city whereas bad environemt quality will obstruct urban economic development [4]. The concept of environment quality can be interpreted either objectively or more subjectively which brings the environment conditions to be measured objectively and the environment quality to be measured subjectively. As evironmental quality is multidimensional in nature it can be characterised by the use of wide ranging methodologies [5].

Research in environmental psychology has increasingly turned towards measuring perceived environmental quality of which one research objective is to study the congruence between the quality of environments and peoples expectations, goals and value systems [6].

1.1. Children and Their Local Play in Urban Residential Environments

The words children and play are inseparable, and childrens right to play is rightly recognised as one of the fundamental rights by the United Nations Convention on the Rights of the Child (UNCRC). By 2050, about 70% of the worlds population will live in urban areas and children currently living in urban areas account for nearly half of the world population. Childrens participation in research can be ensured by working with them to select methods that are appropriate to them and to the research aim states [7]. Play has been defined as one which includes activities of children that are not controlled by adults and that do not necessarily conform to any rules. It explains that play takes place either away from the oversight of adults, near adults who are not involved or near adults who with sensitive support, enrich children’s opportunities to play in their own way. Recent research [8] confirms that there is a direct relationship between play and children’s well being. Unstructured play is a natural behavior, which among other benefits contributes to children’s brain development, enhances creativity and builds resilience to stress factors in their environment. Children’s sense of control, experienced through play, is central to children’s evolving capacities.

Some of the indicators of local environment quality as given by growing up in cities sites are as shown in

Table 1. Indicators of local environment quality.

Rating	Social Qualities	Physical Qualities
Positive	Social integration Freedom from threats Cohesive community Secure tenure Community self help	Green areas Basic facilities Activity settings Freedom from physical dangers Freedom to move Peer gathering places
Negative	Political powerlessness Insecure tenure Social stigma and exclusion Boredom Racial tensions	Lack of gathering spaces Heavy traffic Trash/litter Lack of activities and services

Source—Growing up in Cities project, 2010 [8].

.

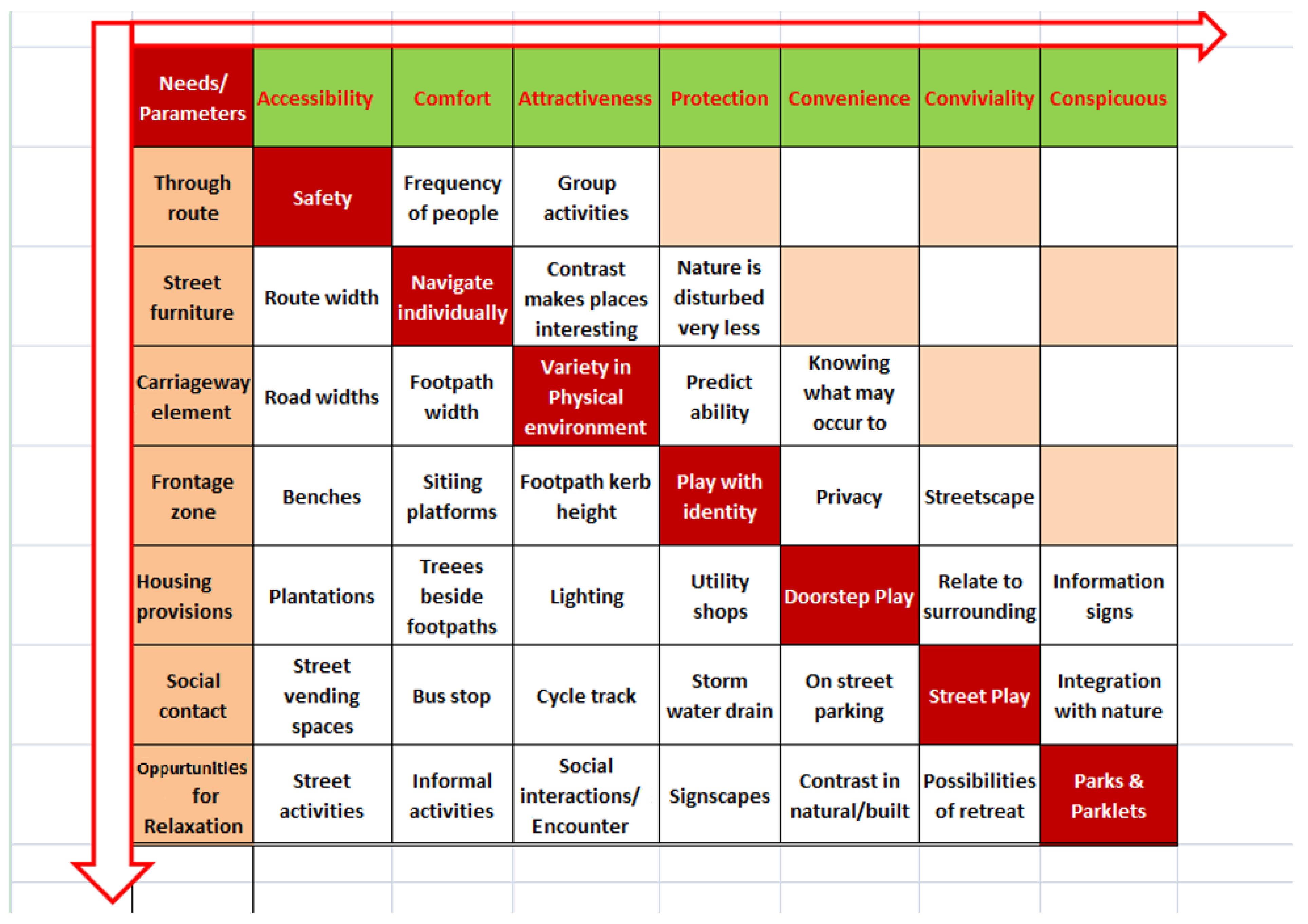
1.2. Children’s Needs

In residential built environments the children’s needs are defined as follows.

(a)

Physiological need—The comfort experienced during physical movements and actions such as walking, sitting, standing, seeing and hearing playing or unfolding activities. Spaces obstruction free and increases competences.

• Accessibility—It is the relative nearness of one place to another indicating easiness of reaching destination from origin. As a spatial analytic measure it plays a vital role for decision makers in deciding where to locate public facilities or amenities to maximize utility.
• Comfort—Increasing ones competences/abilities. When children feel comfortable in their physical surroundings they will venture to explore materials or events around them. Most likely these settings involve varied and moderate levels of stimulation for all senses. Patterns of movement that are moderately diverse help maintain optimum levels of responsiveness and make children feel comfortable.
• Connectivity—The extent to which the pedestrian network provides continuous movement without any physical obstructions links to key trip origins and destinations as well as the extent of linkages between different routes on network.

(b)

Physical needs—The comfort experienced from external influences like climatic protection, traffic accidents, walking path modal conflicts.

• Safety—It means safety from stumbling, tripping, slipping and traffic accidents. Children have great concerns about their personal safety but their strategies for dealing with danger are limited. Living in a state of continual concern about personal safety can wear the body’s immune system, capacity to relax and overall health. Measures like physical barriers, segregation of traffic, nooks and corners and level changes can be incorporated.
• Protection from sun winds and rains.
• Convenience of walking over other modes of transport.

(c)

Physiological needs—The mental and emotional comfort achieved from the sensory and memorable experiences such as legibility, sense of place and belongingness, personal security, relaxation, active and passive engagement, enjoyment, equity and discovery.

• Conviviality—Traversing with active and passive engagement like interaction with people, natural and built environment and other road users.
• Conspicuous—Clear and legible signing, information, orientation and direction.
• Attractiveness—Quality of aesthetics, appealing to senses and interesting.

The children’s needs and their interface with their local environment led to the creation of a matrix, which is shown in Figure 1 below.

1.3. Objective and Hypotheses

The main objective of the research is to define, analyze and model the concept of urban residential environment in the Indian context referring to the tier two city of Nagpur in Maharashtra, India under study.

The research hypotheses are as follows:

(1)

The perceived quality of urban residential environment is a hierarchial multi attribute concept.

(2)

Enhancing the psycho-social attributes and child friendly parameters can improve the residential satisfaction among the residents.

1.4. Methodology of Study

The methodology of the study as shown in Figure 2, begins with the literature data on children in cities in India with the various issues that they face as the blessing or a curse of growing up in urban India. The study majorly focuses on the issues with the childrens basic right to play. The paper brings forth the results of the three primary, supporting surveys relating to childrens daily routine, their opinion on the existing play provisions and then their aspirations from their neighborhoods in future, which sets up the preface to take up the main survey using SPSS to establish the relation between the residents satisfaction and analyzing it if it is being enhanced by the creation of ideal play provisions in the neighborhoods, with the creation of a model and establishing its relevance by validating it on other two neighborhoods as well.

1.4.1. Contextualizing the Location for Groundwork in India

This study is based in Nagpur city, as it exemplifies the typical Indian grade II metropolitan city. It marks the geographic center of India and consist of an old city core and a rapidly spreading extension supporting a population in excess of 4 million. It is home to a moderate industrial base, government offices, education institutions and agrarian trade.

The study focuses on urban neighborhoods of Nagpur city, belonging to the various administrative zones and adhering to the norms and policies of Nagpur municipal corporation and Nagpur improvement trust. The Town and country planning organization (TCPO) and Urban development plans formulation and implementation (UDPFI) guidelines set the basic planning standards for neighborhoods in cities creating an operational ground for ease of comparison.

1.4.2. Delimitation and Characterization of the Study Neighborhoods in Nagpur

Neighborhoods were selected for observation based on administrative zones with varying densities in Nagpur. Data on neighborhood characteristics were collected by two trained research assistants by means of neighborhood observations in the eight neighborhoods. The observers were not part of the research to enhance unbaised collection of the data. The research assistants observed the neighborhoods using a checklist which they completed by mutual agreement. The neighborhood boundaries were defined by the local data bases from the municipal organizations so that the data could be easily interpreted by the local policy makers. In general, these boundaries correspond with what people percieve as their neighborhood and boundaries often coincide with physical boundaries such as a railway, busy road, channel or tunnel.

1.4.3. Defining the Participants

During the process of research, it was observed in the walk through surveys that mostly the children playing in parks, streets and open spaces were of the age of 7–12 years in groups, which prompted to take this age bracket for study. In addition, this was supported by researches done by Chawala (2010), Goyal (2009) showing this age to be of independent mobility and freedom in neighborhood. Hence this age group is taken up for study. Children being the focus user group for research, the sample sizes for various pilot surveys for qualitative aspects were calculated using the Equation (1) mentioned below:

Sample size (SS) = {z² × p × [1 − p]}/c²

(1)

where, z-z value e.g., 1.96 for 95% confidence level; p, percentage picking a choice, expressed as decimal; c, confidence interval, expressed asdecimal (e.g., 0.04 = ±4).

The overall sample size of 872 respondents consisting of children between age of 7–12 years as they are the majority in the set of users assessing play provisions who were interviewed with their parents for qualitative aspects of the research like daily activity schedule (384), opinion on the existing play provisions (120) and the satisfaction with their neighborhoods (368).

1.4.4. Qualitative Surveys

Parents’ and children’s ability to grasp and respond to the complex issues of evaluation study which were never a part of city and neighborhood surveys was depended upon for the surveys. The paper emphasizes on the qualitative aspects of the residential built environments of Nagpur which were analyzed using the various interactive tools like:

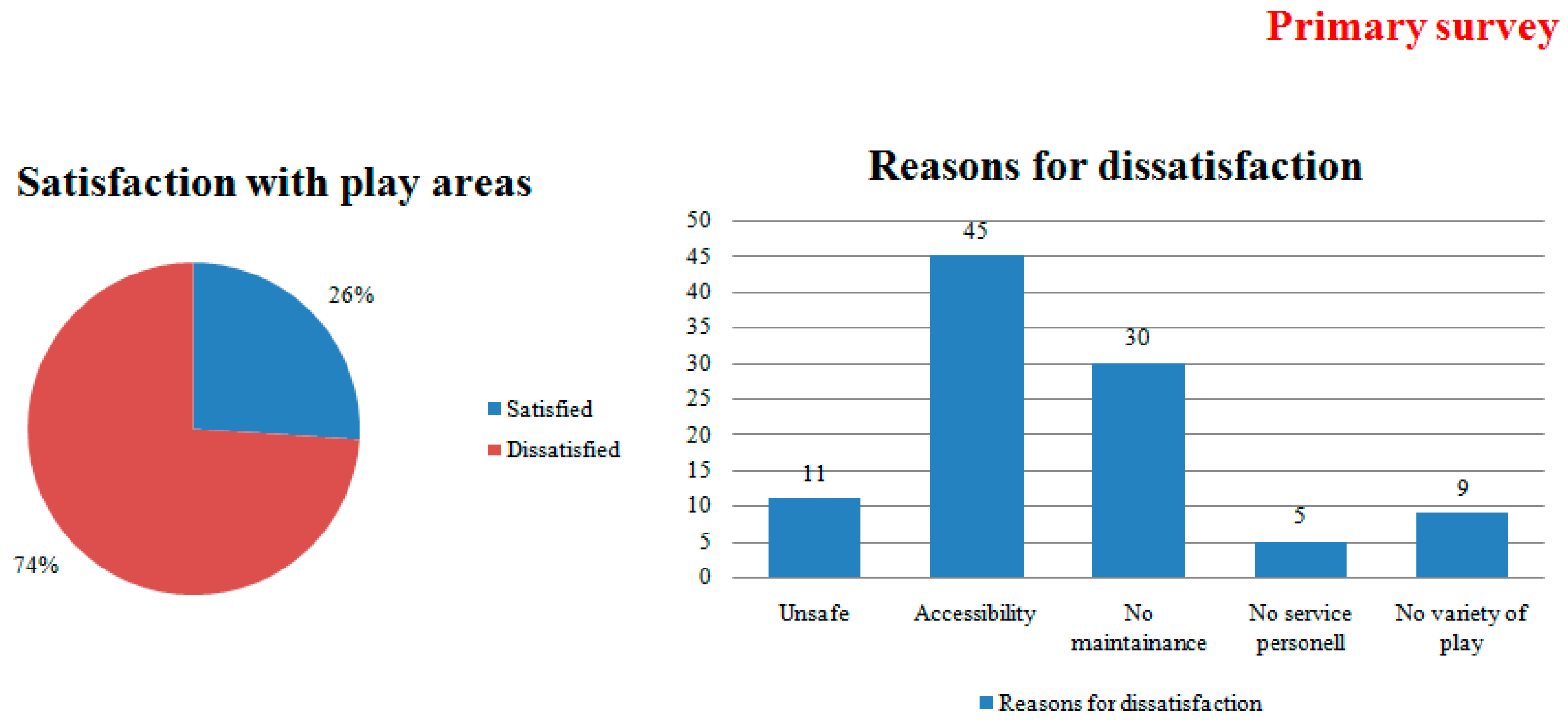
• Interviews with children had a sequence of queries from orders and specific to thought provoking encouraging wishful thinking and dreaming about ideal play spaces in neighborhoods (Children’s satisfaction with existing play provisions).
• Interviews with parents and children (Children’s daily routine survey).
• As it is part of an architectural and planning research, the design and layout of the questionnaire is visually appealing, the creative drawing workshops urged children to respond in a free manner through sketches, notes etc. Although of no statistical worth, it adds value to the ordered and restricted sequence of questionnaire and gives a deeper insight of the assessment.
• RESS Statistical analysis—The data input is done in SPSS to know the normality, reliability, validity of data and the appropriateness of the variables used in the design of the questionnaire which in turn led to the creation of a model of children’s satisfaction scale in the Indian context and in turn the importance of each variable on the output of residents satisfaction.

2. Survey Tools

Structured interviews were used as a qualitative research methodology. These interviews were best suited for engaging in respondents or the focus group of children as it was beneficial to compare/contrast participant responses in order to answer the research question. For these structured qualitative interviews, schedules that list the wording and sequencing of questions were prepared which increased the reliability and credibility of the research data.

2.1. Childrens Daily Activity Schedule Survey

In an effort to understand the residential satisfaction as a quotient of children’s play in the neighborhoods, a questionnaire survey was conducted (the results in form of graph and table is shown in the plate 1 below) to know the average daily activity schedule of children in various neighborhoods of Nagpur. The questions varied from knowing their place of neighborhood, distance from school and tuitions classes to the time spent by them interacting with their peer group in the neighborhood.

The survey revealed that, with the present planning and parents mindsets, the children have more time of their day spent in static activities like travelling to school by bus, school hours, tuition hours and sleep hours which amounts to almost 18–20 h of the day as compared to the dynamic activities for their overall development like recreation, play and socializing which is as low as 2–3 h a day as shown in the graph in Figure 3.

This situation is also attributed to the families migrating to cities for work and hence into the nuclear family system with both parents working and hence preferring the schools that offer the day boarding facility as children can play within the school premises. More so the stereotypes of sending children to good schools even if they are very far from the residence leading to more travel time for kids and hence children finding very less time to relax, play, socialize in their neighborhoods. The existing situation calls for a serious concern to the society and human race in giving a future generation of children in urban areas, with low physical, mental, social, psychological development.

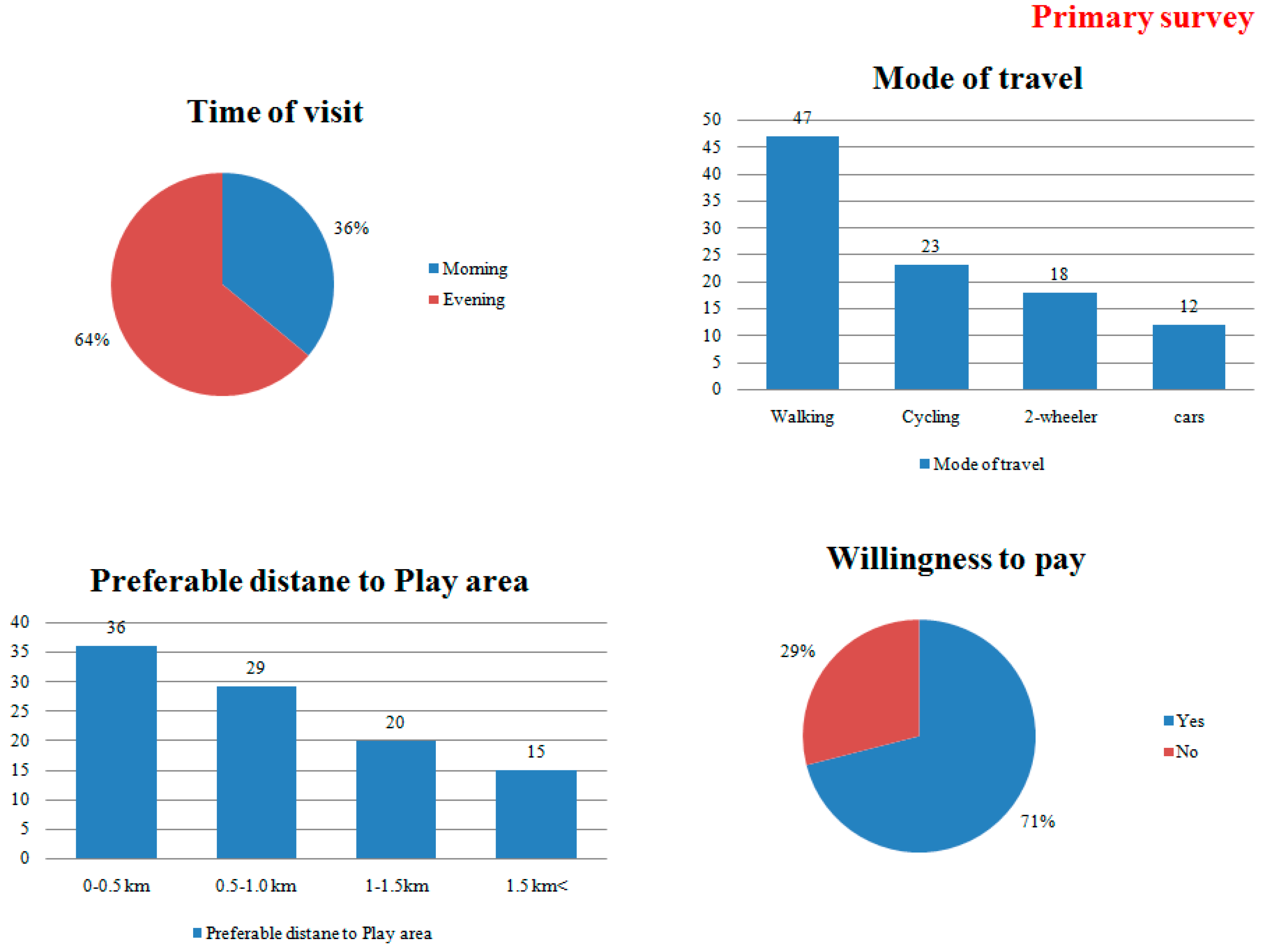
2.2. Childrens Survey about the Existing Play Provisions in Their Neighborhoods

With the basis of the daily activity schedule of children, the research also tried to understand the children’s satisfaction with the existing play facilities as they are in the various neighborhoods of Nagpur. The questions ranged from children’s preferences to spend leisure time indoor/outdoor, their frequency of visit to play areas, time, mode of travel, preferable distance to play areas, so as to be accompanied or un-accompanied with parents or elderly.

The questionnaire survey was conducted in which the results (as seen in the graphs in Figure 4 and Figure 5) showed that, most children (72%) prefer to go outdoors for play but the access to the parks is such that most of them have to be accompanied (59%) by their parents once a week to the nearby parks and playgrounds and on vehicles as they are not within the walkable distance from their place of residence. Children and their parents had the willingness to pay for the parks (71%) if they were well maintained with variety of play and within a walkable range of 500 m from their residences.

The Figure 6 also shows graphs with only (26%) of children and parents reporting of being satisfied with the play provisions. The reasons of their dissatisfaction being accessibility, poor maintenance, lack of variety in play, etc.

The surveys taken up above clearly showed that the children in the first case have very less time for play in the current lifestyle and other priorities and even if they try to play in their neighborhoods, the planning of play spaces and its maintenance and distance does not favors its proper and effective use by the children in the neighborhoods.

2.3. Children’s Aspirations from Their Neighborhoods

The primary surveys conducted above to know the daily activity schedule and then opinion on the existing play provisions in their neighborhoods, further led to an enquiry to know the children’s aspirations from their neighborhoods for which a workshop was conducted in which a lecture on children’s dreams about their neighborhood was conducted. The children here had to imagine and sketch the neighborhood of their dreams in which they would like to reside as is shown in Figure 7 the workshop in progress. The group consisted of almost 100 participants from various neighborhoods of Nagpur.

The outcome was a variety with children’s desire for water, sand, construction, animals, and explorations in their play in neighborhoods as shown in the Figure 8 with games like steppe on the road side away from parked vehicles, their fondness with animals in the garden or park nearby and many games in large groups with other children within protected boundaries.

The qualitative aspects of studying the urban neighborhoods in regard to the users as children and their physical environment as the play provisions in them by means of the questionnaire surveys of children and their parents along with their participation in the workshop clearly defines the typical characteristics of an urban neighborhood and qualities they nurture in the indian context as highlighted in

Table 2. Characteristics of neighborhood and qualities they develop.

Characteristics of Urban Neighborhood	Qualities They Nurture
Uniformity in the sizes of plots Size of neighborhood Vehicular roads throughout	A sense of belonging to the same economic class Governed by the major roads carrying traffic loads acting as edges to the neighborhoods No freedom of movement individually for children & elderly
Lack of maintainance Parking within plots and on footpaths along roads	Repair of public utilities and facilities ingraining a quality to adjust No doorstep play spaces or on streets
Pedestrian facilities lacking behind Emphasis on FSI coverage	No ease of walking or cycling Ignoring the specific needs of users in neighborhood
Access to parks and playgrounds hindered	Children accompanied by elders

.

2.4. Residents Perception Survey

In addition to the issues stated above after the primary survey and observation survey, the neighborhood evaluations revealed absence of many child friendly aspects that make the environment inclusive, comfortable and nurture a sense of belonging towards the neighborhood. The users reiterated having to negotiate with their environs while resolving their needs. The pilot study helped in identification of the variables that required investigation in the residential environment satisfaction scale with a concern for childrens play provisions.

As many social sciences studies completely ignore the physical environment, material conditions are also important components of neighborhoods. Peoples interactions with the physical place their modifications of it and the symbolic meanings they attribute to it are means of developing attachment. When the physical environment is considered, there is much variation in how it is parameterized. It has been represented by built features with symbolic or practical value, such as architectural style, landscape and historical significance, the amount of open space, the condition of streets and buildings and noise level, etc. [9].

Over time several researches have been conducted on the relationship between urban residents and their environment. Bonaiuto et al. studied the relationship between inhabitants and their neighborhoods of residence in the urban environment of Rome from the environmental psychological view and proposed two distinctive instruments. These instruments consisted of 11 scales of measuring the perceived environmental qualities of the urban neighborhoods with one scale measuring neighborhood attachment. This new version of perceived residential environment quality and neighborhood attachment largely improved internal consistency with respect to earlier studies [10].

In the Indian context , the contribution of the social environment to the residential satisfaction of individuals and households is significant. The social environment comprises the relationships, interactions, and social activities that an individual or household participates in, as well as those that surround them in the immediate neighborhood. As per the studies done by researchers in India, the built environments in the Indian context have spatial configurations such that they encourage streets as spaces to socialize and play which also correlates with the findings of the international studies that children prefer places that are busier and frequented not only by other children but by people of all ages. However, besides these benefits, it is generally accepted that children do not play to achieve an external reward or goal, but because they want to play [11].

In this study, the physical environment, socioeconomic and psychological attributes have been covered so that a good understanding of the urban environments in the indian context can be achieved. The research isfocused on seeking a more integrated approach to interpret the environmental quality.

2.4.1. Customizing the RESS

The theoritical model was tailored specifically for evaluation of neighborhoods in India which is dealt with in Figure 9 showing its growth from top to bottom giving all important details of the satisfaction scale.

The theoritical model places the residential satisfaction at the first level with the neighborhood, neighbors and dwelling as the main elements which can be evaluated by the four gerative criterias of spatial, human and functional aspects with the neighborhood attachment. The components of the housing satisfaction are housing unit features, support services, public facilities, social environment and neighborhood facilities. The satisfaction can be measured on the 11 scales which have the 30 different dependent and independent variables with their respective attributes.

Questionnaire for the residents environments satisfaction scale yielded categorical data for qualitative analysis. Vital issues in the design of the questionnaire for contentment with environs are discussed below.

○

Questions are addressing to the specific issues and bounded as it is best suited for a statistical analysis. The questions are numerically evaluated on a five point scale—Strongly agree/very satisfied/yes very much: Agree/satisfied/yes: Neither agree nor disagree/neither satisfied nor dissatisfied/not so much: Disagree/dissatisfied/no: Strongly disagree/very dissatisfied/not at all.

○

The questionnaire initiates with the architectural and town planning aspects, organization and accessibility of roads, green areas to more of social and welfare activities, relations. Level of complexity is further stepped up with queries on recreation and transport facilities, commercial facilities and pace of life with all age groups of people.

○

The journey then makes respondents enter a more abstract form of queries dealing with the sense of belonging and neighborhood attachment.

○

A wish list helps bring out in full force all the aspirations they nurture within themselves for their neighborhood environs.

2.4.2. Method of RESS

Based on this theoritical model, the multiple linear regression approach was done in the following steps:

(1)

Identification and structuring of attributes—the model starts with the top level attribute environmental quality represented by residential satisfaction. The top level attribute branches out into more specific lower level attributes like satisfaction with dwelling, neighborhood and neighbors respectively on which the object may be validly measured.

(2)

Actual residential environments are evaluated on the attributes in the theoritical model given in the Figure 9. The theoritical model of environmental quality was used to design a questionnaire in which respondents were asked to evaluate their present residential situation with each attribute in the model. The variables selected for the questionnaire study are listed as under in

Table 3. Questions set from variables.

Independent Variables	Question Form
X1	Do the buildings have pleasing appearance?
X2	Are the buildings to child scale?
X3	Is the neighborhood too overcrowded?
X4	Are there cycle tracks along roads?
X5	Do roads have walking paths?
X6	On street parking does not obstructs walking?
X7	Are daily needs shops within walkable distance?
X8	Can children walk down to school/bus stops navigating individually?
X9	Are parks well maintained and equipped?
X10	Do parks have variety of play opportunities?
X11	Are there places for games and sports?
X12	Do parks have anti social activities?
X13	Do parks have all weather play provisions?
X14	Is there dispensary, police booth, anganwadi nearby?
X15	What is the frequency of festivities & celebrations?
X16	How much recreation time do children get?
X17	Are there good meeting/personal spaces for children in neighborhood?
X18	Is there proper signage in the neighborhood?
X19	Can the children move with identity in the neighborhood?
X20	Is there flexibility in the use of spaces in the neighborhood?
X21	Is there a hierarchy of play spaces for children of all age groups?
X22	Are there too many abandoned or dead areas in the neighborhood?
X23	Is the neighborhood clean and maintained?
X24	Does the neighborhood feel safe?
X25	Is the neighborhood full of activity?
X26	Do children interact with all age groups of people?
X27	Are children free to express and play in neighborhood?
X28	Do you feel watched and controlled by others?
X29	Is this the most ideal neighborhood for you?
Dependent Variables	Question Form
Y1	What is your overall satisfaction with your neighborhood?

as a set of dependent and independent variables. The variable of satisfaction with the neighborhood is dependent on a number of features of the built environment like:

• I.V.1. The architectural characteristics of the buildings to be pleasing, good, well maintained and occupied by residents. This is considered as an independent variable (X1) to become part of the questionnaire survey.
• I.V.2. The scale of the buildings in the neighborhood to be preferably to the childrens scale so that it increV.ases ledgibility, recognition and brings in confidence in children about the neighborhood as something to be traversed and explored on their own, which is taken as variable (X2).
• I.V.3. The extent of crowding in the neighborhoods is also an important concern as regards childrens free movement in neighborhood as, if it is lonely or too crowded it tends to become unsafe for children to be left on their own in the neighborhood. This is an independent variable (X3).
• I.V.4. The provision of cycle tracks (X4) well designed as per childrens anthropometery and well protected and supervised by the walking paths (X5) along the neighborhood roads are two other variables to be important part of the questionnaire. So also, the on street parking (X6) along roads hindering the traffic movement, walking and childrens play is also an important part of the questionnaire survey in RESS.
• I.V.5. The provisions of the daily needs shops, dispensary, police booths and anganwadis nearby in the neighborhood (X7), (X14) meaning thereby within walkable distance for children and devoid of trafficulated route are variables that would encourage the individual and independent navigation of children in the neighborhoods (X8) giving them a sense of worth and self esteem and be able to negotiate and interact with people and environments.
• I.V.6. The parks and open spaces in the neighborhood are well maintained and equipped (X9) with facilities offering a variety of play oppurtunities (X10). In addition, the places for games and sports are safe (X11) with the hierarchy of spaces for different age groups of children (X21) giving them the freedom to express and play in their neighborhoods and play provisions (X27) that can be enjoyed and used by them throughout the year in all weather conditions (X13).
• I.V.7. The social and cultural vibrancy of the neighborhood being measured by the variable of frequency of festivities and celebrations (X15), making the neighborhood full of activity (X25) and the chances of the neighborhood spaces being used for multiple purposes (X20) which in turn encourages the interaction of all age group of people including children (X26) while they move around with identity (X19).
• I.V.8. The children in the neighborhood get time to recreate (X16) giving them various options for meeting or personal spaces in the neighborhoods (X17) without the unease of being too much overlooked by others (X28).
• I.V.9. The variable of the neighborhood feeling safe (X24) with proper signages and paths highlighted (X18) and with minimum number of abandoned or dead areas in the neighborhood (X22) which do not tend to become dumping grounds of garbage, while maintaining the cleanliness and upkeep, fowl smell, stray animals, out of sight in neighborhoods (X23).
• I.V.10. Of all the variables being taken up , last but not the least is a subjective variable of the residents rating if their neighborhood is close to being the ideal which can be measured in variable (X29).

(3)

The data collected from the questionnaire survey was fed in the IBM SPSS 20 data sheet.

SPSS is a widely used program for statistical analysis in social science. It is also used by market researchers, health researchers, survey companies, government, education researchers, marketing organizations, data miners, and others. The procedure adopted for using the software involved data testing which included the normality tests for all the variables, the reliability tests, factor analysis and then finally the validity test. The second part of the data analysis included the multiple linear regression analysis.

Multiple regression analysis is a statistical technique to analyze the relationaship between a single criterion or dependent variable (i.e., higher level attributes) and two or more predictor or independent variables (i.e., lower level attributes). Multiple regression analysis may be used for prediction. Normally it is used to assess the extent to which the observed variance in the dependent variable is explained by the observed variance in the independent variables also referred to as the model fit. It is also used to assess the so called standardized regression weights. In the present study this is very important property since the beta coefficient may be used to indicate the relative importance of a lower level attribute.

2.4.3. Normality Tests

An assessment of the normality of data is a prerequisite for many statistical tests because normal data is an underlying assumption in parametric testing. There are two main methods of assessing normality: graphically and numerically. Statistical tests have the advantage of making an objective judgment of normality, but are disadvantaged by sometimes not being sensitive enough at low sample sizes or overly sensitive to large sample sizes. As such, some statisticians prefer to use their experience to make a subjective judgment about the data from plots/graphs. Graphical interpretation has the advantage of allowing good judgment to assess normality in situations when numerical tests might be over or under sensitive, but graphical methods do lack objectivity. In statistics, normality tests are used to determine if a data set is well-modeled by a normal distribution and to compute how likely it is for a random variable underlying the data set to be normally distributed.

More precisely, the tests are a form of model selection, and can be interpreted several ways, depending on one’s interpretations of probability like in descriptive statistics terms, one measures a goodness of fit of a normal model to the data—if the fit is poor then the data are not well modeled in that respect by a normal distribution, without making a judgment on any underlying variable. Normality test refers to the bell shaped nature of the curve. The data entries for the 30 variables in the likert scale of 1 to 5 (ranging from low to high) was done for all the 368 respondents in MS excel sheet which was imported in IBM SPSS20 data sheet. The data was then checked for it is for its normal distribution, for all the variables under study which are shown in the Figure 10 below.

The descriptive statistics in

Table 4. Descriptive statistics of variables.

Descriptive Statistics			Statistic	Std. Error
X1	Mean		3.9484	0.0388
	95% Confidence Interval for Mean	Lower Bound	3.8719
		Upper Bound	4.0248
	5% Trimmed Mean		3.9426
	Median		4.0000
	Variance		0.5560
	Std. Deviation		0.7456
	Minimum		3.0000
	Maximum		5.0000
	Range		2.0000
	Interquartile Range		2.0000
	Skewness		0.0840	0.1270
	Kurtosis		−1.1930	0.2540
X2	Mean		2.3478	0.0307
	95% Confidence Interval for Mean	Lower Bound	2.2874
		Upper Bound	2.4082
	5% Trimmed Mean		2.3865
	Median		2.0000
	Variance		0.3470
	Std. Deviation		0.5893
	Minimum		1.0000
	Maximum		3.0000
	Range		2.0000
	Interquartile Range		1.0000
	Skewness		−0.2740	0.1270
	Kurtosis		−0.6690	0.2540
Total	Mean		3.8614	0.0346
	95% Confidence Interval for Mean	Lower Bound	3.7933
		Upper Bound	3.9295

show the skewness of 0.084 with standard error of 0.127 and kurtosis of −1.193 with standard error of 0.254 for variable (X1) on pleasing appearance of buildings in neighborhood. In addition, the variable (X2) on buildings to the children’s scale shows the skewness of −0.274 with standard error of 0.127 and kurtosis of −0.669 with standard error of 0.254.

The results gave the bell shaped graphs showing the mean and standard deviation values along with the frequency distribution in the Figure 10. In the same way the normality tests for all variables was conducted and the cumulative results for all 30 variables were recorded with the following observation.A Shapiro Wilk’s test (p > 0.05) [12,13] and a visual inspection of their histograms, normal Q-Q plots and box plots showed that the variables are normally distributed with a skewness ranging between (0.526 and −1.583) (standard error = 0.127) and kurtosis ranging between (2.845 and −2.009) (standard error = 0.254) [14,15,16]. The z- values for all the variables are found between ±1.96, which indicates our data to be approximately normally distributed in terms of skewness and kurtosis.

The data is a little skewed and kurtotic for the 29 independent and 1 dependent variable but it does not differ significantly from normality. We can assume that our data is approximately normally distributed in terms of skewness and kurtosis and hence the study moved forward with the reliability tests.

2.4.4. Reliability Tests

Cronbach’s alpha [17] is a measure of reliability. Reliability is an assessment of the degree of consistency in multiple measurement of a variable.

The computation of Cronbach’s alpha (Equation (2)) is based on the number of items on the survey (k) and the ratio of the average inter-item covariance to the average item variance.

Cronbach alpha = rk/[1 + (k − 1)r]

(2)

where, k is the number of items considered and r is the mean of the inter-item correlations.

The size of alpha is determined by both the number of items in the scale and the mean inter-item correlations.

For Comparison several other reliability measures are available like Split—half coefficients, Guttmann, Parallel, Strict Parallel.

To obtain a good estimate of the reliability of a survey, the survey was administered twice to the same group of people and then the two sets of results were correlated.

Cronbach’s alpha reliability coefficient normally ranges between 0 and 1. However, there is actually no lower limit to the coefficient. The closer Cronbach’s alpha coefficient is to 1.0 the greater the internal consistency of the items in the scale.

The studies [18] provide the following rules of thumb: “_ > 0.9—Excellent, _ > 0.8—Good, _ > 0.7—Acceptable, _ > 0.6—Questionable, _ > 0.5—Poor and _ < 0.5—Unacceptable” (p. 231). While increasing the value of alpha is partially dependent upon the number of items in the scale, it should be noted that this has diminishing returns. It should also be noted that an alpha of 0.8 is probably a reasonable goal.

Table 5. Showing reliability statistics.

Cronbach’s Alpha	Cronbach’s Alpha Based on Standardized Items	N of Items
0.832	0.837	30

shows the value of Cronbach’s alpha as 0.832 with the number of items being 30. The

Table 6. Showing reliability statistics in split half method.

Cronbach’s Alpha	Part 1	Value	0.790
		N of Items	15 a
	Part 2	Value	0.697
		N of Items	15 b
	Total N of Items		30
Correlation Between Forms			0.541
Spearman-Brown Coefficient	Equal Length		0.702
	Unequal Length		0.702
Guttman Split-Half Coefficient			0.698

^a The items are: X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, and X15; ^b The items are: X16, X17, X18, X19, X20, X21, X22, X23, X24, X25, X26, X27, X28, X29, Y1.

also shows the value of alpha in the split half method where again its value was 0.79 and 0.69 for the variable being split into 2 groups of 15 in numbers. It should also be noted that while a high value for Cronbach’s alpha indicates good internal consistency of the items in the scale, it does not mean that the scale is one-dimensional. Factor analysis is a method to determine the dimensionality of a scale to which the data was further subjected.

2.4.5. Exploratory Factor Analysis

Factor analysis identifies the Factors. It explains the pattern of correlations within a set of observed variables. Types of Factor Analysis includes—(1) Exploratory and (2) Confirmatory. It is used to explore the dimensionality of an instrument by finding the smallest number of factors needed to explain the correlations among a set of variables. Varimax rotation is used to improve interpretability.

Factor Analysis is a commonly used data/variable reduction technique. This multivariate statistical technique is used for three primary reasons:

• Reduce the number of variables, from large to small
• Establish underlying dimensions between measured variables and constructs and
• Provide construct validity evidence

Some of the points of Factor Analysis discussed include the types of factor analysis, i.e., Exploratory Factor Analysis (EFA) and Confirmatory Factor Analysis (CFA). As the names suggest, EFA is used where the study is being conducted with no pre-conceived theories or expectations while CFA is used where the study is being conducted to test a proposed theory. While the uses of Factor Analysis including (a) interdependency and pattern delineation; (b) data reduction; (c) structure; (d) classification; (e) scaling; and (f) hypothesis testing, one aspect in Factor Analysis that needs mention in detail includes KMO and Bartlett’s Test of Sphericity.

KMO and Bartlett’s Test of Sphericity is a measure of sampling adequacy that is recommended to check the case to variable ratio for the analysis being conducted. In most academic and business studies, KMO and Bartlett’s test play an important role for accepting the sample adequacy. While the KMO ranges from 0 to 1, the world-over accepted index is over 0.6. In addition, the Bartlett’s Test of Sphericity relates to the significance of the study and thereby shows the validity and suitability of the responses collected to the problem being addressed through the study. The

Table 7. Showing exploratory factor analysis statistics.

KMO and Bartlett’s Test
Kaiser-Meyer-Olkin Measure of Sampling Adequacy		0.851
Bartlett’s Test of Sphericity	Approx. Chi-Square	5458.758
	df	435
	Sig.	0.000

below shows the KMO of sampling adequacy to be 0.851, which is very much an acceptable index.

For Factor Analysis to be recommended suitable, the Bartlett’s Test of Sphericity must be less than 0.05. Another important aspect that needs mention is the Rotated Component Matrix. While deciding how many factors one would analyze is whether a variable might relate to more than one factor. Rotation maximizes high item loadings and minimizes low item loadings, thereby producing a more interpretable and simplified solution. There are two common rotation techniques—orthogonal rotation and oblique rotation. While orthogonal varimax rotation that produces factor structures that are uncorrelated, oblique rotation produces factors that are correlated. Irrespective of the rotation method used, the primary objectives are to provide easier interpretation of results, and produce a solution that is more parsimonious. The

Table 8. Showing variance statistics.

Component	Initial Eigenvalues			Extraction Sums of Squared Loadings
	Total	% of Variance	Cumulative %	Total	% of Variance	Cumulative %
1	7.561	25.202	25.202	7.561	25.202	25.202
2	3.103	10.344	35.546	3.103	10.344	35.546
3	2.589	8.628	44.175	2.589	8.628	44.175
4	1.801	6.003	50.177	1.801	6.003	50.177
5	1.569	5.231	55.409	1.569	5.231	55.409
6	1.214	4.047	59.456	1.214	4.047	59.456
7	1.099	3.665	63.120	1.099	3.665	63.120
8	0.997	3.323	66.443
9	0.886	2.953	69.396
10	0.798	2.660	72.056
11	0.786	2.619	74.675
12	0.718	2.392	77.067
13	0.714	2.381	79.448
14	0.649	2.165	81.613
15	0.602	2.006	83.619
16	0.580	1.935	85.554
17	0.521	1.737	87.291
18	0.491	1.636	88.927
19	0.445	1.483	90.410
20	0.426	1.420	91.830
21	0.384	1.279	93.109
22	0.364	1.212	94.321
23	0.321	1.071	95.392
24	0.306	1.019	96.411
25	0.255	0.849	97.259
26	0.230	0.766	98.026
27	0.210	0.700	98.726
28	0.181	0.602	99.327
29	0.106	0.353	99.681
30	0.096	0.319	100.000

Extraction method: principal component analysis.

shows the exploratory factor analysis statistics and the total variance explained as under.

The contents of Table 8 are elaborated below.

• Factor—The initial number of factors is the same as the number of variables used in the factor analysis. However, not all 30 factors will be retained. Here seven factors will be retained.
• Initial Eigen values—Eigen values are the variances of the factors. Because we conducted our factor analysis on the correlation matrix, the variables are standardized, which means that the each variable has a variance of 1, and the total variance is equal to the number of variables used in the analysis, in this case, 30.
• Total—This column contains the eigenvalues. The first factor will always account for the most variance (and hence have the highest eigenvalues), and the next factor will account for as much of the left over variance as it can, and so on. Hence, each successive factor will account for less and less variance.
• % of Variance—This column contains the percent of total variance accounted for by each factor.
• Cumulative %—This column contains the cumulative percentage of variance accounted for by the current and all preceding factors. For example, the eighth row shows a value of 66.443. This means that the first eight factors together account for 66.443% of the total variance.
• Extraction Sums of Squared Loadings—The number of rows in this panel of the table correspond to the number of factors retained. Here the values are based on the common variance. The values in this panel of the table will always be lower than the values in the left panel of the table, because they are based on the common variance, which is always smaller than the total variance.
• Rotation Sums of Squared Loadings—The values in this panel of the table represent the distribution of the variance after the varimax rotation. Varimax rotation tries to maximize the variance of each of the factors, so the total amount of variance accounted for is redistributed over the three extracted factors. The graph below shows the scree plots of eigenvalues against the factor numbers.
• The scree plot graphs the eigenvalues against the factor number. You can see these values in the first two columns of the table immediately above. From the seventh factor on, you can see that the line is almost flat, meaning thereby that each successive factor is accounting for smaller and smaller amounts of the total variance as is shown in the Figure 11.
• Component Matrix—This table contains the unrotated factor loadings, which are the correlations between the variable and the factor. Because these are correlations, possible values range from −1 to +1. The correlations that are 3 or less can be removed. This makes the output easier to read by removing the clutter of low correlations that are probably not meaningful anyway.
• Factor Score Coefficient Matrix—This is the factor weight matrix and is used to compute the factor scores. The data was then subjected to the validity tests.

2.4.6. Validity Tests

Correlation Coefficients: There are multiple types of correlation coefficients. By default, Pearson’s selected. Selecting Pearson will produce the test statistics for a bivariate Pearson Correlation.

Test of Significance: Two-tailed or One-tailed, depending on the desired significance test. As the study does not hypothesize a specific directional relationship (i.e., negative or positive) between the variables, a two-tailed significance test is selected. The

Table 9. Showing coefficients of correlations for all variables.

	Y1		Y1		Y1
X1	0.66	X11	0.59	X21	0.17
X2	0.33	X12	0.58	X22	0.14
X3	0.33	X13	0.52	X23	0.12
X4	0.20	X14	−0.02	X24	0.43
X5	0.00	X15	0.23	X25	0.46
X6	0.11	X16	0.43	X26	0.42
X7	0.58	X17	0.27	X27	0.44
X8	0.58	X18	0.15	X28	0.31
X9	0.52	X19	0.10	X29	0.38
X10	0.59	X20	0.19

below shows the coefficients of correlations for all variables.

A correlation coefficient is a statistical measure of the degree to which changes to the value of one variable predict change to the value of another. Correlation coefficients are expressed as values between +1 and −1. A coefficient of +1 indicates a perfect positive correlation: A change in the value of one variable will predict a change in the same direction in the second variable as displayed by most of the variables under study.

The scatter plot in Figure 12 shows the closeness of the variables to the dependent variable. A coefficient of −1 indicates a perfect negative correlation: A change in the value of one variable predicts a change in the opposite direction in the second variable as shown in the variable (X14). Lesser degrees of correlation are expressed as non-zero decimals. A coefficient of zero indicates there is no discernable relationship between fluctuations of the variables as in variable (X5).

2.4.7. Regression Analysis

A statistical measure that attempts to determine the strength of the relationship between one dependent variable (usually denoted by Y) and a series of other changing variables (known as independent variables). The two basic types of regression are linear regression and multiple regressions. Linear regression uses one independent variable to explain and/or predict the outcome of Y, while multiple regressions use two or more independent variables to predict the outcome. The general form of each type of regression is as shown in Figure 13 below.

The

Table 10. Showing the value of R square.

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate	Change Statistics
					R Square Change	F Change	df1	df2	Sig. F Change
1	0.862 a	0.742	0.720	0.31558	0.742	33.581	29	338	0.000

^a Predictors: (Constant), X29, X5, X15, X20, X21, X24, X19, X6, X17, X18, X25, X16, X3, X27, X4, X26, X28, X22, X23, X9, X2, X13, X7, X14, X11, X8, X10, X1, X12; ^b Dependent Variable: Y1.

below shows the value of R square computed after regression analysis. In statistics, regression validation is the process of deciding whether the numerical results quantifying hypothesized relationships between variables, obtained from regression analysis, are acceptable as descriptions of the data. The validation process can involve analyzing the goodness of fit of the regression, analyzing whether the regression residuals are random, and checking whether the model’s predictive performance deteriorates substantially when applied to data that were not used in model estimation. An R² (coefficient of determination) close to one does not guarantee that the model fits the data well, because as Anscombe’s quartet shows, a high R² can occur in the presence of misspecification of the functional form of a relationship or in the presence of outliers that distort the true relationship. The Figure 14 shows the regression standardized residual and the plotting of the dependent variable Y1 as a parabolic curve.

To check for meeting the assumption that the residuals or error terms are normally distributed, we look at the Normal P-P plot of Regression Standardized Residual as shown in Figure 15 below:

The Figure 15 above shows the appropriateness of the model is the degree to which the plot for the actual values coincides with the line of expected values. In our study, the plot of residuals fits the expected pattern well enough to support a conclusion that the residuals are normally distributed and the regression equation (Equation (3)) can be formed as under:

Regression equation –Y1 = −0.987 + (0.005 × 1 + 0.086 × 2 + 0.096 × 3 + 0.040 × 4 − 0.010 × 5 + 0.024 × 6 + 0.087 × 7 + 0.078 × 8 − 0.106 × 9 − 0.094 × 10 − 0.041 × 11 + 0.050 × 12 + 0.039 × 13 + 0.118 × 14 + 0.009 × 15 + 0.083 × 16 − 0.055 × 17 + 0.020 × 18 + 0.013 × 19 + 0.025 × 20 + 0.052 × 21 + 0.025 × 22 + 0.038 × 23 + 0.014 × 24 + 0.055 × 25 + 0.043 × 26 + 0.073 × 27 + 0.053 × 28 + 0.034 × 29)

(3)

The data under study generated the regression equation that was further put to the validation by applying it on the two other neighborhoods of Nagpur.

3. Validating the Model

Validation is a process of establishing documentary evidence demonstrating that a procedure, process, or activity carried out in production or testing maintains the desired level of compliance at all stages.

To validate the model generated after SPSS, it was further applied on two new neighborhoods of Dhantoli and Nehrunagar in the Nagpur city. From the RESS questionnaire of these neighborhoods and respondent data collected, the average values of all the 46 respondents of each neighborhood was put in the model to give the value of (Y1) which was found close to the average of actual values received from the respondents. Thus, regression Equation (4) shown below was establishing the documentary evidence and hence the process was validated. The validation results are shown in the

Table 11. Shows the validation results on 2 neighborhoods.

Neighborhood	Y1 from Model	Y1 from Respondent
Nehrunagar	3.416	3.2
Dhantoli	2.217	2.3

below.

Y1 = −0.987 + (0.005 × 3.6 + 0.086 × 3.5 + 0.096 × 1.6 + 0.040 × 2.1 − 0.010 × 3.5 + 0.024 × 3 + 0.087 × 3.5 + 0.078 × 3.5 − 0.106 × 3.2 − 0.094 × 2.3 − 0.041 × 2.5 + 0.050 × 1.8 + 0.039 × 1.8 + 0.118 × 3.3 + 0.009 × 3.5 + 0.083 × 3.5 − 0.055 × 3.3 + 0.020 × 2.3 + 0.013 × 3.3 + 0.025 × 3.5 + 0.052 × 3.6 + 0.025 × 2.3 + 0.038 × 3.3 + 0.014 × 3.5 + 0.055 × 3.7 + 0.043 × 3.5 + 0.073 × 3.6 + 0.053 × 3.5 + 0.034 × 3.8)

(4)

The methodology of study covered in Section 1.4 with all details of the qualitative surveys has been applied on Nagpur city and found to be validated. The same process of study can be adopted for other tier 2 cities in central India.

3.1. Identification of Significant Variable Mainly Contributing to the Satisfaction Level (Y1)

In order to identify the parameters, which can be improved upon to make the neighborhood environment more responsive for the children’s concerns, we explore the two methods mentioned below.

(1)

Significant independent variables were identified using Pareto statistical tool.

(2)

Average and Ideal values were set for the independent variables marked as (X) with numbers.

3.1.1. Pareto Analysis for Identification of Significant Independent Variable

Pareto Analysis is a statistical technique in decision-making used for the selection of a limited number of tasks that produce significant overall effect. It uses the Pareto Principle (also known as the 80/20 rule) the idea that by doing 20% of the work you can generate 80% of the benefit of doing the entire job. It is used to analyze data about the frequency of problems or causes in a process, when there are many problems and we want to focus on the most significant.

The Pareto analysis of all the 29 variables under study as shown in Figure 16, that helped in defining the child friendliness of a neighborhood in the Indian context, clearly shows that the children’s play related variables X21 relating to hierarchy of open space, X16 relating to the recreation time spent by children, X17 relating to the meeting or personal spaces for children, X13 relating to the all weather play provisions in neighborhood, X10 relating to the variety of play opportunities, X6 relating to the on street parking provisions creating hindrance to play and X4 relating to the provisions of cycle tracks along the road for unobstructed cycling for children fall in the 20% weightage and the other physical and social characteristics of the neighborhoods occupy the 80% of the weightage.

This clearly shows that the conventional planning and design tends to ignore the children’s quotient while designing the neighborhoods, also bringing forth the low participation of children in decision making roles in their residential areas.

3.1.2. Average and Ideal Values for the Independent Variables (X)

To understand the overall existing condition of the built environment in various neighborhoods of Nagpur using the 29 independent variables, it was essential to find average values for each variable in respect to all the 368 respondents data collected. The maximum average score mentioned below in Figure 17, were observed in each variable, which were considered as achievable benchmark scores in Nagpur city.

To improvise the existing scores of the neighborhood, the ideal score which can be aspired to for was to be set. The ideal values of each variable was computed by taking the maximum average score of a variable from all neighborhoods under study and add 10% of average score to arrive at the ideal scores of the variables for the case of Nagpur.

The Figure 18 below shows the average values of each variable computed for all the 368 respondents and the ideal values of each variable.

The two new neighborhoods studied were (Nehrunagar and Dhantoli) and their average values of variables were fitted in regression equation to get the value of Y1. Value of Y1 for Nehrunagar was found to be 3.2 and the value of Y1 for Dhantoli as 2.3 against the average Y1 of 2.9 from equation.

Figure 19 gives the cumulative picture of both the neighborhoods considered for validation and the values of the variables under study lie well within the rings of the average and the ideal values of variables under consideration for the city of Nagpur, which furthermore validates the appropriateness of the model for the urban neighborhoods to be studied and researched upon in the Indian context.

Figure 20 shows the satisfaction scores of the neighborhoods as the value of Y1 and most neighborhoods fall below the average value except the Shantinagar, Nehrunagar and Hanumanagar where the satisfaction is more because of the socio-cultural reasons, but the neighborhoods can strive to reach up to the ideal value of YI variable if the child friendly parameters relating to the physical environment in the neighborhoods are designed, modified and upgraded.

4. Conclusions

The results showed that the quantity and the quality of formal outdoor play facilities or the conventional play facilities in the parks were not positively related to the outdoor play among children in this study. Rather, informal play areas such as the presence of sidewalks were more related to children’s outdoor play. In addition, traffic safety and parked vehicles were important characteristics associated with outdoor play. In addition, the neighborhood evaluations revealed absence of many child friendly aspects that make the environment inclusive, comfortable and nurture a sense of belonging towards the neighborhood bringing down the overall satisfaction of children and parents with their area of residence. The users reiterated having to negotiate with their environs while resolving their needs. Local policy makers from different sectors can use these research findings in creating more activity friendly neighborhoods for children. The pilot survey identified the ground challenges and paved way for a context based research by facilitating the design of a suitable methodology.

This study identified methods by which children would respond on neighborhood experiences. The methodology encompassed the use of several tools for a holistic research covering important aspects in more than one way, which aided in crosschecking and affirming points under study.

The questionnaire and the workshop were the most user responsive tools. Most importantly it helped all the above evaluation data to be collected in a manner conducive to statistical analysis. Quantitative and the qualitative analysis using the SPSS tool completed the assessment holistically. These can be looked upon as the positive contributions of the methodology.

Limitations and Further Applications of Methodology

In India, the environ behavior studies are in a nascent stage. The methodology of this study thus places more emphasis on the spatial and physical attributes through actual ground survey and its environmental significance is found in the Indian context along with the perceptional responses which are socio-economic, culture and lifestyle driven, which contributes positively to the environ-behavior studies in the Asian context.

The tools used in the research are applicable to other typologies in similar conditions. This study can positively contribute in the development of a well organized methodology for furthering built environment assessment research in the Indian context.

The research contributes in:

• In evolving methodology to study child friendly environs.
• In identifying variables in Indian context.
• In developing requisite tools for Residential environment evaluation.

The reliance on foreign case studies imparts a vision but stops short of practical contributions given the diversity of its land and people in the Indian context. There is a need for intensive study looking at the spatial and physical aspects of neighborhoods in the Indian cities. With this reference, the pilot study helped in identifying the unique issues and defining the research direction. It highlighted child friendliness and the importance of children’s primary work, i.e., play, as a neglected aspect of urban neighborhoods in Indian context requiring focused attention. It assisted in the design of an appropriate research methodology. The research emphasizes the need to look afresh at the design and development of residential neighborhood environs especially from the view point of child friendliness.