Numerical Investigation of Blast Performance of Plate-Reinforced Moment-Resisting Connection Using Large Concrete Filled Tubular Section
Abstract
:1. Introduction
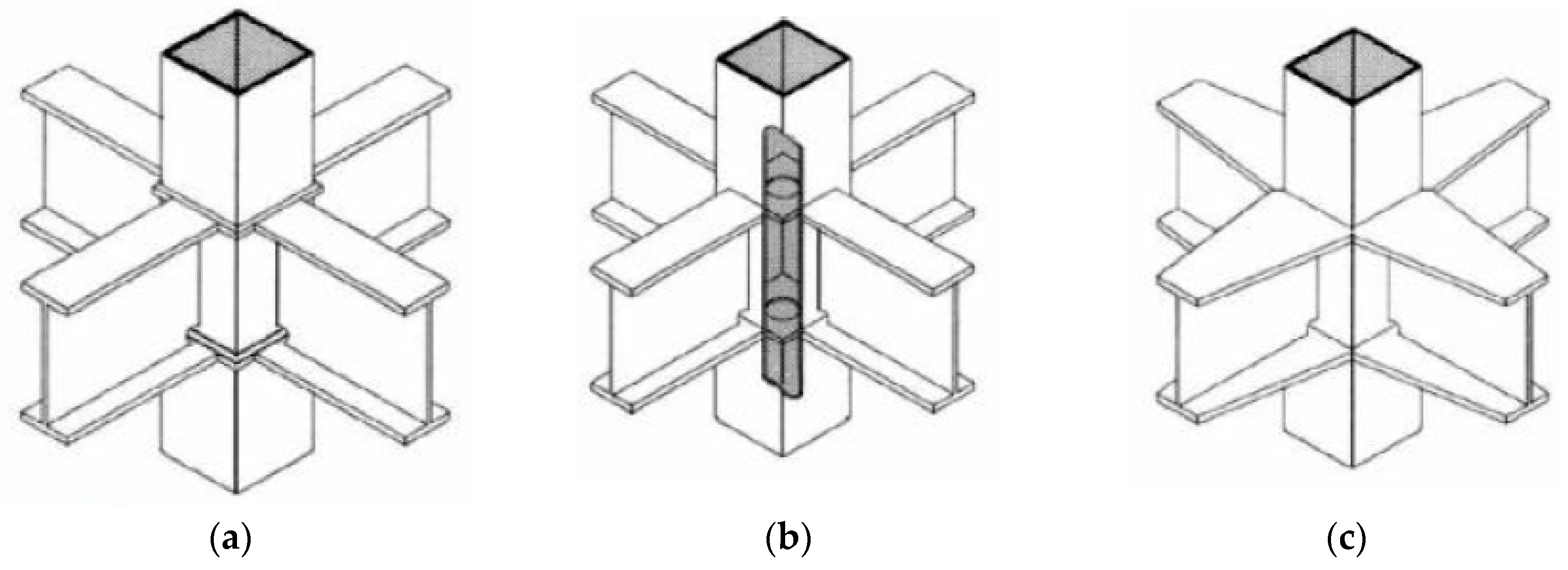
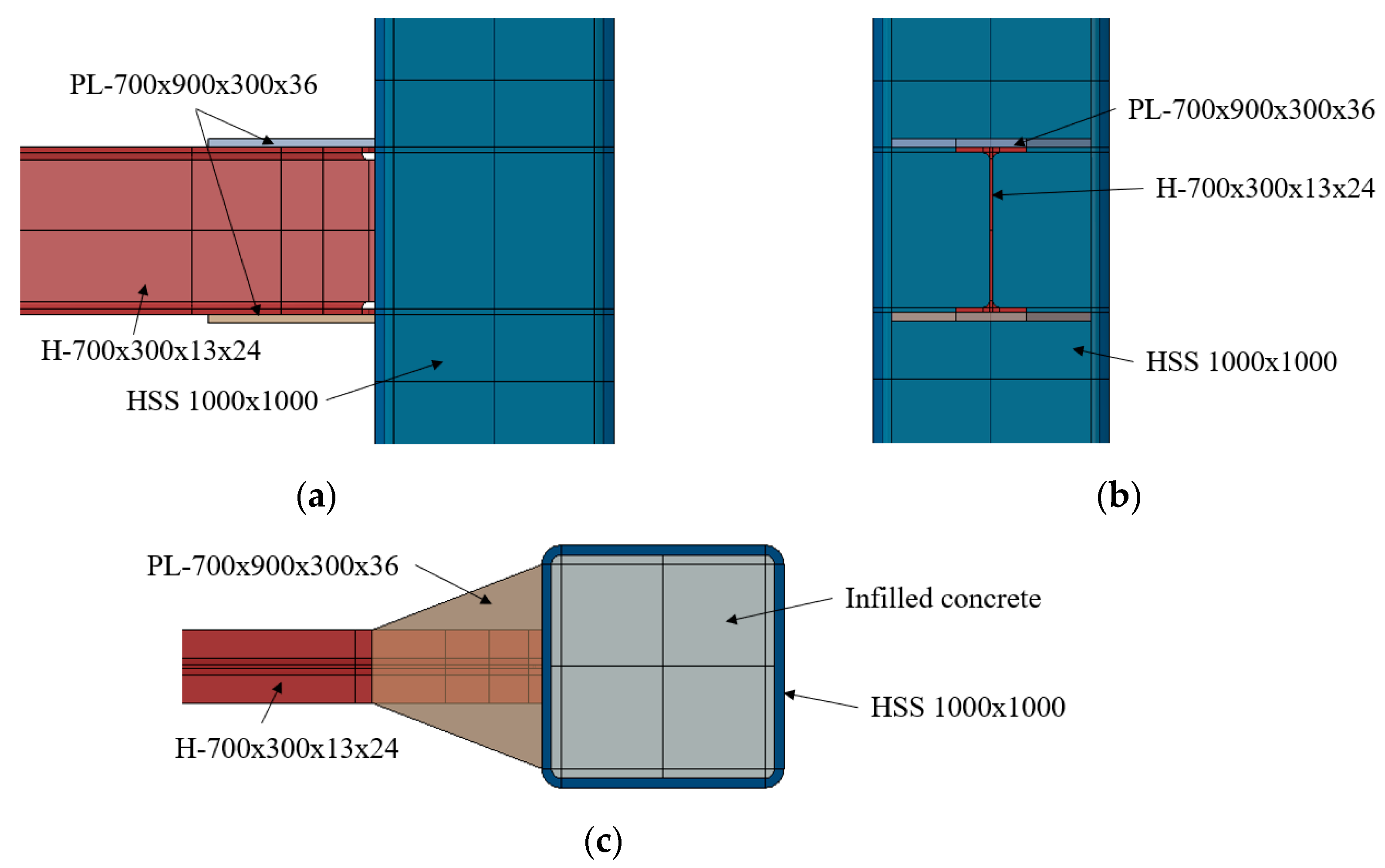
2. Plate-Reinforced Moment Connection with Large CFT Column
3. Blast Scenario
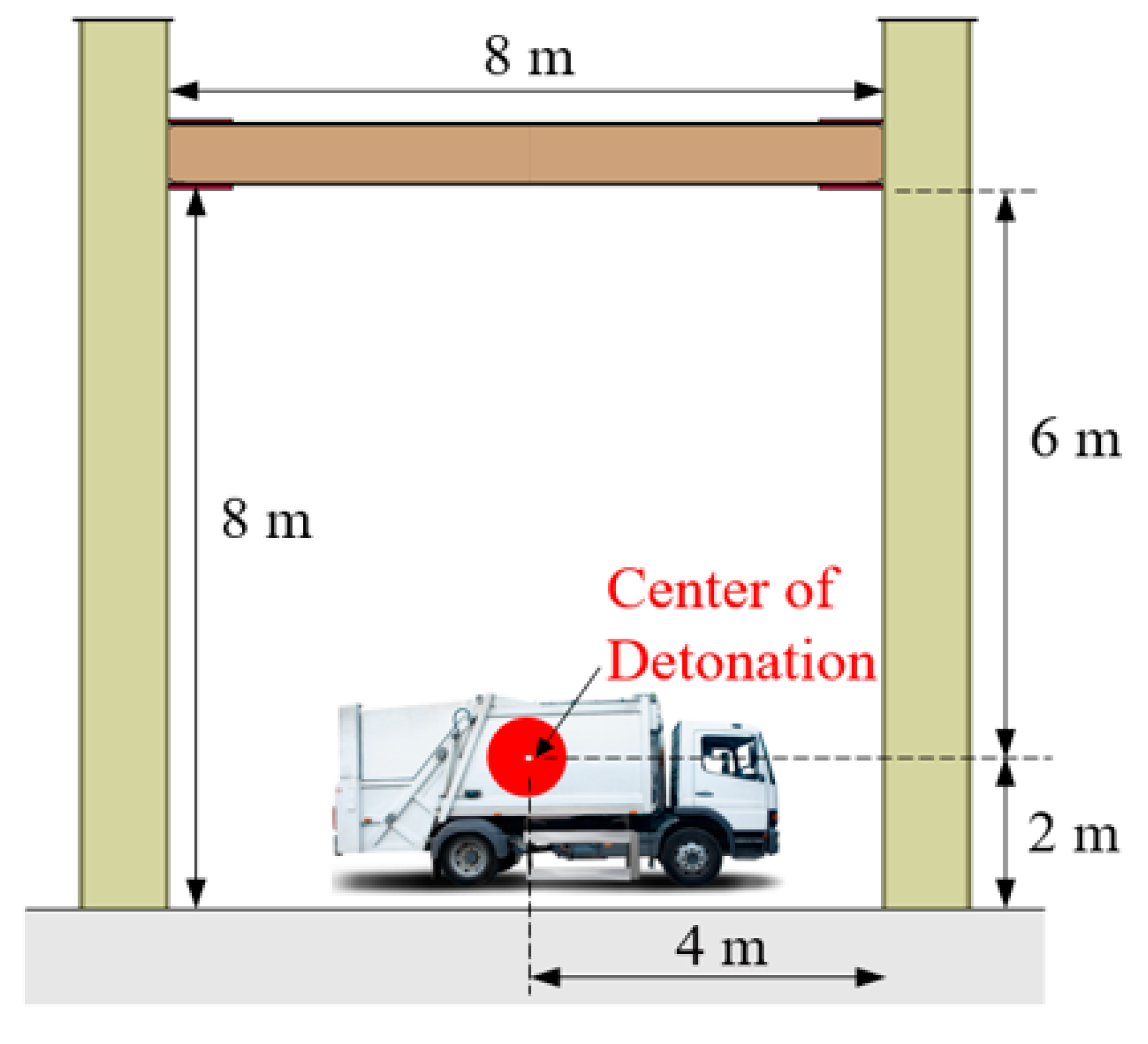
3.1. Model Description
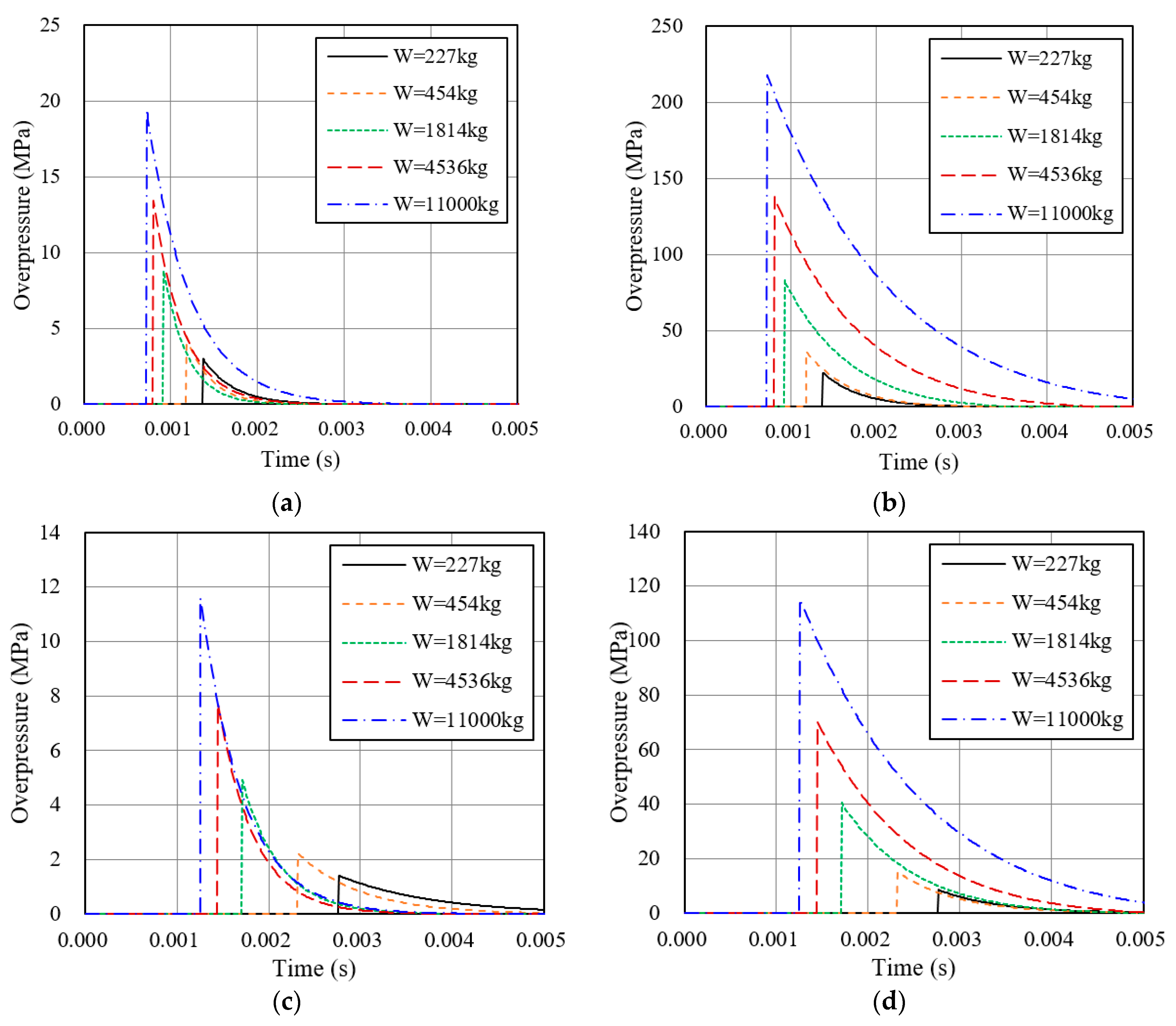
3.2. Blast Loading
4. Numerical Modeling of Connection
4.1. Numerical Model
4.2. Material Properties
4.3. Blast Loading Implementation
4.4. Effect of Strain Rate
4.5. Material Erosion
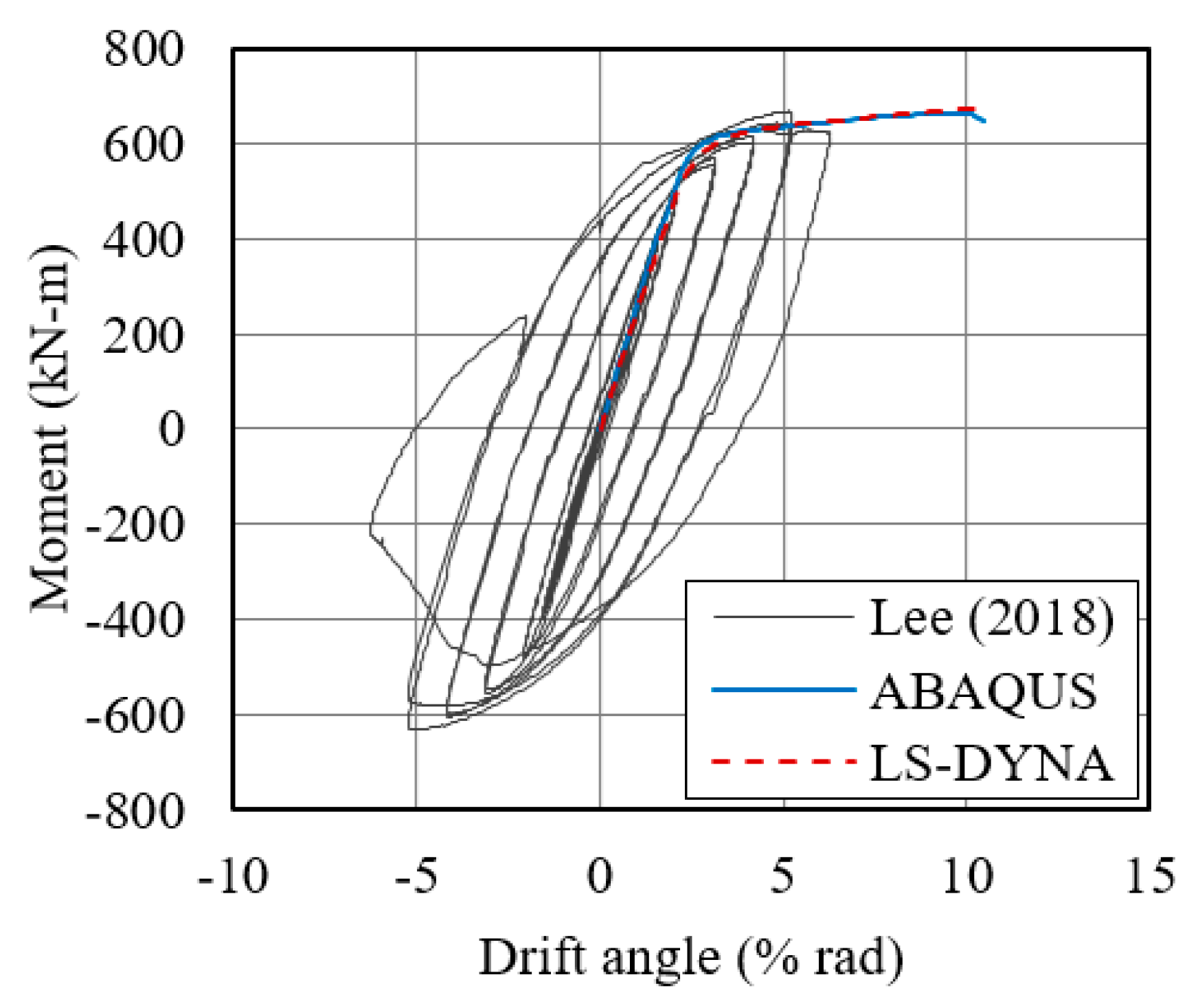
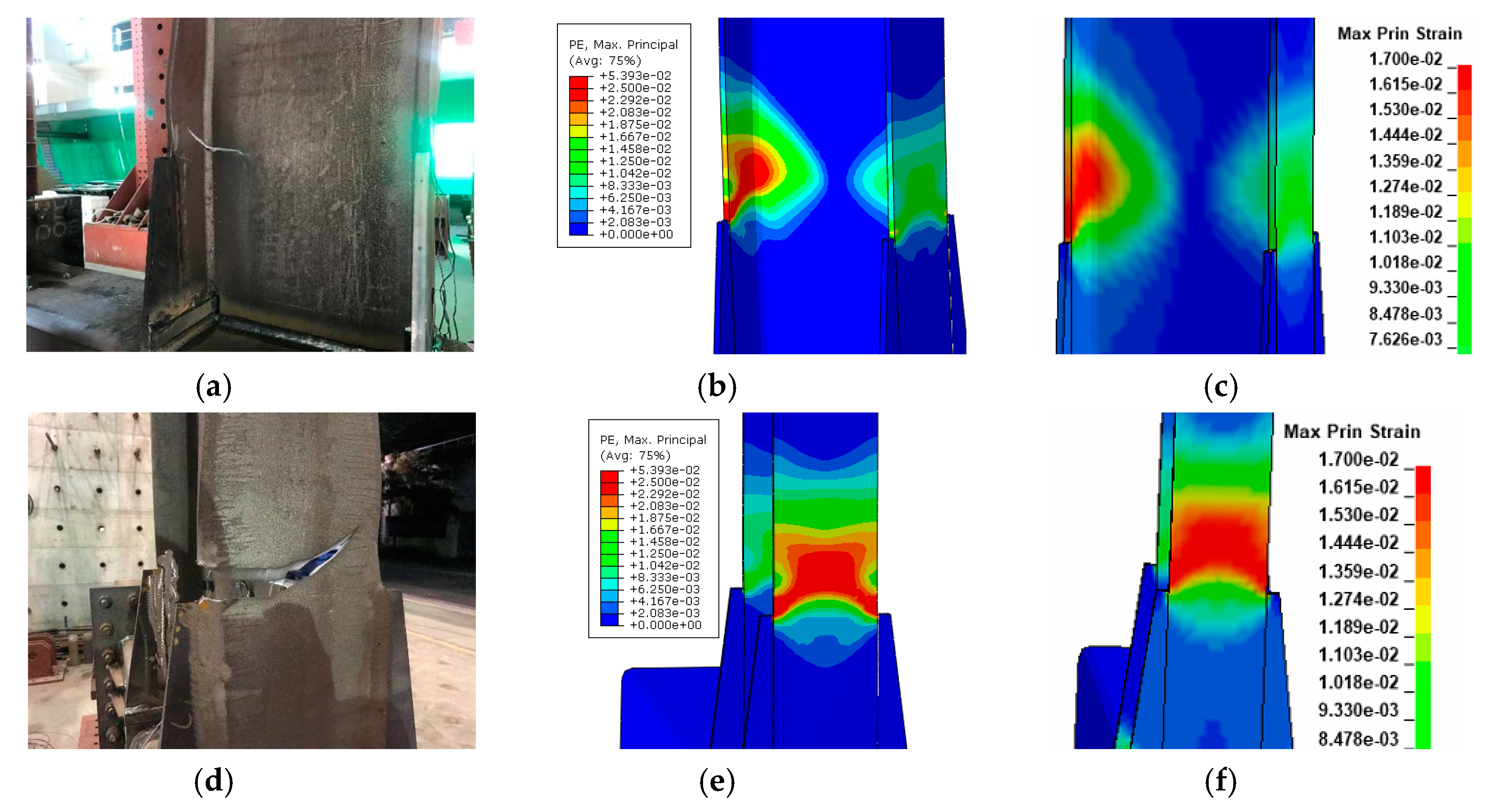
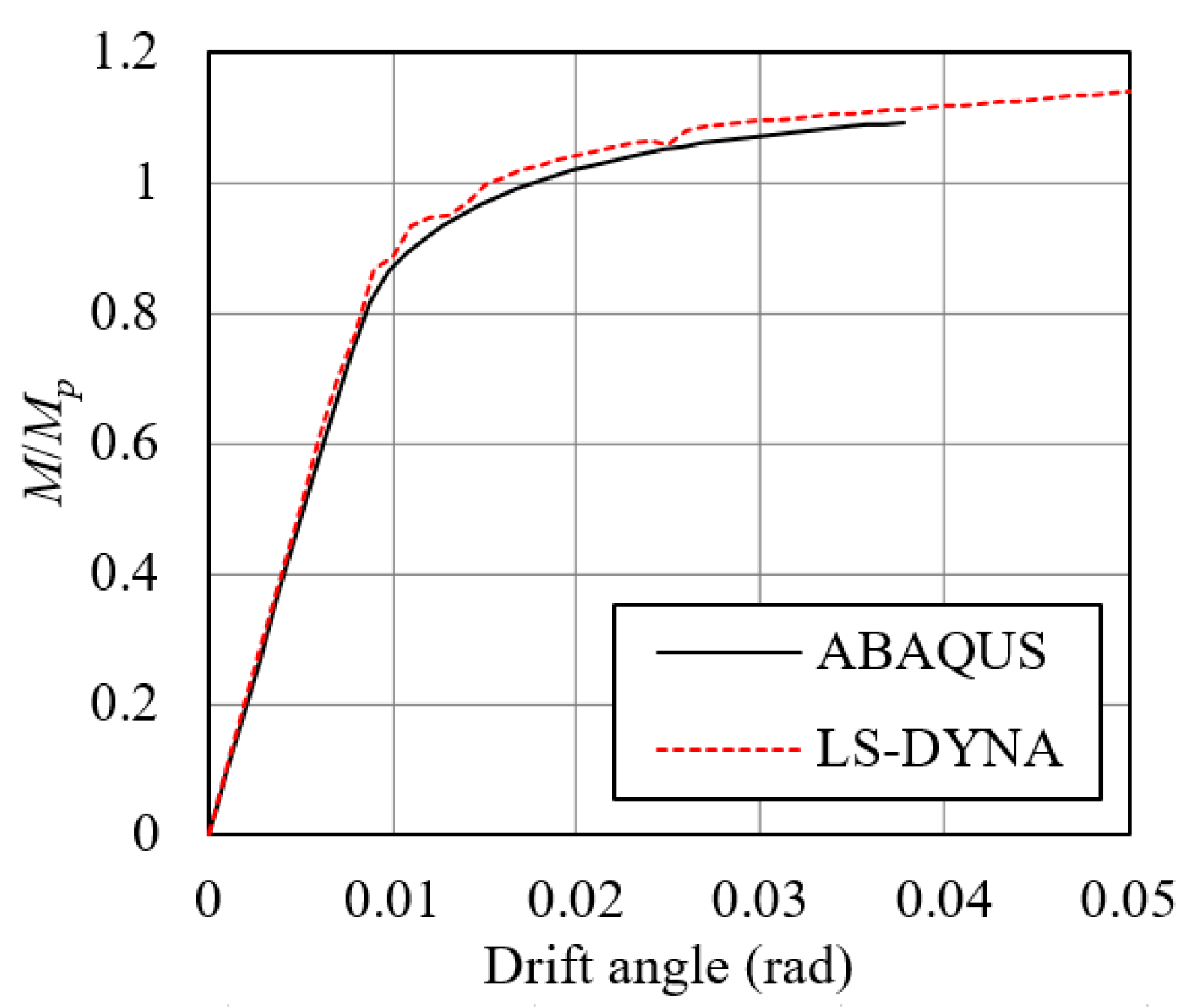
5. Verification and Validation
5.1. Blast Loading
5.2. Structural Performance of Numerical Model
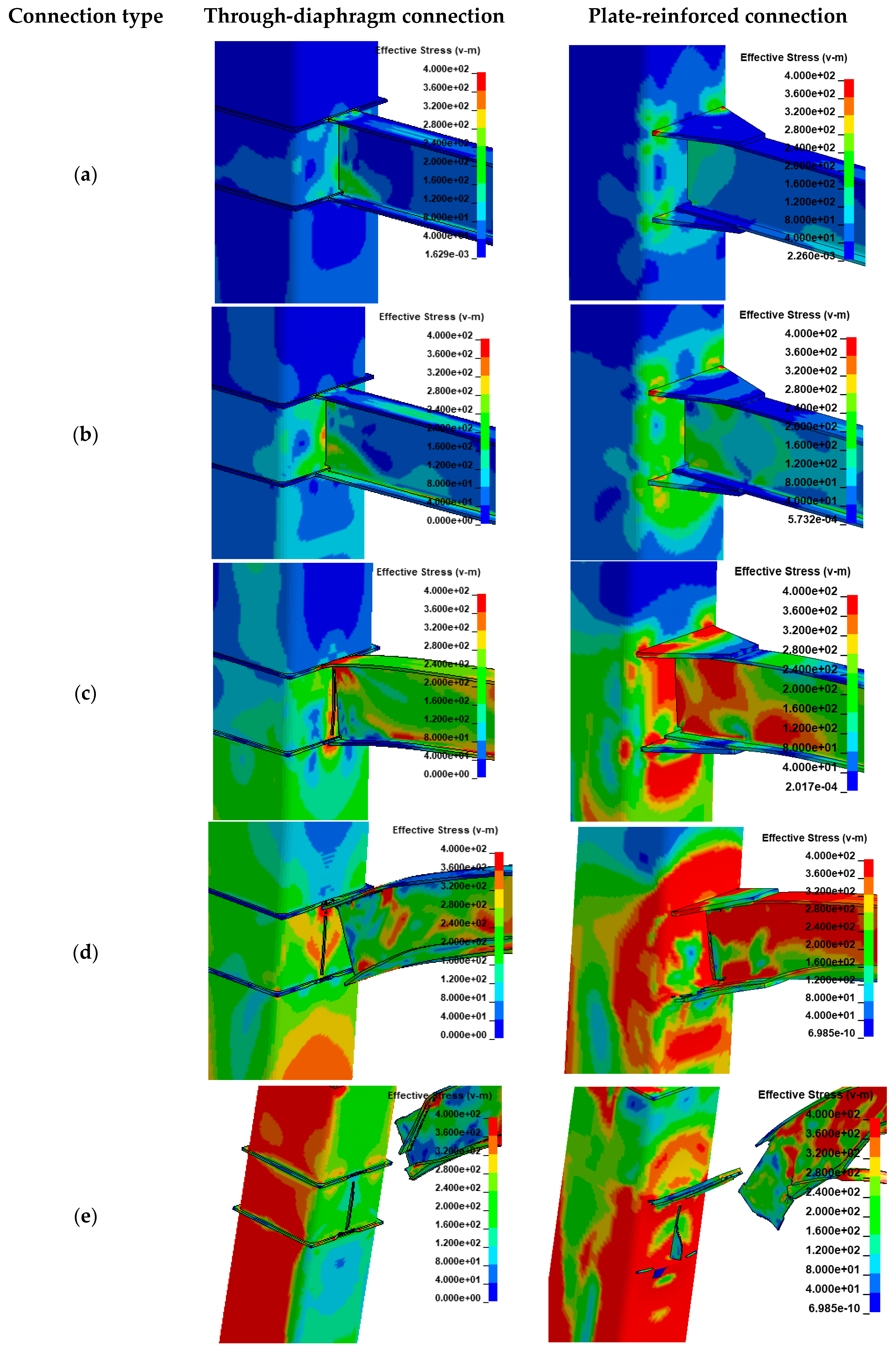
6. Blast Performance of Proposed Connection
6.1. Evaluation Criteria
6.2. Results
6.3. Discussion
7. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shin, K.-J.; Kim, Y.-J.; Oh, Y.-S.; Moon, T.-S. Behavior of welded CFT column to H-beam connections with external stiffener. Eng. Struct. 2004, 26, 1877–1887. [Google Scholar] [CrossRef]
- Shin, H.J.; Jang, B.; Chung, J.A.; Lee, E.T. Performance Evaluation of Connection of Seismic Rectangular Steel Tube Column-H Beam Using One-side Bolts. J. Korean Soc. Steel Const. 2010, 22, 355–363. [Google Scholar]
- Jin, J.; Kim, D.; Kim, H.; Shin, J.; Park, K.; Lee, K. Experimental Evaluation of New Seismic Connections between Rectangular Steel Tube Column and H-shaped Beam. J. Korean Soc. Steel Const. 2018, 30, 77–85. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Chen, Z.; Wang, X.; Zhou, T. Seismic behavior of through-diaphragm connections between CFRT columns and steel beam-experimental study. Adv. Steel Constr. 2014, 10, 351–371. [Google Scholar]
- Chen, Z.; Qin, Y.; Wang, X. Development of connections to concrete-filled rectangular tubular columns. Adv. Steel Constr. 2015, 11, 408–426. [Google Scholar]
- Kim, K.; Lee, H.W.; Kim, Y.K.; Kim, T.; Kim, J.H. Structural strength of beam-to-CFT connections with vertical diaphragm. J. Korean Soc. Steel Const. 2017, 36, 237–247. [Google Scholar]
- Jeddi, M.Z.; Sulong, N.H.R.; Khanouki, M.M.A. Seismic performance of a new through rib stiffener beam connection to concrete-filled steel tubular columns: An experimental study. Eng. Struct. 2017, 131, 477–491. [Google Scholar] [CrossRef]
- Huang, Y.; Young, B. Design of cold-formed stainless steel circular hollow section columns using direct strength method. Eng. Struct. 2018, 163, 177–183. [Google Scholar] [CrossRef] [Green Version]
- Eslami, M.; Namba, H.; Kodur, V.; Mahamid, M.; Moro, M.A. Seismic behavior of composite beam connected to HSS column with large width-to-thickness ratio. Eng. Struct. 2019, 183, 423–442. [Google Scholar] [CrossRef]
- Wu, L.-Y.; Chung, L.-L.; Tsai, S.-F.; Lu, C.-F.; Huang, G.-L. Seismic behavior of bidirectional bolted connections for CFT columns and H-beams. Eng. Struct. 2019, 29, 395–407. [Google Scholar] [CrossRef]
- Wang, Y. Development of New CFT Column-CFT Beam Frame Structure Using Self-Compacting Concrete. Ph.D. Thesis, Kochi University of Technology Academic Resource Repository, Kochi, Japan, 2006. [Google Scholar]
- Kurobane, Y.; Packer, J.A.; Wardenier, J.; Yeomans, N. Design Guide for Structural Hollow Section Column Connections; CIDECT Design Guide No. 9; CIDECT and Verlag TÜV Rheinland GmbH: Köln, Germany, 2004. [Google Scholar]
- Seo, S.Y.; Jung, J.A.; Choi, S.M.; Kim, S.Y. Seismic behavior of H shaped beam to square column connection with outer diaphragm using field welding. J. Korean Soc. Steel Const. 2005, 17, 459–467. [Google Scholar]
- Kim, S.H.; Yom, K.S.; Choi, S.M. Seismic Evaluation of Welded-formed square Column-Beam Connection for External Diaphragm Stress path. J. Korean Soc. Steel Const. 2014, 26, 322–331. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Kim, Y.H.; Choi, S.M. Structural Behavior of Welded Built-up Square CFT Column to Beam Connections with External Diaphragm. J. Korean Soc. Steel Const. 2016, 28, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Lee, G. Structural Performance Evaluation of Prefabricated Steel Square Hollow Section Column to H-Shaped Beam Connections Using Inner Diaphragm. Master’s Thesis, Dankook University, Yongin, Korea, 2018. [Google Scholar]
- JFE Steel Corporation. JFE Column. Available online: https://www.jfe-steel.co.jp/en/products/pipes/catalog/e1e-004.pdf (accessed on 1 December 2019).
- Kim, T.; Whittaker, A.S.; Gilani, A.S.J.; Bertero, V.V.; Takhirov, S.M. Cover-Plate and Flange-Plate Steel Moment-Resisting Connections. J. Struct. Eng. 2002, 128, 474. [Google Scholar] [CrossRef]
- LSTC. LS-DYNA Keyword User’s Manual Ver. R11; Livermore Software Technology Corporation: Livermore, CA, USA, 2018. [Google Scholar]
- Hyde, D.W. ConWep: Conventional Weapons Effects (Application of TM 5-855-1); US Army Corps of Enigneers, Waterways Experiment Station: Vicksburg, MS, USA, 1992. [Google Scholar]
- DoD. Unified Facilities Criteria (UFC): Structures to Resist the Effects of Accidental Explosions (UFC 3-340-02); Departments of Defense: Washington, DC, USA, 2008. [Google Scholar]
- Dassault Systèmes. ABAQUS/CAE User’s Guide 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014. [Google Scholar]
- FEMA. Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings (FEMA-350); Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Shin, J.; Whittaker, A.S.; Cormie, D.; Wilkinson, W. Numerical modeling of close-in detonations of high explosives. Eng. Struct. 2014, 81, 88–97. [Google Scholar] [CrossRef]
- Erhart, T. Review of Solid Element Formulations in LS-DYNA; LS-DYNA Forum: Stuttgart, Germany, 2011. [Google Scholar]
- Ministry of Land, Infrastructure and Transport. Korean Building Code for Steel Structures (KDS 41 30 00: 2019); Ministry of Land, Infrastructure and Transport: Sejong Special Governing City, Korea, 2019. (In Korean) [Google Scholar]
- Murray, Y.D. Evaluation of LS-DYNA Concrete Material Model 159; Report No. FHWA-HRT-05-063; Federal Highway Administration: Washington, DC, USA, 2007.
- Murray, Y.D. User’s Manual for LS-DYNA Concrete Material Model 159; Report No. FHWA-HRT-05-062; Federal Highway Administration: Washington, DC, USA, 2007.
- Gyliene, V.; Ostasevicius, V. Cowper-Symonds material deformation law application in material cutting process using LS-DYNA FE code: Turning and milling. In Proceedings of the 8th European LS-DYNA Users’ Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Choung, J.; Im, S.-W.; Kim, K.S. Plasticity and fracture behaviors of marine structural steel, part V: Effects of strain rate and temperature. J. Ocean Eng. Technol. 2011, 25, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Comité Euro-International du Béton (CEB). CEB-FIP Model Code 1990: Design Code; T. Telford: London, UK, 1993. [Google Scholar]
- AISC. Seismic Provisions for Structural Steel Buildings (ANSI/AISC 341-16); American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]







| Improvised Explosive Device (IED) | Explosive Mass (kg) (TNT Equivalent) | Building Evacuation Distance (m) | Outdoor Evacuation Distance (m) |
|---|---|---|---|
| Pipe bomb | 2.3 | 21 | 259 |
| Suicide belt | 4.5 | 27 | 330 |
| Suicide vest | 9 | 34 | 415 |
| Briefcase/suitcase bomb | 23 | 46 | 564 |
| Compact sedan | 227 | 98 | 457 |
| Sedan | 454 | 122 | 534 |
| Passenger/cargo van | 1814 | 195 | 838 |
| Small moving van/delivery truck | 4536 | 263 | 1143 |
| Moving van/water truck | 13,608 | 375 | 1982 |
| Semitrailer | 27,216 | 475 | 2134 |
| Blast Scenario | W (kg) | R (m) | Target | Z (m/kg1/3) |
|---|---|---|---|---|
| 1 | 227 | 6 | Beam | 0.98 |
| 227 | 4 | Column | 0.66 | |
| 2 | 454 | 6 | Beam | 0.78 |
| 454 | 4 | Column | 0.52 | |
| 3 | 1814 | 6 | Beam | 0.49 |
| 1814 | 4 | Column | 0.33 | |
| 4 | 4536 | 6 | Beam | 0.36 |
| 4536 | 4 | Column | 0.24 | |
| 5 | 11,000 | 6 | Beam | 0.25 |
| 11,000 | 4 | Column | 0.18 |
| W (kg) | Max Deflection (mm) | End Rotation (Degrees) | Evaluation | Failure Mode at t = 20 ms | ||||
|---|---|---|---|---|---|---|---|---|
| Beam | Column | Beam | Column | Beam | Column | Beam | Column | |
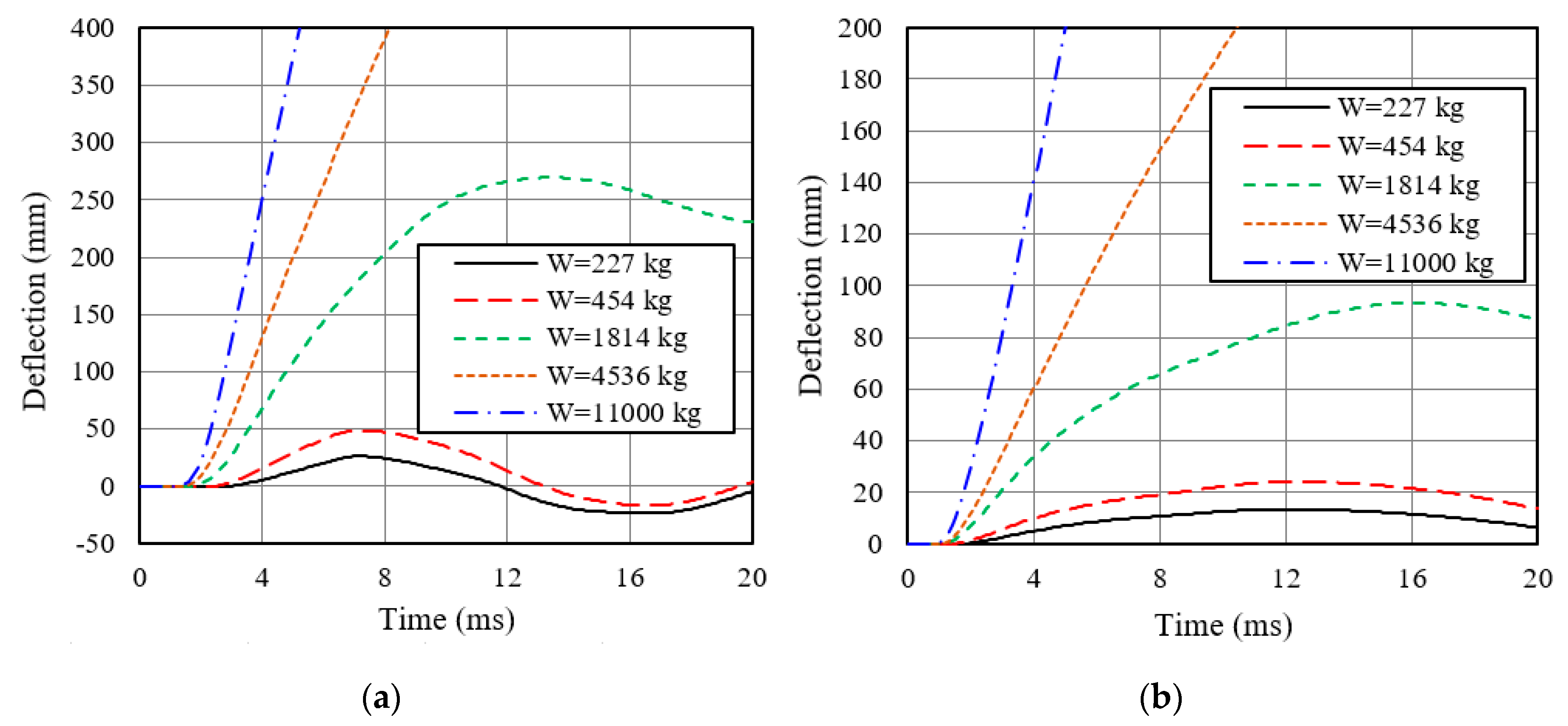
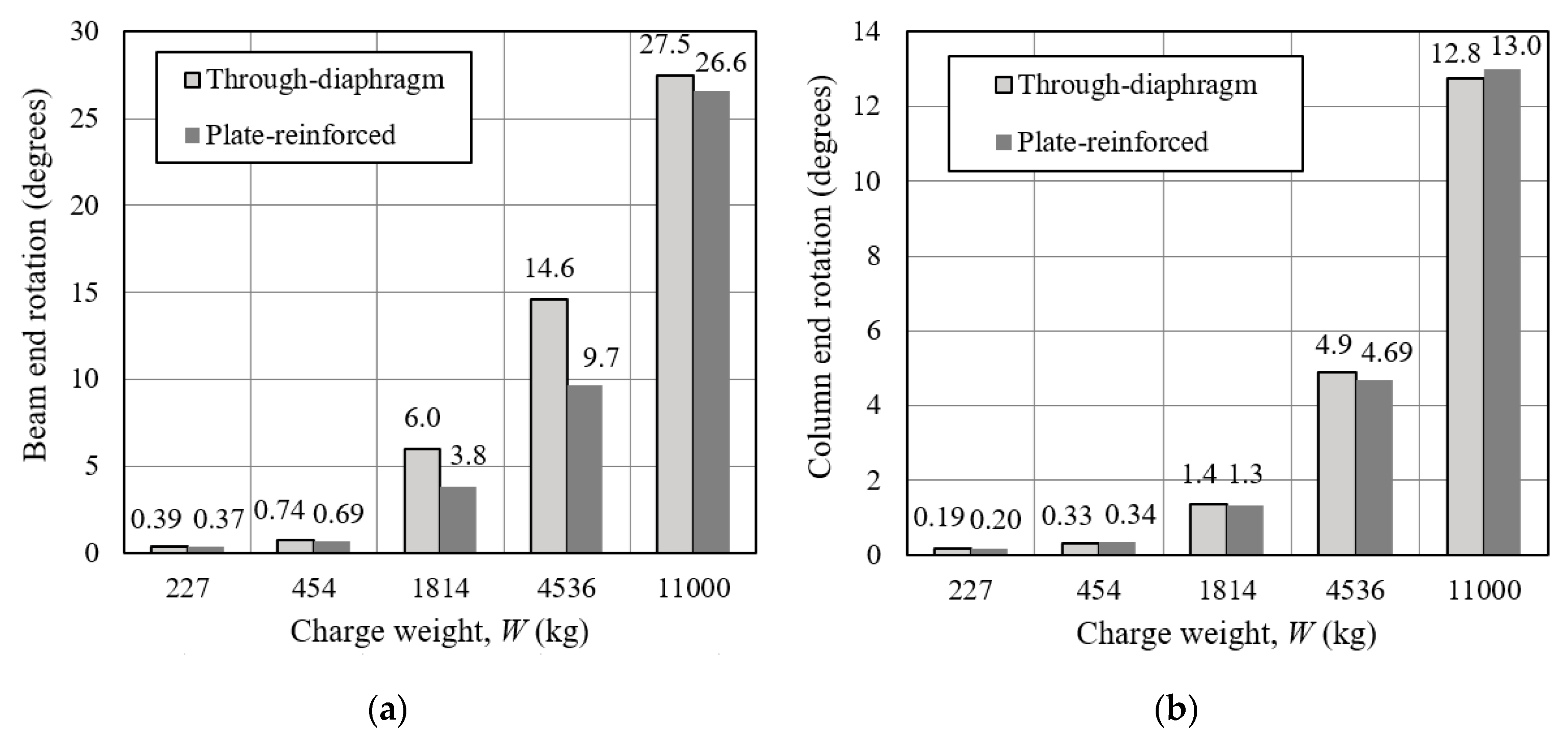
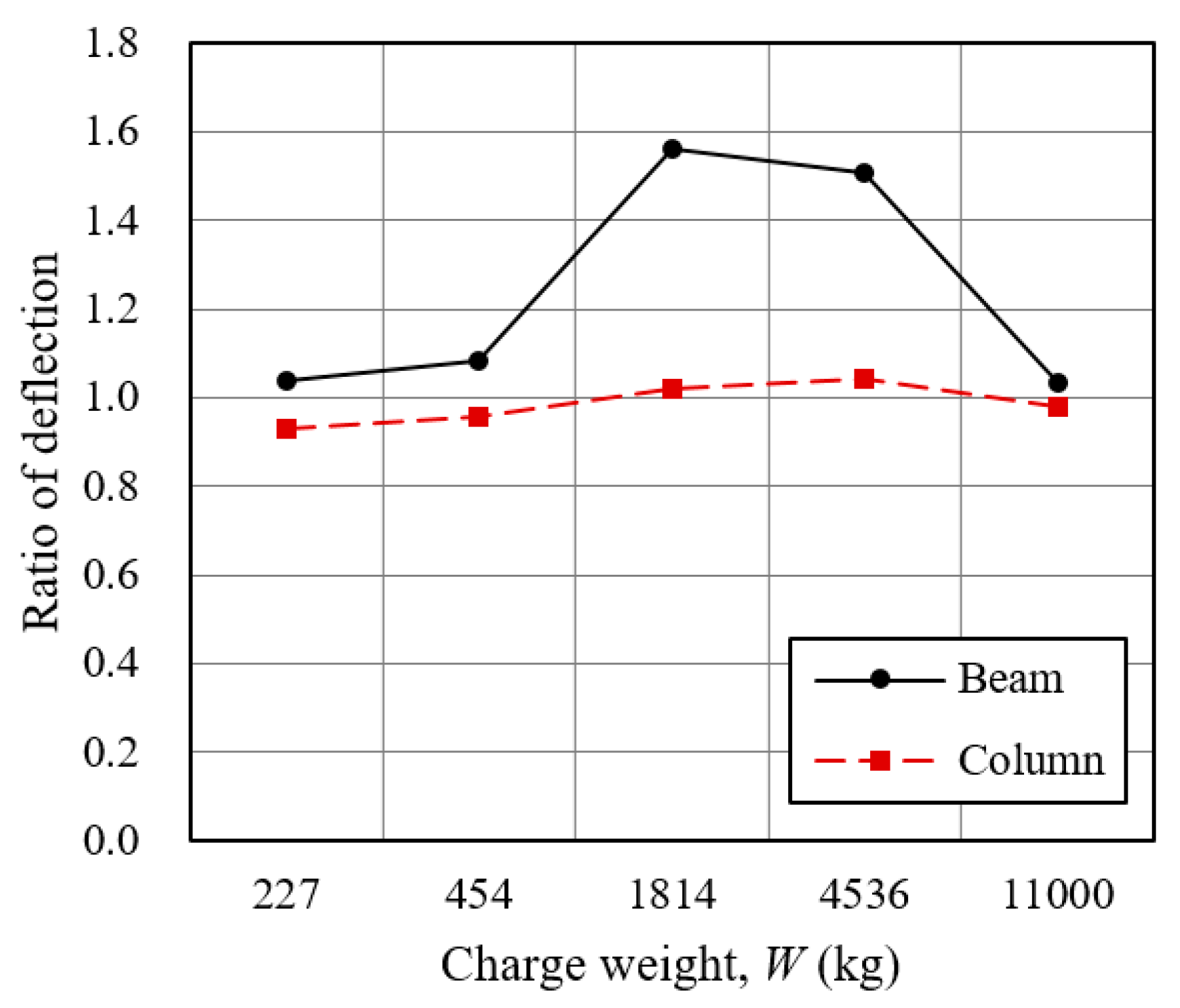
| 224 | 27 | 13 | 0.39 | 0.19 | A 1 | A | No damage | No damage |
| 454 | 52 | 23 | 0.74 | 0.33 | A | A | No damage | No damage |
| 1814 | 421 | 95 | 6.01 | 1.36 | NA 1 | A | Significant damage to beam near column face | Minor damage to concrete at bottom |
| 4536 | 1042 | 342 | 14.6 | 4.89 | NA | NA | Separation of beam from column | Entire damage to concrete |
| 11,000 | 2082 | 906 | 27.5 | 12.8 | NA | NA | Separation of beam from column | Entire damage to concrete |
| W (kg) | Max Deflection (mm) | End Rotation (Degrees) | Evaluation | Failure Mode at t = 20 ms | ||||
|---|---|---|---|---|---|---|---|---|
| Beam | Column | Beam | Column | Beam | Column | Beam | Column | |
| 224 | 26 | 14 | 0.37 | 0.20 | A 1 | A | No damage | No damage |
| 454 | 48 | 24 | 0.69 | 0.34 | A | A | No damage | No damage |
| 1814 | 269 | 93 | 3.85 | 1.33 | NA 1 | A | Minor damage to reinforcing plate | Minor damage to concrete near bottom and connection |
| 4536 | 682 | 328 | 9.68 | 4.69 | NA | NA | Significant damage to beam near column face | Entire damage to concrete |
| 11,000 | 2004 | 923 | 26.6 | 13.0 | NA | NA | Separation of beam from column | Entire damage to concrete |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, J.; Hwang, S.-H.; Kim, J. Numerical Investigation of Blast Performance of Plate-Reinforced Moment-Resisting Connection Using Large Concrete Filled Tubular Section. Appl. Sci. 2020, 10, 3700. https://doi.org/10.3390/app10113700
Shin J, Hwang S-H, Kim J. Numerical Investigation of Blast Performance of Plate-Reinforced Moment-Resisting Connection Using Large Concrete Filled Tubular Section. Applied Sciences. 2020; 10(11):3700. https://doi.org/10.3390/app10113700
Chicago/Turabian StyleShin, Jinwon, Seong-Hoon Hwang, and Jinkyu Kim. 2020. "Numerical Investigation of Blast Performance of Plate-Reinforced Moment-Resisting Connection Using Large Concrete Filled Tubular Section" Applied Sciences 10, no. 11: 3700. https://doi.org/10.3390/app10113700





