Effects of the Top Edge Impedance on Sound Barrier Diffraction
Abstract
:1. Introduction
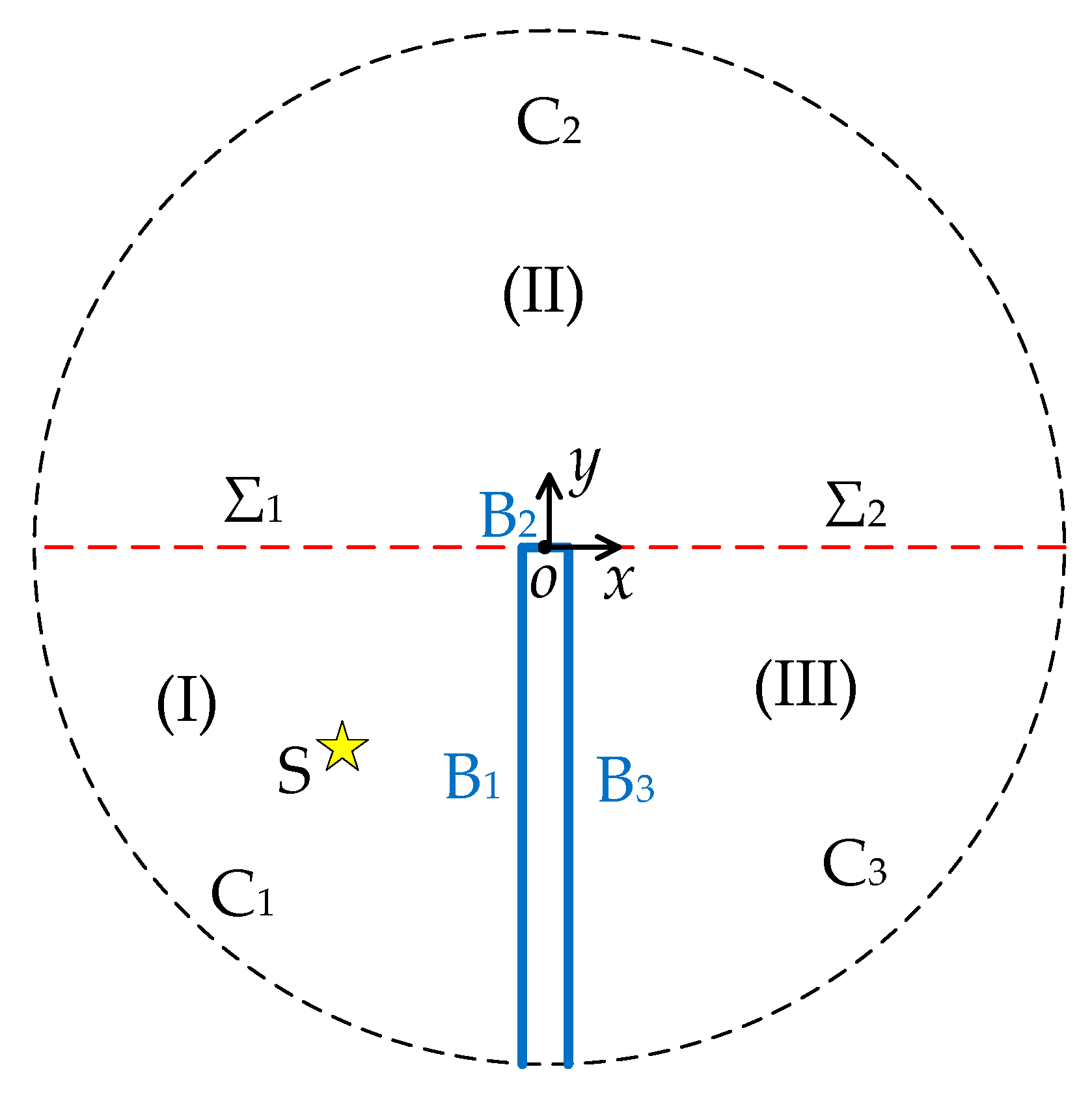
2. Theory
2.1. Theoretical Equation
2.2. Verification
3. The Effects of Top Edge Impedance on Sound Barrier Diffraction
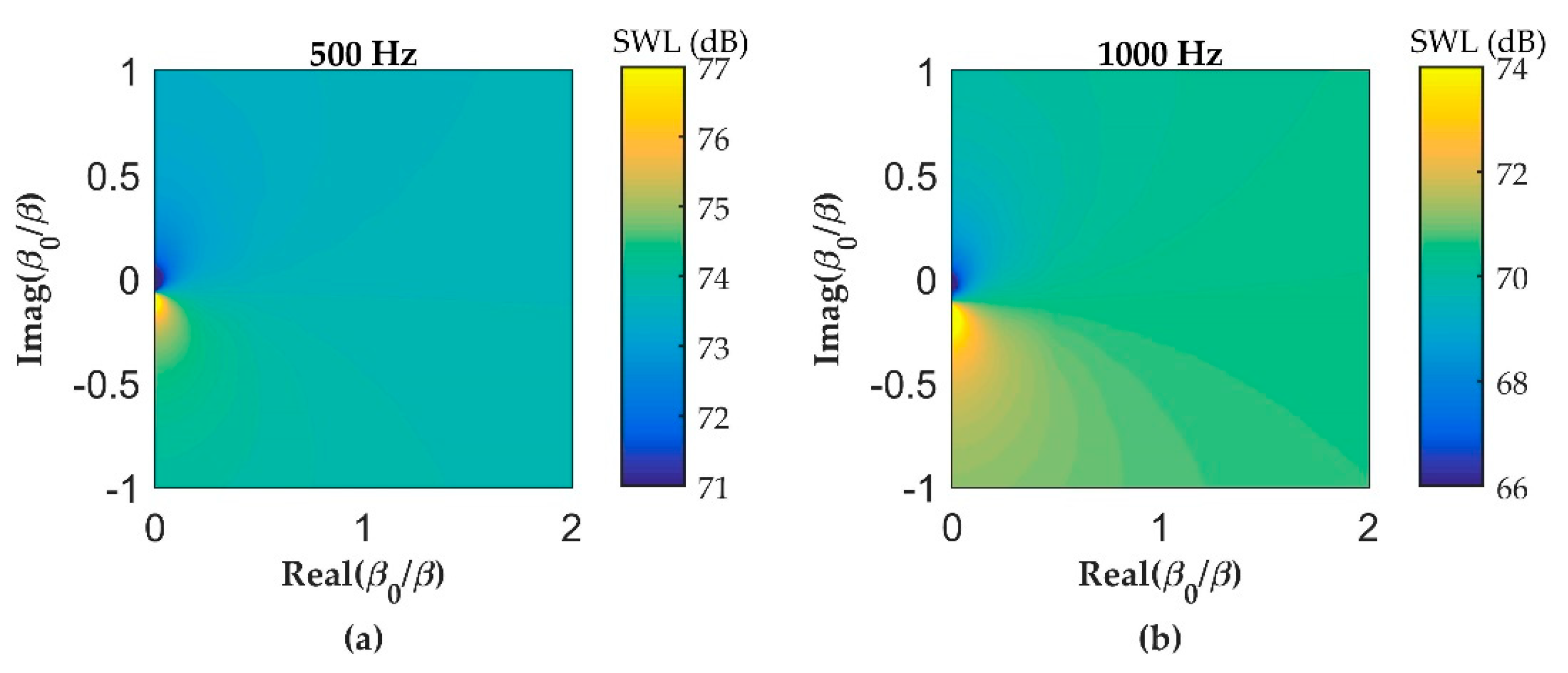
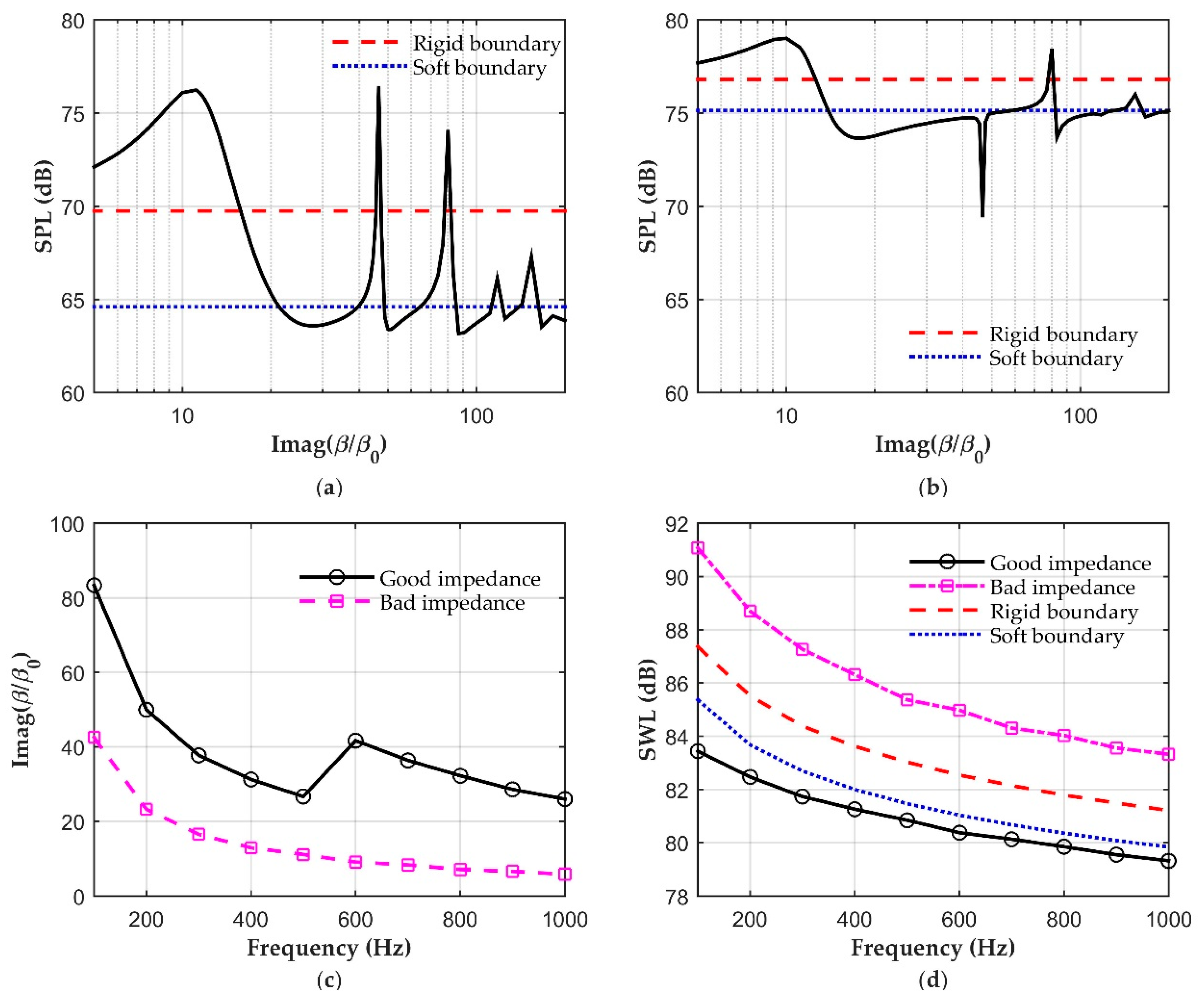
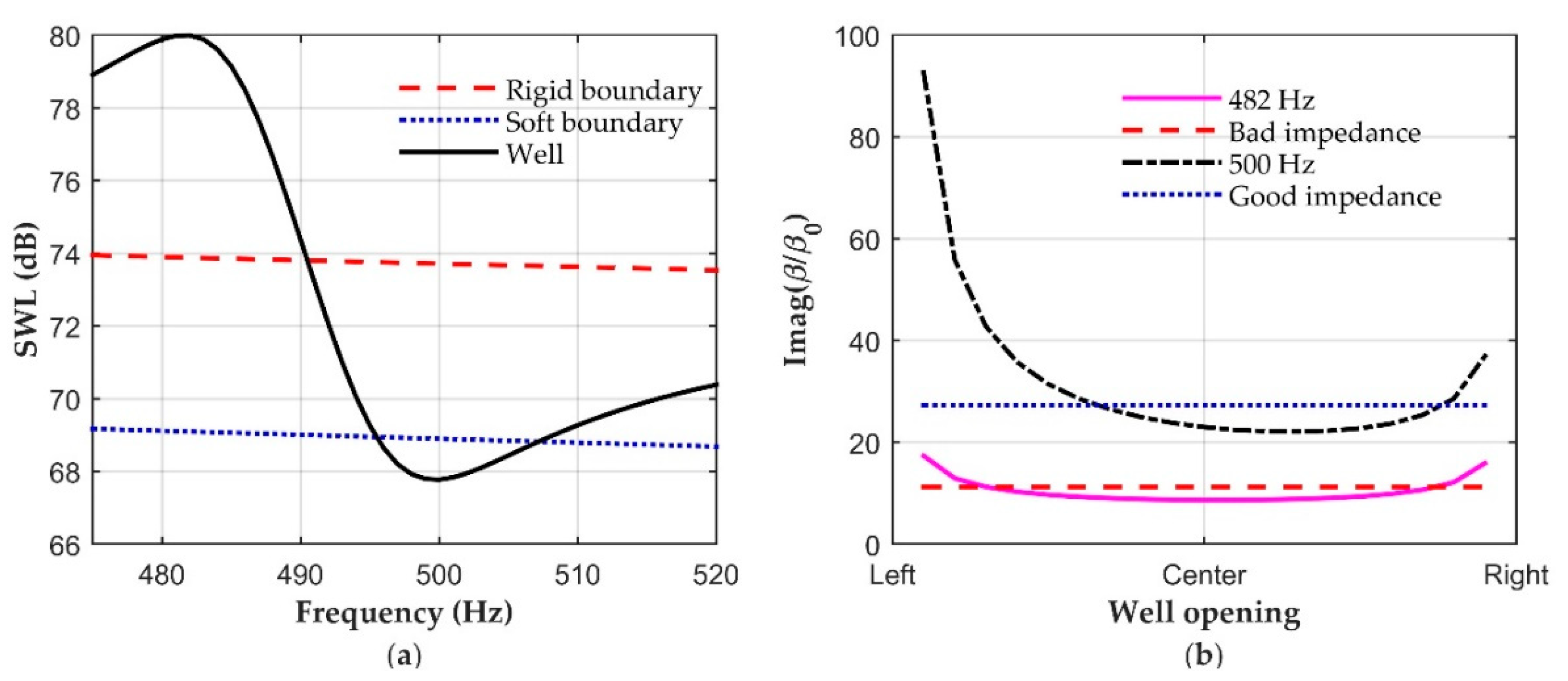
3.1. The Good and Bad Top Edge Impedance
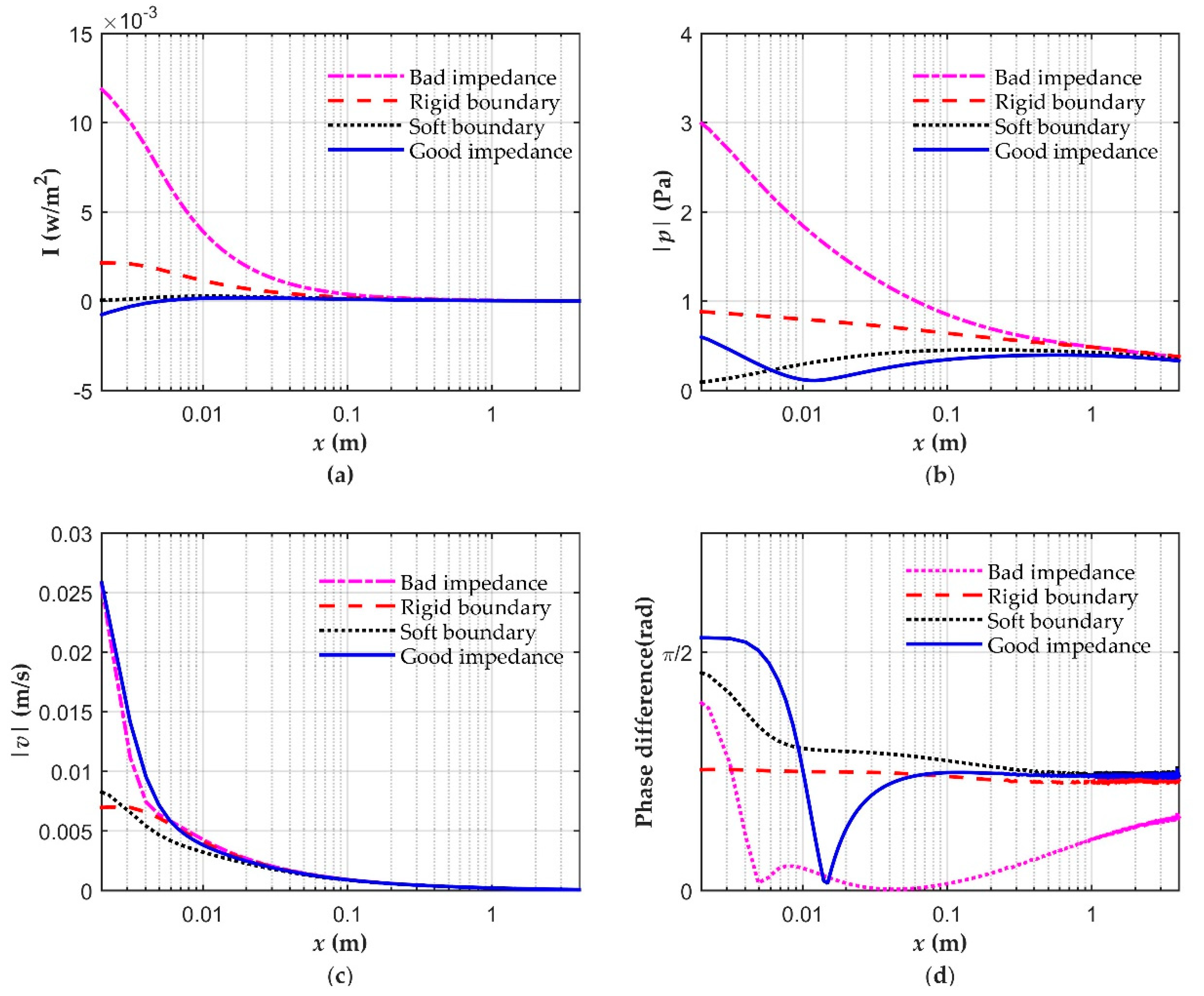
3.2. Mechanism Analysis
4. A Simple Example of Implementing the Good Top Edge Impedance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hayek, S.I. Mathematical-modeling of absorbent highway noise barriers. Appl. Acoust. 1990, 31, 77–100. [Google Scholar] [CrossRef]
- Morgan, P.A.; Hothersall, D.C.; Chandlerwilde, S.N. Influence of shape and absorbing surface—A numerical study of railway noise barriers. J. Sound Vib. 1998, 217, 405–417. [Google Scholar] [CrossRef]
- Tang, S.K. Noise screening effects of balconies on a building facade. J. Acoust. Soc. Am. 2005, 118, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Arenas, J.P. Potential problems with environmental sound barriers when used in mitigating surface transportation noise. Sci. Total Environ. 2008, 405, 173–179. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Kang, J. Combined acoustical and visual performance of noise barriers in mitigating the environmental impact of motorways. Sci. Total Environ. 2016, 543, 52–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aylor, D.E.; Marks, L.E. Perception of noise transmitted through barriers. J. Acoust. Soc. Am. 1976, 59, 397–400. [Google Scholar] [CrossRef]
- Joynt, J.L.R.; Kang, J. The influence of preconceptions on perceived sound reduction by environmental noise barriers. Sci. Total Environ. 2010, 408, 4368–4375. [Google Scholar] [CrossRef] [Green Version]
- Maffei, L.; Masullo, M.; Aletta, F.; Gabriele, M.D. The influence of visual characteristics of barriers on railway noise perception. Sci. Total Environ. 2013, 445–446, 41–47. [Google Scholar] [CrossRef]
- Ishizuka, T.; Fujiwara, K. Performance of noise barriers with various edge shapes and acoustical conditions. Appl. Acoust. 2004, 65, 125–141. [Google Scholar] [CrossRef]
- Watts, G.R.; Crombie, D.H.; Hothersall, D.C. Acoustic performance of new designs of traffic noise barriers: Full scale tests. J. Sound Vib. 1994, 177, 289–305. [Google Scholar] [CrossRef]
- Yang, C.; Pan, J.; Cheng, L. A mechanism study of sound wave-trapping barriers. J. Acoust. Soc. Am. 2013, 134, 1960–1969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Jiao, Y.; Chen, Z. Research on the well at the top edge of noise barrier. Appl. Acoust. 2018, 133, 118–122. [Google Scholar] [CrossRef]
- Fujiwara, K.; Furuta, N. Sound shielding efficiency of a barrier with a cylinder at the edge. Noise Control Eng. J. 1991, 37, 5. [Google Scholar] [CrossRef]
- Monazzam, M.R.; Lam, Y.W. Performance of profiled single noise barriers covered with quadratic residue diffusers. Appl. Acoust. 2005, 66, 709–730. [Google Scholar] [CrossRef] [Green Version]
- Naderzadeh, M.; Monazzam, M.R.; Nassiri, P.; Fard, S.M.B. Application of perforated sheets to improve the efficiency of reactive profiled noise barriers. Appl. Acoust. 2011, 72, 393–398. [Google Scholar] [CrossRef]
- Okubo, T.; Fujiwara, K. Efficiency of a noise barrier with an acoustically soft cylindrical edge for practical use. J. Acoust. Soc. Am. 1999, 105, 3326–3335. [Google Scholar] [CrossRef]
- Okubo, T.; Fujiwara, K. Efficiency of a noise barrier on the ground with an acoustically soft cylindrical edge. J. Sound Vib. 1998, 216, 771–790. [Google Scholar] [CrossRef]
- Baulac, M.; Defrance, J.; Jean, P. Optimisation with genetic algorithm of the acoustic performance of T-shaped noise barriers with a reactive top surface. Appl. Acoust. 2008, 69, 332–342. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, G.H. Optimal rigid and porous material distributions for noise barrier by acoustic topology optimization. J. Sound Vib. 2015, 339, 123–142. [Google Scholar] [CrossRef]
- Duhamel, D. Shape optimization of noise barriers using genetic algorithms. J. Sound Vib. 2006, 297, 432–443. [Google Scholar] [CrossRef]
- Fujiwara, K.; Hothersall, D.C.; Kim, C. Noise barriers with reactive surfaces. Appl. Acoust. 1998, 53, 255–272. [Google Scholar] [CrossRef]
- Li, K.M.; Wong, H.Y. A review of commonly used analytical and empirical formulae for predicting sound diffracted by a thin screen. Appl. Acoust. 2005, 66, 45–76. [Google Scholar] [CrossRef]
- MacDonald, H.M. A class of diffraction problems. Proc. London Math. Soc. 1915, 2, 410–427. [Google Scholar] [CrossRef] [Green Version]
- Hadden, W.J.; Pierce, A.D. Sound diffraction around screens and wedges for arbitrary point source locations. J. Acoust. Soc. Am. 1981, 69, 1266–1276. [Google Scholar] [CrossRef]
- Keller, J.B. Geometrical theory of diffraction. J. Opt. Soc. Am. 1962, 52, 116–130. [Google Scholar] [CrossRef] [PubMed]
- Seznec, R. Diffraction of sound around barriers: Use of the boundary elements technique. J. Sound Vib. 1980, 73, 195–209. [Google Scholar] [CrossRef]
- Piacentini, A.; Invernizzi, M.; Pannese, L. Computational acoustics: Noise reduction via diffraction by barriers with different geometries. Comput. Meth. Appl. Mech. Eng. 1996, 130, 81–91. [Google Scholar] [CrossRef]
- Chevret, P.; Chatillon, J. Implementation of diffraction in a ray-tracing model for the prediction of noise in open-plan offices. J. Acoust. Soc. Am. 2012, 132, 3125–3137. [Google Scholar] [CrossRef]
- Treeby, B.E.; Pan, J. A practical examination of the errors arising in the direct collocation boundary element method for acoustic scattering. Eng. Anal. Bound. Elem. 2009, 33, 1302–1315. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Qiu, X.; Cheng, J. An integral equation method for calculating sound field diffracted by a rigid barrier on an impedance ground. J. Acoust. Soc. Am. 2015, 138, 1608–1613. [Google Scholar] [CrossRef]
- Cheng, J. The Principle of Acoustics, Chinese ed; Science Press: Beijing, China, 2012. [Google Scholar]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Berkhoff, A.P. Control strategies for active noise barriers using near-field error sensing. J. Acoust. Soc. Am. 2005, 118, 1469–1479. [Google Scholar] [CrossRef]
- Zhu, H.; Rajamani, R.; Stelson, K.A. Active control of acoustic reflection, absorption, and transmission using thin panel speakers. J. Acoust. Soc. Am. 2003, 113, 852–870. [Google Scholar] [CrossRef] [PubMed] [Green Version]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Zou, H.; Qiu, X. Effects of the Top Edge Impedance on Sound Barrier Diffraction. Appl. Sci. 2020, 10, 6042. https://doi.org/10.3390/app10176042
Huang X, Zou H, Qiu X. Effects of the Top Edge Impedance on Sound Barrier Diffraction. Applied Sciences. 2020; 10(17):6042. https://doi.org/10.3390/app10176042
Chicago/Turabian StyleHuang, Xiaofan, Haishan Zou, and Xiaojun Qiu. 2020. "Effects of the Top Edge Impedance on Sound Barrier Diffraction" Applied Sciences 10, no. 17: 6042. https://doi.org/10.3390/app10176042



