Nonlinear System Identification of an All Movable Fin with Rotational Freeplay by Subspace-Based Method
Abstract
:1. Introduction
2. Nonlinear Subspace Identification of Mechanical Systems
2.1. State-Space Nonlinear Feedback Description
2.2. Subspace System Identification
2.3. Estimation of Underlying Linear System and Nonlinear Coefficients
3. Modeling of an All Movable Fin with Rotational Freeplay
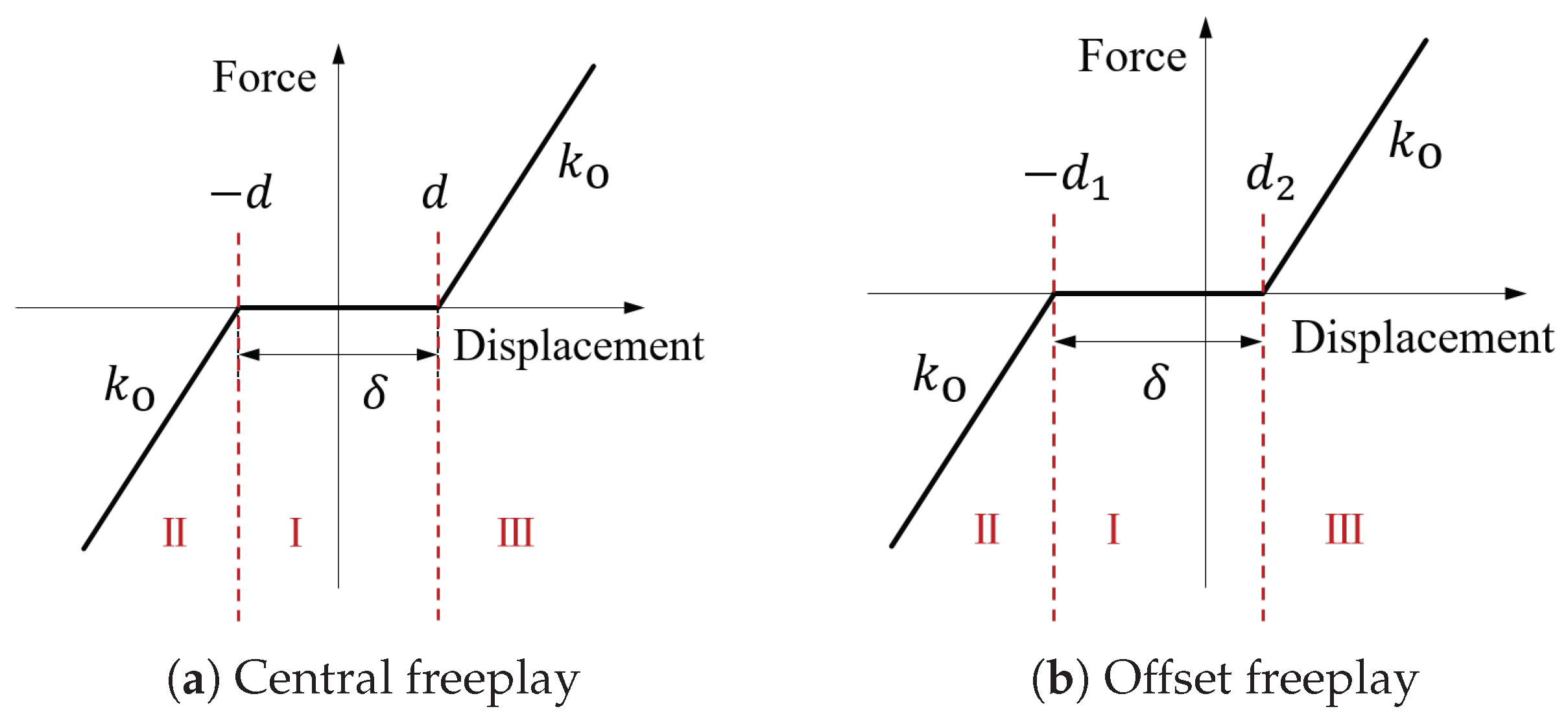
3.1. Freeplay Nonlinearity
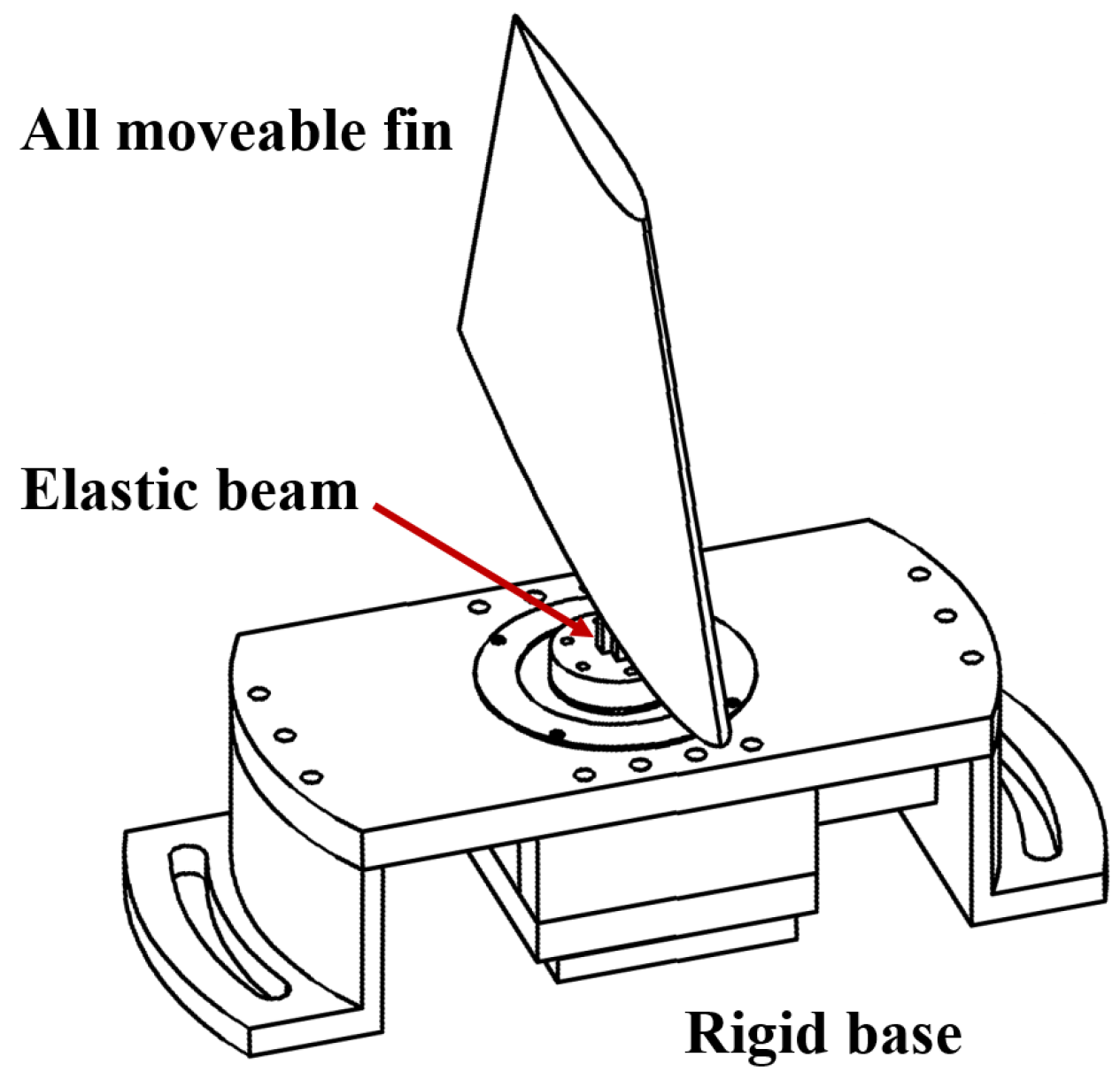
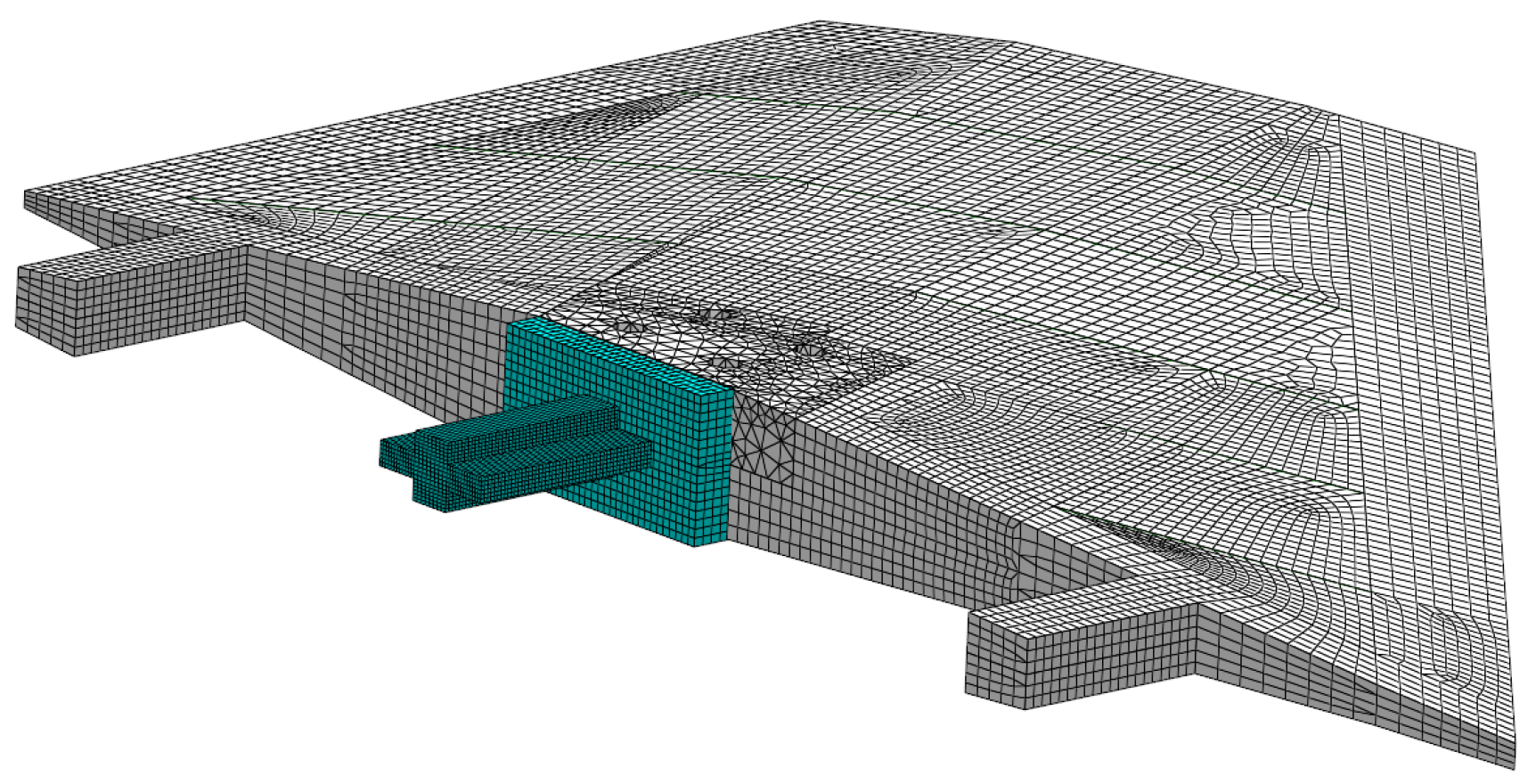
3.2. Description of the All Movable Fin
4. Nonlinear Identification Based on Random Excitation
4.1. Identification of Central Freeplay
4.2. Identification of Offset Freeplay
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CRP | Conditioned reverse path |
| CVA | Canonical variate analysis |
| DOF | Degree of freedom |
| FRF | Frequency response function |
| MDOF | Multi-degree-of-freedom |
| MIMO | Multi-input, multi-output |
| MOESP | Multivariable output error state space |
| NARMAX | Nonlinear autoregressive moving average with exogeneous inputs |
| NIFO | Nonlinear identification through feedback of the output |
| N4SID | Numerical algorithms for subspace state space system identification |
| OLS | Overlying linear system |
| RP | Reverse path |
| SDOF | Single-degree-of-freedom |
| TNSI | Time-domain nonlinear subspace identification |
| ULS | Underlying linear system |
References
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Deshpande, N.; Fofana, M.S. Nonlinear regenerative chatter in turning. Robot. Comput.-Integr. Manuf. 2001, 17, 107–112. [Google Scholar] [CrossRef]
- Fofana, M.S. Sufficient conditions for the stability of single and multiple regenerative chatter. Chaos Solitons Fractals 2002, 14, 335–347. [Google Scholar] [CrossRef]
- Fofana, M.S. Delay dynamical systems and applications to nonlinear machine-tool chatter. Chaos Solitons Fractals 2003, 17, 731–747. [Google Scholar] [CrossRef]
- Urbikain, G.; López de Lacalle, L.N.; Campa, F.J.; Fernández, A.; Elías, A. Stability prediction in straight turning of a flexible workpiece by collocation method. Int. J. Mach. Tools Manuf. 2012, 54–55, 73–81. [Google Scholar] [CrossRef]
- Urbikain, G.; López de Lacalle, L.N.; Fernández, A. Regenerative vibration avoidance due to tool tangential dynamics in interrupted turning operations. J. Sound Vib. 2014, 333, 3996–4006. [Google Scholar] [CrossRef]
- Urbikain, G.; Campa, F.J.; Zulaika, J.J.; López de Lacalle, L.N.; Alonso, M.A.; Collado, V. Preventing chatter vibrations in heavy-duty turning operations in large horizontal lathes. J. Sound Vib. 2015, 340, 317–330. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; de Lacalle, L.L.; Elías-Zuñiga, A. Spindle speed variation technique in turning operations: Modeling and real implementation. J. Sound Vib. 2016, 383, 384–396. [Google Scholar] [CrossRef]
- Urbikain, G.; Olvera, D.; López de Lacalle, L.N.; Beranoagirre, A.; Elías-Zuñiga, A. Prediction Methods and Experimental Techniques for Chatter Avoidance in Turning Systems: A Review. Appl. Sci. 2019, 9, 4718. [Google Scholar] [CrossRef] [Green Version]
- Tian, W.; Yang, Z.C.; Zhao, T. Analysis of nonlinear vibrations and dynamic responses in a trapezoidal cantilever plate using the Rayleigh-Ritz approach combined with the affine transformation. Math. Probl. Eng. 2019, 1, 1–23. [Google Scholar] [CrossRef]
- Masri, S.F.; Caughey, T.K. A nonparametric identification technique for nonlinear dynamic problems. J. Appl. Mech. 1979, 46, 433–447. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for nonlinear systems, part I: Deterministic nonlinear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for nonlinear systems, part II: Stochastic nonlinear systems. Int. J. Control 1985, 41, 329–344. [Google Scholar] [CrossRef]
- Feldman, M. Nonlinear system vibration analysis using the Hilbert transform—I. Free vibration analysis method ‘FREEVIB’. Mech. Syst. Signal Process. 1994, 8, 119–127. [Google Scholar] [CrossRef]
- Feldman, M. Nonlinear system vibration analysis using the Hilbert transform—II. Forced vibration analysis method ‘FORCEVIB’. Mech. Syst. Signal Process. 1994, 8, 309–318. [Google Scholar] [CrossRef]
- Khan, A.A.; Vyas, N.S. Non-linear parameter using Volterra and Wiener theories. J. Sound Vib. 1999, 221, 805–821. [Google Scholar] [CrossRef]
- Noël, J.P.; Kerschen, G. Nonlinear system identification in structural dynamics: 10 more years of progress. Mech. Syst. Signal Process. 2017, 83, 2–35. [Google Scholar] [CrossRef]
- Narendra, K.S.; Gallman, P.G. An iterative method for the identification of nonlinear systems using a Hammerstein model. Autom. Control 1966, 11, 546–550. [Google Scholar] [CrossRef]
- Chang, F.H.I.; Luus, R. A noniterative method for identification using Hammerstein model. Autom. Control 1971, 16, 464–468. [Google Scholar] [CrossRef]
- Billings, S.A.; Fakhouri, S.Y. Non-linear system identification using the Hammerstein model. J. Syst. Sci. 1979, 10, 567–578. [Google Scholar] [CrossRef]
- Zhu, Y. Estimation of an N–L–N Hammerstein–Wiener model. Automatica 2002, 38, 1607–1614. [Google Scholar] [CrossRef]
- Crama, P.; Schoukens, J. Initial estimates of Wiener and Hammerstein Systems using multisine excitation. Instrum. Meas. 2001, 50, 1791–1795. [Google Scholar] [CrossRef]
- Bendat, J.S. Spectral techniques for nonlinear systems analysis and identification. Shock Vib. 1993, 1, 21–31. [Google Scholar] [CrossRef]
- Rice, H.J.; Fitzpatrick, J.A. A procedure for the identification of linear and nonlinear multi-degree-of freedom systems. J. Sound Vib. 1991, 149, 397–411. [Google Scholar] [CrossRef]
- Richards, C.M.; Singh, R. Identification of multi-degree-of-freedom nonlinear systems under random excitation by the “reverse path” spectral method. J. Sound Vib. 1998, 213, 673–708. [Google Scholar] [CrossRef]
- Adams, D.E.; Allemang, R.J. A frequency domain method for estimating the parameters of a nonlinear structural dynamic model through feedback. Mech. Syst. Signal Process. 2000, 14, 637–656. [Google Scholar] [CrossRef]
- Marchesiello, S.; Garibaldi, L. A time domain approach for identifying nonlinear vibration structures by subspace methods. Mech. Syst. Signal Process. 2008, 22, 81–101. [Google Scholar] [CrossRef]
- Noël, J.P.; Kerschen, G. Frequency-domain subspace identification for nonlinear mechanical systems. Mech. Syst. Signal Process. 2013, 40, 701–717. [Google Scholar] [CrossRef]
- Noël, J.P.; Marchesiello, S.; Kerschen, G. Subspace-based identification of a nonlinear spacecraft in the time and frequency domains. Mech. Syst. Signal Process. 2014, 43, 217–236. [Google Scholar] [CrossRef]
- Wu, Z.G.; Yang, N.; Yang, C. Identification of nonlinear multi-degree-of freedom structures based on Hilbert transformation. Sci. China-Phys. Mech. Astron. 2014, 57, 1725–1736. [Google Scholar] [CrossRef]
- Wu, Z.G.; Yang, N.; Yang, C. Identification of nonlinear structures by the conditioned reverse path method. J. Aircr. 2015, 52, 373–386. [Google Scholar] [CrossRef]
- Marchesiello, S.; Garibaldi, L. Identification of clearance-type nonlinearities. Mech. Syst. Signal Process. 2008, 22, 1133–1145. [Google Scholar] [CrossRef]
- Overschee, P.V.; Moor, B.D. Subspace Identification for Linear Systems: Theory-Implementation-Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; pp. 96–97. [Google Scholar]
- Overschee, P.V.; Moor, B.D. N4SID: Numerical algorithms for state space subspace system identification. In Proceedings of the World Congress of the International Federation of Automatic Control, IFAC, Sydney, Australia, 1 July 1993; pp. 361–364. [Google Scholar]
- Verhaegen, M. Identification of the deterministic part of MIMO state space models given in innovations form from input-output data. Automatica 1994, 30, 61–74. [Google Scholar] [CrossRef]
- Larimore, W.E. Canonical variate analysis in identification, filtering and adaptive control. In Proceedings of the 29th Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 596–604. [Google Scholar]
- Dimitriadis, G. Introduction to Nonlinear Aeroelasticity; John Wiley & Sons, Inc.: Chichester, UK; West Sussex, UK, 2017; pp. 264–266. [Google Scholar]
- MSC Nastran User’s Manual. Getting Started with MSC Nastran User’s Guide; MSC Software Co.: Santa Ana, CA, USA, 2012. [Google Scholar]
- Dynamic Design Solutions NV. Getting Started with FEMtools Version 3.7.1; Dynamic Design Solutions NV: Leuven, Belgium, 2014. [Google Scholar]


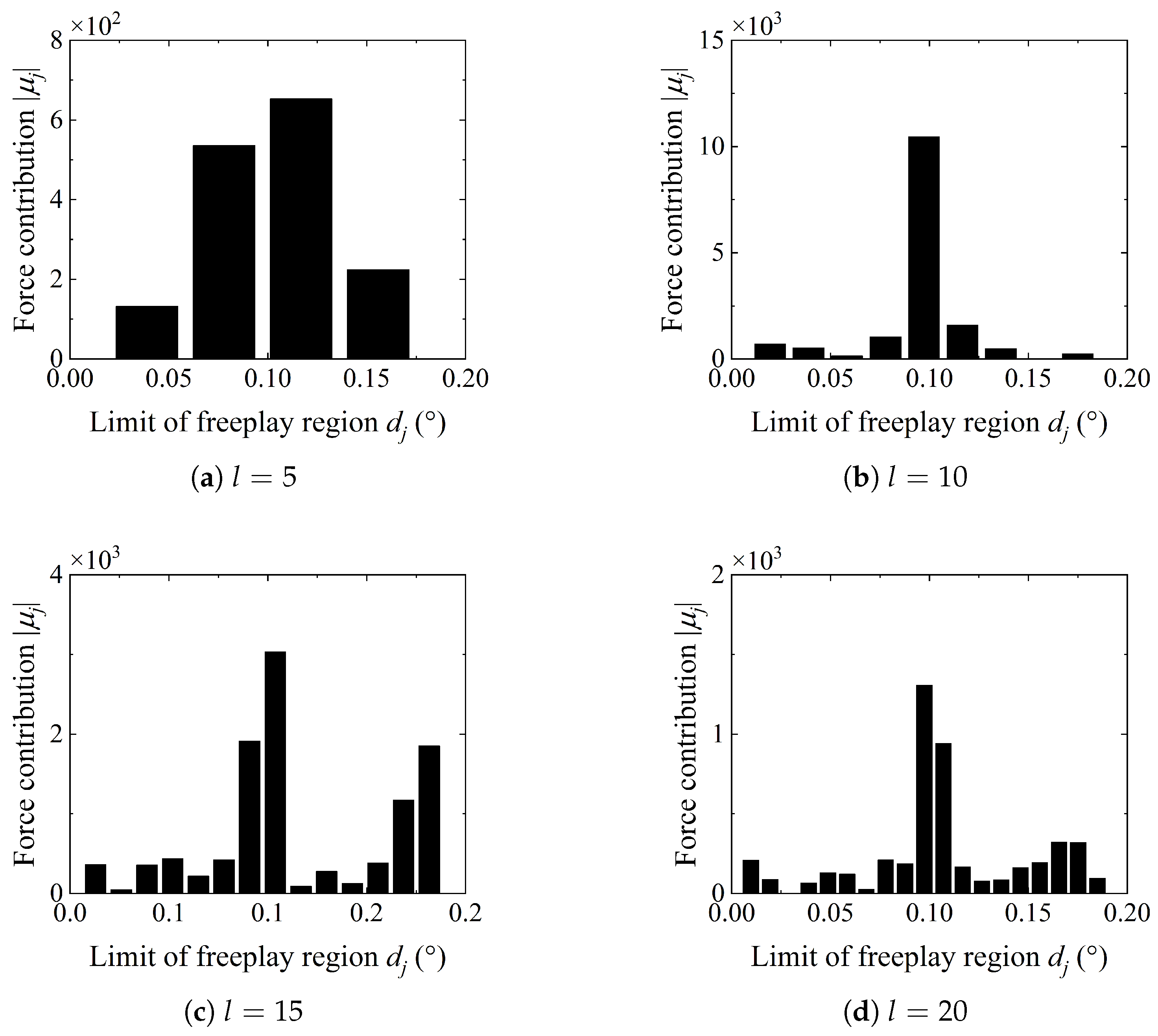
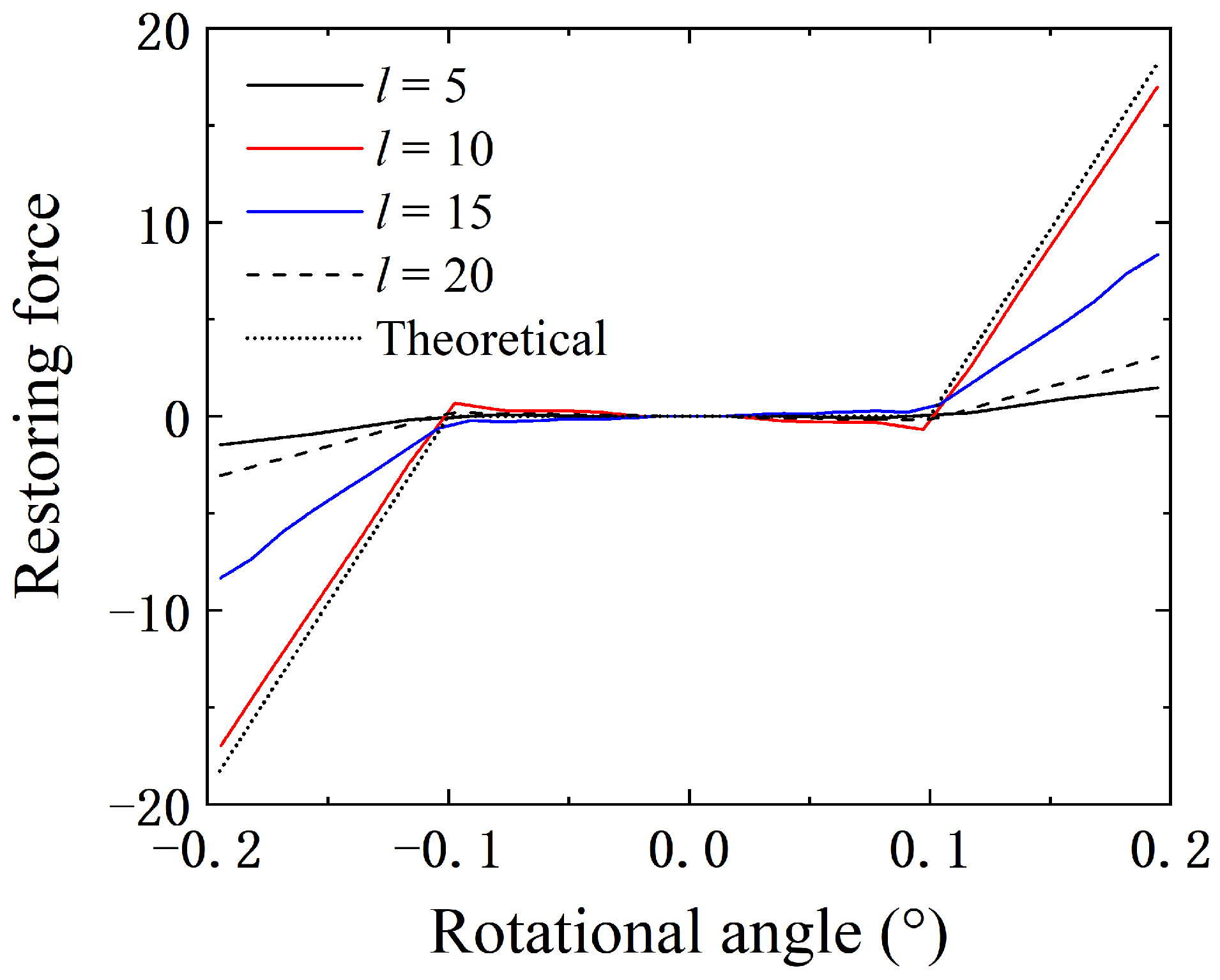
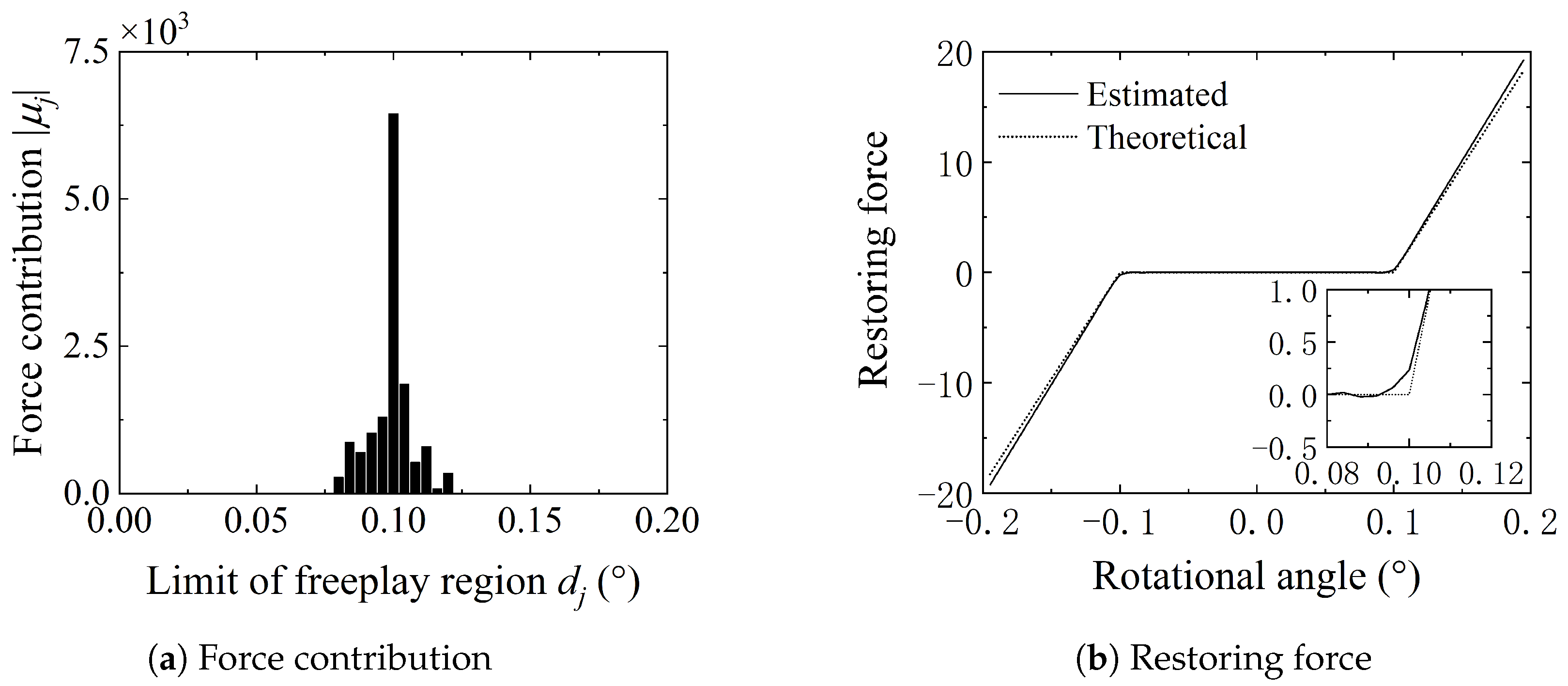
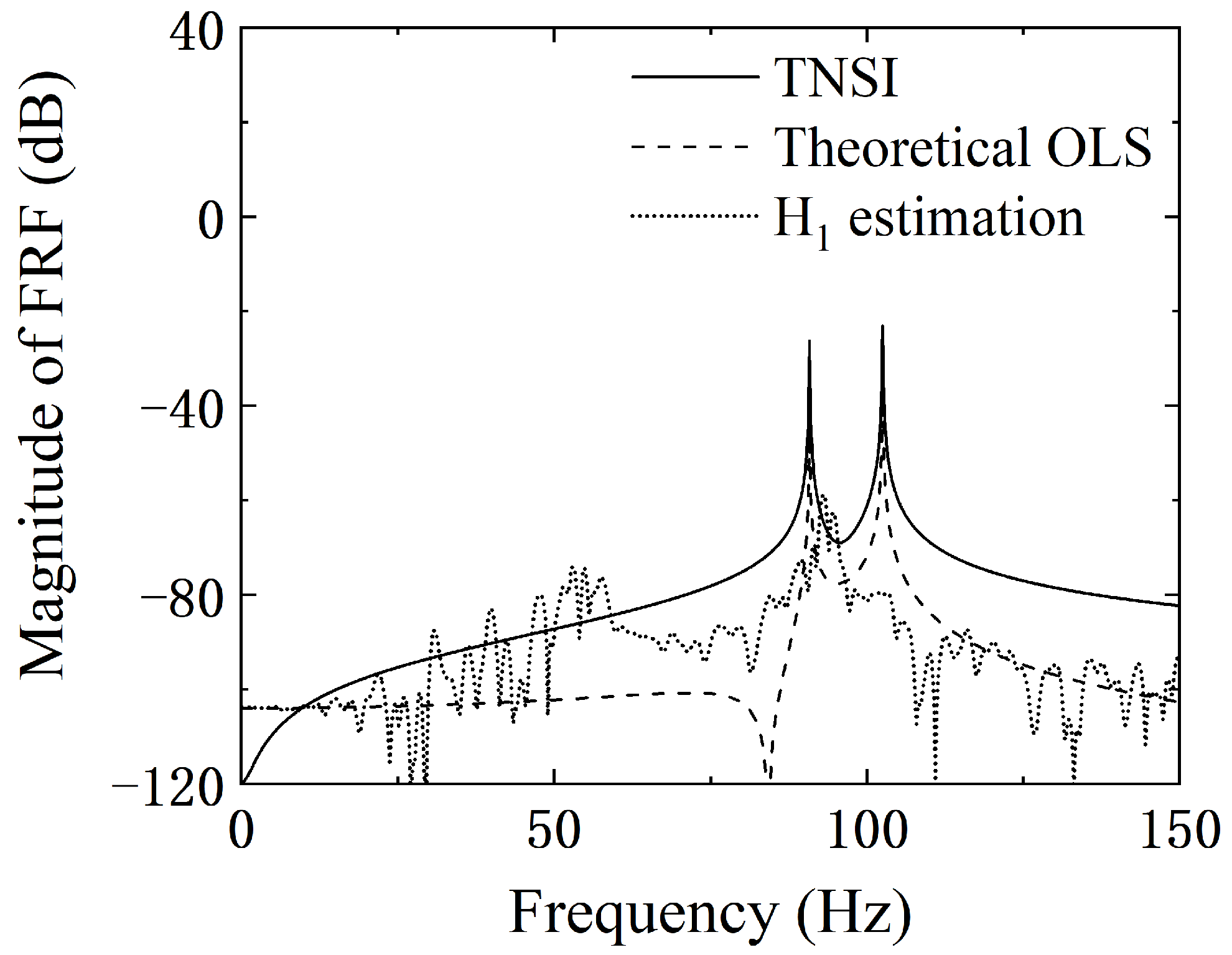
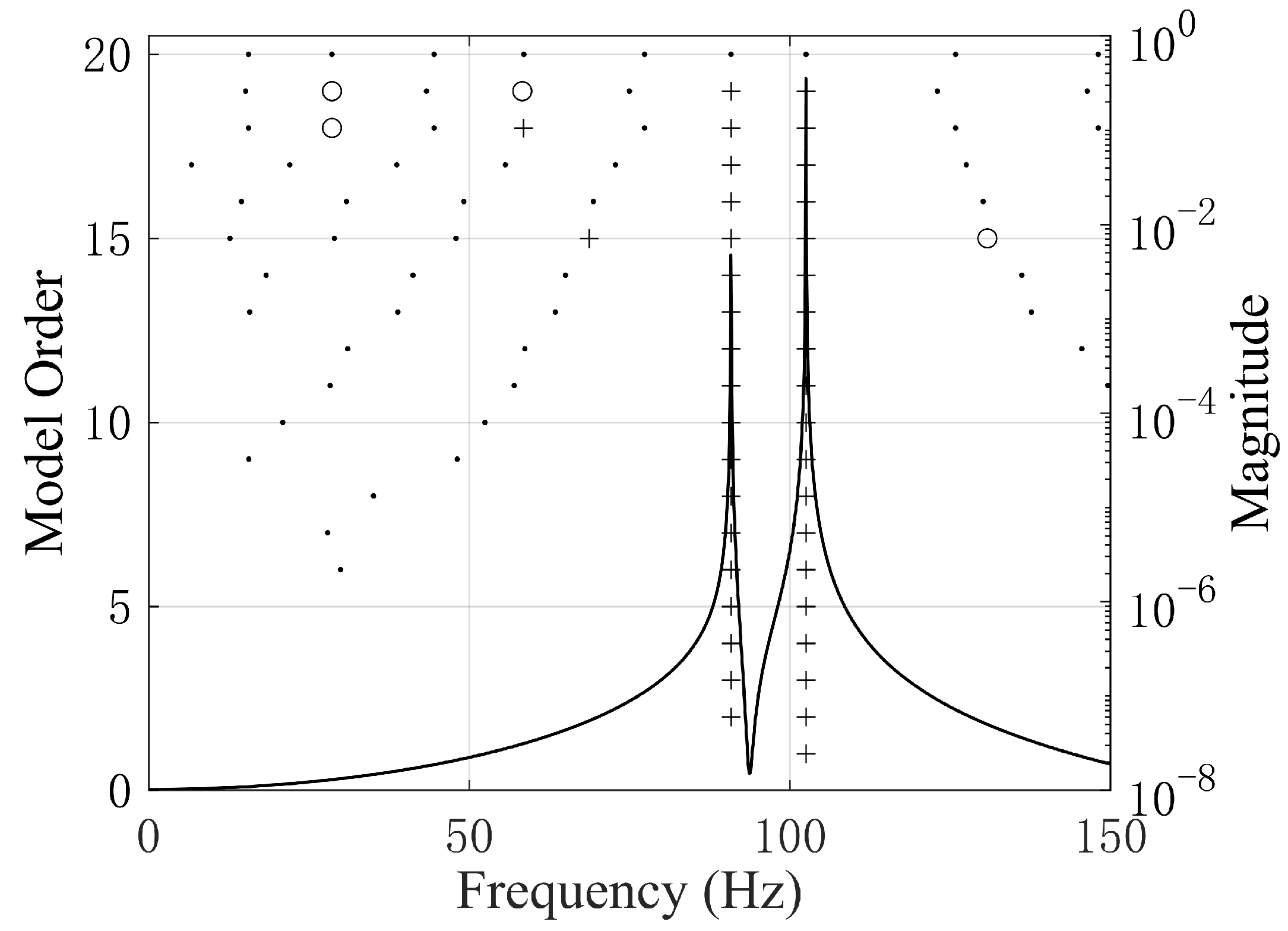
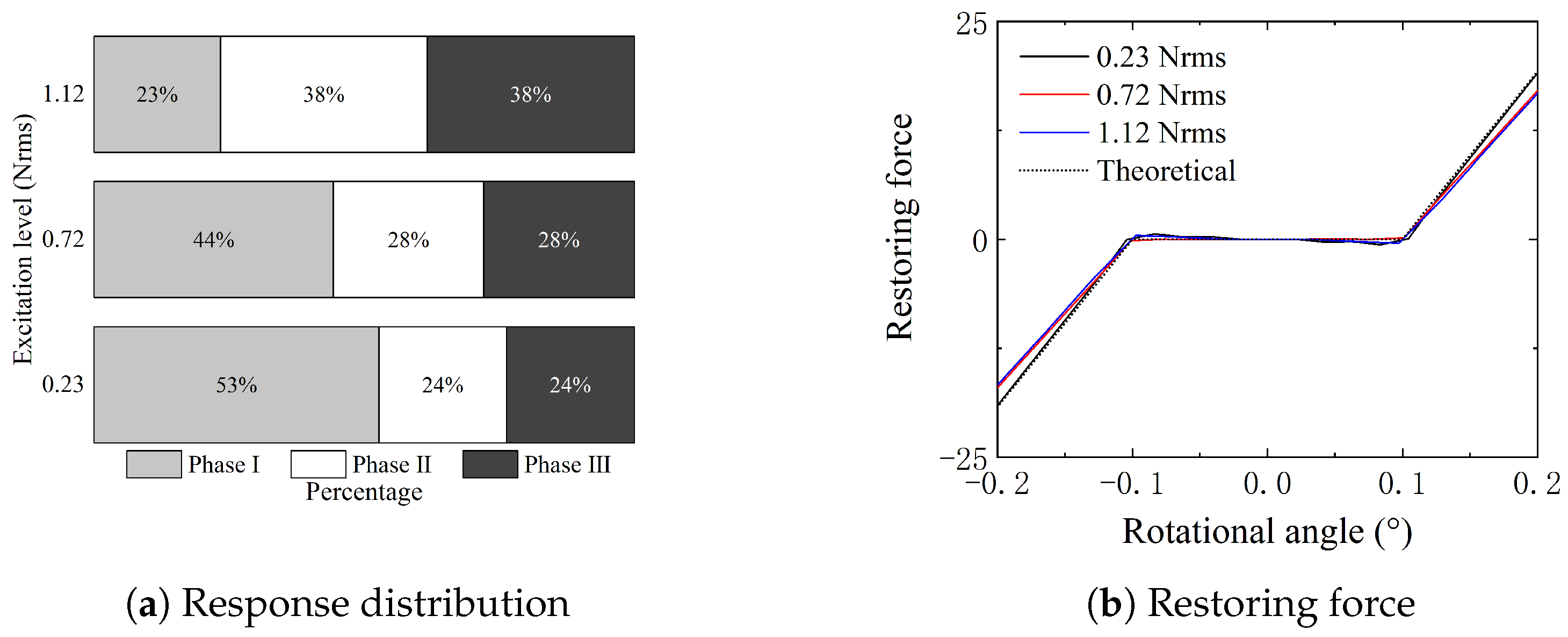

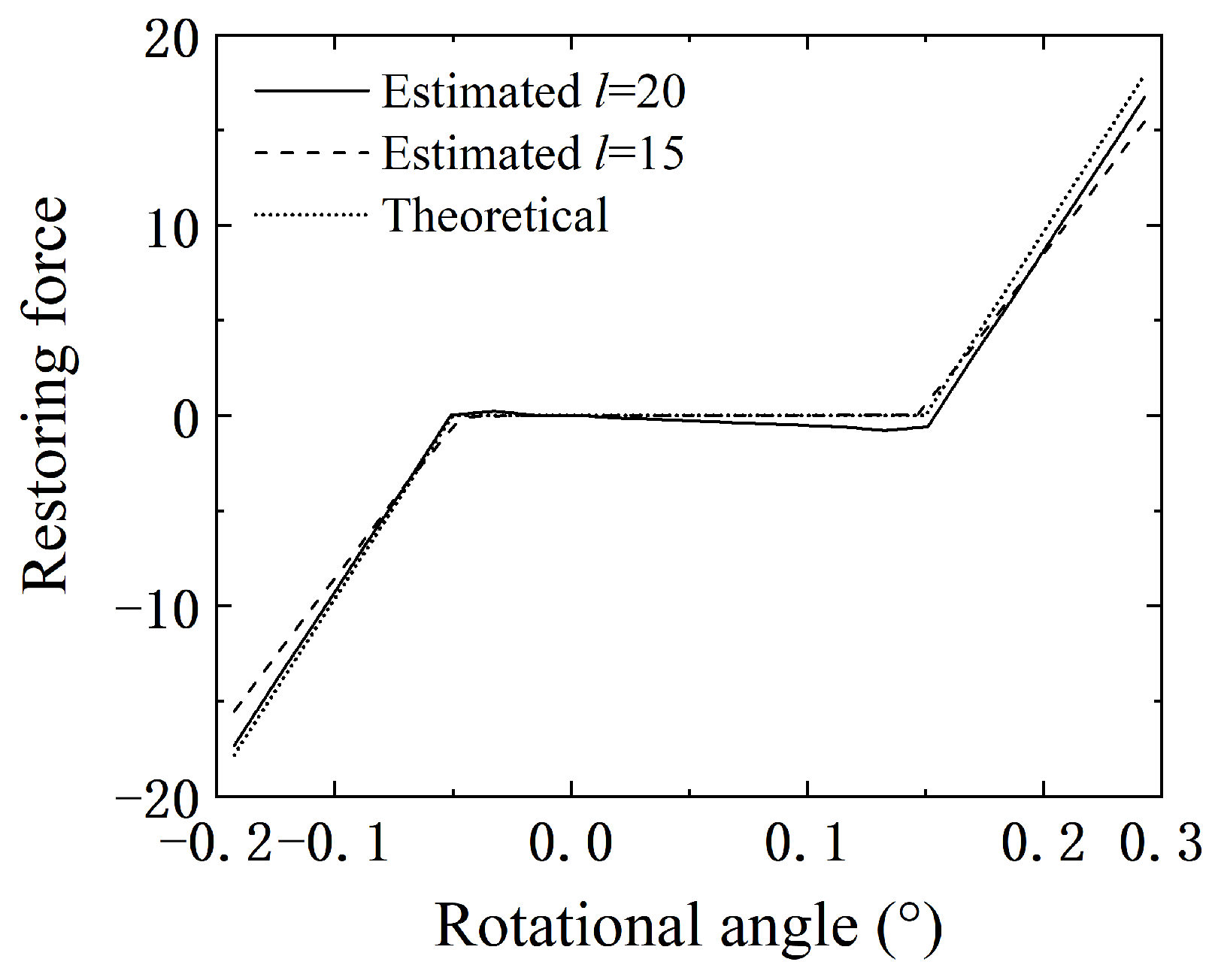

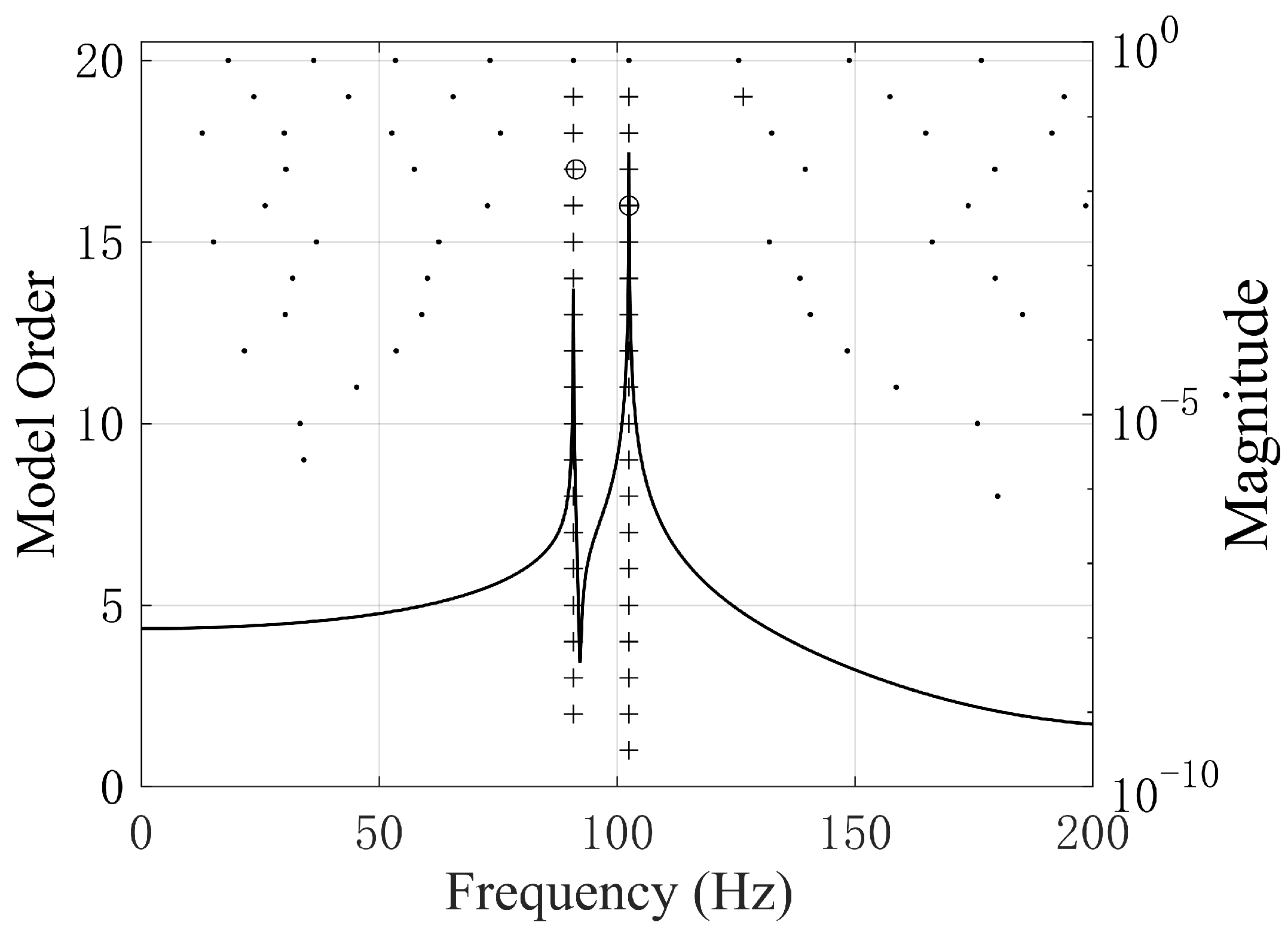
| Mode | Natural Frequency (Hz) | Damping Ratio (%) | Description |
|---|---|---|---|
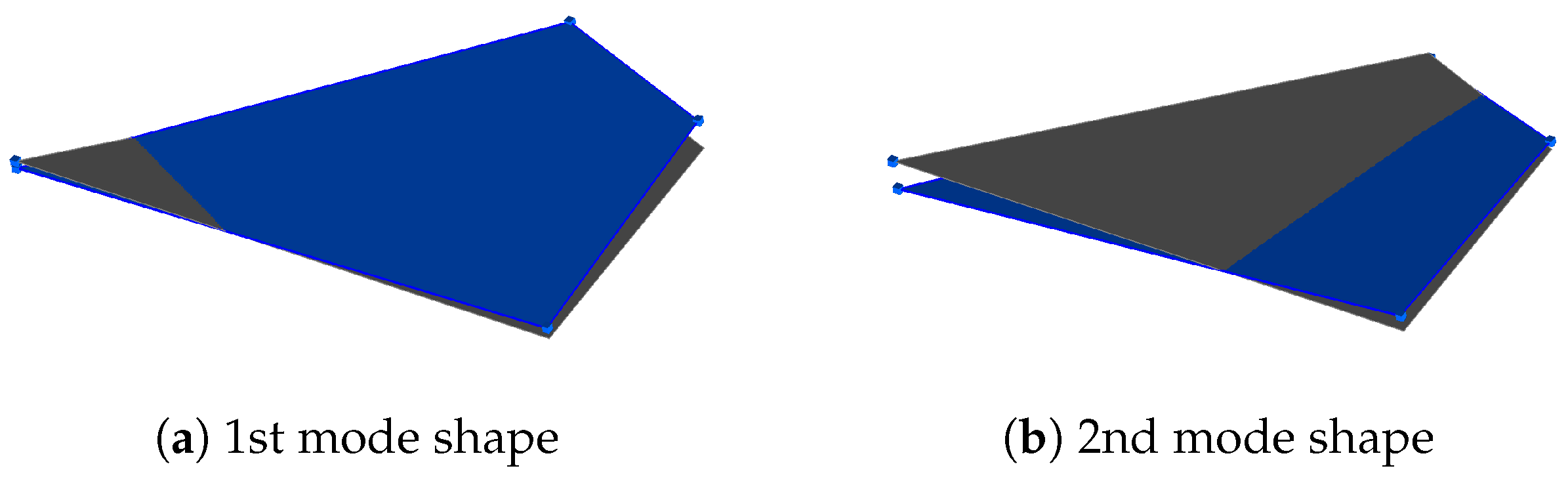
| 1 | 90.6 | 0.72 | Rigid fin bending mode |
| 2 | 102.1 | 0.56 | Rigid fin rotating mode |
| Type | Parameters | Value |
|---|---|---|
| Central freeplay | d | |
| Offset freeplay | ||
| Mode | Natural Frequency (Hz) | Identified Natural Frequency (Hz) | Errors (%) | |
|---|---|---|---|---|
| FE Model | Central Freeplay | Offset Freeplay | ||
| 1 | 90.6 | 90.8 | 90.8 | 0.22 |
| 2 | 102.1 | 102.5 | 102.5 | 0.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yukai, S.; Chao, Y.; Zhigang, W.; Liuyue, B. Nonlinear System Identification of an All Movable Fin with Rotational Freeplay by Subspace-Based Method. Appl. Sci. 2020, 10, 1205. https://doi.org/10.3390/app10041205
Yukai S, Chao Y, Zhigang W, Liuyue B. Nonlinear System Identification of an All Movable Fin with Rotational Freeplay by Subspace-Based Method. Applied Sciences. 2020; 10(4):1205. https://doi.org/10.3390/app10041205
Chicago/Turabian StyleYukai, Sun, Yang Chao, Wu Zhigang, and Bai Liuyue. 2020. "Nonlinear System Identification of an All Movable Fin with Rotational Freeplay by Subspace-Based Method" Applied Sciences 10, no. 4: 1205. https://doi.org/10.3390/app10041205




