Complex Network Characterization Using Graph Theory and Fractal Geometry: The Case Study of Lung Cancer DNA Sequences
Abstract
:1. Introduction
2. Methodology
2.1. Carcinoma of the Lung
2.2. Graph Theory and Fractal Geometry
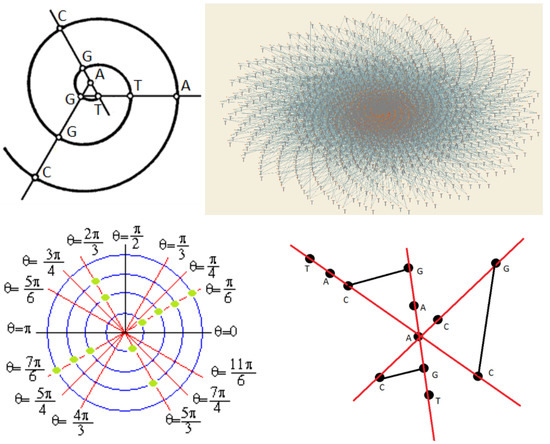
2.3. A New Method for DNA Sequencing
2.4. Statistical DNA Pattern Recognition
2.5. Data Preparation—Application
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wilhelm, T.; Kim, J. What is a complex graph? Physica A 2008, 387, 2637–2652. [Google Scholar] [CrossRef]
- Babič, M.; Calì, M.; Nazarenko, I.; Fragassa, C.; Ekinovic, S.; Mihaliková, M.; Janjić, M.; Belič, I. Surface roughness evaluation in hardened materials by pattern recognition using network theory. Int. J. Interact. Des. Manuf. 2019, 13, 211–219. [Google Scholar] [CrossRef]
- El-Metwally, S.; Ouda, O.M.; Helmy, M. Next generation sequencing technologies and challenges in sequence assembly. Springer Sci. Bus. 2014, 7, 51–59. [Google Scholar]
- Almeida, J.S. Sequence analysis by iterated maps, a review. Brief. Bioinform. 2014, 15, 369–375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tutte, W.T. Graph Theory; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Babič, M.; Marina, N.; Mrvar, A.; Dookhitram, K.; Calì, M. A New Method for Biostatistical miRNA Pattern Recognition with Topological Properties of Visibility Graphs in 3D Space. J. Healthc. Eng. 2019, 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Lennon, F.E.; Cianci, G.C.; Cipriani, N.A.; Hensing, T.A.; Zhang, H.J.; Chen, C.T.; Murgu, S.D.; Vokes, E.E.; Vannier, M.W.; Salgia, R. Lung cancer—A fractal viewpoint. Nat. Rev. Clin. Oncol. 2015, 12, 664–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ristanovic, D.; Milosevic, N.T. Fractal analysis: Methodologies for biomedical researchers. Theor. Biol. Forum 2012, 105, 99–118. [Google Scholar]
- Fractal Geometry in Biological Systems: An Analytical Approach; Iannaccone, P.M.; Khokha, M. (Eds.) CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Matej, B.; Miliaresis, G.C.; Matjaž, M.; Ambu, R.; Michele, C. New method for estimating fractal dimension in 3d space and its application to complex surfaces. Int. J. Adv. Sci. Eng. Inf. Technol. 2019, 9, 2154–2159. [Google Scholar] [CrossRef]
- Broz, P.; Monack, D.M. Newly described pattern recognition receptors team up against intracellular pathogens. Nat. Rev. Immunol. 2013, 13, 551–565. [Google Scholar] [CrossRef]
- Nelson, T.R.; West, B.J.; Goldberger, A.L. The fractal lung: Universal and species-related scaling patterns. Experientia 1990, 46, 251–254. [Google Scholar] [CrossRef]
- Siegel, R.; Ma, J.; Zou, Z.; Jemal, A. Cancer statistics. CA Cancer J. Clin. 2014, 64, 9–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kenneth, N.S.; Rocha, S. Regulation of gene expression by hypoxia. Biochem. J. 2008, 414, 19–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keith, B.; Johnson, R.S.; Simon, M.C. HIF1α and HIF2α: Sibling rivalry in hypoxic tumour growth and progression. Nat. Rev. Cancer 2012, 12, 9–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salceda, S.; Caro, J. Hypoxia-inducible factor 1α (HIF-1α) protein is rapidly degraded by the ubiquitin–proteasome system under normoxic conditions: Its stabilization by hypoxia depends on redox-induced changes. J. Biol. Chem. 1997, 272, 22642–22647. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, N.R.; Semenza, G.L. Adaptive and maladaptive cardiorespiratory responses to continuous and intermittent hypoxia mediated by hypoxia-inducible factors 1 and 2. Physiol. Rev. 2012, 92, 967–1003. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, E.A.; Pritchard, S.A.; Welch, I.M.; Price, P.M.; West, C.M. Is the hypoxia-inducible factor pathway important in gastric cancer? Eur. J. Cancer 2005, 41, 2792–2805. [Google Scholar] [CrossRef]
- Stoeltzing, O.; McCarty, M.F.; Wey, J.S.; Fan, F.; Liu, W.; Belcheva, A.; Bucana, C.D.; Semenza, G.L.; Ellis, L.M. Role of hypoxia-inducible factor 1alpha in gastric cancer cell growth, angiogenesis, and vessel maturation. J. Natl. Cancer Inst. 2004, 96, 946–956. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.; Semenza, G.L.; Simons, J.W.; De Marzo, A.M. Up-regulation of hypoxia-inducible factor 1alpha is an early event in prostate carcinogenesis. Cancer Detect. Prev. 2004, 28, 88–93. [Google Scholar] [CrossRef]
- Rami-Porta, R.; Bolejack, V.; Giroux, D.J.; Chansky, K.; Crowley, J.; Asamura, H.; Goldstraw, P. The IASLC lung cancer staging: The new database to inform the eighth edition of the TNM classification of lung cancer. J. Thorac. Oncol. 2014, 9, 1618–1624. [Google Scholar] [CrossRef] [Green Version]
- Maeda, R.; Yoshida, J.; Ishii, G.; Hishida, T.; Nishimura, M.; Nagai, K. Risk factors for tumor recurrence in patients with early-stage (stage I and II) non–small cell lung cancer. Patient selection criteria for adjuvant chemotherapy according to the seventh edition TNM classification. Chest 2011, 140, 1494–1502. [Google Scholar] [CrossRef]
- Choi, J.P.; Jeong, S.S.; Yoon, S.S. Prognosis of recurrence after complete resection in earlystage non–small cell lung cancer. Korean J. Thorac. Cardiovasc. Surg. 2013, 46, 449–456. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.D.; Nagji, A.S.; Bhamidipati, C.M.; Theodosakis, N.; Kozower, B.D.; Lau, C.L.; Jones, D. RTumor recurrence after complete resection for non–small cell lung cancer. Ann. Thorac. Surg. 2012, 93, 1813–1821. [Google Scholar] [CrossRef] [PubMed]
- Kawase, A.; Yoshida, J.; Miyaoka, E.; Asamura, H.; Fujii, Y.; Nakanishi, Y.; Eguchi, K.; Mori, M.; Sawabata, N.; Okumura, M. Japanese Joint Committee of Lung Cancer Registry visceral pleural invasion classification in non–small-cell lung cancer in the 7th edition of the tumor, node, metastasis classification for lung cancer: Validation analysis based on a large-scale nationwide database. J. Thorac. Oncol. 2013, 8, 606–611. [Google Scholar]
- Endo, C.; Sakurada, A.; Notsuda, H.; Noda, M.; Hoshikawa, Y.; Okada, Y.; Kondo, T. Results of long-term follow-up of patients with completely resected non–small cell lung cancer. Ann. Thorac. Surg. 2012, 93, 1061–1069. [Google Scholar] [CrossRef]
- Fu, Q.F.; Liu, Y.; Fan, Y.; Hua, S.N.; Qu, H.Y.; Dong, S.W.; Li, R.L.; Zhao, M.Y.; Zhen, Y.; Yu, X.L.; et al. Alpha-enolase promotes cell glycolysis, growth, migration, and invasion in non-small cell lung cancer through FAK-mediated PI3K/AKT pathway. J. Hematol. Oncol. 2015, 8, 22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakoda, L.C.; Ferrara, A.; Achacoso, N.S.; Peng, T.; Ehrlich, S.F.; Quesenberry, C.P.; Habel, L.A. Metformin use and lung cancer risk in patients with diabetes. Cancer Prev. Res. 2015, 8, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Ju, Y.S.; Lee, W.C.; Shin, J.Y.; Lee, S.; Bleazard, T.; Won, J.K.; Kim, Y.T.; Kim, J.I.; Kang, J.H.; Seo, J.S. A transforming KIF5B and RET gene fusion in lung adenocarcinoma revealed from whole-genome and transcriptome sequencing. Genome Res. 2012, 22, 436–445. [Google Scholar] [CrossRef] [Green Version]
- Costello, J.F.; Plass, C. Methylation matters. J. Med. Genet. 2001, 38, 285–303. [Google Scholar] [CrossRef] [Green Version]
- Herman, J.G.; Latif, F.; Weng, Y.; Lerman, M.I.; Zbar, B.; Liu, S.; Linehan, W.M. Silencing of the VHL tumor-suppressor gene by DNA methylation in renal carcinoma. Proc. Natl. Acad. Sci. USA 1994, 91, 9700–9704. [Google Scholar] [CrossRef] [Green Version]
- Sullivan Pepe, M.; Etzioni, R.; Feng, Z.; Potter, J.D.; Thompson, M.L.; Thornquist, M.; Winget, M.; Yasui, Y.J. Phases of biomarker development for early detection of cancer. Natl. Cancer Inst. 2001, 93, 1054–1061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siegmund, K.D.; Laird, P.W. Analysis of complex methylation data. Methods 2002, 27, 170–178. [Google Scholar] [CrossRef]
- Wu, D.; Wang, X. Application of clinical bioinformatics in lung cancer-specific biomarkers. Cancer Metastasis Rev. 2015, 34, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ching, T.; Huang, S.; Garmire, L.X. Using epigenomics data to predict gene expression in lung cancer. BMC Bioinform. 2015, 16, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Q.; Wu, H.; Zheng, H. Aberrantly methylated CpG island detection in colon cancer. J. Proteom. Bioinform. 2015, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.C.; Chen, W.S.E.; Lin, C.C.; Liu, H.C.; Chen, H.Y.; Yang, P.C.; Chang, P.C.; Chen, J.J. Topology-based cancer classification and related pathway mining using microarray data. Nucleic Acids Res. 2006, 34, 4069–4080. [Google Scholar] [CrossRef] [Green Version]
- Babič, M.; Kokol, P.; Guid, N.; Panjan, P.A. New method for estimating the Hurst exponent H for 3D objects = Nova metoda za ocenjevanje Hurstovega eksponenta H za 3D-objekte. Mater. Teh. 2014, 48, 203–208. [Google Scholar]
- Feder, Jens, Fractals; Plenum Press: New York, NY, USA, 1988.
- De Nooy, W.; Mrvar, A.; Batagelj, V. Exploratory Social Network Analysis with Pajek: Revised and Expanded Edition for Updated Software; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Semenza, G.L.; Rue, E.A.; Iyer, N.V.; Pang, M.G.; Kearns, W.G. Assignment of the hypoxia-inducible factor 1a gene to a region of conserved synteny on mouse chromosome 12 and human chromosome 14. Genomics 1996, 34, 437–439. [Google Scholar] [CrossRef]
- Breathnach, R.; Chambon, P. Organization and expression of eucaryotic split genes coding for proteins. Ann. Rev. Biochem. 1981, 50, 349–383. [Google Scholar] [CrossRef]
- Wenger, R.H.; Gassmann, M. Oxygen(es) and the hypoxia-inducible factor 1. Biol. Chem. 1997, 378, 609–616. [Google Scholar]
- Milenković, T.; Memišević, V.; Bonato, A.; Pržulj, N. Dominating biological networks. PLoS ONE 2011, 6, e23016. [Google Scholar] [CrossRef] [Green Version]
- Barabási, A.L.; Gulbahce, N.; Loscalzo, J. Network medicine: A network-based approach to human disease. Nat. Rev. Genet. 2011, 12, 56–68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bauer-Mehren, A.; Bundschus, M.; Rautschka, M.; Mayer, M.A.; Sanz, F.; Furlong, L.I. Gene-disease network analysis reveals functional modules in mendelian, complex and environmental diseases. PLoS ONE 2011, 6, e20284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarajlić, A.; Janjić, V.; Stojković, N.; Radak, D.; PrŻulj, N. Network topology reveals key cardiovascular disease genes. PLoS ONE 2013, 8, e71537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hayes, W.; Sun, K.; Pržulj, N. Graphlet-based measures are suitable for biological network comparison. Bioinformatics 2013, 29, 483–491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cavadas, M.A.S.; Nguyen, L.R.; Cheong, A. Hypoxia-inducible factor (HIF) network: Insights from mathematical models. Cell Commun. Signal. 2013, 11, 42. [Google Scholar] [CrossRef] [Green Version]
- Furlan, D.; Sahnane, N.; Carnevali, I.; Cerutti, R.; Uccella, S.; Bertolini, V.; Chiaravalli, A.M.; Capella, C. Up-regulation and stabilization of HIF-1 alpha in colorectal carcinomas. Surg. Oncol. 2007, 16, S25–S27. [Google Scholar] [CrossRef]
- Perez, J.C. Caminos Interdisciplinaios, Seminario CLAVE_INTER, Espacio Interdisciplinario, Universidad de la Republica Montevideo Uruguay. 27 October 2011. Available online: https://issuu.com/eiudelar/docs/en_clave_web (accessed on 21 April 2020).
- Perez, J.C. Codon population in single-stranded whole human genome DNA are fractal and fine-tuned by the Golden Ration 1.618. Interdiscip. Sci. Comput. Life Sci. 2010, 2, 228–340. [Google Scholar] [CrossRef]
- Shendure, J.; Lieberman Aiden, E. The expanding scope of DNA sequencing. Nat. Biotechnol. 2012, 30, 1084–1094. [Google Scholar]
- Mathur, R.; Adlakha, N. A graph theoretic model for prediction of reticulation events and phylogenetic networks for DNA sequences. Egypt. J. Basic Appl. Sci. 2016, 3, 263–271. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, Q.; Zheng, X. DUC-Curve, a highly compact 2D graphical representation of DNA sequences and its application in sequence alignment. Phys. A Stat. Mech. Appl. 2016, 456, 256–270. [Google Scholar] [CrossRef]
- Nandy, A. The GRANCH techniques for analysis of DNA, RNA and protein sequences. Adv. Math. Chem. Appl. 2015, 2, 96–124. [Google Scholar]
- Farahani, M.R. Zagreb Indices and Zagreb Polynomials of Polycyclic Aromatic Hydrocarbons PAHs. J. Chem. Acta 2013, 2, 70–72. [Google Scholar]
- Platt, J.R. Prediction of Isomeric Differences in Paraffin Properties. J. Phys. Chem. 1952, 56, 328–336. [Google Scholar] [CrossRef]
- Ouma, W.Z.; Pogacar, K.; Grotewold, E. Topological and statistical analyses of gene regulatory networks reveal unifying yet quantitatively different emergent properties. PLoS Comput. Biol. 2018, 14, e1006098. [Google Scholar] [CrossRef] [PubMed]
- Csányi, G.; Szendrői, B. Fractal–small-world dichotomy in real-world networks. Phys. Rev. 2004, 70, 016122. [Google Scholar] [CrossRef] [Green Version]
- Gastner, M.T.; Newman, M.E. The spatial structure of networks. Eur. Phys. J. B Condens. Matter Complex Syst. 2006, 49, 247. [Google Scholar] [CrossRef] [Green Version]
- Dragomir, M.; Mafra, A.C.P.; Dias, S.M.; Vasilescu, C.; Calin, G.A. Using microRNA networks to understand cancer. Int. J. Mol. Sci. 2018, 19, 1871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rai, A.; Pradhan, P.; Nagraj, J.; Lohitesh, K.; Chowdhury, R.; Jalan, S. Understanding cancer complexome using networks, spectral graph theory and multilayer framework. Sci. Rep. Nat. 2017, 7, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baish, J.W.; Jain, R.K. Fractals and cancer. Cancer Res. 2000, 60, 3683–3688. [Google Scholar]








| SNP ID/Substitution | Genomic Location | Association to Diseases and Phenotypes |
|---|---|---|
| rs10873142 [C > T] | Intron 8 | Lung cancer (Konac et al., 2009) |
| rs41508050 [C > T] | Exon 10 | Lung cancer (Konac et al., 2009) |
| rs41492849 [C > T] | Exon 12 | Lung cancer (Konac et al., 2009) |
| rs34005929 [G > A] | Exon 12 | Lung cancer (Konac et al., 2009) |
| rs11549465 [C > T] | Exon 12 | Lung cancer (NSCLC) (Koukourakis et al., 2006) (Konac et al., 2009; Kuo et el., 2012) (associated with lung cancer with TP53 LOH) (Putra et al., 2011b), (NSCLC) (Kim el al., 2010) |
| rs11549467 [G > A] | Exon 12 | Lung cancer (Konac et al., 2009), (Associated with adenocarcinoma with 1p34 LOH) (Putra et al., 2011b)) and lung carcinoma (NSCLC) (Kim el al., 2010; Koukourakis et al., 2006; Kou et al., 2005) |
| Rs199775054 [G > C] | Exon 12 | Lung cancer (Park et al., 2009) Lung cancinoma (NSCLC) (Koukourakis et al., 2006) |
| rs10645014 [C > T] | Intron 13 | Lung cancer (Konac et al., 2009) |
| Network Properties | Intron 8 | Exon 10 | Exon 12 | Intron 13 |
|---|---|---|---|---|
| Density | 0.01546718 | 0.01608148 | 0.01621950 | 0.01589322 |
| Average Degree | 40.10639938 | 4.59930314 | 7.02304147 | 13.92246294 |
| The Zagreb group index 1 | 4,197,898 | 7318 | 24,348 | 181,692 |
| The Zagreb group index 2 | 84,948,210 | 22,800 | 104,419 | 1,413,671 |
| The Platt index | 4,093,862 | 5998 | 21,300 | 169,482 |
| Edges | 52,018 | 660 | 1524 | 6105 |
| Type of triads 3–102 | 132,781,531 | 185,036 | 647,562 | 5,256,849 |
| Type of triads 16–300 | 681,579 | 978 | 3498 | 28,152 |
| Watts–Strogatz Clustering Coefficient | 0.99896066 | 0.97880415 | 0.98307498 | 0.99606624 |
| Fractal dimension | 1.365 | 1.862 | 1.907 | 1.851 |
| Network Properties | rs10873142 [C > T] | rs41508050 [C > T] | rs41492849 [C > T] | rs34005929 [G > A] | rs11549465 [C > T] | rs11549467 [G > A] | rs199775054 [G > C] | rs10645014 [C > T] |
|---|---|---|---|---|---|---|---|---|
| Density | 0.01546748 | 0.01676372 | 0.02084908 | 0.01770948 | 0.01757311 | 0.02084908 | 0.02226456 | 0.01609628 |
| Average Degree | 40.10717039 | 4.79442509 | 9.02764977 | 7.66820276 | 7.62672811 | 9.02764977 | 9.64055300 | 14.10034208 |
| Zagreb group index 1 | 4,199,568 | 8198 | 48,822 | 29,668 | 29,424 | 48,844 | 46,042 | 187,550 |
| Zagreb group index 2 | 85,054,098 | 27,736 | 351,924 | 141,323 | 139,795 | 352,309 | 260,722 | 1,495,322 |
| The Platt index | 4,095,530 | 6822 | 44,904 | 26,340 | 26,114 | 44,926 | 41,858 | 175,184 |
| Edges | 52,019 | 688 | 1959 | 1664 | 1655 | 1959 | 2092 | 6183 |
| Type of triads 3–102 | 132,783,343 | 192,594 | 823,641 | 705,525 | 701,722 | 823,661 | 882,619 | 5,322,238 |
| Type of triads 16–300 | 681,875 | 1112 | 7419 | 4339 | 4292 | 7433 | 6911 | 29,099 |
| Watts–Strogatz Clustering Coefficient | 0.99897467 | 0.98532192 | 0.98663000 | 0.98329772 | 0.98323644 | 0.98822358 | 0.98587087 | 0.99628683 |
| Fractal dimension | 1.325 | 1.741 | 1.849 | 1.747 | 1.844 | 1.787 | 1.803 | 1.718 |
| Statistical Properties | Intron 8 | Exon 10 | Exon 12 | Intron 13 |
|---|---|---|---|---|
| Standard Deviation | 11.896 | 2.12891 | 3.464352 | 4.634643 |
| Standard Error | 1.487 | 0.2703719 | 0.433044 | 0.5793303 |
| Variance | 141.5149 | 4.532258 | 12.00174 | 21.47991 |
| Mean Absolute Deviation | 7.617188 | 1.705515 | 2.952637 | 3.946289 |
| Coefficient of Variation | 0.320701 | 0.4599039 | 0.5474532 | 0.3675553 |
| Coefficient of Dispersion | 0.1318597 | 0.3387097 | 0.4869792 | 0.3016827 |
| Pearson’s Contingency Coefficient | 0.9608 | 0.9487 | 0.9536 | 0.9682 |
| Statistical Properties | rs10873142 [C > T] | rs41508050 [C > T] | rs41492849 [C > T] | rs34005929 [G > A] | rs11549465 [C > T] | rs11549467 [G > A] | rs199775054 [G > C] | rs10645014 [C > T] |
|---|---|---|---|---|---|---|---|---|
| Standard Deviation | 12.36723 | 2.374446 | 3.85292 | 4.675162 | 3.493759 | 4.068852 | 5.10522 | 5.060326 |
| Standard Error | 1.545904 | 0.299152 | 0.4816149 | 0.5843953 | 0.4367198 | 0.5086065 | 0.6590812 | 0.6325407 |
| Variance | 152.9484 | 5.637993 | 14.84499 | 21.85714 | 12.20635 | 16.55556 | 26.06328 | 25.6069 |
| Mean Absolute Deviation | 7.890625 | 1.904762 | 3.253418 | 3.523438 | 2.925781 | 3.109375 | 4.915555 | 4.140625 |
| Coefficient of Variation | 0.3348151 | 0.5212198 | 0.5829477 | 0.7056849 | 0.5273598 | 0.6141663 | 0.7582011 | 0.4013146 |
| Coefficient of Dispersion | 0.1387195 | 0.4563492 | 0.5390625 | 0.6125 | 0.484375 | 0.55 | 1.566667 | 0.33125 |
| Pearson’s Contingency Coefficient | 0.9661 | 0.9535 | 0.9701 | 0.9682 | 0.9636 | 0.9661 | 0.9635 | 0.9718 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babič, M.; Mihelič, J.; Calì, M. Complex Network Characterization Using Graph Theory and Fractal Geometry: The Case Study of Lung Cancer DNA Sequences. Appl. Sci. 2020, 10, 3037. https://doi.org/10.3390/app10093037
Babič M, Mihelič J, Calì M. Complex Network Characterization Using Graph Theory and Fractal Geometry: The Case Study of Lung Cancer DNA Sequences. Applied Sciences. 2020; 10(9):3037. https://doi.org/10.3390/app10093037
Chicago/Turabian StyleBabič, Matej, Jurij Mihelič, and Michele Calì. 2020. "Complex Network Characterization Using Graph Theory and Fractal Geometry: The Case Study of Lung Cancer DNA Sequences" Applied Sciences 10, no. 9: 3037. https://doi.org/10.3390/app10093037