Optimised Extraction of Archaeological Features from Full 3-D GPR Data

Abstract

The use of non-invasive methodologies is becoming essential for archaeological research, and ground penetrating radar is one of the most important techniques to obtain high resolution information. In this paper we present the analysis of a full 3-D GPR dataset integrated with a high-resolution photogrammetric survey acquired in a Roman archaeological site located in Aquileia (Northeast Italy) within the partially excavated area known as “Fondo Pasqualis”. We evaluated the importance of dense and accurate data collection and of processing of the GPR signal for characterization of the archaeological features. We further discuss the parametrization and the applicability of GPR attributes, in particular amplitude-based and coherence attributes, to better identify and characterise the archaeological buried targets. Furthermore, autopicking procedures for isosurfaces mapping were critically evaluated with the objective of detecting complex structures. The final interpretation of all the GPR features, with the support of digital terrain modelling and orthophotos from unmanned aerial vehicles, guided the archaeologists to open and excavate newly selected areas, which revealed interesting structures and contributed to the understanding of the historical events that characterized the Aquileia city.

1. Introduction

Ground penetrating radar (GPR) is probably the most popular geophysical technique for archaeological exploration [1] mainly due to its resolution, which is higher than that of the other available techniques, and its high versatility [2]. There are several other available geophysical techniques used for archaeology, in particular electrical resistivity tomography (ERT) [3], magnetometry [4], infrared thermography [5], and multi-spectral surveys [6], but GPR has demonstrated its wide versatility since it has been applied at different steps of archaeological prospecting and at various scale levels, assuring resolution higher than that of the other methods. In fact, there are examples of surveys on previously unexplored wide areas [7] and detailed studies of already excavated or exposed single structures and features (e.g., [8,9]). Some decades ago, GPR surveys encompassed just a few single separated common offset (CO) profiles [10], later, GPR was improved with mono- or bi-directional grids of CO profiles. In the latter acquisition scheme, there is a higher spatial resolution and some data redundancy, in turn allowing in some cases for the gathering of information even when complex and superimposed structures are present. While single profiles (i.e., B-scans) only allow for the interpretation and correlation of structures in 1-D (i.e., in the profile direction or “along track”), acquisitions along regular (or irregular) grids make the combining of collected profiles (crosslines) possible, producing pseudo 3-D data volumes (i.e., C-scans) that can be sliced not only along the profiles’ directions but typically at constant times or depths (time- and depth-slices, respectively) [11]. Time- or depth-slices represent a rapid and efficient way to provide planar comprehensive views of the anomalies’ patterns. They are essential, especially for the analysis of large areas, but they have intrinsic constraints in the case of great subsurface complexity such as when there are different superimposed structures or non-regular features. This is often the case for archaeological surveys due to the presence of collapses, refilling materials, restorations, and so on. When grids are established, typically with a crossline spacing equal to 100 or 50 cm [12], the spatial data sampling is about one order of magnitude higher along-track than across-track, with a trace distance typically in the range of 2–10 cm. As a consequence, data interpolation is neither uniform nor trivial, making it sometimes difficult to identify and accurately locate structures and anomalies. Such a problem was analysed in detail by the authors of [13] who remarked on the importance of accurately recording not only reflections but even diffractions, the latter being very common in some archaeological surveys. Therefore, to obtain spatially unaliased data, quarter-wavelength spatial sampling is considered a minimum requirement for full-resolution GPR recording both inline and crossline [14,15]. For archaeological surveys, a very dense spatial sampling is almost impossible to obtain with any single-channel bistatic GPR equipment due to the following: the logistical complexity when trying to collect regularly spaced close profiles; the very long acquisition time; and the physical dimensions of the antennas, which are typically several decimetres long and wide. Therefore, even though it is possible to combine a series of parallel or intersecting 2-D profiles to create a 3-D volume, it is not a real “full resolution” volume. As a matter of fact, present standards of 3-D GPR in archaeological prospection are therefore based on “pseudo 3-D” volumes obtained by combining a series of 2-D profiles [16,17], so the expression “2.5-D” seems to be more appropriate than the “3-D” for that specific acquisition and processing approach [18].

In order to improve the performance of GPR, different acquisition strategies have been proposed and tested for archaeological applications. In particular, multi-offset (MO) or multi-fold applications offer some relevant advantages. The difference in the MO method is that each subsurface point is imaged by multiple wavefronts, while in the standard CO only a single wavefront is exploited. MO techniques have been the standard for reflection seismic data acquisition and processing for many years [19], but they are seldom applied on GPR data due to their long acquisition time and the differences between seismic and electromagnetic (EM) waves. A comprehensive review of the MO method can be found, for instance, in [20]. In any case, besides the longer acquisition and processing time required, there are interesting examples of MO GPR surveys in different archaeological environments that demonstrate their improved performance, especially when irregular and superimposed targets are present and when the velocity field has strong vertical and lateral variations [21,22].

In recent years an extraordinary advancement in the GPR field took place thanks to the implementation of new multi-channel (also known as multi-array) systems that became available on the market. The first and obvious step ahead is related to determining the productivity rate because this new equipment can “simultaneously” collect a series of parallel CO profiles. Another, even more important improvement is that the full resolution can be easily obtained; in other words, equal (or similar) sampling rates can be fixed for both inline and crossline distances, thus obtaining true 3-D full resolution data volumes. Most of the equipment can be moved by cars or all-terrain vehicles (when logistical conditions are appropriate), further improving the overall productivity rate. Besides engineering applications (e.g., [23,24]), archaeological and cultural heritage studies have become another typical application because requests to investigate large unexplored or only partially investigated areas to accurately estimate their archaeological potential are common. Examples of applications in various conditions and with slightly different objectives are reported in [25,26,27,28,29,30,31,32,33,34,35]. The obtained results are generally of high quality and resolution, but often they are not homogeneous within the investigated areas. In fact, the applied processing and especially some parameters used in the algorithms are neither easy to set nor constant. One of the most important parameters is the EM velocity, which can vary due to the different buildings and surrounding materials but also due to different water content.

In this paper we use a full 3-D GPR survey collected in the Aquileia archaeological park (Northeast Italy), because it is exemplary for several problems, limitations, and constraints often occurring in the interpretation of large GPR archaeological surveys. Our specific aims were:

(1)

Achieve optimized information that is directly useful for archaeologists for planning excavation, often in areas where irregular and already excavated areas are present.

(2)

Image complex structures in which many superimposed and irregular structures are present.

(3)

Obtain full georeferenced results that are easy to understand and manage even by end-users and those who are not trained in geophysics.

(4)

Validate geophysical results with excavations and evaluate the intrinsic resolution limits of GPR by comparing its results with excavations.

In order to achieve these objectives, we focused on data processing, on improved data analysis by means of GPR attributes, and on automated picking/interpretation strategies to limit the subjectivity of the interpretation process while minimizing its temporal length. In the next sections we describe some characteristics of the site used as the test site, then we detail the methodologies we exploited, and finally we address some methodological issues and discuss the obtained results in a wider and more general context.

2. Test Site

The archaeological site analysed in this paper is located at the south-eastern edge of the Roman city of Aquileia (Northeast Italy). Aquileia was an important commercial fluvial harbour from the first century BC until the fifth century AD due to its geographical position and its connection to the Adriatic Sea by the Natissa River. Therefore, vertical superimposition of different structures often occurs due to multiple periods of building, destruction, renovation, and redevelopment, which can produce complex series of archaeological layers, containing remains of different ages and with different archaeological meaning.

The archaeological field is called “Fondo Pasqualis” and was partially excavated in the 1953 and 1954 by Giovanni Brusin [36] (Figure 1). Those excavations uncovered three squares with stone paving (the easternmost was then re-filled), interpreted as marketplaces, and two parallel city walls to the south, lying parallel to the Natissa River.

Between 2018 and 2019 the University of Verona carried out new archaeological excavations in this area based on the geophysical survey done in April 2018 [37]. Two sites were opened: the first (200 sqm) is located between the two southern walls; the second (250 sqm) at the southwest corner of the western square (Figure 1C). Permission for excavation came from Ministero per i beni e le attività culturali, while the research was funded by Fondazione Aquileia. Here, we focus on the second site, which was totally excavated in 2019 and 2020 by a team lead by the University of Verona, finding a very well-preserved market square surrounded by columns. The commercial centre must have played a crucial part in the economic and social life of the late antiquity Aquileia [37].

3. Methods

As a test for the extraction of archaeological features, we used a full 3-D GPR collected in April 2018 with a 3-D MiniMIRA array GPR (Malå Geoscience) equipped with 5 transmitting and 4 receiving 400 MHz shielded antennas arranged in a configuration allowing for the “simultaneous” collection of 8 parallel profiles with a constant distance equal to 8 cm within a swath 56 cm wide. To optimize the spatial resolution, we set a trace spacing also equal to 8 cm, thus obtaining a constant inline and crossline spatial sampling. The system was connected with an electromechanical odometer for triggering and with an RTK GPS allowing for absolute positioning with centimetric accuracy.

During GPR data acquisition, a photogrammetric survey was carried out using a DJI Phantom 4 Pro V.2 quadcopter unmanned aerial vehicle (UAV) equipped with a camera with a Sony Exmor-R sensor of 1” and 20 Mpixel of resolution. The flight for the acquisition of the frames was performed in waypoints mode using the DJI Ground Station Pro software and was carried out at an altitude of 35 m AGL (above ground level). To ensure high overlap between frames, fundamental for photogrammetric reconstruction with a structure from the motion algorithm (SfM), the flight was planned with more than 80% of sidelap and overlap.

Overall, 2.35 ha of terrain were surveyed and 347 high resolution RGB images were captured. A fundamental step of the work was the positioning of a large number of ground control points (GCPs) to achieve high accuracy in the georeferencing photogrammetric model. Seventeen GCPs were set and surveyed with a GNSS Stonex S9 III NRTK receiver connected to a Hexxagon Smartnet reference stations network for real time GNSS correction. The accuracy of the root mean square error (RMSE XYZ) achieved on the GCPs was about 3 cm. The coordinate system used for georeferencing the data was ETRS89/UTM zone 33 Nord (EPSG:25833) and for the conversion of ellipsoidal heights into orthometric ones, referring to the IGM42 datum, the special GK2 IGMI grids were used. A second photogrammetric survey was carried out after archaeological excavation (with the same setting described) so that all the available data (i.e., photogrammetric, geophysical, and archaeological) could be integrated in a GIS environment, thus providing an easy tool for the archaeologists and end-users to visualize and integrate all the information; this is discussed further later in the paper.

The resulting 3-D GPR data volume formed by more than 300 swaths had an extension of about 160 × 90 m. The dataset was not regular due to the already excavated areas with outcropping walls and pavements and isolated trees, both making data acquisition therein logistically impossible (Figure 1).

At first, we applied a standard processing flow including drift removal, background removal, bandpass filtering (corner frequencies were 50-150-600-800 MHz, with a typical non-symmetrical trapezoidal shape to limit the Gibbs phenomena), spherical divergence correction, amplitude recovery, migration (Stolt), and depth conversion using rSlicer software (DECO Geophysical) specifically developed for volume data processing and analysis. In-house algorithms implemented in Matlab were applied to solve specific data issues related in particular to the time misalignment between adjacent traces. Swaths were then interpolated within rectangular grids (chunks), which were manually selected by the operator.

A crucial point for any GPR survey and in particular for the ones focused on archaeological targets is the EM velocity field reconstruction. In fact, knowledge of the EM velocity is essential for depth conversion, but even more important for imaging (migration) algorithms and recovery of physical parameters that are strictly linked to the subsurface material’s characteristics [38]. The EM velocity can be estimated with different techniques, allowing for various accuracy levels. On MO data, several precise methods can be exploited, with most of them based on the shape of the reflectors of common midpoint gathers (CMP). Unfortunately, as reported in the Introduction section, the most common GPR acquisition strategy encompasses CO surveys even when array antennas are adopted. On CO data, the velocity analysis can be completed by exploiting the scattering events (diffractions); the most common analysis methods are diffraction hyperbola fitting and migration velocity scans [20]. The overall accuracy of such techniques and the spatial resolution of the reconstructed velocity field are often limited, since usually only a few diffractors are present and they are not regularly distributed within the investigated area.

The number of diffractions usable for the velocity analysis by hyperbola fitting was not relevant; however, we combined all the obtained analyses (after a careful check evaluating the reliability of strong lateral variations) and used the obtained velocity field for 3-D Stolt time migration and depth conversion. The Stolt algorithm was selected as it requires low computational resources and produces acceptable results for smoothed EM velocity fields, as in the present case. A direct calibration was further conducted thanks to an outcropping drainage pipe in the western portion of the area (Figure 2), at a measured depth of 1.31 m. A velocity of 9 cm/ns was obtained by the fitting of that hyperbola, thus giving an estimated depth for the pipe of 1.35 m. Therefore, there was a depth error equal to 4 cm (3%), which is considered to be within the intrinsic accuracy limits of the applied method.

On the processed data we calculated various GPR attributes. GPR attribute analysis can enhance the GPR performance, because attributes are potential indicators of subsurface changes of physical properties of archaeological interest [18,39], thus emphasizing features and patterns not apparent in the amplitude data. Attributes are increasingly applied to reveal archaeological targets for 2-D and 2.5-D datasets (e.g., [40,41]) but, as far as we know, there are only a few recent examples of their application on full 3-D data in archaeology [42]. For GPR attribute calculation we used software originally developed for reflection seismic data analysis and interpretation (Petrel—Schlumberger and OpenDtect—dGB Earth Sciences). Calculation details and the performance of some selected attributes are reported in the next paragraph.

We further used the Petrel platform for the semi-automatic extraction of isosurfaces, i.e., zones in which an attribute has values higher or lower than a set threshold. Our approach was quite different (and simpler) from the one proposed by [43], which exploited a structuring element strategy in which linear predefined templates are used to extract walls. In our test, only some of the targets were linear (typically this is the case of walls) but many others were planar elements, localized features, or exhibited complex shapes (circular, semi-circular, irregular). We adopted an autotracking function implemented in Petrel: After just a few control points (seeds) with values considered typical for the desired feature are manually picked by the operator, our function is able to automatically extract all the cells (or voxels) with predefined values for a specific attribute. From such points the algorithm is able to select within a predefined search space, which can be either the entire dataset or a portion of it, all the cells having values close to the ones of the seeds and matching pre-set thresholds. An intrinsic advantage of this strategy is that each attribute can be independently used and, by integrating the results, an improved extraction can be achieved. Ideally, the attributes exploited should refer to different signal characteristics such as, for instance, amplitude, coherence, phase, or spectral characteristics. By exploiting different attributes, some of them being potentially independent from each other, it is possible, at least in theory, to overcome constraints due to poor contrasts between targets and their surroundings, for instance, when reflection amplitude data exhibit a low overall signal-to-noise ratio (SNR). In addition, the isosurface can define not only the planar location of a target, but its volume, i.e., its 3-D extension that is in turn related to the actual volumes of the structures.

4. Results

After the standard processing flow, some structures that were well correlated were imaged, but their actual shape and extension were difficult to define (Figure 2). We therefore focused on the optimization of the migration process, which is an essential step to improving the lateral resolution and approximating the true shape and geometry of the buried elements. In Figure 3 we show how different results were obtained by using different constant velocity values from 7 to 12 cm/ns for migration. It is quite apparent that velocities of 9 and 10 cm/ns produced very similar results, while both lower and higher velocities (Figure 3A,D, respectively) produced very degraded results. In particular, a velocity of 7 cm/ns produced a sufficient imaging of the circular structure, while the semi-circular one cannot be detected; the opposite occurs for a velocity of 12 cm/ns, demonstrating how it is difficult to obtain a reliable interpretation when the velocity field is not correct and when spatial sampling is not adequate [44].

Integrated analysis of 2-D inlines and crosslines of the migrated volumes and of time-slices is the typical strategy adopted to interpret the features and amplitude anomalies of potential archaeological interest in GPR data. Exemplary results obtained for localized structures (bases of columns) and for planar elements (a stone floor) are reported in Figure 4 and Figure 5, respectively. The importance of 3-D slices, which can be eventually calculated considering the mean values within vertical windows of a few samples, is easily detectable by analysing the two examples. In particular, localized structures are elusive on 2-D profiles (B-scans) even when the profiles perfectly cross several constant spaced elements. This demonstrated once more that the performance of full 3-D datasets, compared to those of 2-D and 2.5-D surveys, is better. Moreover, even when the archaeological structures are regularly spaced and identical from the building point of view (Figure 4), on single GPR profiles they are different due to various levels of conservation and/or to collapsed materials, while they are very clear on time- or depth-slices.

Wide planar elements can be detected on 2-D profiles more easily due to their extension and if they are characterized by high amplitude (or more generally by a strong amplitude contrast). On volume-slices, the amplitude spans over positive and negative values (Figure 5B), sometimes making interpretation difficult. This behaviour is not surprising because the irregular time/depth of the reflectors produces various phases when it is sliced. This is further emphasized when non-homogeneous velocity fields are present, as in almost all the cases in our test site. In fact, time-slices by definition cannot take into account this behaviour, while depth-slices can be distorted when the actual velocity field differs from the one used for migration/depth conversion.

We tested different attributes including texture, coherency, and amplitude-based attributes, not always obtaining remarkable results. In Figure 6, three texture attributes [39] were calculated on the same depth-slice. It is remarkable to notice that attributes have a strong potential, but are very sensitive to the SNR, which is often low in GPR datasets of archaeological sites [45]. Some attributes (such as the Chaos one) are able to highlight not only the edge of buried structures, but also their extension. In addition, when single apparent structures are not present, attributes can help in the qualitative identification of “homogeneous” zones, which in turn can have archaeological potential.

It is not sufficient to choose which attributes are the more suitable for data analysis, which is both subjective and strictly site-dependent; it is more important to select the appropriate parameters to use during the calculation. Coherence attributes are one of the most powerful attribute categories when applied on full 3-D data [42], this has been well known for many years in the study of reflection seismic data [46]. Coherence is defined by waveform similarity in both the inline and crossline directions, considering patterns with various extensions and shapes. In general, by increasing the number of traces considered in the coherency calculation, more stable results can be obtained but with a lower resolution level. This attribute can be calculated within a fixed length sliding window, usually defined by a lower- and upper-time boundary with respect to a central value lying on a time-slice or a specific horizon; another approach is to compute the attribute over the entire data volume then visualize the coherence along any arbitrary surface [47].

The number of vertical samples of the sliding window is another crucial parameter for coherence calculation (Figure 7). In general, a few (or just one) sample windows produce more detailed results but are more prone to both random and coherent noises, while with larger windows the overall resolution becomes lower, but results are much more stable. In our tests, 16 samples seem to have the best trade off (Figure 7). By considering a velocity of 9 cm/ns for this area and a central frequency of 300 MHz (slightly lower than the nominal one due to the filtering effect of the ground), it is possible to calculate the dominant wavelength, which is equal to 30 cm. The data sampling interval is equal to 0.24 ns, so 16 samples correspond to a time length of 3.84 ns, which can be converted into a thickness of 34.56 cm. These are general results and can be used as a guide when setting the time window length for coherence calculation: a length corresponding or close to the dominant wavelength of the data is a reasonable choice, but the target’s dimensions and lateral variability also play an important role.

An example of semi-automatic extraction of isosurfaces is provided in Figure 8 in which the trace envelope attribute is exploited, but the same approach can be applied to any attribute independently or to combined attributes (a.k.a., meta-attributes). One of the advantages of the procedure is that it is able to “search” in the entire data volume (or portions of it) for values within the set thresholds, making the entire process fast since the operators do not need to analyse single slices, as they do in the traditional picking procedures. In Figure 8B, isosurfaces highlight both localized, linear and planar elements within a depth range from 100 to 200 cm below the topographic surface. The lateral continuity of the automatically extracted structures is in general high, demonstrating that the approach is robust, but some “holes” are present, especially within planar targets. 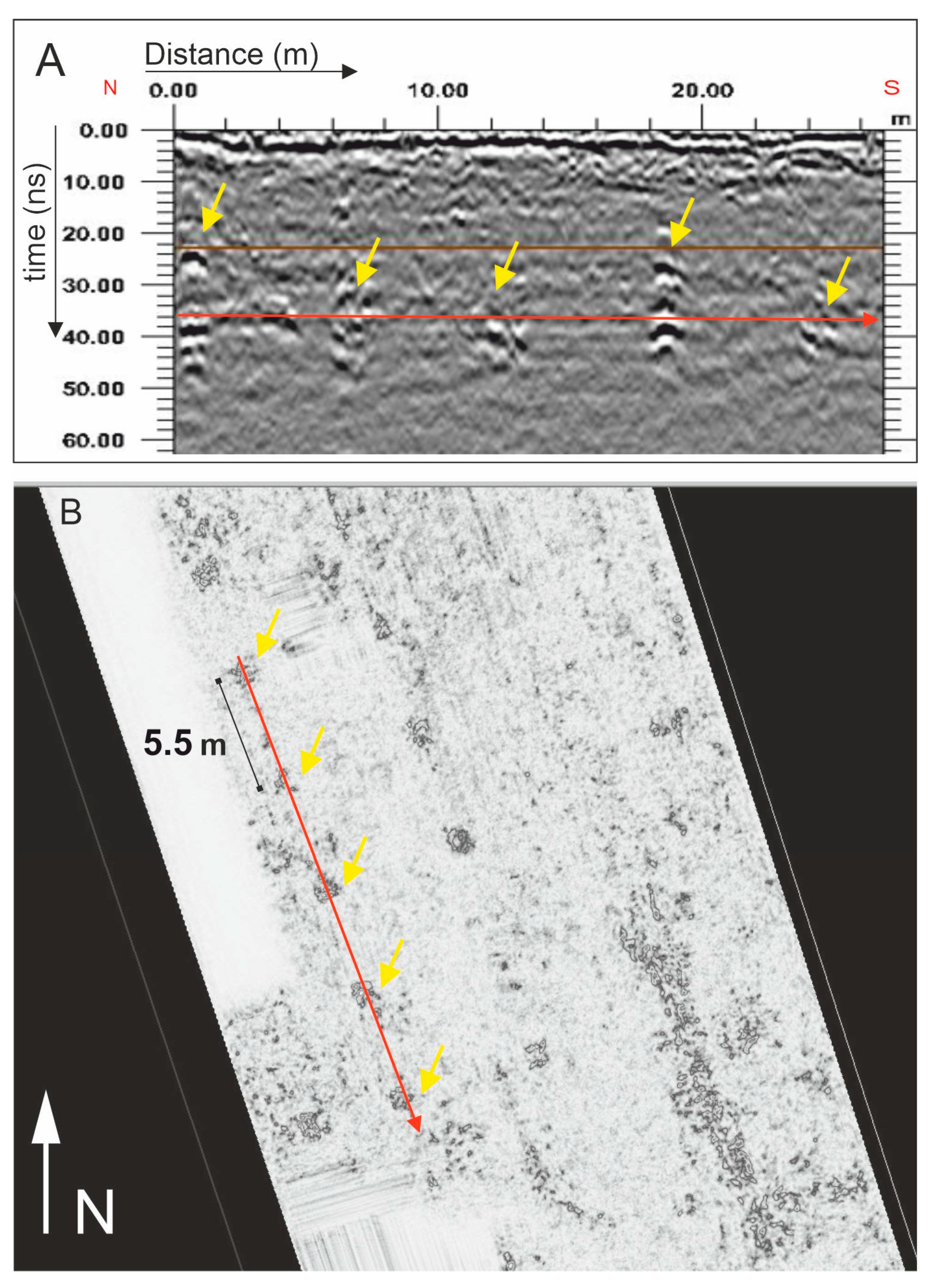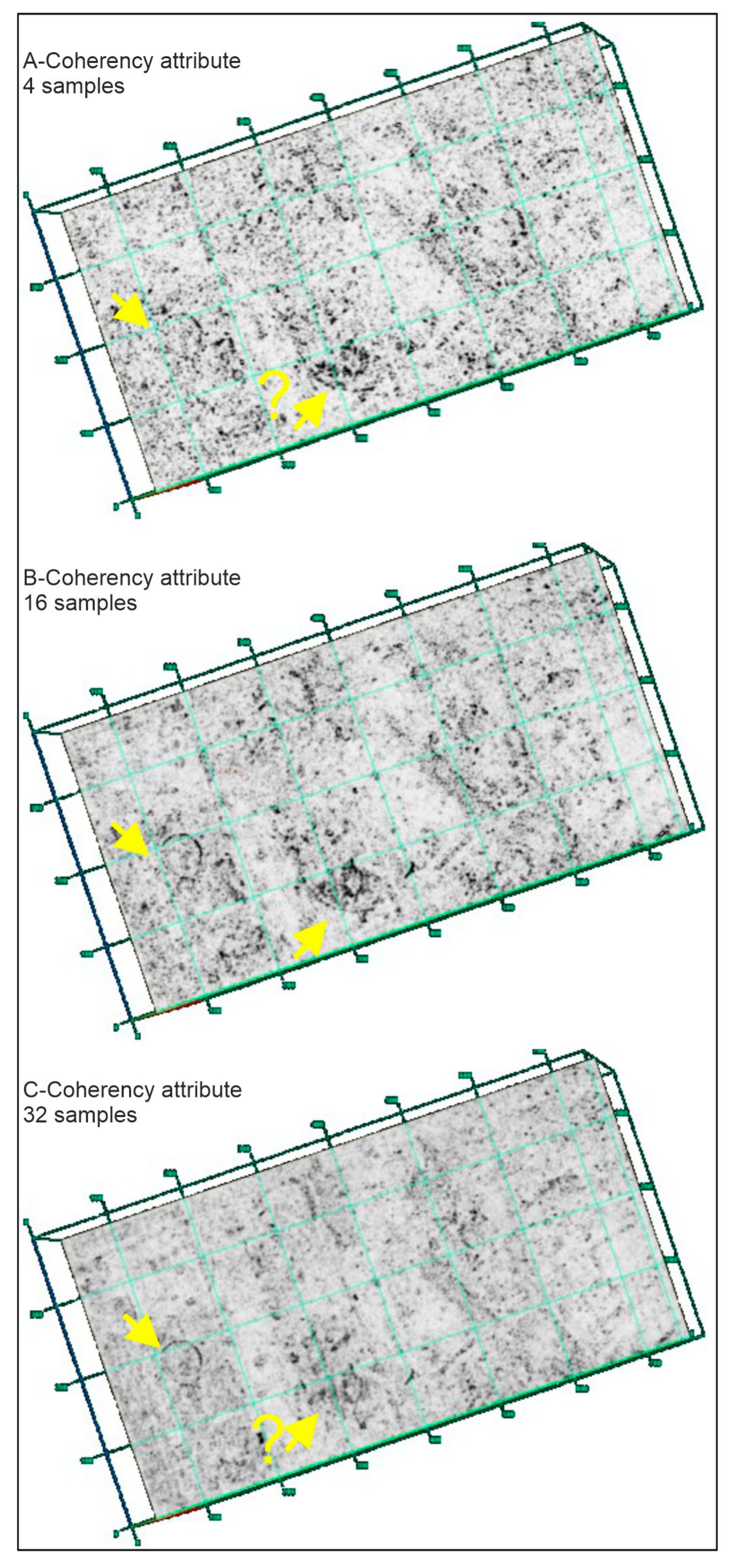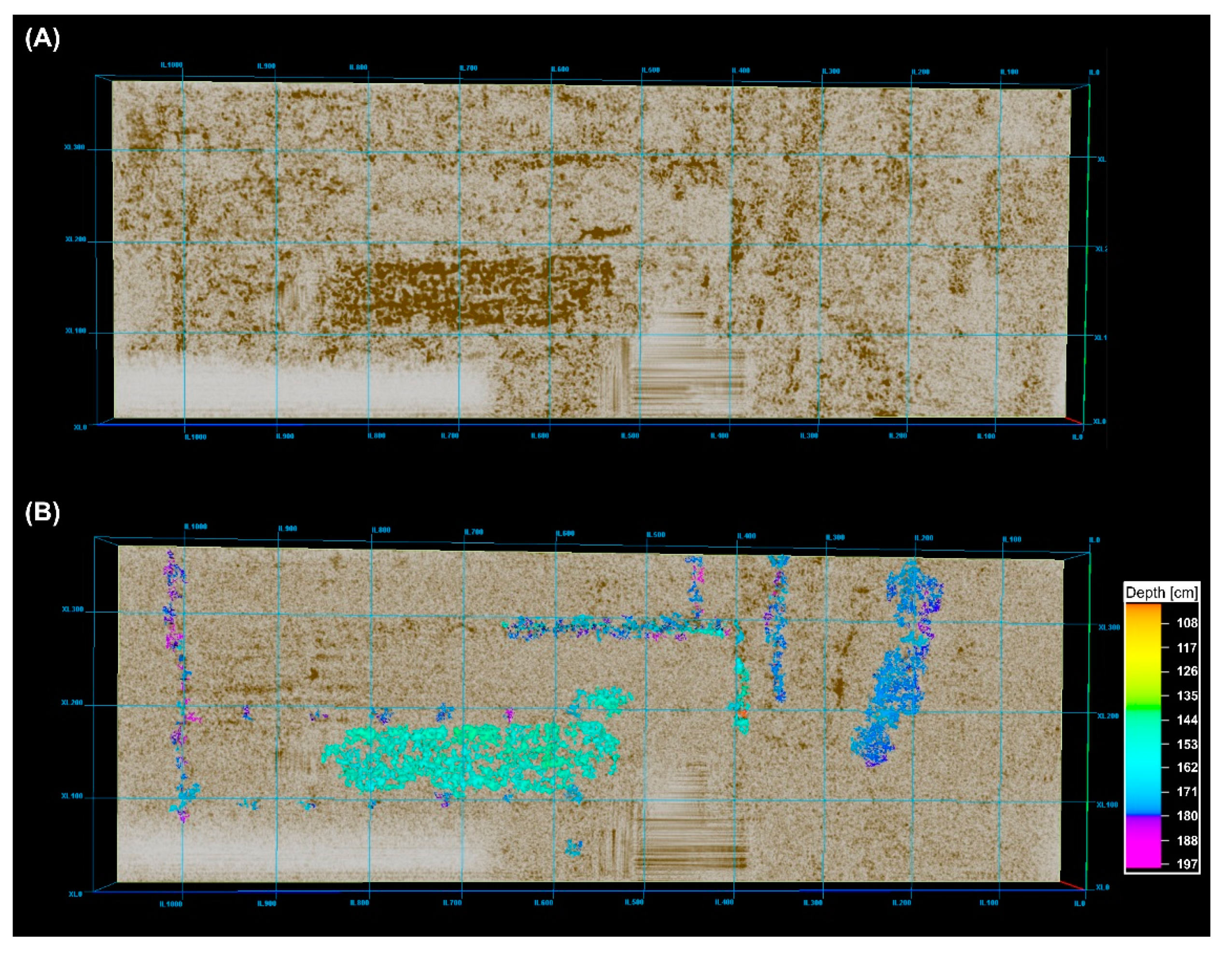In any case, such artifacts do not limit the interpretability and do not misrepresent the archaeological potential of the extracted features.

5. Discussion

Based on the geophysical survey, two zones were excavated in 2019 and 2020 by a team of archaeologists from the University of Verona: the first was placed between the two southern walls (200 sqm); the second (250 sqm) at the southwest corner of the western square (Figure 9(C1)). In 2020 the entire square was excavated (Figure 9A–B1). The important and well-preserved structure is paved by limestone stone slabs of various sizes. Some of them are reworked from earlier architectural elements and one of these was originally a drain cover. Since all the available data (geophysical, photogrammetry before and after excavation, archaeological excavations) are georeferenced and integrated within a dedicated GIS project, we can make quantitative ex post analyses on the accuracy of the geophysical data and the used parameters. The position and size of the excavated archaeological structures have good overall correlation with the geophysical isosurfaces, with the maximum vertical differences equal to 20 cm for test site 1 and 16 cm for test site 2. In particular, we considered the accuracy of the estimated EM velocity field by comparing geophysical data with the excavated structures. For instance, in the test site 2, the absolute elevation of the ground before excavations was 2.6–2.7 m above sea level, while the stones of the floor lie between 1.4 and 1.6 metres above sea level. So, the mean depth of the floor is close to 1 m, as estimated during GPR data analysis.

With the aid of the photogrammetric surveys collected before and after excavation, all the topographic elements were integrated to complete the results and correlate the EM features with the absolute orthometric elevation, further aiding the end users in evaluating the meaning and correlation of the imaged features.

Figure 9 shows the correlation between a portion of the 3-D GPR data volume and the totally excavated square. The inline (W–E direction) perfectly crosses the pavements and its edges are clear; we also note that the central bended break of the stones is imaged by the exemplary 2-D profile by a lowering of signal amplitude (Figure 9A). In addition, the surrounding elements, i.e., column pillars around the square, match with the local geophysical features of the crossline in the N–S direction, pointed to by the yellow arrows. The pillars are also depicted in B–B1 and C–C1 of the migrated slice, on which we applied the envelope attribute to better visualize their signature. We further noticed the foundation of a wall (Figure 9C) 73 cm wide, which runs north–south and shows truncations due to more recent activity. The foundations are in rough-hewn stones and mortar. The elevation was probably made with bricks. The wall would have closed off the eastern end of the arcade.

The joint analysis of new excavations and the correlation with the already uncovered features in the Fondo Pasqualis area (Figure 10A), as well as the outcomes of the geophysical and photogrammetric surveys, allowed the archaeologists to gain details about the architectural and structural characteristics of the building and infrastructure remains and better understand the use and historical events that characterized the study area of Aquileia city. This can help with the 3-D reconstruction and rendering of the buildings (Figure 10B), in which new details are derived from the last archaeological and geophysical surveys.

When all the data are stored in the same digital suite and are accurately georeferenced, different scale correlations become easy and provide new strategies to study and exploit the data for scientists, end users, and tourists (Figure 10C).

6. Conclusions

We showed the advantages achievable when using full 3-D GPR data instead of 2-D or pseudo 3-D GPR archaeological surveys, giving examples of the importance of accurate data processing, in particular for the EM velocity field estimation and the migration algorithms.

By using integrated attributes, it is possible to determine shapes and borders and characterise archaeological targets; amplitude-based and coherency are the most effective and promising attributes. A correct parametrization of the process is mandatory, as shown in the case of the coherency calculation. We found that a vertical window length close to the dominant wavelength of the data is usually the best trade-off between resolution on one side and stability of the results on the other. Volume attributes on a full 3-D GPR dataset allow us to recognize and map even complex archaeological targets by means of isosurfaces extracted from a few manually selected control points by autotracking procedures, which are available on commercial software originally developed for the analysis and interpretation of reflection seismic datasets. It is essential to compare results obtained using different attributes, exploiting and emphasizing different signal characteristics such as amplitude, phase continuity, and spectral behaviour, especially when data are characterized by low SNR. Selection of seeds is a quite subjective procedure that can potentially produce incorrect results. In our experience, the best approach is to first carefully analyse time- or depth-slices, then select seeds on the most promising and apparent structures. To achieve correct results, it is important to collect GPR data with a centimetric positioning accuracy that is guaranteed (in favourable conditions) by recent RTK GPS devices. Integration of geophysical data with DTM and photographs obtained with UAV surveys and georeferenced with the same coordinate system is a key factor in achieving the following:

-

Storage of all the data in the same digital suite;

-

Integrated analyses and correlation of events with the results coming from the new excavated areas.

Further achievements could be obtained by using MO datasets, allowing for more accurate velocity field definition and imaging, and by integrating GPR data with multispectral surveys from UAV when the expected depth of the archaeological targets is limited.