Experimentally Viable Techniques for Accessing Coexisting Attractors Correlated with Lyapunov Exponents

Abstract

Universal, predictive attractor patterns configured by Lyapunov exponents (LEs) as a function of the control parameter are shown to characterize periodic windows in chaos just as in attractors, using a coherent model of the laser with injected signal. One such predictive pattern, the symmetric-like bubble, foretells of an imminent bifurcation. With a slight decrease in the gain parameter, we find the symmetric-like bubble changes to a curved trajectory of two equal LEs in one attractor, while an increase in the gain reverses this process in another attractor. We generalize the power-shift method for accessing coexisting attractors or periodic windows by augmenting the technique with an interim parameter shift that optimizes attractor retrieval. We choose the gain as our parameter to interim shift. When interim gain-shift results are compared with LE patterns for a specific gain, we find critical points on the LE spectra where the attractor is unlikely to survive the gain shift. Noise and lag effects obscure the power shift minimally for large domain attractors. Small domain attractors are less accessible. The power-shift method in conjunction with the interim parameter shift is attractive because it can be experimentally applied without significant or long-lasting modifications to the experimental system.

1. Introduction

The influential research in optical bistability (OB) by Bonifacio and Lugiato [1,2] undergirds the many investigations of the active counterpart of OB, the laser with injected signal (LIS). The LIS system is well-studied and covers a broad range of active systems, including CO₂, diode [3,4,5], and quantum dot lasers [6,7]. It is replete with interesting dynamics from chaos to coexisting attractors [8,9,10]. Intriguing glimpses into self-similarity are reported in References [11,12,13]. Some, if not all, of these characteristics can be found in a wide variety of other models and nonlinear systems [14,15,16,17].

Nonlinear dissipative systems have challenged the imagination since the late 1970s with their potential, unique dynamic features and chaotic behavior [18,19,20,21,22]. The discovery of multistability energized innovative approaches such as feedback loops. Experimentally, Gibbs et al. [23] found that delayed feedback could induce multiple coexisting attractors in an electro-optical bistable device. Coexisting attractors with subharmonic output frequencies were experimentally observed in a modulated CO₂ laser by Arecchi et al. [24]. Later, bifurcation diagrams of a modulated CO₂ laser assisted the experiment; these diagrams were made by sweeping one of the control parameters in an attempt to find bistability [25,26,27,28]. However, the continuous changes of the control parameter limited which attractors could be isolated because of hysteresis effects. Theoretical contributions by Meucci et al. [29] used stepwise changes in a modulated frequency to cause switching between two coexisting attractors in a multistable system.

System control was studied further by Ott, Grebogi, and Yorke [30] and Pyragas [31] who set about controlling chaos using feedback methods that did not require, a priori, analytical knowledge of the system dynamics. The approach was limited because the feedback loop altered the state variables or system parameters. In 2014, Li and Sprott used amplitude control to detect multistability and coexisting attractors [32]. Later, an offset-boosting-based approach was developed as well for the identification of multistable dynamical systems [33]. Burton et al. [34] developed a power-shift method that changed only the control parameter of the system to transition from one attractor to another. However, the method requires some trial and error. A way to avoid this process may exist in the traditional theoretical tools, for example, the analysis of Lyapunov exponents (LEs), which is discussed further in Section 4.2.1.

Lyapunov exponents are able to identify spectral patterns of Hopf bifurcations, period-doubling episodes, tori, and chaos [10,35]. In 2015 Bandy et al. [36] reported that globally analyzed Lyapunov exponents could be used to identify attractor coexistence by comparing forward and backward global scans of the LEs. Lyapunov spectra also predicted the trends of the fundamental frequencies of the output signal of the individual attractors. Structural patterns in the Lyapunov spectra were observed, but the pattern formation was not correlated with the dynamic behavior of the attractor. Later, these specific LE patterns were discovered to predict bifurcation sequences, imminent bifurcations, and common borders of the attractor domains [37]. An imminent bifurcation predicts that by slightly changing a system parameter, one LE pattern changes into another signifying a bifurcation in the system.

Herein, we report further findings of pattern formations that predict imminent potential changes in the dynamics provided the gain parameter is modified slightly. We identify the correlation between these LE configurations and the different values of the gain parameter. Specifically, we see an attractor with a curved trajectory of two equal LEs that appears to be benign with respect to its dynamic behavior. A slight increase in the gain produces a symmetric-like bubble whose potential dynamic characteristic is an established pattern identified in Reference [37]. Also, by slightly decreasing the gain of the system, a symmetric-like bubble known to exist in another attractor changes to the curved trajectory of two-equal LEs, just the reverse of the previous attractor event. Because these two cases represent two different attractors with two different modifications to the gain, what appears to be obvious now, are in fact, new universal pattern constructs with identifiable dynamic connections, albeit future system dynamics.

We also report findings that describe a method for discovering the ideal base attractor used in power shifting the LIS system. We examine the location of the ideal shift and explore correlations with the apexes of the LE bubbles in an attractor’s LE spectra. The experimental conditions of the power shift are developed by including noise on the frequency of the injected signal and a linear ramp on the amplitude of the injected signal. Finally, we create a generic counterpart to the power shift, called the interim parameter shift, in which a system parameter is temporarily modulated to transition to attractors, i.e., to systematically access coexisting attractors and windows in chaos. The interim parameter shift results are compared with the LEs to check for correlations between the reliability and the stability of the system.

2. Model and Methods

2.1. Laser with Injected Signal Model

The laser with injected signal is a semi-classical theory that is based on a homogeneously broadened 2-level atom. The atoms and the cavity frequencies, ω_a and ω_c, respectively, are tuned usually to one another at ω_a = ω_c and, in the absence of the external signal, produce a stable laser output with a carrier frequency ω_a. By injecting into the cavity a continuous wave beam at frequency ω₀ ≠ ω_a, the potential for competition is established between the driving field and the laser oscillator. At resonance and low input-signal levels, beat patterns with frequencies close to |ω_a − ω₀| appear because of a simple mixing of the 2 fields, and thus, the laser acts as the local oscillator. At a high external signal amplitude, the laser is predicted to stably lock to the injected field and produce a constant output intensity, known as injection locking with a carrier frequency ω₀. Between these 2 limits, complicated and interesting nonlinear phenomena appear and, contingent on the system parameters, there are still many unexplained dynamic events. For example, the output signal can display coexisting incommensurate frequencies [35] or as many as 3 different commensurate frequencies for the same driving field by using slightly different initial conditions [8,10,36].

The laser with injected signal is based on the Maxwell-Bloch equations and defined by the customary single-mode, non-resonant unidirectional ring laser. It is a coherent model designed to approach most closely the conditions of spatial uniformity; the chosen parameters are intermediate to the conditions of Class B [38] and Class C [39] lasers. The representative nonlinear equations are as follows:

$$\frac{\partial X}{\partial \tau }=-\tilde{\kappa }\left[\left(1-i\frac{\mathsf{\Phi }}{\tilde{\kappa }}\right)X-Y+2CP\right],$$

(1)

$$\frac{\partial P}{\partial \tau }=-\left(1+i\tilde{\mathsf{\Delta }}\right)P+XD,$$

(2)

$$\frac{\partial D}{\partial \tau }=-\tilde{\gamma }\left[\frac{1}{2}\left(X{P}^{*}+X^{*}P\right)+D+1\right],$$

(3)

where Y is real and positive for definiteness (the system control parameter) and is proportional to the incident field amplitude; X and P are the complex field and polarization amplitudes; D is the real population difference, where negative numbers represent the excited states. We chose to study the equations as 5 real differential equations. The system parameters are the small-signal atomic gain C, the scaled cavity relaxation rate $\tilde{\kappa }$ = κ/γ_⊥, the scaled population decay rate $\tilde{\gamma }$ = γ_∥/γ_⊥, the scaled cavity mistuning parameter Φ = (ω₀ − ω_c)/γ_⊥, and the scaled atomic detuning from the injected-signal carrier $\tilde{\mathsf{\Delta }}$ = (ω_a – ω₀)/γ_⊥. γ_∥ is the relaxation rate of the population inversion and γ_⊥ is the polarization relaxation rate. The time τ is measured in units of the polarization relaxation time γ_⊥⁻¹. The system parameters are C = 3, $\tilde{\mathsf{\Delta }}$ = 0.5, $\tilde{\kappa }$ = 0.1, $\tilde{\gamma }$ = 0.01, Φ/$\tilde{\kappa }$ = −0.5. If Equations (1) and (2) are written in terms of their real and imaginary components, then these equations can be written as real first-order differential equations; adding the real population difference makes a total of 5 real equations which we use to study the nonlinear LIS system. The numerical routine used to solve these equations was the NDSolve function in Mathematica, using the “StiffnessSwitching” method.

In steady state, the output field amplitudes are triple valued with respect to the injected signal, with a domain of instability of 0 < Y < 2.17; the entire lower branch of the tripled-value-curve is unstable.

2.2. Lyapunov Exponents

Lyapunov exponents are theoretical spectra used to study nonlinear dynamics and mathematical maps. They describe the average growth or decay of infinitesimal perturbations to an n-dimensional system orbit and are invariant with respect to their pattern formations and respective domains. In physics, there is universal agreement that even one positive LE predicts chaotic dynamics or fractal geometry [40,41,42]. In this study, the largest three LEs of the 5 available are the dominant contributors to the universal attractor pattern formations described by Bandy et al. [37]. The 2 lowest LEs are not represented here; however for completeness, we note that they are more negative than the others and are always equal for this set of parameters, see Figure 13b and Figure 16b in Reference [36]. The LE order may be different for pattern formation in other nonlinear systems, but the same universal attractor patterns are evident. By attractor pattern formation we mean a universally defined visual arrangement of the LEs as a function of the control parameter. We calculate LEs from a modified form of the Benettin method [43] as applied in the Appendix of Reference [35].

Attractor domains are calculated as an adiabatic scan of the injected signal, so that once located on the attractor, small steps of the control parameter can be taken successively to hold the system on the attractor until it no longer exists. See Reference [36] for details. The scan step size provides the precision for the LE spectral features within the attractor domain. In this study, the details of the system dynamics being explored provide the guidelines for the injected-signal step size. Fourier transforms, Poincarè maps, phase-space portraits, bifurcation diagrams, and temporal plots are the supporting theoretical tools used to confirm the dynamics predicted by the various LE patterns.

Probing nonlinear behavior and multistability, whether in a physical model or a map, is a system-dependent exercise. We chose a single mode, coherent model of the laser with injected signal because it is a generic archetype of the aforesaid LIS model and because there are extensive experimental studies of similar systems. For example, multistability was observed in 1982 by Arecchi et al. [24] using a loss-modulated CO₂ laser; they experimentally established proof-of-existence of coexisting attractors, sparking a new era of LIS research. The LIS studies herein were influenced profoundly by their results. Research varies from exploring system nonlinearities [8,10] to examining intertwined studies of nonlinearities and coexisting attractors [35,36]. In 1985, investigations [35] unearthed many strange looking global LE patterns which, at the time, were considered mysterious if not bizarre spectra. By 2015, these strange looking LE formations (patterns) were no longer considered random prattle. They were found to be significant universal configurations that predicted the dynamic behavior of LIS and other nonlinear systems. The LE formations are known to predict: (i) the domains of coexisting attractors (see Figure 13 of Reference [36]), (ii) a universal attractor boundary, and (iii) characteristic dynamic behaviors (both current and imminent) that are best understood in the context of 2-parameter (“shrimp”) diagrams in Reference [13].

Figure 1 represents a schematic of attractor and window domains for the parameters under consideration. Attractor and window dynamics are included as a function of the injected signal. Each attractor is graphed by the position of its relative characteristic frequency and its domain of activity. The information summarized in Figure 1 is calculated using both LEs and traditional theoretical tools as stated above. Each attractor and window domain is identified by name; attractor 1 (AI) to attractor 8 (AVIII) and periodic windows WI and WII, and their dynamic features. They are named in the order in which they were discovered. Figure 1 is especially useful when one tries to understand the relative positioning of the coexisting attractors; it is also an instant visual of their general dynamics. AI and AII have special distinction from the other attractors in that they appear to be the scaffolding upon which other attractors coexist, except for AVII and AVIII which coexist with chaos. WI and WII interrupt chaos. AI brings LIS to life for low values of the injected signal, while AII has the largest attractor domain and guides the system into injection locking. Note, that some Y values label period-doubling episodes: for example, in AI and AII there is a 2ⁿ period-doubling sequence and in AVII a 5 × 2ⁿ doubling sequence. The transition from 6P to 12P identified in AIV refers to the two dominant limit cycles of a period-doubling sequence, 6 × 2ⁿ into chaos. The callouts for AI, AIV, AII, AVII, and AVIII magnify some details of the attractor dynamics. For example, inverse bifurcation sequences are identified in the callouts AII and AVII.

Different theoretical tools provide information about an attractor or window dynamics and that includes chaos, but it is the exploration of the LEs as a function of the system’s control parameter that reveals the detailed, universally predictive information about each attractor [37] or window. In addition, the study of LE patterns leads ultimately to understanding how an attractor can be accessed reliably under experimental conditions without changing the parameters of the system itself. It is called a power shift [34].

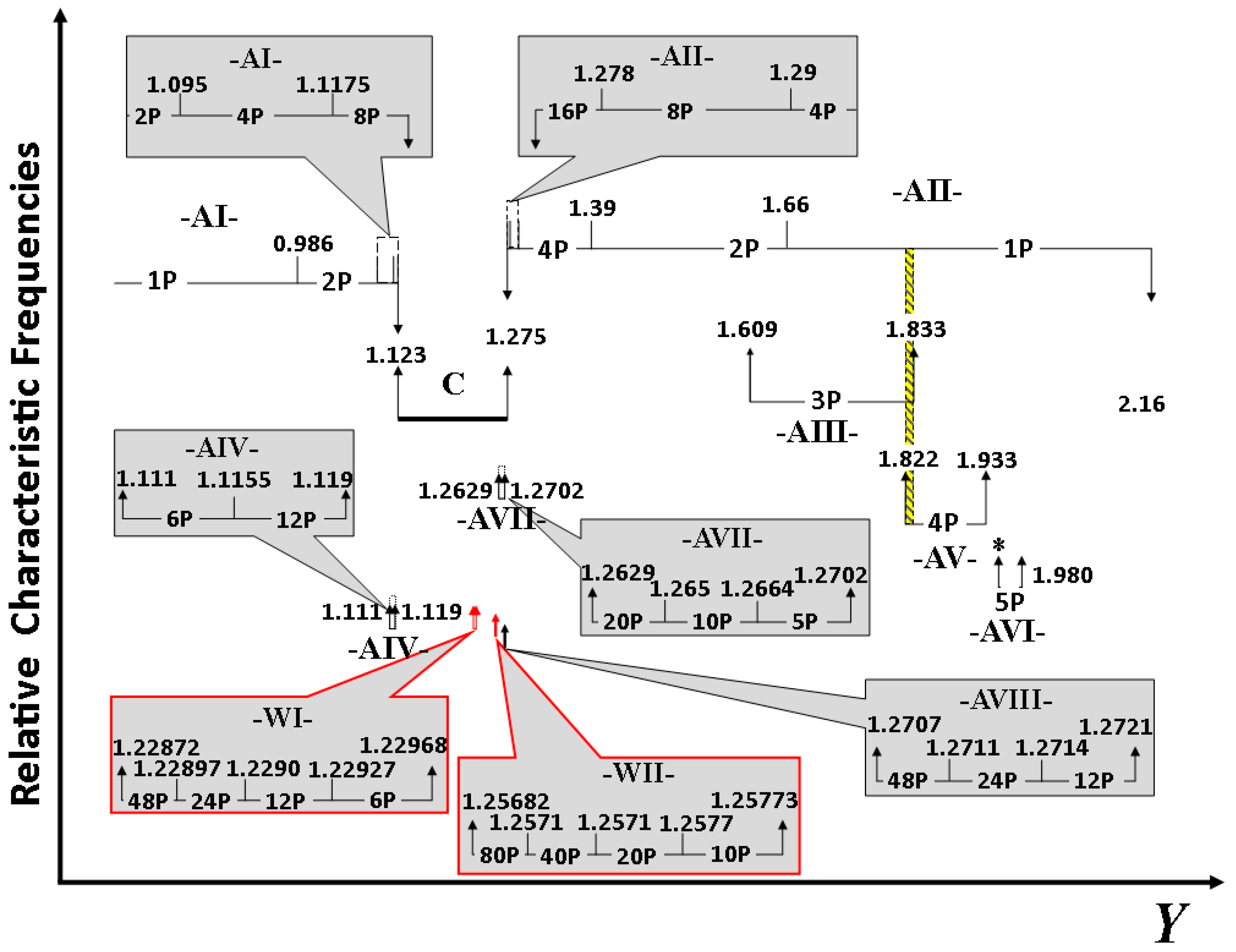
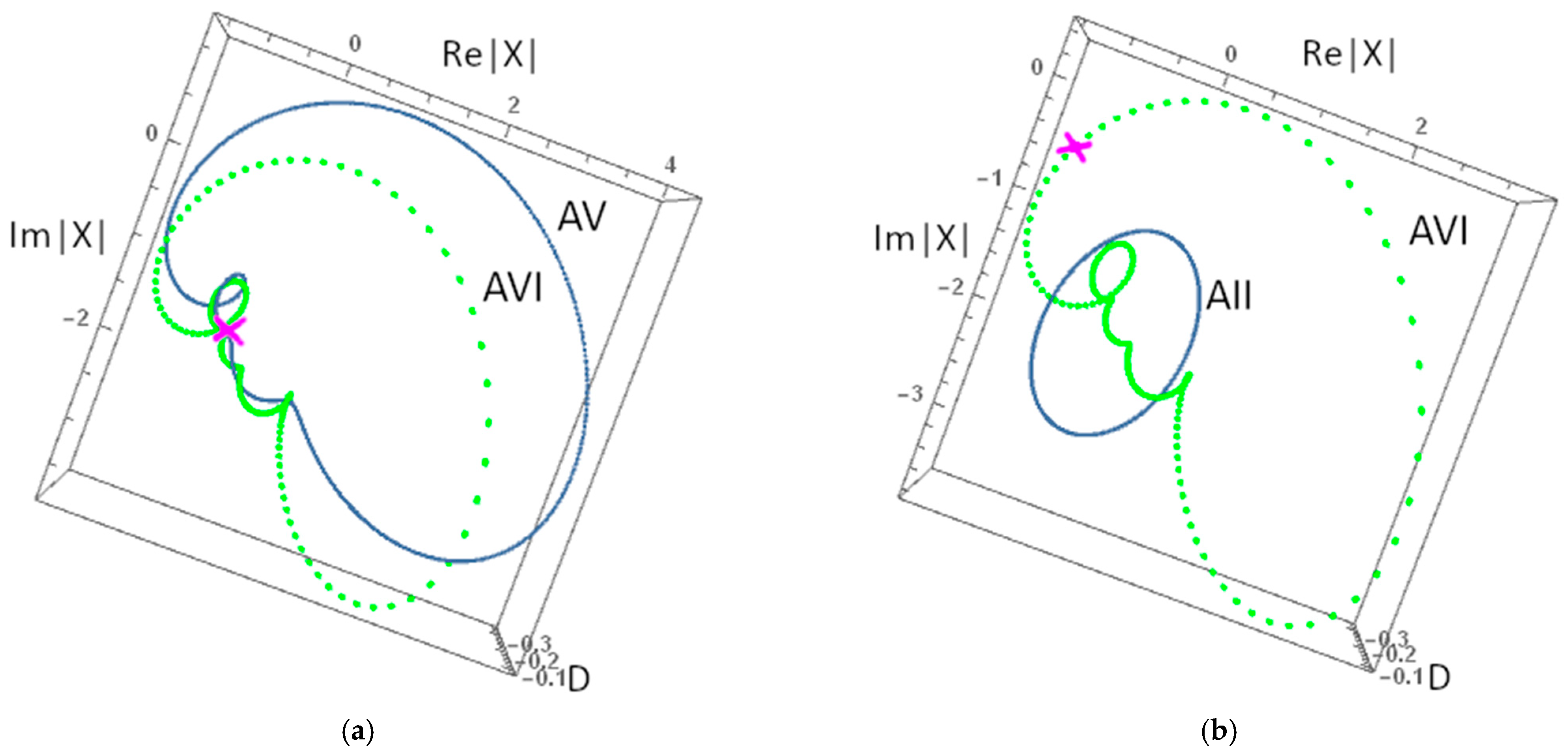
2.2.1. Generic Attractor Characteristics

To date, we have identified the following generic attractor characteristics that are predicted by LEs. A common attractor LE spectral boundary outlines the borders of each of the attractor and window domains. A 2-zero LEs’ signature that is common to several other spectral patterns indicates the beginning and ending of each attractor’s existence [37]. That is, as the injected signal is either increased or decreased, the point of the attractor’s origin or demise is a pair of zero LEs. In between these two extremes, the attractor’s spectral pattern evolves as the dynamics dictate. Figure 2a displays each attractor via its LE pattern in the context of the total unstable LIS domain for this set of parameters. In Figure 2b–d individual LE attractor domains are displayed corresponding to A, B, and C in Figure 2a. Each exhibits the characteristic boundary of converging and diverging Lyapunov spectra and the signature zero pair of LEs. The 8 known attractors are color coded as follows: AI is burnt orange, AII is red, AIII is green, AIV is purple, AV is blue, AVI is yellow, AVII is gray, and AVIII is pink.

A cluster of asymmetric LE bubbles along with their signature zero-pair LEs’ at their apexes represent a forward (in AVII and AVIII) or backward bifurcation sequence, (in AIV); how the sequencing evolves can be interesting. See results in Section 3.1. Figure 2a displays one symmetric bubble in AIII, but this characteristic pattern indicates a different type of dynamics other than the asymmetric bubbles. The following discussion elaborates on symmetric-like LE bubbles.

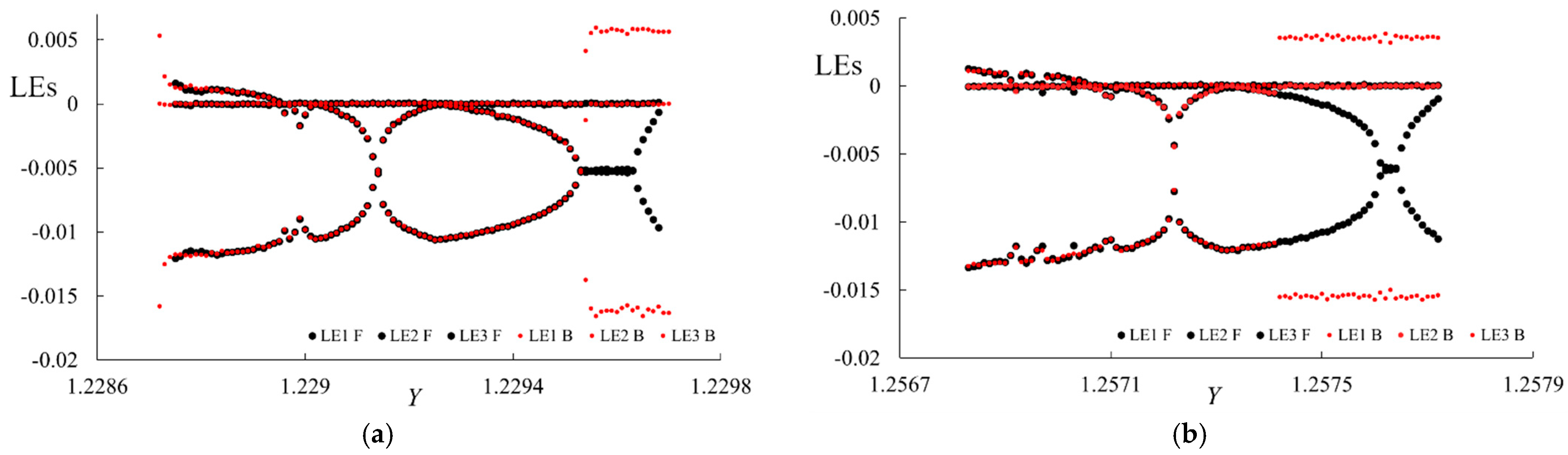
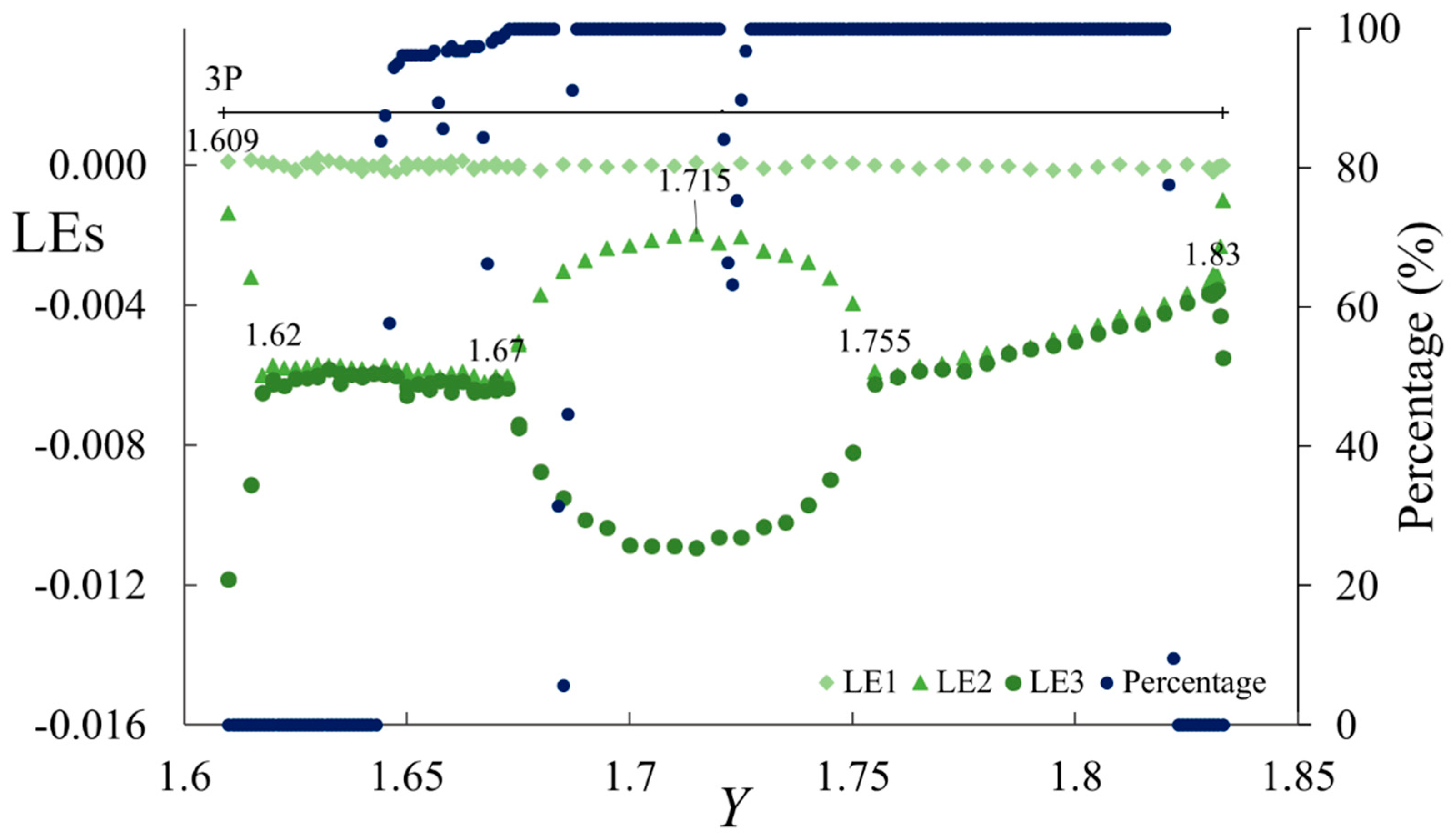
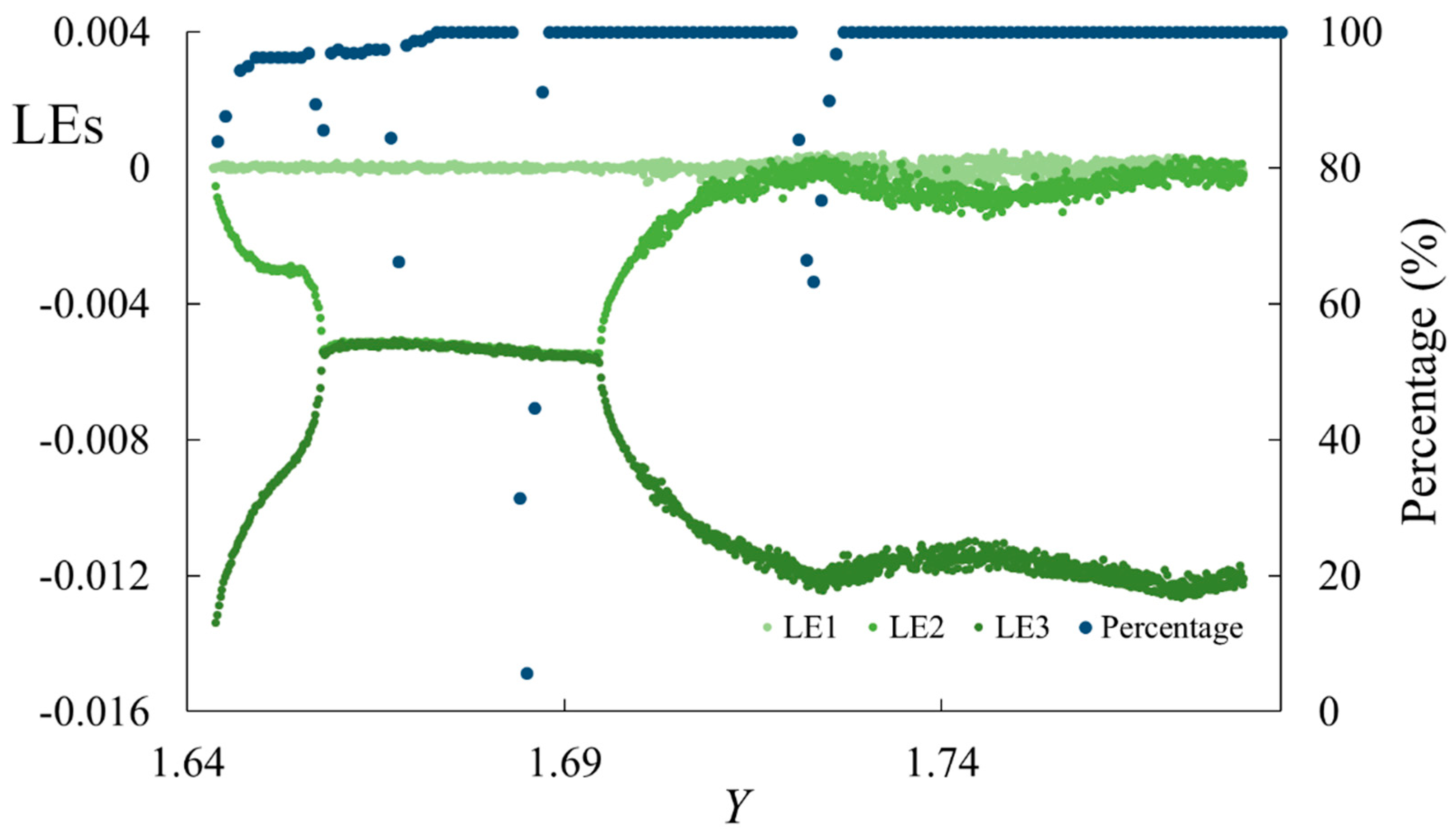
2.2.2. Symmetric-like LE Bubbles

The symmetric-like bubble emerges as a Lyapunov spectral pattern that predicts imminent changes in the dynamics when a parameter is modified slightly. The bubble has an apex located near its center that is not a zero LE. We suspect this apex has something to do with the probability of transitioning dynamics when one of the parameters of the system is changed. There is more discussion on this in Section 4.3. The function of the symmetric-like bubble becomes clearer when linked to the studies of Bonatto et al. [12,13] and Mandel and Erneux [44]. The symmetric-like bubble is now understood to be the forerunner to an imminent bifurcation in the system dynamics, when one of the parameters, such as the gain, is changed. To examine the effects of changing the gain on the attractor dynamics, we collect the LEs associated with “corkscrew” attractors: AIII, AV, and AVI and discuss further in Section 3.1.

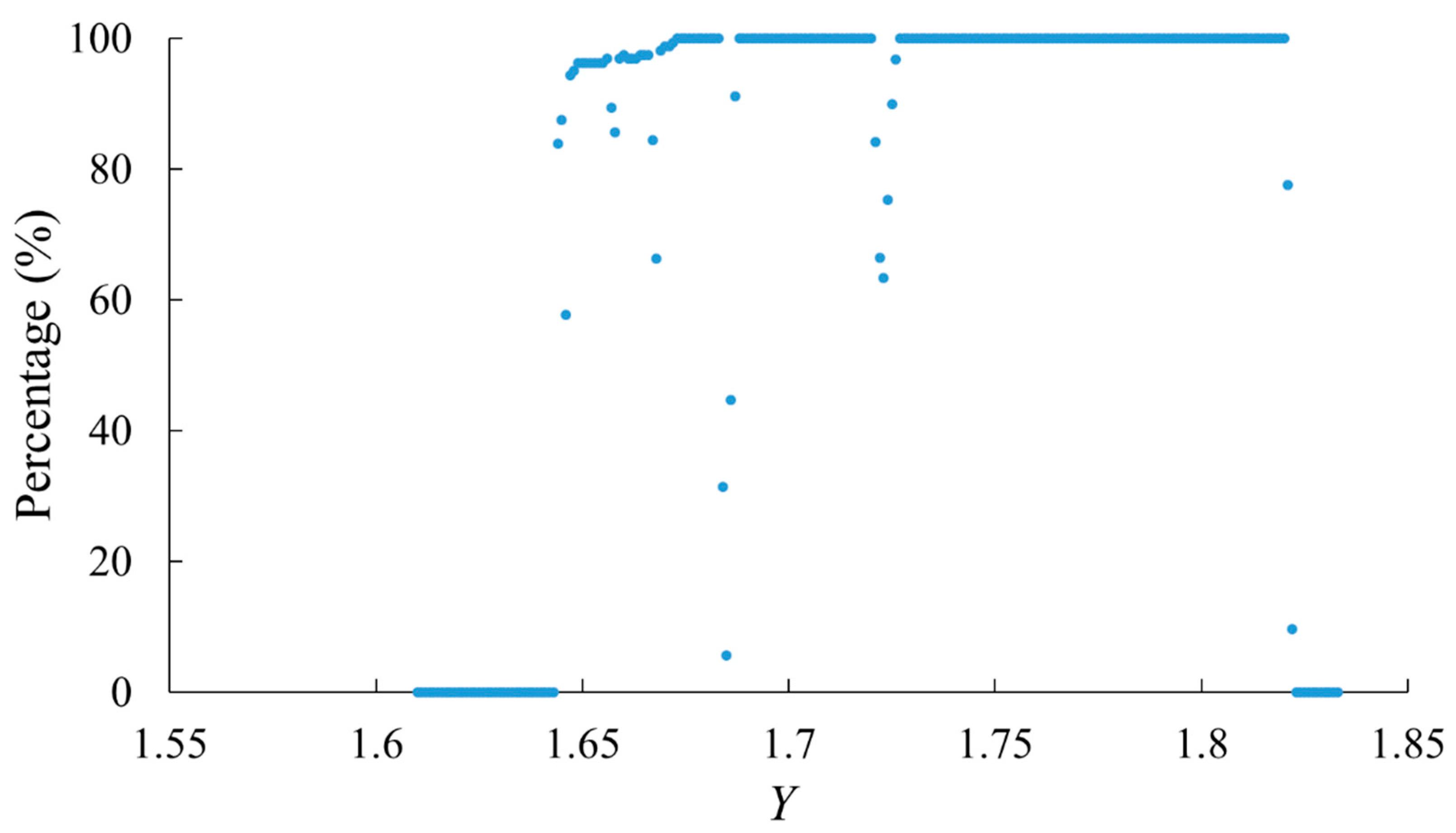
2.2.3. Window Characteristics Predicted by Lyapunov Exponents

In Figure 3 we present 2 unique LE profiles of windows in chaos, WI and WII, that are graphed within their domains as a function of Y. The 2-color scheme in each graph of WI and WII is the result of forward (black) and backward (red) scans of their domains. Note, that the backward scan is not an exact replica of the forward scan. Since these scans are executed adiabatically, the accuracy of landing on WI or WII is imperfect. That is, we believe, the backward scan follows the chaotic trajectories temporarily because the accuracy of the calculations is insufficient to acquire WI and WII at their demise.

It is easy to see that as a function of the control parameter Y, the 2 windows of Figure 3 possess asymmetric bubble patterns. The significance of these results is that windows can be identified using LEs in the same way that attractors are identified. Further, the discovery of the windows in this study was made using the power-shift method [34], as described in Appendix A. By dividing the range ΔY into 1001 segments and evolving for T = 20,000τ at Y = 1.229 we found WI and at Y = 1.2575 we found WII.

2.3. Power Shifting to Access Attractors or Windows

2.3.1. A Theoretical Example of Power Shifting

The power-shift (PS) method requires a nonlinear system with an independent control parameter. Power shifting is a type of incremental perturbation of the control parameter with the result of either accessing known or discovering new attractors (or windows). The method employs specific timings to steer the dynamic trajectory from one known attractor to another that may even coexist.

The power-shift method works in the laser with injected signal by changing the input signal Y at specific points on a known stable limit cycle. In Figure 4a there are 2 sets of limit cycles of known attractors superimposed on each other. The magenta x on base AVI (period four limit cycle in green) marks the position where the injected signal is down shifted from Y₀ = 1.96 to Y_PS = 1.84. The system trajectory jumps from base AVI to resultant AV (period three limit cycle in blue). In Figure 4b for a different location on base AVI, again marked by a magenta x, we show that the system trajectory moves off base AVI to resultant AII using the same down shift values from Y₀ = 1.96 to Y_PS = 1.84. Note, AV and AII coexist at Y = 1.84.

2.3.2. Power-Shift Base Attractor Optimization

In this investigation we use the power-shift method to collect the statistics associated with the successful access of a desired attractor. We initialize the system on the base attractor for 1 control parameter value Y₀ and power shift to Y_PS while at different locations on the limit cycle uniformly distributed in time. For convenience, we set 1 point on the limit cycle as the reference point. An obvious choice for the reference point is the time associated with the attractor’s peak-output power. Next, select any location on the limit cycle as the time after the peak (TAP). We observe to which attractor each TAP evolves. Finally, select a new Y₀ usually in increments of ΔY₀ = 0.01 and repeat the investigation for the same power shift, Y_PS. The results are tabulated across the domain of the base attractor and evaluated for the largest tranche (or time intervals) of TAPs that accesses the desired attractor, or it might be said, for the most efficient Y₀ of the base attractor domain.

An experimentalist might choose to time the power shift at the middle of the tranche, because it gives the largest allowable margin of error for a successful power shift. In the following discussion we include noise and ramp the injected signal.

2.3.3. Power Shift with Noise and Ramped Injected Signal

The power-shift method can be altered theoretically by applying noise to the injected signal frequency at regular intervals in time with an amplitude range simulating experimental conditions more accurately. We add noise with amplitude 0.015 to the injected signal frequency every 0.4τ using the RandomReal function in Mathematica. The addition of noise in the injected signal frequency does modify slightly the system parameters $\tilde{\mathsf{\Delta }}$ and Φ to comport with the model. The change is insignificant.

The second modification of the power-shift method’s experiment is to apply a linear ramp to the power-shift amplitude instead of the Heaviside function initially used. In experiment, an actual laser does not instantaneously reach its new power. To simulate the lag effect, we select power shifts of the type Y(τ,TAP) = Y₀ + slope(τ-TAP), slope = (Y_PS − Y₀)/T_lag. See Section 3.2.1 for the results of the data collection.

2.3.4. Interim Parameter (Gain) Shift

The interim parameter (gain-)shift functions in the following way: Start on a limit cycle and abruptly change the value of the gain for a certain amount of time and then shift it back to its original value. This may result in accessing a different attractor. For our study, we select the gain parameter, because it is convenient and works well as an experimental adjustable. To interim gain shift, we begin at the peak electric field output as the initial condition at t = 0 and allow the system to evolve along the limit cycle until we reach the desired TAP. At that point, we slightly change the gain from its original value to its new value. After an arbitrary t = 10,000τ we shift the gain back to its original value and record the trajectory’s evolution to the resultant attractor. For this study we chose to shift through AIII’s domain; we record different TAP tranches on the limit cycle and determine the statistical distribution resulting from the gain shift. This gives the percentage chance the system leaves its original (base) attractor. See Section 3.3 for results.

3. Results

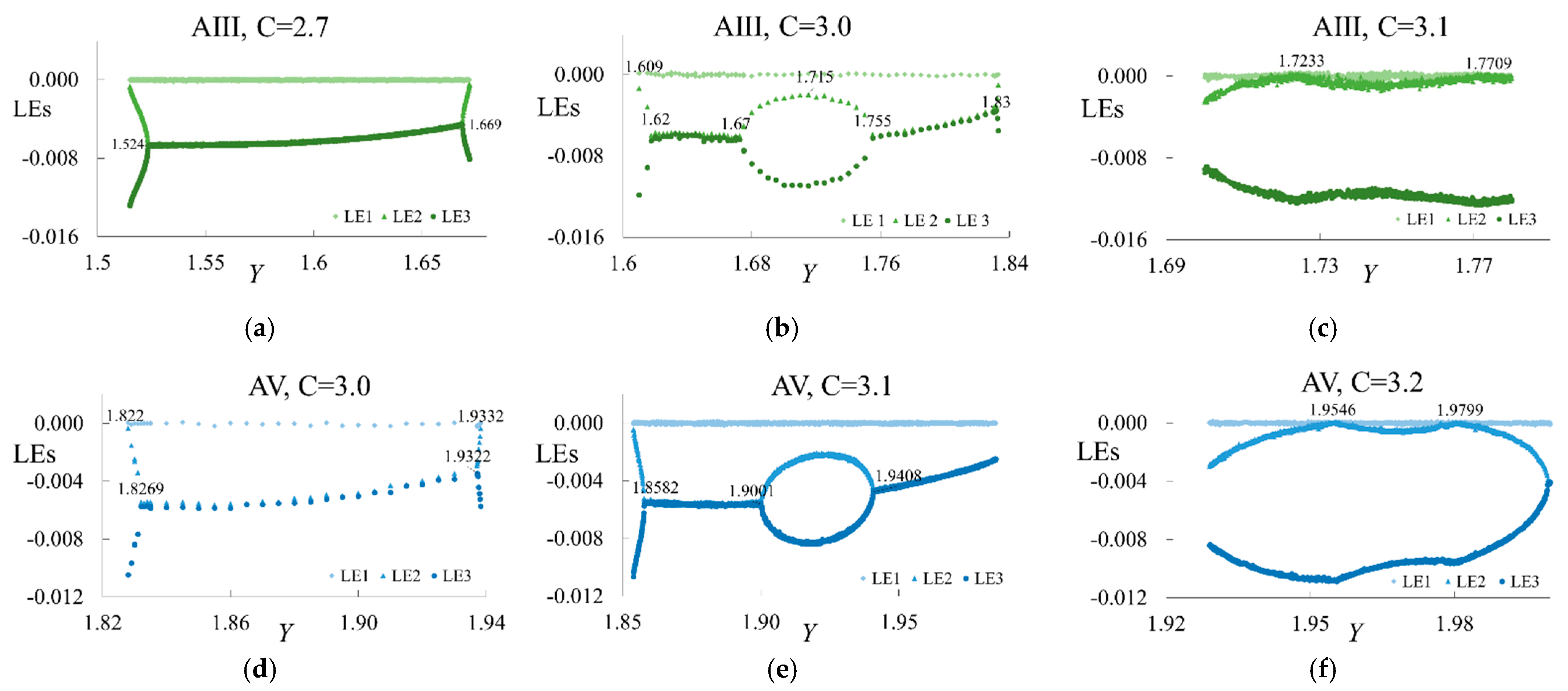
3.1. Gain Changes on Lyapunov Exponent Patterns

In Figure 5a–c we calculate the LEs of AIII using different gains (C values), one value lower than C = 3.0 and the other value larger. The LE pattern, Figure 5a, at a lower value of C = 2.7 no longer exhibits a symmetric-like bubble; it is replaced by a curved trajectory of two equal LEs. A change to a higher value of C = 3.1 shows the LE replacement as the expected asymmetric bubble in Figure 5c, described in Reference [37]. The LE patterns of AIII at C = 2.7 resemble the LE patterns of AV and AVI at the standard (canonical) C = 3.0. Because of their resemblance, we then explored the LEs for AV and AVI to inspect their evolutionary LE pattern changes when C increases from 3.0, to 3.1 and 3.2 for AV, and C increases from 3.0, to 3.2, 3.25, 3.3, and 3.35 for AVI. The results are shown in Figure 5d–f and Figure 6, respectively.

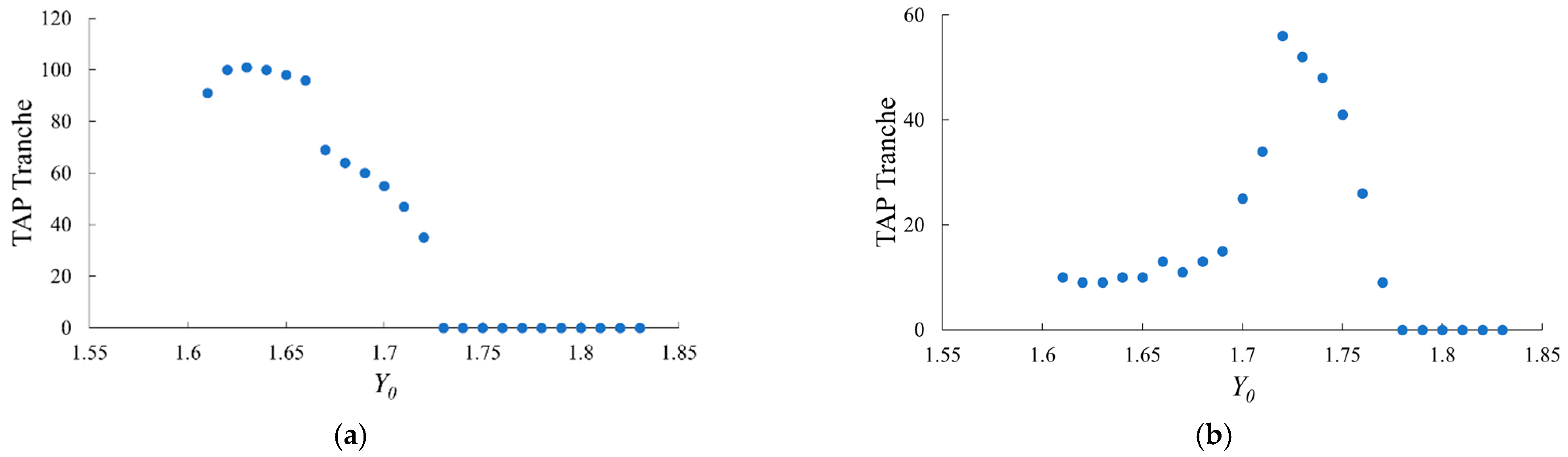
3.2. Power Shift

3.2.1. Optimized Base Attractor for Power Shift

We demonstrate optimized power–shift conditions for a base attractor in Figure 7. Figure 7a plots the largest tranches (time intervals) that transition to AV as a function of Y in AIII’s domain when power shifted to Y_PS = 1.84; the domain is divided into steps of ΔY₀ = 0.01. We find the power shift at Y_o=1.63 has the largest tranche for transitioning to the desired AV. Figure 7b uses the same conditions as Figure 7a except the power shift changes to Y_PS = 1.96 to access the desired AVI. This optimization scheme can be achieved for any valid set of base and goal attractors.

Figure 8a shows results beginning on base AIII at Y₀ = 1.63 and power shifted to Y_PS = 1.84 every 1τ along the period of motion. The resultant attractors, AV or AII, are recorded. The blue and red segments illustrate along the temporal period, 163.551τ, the system’s viable tranches where either AV or AII can be found, respectively. In Figure 8b we show the results beginning on base AIII at Y₀ = 1.72 and power shifted to Y_PS = 1.96 for every 1τ. The resultant attractors, AVI or AII, are recorded. Note, at the end of one period is the beginning of the other, so we can combine the points on both ends to configure the total tranche size. In this case we had 101 contiguous points in a single period of AIII going to the desired AV in Figure 8a and 55 contiguous points going to the desired AVI in Figure 8b.

3.2.2. Addition of Noise

Figure 9 shows the result of adding noise to the system for the same conditions as in Figure 8a. Two example results are shown using identical conditions except for different randomly generated noise.

3.2.3. Linear Ramp on Injected Signal

In Figure 10 we modify the power-shift method with a time lag, T_lag = 15, at Y₀ = 1.63 for base AIII with the Y_PS = 1.84 to simulate experimental conditions. Graphing two periods of the motion dramatizes the range of the tranche that goes to AV using a linear ramp.

3.2.4. Linear Ramp and Noise Included

Figure 11 illustrates the result of adding both a linear ramp with T_lag = 15 and noise as in Figure 8a to the power-shift method. We see similar results in the studies without lag.

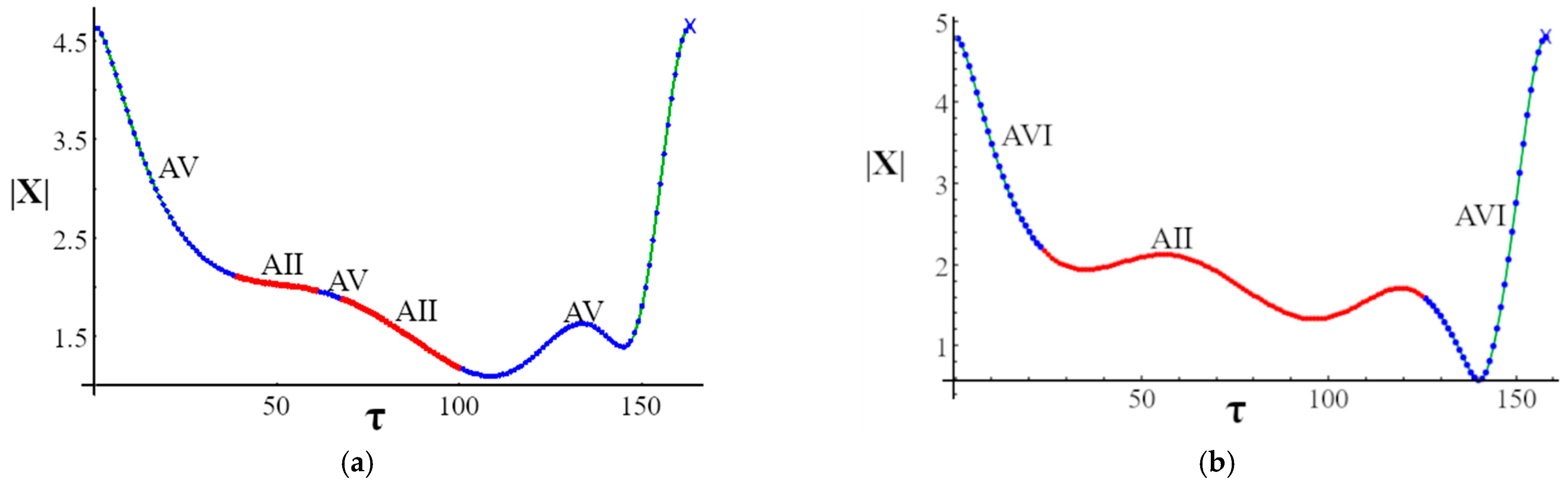
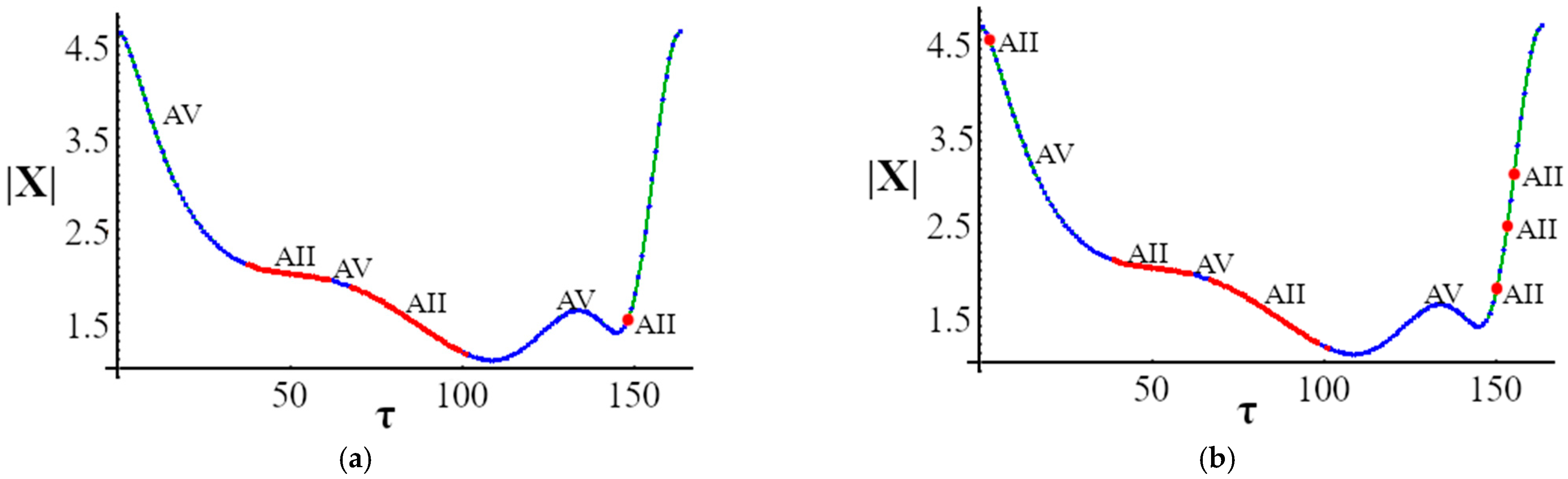
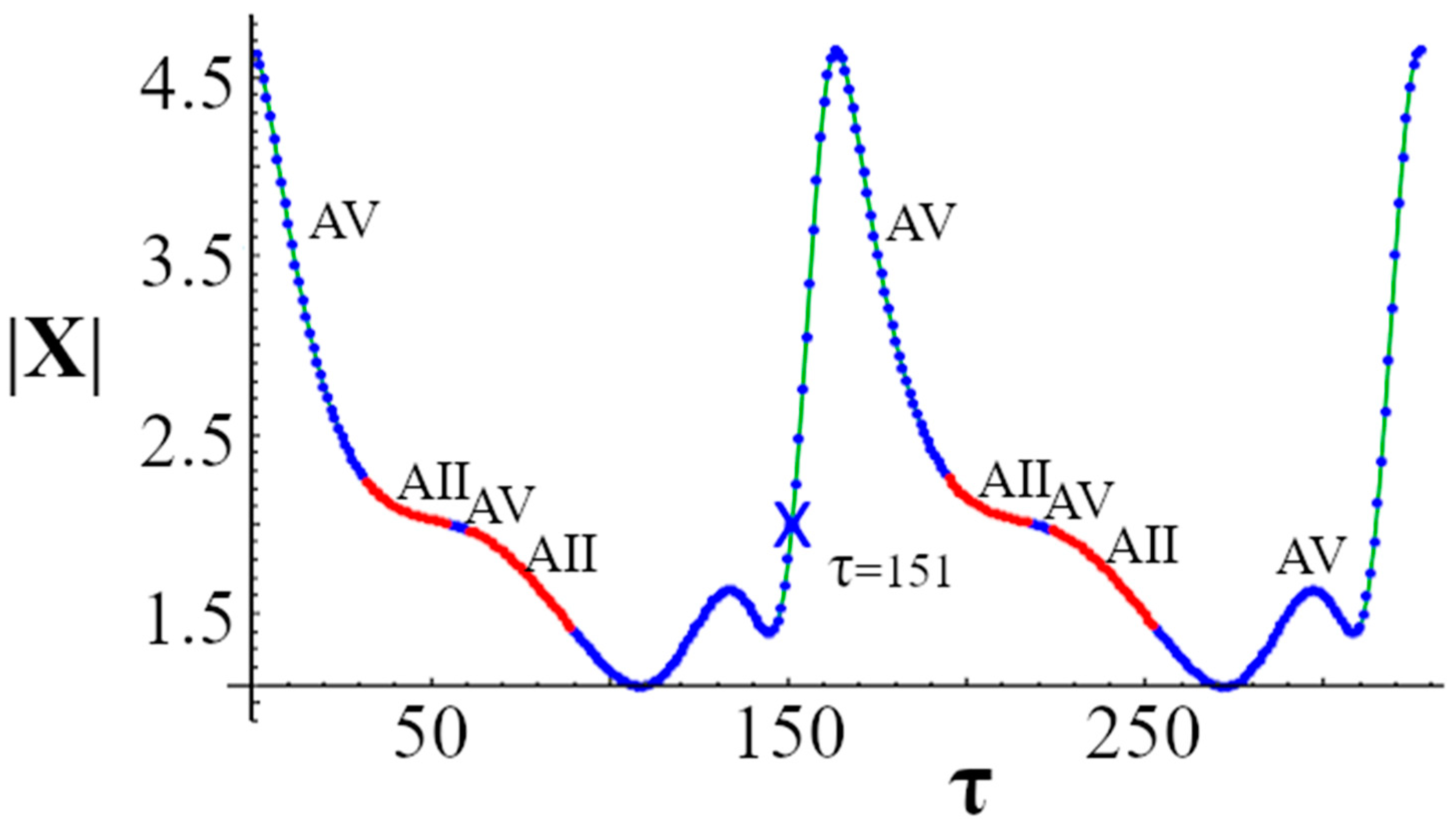
3.3. Interim Gain-Shift Results

Figure 12 illustrates the results of an interim gain shift lasting for 10,000τ by plotting the percent chance AIII survives the shift from C = 3.0 to C = 3.1 as a function of Y. Clearly for this shift, there is a high percentage of AIII surviving with some intermittencies when Y ≥ 1.64. No experimental complications are addressed in this study.

4. Discussion

4.1. Gain Change Effects on LE Patterns

Gain parameter changes clearly affect LE patterns because they alter the parameters of the system. As discussed in Section 3.1 and shown in Figure 5a, the gain is decreased from the canonical C = 3.0 to C = 2.7; here the symmetric-like bubble is eliminated leaving a pattern similarly matching the canonical AV and AVI. In Figure 5b,c the gain is increased from C = 3.0 to C = 3.1, respectively. Due to this slight increase, a symmetric-like bubble changes to an asymmetric bubble supporting the hypothesis that symmetric-like bubbles represent an imminent bifurcation in the system. In Figure 5d–f the gain parameter increases from the canonical C = 3.0 to C = 3.2, where there is a first transition to a symmetric-like bubble, and second to an asymmetric bubble, confirming the thesis that symmetric-like bubbles are predictors of an imminent bifurcation provided there is a small change to one parameter of the system. Note, this result is consistent with the studies in References [13,44] who confirm these types of dynamic changes. It is interesting that a new symmetric-like bubble emerges in Figure 6d forecasting the bifurcation shown in Figure 6e.

4.2. Power Shift

4.2.1. Optimized Power Shift

We find AIII has the largest tranche of points that transition to AV at Y₀ = 1.63 when power shifted to Y_PS = 1.84. For accessing AVI, we find AIII’s largest tranche is at Y₀ = 1.72 when power shifted to Y_PS = 1.96. The largest tranche going to AVI is close to the peak of the symmetric-like LE bubble in AIII. The results for accessing AVI, however, also support the theory because the largest tranche is located only ΔY = 0.005 from the apex. The results for AV, however, do not support the hypothesis that the apex of the symmetric-like bubble is the ideal value from which to power shift, because the largest tranche exists at a much lower value of Y.

The location of the largest tranches for each attractor can be tabulated theoretically to create a “roadmap” of the system describing the most effective way to access every attractor solely through power shifting. See Appendix B,

Table A1. LIS Attractor Access Via a Power Shift Y_PS.

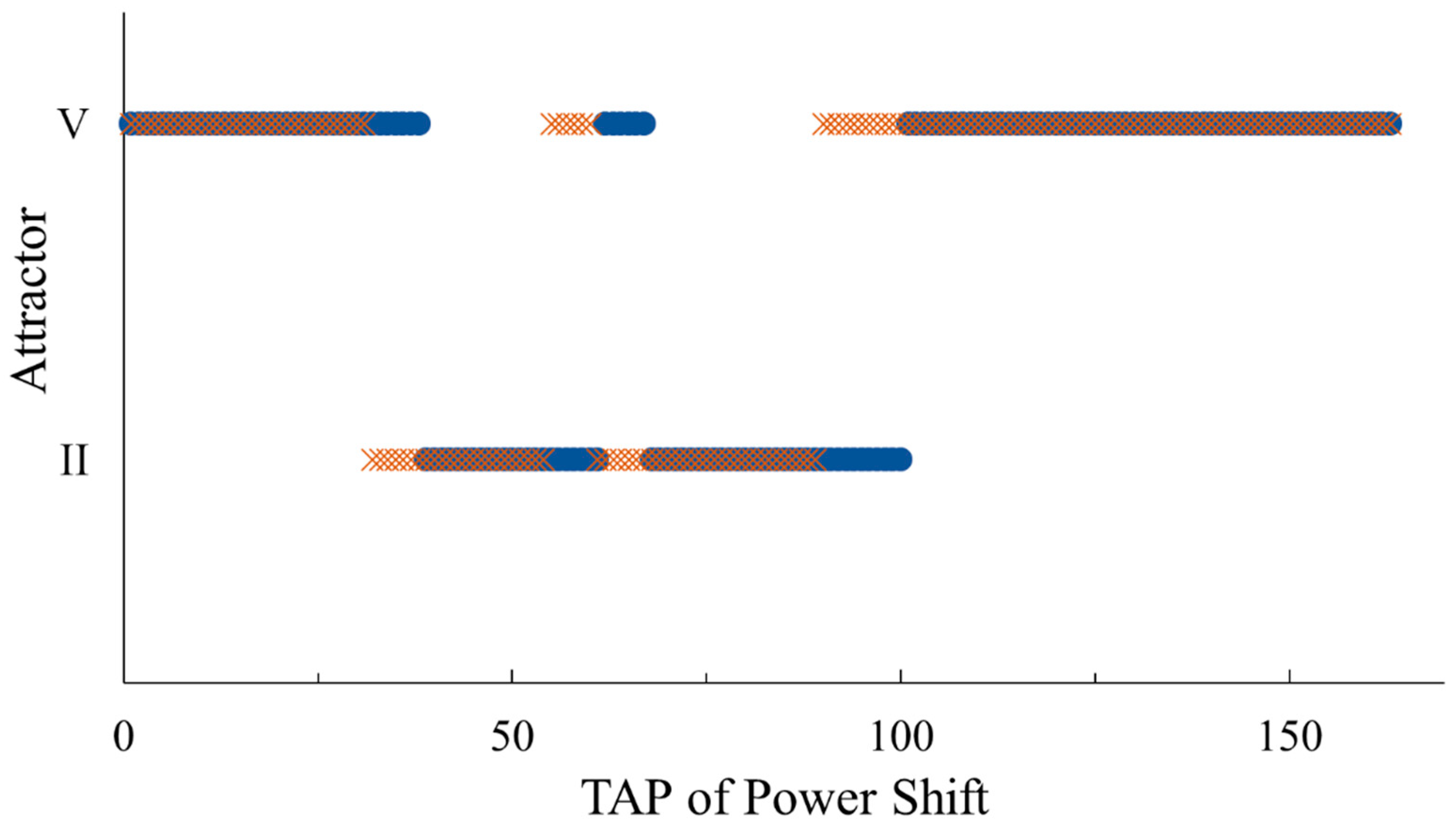
Goal Attractor	Base Attractor	Base Period (τ)	Y0	YPS	TAP ± Leeway
AI	Any		Any
AII	Any		Any	1.54	Any
AIII	AII	108.025	1.51 *	1.8	8 ± 52
AIV	AI	63.132	0.854	1.114	3 ± 4
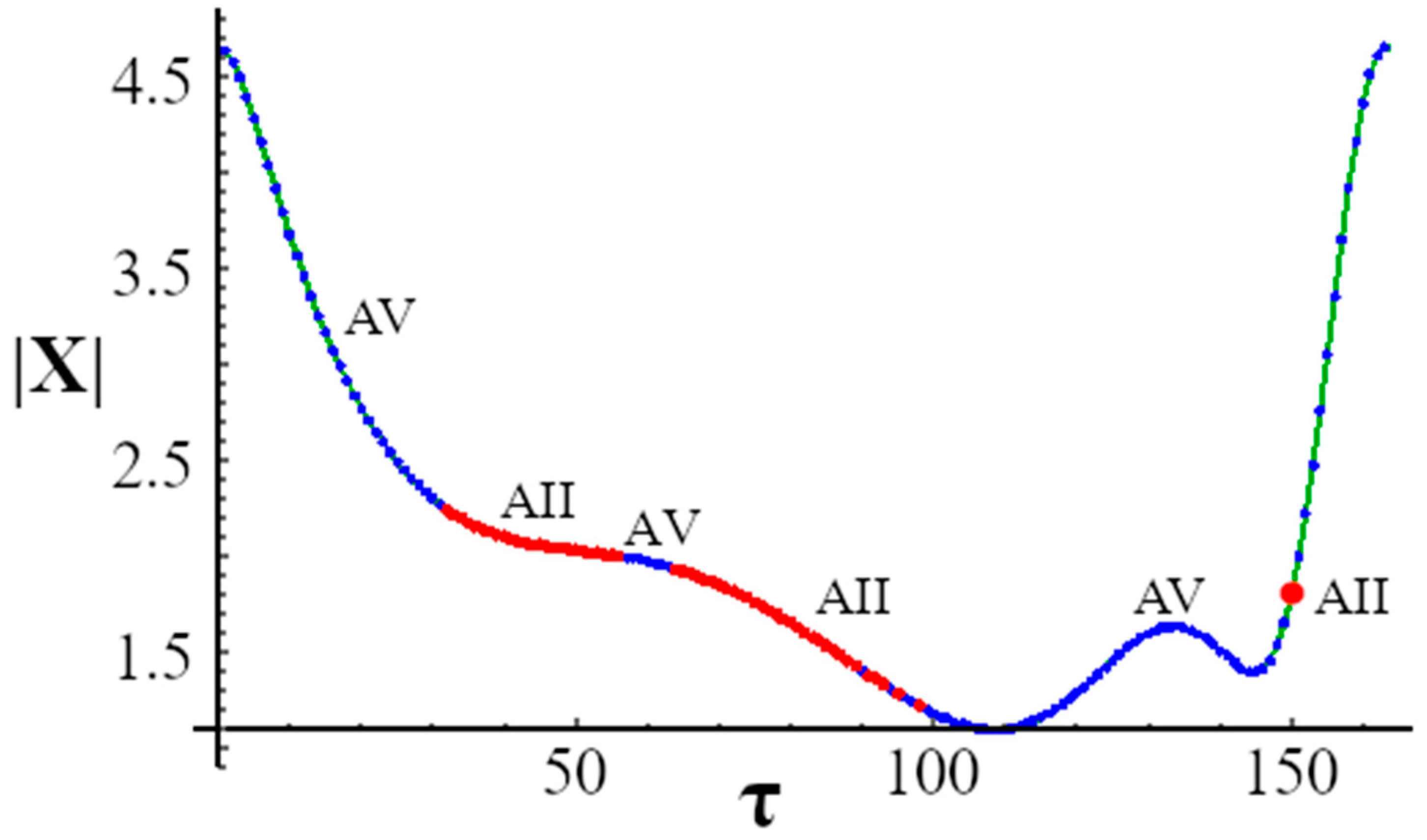
AV	AIII	163.551	1.63 *	1.84	151 ± 50
AVI	AIII	158.396	1.72 *	1.96	154 ± 27
AVII	AIII	156.964	1.8	1.269	138 ± 2

* Y₀ optimized using the method performed in Figure 7.

, as an example.

4.2.2. Effects of Noise

As expected, noise induces some changes indicated by the intermittent transitions to AII in Figure 9, where the tranche of AV dominates without noise, as shown in Figure 8a. At this level of noise, we can say that the power-shift method is still viable. However, because of the intermittencies to AII, it may take multiple tries to access the desired attractor. Note, AIV, AVII, and AVIII are all small domain attractors which are difficult generally to access. Preliminary tests show noise will most likely prevent any access to these three attractors. Clearly AIII, AV, and AVI have larger domains and survive small amounts of noise. AIII, which has the largest domain of AV and AVI, survives a greater noise amplitude.

4.2.3. Effects of a Ramp on the Injected Signal

We compare the power-shift method with and without the linear ramp on the control parameter. In Figure 13 we show the resulting attractor vs. TAP. The blue dots represent the stepwise injected signal at Y₀ = 1.63 for base AIII with the Y_PS = 1.84, i.e., with no T_lag. The orange xs represent the linear ramp with T_lag = 15τ.

The orange xs show that the effect of the ramp is minimal. In fact, access to AV is improved by 2.65%. There is a shift to the left by the orange xs suggesting that a power shift should be conducted slightly earlier to compensate for the lag effects that may appear. Looking at the main tranche we see the orange xs fall off 7τ earlier than the blue dots and also returns 11τ earlier, giving us a net time increase of 4τ. This shows that a slight lag in the power shift might help instead of hinder access.

4.3. Gain Shift versus Symmetric-like Bubble

Originally, we believed that the apex of the symmetric-like bubble might be the ideal place to gain shift due to it having greater instability. However, the data shown in Figure 14 tells a different story. The system shows an instability at a location that seems to not match with the LEs. The dip at Y = 1.721 does not line up exactly with the apex of the symmetric-like bubble, instead, it is slightly to the right.

When we instead superimpose the gain shift with the LEs for C = 3.1 in Figure 15, we see a dip where the asymmetric bubble reaches its apex, the signatory two-zero LEs.

This tells us that, when the parameter shifts, we must consider the stability of the attractor at both the original parameter value and the shifted value. In other words, when the gain-shift method is applied, one needs to consider the attractor’s stability at both gains.

5. Conclusions

By power shifting, we can discover windows and access many attractors reliably even with noise on the frequency and a linear ramp on the injected signal amplitude of LIS. We select a base attractor which enhances the power shift’s reliability of accessing a desired attractor. Using the modified power-shift technique with the interim parameter shift, we expand access to attractors by temporarily modulating the gain (parameter), in this case. The power-shift method in conjunction with the interim parameter shift is attractive because it can be experimentally applied without significant or long-lasting modifications to the experimental system itself. When gain-shift results are compared to the LE patterns for a specific gain, we find critical points of the spectra where the attractor is unlikely to survive the gain shift. Noise and lag effects obscure the power-shift technique minimally for large domain attractors. Small domain attractors are inaccessible. Experimentally, we believe that the enhanced power-shift method, which enables an experimentalist to both discover and access coexisting attractors, is appealing because this provides flexibility to move from one type of system dynamics to another. By varying other system parameters, this method could facilitate, for example, a mapping of the dynamical states in parameters space of frequency detuning [7].

The Lyapunov exponents continue to herald system dynamics, attractor and window domains, and the level of instability associated with the various patterns. We know, for example, that every attractor has a unique LE pattern that is choreographed by the subtle variations of the attractor dynamics and are circumscribed by converging and diverging LE spectral patterns including the signature two-zero LEs at the origin and demise of the attractor [37]. We understand symmetric-like and asymmetric bubbles as imminent bifurcations and existing bifurcations, respectively. These results reiterate the universality of the LEs spectra patterns. There are still unknown patterns observed in other nonlinear systems which need to be defined that may or may not be associated with the LIS systems, but what we do know, is that the Lyapunov spectra has many mysteries yet to be discovered.

The power-shift method, along with the interim gain shift, is an answer to the question of how to access individual attractors stably and accurately even under experimental conditions. Identifying the dominance of one attractor over another in the same system and understanding the conditions that might change this dominance remains an open issue.