Detection of Density Changes in Soils with Impedance Spectroscopy
Abstract
:1. Introduction
1.1. Impedance Spectroscopy
1.2. Structure of Dikes
1.3. Contact Erosion
1.4. State-of-the-Art Techniques
2. Materials and Methods
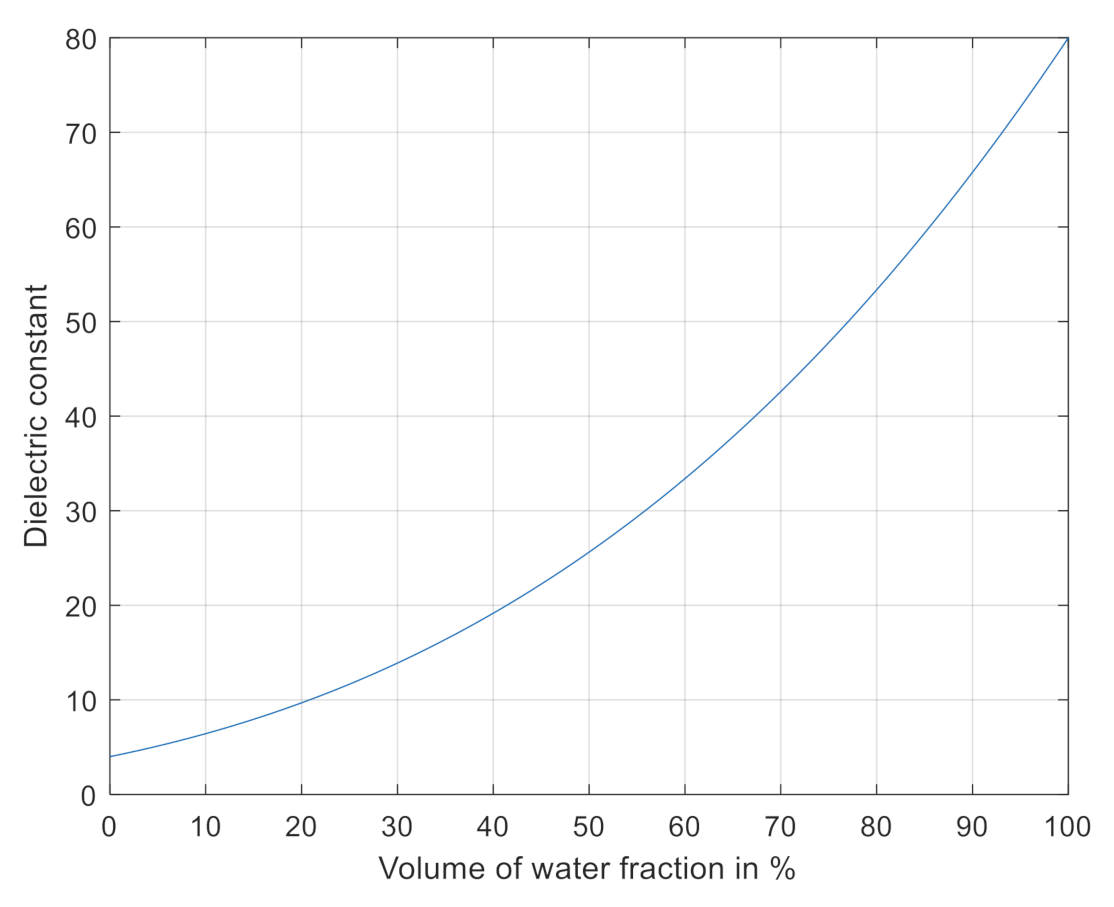
2.1. Dielectric Properties of Soils
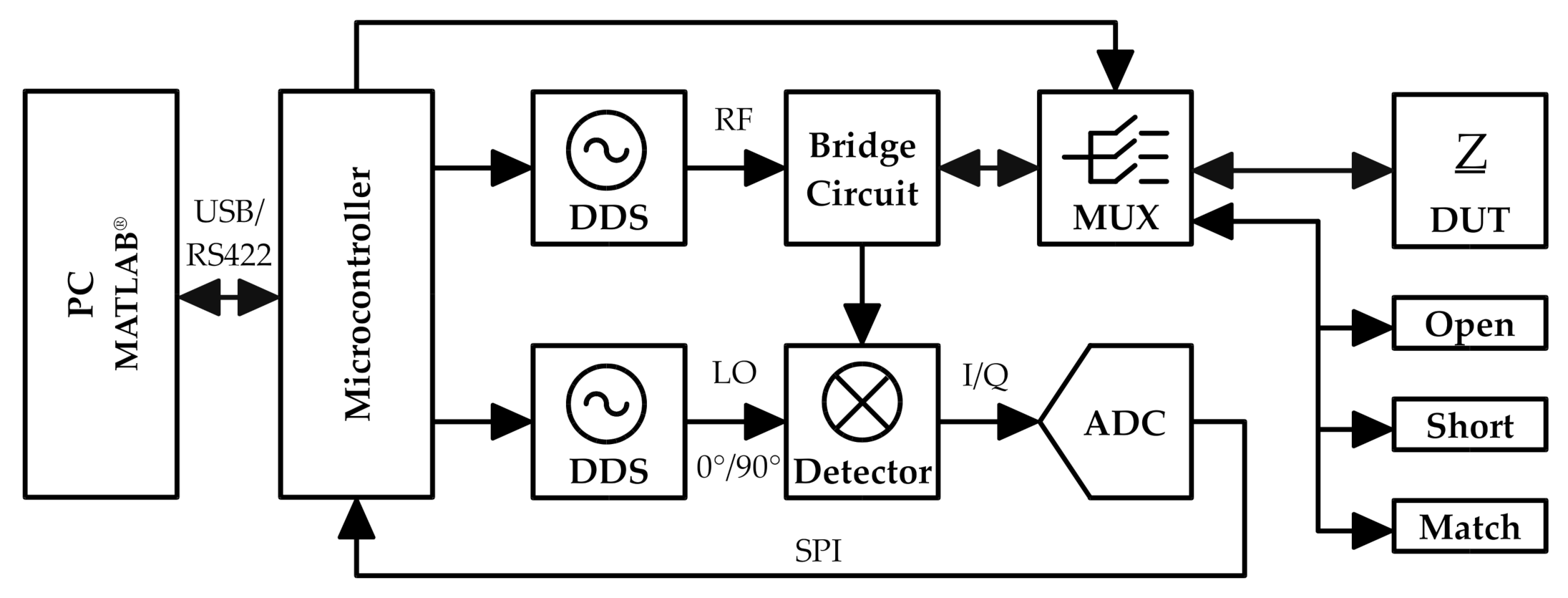
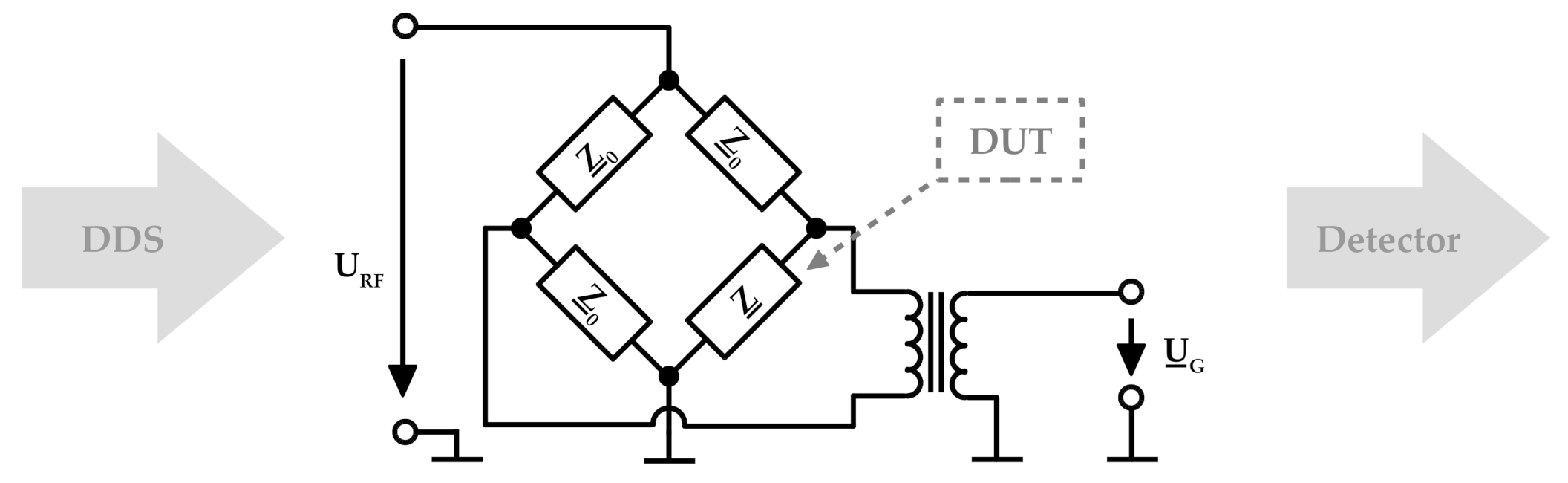
2.2. Measurement Set-Up
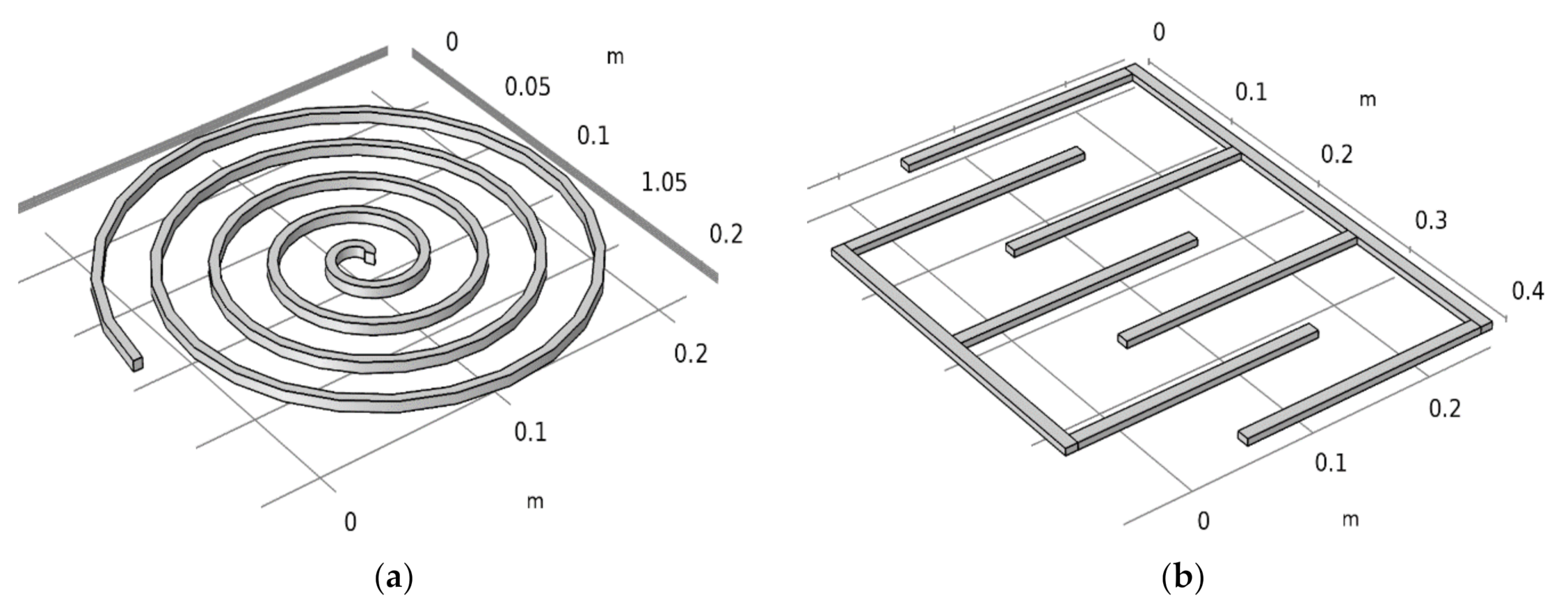
2.3. Sensor Design
2.4. Measurement of Complex Impedances
3. Results and Discussion
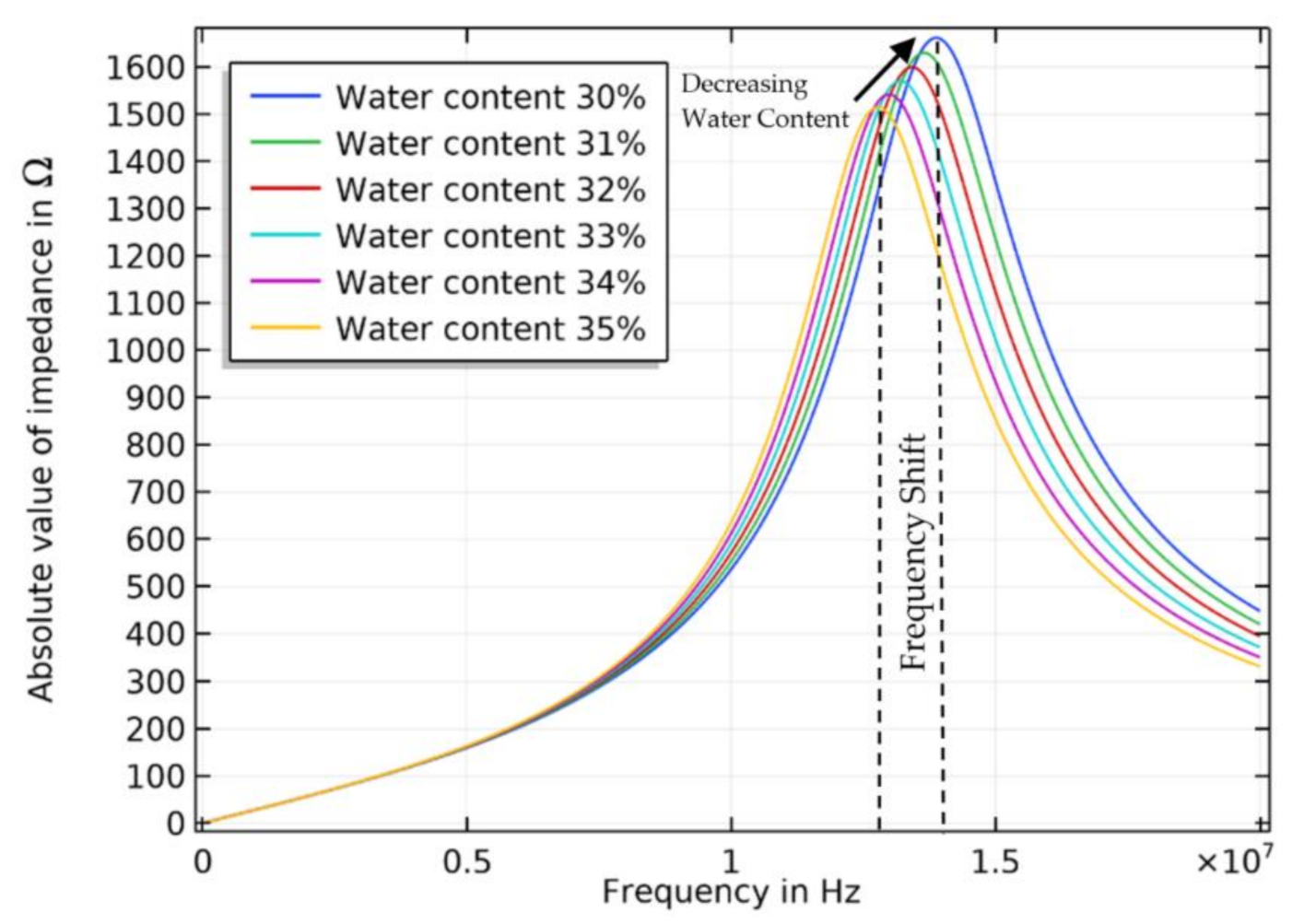
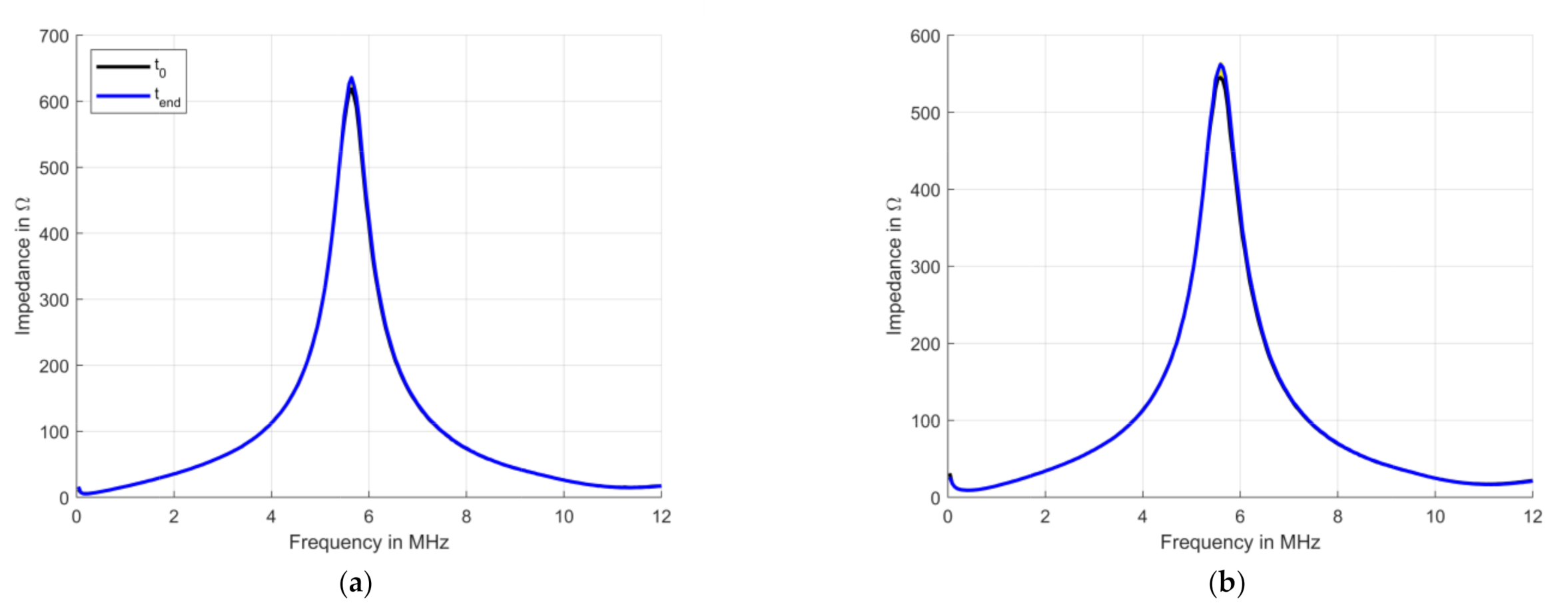
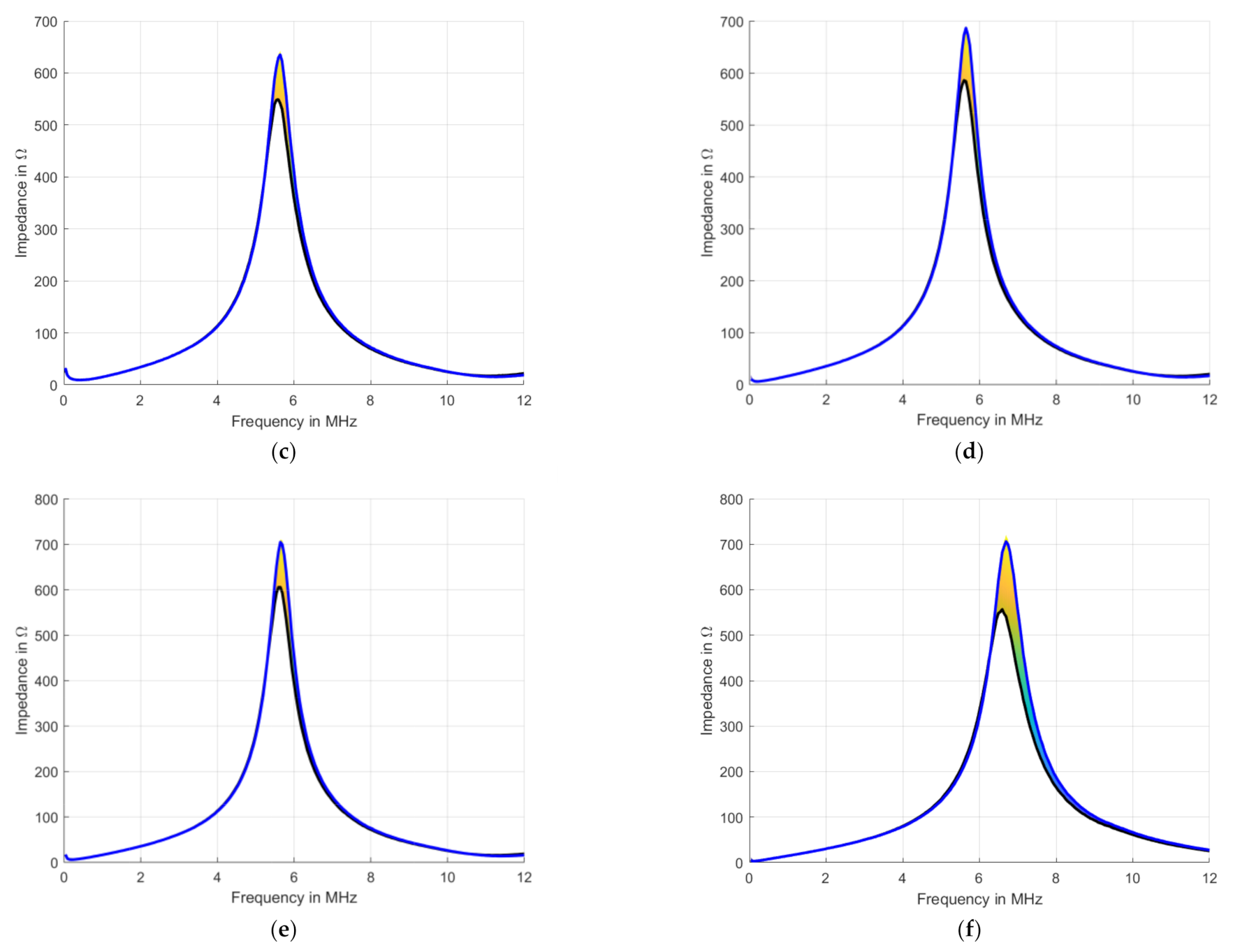
3.1. Measurement Properties and Experimental Results
3.2. Impedance Modelling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- BAW. Merkblatt Materialtransport im Boden; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2013; pp. 12–19. [Google Scholar]
- Kanoun, O.; Tetyuev, A.; Tränkler, H.-R. Bodenfeuchtemessung mittels Impedanzspektroskopie (Soil Moisture Measurement with Impedance Spectroscopy). Tm Tech. Mess. 2004, 71, 475–485. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung. DIN 19712: Flood Protection Works on Rivers; Beuth Verlag GmbH: Berlin, Germany, 2013; pp. 25–29. [Google Scholar]
- Beguin, R.; Philippe, P.; Faure, Y.H. Pore-scale flow measurements at the interface between a sandy layer and a model porous medium: Application to statistical modeling of contacterosion. J. Hydraul. Eng. ASCE 2013, 139, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Guidoux, C.; Faure, Y.H.; Beguin, R.; Ho, C.-C. Contact Erosion at the Interface between Granular Coarse Soil and Various Base Soils under Tangential Flow Condition. J. Geotech. Geoenvironmental Eng. ASCE 2010, 136, 741–742. [Google Scholar] [CrossRef]
- Quinta-Ferreira, M. Ground Penetration Radar in Geotechnics. Advantages and Limitations. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 12019. [Google Scholar] [CrossRef] [Green Version]
- Baker, G.S.; Jordan, T.E.; Talley, J. An Introduction to Ground Penetrating Radar (GPR). Special Paper 432: Stratigraphic Analyses Using GPR; Geological Society of America: Boulder, CO, USA; pp. 1–18.
- Carlsten, S.; Johansson, S.; Wörmann, A. Radar techniques for indicating internal erosion in embankment dams. Appl. Geophys. 1995, 33, 143–156. [Google Scholar] [CrossRef]
- Liu, X.; Ren, T.; Horton, R. Determination of soil bulk density with thermo-time domain reflectometry Sensors. Soil Sci. Soc. Am. J. 2008, 72, 1000–1005. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, X.; Zhang, M.; Heitman, J.; Horton, R.; Ren, T. Thermo–Time Domain Reflectometry Method: Advances in Monitoring In Situ Soil Bulk Density. Soil Sci. Soc. Am. J. 2018, 82, 733–733. [Google Scholar] [CrossRef] [Green Version]
- Ren, T.; Noborio, K.; Horton, R. Measuring Soil Water Content, Electrical Conductivity, and Thermal Properties with a Thermo-Time Domain Reflectometry Probe. Soil Sci. Soc. Am. J. 1999, 63, 450–457. [Google Scholar] [CrossRef]
- Pluta, S.E.; Hewitt, J.W. Non-Destructive Impedance Spectroscopy Measurement for Soil Characteristics. In Proceedings of the GeoHunan International Conference, Changsha, China, 3–6 August 2009. [Google Scholar] [CrossRef] [Green Version]
- Swinford, J.M.; Meyer, J.H. An evaluation of a nuclear density gauge for measuring infield compaction in soils of the South African sugar industry. South Afr. Sugar Technol. Assoc. 1985, 19, 218–224. [Google Scholar]
- Mejias-Santiago, M.; Berney, E.S.; Bradley, C.T. Evaluation of a Non-Nuclear Soil Density Gauge on Fine-Grained Soils; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2013. [Google Scholar]
- Looyenga, H. Dielectric Constants of Heterogeneous Mixtures. Physica 1965, 31, 401–406. [Google Scholar] [CrossRef]
- Hölting, B.; Coldwey, W.G. Allgemeine Hydrogeologie, In Hydrogeologie: Einführung in Die Allgemeine und Angewandte Hydrogeologie; Springer Spektrum: Heidelberg, Germany, 2013; Volume 8, pp. 11–12. [Google Scholar]
- Rhoades, J.D.; Raats, P.A.C.; Prather, R.J. Effects of liquid-phase electrical conductivity, water content, and surface conductivity on bulk soil electrical conductivity. Soil Sci. Soc. Am. J. 1976, 40, 651–655. [Google Scholar] [CrossRef]
- North Rhine-Westphalia State Agency for Nature. Environment and Consumer Protection, Measurement Station for Water Quality of the Rhine in Düsseldorf-Flehe. Available online: http://luadb.lds.nrw.de/LUA/hygon/pegel.php?messstellen_nr=000309&guete=tabelle# (accessed on 6 April 2020).
- Radschun, M.; Morgenstern, T.; Schaefer, R.; Kanoun, O.; Himmel, J. Improved VNA hardware for applications in civil engineering. In Proceedings of the 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech, Marokko, 28–31 March 2017; pp. 719–723. [Google Scholar] [CrossRef]
- Weidenmüller, J. Optimization of Encircling Eddy Current Sensors for Online Monitoring of Hot Rolled Round Steel Bars. Ph.D. Thesis, Chemnitz University of Technology, Chemnitz, Germany, 2014. [Google Scholar]
- Radschun, M.; Jobst, A.; Kanoun, O.; Himmel, J. Process Monitoring in Steel-Mills using Impedance Analysis: VNA Improvement for Data Acquisition. In Proceedings of the 10th International Workshop on Impedance Spectroscopy (IWIS), Chemnitz University of Technology, Chemnitz, Germany, 27–30 September 2017; ISBN 978-3-9817-630-3-4. [Google Scholar]
- Radschun, M.; Jobst, A.; Kanoun, O.; Himmel, J. Velocity Measurement in Rolling Mills using Impedance Analysis. In Proceedings of the 11th International Workshop on Impedance Spectroscopy (IWIS), Chemnitz University of Technology, Chemnitz, Germany, 25–28 September 2018; ISBN 978-3-9817630-5-8. [Google Scholar]
- Radschun, M.; Jobst, A.; Kanoun, O.; Himmel, J. Non-contacting Velocity Measurement of hot Rod and Wire using Eddy-current Sensors. In Proceedings of the 8th IEEE Workshop—Industrial and Medical Measurement and Sensor Technology Vehicle Sensor Technology, Mülheim, Germany, 6–7 June 2019; pp. 34–35. [Google Scholar]
- Jobst, A.; Radschun, M.; Kanoun, O.; Himmel, J. Velocity Approximation of Hot Steel Rods Using Frequency Spectroscopy of the Cross-Section Area. In Proceedings of the 12th International Workshop on Impedance Spectroscopy (IWIS), Chemnitz University of Technology, Chemnitz, Germany, 26–27 September 2019. [Google Scholar]
- Radschun, M.; Jobst, A.; Himmel, J.; Kanoun, O. Summary of developing a test stand for realistic emulation of the cross-sectional area variation of hot rolled wire. Tm Tech. Mess. 2020, 87, 332–342. [Google Scholar] [CrossRef]







| Frequency Range | to |
| Frequency Resolution | 35 m𝐻𝑧 |
| Impedance Range | |
| Impedance Resolution | |
| Sample Rate | @ 10 Points @ 100 Points per frequency sweep @ 1000 Points |
| Measurement | Gravel Grain Size [mm] | Hydraulic Gradient | Volume Change [%] | Impedance Change [%] |
|---|---|---|---|---|
| 1 (a) | 2–4 | 7 | 0.26 | 3.65 |
| 2 (b) | 4–8 | 7 | 0.37 | 4.33 |
| 3 (c) | 4–8 | 9 | 1.56 | 17.21 |
| 4 (d) | 4–8 | 11 | 1.68 | 18.17 |
| 5 (e) | 4–8 | 13 | 3.11 | 17.93 |
| 6 (f) | 4–8 | 13 | 5.34 | 29.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemens, C.; Radschun, M.; Jobst, A.; Himmel, J.; Kanoun, O. Detection of Density Changes in Soils with Impedance Spectroscopy. Appl. Sci. 2021, 11, 1568. https://doi.org/10.3390/app11041568
Clemens C, Radschun M, Jobst A, Himmel J, Kanoun O. Detection of Density Changes in Soils with Impedance Spectroscopy. Applied Sciences. 2021; 11(4):1568. https://doi.org/10.3390/app11041568
Chicago/Turabian StyleClemens, Christoph, Mario Radschun, Annette Jobst, Jörg Himmel, and Olfa Kanoun. 2021. "Detection of Density Changes in Soils with Impedance Spectroscopy" Applied Sciences 11, no. 4: 1568. https://doi.org/10.3390/app11041568






