An Efficient Semi-Analytical Scheme for Determining the Reflection of Lamb Waves in a Semi-Infinite Elastic Waveguide
Abstract
:1. Introduction
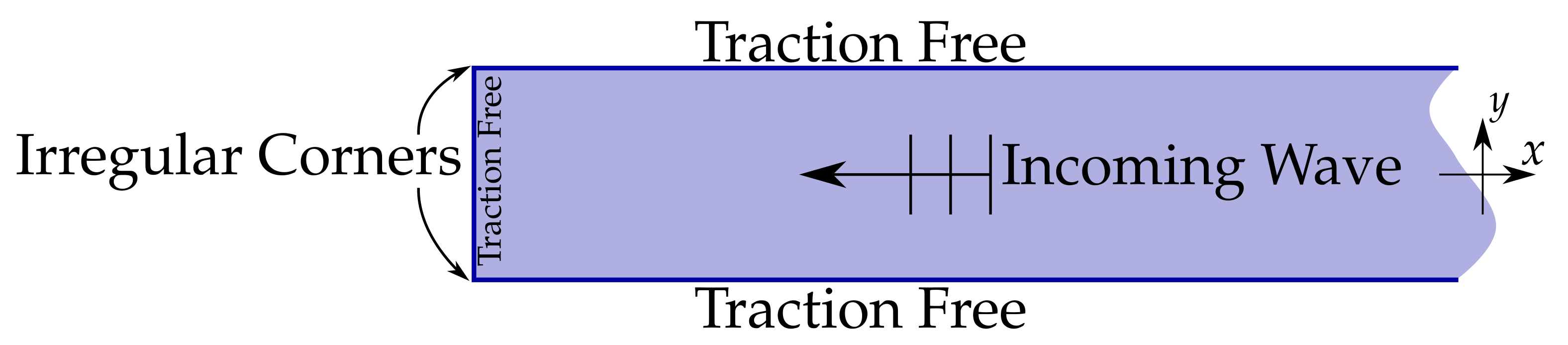
2. Materials and Methods
2.1. A Useful ‘Equivalent’ Problem: A Forced Infinite Elastic Plate
Virtual Plates
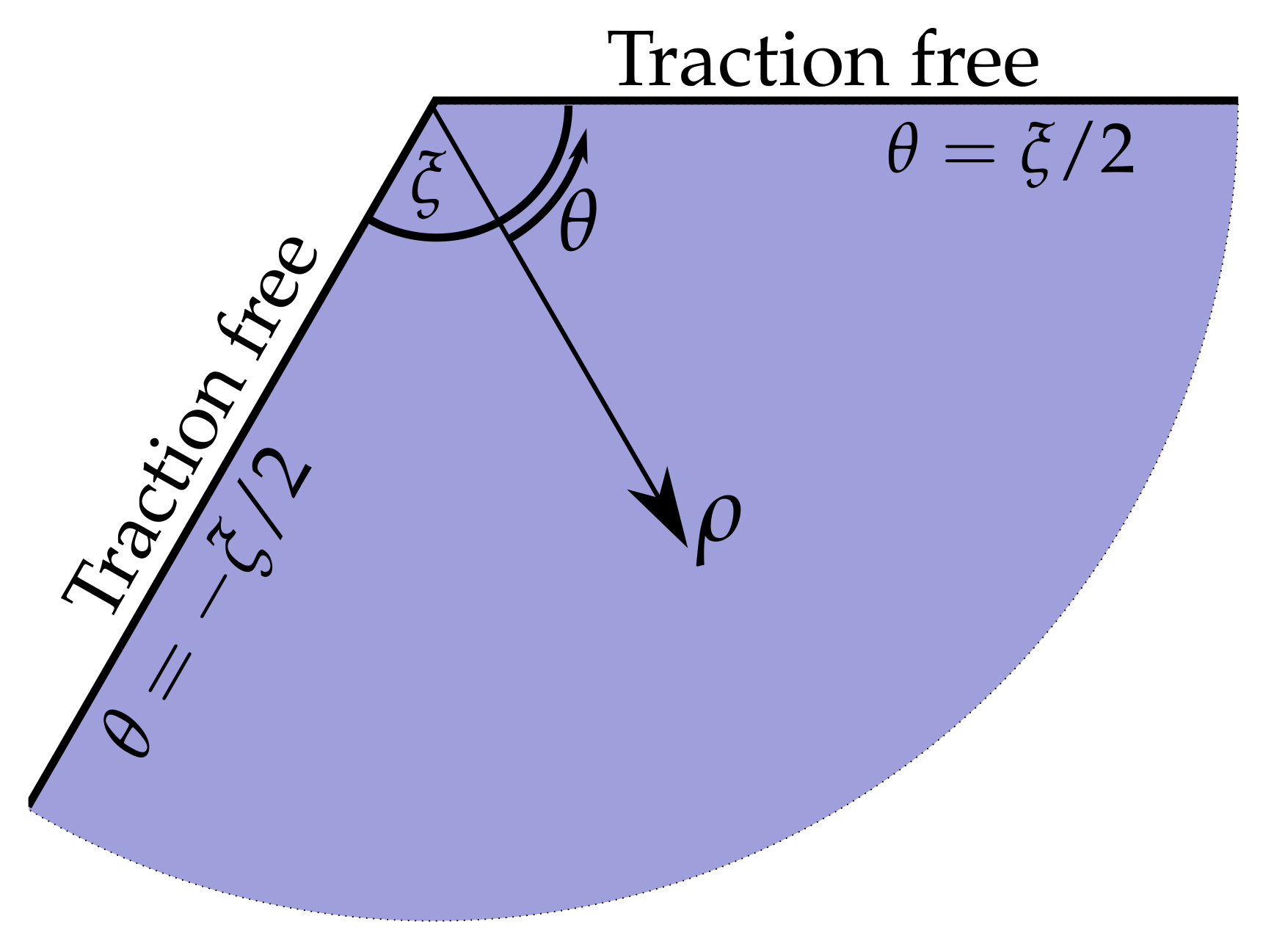
2.2. Similarity Solutions in the Corner of an Elastic Body
2.2.1. Elastostatic Expansion
2.2.2. Elastodynamic Expansion
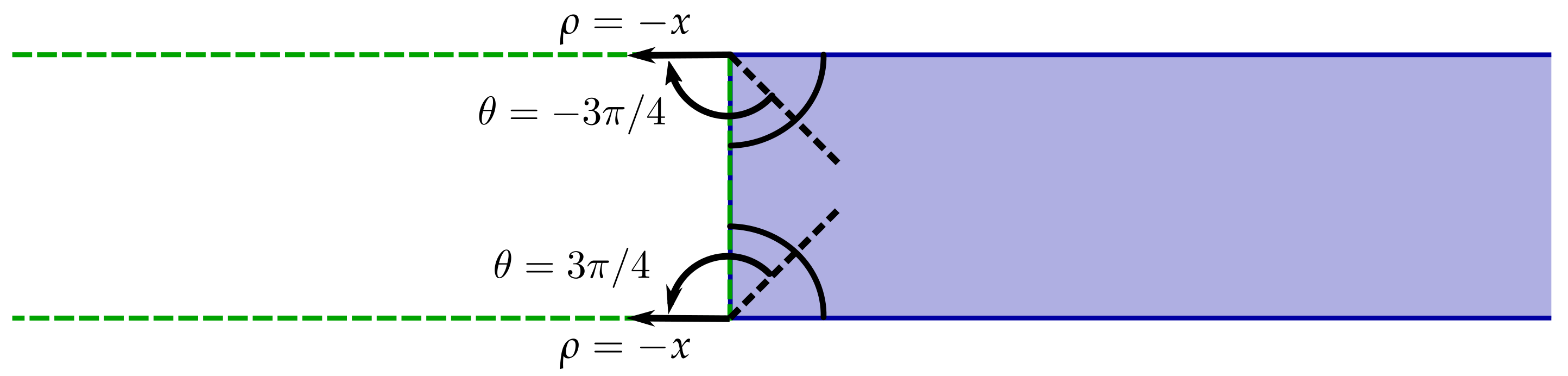
2.3. Expressing the Virtual Forcing in Terms of Corner Modes
2.3.1. Inverse Transformation of the Forced Plate
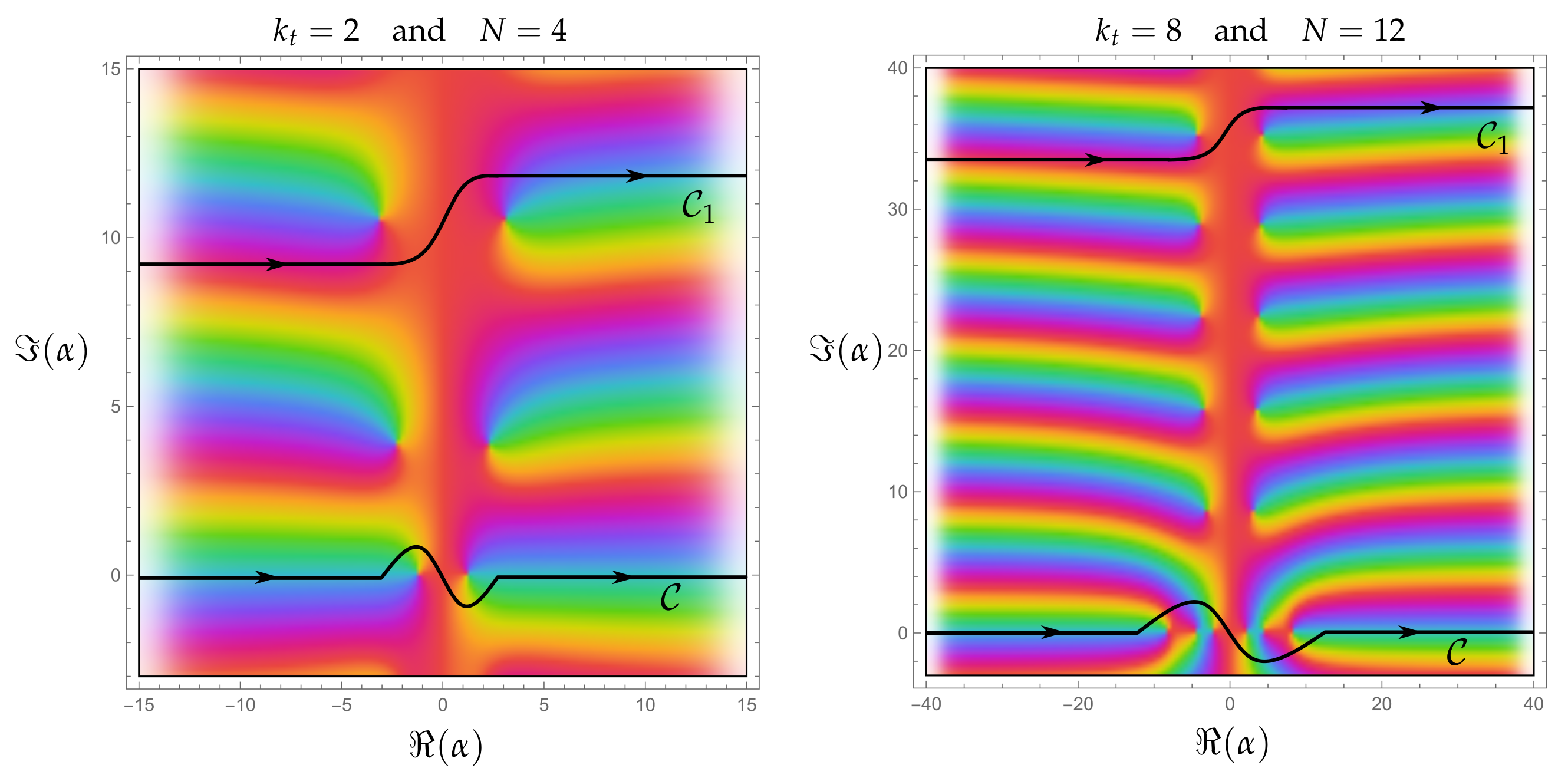
2.3.2. Satisfaction of the Free-End Boundary Conditions by Collocation
3. Results
3.1. Reconstructions
3.2. Trapped Modes
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- AWE. Private Correspondence; Technical Report; AWE: Aldermastion, UK, 2016. [Google Scholar]
- ACVR. Experimental Data; Technical Report; ACVR: Reno, NV, USA, 2017. [Google Scholar]
- Abrahams, I.D.; Wickham, G.R. The propagation of elastic waves in a certain class of inhomogeneous anisotropic materials. I. The refraction of a horizontally polarized shear wave source. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1992, 436, 449–478. [Google Scholar] [CrossRef]
- Abrahams, I.D.; Wickham, G.R. Scattering of elastic waves by a small inclined surface-breaking crack. J. Mech. Phys. Solids 1992, 40, 1707–1733. [Google Scholar] [CrossRef]
- Williams, M.L. Surface singularities resulting from various boundary conditions in angular corners of plates in extension. J. Appl. Mech. Asme 1952, 19, 526–528. [Google Scholar] [CrossRef]
- Gregory, R.D.; Gladwell, I. The reflection of a symmetric Rayleigh-Lamb wave at the fixed or free edge of a plate. J. Elast. 1983, 13, 185–206. [Google Scholar] [CrossRef]
- Pagneux, V. Revisiting the edge resonance for Lamb waves in a semi-infinite plate. J. Acoust. Soc. Am. 2006, 120, 649. [Google Scholar] [CrossRef] [Green Version]
- Zernov, V.; Pichugin, A.; Kaplunov, J. Eigenvalue of a semi-infinite elastic strip. Proc. R. Soc. Math. Phys. Eng. Sci. 2006, 462, 1255–1270. [Google Scholar] [CrossRef] [Green Version]
- Lawrie, J.B.; Kaplunov, J. Edge waves and resonance on elastic structures: An overview. Math. Mech. Solids 2012, 17, 4–16. [Google Scholar] [CrossRef]
- Lamb, H. On waves in an Elastic Plate. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1917, 93, 114–128. [Google Scholar] [CrossRef] [Green Version]
- Chapman, C.J.; Sorokin, S.V. The finite-product method in the theory of waves and stability. Proc. R. Soc. Math. Phys. Eng. Sci. 2010, 466, 471–491. [Google Scholar] [CrossRef]
- Gregory, R.D.; Gladwell, I. The Cantilever Beam Under Tension, Bending or Flexure at Infinity. J. Elast. 1982, 12, 317–343. [Google Scholar] [CrossRef]
- Nawaz, R.; Lawrie, J.B. Scattering of a fluid-structure coupled wave at a flanged junction between two flexible waveguides. J. Acoust. Soc. Am. 2013, 134, 1939–1949. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawrie, J.B.; Afzal, M. Acoustic scattering in a waveguide with a height discontinuity bridged by a membrane: A tailored Galerkin approach. J. Eng. Math. 2017, 105, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Abrahams, I.D.; Assier, R.C.; Cotterill, P.A. A new method for improving convergence of modal expansions for discontinuous waveguide problems. 2022; to be submitted. [Google Scholar]
- Linton, C. Accurate solution to scattering by a semi-circular groove. Wave Motion 2009, 46, 200–209. [Google Scholar] [CrossRef]
- Homentcovschi, D.; Miles, R.N. A re-expansion method for determining the acoustical impedance and the scattering matrix for the waveguide discontinuity problem. J. Acoust. Soc. Am. 2010, 128, 628–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Porter, R.; Evans, D.V. Complementary approximations to wave scattering by vertical barriers. J. Fluid Mech. 1995, 294, 155–180. [Google Scholar] [CrossRef]
- Fernyhough, M.; Evans, D.V. Scattering by periodic array of rectangular blocks. J. Fluid Mech. 1995, 305, 263–279. [Google Scholar] [CrossRef]
- Chang, K.H.; Tsaur, D.H.; Wang, J.H. Scattering of SH waves by a circular sectorial canyon. Geophys. J. Int. 2013, 195, 532–543. [Google Scholar] [CrossRef] [Green Version]
- Lyapin, V.P.; Manuilov, M.B.; Sinyavsky, G.P. Quasi-analytical method for analysis of multisection waveguide structures with step discontinuities. Radio Sci. 1996, 31, 1761–1772. [Google Scholar] [CrossRef]
- Lucido, M.; Panariello, G.; Schettino, F. Analysis of the Electromagnetic Scattering by Perfectly Conducting Convex Polygonal Cylinders. IEEE Trans. Antennas Propag. 2006, 54, 1223–1231. [Google Scholar] [CrossRef]
- Cotterill, P.A.; Abrahams, I.D. Acoustic transmission through gaps in sound-reduction coatings. 2022; to be submitted. [Google Scholar]
- Carrier, G.F.; Krook, M.; Pearson, C.E. Functions of a Complex Variable; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Fung, Y.C. Foundations of Solid Mechanics; Prentice-Hall: Hoboken, NJ, USA, 1965. [Google Scholar]
- Lawrie, J.B.; (Brunel University London, London, UK). Personal communication, 2022.


 ); a mixed expansion with and (
); a mixed expansion with and (  ); an expansion with and (
); an expansion with and (  ); and an expansion with and (
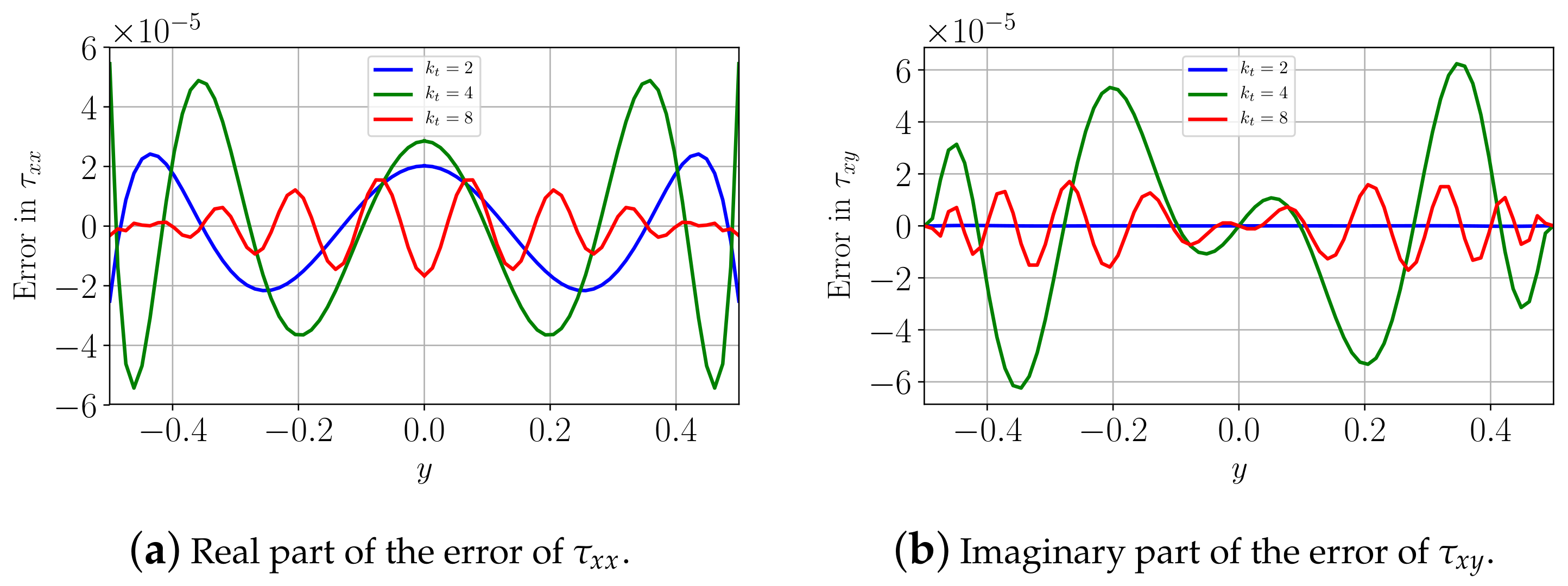
); and an expansion with and (  ). Subfigures (a,b) are the reconstructions of the scattered stress fields along the traction-free face. The negative of the incoming stress fields, which should lie on the same line, are plotted as (
). Subfigures (a,b) are the reconstructions of the scattered stress fields along the traction-free face. The negative of the incoming stress fields, which should lie on the same line, are plotted as (  ) for comparison. Subfigures (c,d) show the errors of the reconstructions of the total stress fields (sum of the incoming field and the outgoing field). In this example, and .
) for comparison. Subfigures (c,d) show the errors of the reconstructions of the total stress fields (sum of the incoming field and the outgoing field). In this example, and .
 ); a mixed expansion with and (
); a mixed expansion with and (  ); an expansion with and (
); an expansion with and (  ); and an expansion with and (
); and an expansion with and (  ). Subfigures (a,b) are the reconstructions of the scattered stress fields along the traction-free face. The negative of the incoming stress fields, which should lie on the same line, are plotted as (
). Subfigures (a,b) are the reconstructions of the scattered stress fields along the traction-free face. The negative of the incoming stress fields, which should lie on the same line, are plotted as (  ) for comparison. Subfigures (c,d) show the errors of the reconstructions of the total stress fields (sum of the incoming field and the outgoing field). In this example, and .
) for comparison. Subfigures (c,d) show the errors of the reconstructions of the total stress fields (sum of the incoming field and the outgoing field). In this example, and .
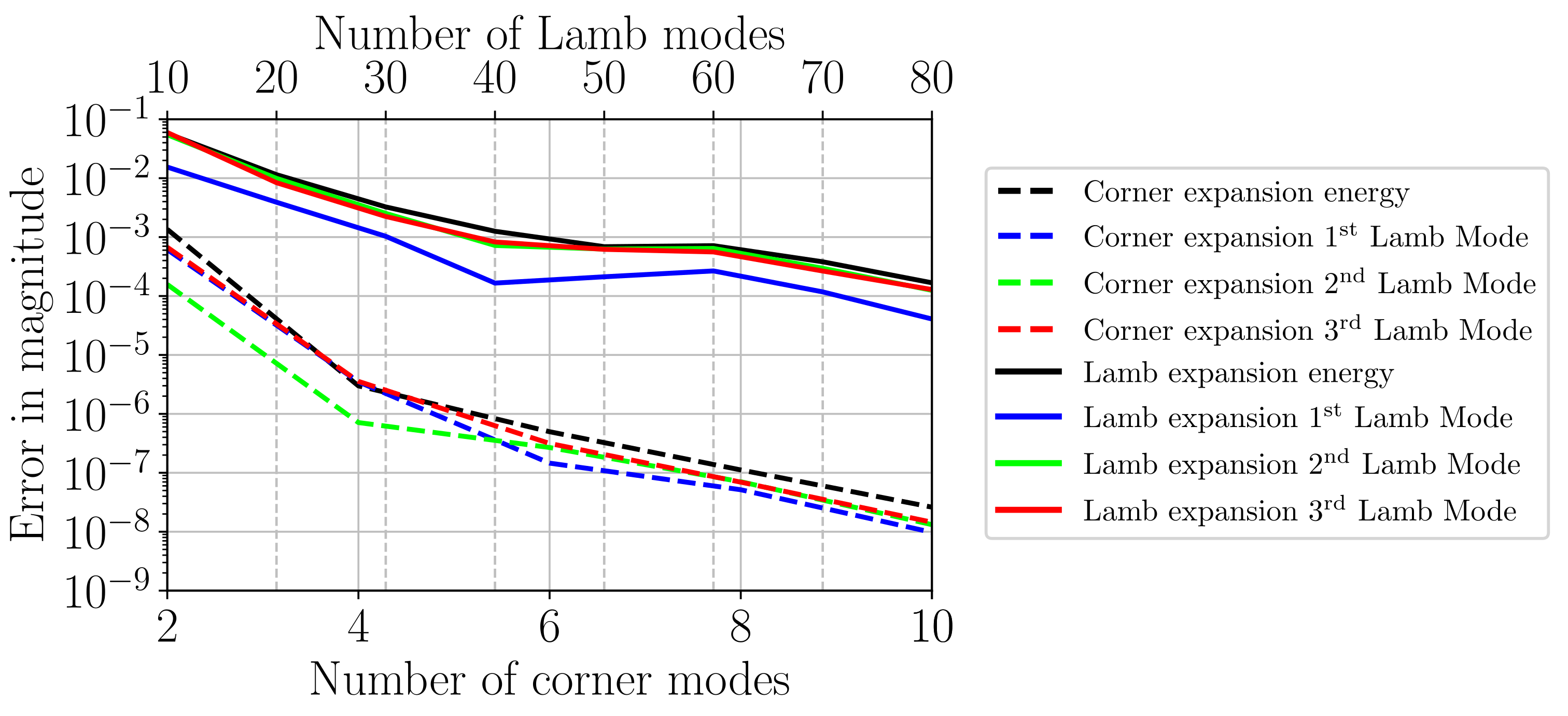
 ), (
), (  ), (
), (  ), and (
), and (  ) corner modes. The dotted lines are the projected values of the determinant, found by extending the curves on either side of zero; this aids the determination of location of zero. The value of Poisson’s ratio at which the determinant vanishes can be seen to have converged, once or larger, to .
) corner modes. The dotted lines are the projected values of the determinant, found by extending the curves on either side of zero; this aids the determination of location of zero. The value of Poisson’s ratio at which the determinant vanishes can be seen to have converged, once or larger, to .
 ), (
), (  ), (
), (  ), and (
), and (  ) corner modes. The dotted lines are the projected values of the determinant, found by extending the curves on either side of zero; this aids the determination of location of zero. The value of Poisson’s ratio at which the determinant vanishes can be seen to have converged, once or larger, to .
) corner modes. The dotted lines are the projected values of the determinant, found by extending the curves on either side of zero; this aids the determination of location of zero. The value of Poisson’s ratio at which the determinant vanishes can be seen to have converged, once or larger, to .
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© Crown Owned Copyright AWE/MoD 2022. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davey, R.C.; Assier, R.C.; Abrahams, I.D. An Efficient Semi-Analytical Scheme for Determining the Reflection of Lamb Waves in a Semi-Infinite Elastic Waveguide. Appl. Sci. 2022, 12, 6468. https://doi.org/10.3390/app12136468
Davey RC, Assier RC, Abrahams ID. An Efficient Semi-Analytical Scheme for Determining the Reflection of Lamb Waves in a Semi-Infinite Elastic Waveguide. Applied Sciences. 2022; 12(13):6468. https://doi.org/10.3390/app12136468
Chicago/Turabian StyleDavey, Robert C., Raphaël C. Assier, and I. David Abrahams. 2022. "An Efficient Semi-Analytical Scheme for Determining the Reflection of Lamb Waves in a Semi-Infinite Elastic Waveguide" Applied Sciences 12, no. 13: 6468. https://doi.org/10.3390/app12136468




