Wavelet Energy Evolution Characteristics of Acoustic Emission Signal under True-Triaxial Loading during the Rockburst Test
Abstract
:1. Introduction
2. Specimen and Methods
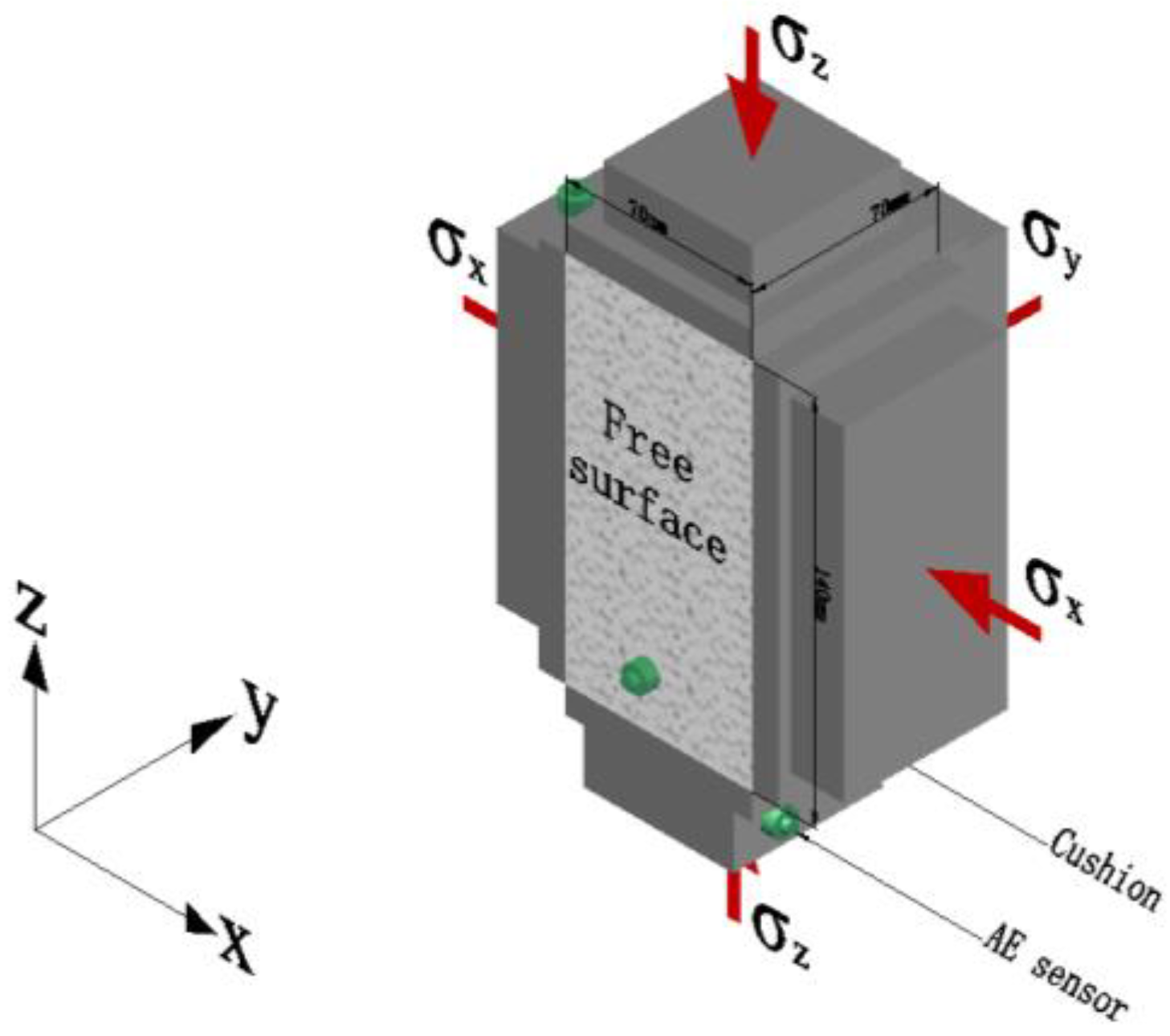
2.1. Specimen
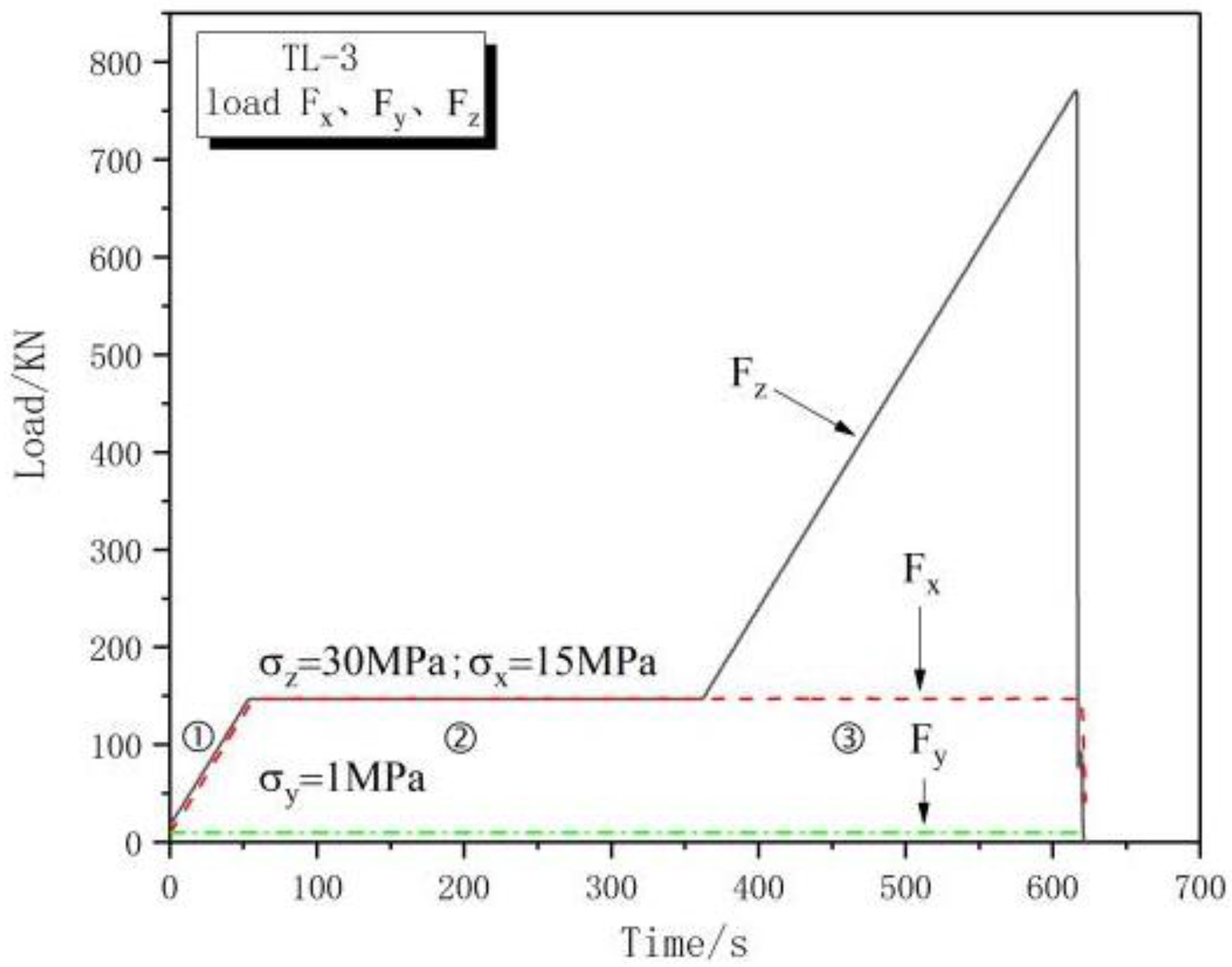
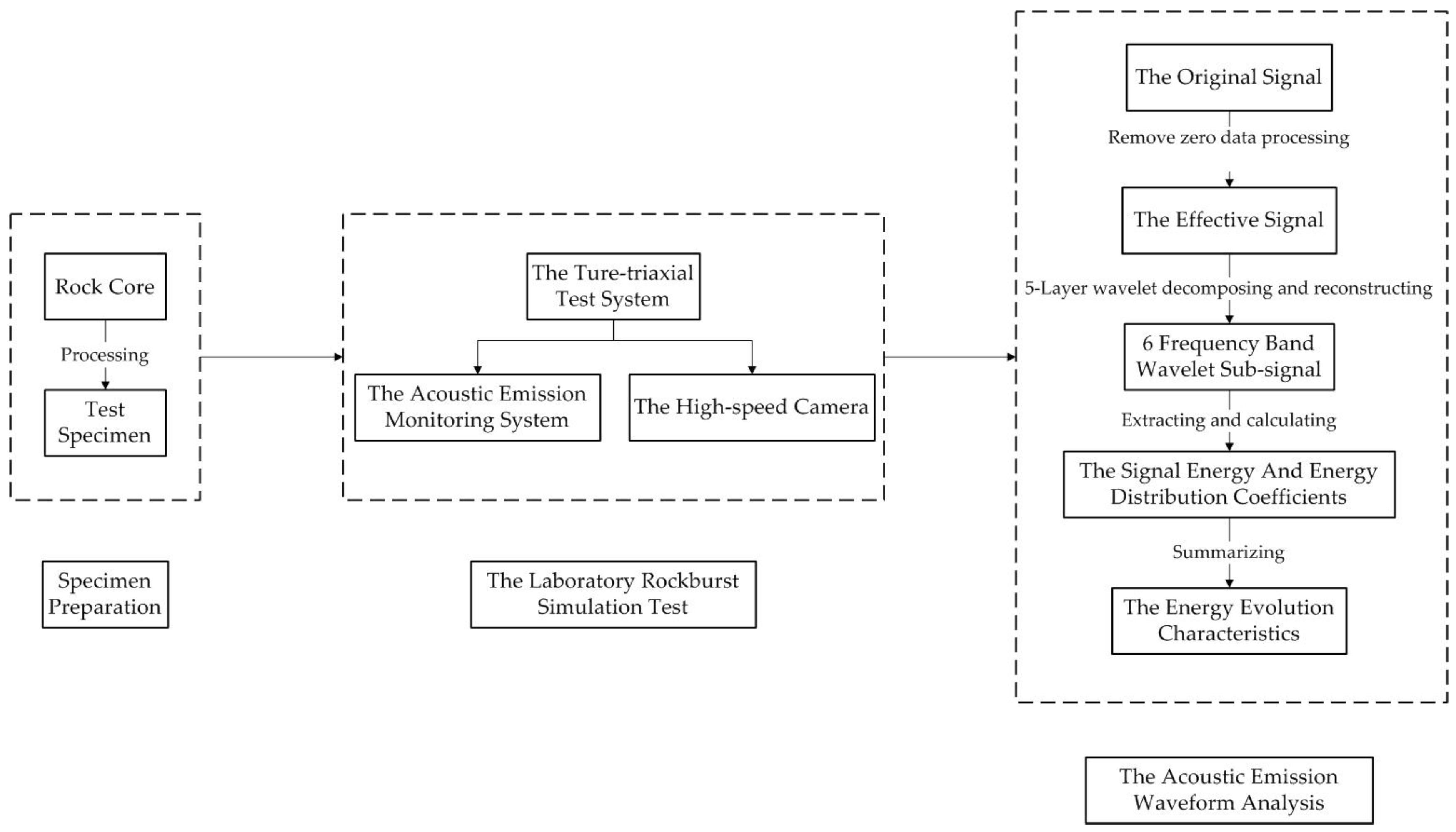
2.2. Methods
3. Phenomenon and Results
3.1. Phenomenon
3.2. Results
4. Wavelet Energy Evolution Characteristics
4.1. Wavelet Transform
4.2. Remove Zero Data Processing
4.3. Wavelet Energy Analysis
4.4. Characteristics of the Wavelet Energy Evolution
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mutke, G.; Dubiński, J.; Lurka, A. New Criteria to Assess Seismic and Rock Burst Hazard in Coal Mines/Nowe Kryteria Dla Oceny Zagrożenia Sejsmicznego I Tąpaniami W Kopalniach Węgla Kamiennego. Arch. Min. Sci. 2015, 60, 743–760. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, E.; Li, Z.; Liu, Z.; Song, D.; Qiu, L. Rock Burst Monitoring by Integrated Microseismic and Electromagnetic Radiation Methods. Rock Mech. Rock Eng. 2016, 49, 4393–4406. [Google Scholar] [CrossRef]
- Gong, Q.M.; Yin, L.J.; Wu, S.Y.; Zhao, J.; Ting, Y. Rock burst and slabbing failure and its influence on TBM excavation at headrace tunnels in Jinping II hydropower station. Eng. Geol. 2012, 124, 98–108. [Google Scholar] [CrossRef]
- Keneti, A.; Sainsbury, B. Review of published rockburst events and their contributing factors. Eng. Geol. 2018, 246, 361–373. [Google Scholar] [CrossRef]
- Reddy, N.S.S.M. The influence of geology on a simulated rockburst. J. S. Afr. Inst. Min. Metall. 2001, 101, 267–272. [Google Scholar]
- Zhao, Y.; Zhang, L.; Liao, J.; Wang, W.; Liu, Q.; Tang, L. Experimental Study of Fracture Toughness and Subcritical Crack Growth of Three Rocks under Different Environments. Int. J. Geomech. 2020, 20, 4020128. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Tang, L.; Liu, Q.; Cheng, G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 2019, 101, 59–66. [Google Scholar] [CrossRef]
- Lin, H.; Yang, H.; Wang, Y.; Zhao, Y.; Cao, R. Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression. Theor. Appl. Fract. Mech. 2019, 104, 102358. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, Y.; Tang, L.; Liao, J.; Wang, X.; Tan, T.; Chang, L.; Luo, S.; Wang, M. Mechanical characteristics of single cracked limestone in compression-shear fracture under hydro-mechanical coupling. Theor. Appl. Fract. Mech. 2022, 119, 103371. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Zhang, C.; Canbulat, I.; Hebblewhite, B.; Ward, C.R. Assessing coal burst phenomena in mining and insights into directions for future research. Int. J. Coal Geol. 2017, 179, 28–44. [Google Scholar] [CrossRef]
- Zhao, T.; Guo, W.; Tan, Y.; Yin, Y.; Cai, L.; Pan, J. Case Studies of Rock Bursts Under Complicated Geological Conditions During Multi-seam Mining at a Depth of 800 m. Rock Mech. Rock Eng. 2018, 51, 1539–1564. [Google Scholar] [CrossRef]
- Ghorbani, M.; Shahriar, K.; Sharifzadeh, M.; Masoudi, R. A critical review on the developments of rock support systems in high stress ground conditions. Int. J. Min. Sci. Technol. 2020, 30, 555–572. [Google Scholar] [CrossRef]
- Si, X.; Huang, L.; Li, X.; Gong, F.; Liu, X. Mechanical properties and rockburst proneness of phyllite under uniaxial compression. Trans. Nonferrous Met. Soc. China 2021, 31, 3862–3878. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; Shen, R.; He, M. Electromagnetic radiation signal monitoring and multi-fractal analysis during uniaxial compression of water-bearing sandstone. Measurement 2022, 196, 111245. [Google Scholar] [CrossRef]
- Hui, Z.; Jing-Jing, L.U.; Rong-Chao, X.U.; Chuan-Qing, Z.; Fan-Zhen, M. Critical problems of study of slabbing failure of surrounding rock in deep hard rock tunnel and research progress. Rock Soil Mech. 2015, 36, 2737–2749. [Google Scholar]
- Gong, F.; Luo, Y.; Li, X.; Si, X.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Si, X.; Gong, F. Strength-weakening effect and shear-tension failure mode transformation mechanism of rockburst for fine-grained granite under triaxial unloading compression. Int. J. Rock Mech. Min. 2020, 131, 104347. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Huang, G.; Yu, B.; Liu, Y.; Song, Z. Experimental investigation on rockburst process and failure characteristics in trapezoidal tunnel under different lateral stresses. Constr. Build. Mater. 2020, 259, 119530. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Liang, P.; Liu, X.X.; Liu, S.J.; Tian, B.Z. An experimental study of predicting rockburst in granitic roadway based on multiparameter normalization. Rock Soil Mech. 2016, 37, 96–104. [Google Scholar]
- He, S.; Lai, J.; Zhong, Y.; Wang, K.; Xu, W.; Wang, L.; Liu, T.; Zhang, C. Damage behaviors, prediction methods and prevention methods of rockburst in 13 deep traffic tunnels in China. Eng. Fail. Anal. 2021, 121, 105178. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, J.; Xu, N.; Liu, Q.; Gao, Y. A new energy index for evaluating the tendency of rockburst and its engineering application. Eng. Geol. 2017, 230, 46–54. [Google Scholar] [CrossRef]
- Liu, F.; Tang, C.; Zhang, Y.; Ma, T. Rockburst and microseismicity characteristics in the Qinling water conveyance tunnel of the Hanjiang-to-Weihe River Diversion Project. Int. J. Rock Mech. Min. 2021, 148, 104973. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Wang, E.; Li, Z. Rockburst mechanism in coal rock with structural surface and the microseismic (MS) and electromagnetic radiation (EMR) response. Eng. Fail. Anal. 2021, 124, 105396. [Google Scholar] [CrossRef]
- Liu, X.; Liang, Z.; Zhang, Y.; Liang, P.; Tian, B. Experimental study on the monitoring of rockburst in tunnels under dry and saturated conditions using AE and infrared monitoring. Tunn. Undergr. Space Technol. 2018, 82, 517–528. [Google Scholar] [CrossRef]
- Tang, S.; Tong, M.; Hu, J.; He, X. Characteristics of acoustic emission signals in damp cracking coal rocks. Min. Sci. Technol. (Xuzhou China) 2010, 20, 143–147. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, X.; Zhou, J. Practices on rockburst prevention and control in headrace tunnels of Jinping II hydropower station. J. Rock Mech. Geotech. Eng. 2012, 4, 258–268. [Google Scholar] [CrossRef] [Green Version]
- He, M.; E Sousa, L.R.; Miranda, T.; Zhu, G. Rockburst laboratory tests database—Application of data mining techniques. Eng. Geol. 2015, 185, 116–130. [Google Scholar] [CrossRef]
- Shiotani, T.; Ohtsu, M.; Ikeda, K. Detection and evaluation of AE waves due to rock deformation. Constr. Build. Mater. 2001, 15, 235–246. [Google Scholar] [CrossRef]
- Labuz, J.F.; Cattaneo, S.; Chen, L.H. Acoustic emission at failure in quasi-brittle materials. Constr. Build. Mater. 2001, 15, 225–233. [Google Scholar] [CrossRef]
- Ohnaka, M.; Mogi, K. Frequency-characteristics of acoustic-emission in rocks under uniaxial compression and its relation to the fracturing process to failure. J. Geophys. Res. 1982, 87, 3873–3884. [Google Scholar] [CrossRef]
- Ohnaka, M. Acoustic-emission during creep of brittle rock. Int. J. Rock Mech. Min. 1983, 20, 121–134. [Google Scholar] [CrossRef]
- Colombo, S.; Forde, M.C.; Main, I.G.; Shigeishi, M. Predicting the ultimate bending capacity of concrete beams from the “relaxation ratio” analysis of AE signals. Constr. Build. Mater. 2005, 19, 746–754. [Google Scholar] [CrossRef]
- Du, F.; Wang, K.; Wang, G.; Jiang, Y.; Xin, C.; Zhang, X. Investigation of the acoustic emission characteristics during deformation and failure of gas-bearing coal-rock combined bodies. J. Loss Prevent. Proc. 2018, 55, 253–266. [Google Scholar] [CrossRef]
- Zhu, G.; Dou, L.; Wang, C.; Ding, Z.; Feng, Z.; Xue, F. Experimental study of rock burst in coal samples under overstress and true-triaxial unloading through passive velocity tomography. Saf. Sci. 2019, 117, 388–403. [Google Scholar] [CrossRef]
- Chu, Y.; Zhang, D.; Liu, H.; Wu, X.; Zhai, P.; Sheng, T. Experimental study on mechanical properties, acoustic emission characteristics and energy evolution of coal samples after freezing with liquid nitrogen. Fuel 2022, 321, 123955. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, J. A new method for determining the crack classification criterion in acoustic emission parameter analysis. Int. J. Rock Mech. Min. 2020, 130, 104323. [Google Scholar] [CrossRef]
- Li, H.; Zhou, L.; Lu, Y.; Yan, F.; Zhou, J.; Tang, J. Influence of supercritical CO2 saturation on the failure process of hot dry rock with acoustic emission monitoring. Powder Technol. 2020, 374, 241–249. [Google Scholar] [CrossRef]
- Zhao, K.; Ma, H.; Liang, X.; Li, X.; Liu, Y.; Cai, R.; Ye, L.; Yang, C. Damage evaluation of rock salt under multilevel cyclic loading with constant stress intervals using AE monitoring and CT scanning. J. Petrol. Sci. Eng. 2022, 208, 109517. [Google Scholar] [CrossRef]
- Stankevych, O.; Skalskyi, V.; Klym, B.; Velykyi, P. Identification of fracture mechanisms in cementitious composites using wavelet transform of acoustic emission signals. Procedia Struct. Integr. 2022, 36, 114–121. [Google Scholar] [CrossRef]
- Dinmohammadpour, M.; Nikkhah, M.; Goshtasbi, K.; Ahangari, K. Application of wavelet transform in evaluating the Kaiser effect of rocks in acoustic emission test. Measurement 2022, 192, 110887. [Google Scholar] [CrossRef]
- Wei, J.; Wang, H.; Lin, B.; Sui, T.; Zhao, F.; Fang, S. Acoustic emission signal of fiber-reinforced composite grinding: Frequency components and damage pattern recognition. Int. J. Adv. Manuf. Technol. 2019, 103, 1391–1401. [Google Scholar] [CrossRef]
- Li, L.; Cai, H.; Han, H.; Jiang, Q.; Ji, H. Adaptive short-time Fourier transform and synchrosqueezing transform for non-stationary signal separation. Signal Processing 2020, 166, 107231. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Chen, Y. Seismic Time—Frequency Analysis via Empirical Wavelet Transform. IEEE Geosci. Remote Sens. Lett. 2016, 13, 28–32. [Google Scholar] [CrossRef]
- Knigge, B.; Talke, F.E. Slider vibration analysis at contact using time-frequency analysis and wavelet transforms. J. Tribol. ASME 2001, 123, 548–554. [Google Scholar] [CrossRef]
- Lee, S.W.; Park, K.H.; Lee, J.G. Blast-Induced Damage Identification of Rock Mass using Wavelet Transform Analysis. Procedia Eng. 2011, 14, 3142–3146. [Google Scholar] [CrossRef] [Green Version]
- Lee, I.; Han, S.; Kim, H.; Yu, J.; Min, B.; Lee, J. Evaluation of rock bolt integrity using Fourier and wavelet transforms. Tunn. Undergr. Space Technol. 2012, 28, 304–314. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Processing 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Processing 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Gowd, T.N. Factors Affecting the Acoustic Emission Response of Triaxially Compressed Rock. Int. J. Rock Mech. Min. 1980, 4, 219–223. [Google Scholar] [CrossRef]
- Sun, X.; Xu, H.; He, M.; Zhang, F. Experimental investigation of the occurrence of rockburst in a rock specimen through infrared thermography and acoustic emission. Int. J. Rock Mech. Min. 2017, 93, 250–259. [Google Scholar] [CrossRef]






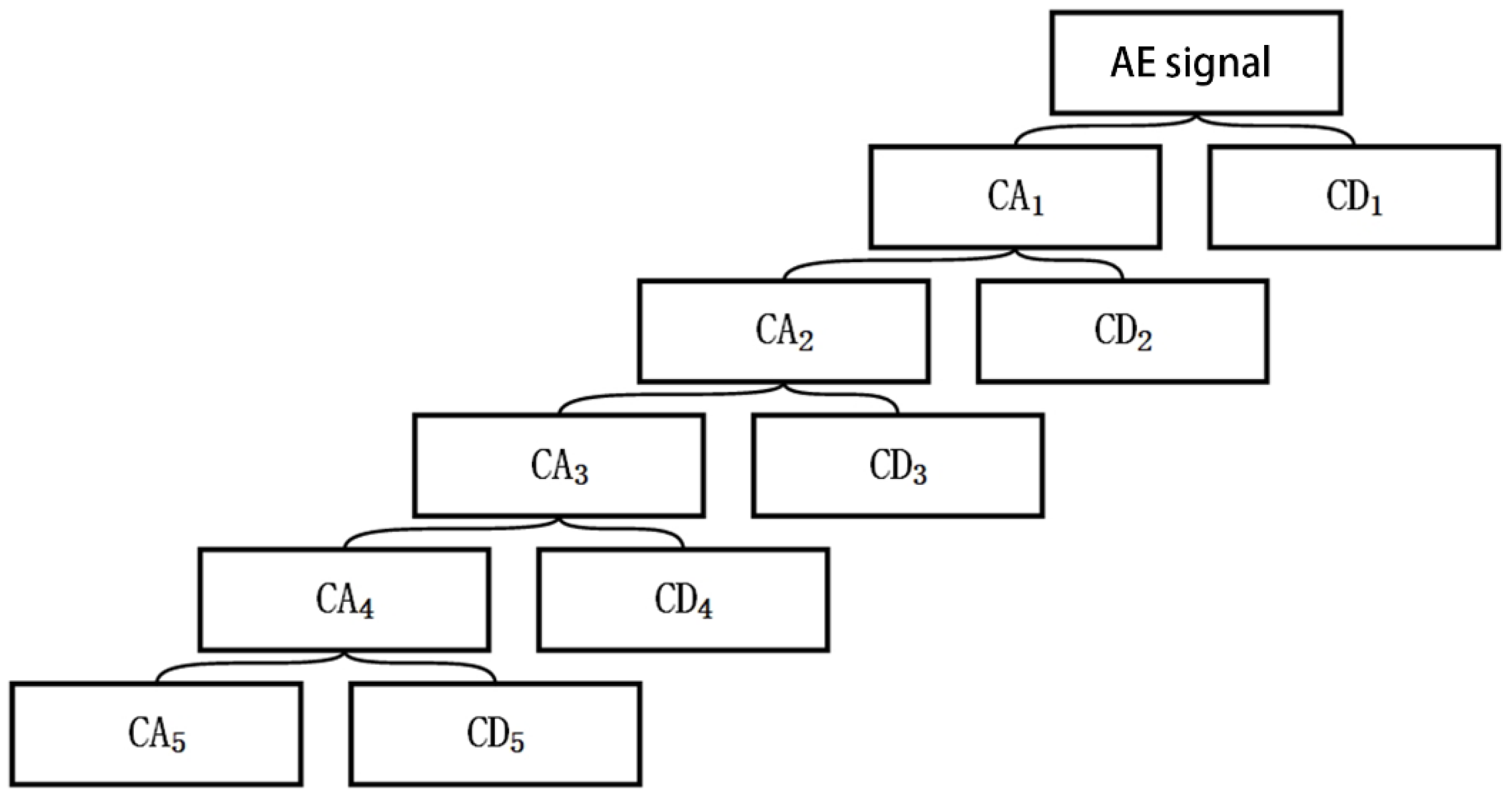
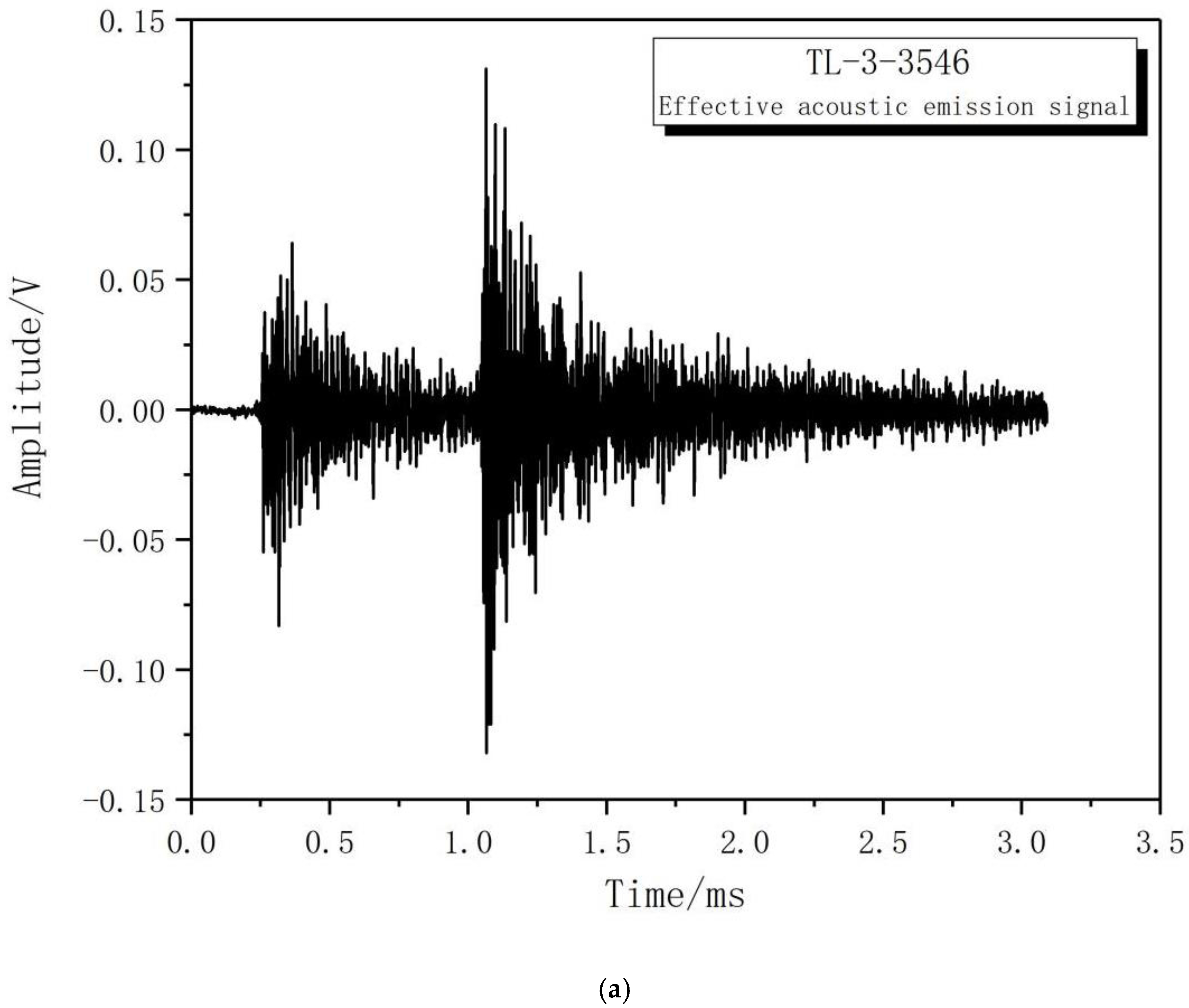

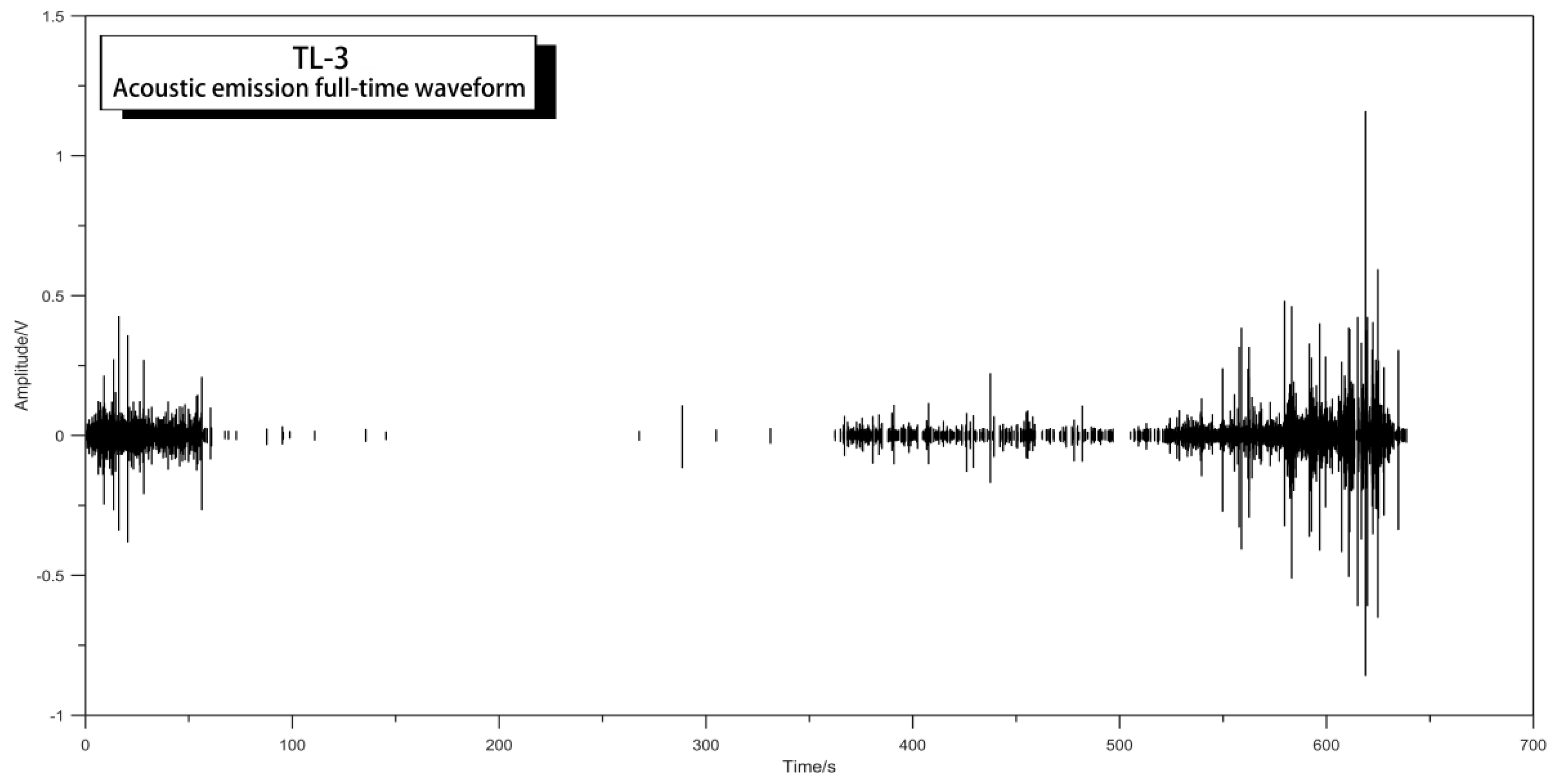

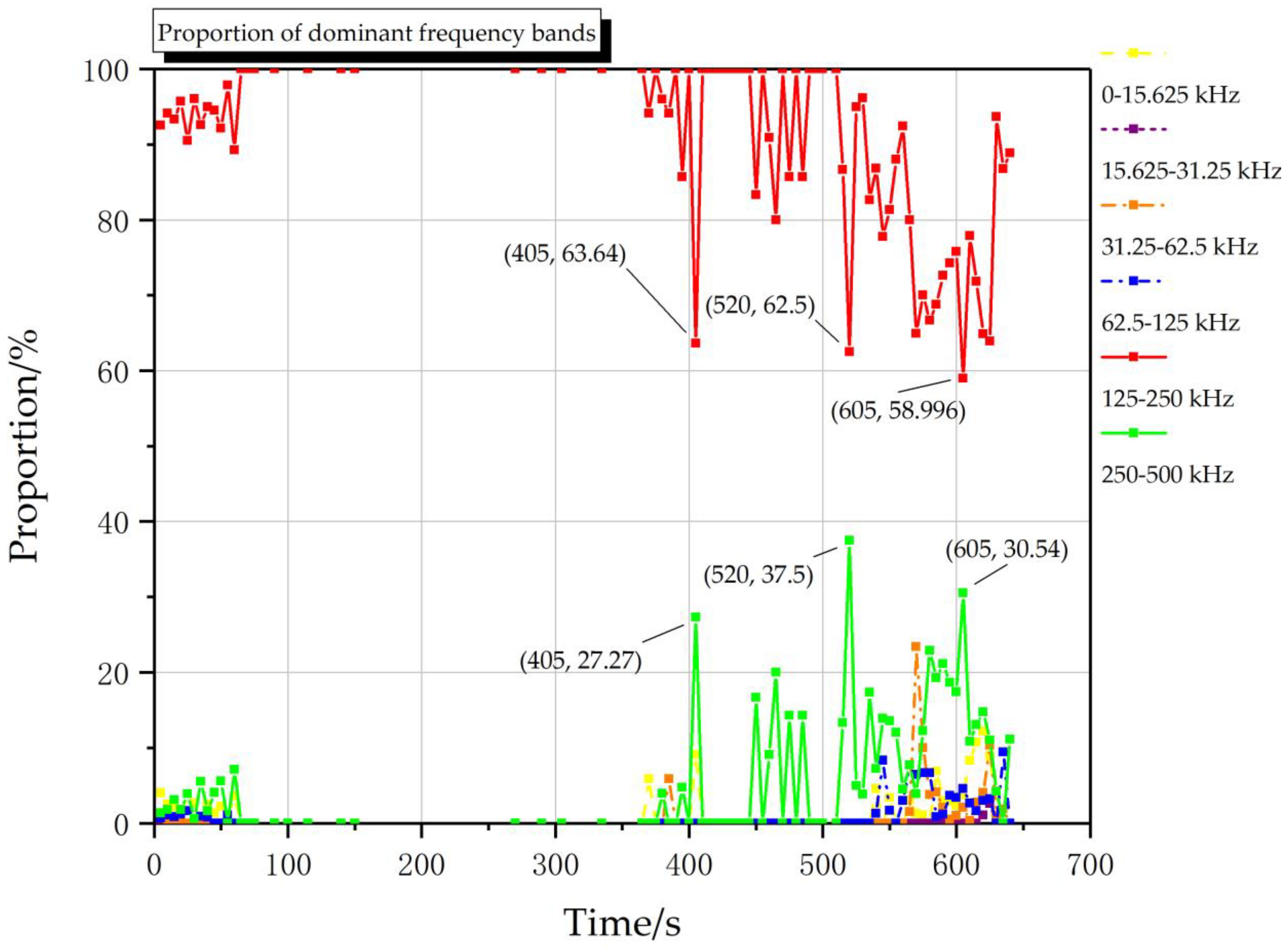
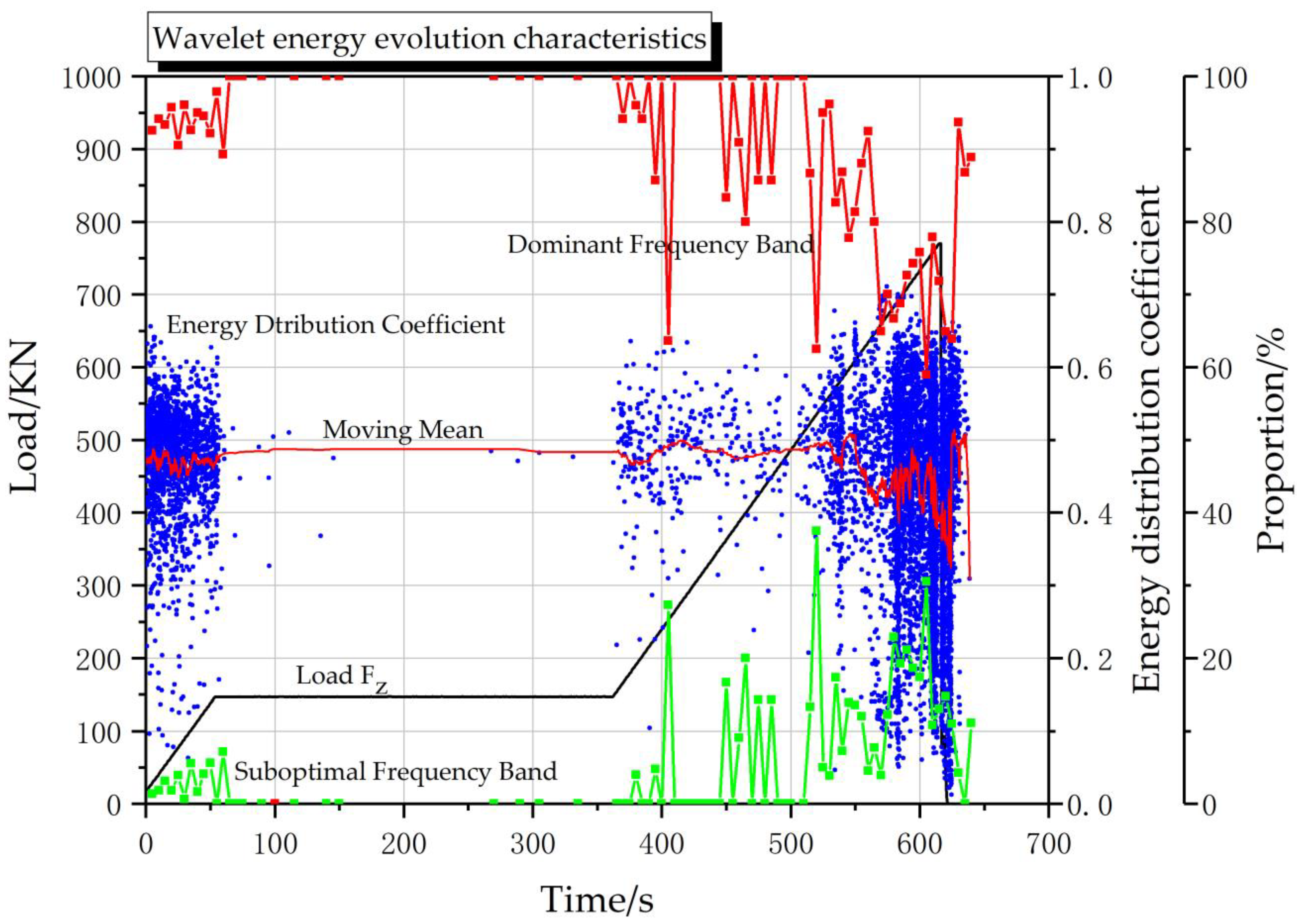
| Number i | Wavelet Sub-Signal | Frequency Range/kHz |
|---|---|---|
| 1 | CA5 | 0~15.625 |
| 2 | CD5 | 15.625~31.250 |
| 3 | CD4 | 31.25~62.50 |
| 4 | CD3 | 62.5~125.0 |
| 5 | CD2 | 125~250 |
| 6 | CD1 | 250~500 |
| CD1 | CD2 | CD3 | CD4 | CD5 | CA5 | |
|---|---|---|---|---|---|---|
| E | 0.1983 | 0.2812 | 0.1352 | 0.0830 | 0.0046 | 0.0025 |
| K | 0.2813 | 0.3990 | 0.1918 | 0.1177 | 0.0066 | 0.0036 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Mei, F.; Hussain, W. Wavelet Energy Evolution Characteristics of Acoustic Emission Signal under True-Triaxial Loading during the Rockburst Test. Appl. Sci. 2022, 12, 7786. https://doi.org/10.3390/app12157786
Hu C, Mei F, Hussain W. Wavelet Energy Evolution Characteristics of Acoustic Emission Signal under True-Triaxial Loading during the Rockburst Test. Applied Sciences. 2022; 12(15):7786. https://doi.org/10.3390/app12157786
Chicago/Turabian StyleHu, Chuanyu, Fuding Mei, and Wakeel Hussain. 2022. "Wavelet Energy Evolution Characteristics of Acoustic Emission Signal under True-Triaxial Loading during the Rockburst Test" Applied Sciences 12, no. 15: 7786. https://doi.org/10.3390/app12157786





