Computational Modelling and Simulation of Fluid Structure Interaction in Aortic Aneurysms: A Systematic Review and Discussion of the Clinical Potential

Abstract

Aortic aneurysm is a cardiovascular disease related to the alteration of the aortic tissue. It is an important cause of death in developed countries, especially for older patients. The diagnosis and treatment of such pathology is performed according to guidelines, which suggest surgical or interventional (stenting) procedures for aneurysms with a maximum diameter above a critical threshold. Although conservative, this clinical approach is also not able to predict the risk of acute complications for every patient. In the last decade, there has been growing interest towards the development of advanced in silico aortic models, which may assist in clinical diagnosis, surgical procedure planning or the design and validation of medical devices. This paper details a comprehensive review of computational modelling and simulations of blood vessel interaction in aortic aneurysms and dissection, following the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). In particular, the following questions are addressed: “What mathematical models were applied to simulate the biomechanical behaviour of healthy and diseased aortas?” and “Why are these models not clinically implemented?”. Contemporary evidence proves that computational models are able to provide clinicians with additional, otherwise unavailable in vivo data and potentially identify patients who may benefit from earlier treatment. Notwithstanding the above, these tools are still not widely implemented, primarily due to low accuracy, an extensive reporting time and lack of numerical validation.

1. Introduction

The diagnosis and treatment of aortic diseases is performed in accordance with clinical guidelines provided by several organisations, such as the American Heart Association, American College of Cardiology and European Society of Cardiology [1,2]. The treatment guidelines for Ascending Thoracic Aortic Aneurysm (ATAA) and Abdominal Aortic Aneurysm (AAA) suggest surgical intervention for patients with a maximum diameter greater than 55 $\mathrm{m}\mathrm{m}$. This simple geometrical criterion is supported by Laplace’s law and empirical evidence of a significant increase in rupture risk from $0.6\%$ to $6.9\%$ in aortas with 50 $\mathrm{m}\mathrm{m}$ and 60 $\mathrm{m}\mathrm{m}$ diameters, respectively [3]. This criterion, although clinically still accepted and used, is also controversial and is now extensively recognised as insufficient [4,5]. For instance, Lucio et al. [6] showed that around $13\%$ of ATAA occurs with an aortic size below 50 $\mathrm{m}\mathrm{m}$ rupture, whereas $54\%$ of those over 70 $\mathrm{m}\mathrm{m}$ may not rupture over long periods. Therefore, these findings reveal an unmet clinical need for suitable, robust and accurate risk assessment metrics that will assist clinicians in clinical diagnosis and decision making.

The development of patient-specific computational models assisted by in vivo data obtained via non-invasive measurements that could mimic the biomechanical behaviour of Cardiovascular Diseases (CVD) in the framework of a digital twin platform has been presented as adding value to clinical examination [7,8]. These models are able to provide clinicians with insightful in vivo patient-specific data, such as Wall Shear Stress (WSS) and pressure distributions, displacement field, intramural stress state or flow patterns, which are otherwise unavailable. Over the last few decades, these advanced computational models and simulation tools have also enabled a better understanding of the underlying mechanisms of a variety of CVD, including aortic aneurysms and dissection. Several computational techniques, such as the Finite Element Method (FEM), Machine Learning (ML) and Smoothed Particle Hydrodynamics (SPH), have been applied. These techniques, spanning the entire range of numerical approaches, encompass Computational Solid Mechanics (CSM) and Computational Fluid Dynamics (CFD) to Fluid–Structure Interaction (FSI). CSM is useful to study the Wall Stress (WS) distributions and deformations [9,10]. CFD solves the governing equations of fluid mechanics and studies haemodynamics patterns and metrics [11,12]. FSI combines the above-mentioned approaches and simultaneously evaluates haemodynamics and wall motion [13,14]. Such studies did not specifically address the impact of considering the heterogeneity of wall thickness and material properties, the effect of surrounding structures and the aortic root motion at applying the numerical tools. Exploring the limitations of current numerical models that are constraining their introduction into clinical practice, and providing an extensive overview of the utilised numerical techniques to reproduce aortic biomechanics, are the main goals of this review.

In this article, a systematic review following the PRISMA [15] methodology is presented, concerning the computational modelling and simulation of the biomechanical behaviour of healthy and diseased aortas, and we explore their methodologies, hypotheses and risk evaluation metrics in view of their usage in clinical practice in order to answer the following scientific questions: “Which mathematical models have been applied to simulate the biomechanical behaviour of healthy and diseased aortas?” and “Why are these models not clinically implemented?”. Section 2 explains how the search, selection and screening processes were performed. In Section 3, a summary of the selected articles is presented, and in Section 4, the raised questions are discussed. Finally, in Section 5, a summary of the systematic review is given.

2. Materials and Methods

2.1. Search Strategy

This review was guided in accordance with the PRISMA methodology [15]. A comprehensive electronic search was performed in the Scopus electronic database until 23 February 2022, with no restrictions regarding date of publication and language. This search was performed by combining the search terms “numerical model” and “aorta”.

2.2. Inclusion and Exclusion Selection Criteria

In this search, only studies on human healthy and diseased aortas were accepted. Moreover, studies that reported the use of any numerical method to evaluate biomechanical parameters that are not directly accessible through medical imaging exams, such as velocity and displacement fields, WSS and WS distributions or even wall material properties on healthy and diseased aortas, were included. Reports of the applicability or development of novel risk indexes were also selected. Lastly, studies that assessed the effect of haemodynamic or mechanical stresses on wall microstructure or used idealised geometries were also included.

The studies that were not included, in this review, analysed specific populational groups (e.g., pregnant women or newborns); studied the biomechanical behaviour of post-surgery aortas; assessed the efficiency of certain treatment methodologies or focused on undesirable anatomic regions (e.g., heart, brain, iliac arteries or bones). Lastly, reviews, comments and conference proceedings were also excluded.

2.3. Quality Assessment

All gathered results were classified based on the selected method to perform numerical validation following the recommendations of the GRADE handbook [16,17]. The attributed grades were “high”, “moderate” or “low”, assigned to works that compared the numerical results with in vivo patient-specific data, in vitro measurements and other in silico results or did not perform any sort of validation, respectively.

2.4. Study Selection

The screening process of the elected results was performed in two different stages. In the first stage, both titles and abstracts of all researched works were analysed and only the ones meeting the selection criteria were selected for the full-text revision. In the second stage, during full-text analysis, the work’s compatibility with the inclusion and exclusion criteria was again checked. Moreover, prior to reading, analysis spreadsheets were developed in order to unify and synthesise the data extraction process. The screened articles were then divided into 4 categories, which are explored individually in Section 3.3.

3. Results

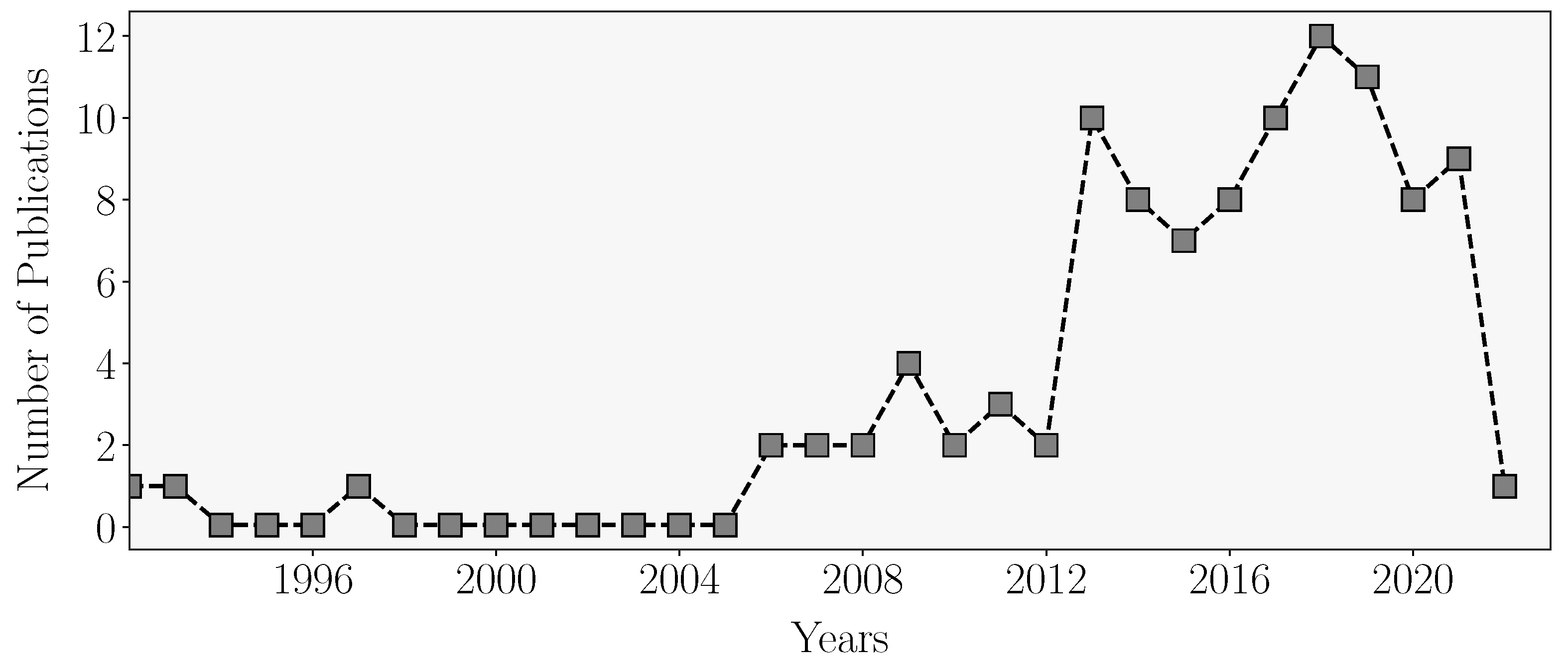
3.1. Publication Overview

The complete database contained a total of 214 articles. After the first screening process, 61 were excluded. From the remaining 153 articles, seven were not available for full-text analysis and 32 were excluded during the second screening phase. In the end, the database of articles comprised a total of 115 articles. In Figure 1, the PRISMA flowchart for systematic reviews is presented. This also describes the evolution of accepted articles throughout the several screening stages, where n is the number of available articles.

Figure 1. PRISMA flow chart of the systematic search strategy.

The gathered results evidenced a growing interest in the presented topic over the last few decades (Figure 2). The earliest report on the development of a human aorta numerical model was in 1992 by Owen [18], and until 2005, only two other works were found [19,20]. From 2006 until the present, the remaining 111 reviewed articles were published, with 2018 being the year with the highest number of publications (12).

Figure 2. Evolution of number of publications per year.

Regarding the studied anatomical region, it is evident a tendency to model either ATAA [21,22], AAA [23,24] or Aortic Dissection (AD) [25,26] since these present higher incidence among aortic diseases and are potentially more catastrophic. Moreover, several works recreated the biomechanics of healthy subjects [27,28,29] as it is relevant to identify the main differences between healthy and diseased states. Regarding the chosen computing platforms, open-source software such as OpenFOAM [11] and SimVascular [30] was used in around $10\%$ of the revised papers. The ANSYS finite element software was the preferred choice, being used in 40% of the works, particularly for CFD and FSI simulations. Abaqus was the second most used platform (20%), being commonly applied to CSM [9,31] or to FSI [32,33] studies (coupled with the Abaqus flow module or with ANSYS CFD modules). The entirety of the studied anatomies and the utilised computing platforms are presented in Figure 3.

Figure 3. (a) Studied anatomical regions. (b) Selected software to perform the numerical modelling.

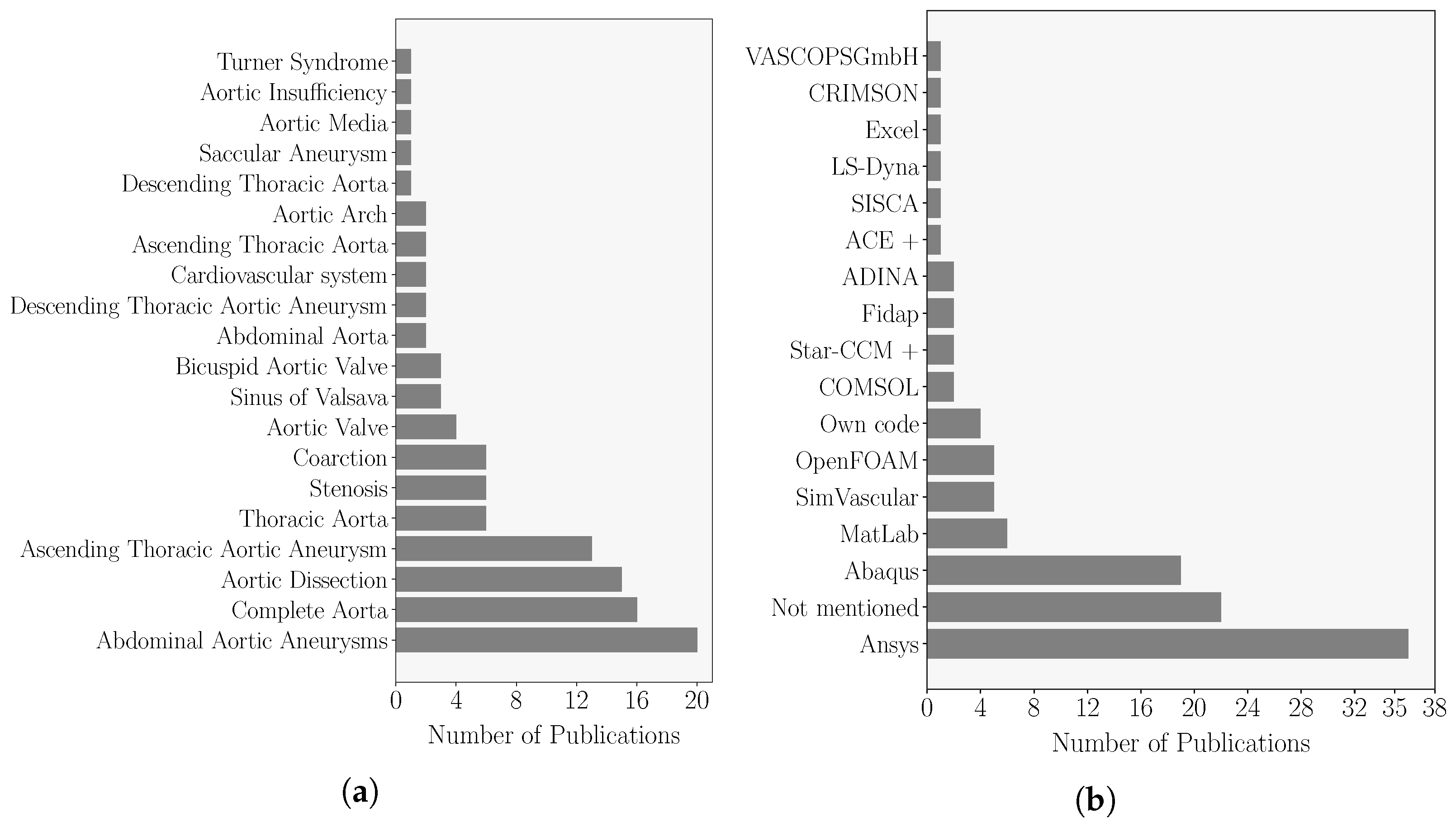
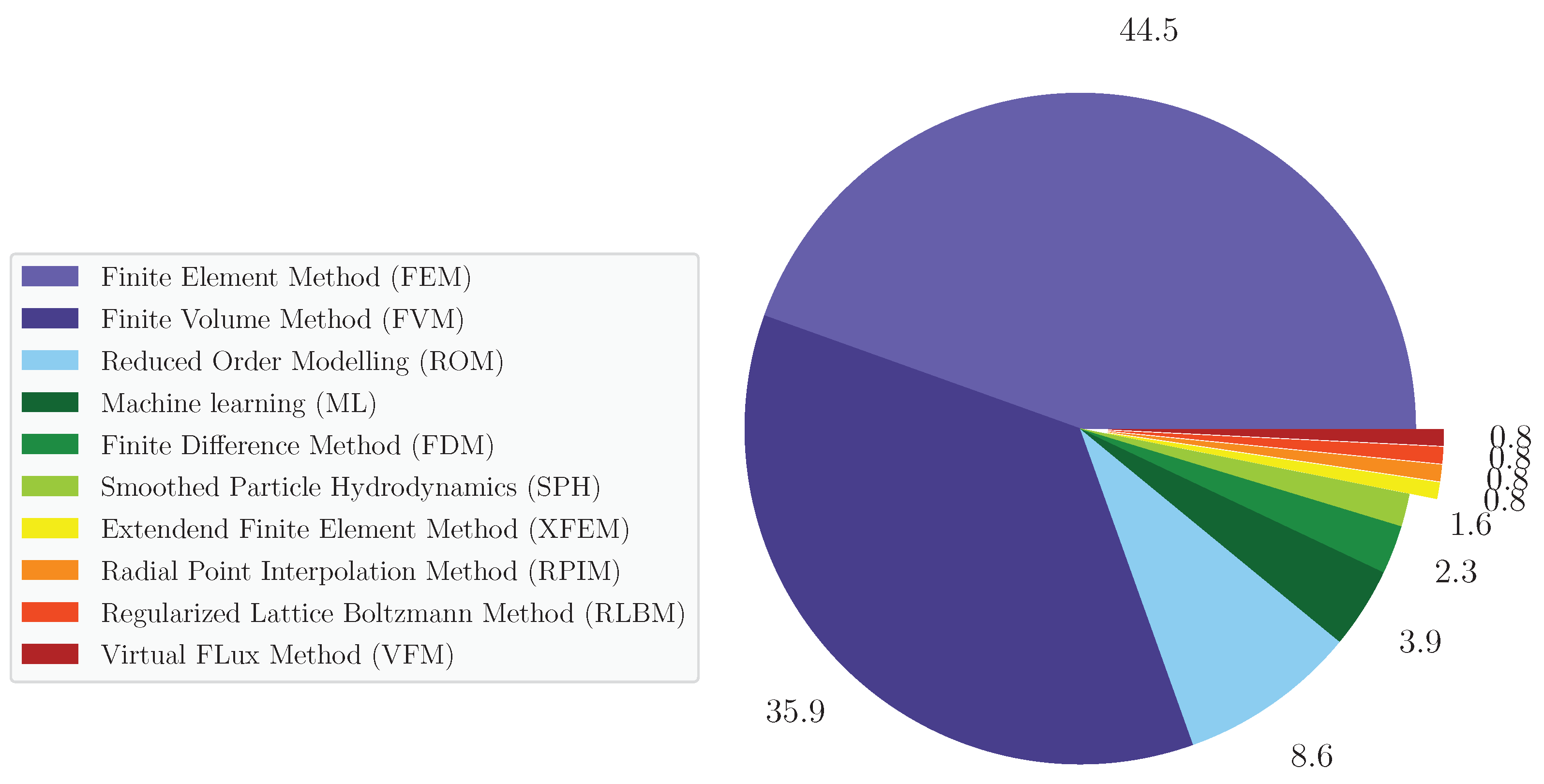
3.2. Computational Techniques to Model Diseased Aortas

Regarding the utilised numerical methods, our analysis revealed the usage of 12 different techniques. These and their relative frequency are depicted in Figure 4. The vast majority of the reviewed works resorted to the FEM and Finite Volume Method (FVM), which are grid-based methods to solve partial differential equations and allow the calculation of CSM [34,35,36], CFD [31,37,38] and FSI [21,39,40] simulations. FEM solves the differential equation by diving the analysed systems into finite elements and their predominance can be supported by several aspects. The main reasons are the wide implementation in computational platforms, the ability to handle complex geometries and, as of today, it represents the preferred choice to perform CSM simulations. Moreover, it was reported the use of FEM in CFD simulations (Garlekin Method) [41,42]. FVM integrates, over finite volumes, the system governing equations and, using the divergence theorem, converts these volume integrals into surface integrals. Therefore, the physical properties of interest can be assessed as flux on the cell’s surface, which is meant to improve convergence. This fact explains the recurrent choice of FVM to develop CFD simulations. As shown in Figure 3, the top five reported platforms (Abaqus, ANSYS, SimVascular, MatLab, OpenFOAM) all primarily resort to FEM and FVM techniques to develop the available modules.

Figure 4. Relative frequency (values presented in percentage) of the identified numerical approaches. $n=115$ articles.

Several other grid-based methods were reported. Finite Difference Method (FDM), similarly to FEM and FVM, also aims to solve partial differential equations, in this case by approximation to finite differences [19,43,44]. Extended Finite Element Method (XFEM) combines the formulations of generalised FEM and the Partition of Unity method and is mainly used in situations where grid refinement is not enough to achieve convergence. This feature is highly desirable in crack propagation simulations and coincidentally was used only in one work [45] to study the progression of AD. Regularised Lattice Boltzman Method (RLBM) and Virtual Flux Method (VFM) were the only Cartesian grid methods depicted in our summary [46]. The latter virtually calculate fluxes to impose pressure conditions on body surfaces, being able to reproduce their motion, and the former represents a set of methods for CFD simulations. These techniques were combined by Fukui and Morinishi [46] to model the AV leaflet motion (VFM) and the transvalvular flow (RLBM).

The second most used technique was the Reduced Order Model (ROM). Combining the works that resorted to 0D (4) [47,48], 1D (6) [49,50] and 2D (1) [51] models to recreate the haemodynamics of diseased and healthy aortas resulted in a total of 12 reports. ROM techniques are useful to overcome computational complexity-related problems by reducing the model degrees of freedom. In comparison with FEM or FVM simulations, which can easily take days or even weeks to conclude, these techniques allow for accurate computations in a few minutes or even seconds of incomplete characterisations of flow fields and WSS distributions. The 0D models, also known as electric analogues, are often used in in silico simulations of the cardiovascular system as Boundary Condition (BC) that recreates the compliance and resistance of arterial blood flow. The 1D models are mainly used to study Pulse Wave Velocity (PWV), which is an important metric to assess aortic stiffness, as recommended in clinical guidelines [2]. These models have been applied in FSI simulations to estimate the haemodynamics [52,53]. The 2D models are nowadays less utilised as 3D simulation has become more accessible due to improvements in computer processing and the availability of 3D solvers.

ML models have been growing in popularity over the last few decades due to their capabilities of efficiently analysing data. Another advantage of ML tools is that they can be used in a wide range of applications. Our summary gathered seven reports where ML tools were developed. Regarding their use in cardiovascular medicine, we found applications of these tools to improve the reporting time of Computed Tomography (CT) scans [54], estimate aortic reference configurations [29], act as a wall constitutive model [55], predict the local strength of ATAA tissue [56,57] and evaluate the propensity to rupture of aortic tissue [58].

There were another two reported numerical techniques and both were meshfree methods, which represent a new field of research opportunity, as these methods eliminate the necessity of grid generation, which can often be time-consuming and troublesome. One example is SPH, which was used in two works and is a meshfree Lagrangian approach that discretises the fluid as a set of moving particles and solves the governing equations for each of these particles [59,60]. This method is suitable to model large boundary displacements, which may be useful to model aortic wall dynamics [59,60]. Galerkin weak formulation and polynomial shape functions are used to develop Radial Point Interpolation Method (RPIM) models [61]. These also do not require grid generation as the polynomial functions are created based on a group of arbitrary nodes distributed along the computational domain. In Table 1 are presented the most relevant numerical results that can be calculated with each technique and their main advantages and limitations.

Table 1. Applications, advantages and limitations of the identified computational techniques.

Numerical Techniques	WSS	BP	PWV	WS	Strain	Advantages	Limitations
Finite Element Method	✪	✪	✪	✪	✪	Wide implementation in computing platforms. Ability to handle complex geometries. Preferred to develop CSM models	Requires mesh generation and is more computationally demanding than FVM and FDM
Finite Volume Method	✪	✪	✪	✔	✔	Wide implementation in commercial and open-source software. Preferred to perform CFD simulations	It induces complexity in mesh generation and requires more interpolation algorithms
Finite Difference Method	✔	✔	✔	✔	✔	Easier to implement efficient simulations in rectangular or box-shaped computational domains	Challenging to implement in complex geometric models, particularly for geometries with curved shapes
Extended Finite Element Method	✔	✔	✔	✪	✪	Useful to study crack propagation. It does not require mesh refinement or adaptative meshes	Not recommended for crack branching problems, 3D domains and highly heterogeneous or non-linear media
0D	✖	✪	✖	✖	✖	Possibility of coupling with 3D models in order to mimic the flow resistance imposed by the downstream vasculatures	Only describes the global behaviour of the system
1D	✔	✔	✪	✖	✖	Allow quick computations of PWV	Provide incomplete descriptions of the aortic haemodynamics
2D	✔	✔	✪	✖	✔	Easier to implement than 3D simulations and quicker to compute results	As computer processing and 3D solvers have increased, these simulations have lost relevance
Virtual FLux Method	✪	✪	✔	✖	✖	Resorts to GPU, which allows quicker computations. Enables flow calculation in curved surfaces using Cartesian grids	Challenging to implement patient-specific geometries
Regularised Lattice Boltzmann Method	✪	✪	✖	✖	✖	Designed to run on parallel architectures. Simple implementation and fixed regular grid	Stability problems in particular in heterogeneous media and thermal applications
Radial Point Interpolation Method	✔	✔	✪	✪	✪	Does not require mesh generation	Still a newly developed technology that requires further development
Smooth Particle Hydrodynamics	✔	✪	✪	✪	✪	Meshless and GPU-based method that allows for quicker computations	It does not capture well flow viscous features. Hard to implement inlet and outlet BC
Machine Learning	✪	✪	✪	✪	✪	Wide range of possible applications. Regarding numerical modelling, it is mainly applied to pre- and post-processing tasks	Hard to implement. Highly impacted by the quality of the training data sets

WS—Wall Shear Stress; BP—Blood Pressure; PWV—Pulse Wave Velocity; WS—Wall Stress; ✪—Preferred; ✔—Adequate but not preferred; ✖—Not adequate.

3.3. Summary of the Results

Among the gathered results on the numerical modelling of human aortas, the authors identified four main search topics, which will be discussed in the following order:

• Biomechanical behaviour of healthy and diseased aortas;
• Aortic wall characterisation;
• Risk assessment strategies and diagnosing techniques;
• Numerical modelling augmentation.

For papers that overlapped two or more categories, it was decided to address their work on the topic for which the contributions were more relevant. Exceptions were made for works that presented important contributions over more than one topic.

3.4. Biomechanical Behaviour of Healthy and Diseased Aortas

The study of the biomechanical behaviour of healthy and diseased aortas is an important research topic in the scientific community. To improve risk predictions of acute complications such as AAA [62,63], AD [26,37,64], ATAA [65,66,67], abdominal and aortic stenosis [68,69], coarction [70,71] or Sinus of Valsava [46] and improve diagnose efficiency, a deep understanding of its development and growth is mandatory. To date, the real pathophysiology of acute aortic complications is still not fully fathomed. It is expected that computational analyses could provide novel insights in this topic, as they enable access to complementary indices to quantify the risk of rupture, such as WSS and WS distributions or other relevant metrics. The works that have been gathered in this subsection are focused on studying the characteristic haemodynamic and structural features of healthy and diseased subjects. In Table 2, a summary of the analysed articles is presented.

Table 2. Studies focused on study the biomechanical environment of healthy and diseased aortas ($n=31$ articles).

First Author	Year	Simulation	Solver	Geometry	Boundary Conditions	Flow		Wall	Main Remarks	Aim of the Work	GRADE
J. Brunet	2021	CSM (XFEM)	Abaqus	AD (I)	LP; Axial DF	-	-	HGO	The propagation of AD is more likely to occur in larger and deeper tears	Study the effect of tear orientation on AD progression	Low
A. Totorean	2021	CFD (FEM; FVM)	SimVas-cular; Fluent	AAA (PS-CT)	I:CV (0.25 m s−1); O: 0P	L	N	-	Downstream of the abdominal bifurcation, recirculation zones, supraphysiological WSS and long particle residence time were found	Assess geometrical parameters’ influence on AAA and its branches’ haemodynamics	Low
B. Melka	2020	CFD (FVM)	Fluent	Coarction (I)	I:FR; O:WM	L	MM-E-E	-	One-phased and MM-EE rheological models produced similar results for high-velocity regimens	Investigate the influence of coarction on aortic haemodynamics	Low
Y. Chen	2019	FSI (FEM; FVM)	Ansys	Aortic Valve (I)	I:PoT; O:—	L	N	NH; S-VK	High bending stiffness causes a reduction in opening area of the AV; low bending stiffness may induce flapping oscillations	Assess the effect of the leaflets’ bending stiffness on FSI simulation	Low
R. Campobasso	2018	FSI (FEM; FVM)	Ansys	ATAA (PS-MRI)	I:VF; O:FR & WM	L	C	LEI	Stiffer aortas usually present abnormal WS distributions; increased peripheral resistance is correlated with increase in WSS	Evaluate the haemodynamic and structural changes in ATAA behaviour for different wall material properties	High
H. Yeh	2017	FSI (FEM)	COMSOL	ATAA (PS-Echo)	I:FR; O:CP	L	N	HGO	Significant differences in wall strain, blood pressure, WSS and turbulence were found between normative and hypertensive loading	Analysis of ATAA biomechanics under hypertensive and normative conditions	Low
C. García Herrera	2017	CSM (FEM)	House-hold code	ATAA (I)	LP (120–160 mmHg); PrS; DF	-	-	D	The stress field in MFS patients was mainly circumferentially oriented, almost uniform and presented higher WS magnitude	Numerically characterise ATAA biomechanics in MFS patients	Low
G. Jalalahmadi	2017	CSM (FEM)	Ansys	AAA (PS-CT/MRI; I)	LP (120 mmHg)	-	-	N-H; R-V	PWS increased with maximum diameter, asymmetry and turtuosity and decreased with wall thickening	Evaluation of the influence of different geometrical features on PWS	Low
J. Long	2017	CFD (FVM)	CFX	AD (PS-CT)	I:FR; O:PoT	$k-ϵ$	N	-	WSS in the FL were significantly higher; peak vortical flow appeared at aortic tear initiation points	Further investigate the pathogenesis and progression of AD	Low
B. Šeta	2017	CFD (FVM)	Star-CCM+	Aortic Arch (PS-CT)	I:VP; O:FR	L	C-Y	-	The flow on the aortic arch presented higher velocity near the inner wall, and clockwise helical and recirculating flow	Investigate the haemodynamics in the aortic arch	Low
Y. Shi	2016	CFD (FVM)	Fluent	AD (PS-CT)	I:PoT; O:PoT	L	N	-	Pressure and WSS seem to be well correlated with tear location	Evaluate the influence of tear location and tear size on AD haemodynamics	Low
S. Numata	2016	CFD (FVM)	Fluent	TAA(PS-CT)	I:CV ($5\mathrm{L}/min$); O:WM	RNG $k-ϵ$	N	-	Abnormal WSS was correlated with intimal layer (mal)functioning; high OSI was correlated with regions of high probability of rupture	Assess the haemodynamic variations between healthy and TAA patients	Low
L. Prahl	2016	CFD (FVM)	-	TS (PS-MRI)	I:FR; O:CP	L	Q	-	Anatomical variations contributed to increased WSS and recirculation zones where the n-N effects were significant	Assess how anatomical changes in TS patients influence aortic haemodynamics	Low
S. Ahmed	2016	CFD (FEM)	CRIMSON	AD (I)	I:FR; O:WM	L	N	-	AD induces increased blood pressure; the FL location is only impactful on blood pressure and velocities on the inner curvature	Evaluate AD haemodynamic alterations associated with anatomical variations	Low
H. Chen	2016	FSI (FEM)	Abaqus	AD (I)	I:FR; O:PoT	EM	N	LEI	Distally to the flap, lower velocities and higher flow turbulence were found	Assess the haemodynamic and structural features of a flap–blood interaction	Moderate
F. Callaghan	2015	CFD (FVM)	CFX	TAA (PS-MRI)	I:FR; O:FR; WM	$k-\omega$ SST	N	-	Vortices were formed at the entrance of the SA, which caused flow turbulence and recirculation zones	Study the haemodynamics on SA	High
K. Chaudhari	2015	CFD (FVM)	Fluent	Abdominal Stenosis (I)	-	L	N	-	As the blockage increases, the mean flow velocity and WSS magnitude also increase; the changes were significant for arterial blockage above 50%	Evaluate the haemodynamics on abdominal stenosis of different blockage degrees	Low
Y. Cong	2015	FSI (FEM; FVM)	Ansys	AAA (I)	I:PoT; O:CP	L	N	LEI	AAA haemodynamics were characterised by the formation of two vortices, which were appointed as the dominant aspect of fluid dynamics	Study the influence of vessel dilation and aspect ratio on the haemodynamics	Low
M. Moosavi	2014	FSI (FEM)	ADINA	Sinus of Valsava (PS-MRI)	I:FR; O:PoT	L	N	LEI	Vortices are formed in the LV and travel towards aorta; higher pressure and WSS were found in the aorta	Compute the haemodynamics inside the LV and aortic sinuses	High
T. Fukui	2013	FSI (RLBM; VFM)	Own code	Sinus of Valsava (I)	I:FR; O:PoT	LES	N	-	The formation of two vortices near the aortic root was evidenced and correlated with high WSS and diminished blood supply to the myocardium	Assess WSS distributions on sinus of Valsava patients	Low
H. Suito	2013	CFD (FDM)	-	TA (PS-CT)	I:FR; O:0P	L	N	-	All the tested geometries produce a swirled flow on the TA	Investigate effect of aortic torsion on the blood flow	Low
G. Marom	2013	FSI	Abaqus	BAV (I)	I:PoT; O:PoT	L	N	LEI	BAV caused more turbulence near the aortic root, and higher velocity and WSS	Evaluate the influence of BAV on blood flow	Moderate
S. Pasta	2013	FSI (FEM; FVM)	Ansys	AD (PS-CT)	I:VF; O:FR	L	N	RV	In BAV patients, an intrinsic disturbed blood flow that contributes to an asymmetric and elevated WS distribution was evidenced	Study the main differences in haemodynamics and WS between BAV and TAV patients	Low
Y. Zhang	2013	CFD (FVM)	Fluent	AD (PS-CT)	I:FR; O:0P	L	N	-	The pressure imbalance between the TL and FL is responsible for the delamination of aortic wall	Elucidate the mechanisms of longitudinal propagation of AD	Low
E. Shang	2013	CSM (FEM)	Abaqus	DTAA (PS-CT)	LP (120  mmHg)	-	-	RV	Positive correlation between PWS and aneurysm growth	Presented new correlations between PWS and aneurysm growth	Low
D. Molony	2011	FSI (FEM; FVM)	Abaqus; Fluent	AAA (PS-CT)	I:FR; O:PoT	L	N	RV	Aneurysm induced WSS magnitude increase (3-fold) and contributed to disturbed flow patterns	Evaluate the differences in haemodynamics between healthy subjects and AAA	Low
M. Alishahi	2011	FSI (FEM; FVM)	Ansys	Stenosis (PS-CT)	I:FR; O:PoT	L	PL	LEI	Wall deformation was low but still produced significantly different numerical results	Investigate the effects of pulsatile flow and flexible walls on aortic flow	Low
J. Lantz	2011	FSI (FEM; FVM)	Ansys	Aorta (PS-MRI)	I:FR; O:WM; EP	$k-ϵ$	N	LEI	The model accurately estimated flow patterns, presenting close agreement with MRI data for lower-velocity regimens; WSS is highly influenced by wall motion	Evaluate the flow dynamics on healthy aorta, in particular WSS distributions	High
Z. Cheng	2010	CFD (FVM)	CFX	AD (PS-CT)	I:FR; O:0P	$k-\omega$	Q	-	Disturbed flow and strong recirculation within both the TL and FL were found	Study the flow in AD and assess the crucial features to aneurysm dilation	Low
Z. Keshavarz-Motamed	2010	CFD (FVM)	Fluent	Stenosis; Coarction (I)	I:FR; O:—	$k-\omega$	N	-	The combination of coarction and stenosis highly influenced WSS and pressure distributions and induced the formation of secondary flow patterns	Study the effect of pulsatile flow on haemodynamics of stenosed and coarcted aortas	Low
T. Gasser	2009	CFD (FVM); CSM (FEM)	CFX; VASCOPS	AAA (PS-CT)	I:FR; O:PoT	L	C-Y	-	Significant haemodynamic and structural differences were found between healthy subjects and AAA patients	Study haemodynamic and structural features of AAA	Low
C. Gaudio	2006	CFD (FVM)	Fluent	Aortic Arch (I)	I:FR; O:FR	L	PL	-	Modelling the aortic root motion influenced the numerical results; intimal thickening occurred in low OSI and WSS regions	Show the potential of numerical tools to recreate the haemodynamics of the aortic arch	Low

0G—Zero Gradient; 0P—Zero Pressure; AoI—Aortic Insufficiency; AS—Aortic Stenosis; BT—Biaxial Tension; C—Carreau; CFN—Collagen Fiber Network model; CP—Constant Pressure; CS—Cardiovascular System; CV—Constant Velocity; C-Y—Carreau–Yasuda; D—Demiray; DF—Displacement Field; EM—Empirical Model; EP—External Pressure; FR—Flow Rate; F—Fung Exponentially Stiffening Material; HGO—Holzapfel–Gasser–Ogden; HI—Hyperelastic Isotropic; iFR—instantaneous Wave-Free Ratio; I—Idealised; Imp—Impedance; K-V—Kelvin–Voigt; L—Laminar; LDL—Low-Density Lipoprotein; LEI—Linear, Elastic and Isotropic; LP—Luminal Pressure; LV—Left Ventricle; MFS—Marfan Syndrome; MM-EE—Multi-Phase Euler–Euler Model; M-R—Mooney–Rivlin; MRV—Magnetic Resonance Velocimetry; n-N—non-Newtonian; N—Newtonian; N-H—Neo–Hookean; O—3rd-Order Ogden Model; OSI—Oscillatory Shear Index; PH—Polynomial Hyperelastic Constitutive Model; PL—Power Law; PoT—Pressure over Time; PrS—Prestress; PS—Patient-Specific; Q—Quemada; R—Resistance; RBF—Radial Basis Function; RF—Reflection Free; RV—Raghavan and Vorp; RVol—Representative Volume; SA—Saccular Aneurysms; S-VK—Saint Vennant–Kirchhoff; TA—Thoracic Aorta; Tor—Torsion; TKE—Turbulent Kinetic Energy; TS—Turner Syndrome; UT—Uniaxial Tension; VP—Velocity Profile; WM—WindKessel Model; Y—Yeoh Model.

3.4.1. Healthy Aorta

The first work from the selected database reporting numerical modelling in healthy aortas was in 2006 by Del Gaudio et al. [72]. In this work, CFD simulations considering a non-Newtonian fluid were performed on idealised geometries. The aim was to elucidate how numerical tools can be used to recreate the haemodynamics on the aortic arch. Their findings on the axial flow profiles revealed complex temporal variances and skewness towards the inner curvature of the arch. They also postulated that vascular geometry (e.g., branching, non-planar, curvature, asymmetry), as it highly influences local fluid dynamics, could be the primary cause in the development of atherosclerosis. Later, in 2011, Lantz et al. [73] reported the development of FSI simulations on Magnetic Resonance Imaging (MRI)-driven geometric models. Patient-specific velocity profiles were used as an inlet BC and the external pressure exerted by surrounding vessels (e.g., pulmonary trunk and superior vena cava) was modelled as a linear elastic support BC on the outer wall. The model proved to be able to reproduce physiologically admissible flow patterns that presented close agreement with MRI data for lower-velocity regimes. Marom et al. [74] also resorted to FSI simulations specifically to model the leaflet motion of the Aortic Valve (AV). The left ventricle and the aorta were modelled as rigid cylindrical tubes and the blood was considered slightly compressible to improve numerical convergence. The results evidenced that higher stresses appeared on collagen fibres and that Bicuspid Aortic Valve (BAV) induced flow turbulence and led to higher velocities and WSS magnitudes. Moosavi et al. [75] also used FSI formulations to simulate the blood flow on the Sinotubular Junction (STJ). A rigid model of the aorta and valve leaflets (peak systolic configuration) coupled with a contractile left ventricle mimicked the blood ejection into the aorta. Among their findings was the evidence of turbulence created at the left ventricle that travelled towards the aorta and higher WSS were found in the aorta. Šeta et al. [76] performed patient-specific CFD simulations using FVM to calculate the haemodynamics of the aortic arch. Larger velocities near the inner wall and the presence of clockwise helical flow and recirculation zones was evidenced. Chen and Luo [53] also performed FSI simulations on AV virtualisations, but in this particular case, the blood flow was modelled with a ROM (1D). A good agreement was found with regular FSI simulations and showed that increased bending stiffness reduces the opening area and considerably increases flow resistance. On the other hand, excessively low values of bending stiffness are also not desirable as the leaflets may present flapping oscillation. Totorean et al. [77] performed CFD analysis on patient-specific models of the abdominal aorta and its branches. The geometries were reconstructed via CT data segmentation and comprised a total of 16 outlets. The authors postulated that the flow was almost entirely stable upstream of the abdominal aortic bifurcation. Downstream of the bifurcation, secondary blood flow with recirculation zones was formed. Moreover, WSS analysis revealed distributions with low, high and supra physiological magnitudes during the cardiac cycle and particles that presented long residence times near the wall, which is known to be a contributing factor to atherosclerosis.

3.4.2. Aortic Aneurysms

Our database revealed that 12 works focused on studying the biomechanical behaviour of aortic aneurysms (e.g., ATAA, AAA, Descending Thoracic Aortic Aneurysm (DTAA) and saccular aneurysms). Gasser et al. [63] developed both CFD and CSM models based on the FEM technique, to study the haemodynamics and structure of patient-specific AAA. Their results highlighted the existence of recirculation zones and increased WSS, which was not found in healthy patients. Structurally, it was shown that patients with a known rupture appeared to have superior Peak Wall Stress (PWS). Molony et al. [21] improved the methodology described in the previous work by developing a two-way FSI simulation, using partitioned schemes. Cong et al. [62] also developed two-way FSI to assess the effects of dilatation and aspect ratio on the haemodynamics of idealised models of AAA. The numerical results showed the formation of two vortices, which were appointed as the dominant aspect of fluid dynamics. Moreover, elevated Oscillatory Shear Index (OSI), which is highly correlated with endothelial malfunctioning, was also found. Callaghan et al. [67] performed CFD simulations in patient-specific geometries. The haemodynamics of saccular transverse aortic aneurysms was analysed. Higher WSS magnitudes and increased turbulence (vortices and recirculation) were found at the dilated region.

Pasta et al. [39] explored the differences in haemodynamics and WS induced by BAV using a two-way FSI approach and structured meshes. Evidence of an intrinsic disturbed blood flow was found in BAV patients; this contributes to an asymmetric and elevated WSS distribution. The inner layer was subjected to significantly higher principal stress and a greater inner–outer wall pressure gradient was found on the STJ area, supporting the hypothesis that this region is the most susceptible to dissection. This was later also postulated by Numata et al. [78], where CFD simulations highlighted that abnormal WSS distributions promote medial degeneration, which may be one of the main causes of AD development, and that the STJ presented with higher values of OSI and WSS. Prahl Wittberg et al. [79] evaluated the influence of anatomical features on aortic haemodynamics. A two-phase mixture model to measure the evolution of red blood cells on the blood flow, Quemada non-Newtonian rheological model and four different groups (healthy, BAV, aneurysm and elongated transverse aorta) were considered to perform the CFD simulations. It was shown that anatomical variations had a great impact on flow patterns. On some occasions, recirculation zones, characterised by lowered blood cell concentrations and elevated WSS, were found, in which the non-Newtonian behaviour of blood significantly altered the results.

Jalalahmadi et al. [66], following an approach similar to Prahl Wittberg et al. [79], investigated the influence of several geometrical factors (thickness, maximum diameter, turtuosity and asymmetry) on the WS distribution of ATAA. Several sets of idealised distinct geometries were generated to study each factor individually. They assessed that PWS increases with higher maximum diameter, asymmetry and turtuosity and decreased thickness. Yeh et al. [80] performed patient-specific FSI simulations under normative and hypertensive conditions. The presented results implied that wall motion was highly influenced by blood pressure and local geometrical characteristics and that WS distribution was highly inter-patient heterogeneous. Campobasso et al. [65] also developed a two-way coupled FSI model to study the influence of peripheral vascular resistance and wall mechanical properties on WS. Their findings suggested that aortic stiffening contributed to abnormal WS distributions and predisposed the aortic wall to rupture. The increase in peripheral resistance translated into elevated blood pressure, which makes the aortic wall more susceptible to rupture as well [80]. García–Herrera et al. [81] were interested in studying ATAA biomechanics in Marfan syndrome patients, as this syndrome is known for weakening the aortic wall. CSM simulations were performed on idealised geometries resorting to an in-house-built code, in which incremental homogeneous inner pressure (120–160 mmHg), aortic root motion and prestress BC were applied. The numerical results evidenced that Marfan syndrome presence induced significant changes in WS due to material properties’ degradation. Furthermore, the stress field was mainly circumferentially oriented, which is justified by the spatial distribution and orientation of collagen fibres.

3.4.3. Aortic Dissection

The real pathogenesis of AD is still an open debate. Several numerical models provided great contributions towards a better understanding of the main contributors to the development and progression of AD. Cheng et al. [82] evidenced that AD induced abnormal haemodynamics with the presence of recirculation zones both in True Lumen (TL) and False Lumen (FL). Geometrical features were also identified as a primary cause of disturbed haemodynamics. Zhang et al. [37] focused on studying the underlying haemodynamics responsible for the longitudinal propagation of AD by developing CFD models with pulsatile flow conditions. Tear (entry point towards the FL ) size and location impacted the FL blood flow patterns. The transmural pressure gradient, specifically in the circumferential direction, was suggested as one of the mechanisms responsible for the cleavage of lamellar units. Abnormal WSS distributions were proposed as the main cause of intimal tear initiation, justified by the elevated values of Time-Averaged Wall Shear Stress (TAWSS) found near the tear. Ahmed et al. [83] studied the influence of anatomical risk factors in 14 idealised models of AD (tear size and location, number of entries and FL location). Evidence pointed out that FL increases flow resistance and revealed significant differences in the haemodynamics between the TL and FL. These differences diminish with the increase in the tear size. Shi et al. [26] also assessed the influence of tear location on haemodynamics with CFD simulations on patient-specific geometric models. Their results proved that aortic root proximity induces more turbulence in the FL. Pressure and WSS distributions seem to be well correlated with tear location since the tear usually occurred in regions where these quantities presented higher magnitude. Long Ko et al. [64] also investigated the haemodynamics of pulsatile flow on AD. Their results suggested that a high WSS gradient between TL and FL acts as the main contributor to layer delamination and consequent AD progression and that high vorticity may be associated with intimal tear initiation and growth. Brunet et al. [45] investigated the most influential factors in AD propagation. CSM simulations on idealised models with two uniform thickened layers (media and adventia layers) were accomplished. Failure criteria based on Hashin failure theory, hyperelastic anisotropic constitutive models and residual and prestresses were considered. The authors postulated that initial tearing is correlated with tissue fatigue and that tissue ultimate tensile stress can be achieved during intense workouts (e.g., weight lifting). Media layer strength appeared as a fundamental factor in AD propagation and the shear fracture was identified as a key process in delamination. Wan Ab Naim et al. [84] published a comprehensive overview on the topic of AD numerical modelling with a focus on the biomechanical factors leading to the initial tear.

Besides the study of the effects of AD in the haemodynamics, the interaction between the blood flow and tear is also important as it may provide further insight into the mechanisms that induce the development of AD. Chen et al. [85] applied FSI simulations to study this interaction in an idealised aortic model that included the TL and FL was applied. The haemodynamic parameters at the TL and FL tend to homogeneity as the FL increase in size. Smaller FL presents lower velocities and may be stagnant. Moreover, stress analysis around the flap evidenced an elevated concentration of stress, which may lead to AD progression.

3.5. Aortic Wall Characterisation

This section includes the works with a focus on studying materials that can mimic the behaviour of biological tissues, studying the microstructure of the aortic wall and exploring methods to non-invasively estimate wall properties. The results of this analysis are summarised in Table 3.

Table 3. Numerical models applied to study aortic wall microstructure ($n=14$ articles).

First Author	Year	Simulation	Solver	Geometry	Boundary Conditions	Flow		Wall	Main Remarks	Aim of the Work	GRADE
G. Comunale	2021	FSI (FEM)	Abaqus	TA (PS-MRI)	I:FP; O:CP	L	N	O; HGO	Geometrical factors highly influence the haemodynamic patterns; wall compliance was the dominant factor for the overall aortic mechanical behaviour	Assess the viability of using in vitro silicone models to mimic vascular tissue	Moderate
E. Ban	2021	CSM (FEM)	-	AD (RVol)	Fluid injection	-	-	N-H; F	The maximum pressure prior to tearing is highly dependent on local geometry and material properties	Assess which location of the aortic wall is more likely to dissect	Low
R. Wang	2020	CSM (FEM)	Abaqus	AD (RVol)	UT	-	-	HGO	Glucose-treated elastin presented increased peeling force, energy release rate and interlamellar strength	Evaluate the effect of elastin glycation on AD progression	Moderate
S. Maiti	2020	CSM (FEM)	Own code	AD (RVol)	UT	-	-	LEI	In biaxial conditions, the rupture is likely to occur in any direction; organisation and fibre properties are the main contributors to aortic strength	Assess the relevant changes in aortic wall microstructure during rupture	Low
S. Farzaneh	2019	CSM (FEM)	Abaqus	ATAA (PS-CT)	DF; LP (80 mmHg)	-	-	HGO	Extensional stiffness (higher in the ascending aorta) and high rupture risk were statistically correlated	Develop a technique to non-invasively identify aortic wall mechanical properties	High
O. Gültekin	2019	CSM (FEM)	-	AD (RVol)	DF; LP (80–600 mmHg); Tor	–	-	HGO	AD development is consequence of in-plane shear stresses created by the heterogeneity of aortic wall properties and FL propagation occurs mainly due to the secondary blood flow	Study the mechanisms that explain the beginning and progression of AD	Low
M. Frank	2019	CSM (FEM)	-	Aortic Media (RVol)	BT	-	-	Y; NH	The developed model captured the overall response only for physiological pressure ranges	Present a new micromechanically based wall constitutive model	Moderate
J. Thunes	2017	CSM (FEM)	MatLab	Aorta (RVol)	Axial DF	-	-	N-H; LEI	Collagen fibres present higher strength and stiffness but lower failure stretch when compared to elastin; collagen breakage is the governing tissue failure mechanism	Study the microstructural response of the aortic wall to rupture	Moderate
J. Thunes	2016	CSM (FEM)	MatLab	Aorta (RVol)	Axial DF	-	-	N-H; LEI	Collagen fibres oriented in loading direction were more solicited	Study the response of aortic wall microstructure under UT conditions	Low
H. Taghizadeh	2015	CSM (FEM)	Own-Code	Aorta (RVol)	LP (100–160 mmHg)	-	-	HGO	Elastin fibres have a dominant role for lower strains	Study microstructure components of the aortic wall under hypertensive conditions	Low
A. Cloonan	2014	FSI (FEM)	Abaqus	AAA (PS-CT)	I:FR; O:RF	L	N	HI	The materials presented similar mechanical properties to vascular tissue; PWV results were consistent with FSI simulation findings	Assess whether certain phantom materials are good replicates of vascular tissue	Moderate
S. Yang	2014	FSI (FVM)	ACE +	TA (PS-MRI)	I:FR; O:FR	L	N	LEI	The proposed method may be used to evaluate whether the considered material parameters are suitable	Present a new method for arterial wall compliance assessment	Low
A. Azadani	2012	CSM (FEM)	Matlab	AS (I)	BT	-	-	2D F	Ascending aorta (more compliant) and AS tissue presented significantly different material properties	Evaluate ATAA and AS material properties differences	Moderate
F. Helderman	2008	CSM (FEM)	-	AAA (PS-CT)	LP	-	-	LEI	Aneurysmal growth was correlated with elevated aortic stiffness	Evaluate the aortic microstructure alterations promoted by abnormal WS distributions	Low

0G—Zero Gradient; 0P—Zero Pressure; AoI—Aortic Insufficiency; AS—Aortic Stenosis; BT—Biaxial Tension; C—Carreau; CFN—Collagen Fibre Network model; CP—Constant Pressure; CS—Cardiovascular System; CV—Constant Velocity; C-Y—Carreau–Yasuda; D—Demiray; DF—Displacement Field; EM—Empirical Model; EP—External Pressure; FR—Flow Rate; F—Fung Exponentially Stiffening Material; HGO—Holzapfel–Gasser–Ogden; HI—Hyperelastic Isotropic; iFR—instantaneous Wave-Free Ratio; I—Idealised; Imp—Impedance; K-V—Kelvin–Voigt; L—Laminar; LDL—Low-Density Lipoprotein; LEI—Linear, Elastic and Isotropic; LP—Luminal Pressure; LV—Left Ventricle; MFS—Marfan Syndrome; MM-EE—Multi-Phase Euler–Euler Model; M-R—Mooney–Rivlin; MRV—Magnetic Resonance Velocimetry; n-N—non-Newtonian; N—Newtonian; N-H—Neo–Hookean; O—3rd-Order Ogden Model; OSI—Oscillatory Shear Index; PH—Polynomial Hyperelastic Constitutive Model; PL—Power Law; PoT—Pressure over Time; PrS—Prestress; PS—Patient-Specific; Q—Quemada; R—Resistance; RBF—Radial Basis Function; RF—Reflection Free; RV—Raghavan and Vorp; RVol—Representative Volume; SA—Saccular Aneurysms; S-VK—Saint Vennant–Kirchhoff; TA—Thoracic Aorta; Tor—Torsion; TKE—Turbulent Kinetic Energy; TS—Turner Syndrome; UT—Uniaxial Tension; VP—Velocity Profile; WM—WindKessel Model; Y—Yeoh Model.

3.5.1. Cardiac Phantom Materials

Human and diseased aortas present complex anatomy and mechanical behaviours (e.g., heart motion, anisotropic hyperelastic wall, heterogeneity of wall properties and thickness, active contraction of the vascular smooth muscle cells within the aortic media layer). Access to materials able to mimic cardiovascular tissue is relevant for clinicians to practice, plan surgical procedures and validate devices or techniques. There is an ongoing quest to develop such materials, known as cardiac phantom materials, that are capable of representing patient-specific human aortas.

Following this rationale, Cloonan et al. [86] performed experimental (uniaxial, tear and dynamic tests) and in silico FSI tests on different cardiac phantoms. These phantoms had the particularity of allowing them to measure results with PWV. The results suggested that the tested materials presented similar mechanical properties and similar pulse wave propagation. Nonetheless, the materials appeared to be less stiff under dynamic loading, where the viscoelastic effects were more prominent. Moreover, the authors presented two different techniques to produce these cardiac phantom materials (investment casting process and 3D printing) and postulated that these materials have great potential to improve computational modelling approaches, clinical imaging modalities and medical device design and bench testing. Comunale et al. [28] intended to answer the following questions: “Can a silicone prototype suitably mimic a biological aorta?”; “To what extent do the anatomical characteristics have to be detailed?”. The differences in considering patient-specific geometries and material properties were assessed by implementing FSI simulations. It was assessed that geometrical factors highly influence the haemodynamic patterns and wall compliance was the dominant factor for the overall mechanical behaviour. They recommended that both patient-specific geometries and material properties should be considered.

3.5.2. Wall Microstructure

The aortic wall is a complex structure constituted by three distinct layers with distinct material properties, microstructure and morphology and adaptative to the mechanical environment. For instance, older patients present stiffer aortas resulting from increased collagen content and reduced elastin content. Another example of the nuances of this structure is how an elevated WSS magnitude deregulates matrix metalloproteinase synthesis, which contributes to the cleavage of collagen fibres and consequent weakening of the wall. Henceforth, studying the effects of the mechanical environment on the wall microstructure is relevant to a better understanding of the underlying mechanisms of the development of acute complications.

In 2008, Helderman et al. [24] developed a CSM model using FEM that aimed to estimate aneurysmal diameter growth. They chose an adaptative constitutive model which considered collagen degradation in regions where the stress surpassed a certain threshold. Despite the elevated clinical interest in the presented model, no relevant results were presented due to the excessive number of limitations. Taghizadeh et al. [36] created an aortic media lamellar model, constituted by adjacent stripes that alternated between representing elastic lamellae and the constituents comprising two elastic laminae, e.g., collagen fibres and vascular smooth muscle cells. For hypertensive pressure conditions (160 mmHg), the results suggested elastin as a major load-bearing component in lower strain regimes. Increased strain induces the engagement of collagen fibres, evidencing that these are the primary load-bearing component for higher strains. Moreover, the authors postulated that wall thickening and alteration of the microstructure promoted higher blood pressure. Thunes et al. [87] assessed the changes in the aortic wall microstructure, especially on collagen fibres, by imposing BC that recreated uniaxial tensile tests. CSM simulations on representative volumes of the aortic media were calculated. The heterogeneity in mechanical properties was found to increase with stretch, mainly due to the spatial orientation of collagen fibres and activation. In 2017, the same group [9] suggested that under these conditions, aortic tissue failure is governed by the cleavage of collagen fibres as they are stiffer and present inferior maximum stretch. Elastin fibres are more compliant, thus being the main contributor to hyperelastic behaviour of the aortic wall.

Gültekin et al. [10] implemented an extension–inflation–torsion in silico test that intended to study the underlying mechanisms of the development and progression of AD. The numerical model used an anisotropic wall constitutive model and failure criterion. In-plane shear stress originating from the heterogeneity of aortic wall mechanical properties was found to be the main contributor to initial tearing [45] and the second blood flow on the FL the main contributor to AD progression. Similar to Thunes et al. [9], Maiti et al. [88] developed a CSM virtualisation of a mechanical test (biaxial tensile). The results also suggested cleavage of collagen fibres as the main contributor to the failure of the aortic wall. Under biaxial conditions, collagen fibres in both directions are similarly loaded and rupture is likely to occur in any direction as well. Wang et al. [89] simulated peeling and direct tension tests, aiming to study the effect of glycation (covalent attachment of sugars, usually glucose, to a protein or lipid) on the interlamellar bonding properties of medial elastin, which is often compromised in CVD. The motivation behind this study was the reports of the reduced risk of AD in patients with diabetes. Their findings suggested that glycation of arterial elastin reduces the risk of AD since it significantly increases the peeling force and interlamellar strength. Ban et al. [90] studied the effect of circulating blood flow on the propensity to dissect of different regions and created a model that simulated a fluid injection on idealised volumes of the aortic media. Ultimate tensile stress was found to be highly dependent on local geometry and material properties. It was remarked that intramural swelling can lead to delamination, and radially oriented structural components are extremely relevant to the delamination process, either to allow or arrest it.

3.5.3. Non-Invasive Estimation of Wall Material Properties

When the interest of the simulation requires modelling of the aortic wall, a suitable wall constitutive model needs to be chosen and calibrated. However, patient-specific material properties are not directly available and are very challenging to estimate, and since the numerical results are highly dependent on these parameters, an accurate estimate is vital to produce accurate results. Estimating wall properties in a non-invasive way is still a challenge and further developments are needed. Our research gathered eight works where methodologies to estimate in vivo or ex vivo mechanical properties were presented. Azadani et al. [91] implemented a code in MatLab that adjusted the parameters of a bidimensional Fung strain energy constitutive model to experimental stress–strain data, obtained from peel and direct tension tests performed on human ascending aorta and aortic sinus samples. Yang et al. [92] presented a novel method to estimate aortic wall compliance. This method resorted to uncoupled FSI simulations to estimate PWV. The cardiac circle was divided into five time steps, and for each one, the following steps were executed and repeated until no significant differences were found: (i) the governing equations of the fluid domain are solved considering steady flow; (ii) the results of these simulations are updated on the solid domain; (iii) CFD simulations are newly performed with an updated computational domain according to the previous structural analysis. The results suggested close agreement in the estimated PWV, according to what was expected in this particular case (552 cm s⁻¹. Therefore, the authors affirmed that this methodology could be a promising metric to assess if the used material parameters are adequate and may also be used to inversely estimate wall compliance. The group of Liu et al. [93] also developed a method to non-invasively estimate wall properties. In their first work [93], the multi-resolution direct search approach was presented, which aimed to efficiently solve optimisation problems. Multi-resolution direct search was used to estimate a set of constitutive parameters (Holzapfel–Gasser–Ogden model) that best represents the patient-specific structural behaviour by minimising the node to node differences between estimated (via CSM simulations) and synthetic “real” geometries. In the second work [94], the multi-resolution direct search approach was combined with CT data and the preliminary results were relatively close to experimental stress–strain curves. Farzaneh et al. [95] estimated local aortic stiffness from CT scans and found higher stiffness in ATAA when compared to healthy subjects. The inverse methodology applied in this work also allowed the authors to identify regional gradients of material properties that greatly impacted the numerical results.

3.6. Risk Assessment Strategies and Diagnosing Techniques

As mentioned in Section 1, current clinical guidelines for aortic disease diagnosis and treatment are fallible and unreliable, which creates an urgent need for more robust risk assessment and diagnosing techniques. This section presents a summary of 16 works that explored the potential of numerical models to act as complementary tools in clinical diagnosis [96], assessing the risk of acute complications by exploring their correlation with numerically obtained metrics such as PWS [34], WSS [97] or transvalvular pressure gradient [98]. The modelling options and results of the analysed articles are summarised in Table 4.

Table 4. Works regarding improvements or development of diagnosis metrics or techniques ($n=16$ articles).

First Author	Year	Simulation	Solver	Geometry	Boundary Conditions	Flow		Wall	Main Remarks	Aim of the Work	GRADE
V. Badeli	2021	CSM (FEM)	COMSOL	AD (I)	Specific Voltage	-	-	-	The use of Bayesian approach outperformed regular multi-sensor impedance cardiography methodology	Intended to simulate the propagation of trans-thoracic electric pulses	Low
M. Liu	2021	CSM (FEM)	-	ATAA (PS-CT)	LP (80–120 mmHg); PrS	-	-	HGO	The developed ML tool outperformed other rupture risk estimation methods	Identify the locations where the aortic rupture is more likely to occur	Low
S. Pasta	2020	CFD (FVM)	Fluent	ATAA (PS-CT)	I:CV; O:WM	L	C	-	A combination of haemodynamic, wall parameters and circulating biomarkers may be a suitable method to assess the risk of acute complications	Investigate the relation between WSS and aortic wall strain and the presence of biomarkers	Low
A. Bauer	2019	CFD (FVM)	Open- FOAM	AAA (I)	I:FR; O:0G	L	N	-	Laser Doppler velocimetry is the preferred technique to estimate WSS	Evaluate the gold-standard method to estimate WSS	Moderate
M. Bopp	2019	CFD (FVM)	Open- FOAM	AAA (I)	I:FR; O:0G	RANS	N	-	Magnetic resonance velocimetry captured better the flow turbulence and better predicted WSS when compared to WSS	Present validated numerical descriptions of AAA blood flow to improve MRV efficiency	Moderate
N. Kizilova	2018	CFD (2D)	-	Aorta	I:FR; O:Imp	L	K-V	LEI	The developed model found good agreement with in vivo data and outperformed regular rigid wall simulations	Develop a validated realistic model of the aorta that is able to evaluate PWV	High
C. Zhu	2018	CFD (FVM)	-	AS (I)	I:CV; O:—	DNS	N	-	Murmur source location is not correlated with stenosis degree and is not coincident with stenosis location	Enhance auscultation by studying post-stenosis haemodynamics	Low
J. Sotelo	2018	CFD (FEM)	MatLab	Aorta (PS-MRI)	I:PoT; O:PoT	L	N	-	The circumferential component of WSS presented good correlation with disturbed flow	Implement a method to estimate WSS different components	Low
F. Condemi	2017	CFD (FVM)	Fluent	ATAA; AI (PS-MRI)	I:VF; O:FR; WM	L	C	-	Inflow jet impingement against the aortic wall creates a non-homeostatic WSS distribution	Study the role of altered haemodynamics in aortic rupture risk	High
I. Sazonov	2017	CFD (1D)	-	AAA	I:FR; O:RF	L	N	LEI	Aortic compliance alterations may be a good monitoring metric for diagnosing aneurysms that can be estimated via ultra-sound measurements	Develop a new diagnosis technique for aneurysms based on 1D modelling	Moderate
S. Pasta	2016	FSI (FEM; FVM)	Abaqus; Fluent	BAV (PS-CT)	I:FR; O:WM	L	N	P	BAV patients showed increased WSS and WS when compared to TAV patients	Evaluation of new ascending aortic dilatation risk predictors	Low
H. Mohammadi	2015	CFD (2D)	LS-Dyna	AS	I:PoT; O:0P	L	N	LEI	Systolic transvalvular pressure gradient is useful to evaluate the degree of stenosis	Improve the diagnosis efficiency of aortic stenosis	Low
J. Sotelo	2015	CFD (FEM)	MatLab	Aorta (PS-MRI)	I:PoT; O:PoT	L	N	-	Wall deformation highly impacted the WSS magnitude	Develop a new technique to evaluate WSS distributions in the aorta	Low
C. Babbs	2014	CFD (0D)	Excel	CS	I:PoT; O:R	-	-	F	The proposed methodology presented good estimation when constant compliance was applied	Develop a new technique to measure cardiac stroke volume	Low
E. Shang	2013	CSM (FEM)	Abaqus	DTAA (PS-CT)	LP (120 mmHg)	-	-	RV	Positive correlations between PWS and aneurysm growth were found	Study the rupture of aneurysms	Low
B. Doyle	2009	CSM (FEM)	Abaqus	AAA (I)	DF	-	-	O	The numerical results accurately predicted the sites of rupture	Simulate the rupture in aneurysms using in silico and in vitro experiments	Moderate

0G—Zero Gradient; 0P—Zero Pressure; AoI—Aortic Insufficiency; AS—Aortic Stenosis; BT—Biaxial Tension; C—Carreau; CFN—Collagen Fibre Network Model; CP—Constant Pressure; CS—Cardiovascular System; CV—Constant Velocity; C-Y—Carreau–Yasuda; D—Demiray; DF—Displacement Field; EM—Empirical Model; EP—External Pressure; FR—Flow Rate; F—Fung Exponentially Stiffening Material; HGO—Holzapfel–Gasser–Ogden; HI—Hyperelastic Isotropic; iFR—instantaneous Wave-Free Ratio; I—Idealised; Imp—Impedance; K-V—Kelvin–Voigt; L—Laminar; LDL—Low-Density Lipoprotein; LEI—Linear, Elastic and Isotropic; LP—Luminal Pressure; LV—Left Ventricle; MFS—Marfan Syndrome; MM-EE—Multi-Phase Euler–Euler model; M-R—Mooney–Rivlin; MRV—Magnetic Resonance Velocimetry; n-N—non-Newtonian; N—Newtonian; N-H—Neo–Hookean; O—3rd-Order Ogden Model; OSI—Oscillatory Shear Index; PH—Polynomial Hyperelastic Constitutive Model; PL—Power Law; PoT—Pressure over Time; PrS—Prestress; PS—Patient-Specific; Q—Quemada; R—Resistance; RBF—Radial Basis Function; RF—Reflection Free; RV—Raghavan and Vorp; RVol—Representative Volume; SA—Saccular Aneurysms; S-VK—Saint Vennant–Kirchhoff; TA—Thoracic Aorta; Tor—Torsion; TKE—Turbulent Kinetic Energy; TS—Turner Syndrome; UT—Uniaxial Tension; VP—Velocity Profile; WM—WindKessel Model; Y—Yeoh Model.

3.6.1. Mathematical Models as Tools to Assist Clinical Diagnosis

According to current clinical guidelines, PWV (measures how the shock wave generated by the closing of AV propagates along the aorta) is a useful metric to estimate aortic stiffness, cardiac output and even the presence of aneurysms and AD as they induce wave reflection and consequent changes in normal PWV. Therefore, this metric may be used as a diagnosis methodology. Numerically, excluding a few exceptions [86,92], all the works that aimed to estimate this metric resorted to ROM as it allows the computation of accurate and time-efficient results. Babbs [99] developed 0D models of the systemic circulation to measure cardiac output. The results presented close agreement with in vitro data when constant wall compliance was considered. The introduction of non-linear effects led to overestimations of wall compliance for higher pressure ranges. Sazonov et al. [50] aimed to develop cost-effective aneurysm diagnosing techniques, based on assessable measurements and pressure and/or velocity waveforms obtained via 1D modelling. This 1D model was validated with a representative experimental model of blood vessels and aimed to assess the changes in PWV between healthy and diseased subjects. Compliance gradients were appointed by the authors as the only parameter assessed via 1D modelling able to efficiently indicate aortic wall strength. Kizilova and Mizerski [51] developed a 2D numerical model of the aorta using tapered tubes to estimate PWV. The model was able to predict high reflection sites that are potentially damaging to the aortic wall.

Badeli et al. [100] applied FEM modelling to simulate the propagation of electrical currents across the thorax and identified trans-thoracic impedance in order to diagnose AD. The numerical results were analysed by Bayesian stochastic models. The model virtualised an impedance cardiography exam (measures how changes in aortic blood volume and flow influence transmission of a known electrical current across the thorax) and the results proposed that the Bayesian approach outperformed the conventional impedance cardiography multi-sensor technique.

Aneurysmal growth [101], intimal tearing initiation [87] and even propensity to rupture [97] were closely correlated with abnormal WSS distributions and large magnitudes. The group of Bopp et al. [102] developed an experimental facility where flow measurements could be obtained with MRI technology and in vitro CFD models. The objective was to provide an extensive reference database of aortic haemodynamics obtained with validated numerical simulations—therefore improving the accuracy of WSS calculations of magnetic resonance velocimetry as it assists in surpassing limitations related to MRI low spatial resolution. In their first work [103], a comparison between laser Doppler velocimetry, magnetic resonance velocimetry and CFD estimation of WSS was performed. Bauer et al. [103] suggested that the laser Doppler velocimetry technique could indeed be the “gold standard” for WSS estimation. Despite this, it is still limited by the low spatial resolution of MRI.

Afterwards, Bopp et al. [102] assessed the differences in flow measurements obtained via magnetic resonance velocimetry and CFD. The turbulent nature of the blood flow was better captured by magnetic resonance velocimetry. Bopp et al. [102] addressed the fact that using more robust turbulence models (e.g., Large Eddy Simulations (LES) rather than Reynolds-Averaged Navier–Stokes (RANS) equations) may overcome this limitation. The group of Sotelo et al. [42] developed a novel method to estimate WSS distributions, which consisted of post-processing velocity fields (obtained with MRI) resorting to CFD models. In this work, evidence that wall motion highly impacts WSS distribution was presented. Later, in 2017 [41], this methodology was augmented by allowing the calculation of different WSS components.

The latter two works focused on improving the efficiency of maximum diameter measurements [54] and auscultation exam [96]. Rueckel et al. [54] suggested an ML tool that estimated the diameter in nine important anatomic locations automatically using CT data. This tool obtained results similar to specialists, with a considerable reduction in reporting time (13 to 2 min), and may be useful to assist clinicians with aneurysm diagnosis. Murmur properties were correlated with pathological states by Zhu et al. [96] through the analysis of CFD simulations. Murmurs are caused by flow abnormalities and can be detected with stethoscopes. Thus, understanding the correlations between murmurs and different pathologies can improve auscultation capacity to diagnose CVD.

3.6.2. Risk Estimation of Aneurysm Rupture

The rupture phenomenon of aneurysms was studied in six different works [34,97,104,105]. Doyle et al. [105] experimentally (silicone test samples) and in silico tested idealised models of the abdominal aorta until rupture. Inflation tests were virtualised resorting to CSM simulations. The aim was to identify the probable location of rupture in AAA using Von Mises stress and PWS criteria. Material properties were identified by fitting different constitutive models with uniaxial tensile test data. The third-order Ogden model was found to be the constitutive model that produced better approximations ($R^2=0.9812$). Numerical results showed that higher stress appeared at regions of higher strain rather than higher diameter. The PWS rupture criteria presented good agreement with experimental data. Shang et al. [34] performed CSM simulations on patient-specific DTAA models with the objective of assessing the correlation between aneurysm growth and PWS. This metric presented a stronger correlation with aneurysm growth than maximum diameter and was suggested as a possible indicator of acute complications. Condemi et al. [106] developed a numerical model using CFD assisted by MRI data to assess the influence of abnormal haemodynamics on rupture risk. They analysed both numerical results and experimental data from bulge inflation tests. Higher flow eccentricity was correlated with higher and more disturbed WSS distributions. The areas of higher WSS were coincident with the region of flow impingement and also correlated with higher values of TAWSS and OSI, which were previously correlated with a high probability of rupture [78]. However, a direct correlation between WSS and wall strength was not found, possibly suggesting that further structural analysis is also required. On the 31 analysed patients with CFD simulations by Pasta et al. [101], the authors found higher WSS magnitude and pressure index in all ascending aorta for BAV patients and evidence of PWS being a great candidate to predict the risk of ATAA rupture. Moreover, Pasta et al. [97] assessed correlations between biomarkers (e.g., MMP, TIMP and miRNA), WSS (obtained via CFD) and aortic strain (obtained from post-processing CT data) in ATAA. Evidence of higher WSS and wall strain from the STJ to the mid-ascending aorta was presented. The increase in WSS was correlated with higher matrix metalloproteinase synthesis, which can dysregulate the homeostasis of the aortic wall and promote elastin and collagen degradation. A combination of biomarkers (extracted from blood samples) and non-invasive evaluation of WSS distributions may assist in the rupture risk assessment of ATAA.

The use of ML tools to estimate rupture risk in ATAA was reported in three articles. Luo et al. [58] used a similar technique to Azadani et al. [91] and Doyle et al. [105], in order to fit constitutive models to tension–strain data from bulge inflation tests. The estimated material parameters and geometric parameters were analysed by the developed ML tool, which classified the data into rupture and non-rupture groups. This analysis suggested that the members of the ruptured group presented similar material properties. One important remark is that the model identified strong correlations between tissue strength and pre-rupture response features. He et al. [57] developed two ML models which were also trained with tension–strain data collected through ex vivo inflation tests on ATAA tissue samples (rupture was ensured). The first aimed to identify the locations of higher tension buildup along the aortic wall. The second estimated ultimate tensile stress in the identified regions. The results suggested that local rupture strength can be reliably estimated from the pre-rupture features, as postulated by Luo et al. [58], matching 13 out of 15 estimated rupture sites with experimental data [56]. Liu et al. [104] identified the regions more prone to rupture through the implementation of ML tools trained with CSM-driven systolic and diastolic geometries. For this, CSM-driven systolic and diastolic geometries were used to train the ML tool, whose objective was to act as a rupture criterion. The presented results showed that this tool outperformed other rupture risk estimation methods on the available and limited sample.

3.7. Numerical Modelling Augmentation

Numerical modelling also presents some limitations that limit its use in clinical practice. This section compiles the results from 48 articles that implemented new techniques to reduce reporting times or improve accuracy (18), assessed whether certain physiological features such as turbulence or the non-Newtonian behaviour of blood are relevant to be considered (25) and studied the sensitivity of the numerical results to inlet conditions (6). The results are summarised in Table 5.

Table 5. Summary of the contributions that aimed to augment numerical modelling of healthy and diseased aortas ($n=38$ articles).

First Author	Year	Simulation	Solver	Geometry	BC Conditions	Flow		Wall	Main Remarks	Aim of the Work	GRADE
R. Valente	2022	FSI (FEM)	SimVas- cular	ATAA (PS-CT)	I:FR; O:WM	L	N	N-H	The developed method contributed to improved convergence	Develop a novel method to separately mesh the fluid and solid domains	Low
A. Mariotti	2021	FSI (FEM)	SimVas- cular	TA (PS-MRI)	I:VP-MRI; O:WM	L	N	LEI	WSS presented significant differences for different inlet flow wave forms	Evaluate the numerical results’ sensitivity to the inlet flow rate waveform	Low
A. Mourato	2021	CFD (FVM)	Open- FOAM	ATAA (PS-CT)	I:FR; O:PoT	$k-\omega$ SST	CY	-	Turbulence and n-N behaviour of blood is not relevant to be modelled in ATAA	Evaluate the relevance of modelling turbulence and n-N behaviour	Low
K. Baumler	2020	FSI (FEM)	SimVas- cular	AD (PS-CTA)	I:VP; O:WM; PrS; EP	L	N	N-H	The inclusion of two-way FSI, PrS and adequate wall and flap material properties improved the numerical results’ agreement with in vivo data	Assess the relevance of modelling realistic wall and dissection flap deformation on AD	High
U. Hackstein	2020	CFD (0D)	SISCA	AAA	I:PoT; O:-PoT	L	N	-	Certain estimated model parameters presented significant differences between healthy and diseased subjects	Estimate coefficients of 0D models using ARMA approach, which may assist in clinical diagnosis	Low
M. Biancolini	2020	CFD (FVM)	Fluent	ATAA (PS-MRI)	I:VF; O:FR; WM	L	C-Y	-	ROM and RBF mesh morphing allow one to explore new results interactively and almost in real time	Assess the relevance of using mesh morphing and ROM techniques	Low
M. Lucio	2020	CSM (FEM)	Abaqus	AAA (I)	LP (120 mmHg); DF	-	-	HGO	Intima presents early exponential stiffening, which contributes to the load bearing of the aortic wall	Evaluate the intima layer’s load-bearing effect on aged aortas	Low
J. Silva	2019	CSM (RPIM)	-	AAA (I)	LP	-	-	LEI	FEM and RPIM models produced similar results	Test the viability of using RPIM methods	Low
M. Nowak	2019	FSI (FEM; FVM)	Ansys	Coarction (PS-MRI)	I:VP; O:OP	L	C	LEI	FSI simulations increase in relevance for decreased wall stiffness	Assess the relevance of resorting to FSI simulations	High
C. Aricò	2019	CFD (SPH)	-	AAA (PS-CT)	I:VP; O:PoT; DF	L	N	-	Moving wall simulations produced more realistic haemodynamics	Present a novel tool to predict AAA haemodynamics	Low
G. de Nisco	2018	CFD (FVM)	-	ATAA (PS-MRI)	I:VP; O:FR	L	N	-	Stroke volume and cardiac cycle duration presented significant influence on the numerical results	Explore the sensitivity of the blood-to-wall LDL transfer to inlet BC	Low
K. Capellini	2018	CFD (FVM)	Fluent	ATAA (PS-MRI)	I:VP; O:WM	L	N	-	Significant haemodynamic changes appeared only for a 60% increase in aneurysm diameter	Address the effects of geometrical changes on haemodynamics	Low
C. Àrico	2018	CFD (SPH)	-	AAA (I)	I:FR; O:PoT; DF	L	N	-	The model was able to accurately reproduce the biomechanical behaviour of the aorta	Present a novel technique to perform FSI simulations using SPH and moving BC	Low
S. Attaran	2018	FSI (FEM)	ADINA	Aorta (I)	I:FR; O:2D	L	N	LEI	The developed BC is able to accurately model pulse wave reflection	Present a new model to apply as an outlet BC	Low
T. Koltukluoǧlu	2018	CFD (FEM)	Open- FOAM	Aorta (PS-MRI)	-	L	N	-	The presented technique outperformed classical CFD approaches	Present an inverse method to estimate in vivo BC	Moderate
V. Mendez	2018	FSI (FEM; FVM)	Ansys	ATAA (PS-MRI/CT)	I:FR; O:WM	L	N	HGO	Both WSS and WS presented significant differences between the simplest approaches and FSI models	Assess if FSI formulation is more accurate than CFD or CSM analysis	Low
J. Febina	2018	CFD (FVM)	Star-CCM+	SA (PS-CT)	I:FR; O:FR	L	N	-	For modelling SA assuming pulsatile, laminar and n-N flow are key factors	Provide insights into SA modelling in adequate numerical settings	Low
L. Liang	2018	CSM (FEM)	Abaqus	TA (I)	LP (10–16 kPa)	-	-	HGO	FEM models can successfully train ML tools with considerable reduction in computational time	Estimate the reference configuration of human TA resorting to ML tools	Low
W. Wolánski	2017	FSI (FEM; FVM)	Ansys	Aorta (PS-CT)	I:FR; O:FR	L	N	NH	Rigid wall simulations overestimate pressure and WSS-driven metrics	Assess how the intramural pressure changes with wall stiffness	Low
J. Bols	2016	FSI (FEM)	Abaqus; Fluent	Coarction (PS)	I:FR; O:FR; WM	L	N	PH	Automated mesh generation can be useful to reduce the reporting time	Reduce the computational effort of grid generation	Low
M. Alimohammadi	2015	FSI (FEM; FVM)	Ansys	AD (PS-CT)	I:FR; O:WM	$k-\omega$ SST	C-Y	RV	FSI models have increased accuracy, but for AD, the required computational time can be excessive	Assess the haemodynamic changes and the stresses in the flap–blood interaction	Low
L. Taelman	2014	FSI (FEM; FVM)	Abaqus; Fluent	Coarction (I)	I:PoT; O:RF	L	N	MR	Numerical dissipation and diffusion are mainly determined by spatial and time discretisation	Study the effects of coarction on pulse wave reflection	Low
W. Chen	2014	CFD (FVM)	Open- FOAM	Aorta(I)	I:FR; O:—	DNS	N	-	No significant changes were found using DNS for turbulence modelling	Study the impact of modelling the turbulence of blood flow	Low
E. Bollache	2014	CFD (1D)	-	DTA	I:FR; O:WM	L	N	-	PWV, total arterial resistance and compliance were calculated and validated against MRI data	Evaluate the application of 1D modelling on cardiovascular medicine	High
Y. Aboelkassem	2014	CFD (0D)	-	AV	-	-	-	-	No relevant conclusions were presented besides the fact that it was suggested as realistic	Mathematical model that recreates AV dynamics	Low
E. Bollache	2013	CFD (1D)	-	Aorta	I:FR; O:WM	L	N	-	Numerical results closely reproduced velocity, PWV and area changes	Evaluate the efficiency of using 1D models to estimate PWV	High
J. Lantz	2013	CFD (FVM)	CFX	Coarction (PS-MRI)	I:VP; O:FR; PoT	LES	N	-	TKE may be a good indicator of abnormal or pathophysiological flow conditions	Compare the results of CFD and MRI data	High
G. Marom	2012	FSI (FEM)	Abaqus	BAV (I)	I:PoT; O:PoT	L	N	CFN	The CSM simulation overestimated by 30% the coaptation area, 55% the contact pressure and 170% the closure time	Evaluate the difference in modelling AV with CSM or FSI	Low
H. Suito	2013	CFD (FDM)	-	TA (SemiPS-CT)	I:FR; O:0P	L	N	-	All the tested geometries produce a swirled flow somewhere on the TA	Investigate the blood flow in TA, focusing on the effect of torsion	Low
B. Doyle	2012	CSM (FEM)	Abaqus	AAA (PS-CT)	LP (120 mmHg)	-	-	PH	Using patient-specific parameters had significant impact on the results	Evaluate the impact of considering patient-specific material properties	Low
F. He	2009	CFD (FDM)	-	Aorta (I)	I:VP; O:PoT	L	N	-	Under transient conditions, inlet and outlet BC significantly altered the numerical results	Assess the sensitivity of numerical results to the chosen BC	Low
F. Salvucci	2009	CFD (1D)	MatLab	Aorta	VP; PoT	L	N	-	The developed model presented good agreement with in vivo data	Novel method to estimate WSS distribution	High
F. Carneiro	2008	CFD (FVM)	Fluent	Abdominal aorta (I)	I:CV (0.234 m s−1); O:—	$k-ϵ$	N; C-Y	-	Small differences in WSS were found between different rheological models	Explore the haemodynamics in the bifurcation of the abdominal aorta	Moderate
K. Matthys	2007	CFD (1D)	-	Aorta	I:FR; O:FR; PoT	L	N	-	Energy losses at bifurcations had a secondary effect on the blood flow and wall viscoelasticity might have a significant effect on PWV	Explore the effects on PWV of energy loss and fluid inertia	Moderate
K. Khanafer	2007	CFD (FEM)	Fidap	AAA (I)	I:FR; O:0G	$k-ϵ$	n-N	-	It is relevant to model n-N behaviour and turbulence in AD	Evaluate the influence of pulsatile, turbulent and n-N flow	Low
R. Berguer	2006	CFD (FEM)	Fidap	AAA (I)	I:FR; O:0G	$k-ϵ$	n-N	-	High blood pressure and turbulence were postulated as contributors to aneurysm rupture	Same as Khanafer et al. [109]	Low
A. Geertsema	1997	CFD (0D)	-	CS	-	-	-	-	The model was able to simulate haemodynamic waveforms for different heart frequencies and heart diseases	Developed a new numerical model of the cardiovascular system	High
A. Owen	1992	CFD (1D)	-	AV	PoT	L	N	-	Blood pressure, PWV and wall properties presented good agreement with theory and empirical data	Develop a model that estimates the haemodynamics of the AV	Low

0G—Zero Gradient; 0P—Zero Pressure; AoI—Aortic Insufficiency; AS—Aortic Stenosis; BT—Biaxial Tension; C—Carreau; CFN—Collagen Fibre Network Model; CP—Constant Pressure; CS—Cardiovascular System; CV—Constant Velocity; C-Y—Carreau–Yasuda; D—Demiray; DF—Displacement Field; EM—Empirical Model; EP—External Pressure; FR—Flow Rate; F—Fung Exponentially Stiffening Material; HGO—Holzapfel–Gasser–Ogden; HI—Hyperelastic Isotropic; iFR—instantaneous Wave-Free Ratio; I—Idealised; Imp—Impedance; K-V—Kelvin–Voigt; L—Laminar; LDL—Low-Density Lipoprotein; LEI—Linear, Elastic and Isotropic; LP—Luminal Pressure; LV—Left Ventricle; MFS—Marfan Syndrome; MM-EE—Multi-Phase Euler–Euler Model; M-R—Mooney–Rivlin; MRV—Magnetic Resonance Velocimetry; n-N—non-Newtonian; N—Newtonian; N-H—Neo–Hookean; O—3rd-Order Ogden Model; OSI—Oscillatory Shear Index; PH—Polynomial Hyperelastic Constitutive Model; PL—Power Law; PoT—Pressure over Time; PrS—Prestress; PS—Patient-Specific; Q—Quemada; R—Resistance; RBF—Radial Basis Function; RF—Reflection Free; RV—Raghavan and Vorp; RVol—Representative Volume; SA—Saccular Aneurysms; S-VK—Saint Vennant–Kirchhoff; TA—Thoracic Aorta; Tor—Torsion; TKE—Turbulent Kinetic Energy; TS—Turner Syndrome; UT—Uniaxial Tension; VP—Velocity Profile; WM—WindKessel Model; Y—Yeoh Model.

3.7.1. Relevance of Modelling Certain Physiological Features

The results that we gathered mainly focused on determining wall motion, patient-specific material properties, turbulence and non-Newtonian blood behaviour’s impact on the numerical results.

The aortic wall possesses hyperelastic properties, mainly due to the presence of elastin fibres [9], which allows the aorta to expand and contract during the cardiac cycle. This effect is known as the Windkessel effect and contributes to reducing the range between systolic and diastolic pressures, as well as assisting with blood flow. Given this, two questions arise from this rationale. Firstly, diseased aortas usually present stiffer aortas and lower diameter variations over the cardiac cycle. The studied group in Mendez et al. [13] presented an average variation of $4.2\pm 2.4\%$. It may be not significant to consider as it introduces complexity to the model without a relevant impact on the numerical results. On this topic, Lantz et al. [73] compared the results of CFD and FSI simulations and found that instantaneous WSS are extremely influenced by wall motion. However, averaged values such as TAWSS and OSI seem not to be significantly influenced by FSI simulations. Marom et al. [107] performed the same comparison on idealised models of the aortic root and concluded that aortic compliance did not impact the transvalvular haemodynamics. Alimohammadi et al. [108] noticed a 15-fold increase in reporting time from CFD to FSI models. They also found that FSI-driven WSS distributions presented closer agreement with in vivo patient-specific data. Wolański et al. [14] found that rigid wall simulations tend to overestimate blood pressure and WSS magnitude. Mendez et al. [13] also assessed the differences between CSM, CFD and FSI simulations. Their results suggested that both WSS and WS presented significant differences between the simplest approaches (CSM and CFD) and FSI models. As reported by Nowak et al. [40], these differences were greater for more compliant aortas. Bäumler et al. [25] studied the importance of modelling realistic wall and tear motion to AD haemodynamics and also found that FSI simulations contributed to improving the agreement of numerical results with MRI data.

Assuming that wall motion is indeed relevant to the model, it becomes necessary to choose a wall constitutive model which requires the estimation of material properties. The assessment of these parameters is still a challenging objective to fulfill and, to date, there is still no “gold standard” methodology to perform this task. Thus, it becomes relevant to study the impact of considering populational averaged values. Doyle et al. [22] developed CSM models with patient-specific geometries of AAA. The objective was to evaluate the numerical variations when patient-specific constitutive parameters are used instead of averaged values. The results evidenced significant differences, namely increased PWS by 67%, wall strain by 320% and displacement by 177%. Another interesting finding was that several constitutive models overestimated the ultimate tensile strength of the tissue. Lucio et al. [6] tested the relevance of considering the three aortic wall layers—in particular, whether the intima layer also has a considerable load-bearing effect—by developing CSM digital twins of uniaxial tensile tests. Their analysis showed that the intima layer is stiffer among the layers and contributes significantly to the load bearing of the wall. Significant differences were found in considering three or only one layer—approximately $30\%$ concerning the stresses and a maximum of $53\%$ in displacements.

On the topic of aorta blood flow, there are also open questions regarding the modelling of flow rheology and turbulence in large arteries. Although blood presents non-Newtonian behaviour, which is more evident for lower velocity regimes, we found contradictory evidence in our research regarding this topic. For instance, in the works of Lou and Yang [19], Mourato et al. [110] and Carneiro et al. [23], the authors depicted that using rheological models did not significantly alter the numerical results in ATAA, AAA and healthy aortas. Alimohammadi et al. [108] and Febina et al. [12] studied the same topic in AD and saccular aneurysms and found that modelling the non-Newtonian behaviour of blood impacted the numerical results. This evidence suggests that the pseudoplastic and viscoelastic features of blood are only relevant for lower shear rates, which are uncommon in large arteries but do occur in stagnant flow and recirculation zones. Regarding turbulence, the vast majority of numerical models opted for imposing laminar flow. However, it is known that in diseased and healthy (although rare) aortas, turbulent flow may occur during instances of the cardiac cycle. Zhu et al. [96] and Chen et al. [11] used Direct Numerical Simulations (DNS) to model the turbulence in abdominal aortic stenosis and idealised geometries and found no significant differences in the numerical results. The group of Khanafer et al. [109] developed CFD models using the Galerkin method and suggested that the turbulence had a significant impact on pressure distributions [111]. Moreover, Lantz et al. [112] used LES modelling to study the correlation between turbulent kinetic energy and abnormal flow on stenosed models. They found variations of around 15% in turbulent kinetic energy estimations and good agreement with MRI data when turbulence was modelled.

3.7.2. Novel Numerical Techniques

Despite the capabilities of numerical modelling to predict the behaviour of complex biomechanical systems, their implementation in clinical practice is still very limited, with few examples of success. Possible reasons for this fact are presented and discussed below. Here, we present works aiming at the development of numerical models using innovative computational techniques (e.g., SPH, ML, ROM) and exploring new methods to improve the efficiency of FEM modelling.

Regarding FEM modelling improvements, in our research, we found efforts in developing novel and more realistic BC, more robust methods to model the aortic wall and develop new meshing processes. Starting with BC-related works, Stevens et al. [113] developed an equation that modelled the cardiac output towards the ascending aorta. The numerical results presented close agreement with in vivo data after calibration. Aboelkassem et al. [47] created a simplistic mathematical model aiming to recreate the coupling between the left ventricle and the ascending aorta by recreating the dynamics of the AV. Koltukluoǧlu and Blanco [5] applied optimisation algorithms to estimate inlet and outlet BC. The proposed approach provides a systematic strategy to improve the model predictions regarding clinically relevant haemodynamic data. The method provided physiological flow patterns with reduction in 4D flow MRI measurement noise and outperformed regular CFD simulations. Attaran et al. [114] proposed a novel outlet BC for compliant arteries. This BC consisted of the addition of a tube composed of porous media at the outlets. This condition aimed to recreate the reflection of pulse waves promoted by the downstream vasculatures and presented higher computational efficiency than (1D–3D) models.

Liang et al. [29] developed an ML tool trained with CSM data to estimate the zero-pressure geometries of patient-specific aortas. Aortic reference configurations are important to accurately represent the complex stress state of deformed aortas. Ben-Or Frank et al. [35] used second-harmonic imaging microscopy data to assist a new micromechanical model with patient-specific data of collagen fibre orientation, to better predict the mechanical response of the aortic wall. They postulated that the developed methodology can capture the overall response of soft tissue by resorting to fewer constitutive parameters. They also found increased stiffness for larger strains (J-shaped curve) and poor approximations for the supra-physiological loading range. Liu et al. [55] presented an ML tool surrogate of traditional wall constitutive models. This tool was trained with data from 63 ATAA human samples and outperformed well-recognised models such as the Holzapfel–Gasser–Ogden model.

On meshing-related topics, Santis et al. [115], Suito et al. [43] and Bols et al. [32] explored the application and generation of structured grids on patient-specific aortic models. Silva et al. [61] compared the results of RPIM and FEM models of AAA. The results of both approaches were very similar. However, the meshing process in RPIM is less complex, which constitutes an advantage to the approach. Capellini et al. [31] presented a mesh morphing technique to assist and facilitate the meshing process for FEM simulations. Valente et al. [30] developed a new method to assist the construction of both solid and lumen domains for FSI analysis, using SimVascular. The opportunity to independently choose the element size and the introduction of prestress methods contributed to a reduction in computational effort.

Regarding the development of new techniques, there were several examples of works focusing on developing and improving previously developed ROM. In 1992, we found the first reference to these applications. In this work, Owen [18] developed a 1D model of the aorta and AV. At the inlet, a pressure evolution over time was applied to mimic the cardiac pulse. At the outlet, the flow was calculated using a resistance BC. They reported results on blood pressure, PWV, wall properties and axial velocity and radius variations, which presented good agreement with theory and empirical data. Geertsema et al. [48] presented an electric analogue of the cardiovascular system (0D model) and found good agreement with in vivo data in the numerical results. Matthys et al. [116] compared in vitro measurements on a silicone model with results obtained from 1D models of the cardiovascular tree. The main purpose was to study the effects on pulse wave propagation of energy dissipation at vessel bifurcations. The numerical model presented small errors in pressure and flow measurements, thus proving to be able to accurately capture the main haemodynamic features. Salvucci et al. [117] estimated planar WSS using 1D models of the thoracic aorta. The group of Bollache et al. [49] developed 1D models based on patient-specific data obtained via CT and MRI scans. The purpose of both works [49,118] was to estimate PWV, which may be used to assess aortic wall compliance. The results were in good agreement with in vivo data. Chen and Luo [53] coupled a 1D model of the trans valvular aortic flow with a FEM model of the leaflets and compared the results with regular FSI simulations. The proposed 1D model presented good accuracy while reducing the computational time. Biancolini et al. [52] performed the same analysis for ATAA models and found similar conclusions. Hackstein et al. [119] developed 0D models of the cardiovascular system to extract correlations between model parameters (estimated with AutoRegressive Moving-Average models) and pathological flow conditions.

Besides ROM, two other works from Arico et al. [59] described the use of innovative techniques. These works resorted to the SPH technique to model AAA haemodynamics. Interestingly, although the aortic wall was not considered, a displacement field obtained via CT angiography was applied to the outside surface of the lumen. The results showed that velocity fields in rigid wall simulations underestimated blood pressure and overestimated velocity magnitude. Maximum WSS was similar but differed in distribution [60].

3.7.3. Sensitivity Analysis

Accuracy is crucial for biomechanical applications of numerical models. Thus, it is of great relevance to perform sensitivity analysis to understand how the conditions chosen in developing numerical models impact the results. He and Li [44] evaluated that, in CFD simulations, using pulsatile inlet conditions produces better results, and they suggested that these should be as physiologically accurate as possible. Taelman et al. [33] performed FSI simulations on idealised aortic models and studied the effect of grid spatial resolution. They suggested that the undesirable effects of numerical dissipation and diffusion are mainly ruled by spatial discretisation. Mesh sensitivity analysis is recommended in FEM modelling and it was also suggested that higher-order discretisation schemes assist in accuracy improvement. Nisco et al. [38] studied the influence of inlet BC on Low-Density Lipoprotein (LDL) transport and found that realistic inlet BC produced closer agreement with in vivo data. Mariotti et al. [27] focused on studying the numerical results sensitivity of CFD and FSI simulations to the inlet waveform (cardiac cycle duration and stroke volume). The results proved that stroke volume strongly influenced the numerical results. Contrary to the stroke volume, the period of the cardiac cycle had a moderate impact and the interacting effect of the two was insignificant. Ascending aorta presented less sensitivity to period and stroke volume than the aortic arch and descending aorta. Moreover, when the wall motion was considered, the standard deviation was not significantly changed. The same group published two other works on the same topic, where they studied the influence of inlet waveform uncertainties [120] and the spatial distribution of inlet velocity fields [121].

4. Discussion

The present systematic review followed the PRISMA guidelines with the objective of understanding which numerical techniques have been applied to simulate the blood and aortic wall interaction in healthy and diseased aortas, and the intrinsic reasons behind the lack of implementation of these models in real-life clinical practice were explored.

The gathered results support the ability of numerical models to provide novel insightful information on the development and growth of several pathological conditions, such as ATAA [12,27] or AD [10,64,89]. Numerical simulations assisted by medical imaging data showed capabilities of estimating in vivo aortic wall material properties [91,93] and WSS [41,80] and WSS distributions [29,39]. Furthermore, several groups proved that simple geometrical criteria cannot reliably predict the risk of acute events [31,52] and suggested stronger haemodynamic [78,97] and structural [37,106] metrics for acute complications’ risk assessment. However, these tools are not widely implemented in clinical practice, and three aspects were identified as the most relevant to the lack of presence in real-life medical applications of numerical modelling.

The first aspect is the need for higher levels of accuracy in the numerical results. Numerical modelling is highly impacted by the chosen initial conditions (e.g., initial geometric model, definition of the fluid and solid domains) and applied BC. To systematically produce proper results, these conditions must be rigorously selected and as close as possible to the in vivo patient-specific conditions. This necessity was evidenced by He and Li [44], Taelman et al. [33] and Mariotti et al. [27], which have shown that numerical results are significantly affected by slight variations in inlet BC, either in spatial or time distributions. Comunale et al. [28] and Wolański et al. [14] proved that patient-specific constitutive parameters induce closer agreement between numerical results and in vivo data. On one hand, we are still lacking a concrete understanding of which biomechanical features of diseased and healthy aortas are relevant to be modelled. For instance, in Section 3.7, we discussed the contradictory evidence that was found on modelling the flow rheology [23,110], turbulence [11,110,112] and wall dynamics [40,73]. Another contributor to inaccuracies is the often disregarded of features that may significantly impact the numerical results, such as wall thickness and mechanical properties’ heterogeneity, aortic root displacement and external pressure exerted by surrounding vasculatures (e.g., pulmonary trunk and superior vena cava). For instance, evidence of increased longitudinal stress at the ascending aortic outer curve when modelling realistically heart motion was presented by Mendez et al. [13]. Nonetheless, more work is needed to address the real impact of including such simplifications. On the other hand, to this day, it is still difficult to estimate in vivo patient-specific parameters required to model the structural behaviour of the aortic wall as well as inlet and outlet BC. Hence, it represents a complex task to assist numerical calculations with accurate initial conditions, which is crucial to achieving good numerical results. Great efforts have been presented to improve the accuracy of numerical models and one common idea is to allow the model to estimate these requirements through the use of optimisation algorithms. Take as an example the works of Liu et al. [94] and Koltukluoǧlu and Blanco [5], which implemented inverse methodologies to estimate aortic material properties and inlet and outlet BC from MRI data, respectively. MRI and CT data usually present noise and suffer from low time and spatial discretisation, which also act as a source of uncertainties in the results. Therefore, even using these inverse methodologies, which nowadays seem to represent the best solution, can still lead to an offset between the estimated and real parameters.

The second major limitation is the elevated reporting time that most of the identified techniques require to produce the numerical results. In common clinical practice, often, clinicians deal with time-sensitive situations, where the mortality rate increases rapidly [9] (e.g., AD) and there is no option to wait for days or weeks for results. Biancolini et al. [52] also have pointed out the high computational cost required to perform viable simulations as one of the greatest bottlenecks in clinical implementation. Mesh generation is often one of the most time-consuming steps in grid-based models such as FEM or FVM. Furthermore, in 2D and 3D simulations, the calculation itself is also a highly time-consuming step due to the elevated amount of performed calculations and domain subdivisions. Moreover, these models regularly deal with convergence-related problems and the patient-to-patient adaptability usually requires time-consuming calibration processes. In addition, regarding the reporting time, as expected, we found evidence that computational effort grows with model complexity. For instance, laminar simulations take less time to compute results than turbulent simulations. FSI simulations can lead to a 15-fold increase in computational time, as reported by Alimohammadi et al. [108]. This also enhances the need for studying the equilibrium between model complexity and simulation time. On this topic, there also have been great efforts to improve the efficiency of numerical models. Santis et al. [115], Suito et al. [43] and Bols et al. [32] explored the application of structured grids, which are known for reducing computational effort as it requires fewer elements to achieve convergence. Aricò et al. [60] and Silva et al. [61] implemented meshless models and reported significant reductions in computational effort. ROM was also suggested as an efficient technique to estimate haemodynamics accurately and reduce reporting time [48,53,117,118]. Liu et al. [93] proposed a new optimisation method (Multi-Resolution Direct Search) designed to reduce the high computational effort inherent to inverse methodologies. Moreover, Liang et al. [29] suggested the use of GPU-based (instead of CPU) methods such as SPH [59,60].

Lastly, the third major limitation and possibly the most relevant is the lack of extensive clinical trials that prove the efficiency of these tools to precisely predict the development of severe pathological conditions. Studies on large patient cohorts are still needed and essential to the implementation of numerical models in clinical guidelines. Only 12% of the works analysed in this review performed numerical validation with patient-specific in vivo data and the majority (76%) did not present a meaningful validation process, which also contributes to the lack of proof of numerical modelling efficiency.

To conclude, it is pointed out that the present systematic review was limited to only one electronic database, with the exclusion of MSc and PhD theses. In future works, the authors will seek to further understand the biomechanics of the most common aortic diseases ( ATAA, AAA and AD) and explore which rheology and turbulence models, BC and numerical techniques and approaches produce better results.

5. Conclusions

From this systematic review, the following remarks can be drawn:

• Numerical models are feasible tools to recreate the complex conditions of the biomechanical system. These models can have the potential to provide insightful data toward clinical practice.
• Among the relevant data that numerical models can provide, we have highlighted: (i) the WSS and WS-based metrics, which were strongly correlated with aortic microstructure (mys) functioning and elevated propensity to rupture; (ii) PWV due to its ability to evaluate aortic stiffness by clinical guidelines; (iii) and wall strain.
• One-dimensional modelling and ML were the next most selected techniques. One-dimensional models proved to allow quick computations of PWV on a patient-specific basis. ML presented a wide range of applications that outperformed usual methods while reducing the computation time.
• There is no consensus on the gold standard technique to model the haemodynamics and structure dynamics of the aortic wall. From the review, FEM and FVM are the two preferred techniques to perform CSM and CFD patient-specific simulations, respectively. These techniques were collectively chosen in around $80\%$ of the analysed works, are widely implemented in commercial and open-source computing platforms and allow the use of complex geometric models such as diseased aortas.
• Accuracy, computing time and lack of validation were the main identified contributors to the lack of application of numerical models in real-life medical applications. Accuracy issues are mostly correlated with poor selection of rheological, turbulence or wall constitutive models and difficulties in correctly assessing the in vivo patient-specific parameters for these models and patient-specific geometric models or BC. Excluding ROM, computing 3D haemodynamics or structural data can easily take days or even weeks, particularly in grid-based methods, which is not suitable for time-sensitive situations. Moreover, there is a lack of both numerical validations as assessed by the GRADE approach (only 12% of the total works presented numerical validation against in vivo patient-specific data) and extensive clinical trials.
• To date, there is still a lack of reports on the bibliography of studies on the impact of considering wall thickness and material properties’ heterogeneity, surrounding aortic structures, the internal pressure of the human body, the calibration of impedance-based outlet conditions and aortic root motion on the numerical results.