Experimental and Numerical Study on UHPC–RC Decks within Hogging Moment Region
Abstract
:1. Introduction
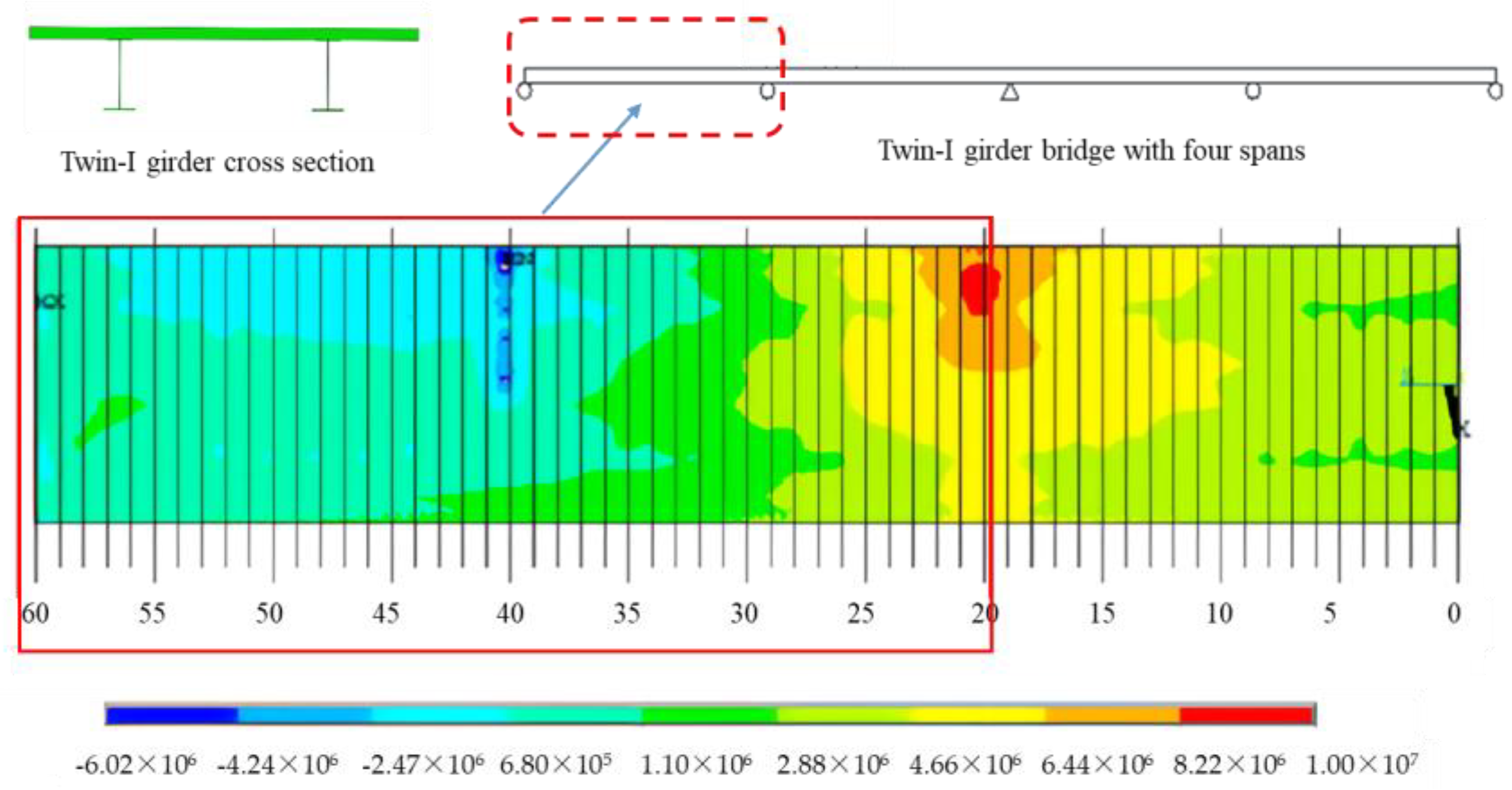
2. Stress State for Steel–Concrete Composite Girder Bridges Using an RC Deck
3. Experimental Study
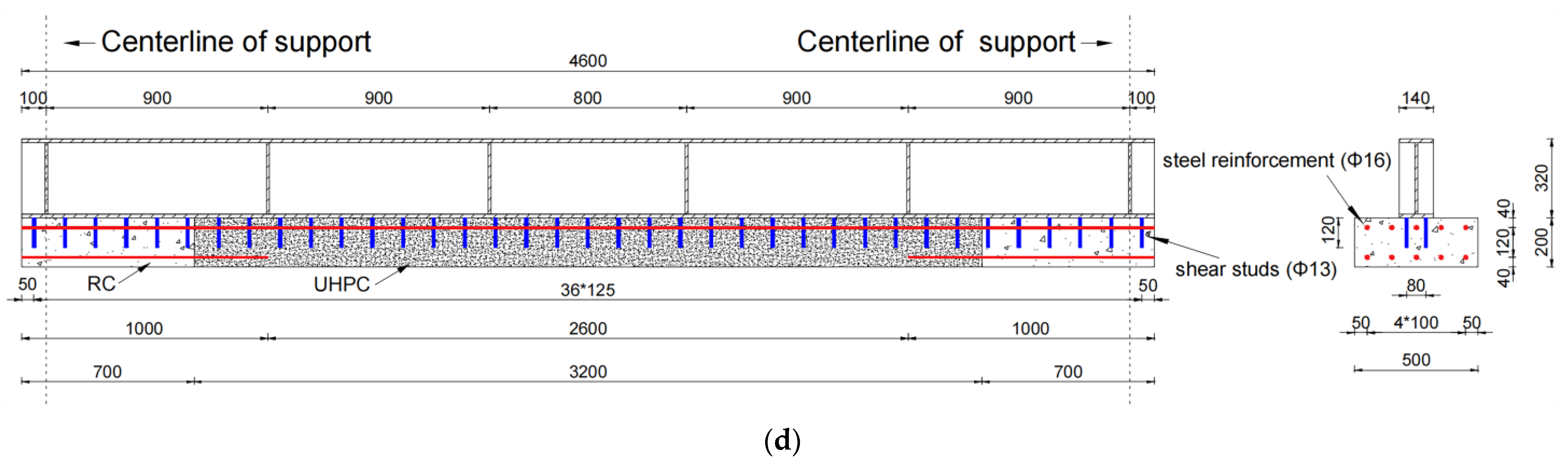
3.1. Design Principles
3.2. Parameters of Specimens
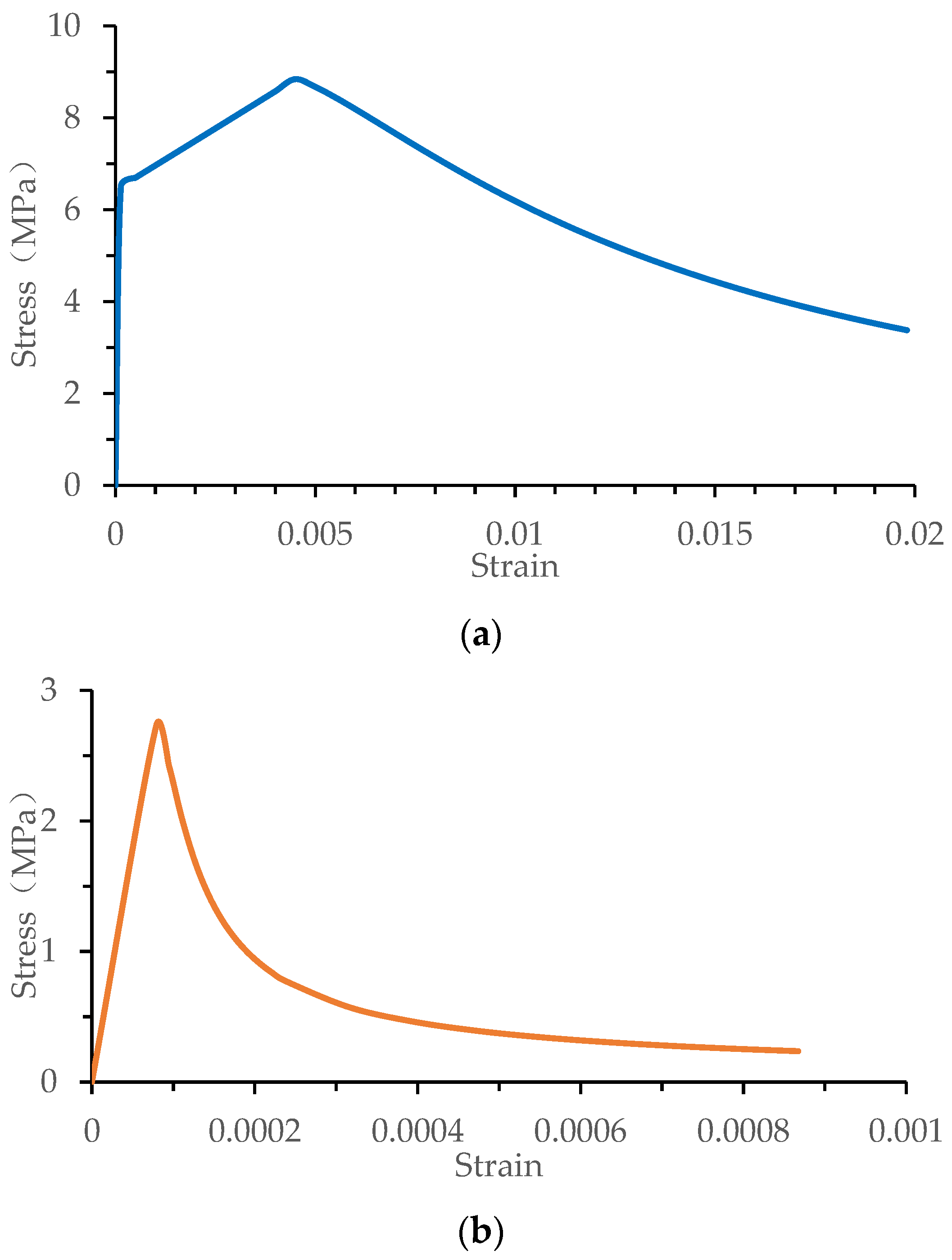
3.3. Material
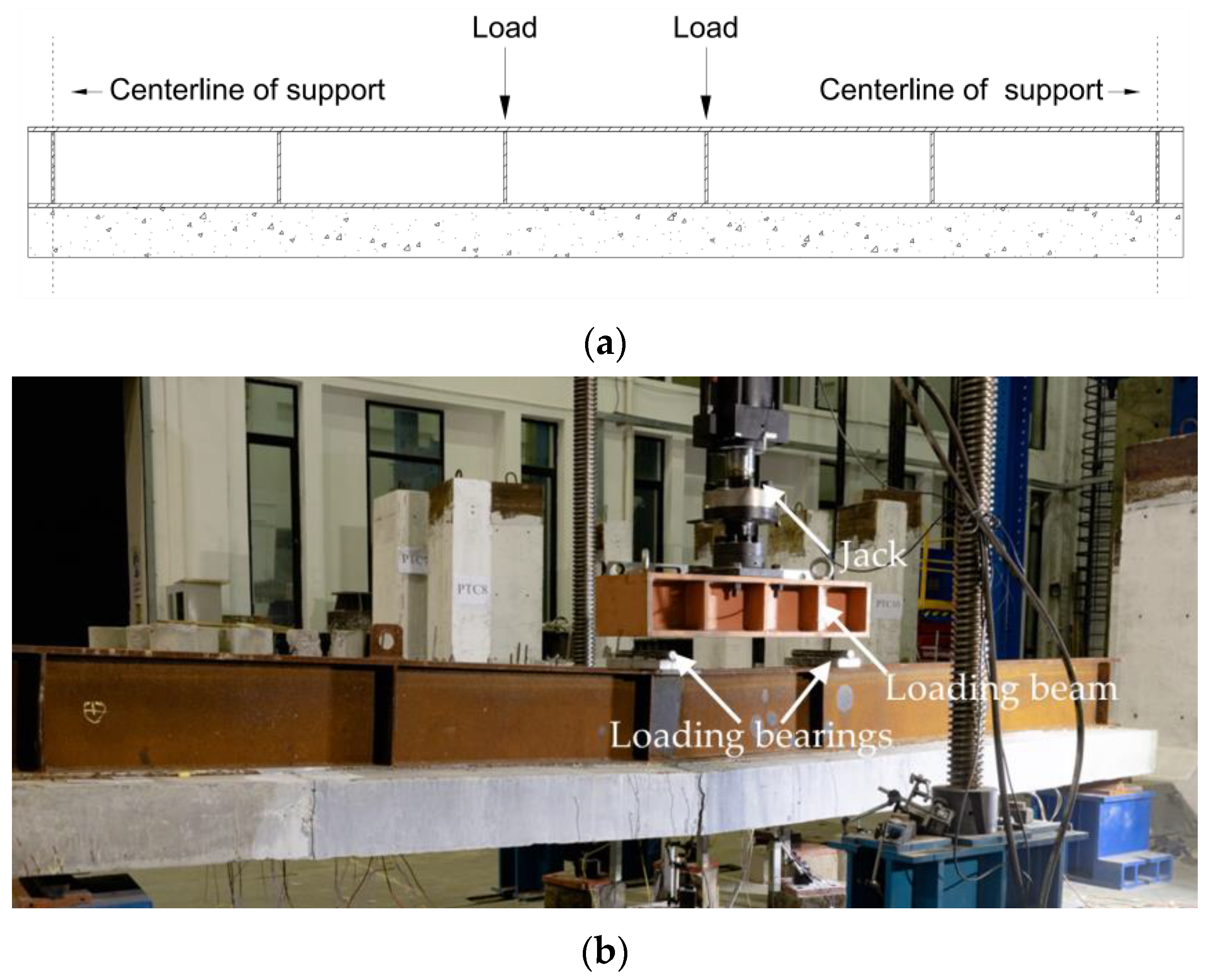
3.4. Load
3.5. Experimental Results
4. Finite Element Model
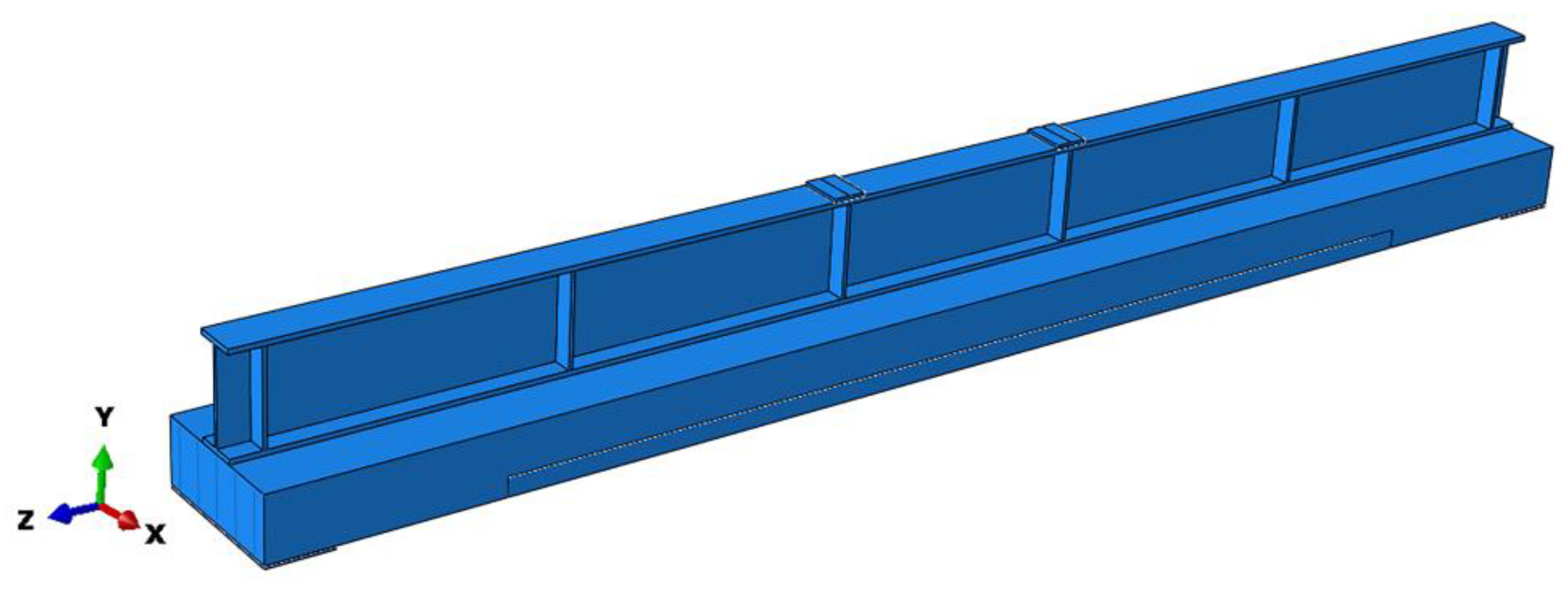
4.1. Elements and Mesh
4.2. Boundary Conditions
4.3. Material
4.4. Load
5. Comparison and Analysis of Results
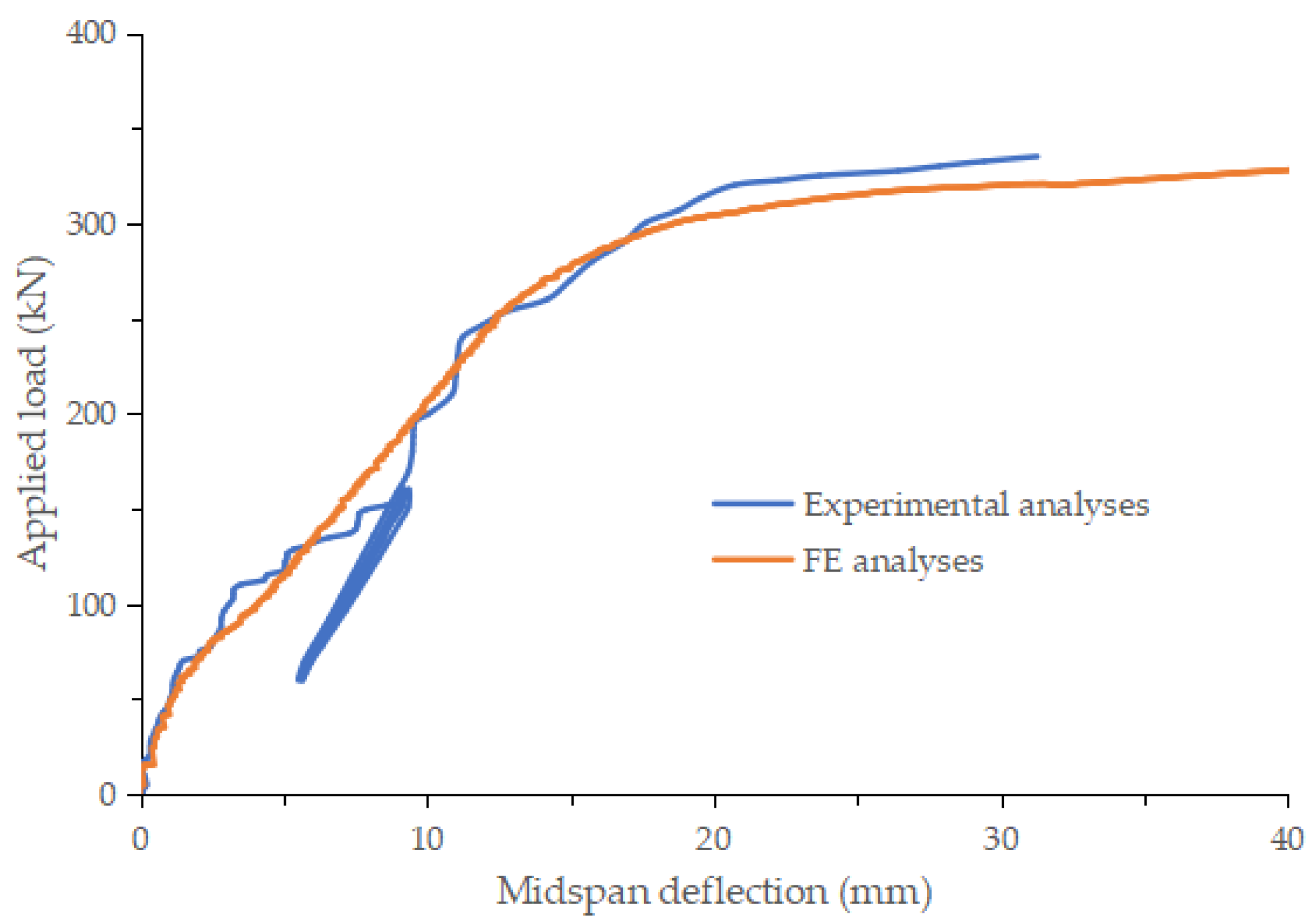
5.1. UHPC Layer Ratio of 0
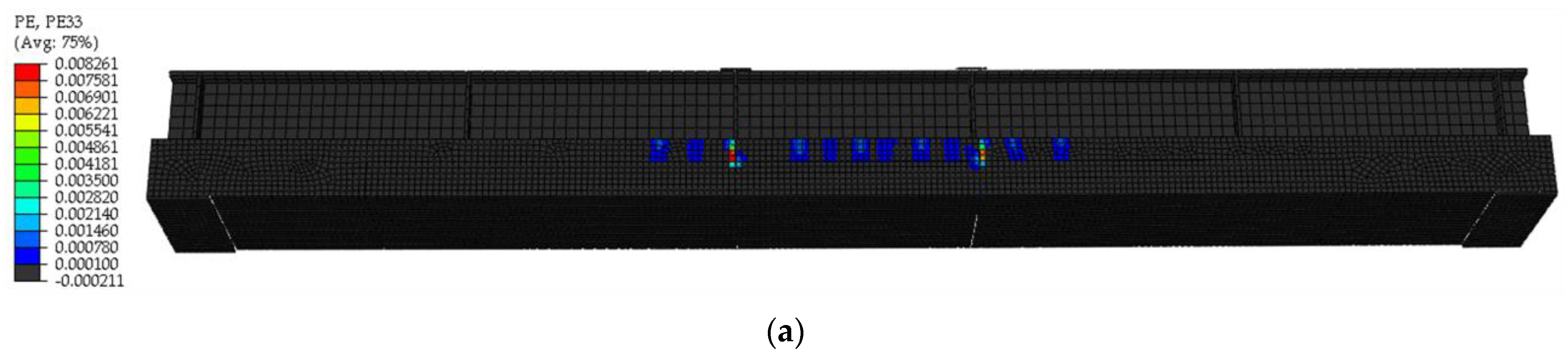
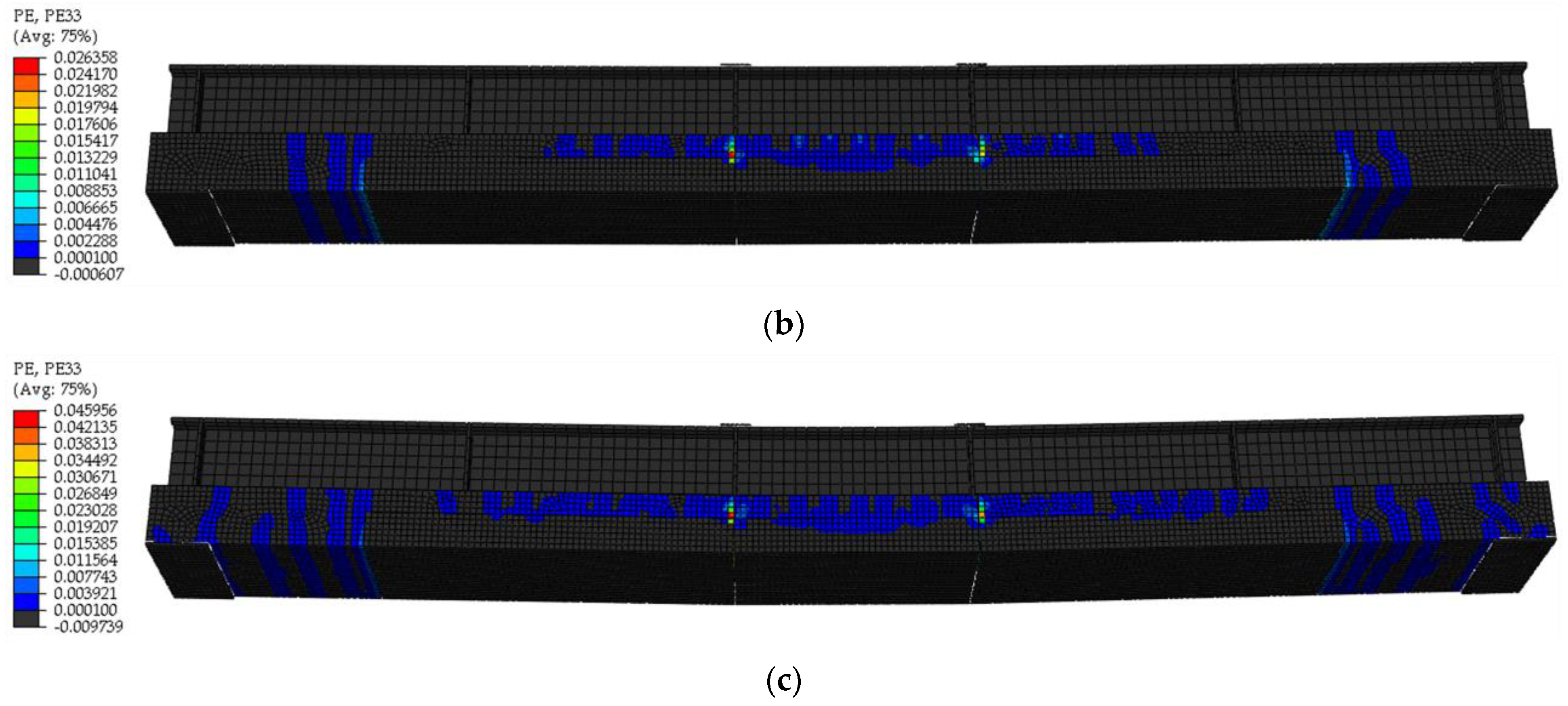
5.1.1. Crack Development
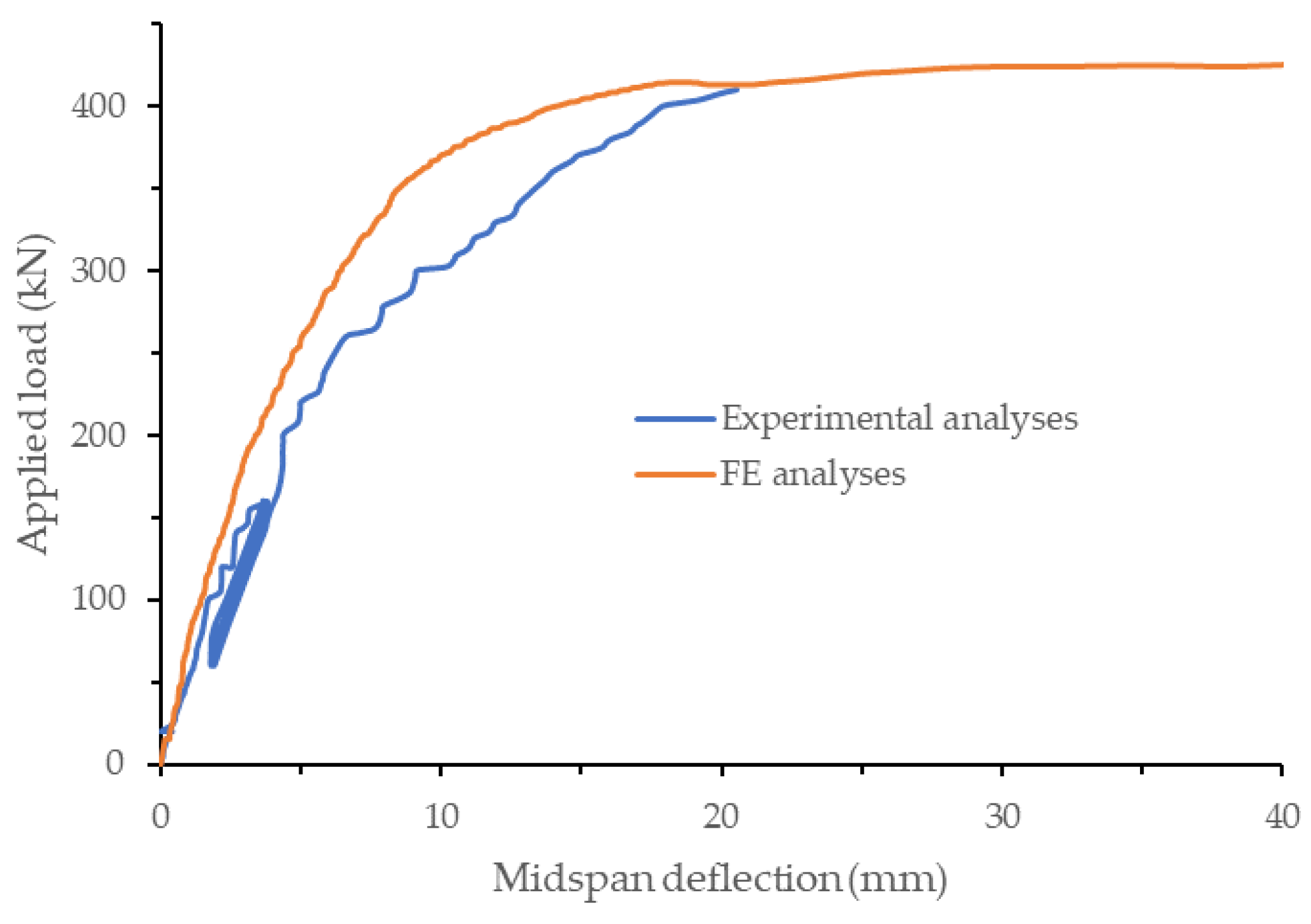
5.1.2. Load-Displacement Curve
5.2. UHPC Layer Ratio of 0.3
5.2.1. Crack Development
5.2.2. Load-Displacement Curve
5.3. UHPC Layer Ratio of 0.6
5.3.1. Crack Development
5.3.2. Load-Displacement Curve
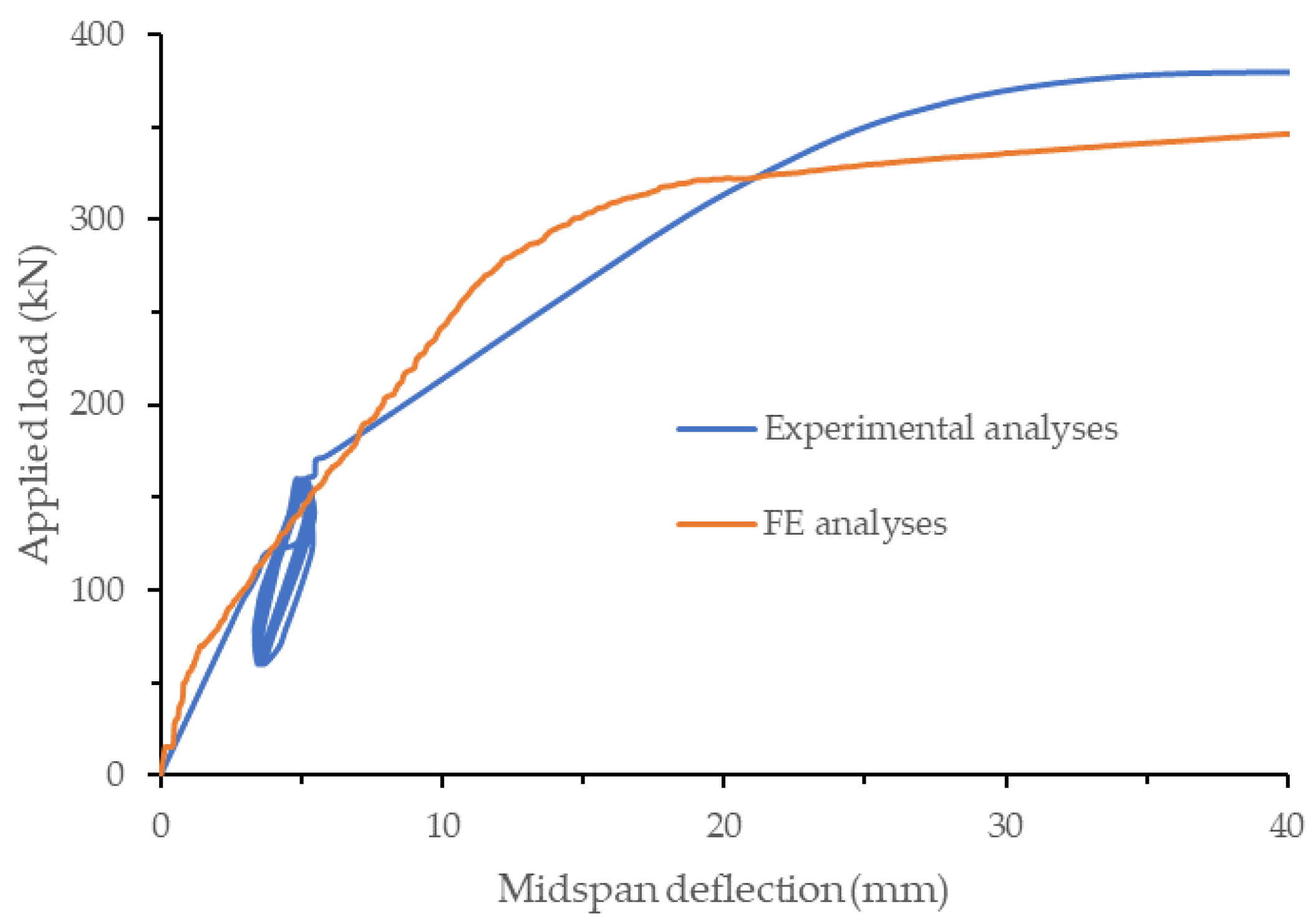
5.4. UHPC Layer Ratio of 1.0
5.4.1. Crack Development
5.4.2. Load-Displacement Curve
6. Conclusions
- (1)
- A UHPC–RC composite deck can effectively increase the anti-cracking capacity of steel–concrete girder bridges within the hogging moment region.
- (2)
- With increasing UHPC layer thickness, the anti-cracking capacity of bridge decks gets better; with economic cost consideration, the UHPC layer ratio of the bridge deck can be taken as 0.3.
- (3)
- The developed FE models could reasonably predict the behavior of the four specimens, and they can be used to design UHPC–RC composite decks of steel–concrete composite bridge structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, H.; Shi, X.; Zhang, Y. Long-Term Behaviour of Precast Concrete Deck Using Longitudinal Prestressed Tendons in Composite I-Girder Bridges. Appl. Sci. 2018, 8, 2598. [Google Scholar] [CrossRef]
- Hällmark, R.; Collin, P.; Möller, M. The Behaviour of a Prefabricated Composite Bridge with Dry Deck Joints. Struct. Eng. Int. 2013, 23, 47–54. [Google Scholar] [CrossRef]
- Yan, L.; Jia, X.J.; Lu, Z.F.; Deng, X.G. Crack resistance measure for steel-concrete composite continuous girder bridge in negative bending area. World Build. Mater. 2018, 39, 47–51. [Google Scholar]
- Xu, C.; Su, Q.; Wu, C.; Sugiura, K. Experimental study on double composite action in the negative flexural region of two-span continuous composite box girder. J. Constr. Steel Res. 2011, 67, 1636–1648. [Google Scholar] [CrossRef]
- Hajdin, N. Einige Beispiele der Kombination von Stahl und Beton im Brückenbau. Schweiz. Ing. Archit. 1985, 103, 37–39. [Google Scholar] [CrossRef]
- Larena, J.B.; Larena, A.B. Beitrag zur Entwicklung der Querschnittsgestaltung im Verbundbrückenbau. Stahlbau 2011, 80, 185–197. [Google Scholar] [CrossRef]
- Elsheikh, A. Bistable Morphing Composites for Energy-Harvesting Applications. Polymers 2022, 14, 1893. [Google Scholar] [CrossRef]
- Kamal, A.; Elsheikh, A.H.; Showaib, E. Development of Fatigue Machine to Accommodate the Application of Overloads During Fatigue Crack Propagation Tests of Polymeric Materials. J. Fail. Anal. Prev. 2022, 22, 510–518. [Google Scholar] [CrossRef]
- Kamal, A.; Showaib, E.; Elsheikh, A. Effect of single-period overload parameters on fatigue crack retardation for high-density polyethylene. Theor. Appl. Fract. Mech. 2022, 118, 103249. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.; Lee, G.C. Application of Ultra-High Performance Concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Azmee, N.M.; Shafiq, N. Ultra-high performance concrete: From fundamental to applications. Case Stud. Constr. Mater. 2018, 9, e00197. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, S.; Zhu, Y.; Fan, L.; Shao, X. Flexural responses of steel-UHPC composite beams under hogging moment. Eng. Struct. 2020, 206, 110134. [Google Scholar] [CrossRef]
- Xiao, J.-L.; Zhou, M.; Nie, J.-G.; Yang, T.-Y.; Fan, J.-S. Flexural behavior of steel-UHPC composite slabs with perfobond rib shear connectors. Eng. Struct. 2021, 245, 112912. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, Q.; Bao, Y.; Deng, P.; Wei, C.; Li, M. Flexural behavior of corrugated steel-UHPC composite bridge decks. Eng. Struct. 2021, 246, 113066. [Google Scholar] [CrossRef]
- Liu, X.-Y. Experimental study on bending resistance of steel-UHPC composite slabs. IOP Conf. Ser. Earth Environ. Sci. 2021, 787, 012041. [Google Scholar] [CrossRef]
- Hu, Y.; Meloni, M.; Cheng, Z.; Wang, J.; Xiu, H. Flexural performance of steel-UHPC composite beams with shear pockets. Structures 2020, 27, 570–582. [Google Scholar] [CrossRef]
- Shao, X.; Deng, L.; Cao, J. Innovative steel-UHPC composite bridge girders for long-span bridges. IABSE Symp. Rep. 2016, 106, 614–622. [Google Scholar] [CrossRef]
- Tong, L.; Chen, L.; Wang, X.; Zhu, J.; Shao, X.; Zhao, Z. Experiment and finite element analysis of bending behavior of high strength steel-UHPC composite beams. Eng. Struct. 2022, 266, 114594. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Cheng, Z.; Ye, M. Experimental and Numerical Studies on the Negative Flexural Behavior of Steel-UHPC Composite Beams. Adv. Civ. Eng. 2021, 2021, 8828175. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Q.; Yang, Z.; Li, M.; Cheng, Z.; Bao, Y. Flexural cracking behavior of reinforced UHPC overlay in composite bridge deck with orthotropic steel deck under static and fatigue loads. Eng. Struct. 2022, 265, 114537. [Google Scholar] [CrossRef]
- Ghasemi, S.; Zohrevand, P.; Mirmiran, A.; Xiao, Y.; Mackie, K. A super lightweight UHPC–HSS deck panel for movable bridges. Eng. Struct. 2016, 113, 186–193. [Google Scholar] [CrossRef]
- Liu, J.; Lai, Z.; Chen, B.; Xu, S. Experimental behavior and analysis of steel-laminated concrete (RC and UHPC) composite girders. Eng. Struct. 2020, 225, 111240. [Google Scholar] [CrossRef]
- Department of Transportation of Guangdong Province. Technical Specification for Ultra-High Performance Light-Weighted Composite Deck Structure; China Communications Press: Beijing, China, 2015. [Google Scholar]
- CCCC Highway Consultants Co., Ltd. General Code for Design of Highway Bridges and Culverts: JTG D60-2015; China Communications Press: Beijing, China, 2015. [Google Scholar]
- Swiss Society of Architects and Engineers. UHPFRC-Materials Design and Construction: SIA 2052; Swiss Federal Institute of Technology in Lausanne: Lausanne, Switzerland, 2016. [Google Scholar]
- Shi, X.F.; Ma, H.Y.; Liu, C. Parametric Study and Optimization on Behaviour of Twin-I girder Composite Bridges. J. Tongji Univ. (Nat. Sci.) 2018, 46, 444–451. (In Chinese) [Google Scholar] [CrossRef]
- Brühwiler, E.; Denarié, E. Rehabilitation and Strengthening of Concrete Structures Using Ultra-High Performance Fibre Reinforced Concrete. Struct. Eng. Int. 2013, 23, 450–457. [Google Scholar] [CrossRef]
- China Metallurgical Information and Standardization Institute. Dimension, Shape, Weight and Tolerances for Hot-Rolled Steel Plates and Sheets: GB/T 709-2019; Standards Press of China: Beijing, China, 2019. [Google Scholar]
- National Standardization Administration of China. Steel for the Reinforcement of Concrete-Part 2: Hot Rolled Ribbed Bars: GB/T 1499.2-2018; Standards Press of China: Beijing, China, 2018. [Google Scholar]







| Group | Size of the Deck |
|---|---|
| A | Conventional concrete deck of 200 mm |
| B | UHPC layer of 60 mm + conventional concrete layer of 140 mm |
| C | UHPC layer of 120 mm + conventional concrete layer of 80 mm |
| D | UHPC layer of 200 mm |
| Type | Yield Strength (MPa) | Ultimate Strength (MPa) |
|---|---|---|
| Q235 | 235 | 360 |
| HRB400 | 425 | 595 |
| Material | Dilation Angle | Eccentricity | fb01/fc02 | K3 | Viscosity Parameter |
|---|---|---|---|---|---|
| UHPC | 54 | 0.1 | 1.07 | 0.667 | 0.01 |
| RC | 30 | 0.1 | 1.16 | 0.667 | 1 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, G.; Zhou, R.; Ma, H.; Xin, G.; Emadi, S.; Shi, X. Experimental and Numerical Study on UHPC–RC Decks within Hogging Moment Region. Appl. Sci. 2022, 12, 11446. https://doi.org/10.3390/app122211446
Long G, Zhou R, Ma H, Xin G, Emadi S, Shi X. Experimental and Numerical Study on UHPC–RC Decks within Hogging Moment Region. Applied Sciences. 2022; 12(22):11446. https://doi.org/10.3390/app122211446
Chicago/Turabian StyleLong, Guanxu, Ruigen Zhou, Haiying Ma, Gongfeng Xin, Seyyedbehrad Emadi, and Xuefei Shi. 2022. "Experimental and Numerical Study on UHPC–RC Decks within Hogging Moment Region" Applied Sciences 12, no. 22: 11446. https://doi.org/10.3390/app122211446





