Influence of Circular Saw Blade Design on Reducing Energy Consumption of a Circular Saw in the Cutting Process
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Consumption of the Cutting Power
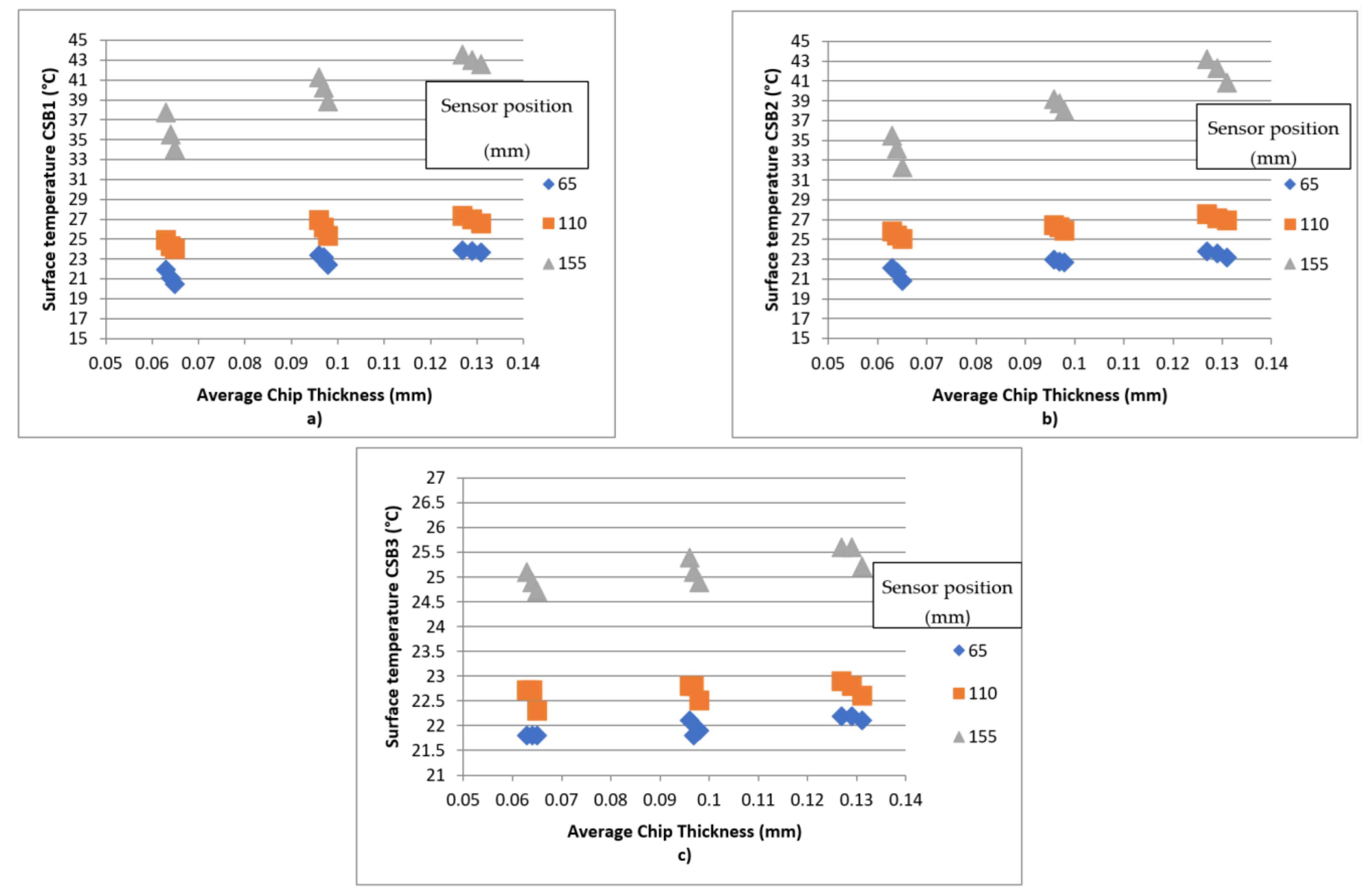
3.2. Circular Saw Blade Surface Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nasir, V.; Cool, J. A review on wood machining: Characterization, optimization, and monitoring of the sawing process. Wood Mater. Sci. Eng. 2020, 15, 1–16. [Google Scholar] [CrossRef]
- Sandak, J.; Negri, M. Wood surface roughness—What is it? In Proceedings of the 17th International Wood Machining Seminar (IWMS 17), Rosenheim, Germany, 26–28 September 2005; pp. 242–250. [Google Scholar]
- Spinelli, R.; Cavallo, E.; Eliasson, L.; Facello, A.; Magagnotti, N. The effect of drum design on chipper performance. Renew. Energy 2015, 81, 57–61. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Wieczorek, B.; Krawiec, P. Energy consumption of the wood size reduction processes with employment of a low-power machines with various cutting mechanisms. Renew. Energy 2022, 181, 630–639. [Google Scholar] [CrossRef]
- Gao, Y.; Kang, F.; Kan, J.; Wang, Y.; Tong, S. Analysis and experiment of cutting mechanical parameters for Caragana korshinskii (CK) branches. Forests 2021, 12, 1359. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Influence of innovative woodchipper speed control systems on exhaust gas emissions and fuel consumption in urban areas. Energies 2020, 13, 3330. [Google Scholar] [CrossRef]
- Mergl, V.; Pandur, Z.; Klepárník, J.; Kopseak, H.; Bačić, M.; Šušnjar, M. Technical solutions of forest machine hybridization. Energies 2021, 14, 2793. [Google Scholar] [CrossRef]
- Lajunen, A.; Suomela, J.; Pippuri, J.; Tammi, K.; Lehmuspelto, T.; Sainio, P. Electric and hybrid electric non-road mobile machinery–present situation and future trends. World Electr. Veh. J. 2016, 8, 172–183. [Google Scholar] [CrossRef] [Green Version]
- Krilek, J.; Kováč, J.; Kučera, M. Wood crosscutting process analysis for circular saws. BioResources 2014, 9, 1417–1429. [Google Scholar] [CrossRef]
- Kminiak, R.; Kubš, J. Cutting power during cross-cutting of selected wood species with a circular saw. BioResources 2016, 11, 10528–10539. [Google Scholar] [CrossRef] [Green Version]
- Nasir, V.; Cool, J. Optimal power consumption and surface quality in the circular sawing process of Douglas-fir wood. Eur. J. Wood Wood Prod. 2019, 77, 609–617. [Google Scholar] [CrossRef]
- Cristóvăo, L.; Broman, O.; Grönlund, A.; Ekevad, M.; Sitoe, R. Main cutting force models for two species of tropical wood. Wood Mat. Sci. Eng. 2012, 7, 143–149. [Google Scholar] [CrossRef]
- Eyma, F.; Méausoone, P.; Larricq, P.; Marchal, R. Utilization of a dynamometric pendulum to estimate cutting forces involved during routing. Comparison with actual calculated values. Ann. For. Sci. 2005, 62, 441–447. [Google Scholar] [CrossRef]
- Méausoone, P.J. Choice of optimal cutting conditions in wood machining using the coupled tool-material method. In Proceedings of the 15th International Wood Machining Seminar, Los Angeles, CA, USA, 30 July–1 August 2001; pp. 37–47. [Google Scholar]
- Kivimaa, E. Cutting force in woodworking. In The State Institute for Technical Research; Publication No.18 Helsinki; VTT Technical Research Centre of Finland: Helsinki, Finland, 1950. [Google Scholar]
- Axelsson, B.O.; Lundberg, A.S.; Grönlund, J.A. Studies of the main cutting force at and near a cutting edge. Eur. J. Wood Prod. 1993, 51, 43–48. [Google Scholar] [CrossRef]
- Aguilera, A.; Méausoone, P.J.; Martin, P. Wood material influence in routing operations: The MDF case. Holz Roh-Werkst. 2000, 58, 278–283. [Google Scholar] [CrossRef]
- Vazquez-Cooz, I.; Meyer, R.W. Cutting forces for tension and normal wood of maple. For. Prod. J. 2006, 56, 26–34. [Google Scholar]
- Hlásková, L.; Orlowski, K.; Kopecký, Z.; Sviták, M.; Ochrymiuk, T. Fracture toughness and shear yield strength determination for two selected species of central European provenance. BioResources 2018, 13, 6171–6186. [Google Scholar] [CrossRef]
- Orlowski, K.A.; Ochrymiuk, T.; Atkins, A.; Chuchala, D. Application of fracture mechanics for energetic effects predictions while wood sawing. Wood Sci. Technol. 2013, 47, 949–963. [Google Scholar] [CrossRef] [Green Version]
- Aguilera, A. Cutting energy and surface roughness in medium density fiberboard rip sawing. Eur J. Wood Prod. 2011, 69, 11–18. [Google Scholar] [CrossRef]
- Naylor, A.; Hackney, P.; Clahr, E. Machining of wood using a rip tooth: Effects of workpiece variations on cutting mechanics. In Proceedings of the 20th International Wood Machining Seminar, Skellefteå, Sweden, 7–10 June 2011. [Google Scholar]
- Moradpour, P.; Scholz, F.; Doosthoseini, K.; Tarmian, A. Measurement of wood cutting forces during bandsawing using piezoelectric dynamometer. Drvna Ind. 2016, 67, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Hutton, S.G.; Lee, V.; Kirbach, E. Effect of tooth front bevel angle on cutting accuracy and chip formation for circular rip saws. Holz Roh-Werkst. 1992, 50, 313–316. [Google Scholar] [CrossRef]
- Li, L.; Xi, B.T.; Yang, Y.F. Transverse deflection of circular saw and sawing profile on workpiece. J. Beijing For. Univ. 2007, 29, 141–145. [Google Scholar]
- Orlowski, K.A.; Sandak, J.; Tanaka, C. The critical rotational speed of circulr saw: Simple measurement method and its practical implementations. J. Wood Sci. 2007, 53, 388–393. [Google Scholar] [CrossRef]
- Ukvalbergiene, K.; Vobolis, J. Research of inter-impact of wood circular saws vibration modes. Wood Res. 2007, 52, 89–100. [Google Scholar]
- Pohl, M.; Rose, M. Piezoelectric shunt damping of a circular saw blade with autonomous power supply for noise and vibration reduction. J. Sound Vib. 2016, 361, 20–31. [Google Scholar] [CrossRef]
- Kopecký, Z.; Rousek, M. Impact of dominant vibrations on noise level of dimension circular saw blades. Wood Res. 2012, 57, 151–160. [Google Scholar]
- Konov, V.N. Research of the temperature field on the circular saw blades in the wood cutting process. In Working Machines, Tools in Machining of the Wood; University Textbook of the Scientific Works: Leningrad, Russia, 1982; Volume 9, pp. 3–6. [Google Scholar]
- Danielson, J.D.; Schajer, G.S. Saw blade heating and vibration behavior in a circular gang edger. In Proceedings of the Saw Tech 93—3rd International Conference on Sawing Technology, San Francisco, CA, USA, 14–16 October 1993. [Google Scholar]
- Ratnasingam, J.; Pew Ma, T.; Ramasamy, G. Tool temperature and cutting forces during the machining of particleboard and solid wood. J. Appl. Sci. 2010, 10, 2881–2886. [Google Scholar] [CrossRef] [Green Version]
- Mote, C.D.; Rahimi, A. Real time vibration control of rotating circular plates by temperature control and system identification. J. Dyn. Syst. Meas. Control. 1984, 106, 123–128. [Google Scholar] [CrossRef]
- Li, L.; Xi, B.T.; Yang, Y.F. Thermal and rotary stresses in circular saw blades. J. Beijing For. Univ. 2002, 24, 14–17. [Google Scholar]
- Sheikh-Ahmad, J.Y.; Lewandowski, C.M.; Stewart, J.S. Experimental and numerical methods for determing temperature distribution in a wood cutting tool. Exp. Heat Transf. 2003, 16, 255–271. [Google Scholar] [CrossRef]
- Lehmann, B. Heating and cooling of circular saws. In Proceedings of the Volume I—Oral Presentations of the 18th International Wood Machining Seminar, Vancouver, BC, Canada, 7–9 May 2007. [Google Scholar]
- Ishihara, M.; Noda, N.; Ootao, Y. Analysis of dynamic characteristics of rotating circular saw subjected to thermal loading and tensioning. J. Therm. Stress. 2010, 33, 501–517. [Google Scholar] [CrossRef]
- Khvijuzov, M.A.; Galashev, A.N. Raschet temperatury nagreva poverkhnosti piľnogo diska pri osushchestvlenii pirometricheskogo kontrolya (Temperature calculation of the blade heating surface in the implementation of the control Pyrometer). Lesnoy Zhurnal 2013, 1, 60–65. [Google Scholar]
- Khvijuzov, M.A.; Galashev, A.N.; Soloviev, I. Kompensacija medodičeskoj progrešnosti pri IK-kontrole nagreva kruglych pil (Compensation of method error in the infrared heating control of circular saws). Lesnoy Zhurnal 2015, 6, 107–115. [Google Scholar]
- Svoreň, J.; Javorek, Ľ.; Krajčovičová, M.; Klobušiaková, K.; Kubovský, I.; Kminiak, R. The effect of the circular saw blade body structure on the concentric distribution of the temperature along the radius during the wood cutting process. Wood Res. 2017, 62, 427–436. [Google Scholar]
- Mohammadpanah, A.; Lehmann, B.; White, J. Development of a monitoring system for guided circular saws: An experimental investigation. Wood Mater. Sci. Eng. 2019, 14, 99–106. [Google Scholar] [CrossRef]
- Martinez, H.V.; Hankele, M. Simulation of the circular sawing process. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015. [Google Scholar]


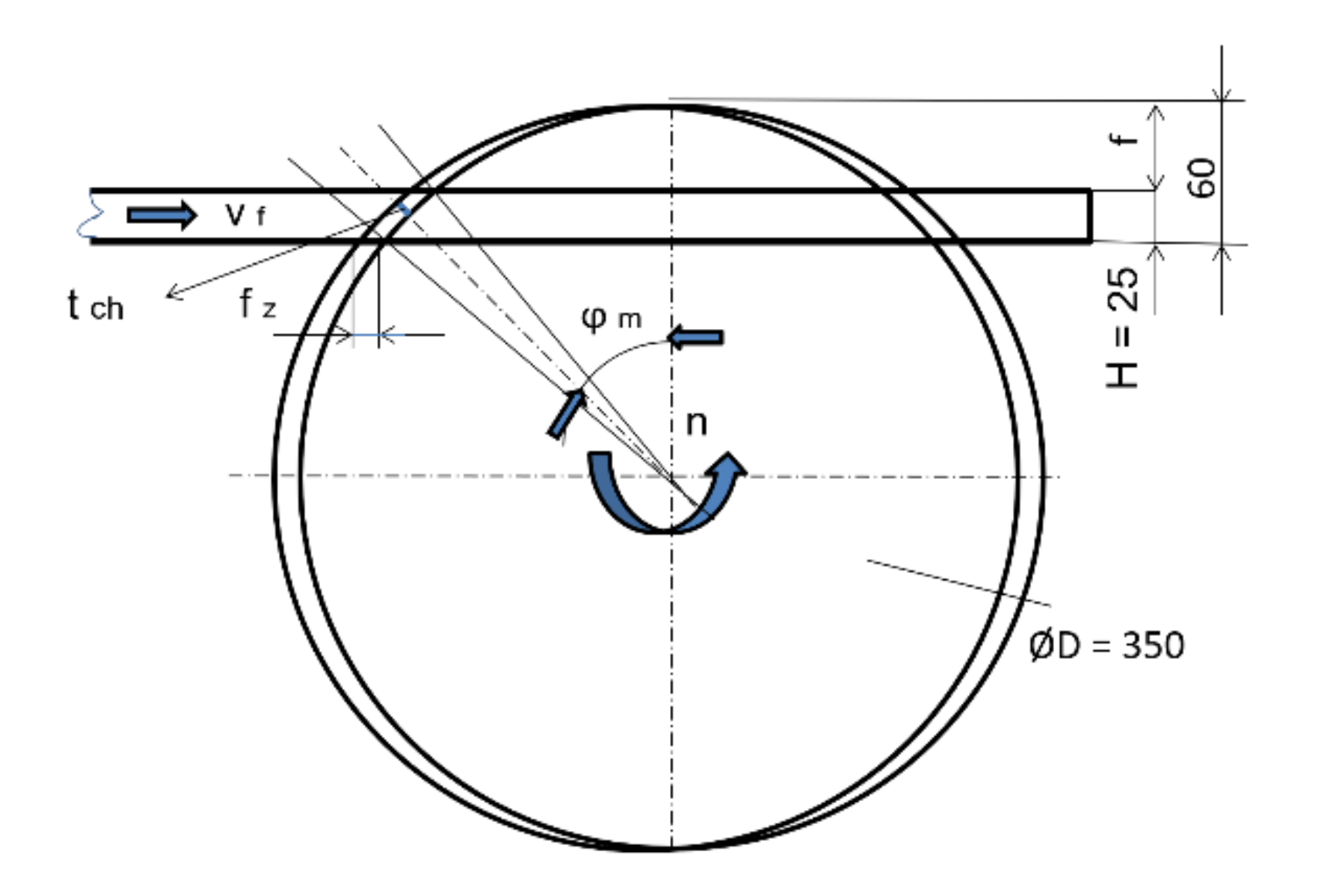







| Parameters | CSB1 | CSB2 | CSB3 |
|---|---|---|---|
| Circular saw blade diameter (mm) | 350 | 350 | 350 |
| Clamping hole diameter (mm) | 30 | 30 | 30 |
| Number of teeth (−) | 36 | 36 | 36 |
| Body thickness (mm) | 2.4 | 2.4 | 2.4 |
| Length of the cutting edge (mm) | 4.0 | 3.8 | 4.0 |
| Tooth height (mm) | 13 | 13 | 13 |
| Tooth geometry | αf = 15° | ||
| βf = 65° | |||
| γf = 10° | |||
| Condition Number | Rotational Speed (rev/min) | Feed Speed (m/min) | Cut Height (m) | Average Chip Thickness (mm) |
|---|---|---|---|---|
| 1 | 4050 | 14 | 0.025 | 0.065 |
| 2 | 4100 | 14 | 0.025 | 0.064 |
| 3 | 4150 | 14 | 0.025 | 0.063 |
| 4 | 4050 | 21 | 0.025 | 0.098 |
| 5 | 4100 | 21 | 0.025 | 0.096 |
| 6 | 4150 | 21 | 0.025 | 0.095 |
| 7 | 4050 | 28 | 0.025 | 0.130 |
| 8 | 4100 | 28 | 0.025 | 0.128 |
| 9 | 4150 | 28 | 0.025 | 0.127 |
| Parameter | Value |
|---|---|
| Power supply | 6...28 Vss |
| Measuring range | −40 ... + 1000 °C (adjustable) |
| Output | 4...20 mA, USB |
| Optika | 30:1 |
| Emissivity | Adjustable via USB and computer |
| Spectral range | 8...14 µm |
| Accuracy | ±1% of value or ± 0.5 °C (whichever is greater) |
| Housing operating temperature | 0... + 70 °C |
| Response time | 240 ms (90%) |
| Dimensions | Ø25 × 106.5 mm |
| Mounting | Thread M20 × 1 |
| Coverage | IP65 |
| Case material | Stainless steel AISI304 |
| Parameter | Cutting Power | |
|---|---|---|
| F Value | p Value | |
| Feed speed | 526.24 | 0.000 |
| Rotation speed | 30.57 | 0.000 |
| Circular Saw Blade | 19.44 | 0.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svoreň, J.; Naščák, Ľ.; Barcík, Š.; Koleda, P.; Stehlík, Š. Influence of Circular Saw Blade Design on Reducing Energy Consumption of a Circular Saw in the Cutting Process. Appl. Sci. 2022, 12, 1276. https://doi.org/10.3390/app12031276
Svoreň J, Naščák Ľ, Barcík Š, Koleda P, Stehlík Š. Influence of Circular Saw Blade Design on Reducing Energy Consumption of a Circular Saw in the Cutting Process. Applied Sciences. 2022; 12(3):1276. https://doi.org/10.3390/app12031276
Chicago/Turabian StyleSvoreň, Ján, Ľubomír Naščák, Štefan Barcík, Peter Koleda, and Štefan Stehlík. 2022. "Influence of Circular Saw Blade Design on Reducing Energy Consumption of a Circular Saw in the Cutting Process" Applied Sciences 12, no. 3: 1276. https://doi.org/10.3390/app12031276





