Multi-Point Displacement Synchronous Monitoring Method for Bridges Based on Computer Vision
Abstract
:1. Introduction
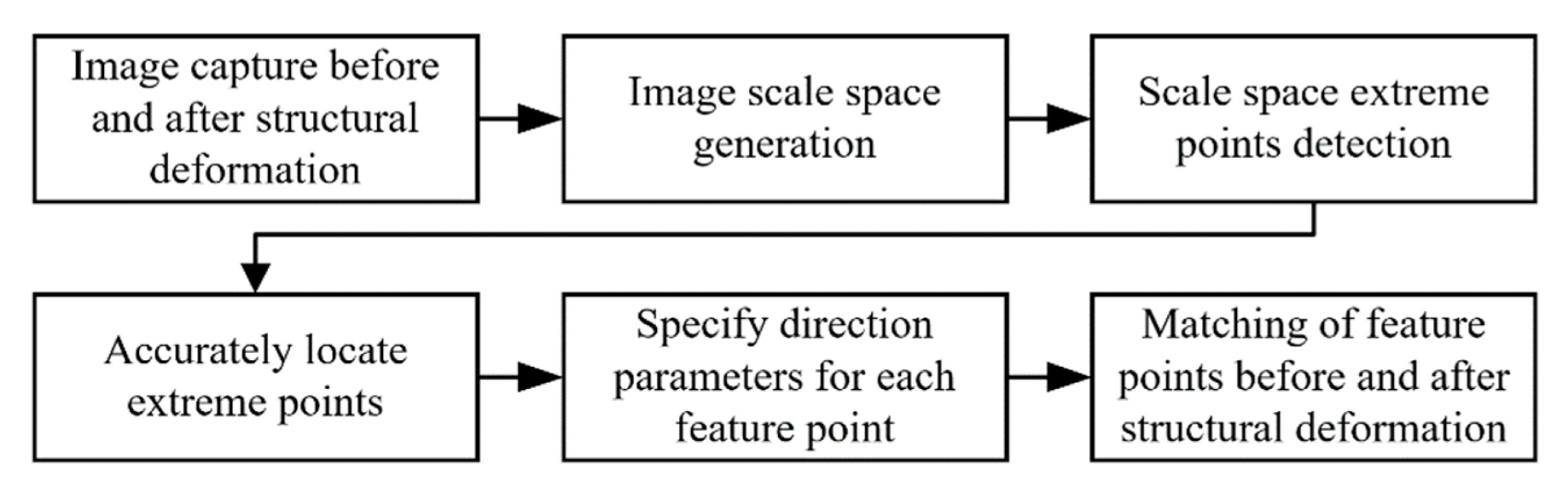
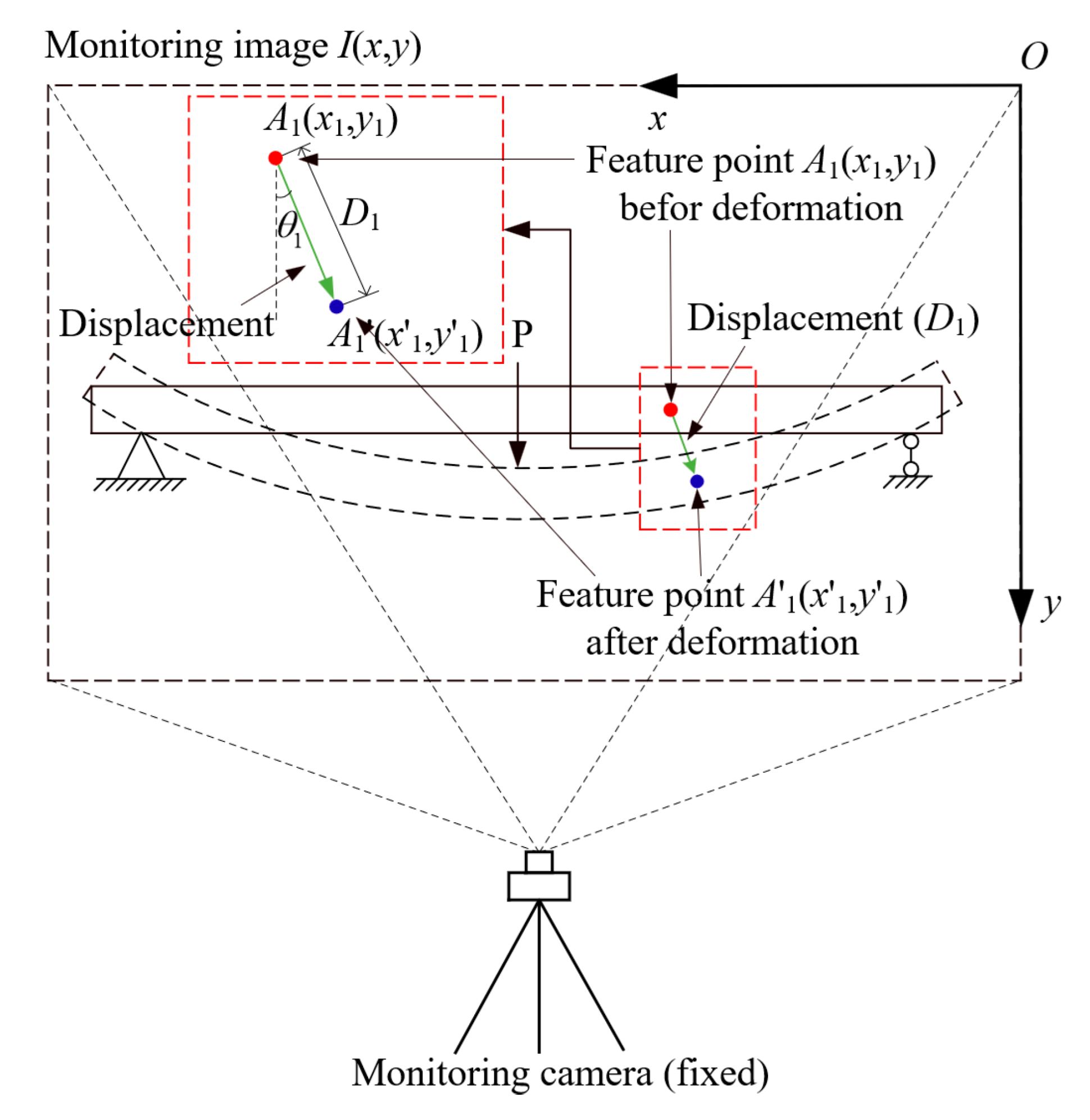
2. Multi-Point Displacement Synchronous Monitoring Method
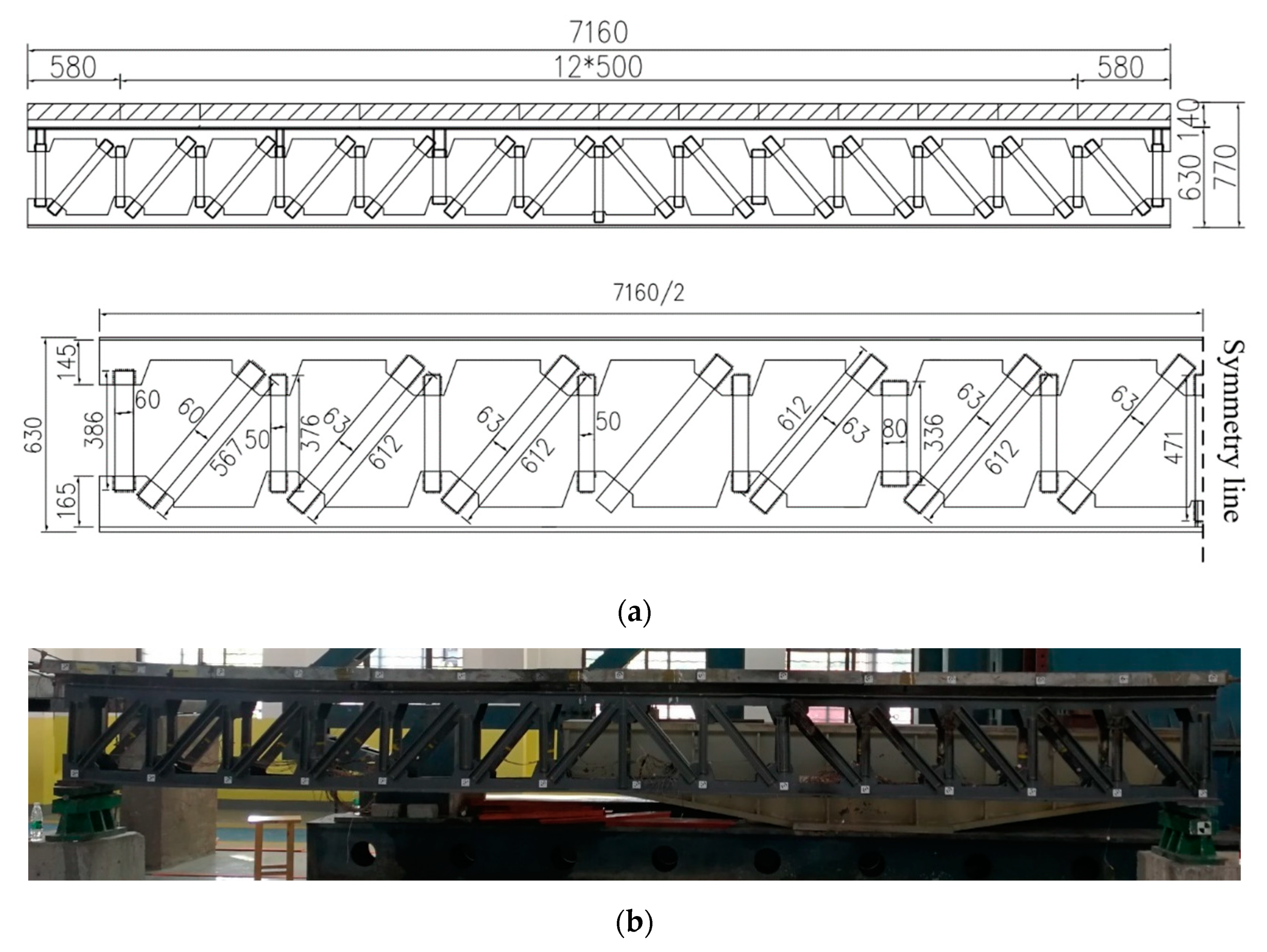
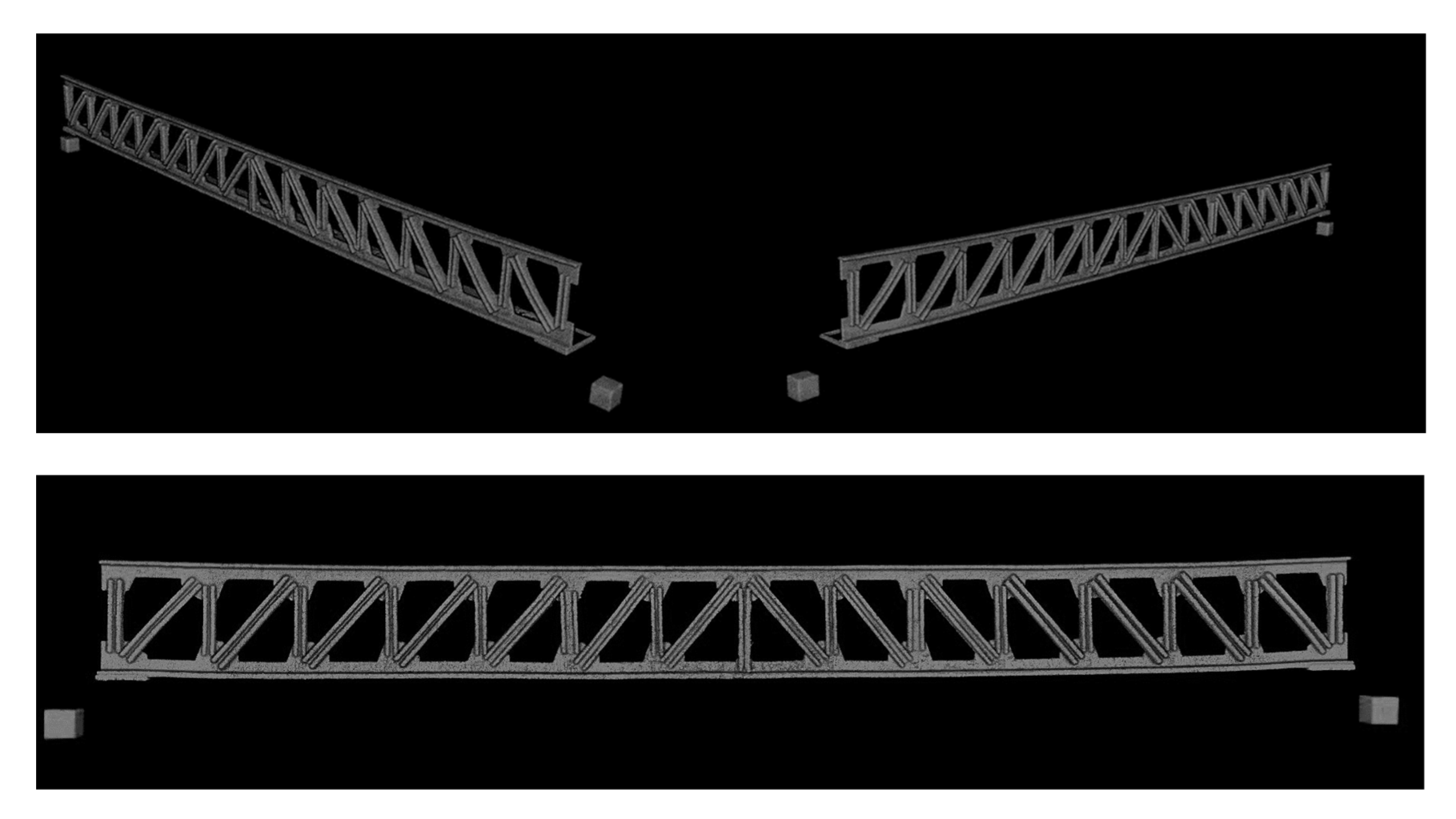
3. Structural Multi-Point Displacement Monitoring Test
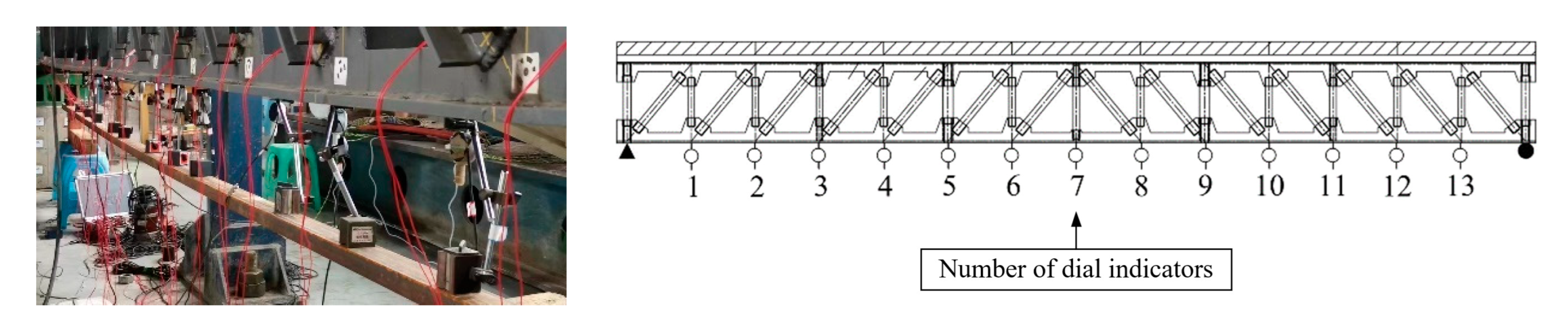
3.1. Data Collection Equipment
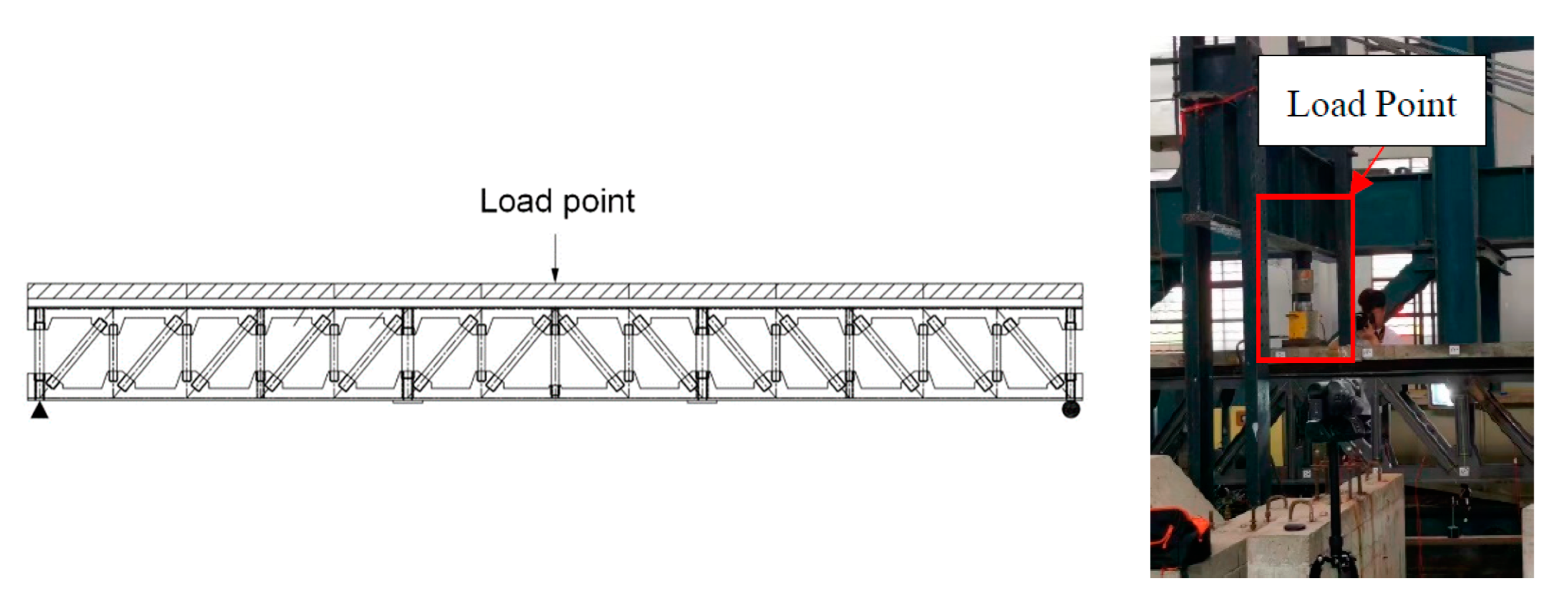
3.2. Loading of the Beam
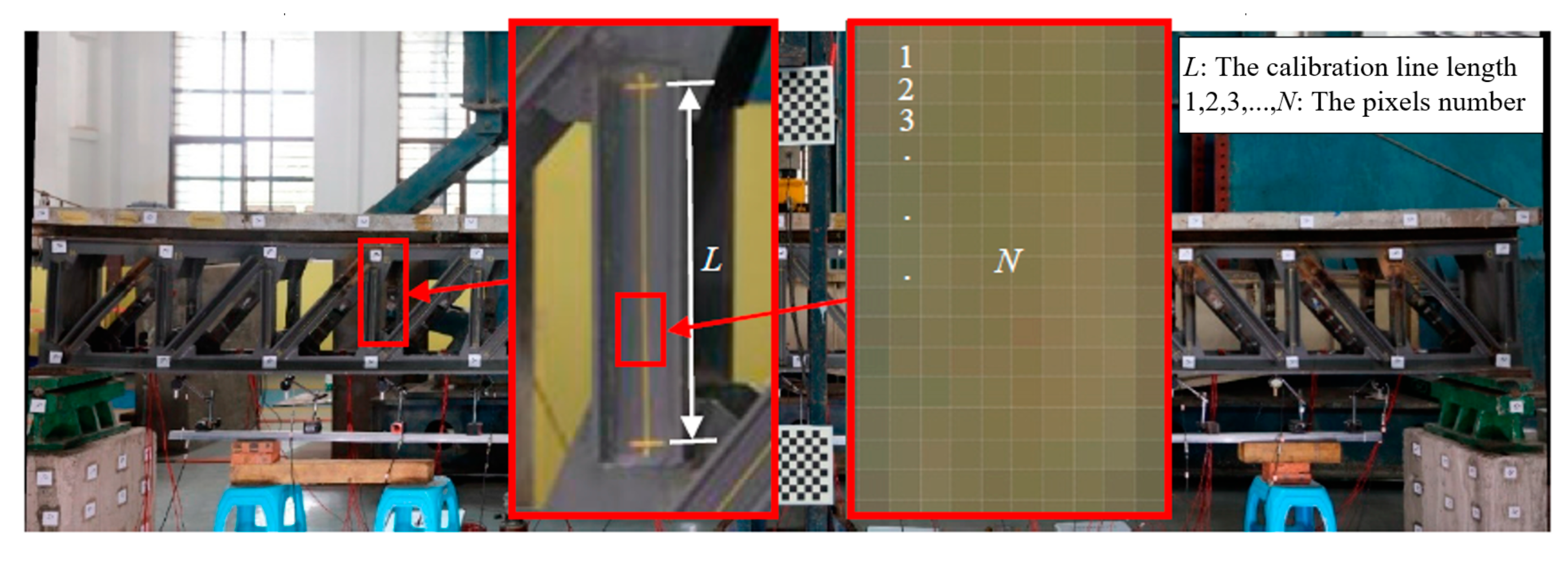
3.3. Calibration Monitoring Resolution
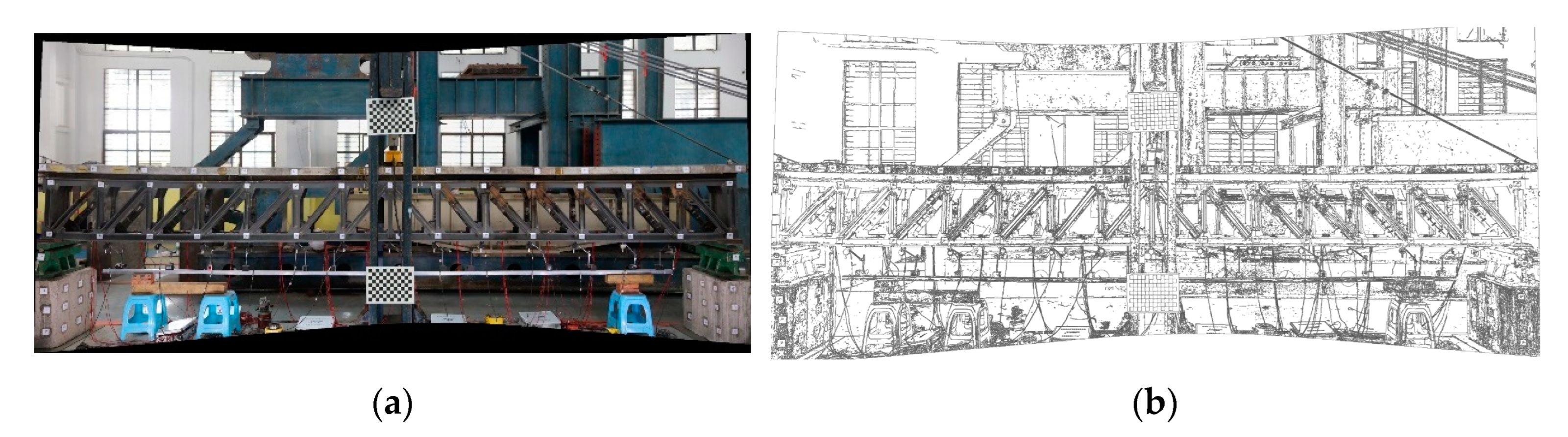
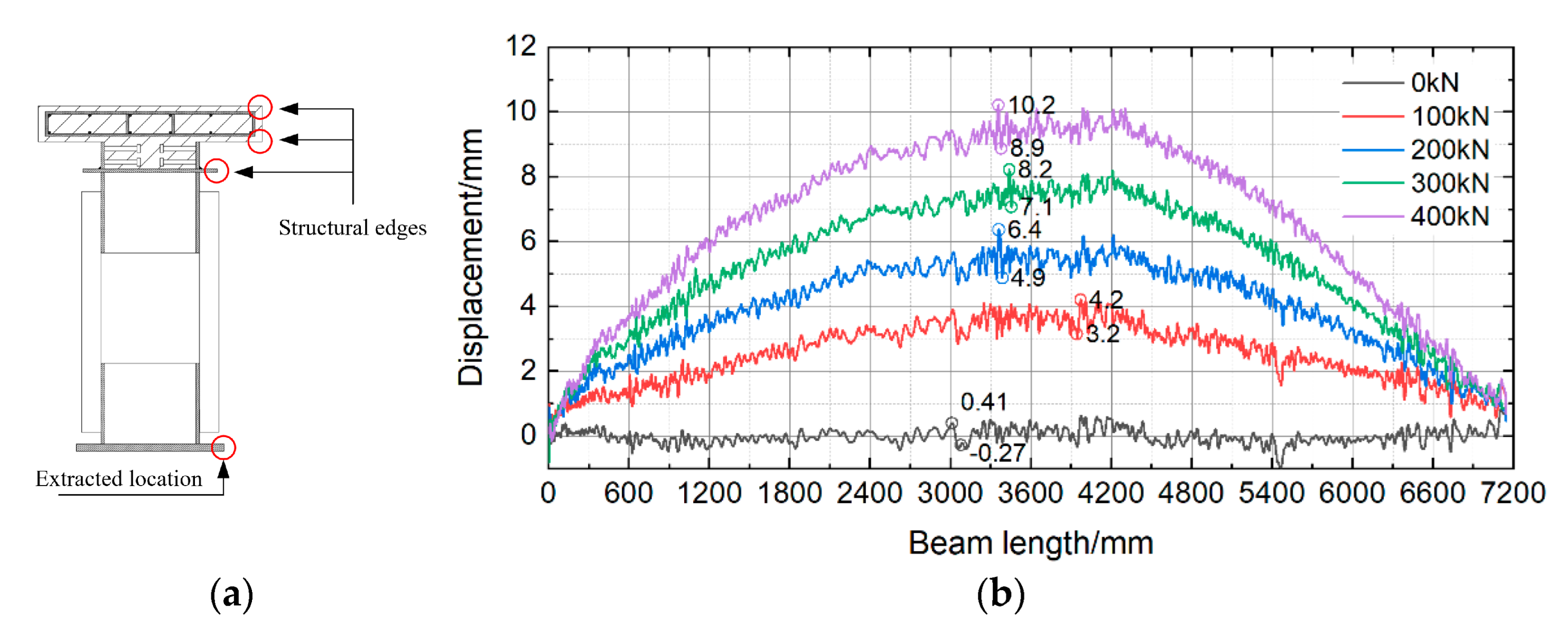
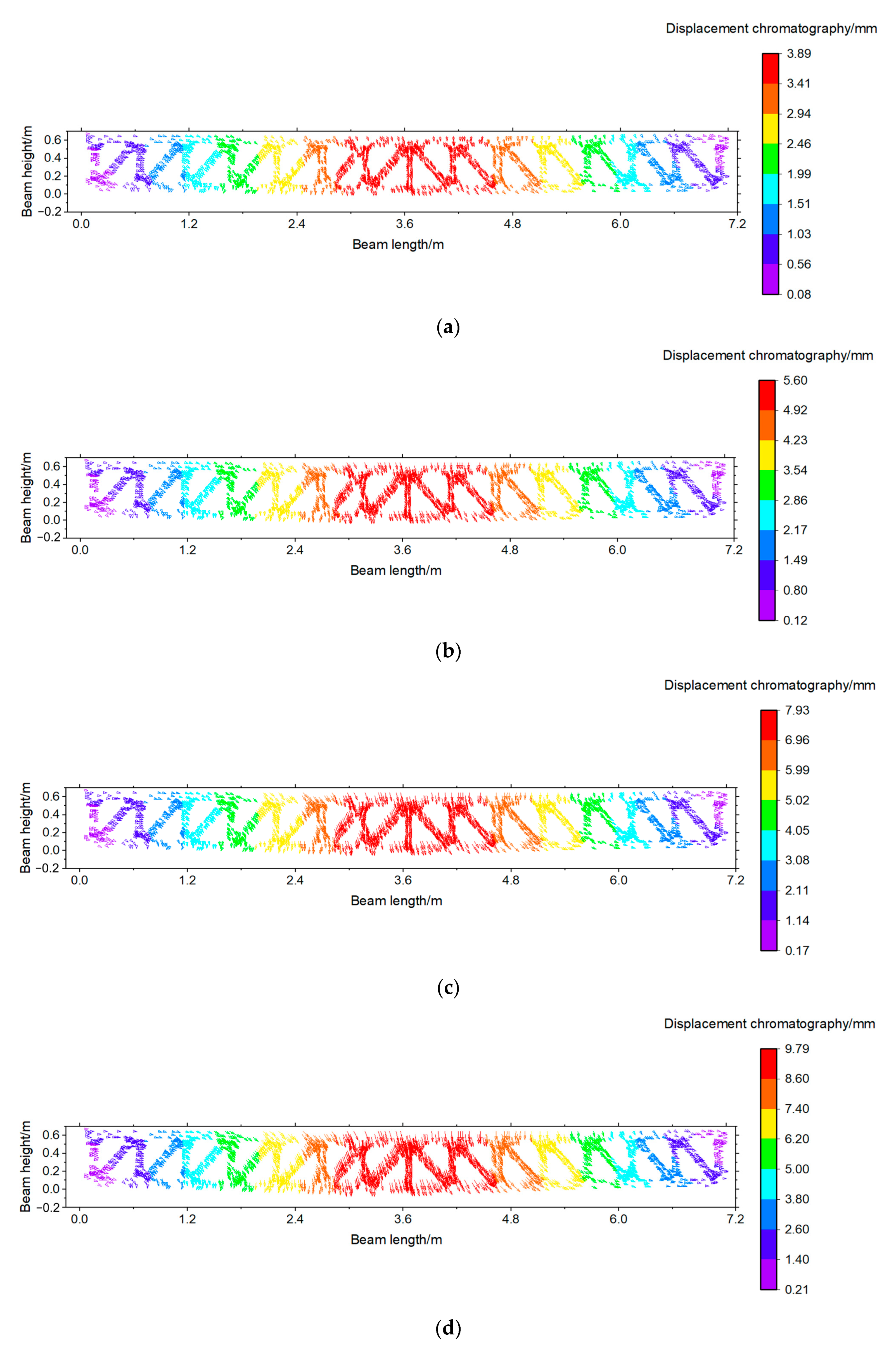
3.4. Initial Monitoring Results for the Beam’s Multi-Point Displacement
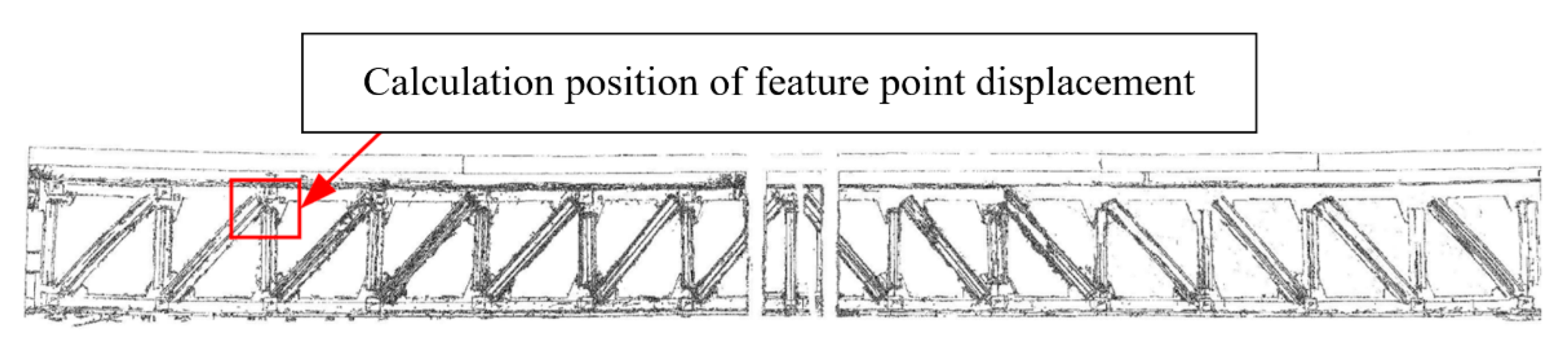
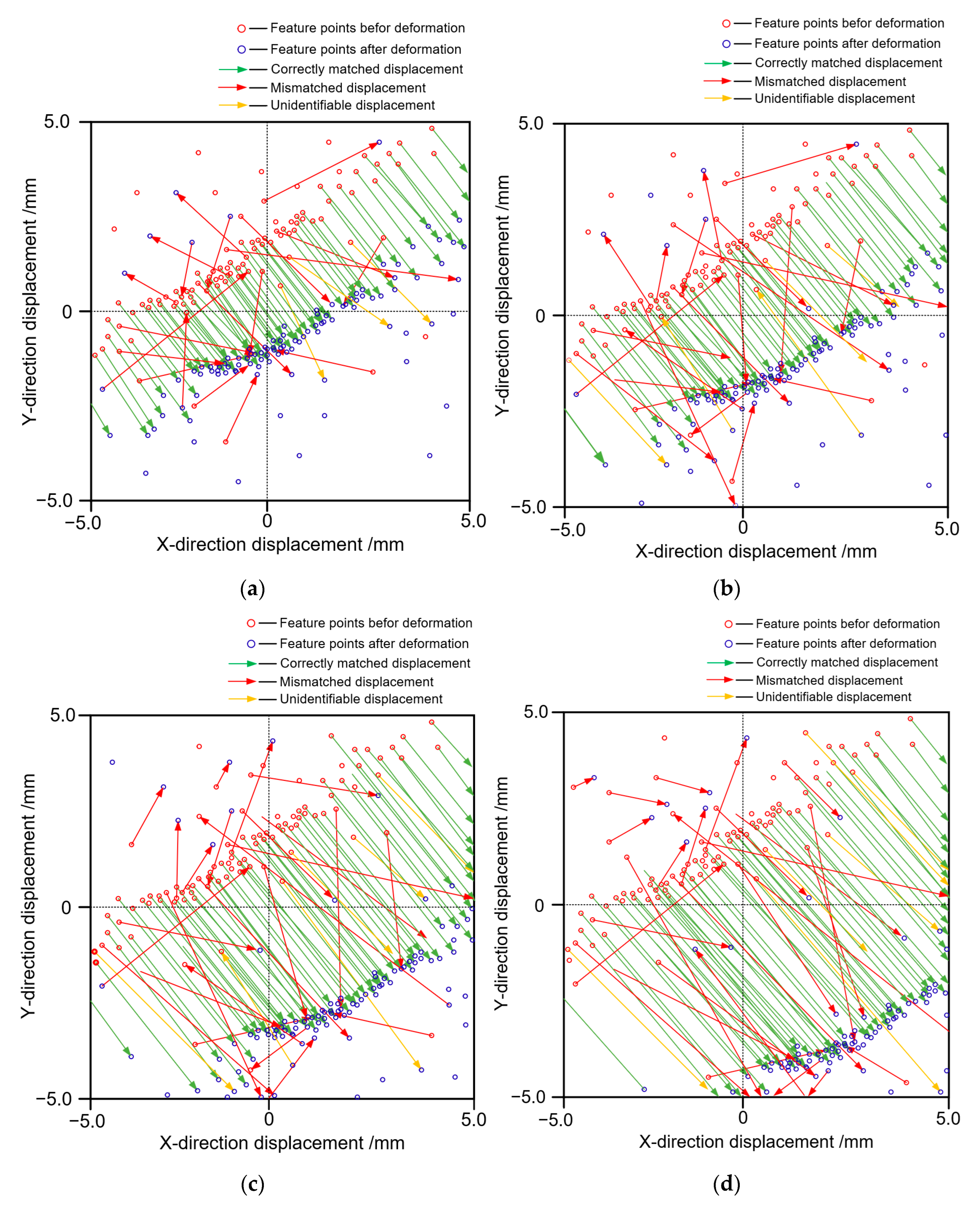
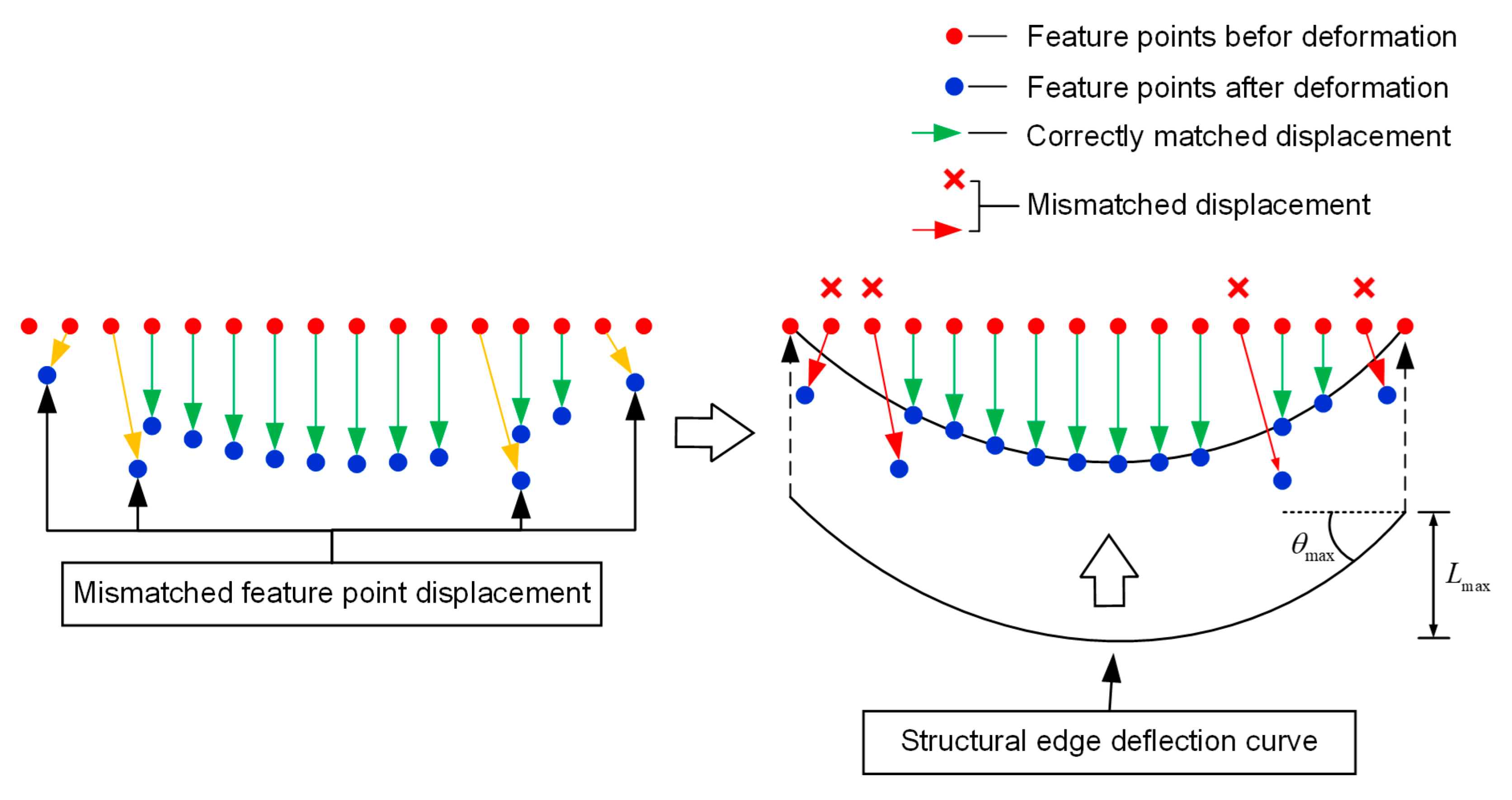
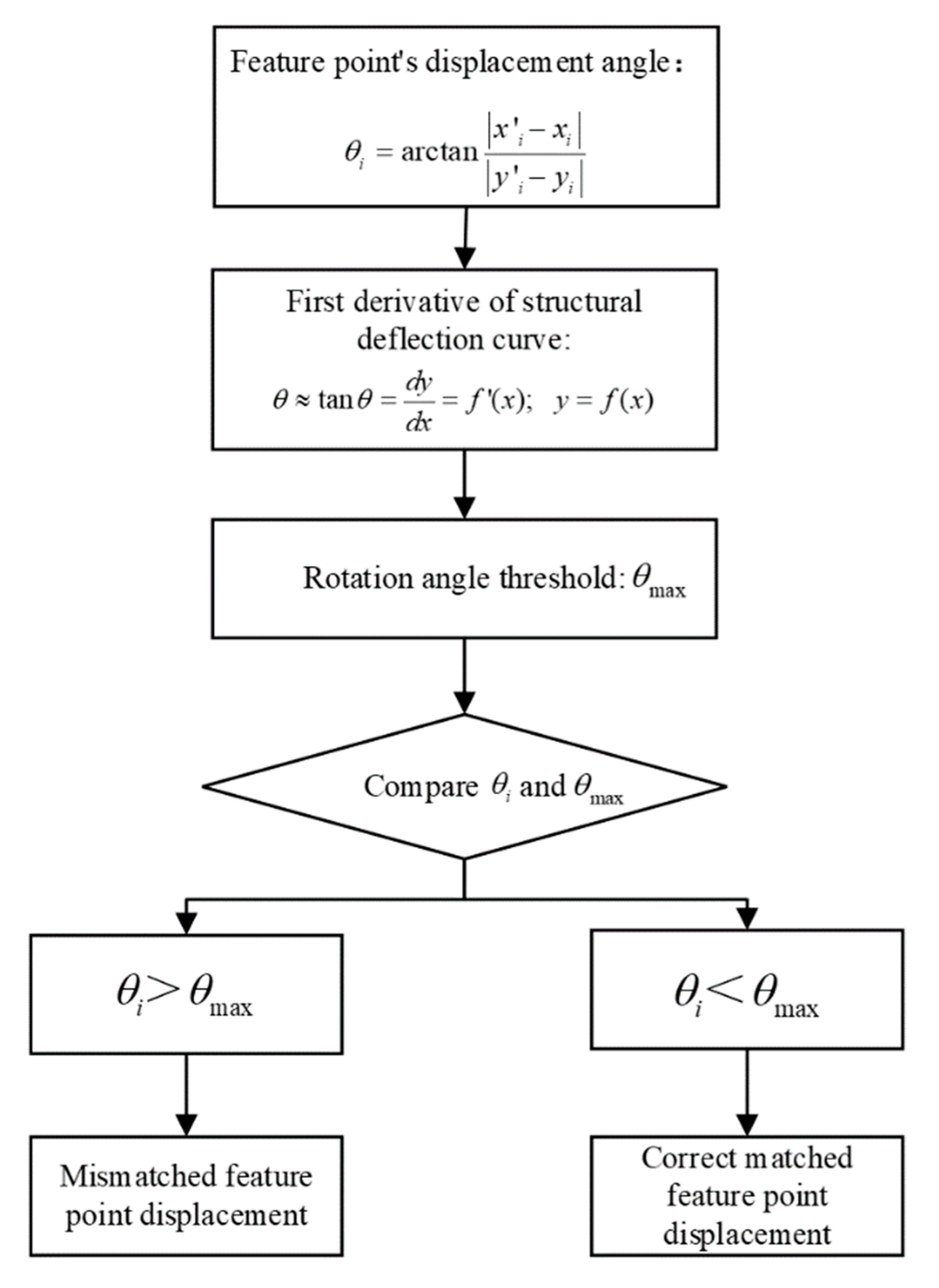
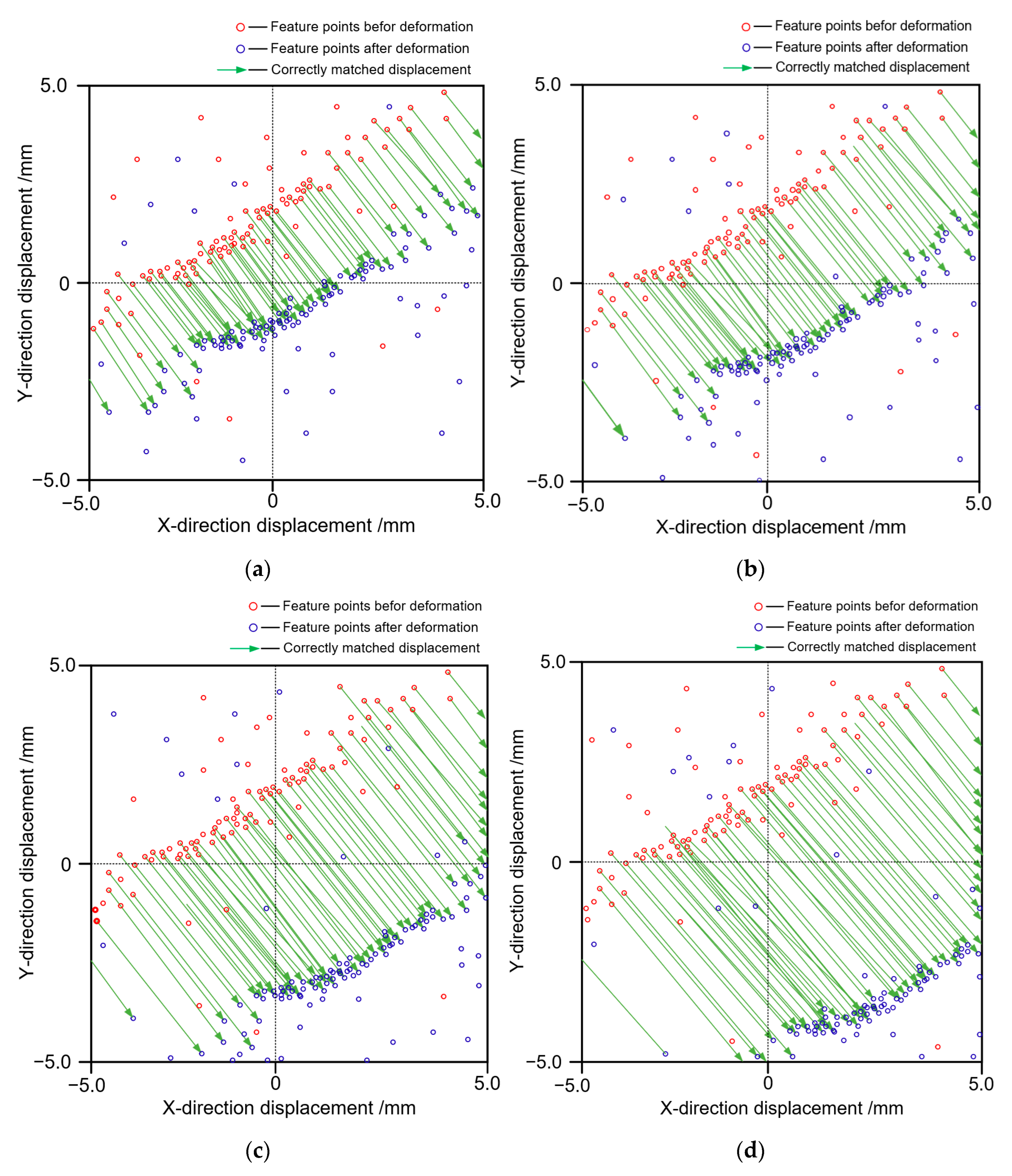
4. A Method for Multi-Point Displacement Mismatch Elimination
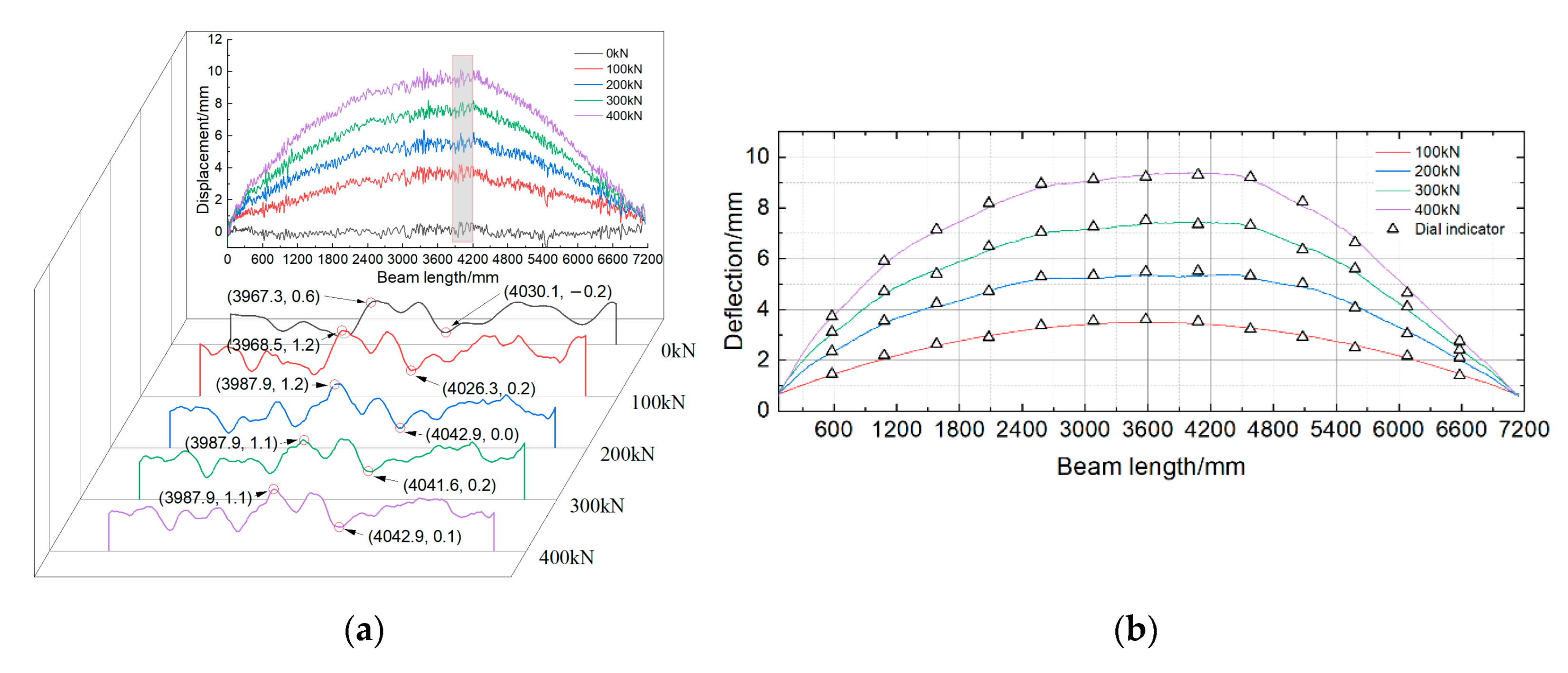
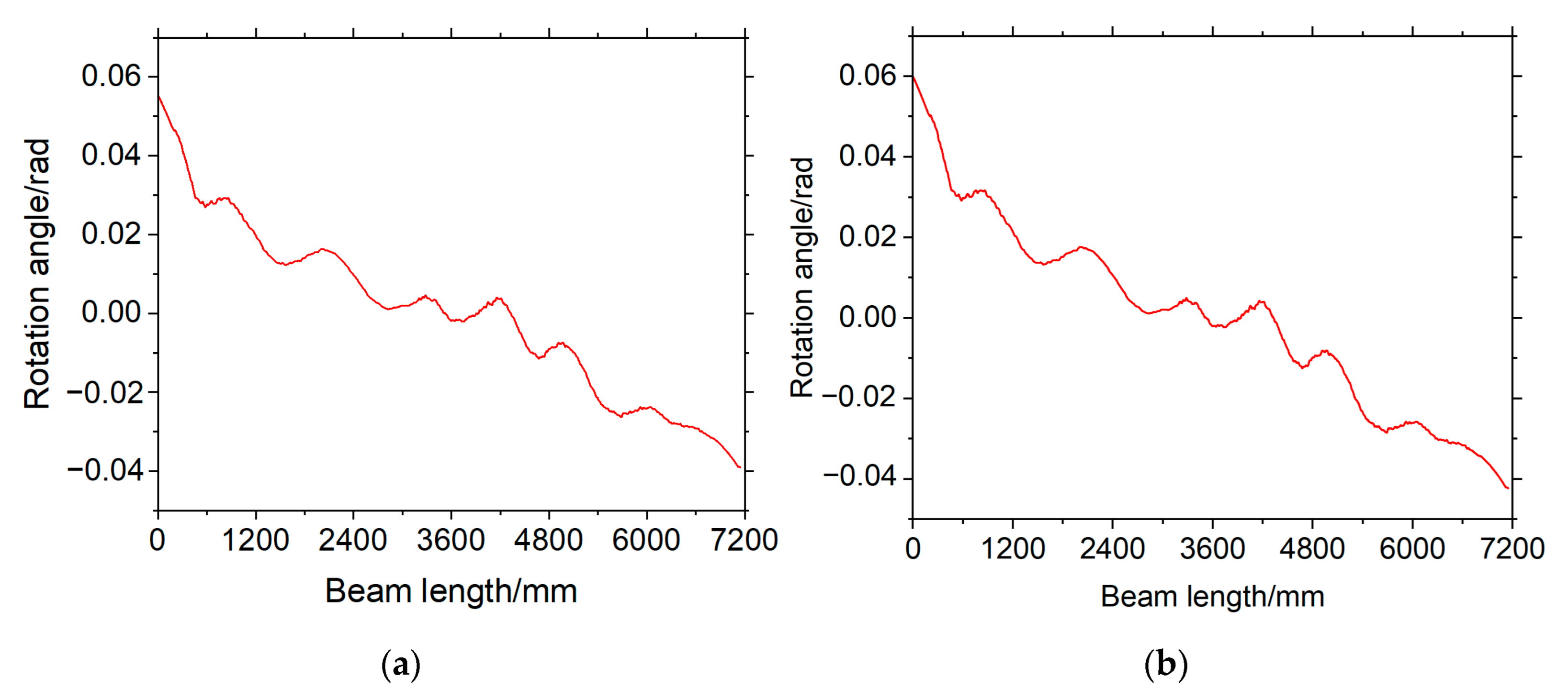
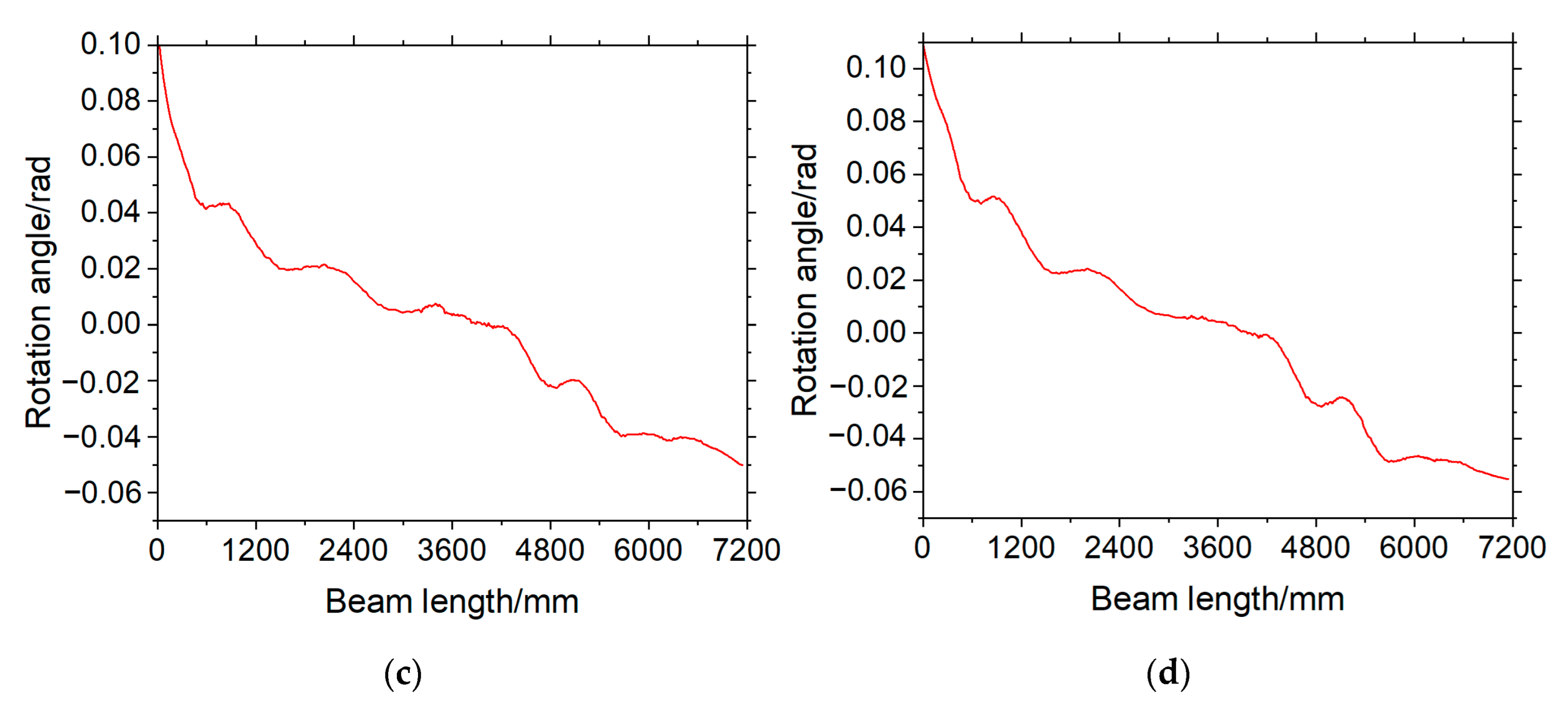
4.1. The Beam’s Edge Deflection
4.2. Mismatch Elimination for Multi-Point Displacements
4.3. Elimination Results of the Beam’s Multi-Point Displacement Mismatches
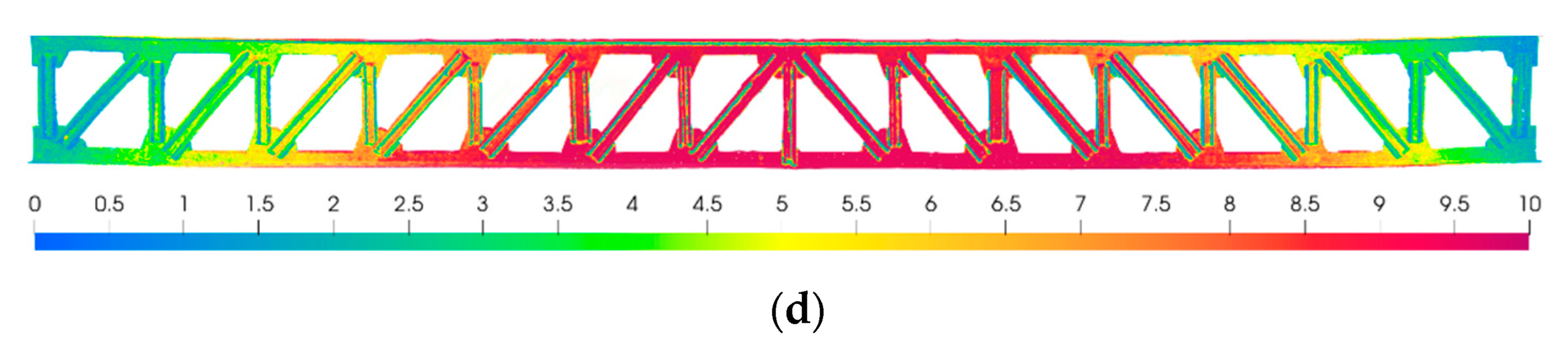
5. Validation of the Monitoring Results
6. Conclusions
- The Scale-invariant Feature Transform (SIFT) algorithm can extract the structural feature points. These feature points can be used as measurement points for displacement monitoring. By establishing an image coordinate system, the displacement of feature points before and after deformation can be calculated.
- A 7 m long test beam was made in the laboratory. By drawing calibration lines on the vertical members of the test beam, the monitoring resolution of the image can be calculated. The monitoring resolution of the test beam image in this paper is 0.18 mm.
- The structural surface’s weak or repeated natural texture features can lead to the mismatches of some displacements. Hence, a displacement mismatch elimination method was proposed. This method uses the extracted deflection curve to constrain the displacement’s length and rotation angle. Hence, we achieved structural multi-point displacement mismatch elimination.
- We validated the test results using a three-dimensional laser scanning method. The maximum error of the monitoring results was 8.70%, and the average error was 4.21%. The monitoring results are consistent with the actual structural deformation.
- This method can expand the monitoring data. The monitoring results are similar to those of the structural full-field displacement monitoring and are expected to fundamentally solve the bridge safety evaluation problem of incomplete test data.
- This study yielded good monitoring results in the laboratory. However, the test beam’s image in the laboratory exhibits obvious noise, leading to the structural edge’s line shape undulation. The bridge environment is more complex than that of the laboratory, and the image noise is obvious. Therefore, the noise interference problem in the application of this method to practical actual bridges should be researched in future studies. It is recommended to use higher pixel hardware devices and more accurate feature point extraction algorithms in future studies to reduce the impact of noise.
- The multi-point displacement synchronous monitoring method of structures can be combined with structural damage identification. Compared to traditional single-point monitoring, multi-point displacement monitoring of structures can obtain more comprehensive monitoring data, and rotation angle information can be obtained through structural multi-point displacement. Whether the rotation angle can be used as a damage identification index combined with multi-point displacement monitoring methods still needs further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stephen, G.A.; Brownjohn, J.M.W.; Taylor, C.A. Measurements of static and dynamic displacement from visual monitoring of the Humber Bridge. Eng. Struct. 1993, 15, 197–208. [Google Scholar] [CrossRef]
- Olaszek, P. Investigation of the dynamic characteristic of bridge structures using a computer vision method. Measurement 1999, 25, 227–236. [Google Scholar] [CrossRef]
- J´auregui, D.V.; White, K.R.; Woodward, C.B.; Leitch, K.R. Noncontact photogrammetric measurement of vertical bridge deflection. J. Bridge Eng. 2003, 8, 212–222. [Google Scholar] [CrossRef]
- Lee, J.J.; Cho, S.J.; Shinozuka, M.; Yun, C.B.; Lee, C.G.; Lee, W.T. Evaluation of bridge load carrying capacity based on dynamic displacement measurement using real–time image processing techniques. Int. J. Steel Struct. 2006, 6, 377–385. [Google Scholar]
- Dongming, F.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control. Health Monit. 2016, 23, 876–890. [Google Scholar]
- Terán, L.; Ordóñez, C.; García-Cortés, S.; Menéndez, A. Detection and magnification of bridge displacements using video images. Proc. Spie 2016, 151, 1015109. [Google Scholar]
- Pan, B.; Tian, L.; Song, X. Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation. NDT E Int. 2016, 79, 73–80. [Google Scholar] [CrossRef]
- Long, T.; Pan, B. Remote Bridge Deflection Measurement Using an Advanced Video Deflectometer and Actively Illuminated LED Targets. Sensors 2016, 16, 1344. [Google Scholar]
- Zhao, X.; Liu, H.; Yu, Y.; Xu, X.; Hu, W.; Li, M.; Ou, J. Bridge Displacement Monitoring Method Based on Laser Projection-Sensing Technology. Sensors 2015, 15, 8444–8463. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, H.; Yu, Y.; Zhu, Q.; Hu, W.; Li, M.; Ou, J. Displacement monitoring technique using a smartphone based on the laser projection-sensing method. Sens. Actuators A Phys. 2016, 246, 35–47. [Google Scholar] [CrossRef]
- Liu, P.; Liu, C.; Zhang, L.; Zhao, X. Displacement monitoring method based on laser projection to eliminate the effect of rotation angle. Adv. Struct. Eng. 2019, 22, 3319–3327. [Google Scholar] [CrossRef]
- Liu, P.; Xie, S.; Zhou, G.; Zhang, L.; Zhang, G.; Zhao, X. Horizontal displacement monitoring method of deep foundation pit based on laser image recognition technology. Rev. Sci. Instrum. 2018, 89, 125006. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, D.; Calçada, R.; Ferreira, J.; Martins, T. Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 2014, 75, 164–180. [Google Scholar] [CrossRef]
- Feng, M.Q.; Fukuda, Y.; Feng, D.; Mizuta, M. Nontarget Vision Sensor for Remote Measurement of Bridge Dynamic Response. J. Bridge Eng. 2015, 20, 04015023. [Google Scholar] [CrossRef]
- Khuc, T.; Catbas, F.N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision. Struct. Control Health Monit. 2017, 24, e1852. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.C.; Jeong, S.; Lee, Y.J.; Sim, S.H. Long-term displacement measurement of full-scale bridges using camera ego-motion compensation. Mech. Syst. Signal Process. 2020, 140, 106651. [Google Scholar] [CrossRef]
- Kromanis, R.; Kripakaran, P. A multiple camera position approach for accurate displacement measurement using computer vision. J. Civ. Struct. Health Monit. 2021, 11, 661–678. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, Y.; Lee, H.; Yun, H. Marker-Based Structural Displacement Measurement Models with Camera Movement Error Correction Using Image Matching and Anomaly Detection. Sensors 2020, 20, 5676. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W. Review of machine-vision based methodologies for displacement measurement in civil structures. J. Civ. Struct. Health Monit. 2018, 8, 91–110. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr.; Hoskere, V.; Narazaki, Y. Advances in Computer Vision-Based Civil Infrastructure Inspection and Monitoring. Engineering 2019, 5, 199–222. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, P.; Yan, X.; Zhao, X. Middle displacement monitoring of medium–small span bridges based on laser technology. Struct. Control Health Monit. 2020, 27, e2509. [Google Scholar] [CrossRef]
- Bai, X.; Yang, M.; Ajmera, B. An Advanced Edge-Detection Method for Noncontact Structural Displacement Monitoring. Sensors 2020, 20, 4941. [Google Scholar] [CrossRef]
- Yu, L.; Lubineau, G. A smartphone camera and built-in gyroscope based application for non-contact yet accurate off-axis structural displacement measurements. Measurement 2021, 167, 108449. [Google Scholar] [CrossRef]
- Lee, J.H.; Yoon, S.; Kim, B.; Gwon, G.H.; Kim, I.H.; Jung, H.J. A new image-quality evaluating and enhancing methodology for bridge inspection using an unmanned aerial vehicle. Smart Struct. Syst. 2021, 27, 209–226. [Google Scholar]
- Chu, X.; Zhou, Z.; Deng, G.; Duan, X.; Jiang, X. An Overall Deformation Monitoring Method of Structure Based on Tracking Deformation Contour. Appl. Sci. 2019, 9, 4532. [Google Scholar] [CrossRef]
- Deng, G.; Zhou, Z.; Shao, S.; Chu, X.; Jian, C. A Novel Dense Full-Field Displacement Monitoring Method Based on Image Sequences and Optical Flow Algorithm. Appl. Sci. 2020, 10, 2118. [Google Scholar] [CrossRef]
- Luo, R.; Zhou, Z.; Chu, X.; Liao, X.; Meng, J. Research on Damage Localization of Steel Truss–Concrete Composite Beam Based on Digital Orthoimage. Appl. Sci. 2022, 12, 3883. [Google Scholar] [CrossRef]



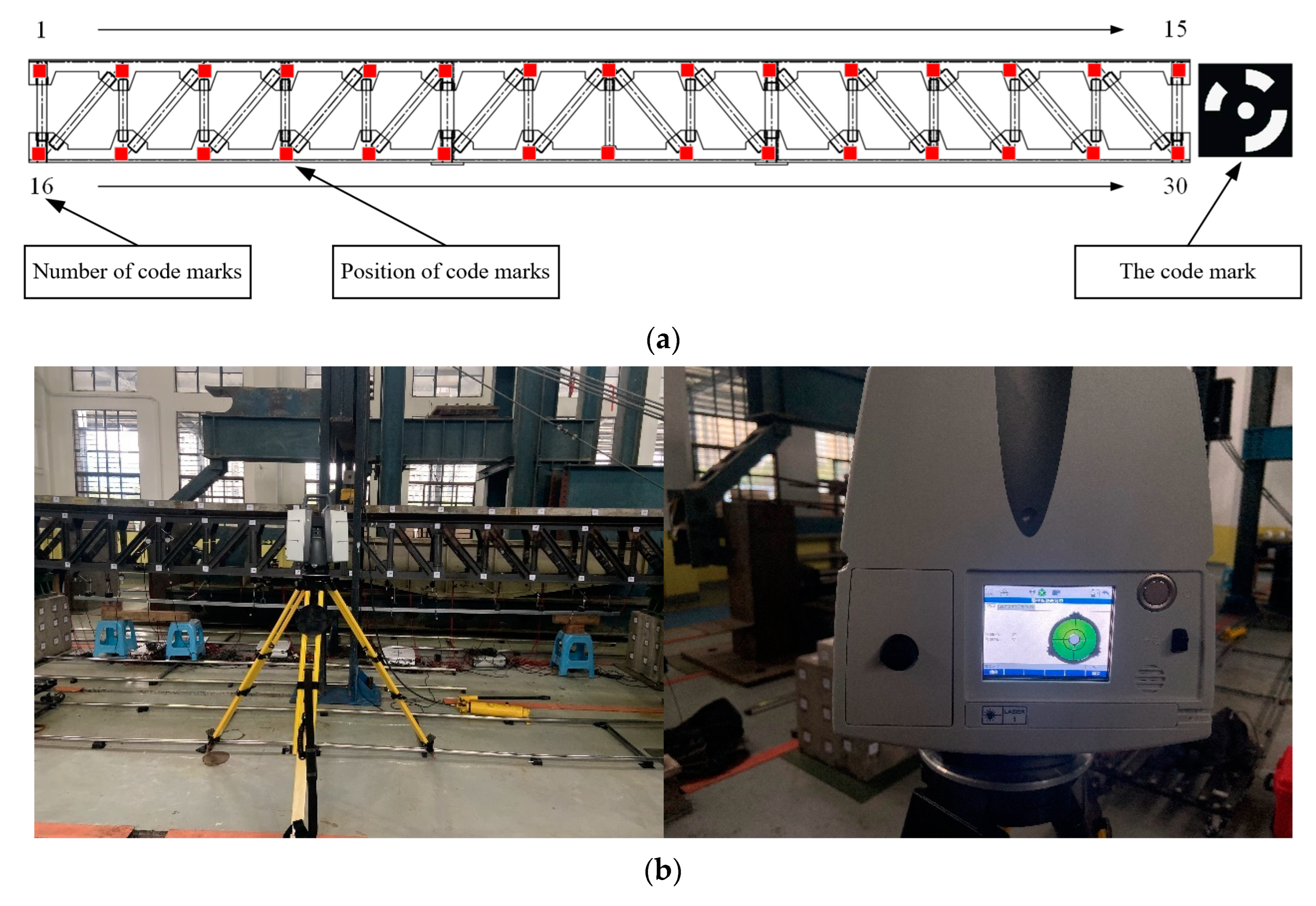

| Pixels | Sensor | Data Interface | Image Frame |
|---|---|---|---|
| 102 million | 43.8 × 32.9 mm | USB 3.0 | 11,648 × 8736 |
| Pixel size | Lens model | Relative aperture of lens | Focal length |
| 3.76 μm | GF 32–64/4 R LM WR | F4.0–F32 | 32–64 mm |
| Member Nos. | N | L (mm) | Calibration Results L/N (mm/pixel) | Average |
|---|---|---|---|---|
| 1–16 | 1975 | 386.24 | 0.20 | 0.18 mm/pixel |
| 2–17 | 1978 | 349.25 | 0.18 | |
| 3–18 | 1987 | 327.83 | 0.16 | |
| 4–19 | 1980 | 332.91 | 0.17 | |
| 5–20 | 1968 | 366.79 | 0.19 | |
| 6–21 | 1989 | 327.91 | 0.16 | |
| 7–22 | 1980 | 359.12 | 0.18 | |
| 8–23 | 1992 | 345.13 | 0.17 | |
| 9–24 | 1989 | 312.15 | 0.16 | |
| 10–25 | 1992 | 387.54 | 0.19 | |
| 11–26 | 1991 | 381.28 | 0.19 | |
| 12–27 | 1983 | 331.53 | 0.17 | |
| 13–28 | 1982 | 349.27 | 0.18 | |
| 14–29 | 1981 | 339.25 | 0.17 | |
| 15–30 | 1989 | 351.72 | 0.18 |
| Load | Dial Indicator No. | Dial Indicator Value (mm) | Calculated Value (mm) | Error (%) |
|---|---|---|---|---|
| 100 kN | 1 | 1.45 | 1.42 | 2.07% |
| 2 | 2.19 | 2.17 | 0.91% | |
| 3 | 2.63 | 2.57 | 2.28% | |
| 4 | 2.90 | 2.97 | 2.41% | |
| 5 | 3.37 | 3.26 | 3.26% | |
| 6 | 3.55 | 3.42 | 3.66% | |
| 7 | 3.61 | 3.49 | 3.32% | |
| 8 | 3.53 | 3.44 | 2.55% | |
| 9 | 3.22 | 3.27 | 1.55% | |
| 10 | 2.91 | 2.99 | 2.75% | |
| 11 | 2.53 | 2.59 | 2.37% | |
| 12 | 2.16 | 2.08 | 3.70% | |
| 13 | 1.40 | 1.45 | 3.57% | |
| 200 kN | 1 | 2.34 | 2.32 | 0.85% |
| 2 | 3.55 | 3.63 | 2.25% | |
| 3 | 4.24 | 4.12 | 2.83% | |
| 4 | 4.73 | 4.72 | 0.21% | |
| 5 | 5.29 | 5.19 | 1.89% | |
| 6 | 5.34 | 5.24 | 1.87% | |
| 7 | 5.49 | 5.34 | 2.73% | |
| 8 | 5.51 | 5.32 | 3.45% | |
| 9 | 5.33 | 5.26 | 1.31% | |
| 10 | 5.03 | 4.88 | 2.98% | |
| 11 | 4.07 | 4.16 | 2.21% | |
| 12 | 3.04 | 3.13 | 2.96% | |
| 13 | 2.11 | 2.01 | 4.74% | |
| 300 kN | 1 | 3.11 | 3.03 | 2.57% |
| 2 | 4.72 | 4.85 | 2.75% | |
| 3 | 5.41 | 5.53 | 2.22% | |
| 4 | 6.48 | 6.34 | 2.16% | |
| 5 | 7.05 | 6.99 | 0.85% | |
| 6 | 7.16 | 7.17 | 0.14% | |
| 7 | 7.32 | 7.39 | 0.96% | |
| 8 | 7.36 | 7.42 | 0.82% | |
| 9 | 7.31 | 7.25 | 0.82% | |
| 10 | 6.37 | 6.46 | 1.41% | |
| 11 | 5.61 | 5.49 | 2.14% | |
| 12 | 4.11 | 4.00 | 2.68% | |
| 13 | 2.41 | 2.46 | 2.07% | |
| 400 kN | 1 | 3.73 | 3.71 | 0.54% |
| 2 | 5.88 | 6.11 | 3.91% | |
| 3 | 7.16 | 7.06 | 1.40% | |
| 4 | 8.19 | 8.03 | 1.95% | |
| 5 | 8.96 | 8.78 | 2.01% | |
| 6 | 9.13 | 9.09 | 0.44% | |
| 7 | 9.47 | 9.32 | 1.58% | |
| 8 | 9.22 | 9.37 | 1.63% | |
| 9 | 8.94 | 9.13 | 2.13% | |
| 10 | 8.35 | 8.07 | 3.35% | |
| 11 | 6.64 | 6.79 | 2.26% | |
| 12 | 4.65 | 4.74 | 1.94% | |
| 13 | 2.76 | 2.86 | 3.62% |
| Load Level | Rotation Angle Threshold (Rad) |
|---|---|
| 100 kN | 0.055 |
| 200 kN | 0.059 |
| 300 kN | 0.098 |
| 400 kN | 0.110 |
| Load | Code Mark No. | Validation Value (mm) | Calculated Value (mm) | Error (%) |
|---|---|---|---|---|
| 400 kN | 1 | 1.00 | 1.03 | 3.26% |
| 2 | 4.96 | 4.75 | 4.29% | |
| 3 | 7.82 | 8.29 | 5.95% | |
| 4 | 9.52 | 9.84 | 3.35% | |
| 5 | 10.89 | 11.23 | 3.05% | |
| 6 | 11.92 | 11.13 | 6.60% | |
| 7 | 12.14 | 12.32 | 1.42% | |
| 8 | 12.60 | 13.11 | 4.12% | |
| 9 | 12.26 | 12.57 | 2.49% | |
| 10 | 11.89 | 12.22 | 2.80% | |
| 11 | 11.11 | 11.38 | 2.51% | |
| 12 | 8.83 | 9.28 | 5.12% | |
| 13 | 6.18 | 6.52 | 5.38% | |
| 14 | 3.67 | 3.99 | 8.70% | |
| 15 | 0.92 | 0.95 | 3.52% | |
| 16 | 0.96 | 0.91 | 4.97% | |
| 17 | 5.00 | 4.68 | 6.38% | |
| 18 | 7.95 | 8.26 | 3.85% | |
| 19 | 9.32 | 9.74 | 4.42% | |
| 20 | 10.96 | 11.19 | 2.06% | |
| 21 | 11.90 | 11.60 | 2.57% | |
| 22 | 12.29 | 12.78 | 4.00% | |
| 23 | 12.40 | 12.85 | 3.65% | |
| 24 | 12.53 | 12.15 | 2.99% | |
| 25 | 12.50 | 12.07 | 3.48% | |
| 26 | 11.12 | 11.65 | 4.81% | |
| 27 | 8.31 | 8.82 | 6.08% | |
| 28 | 6.00 | 5.50 | 8.31% | |
| 29 | 3.82 | 3.92 | 2.70% | |
| 30 | 0.81 | 0.84 | 3.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, X.; Zhou, Z.; Zhu, W.; Duan, X. Multi-Point Displacement Synchronous Monitoring Method for Bridges Based on Computer Vision. Appl. Sci. 2023, 13, 6544. https://doi.org/10.3390/app13116544
Chu X, Zhou Z, Zhu W, Duan X. Multi-Point Displacement Synchronous Monitoring Method for Bridges Based on Computer Vision. Applied Sciences. 2023; 13(11):6544. https://doi.org/10.3390/app13116544
Chicago/Turabian StyleChu, Xi, Zhixiang Zhou, Weizhu Zhu, and Xin Duan. 2023. "Multi-Point Displacement Synchronous Monitoring Method for Bridges Based on Computer Vision" Applied Sciences 13, no. 11: 6544. https://doi.org/10.3390/app13116544






