Extreme Wave Loading on a Vertical Circular Cylinder
Abstract
:1. Introduction
2. Experimental Modeling and Data Analysis
2.1. Experimental Setup
2.2. Incident Wave Field
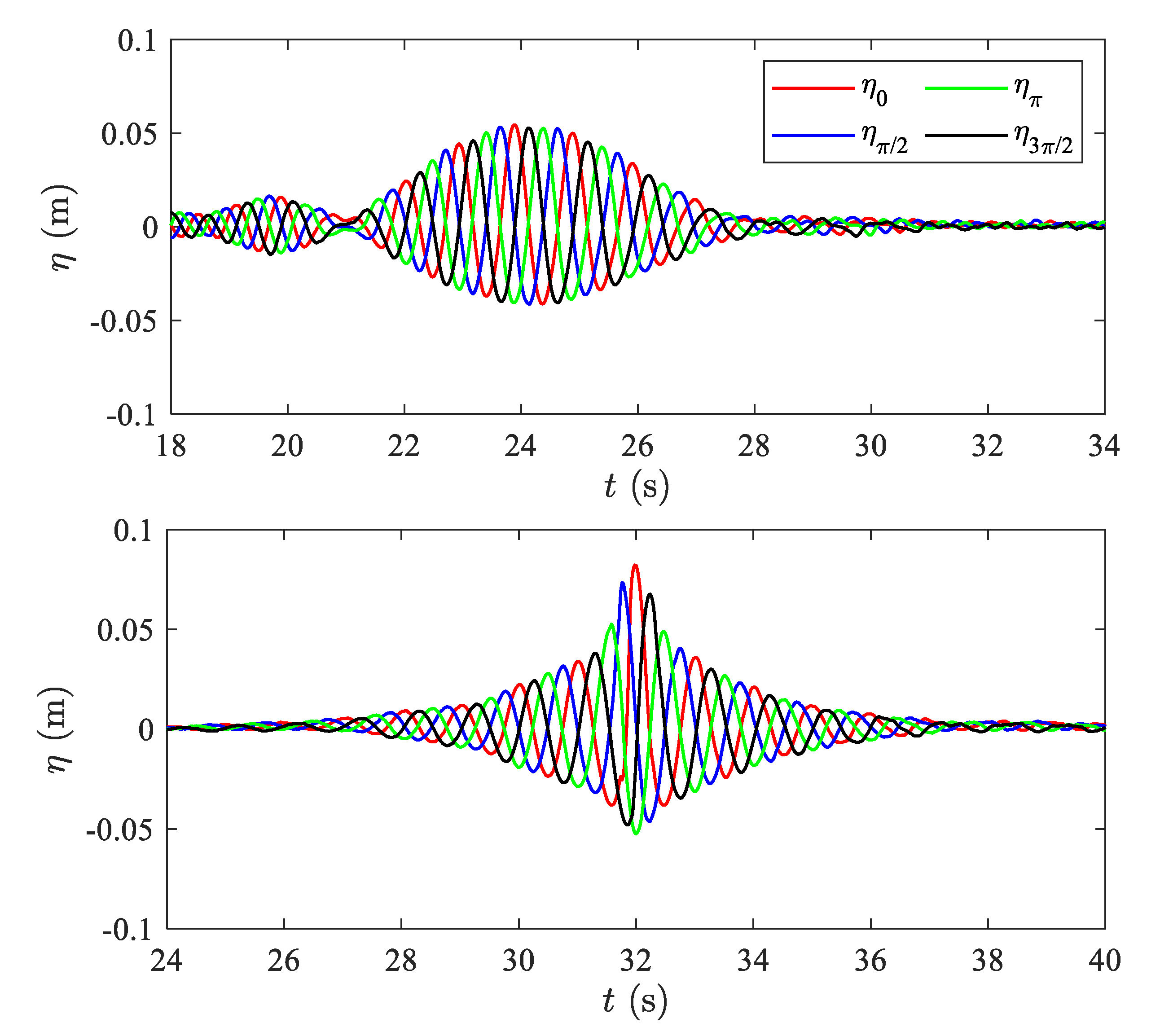
2.3. Four-Phase-Based Decomposition Method
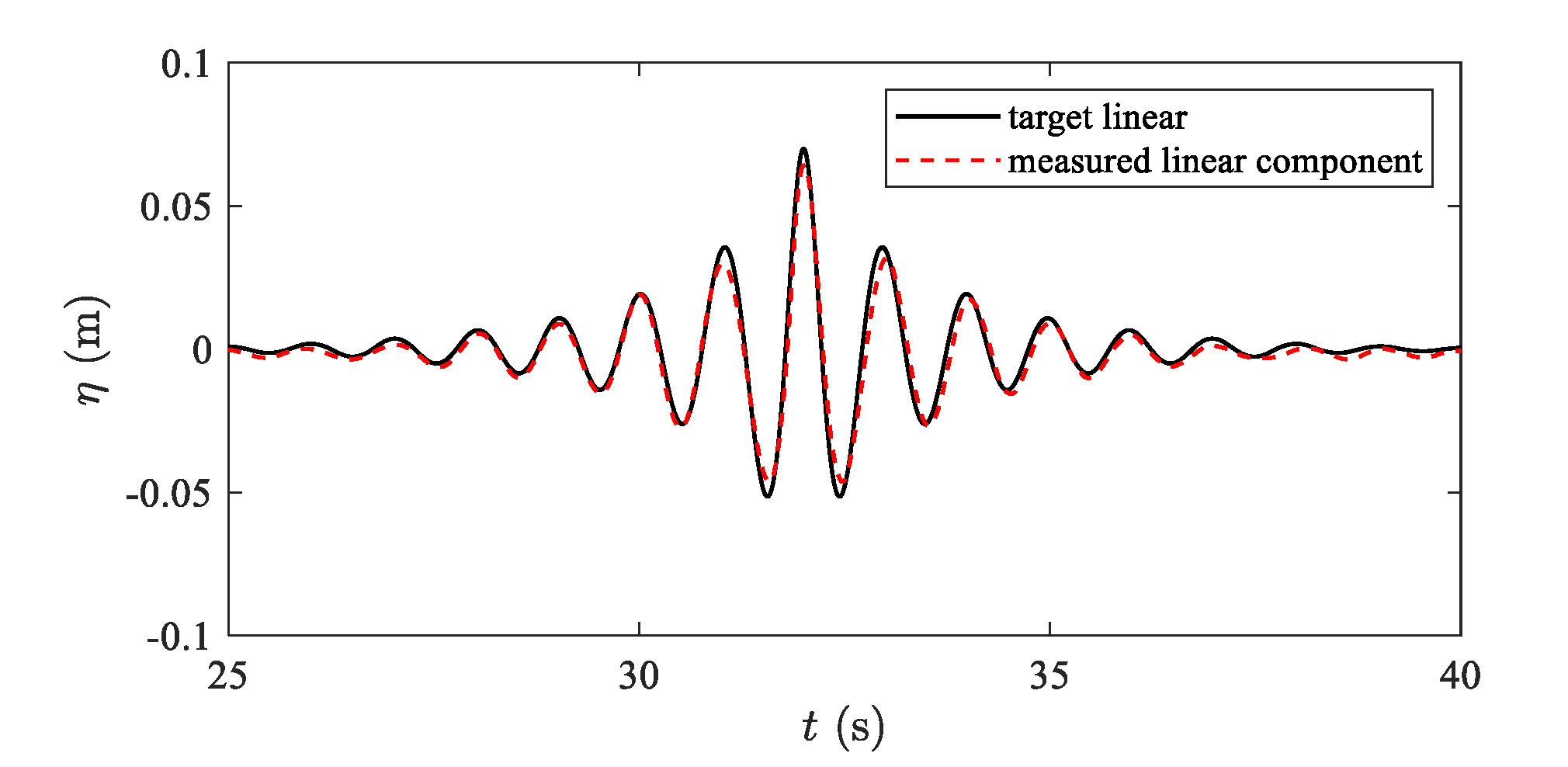
2.4. Iterative Correction for Generating Controlled and Accurate Focused Wave Group
2.5. Variability of the Surface Elevations and Forces
3. Higher-Order Wave Components Driving Nonlinear Loading on a Structure
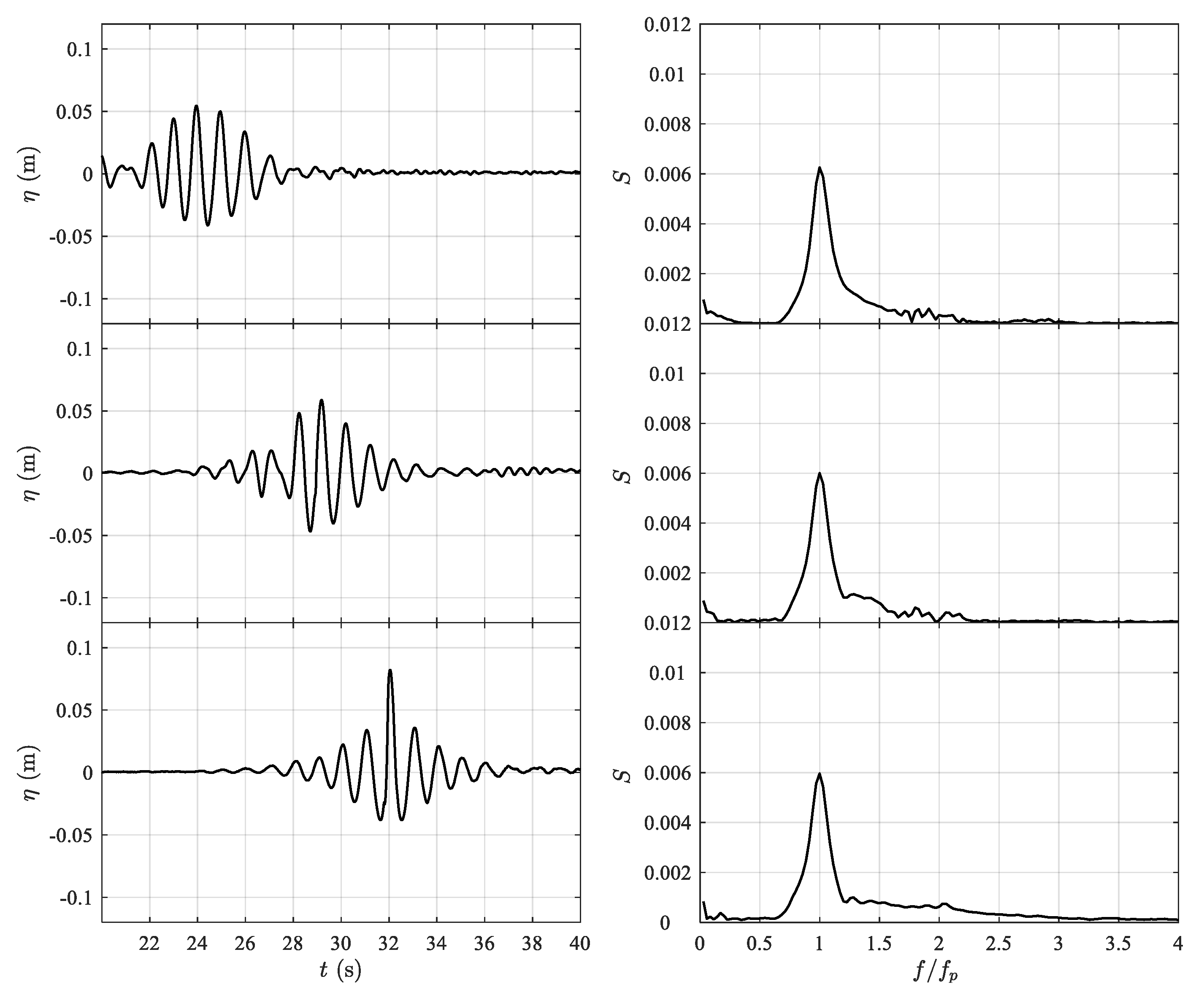
3.1. Nonlinear Wave Evolutions
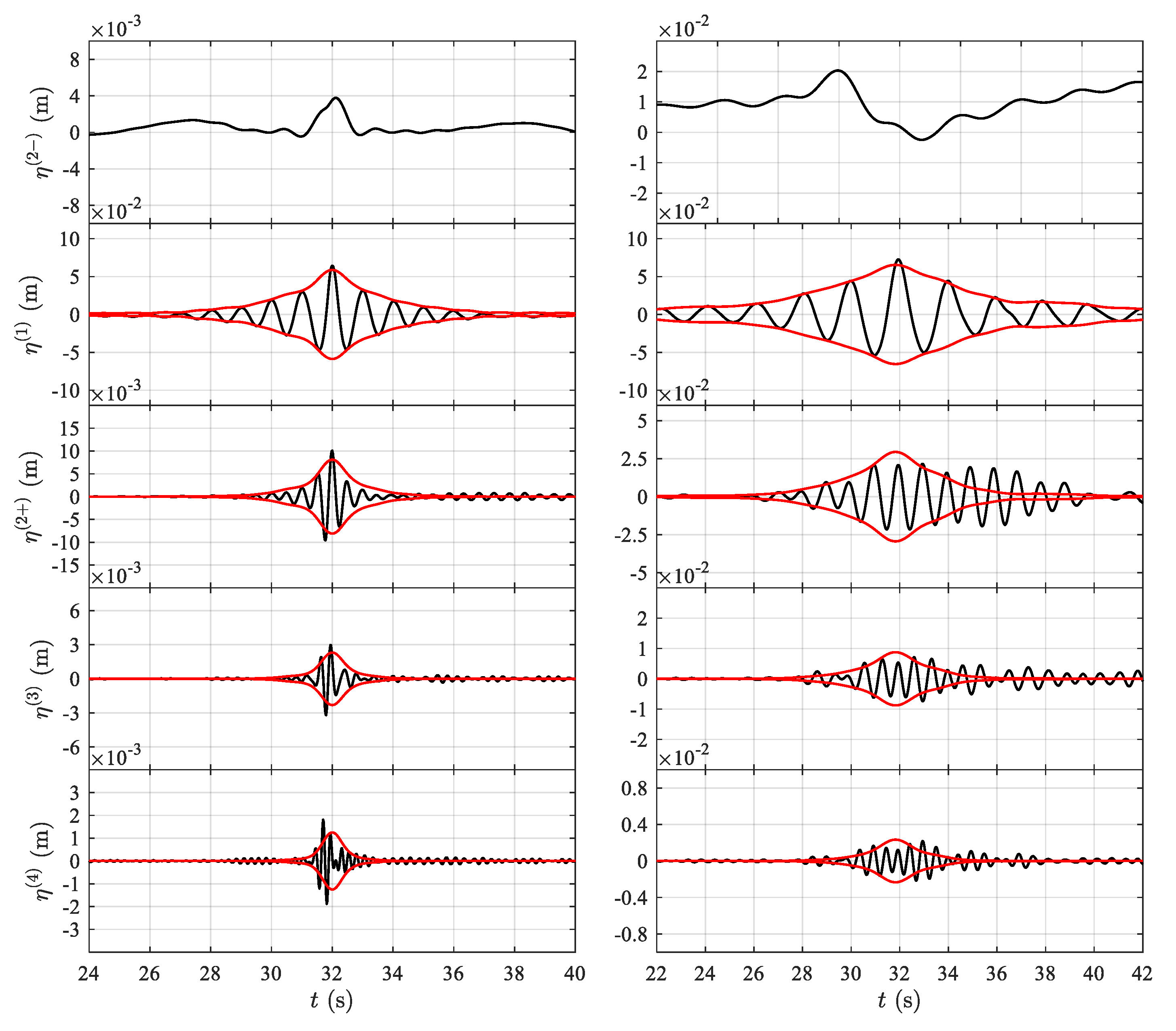
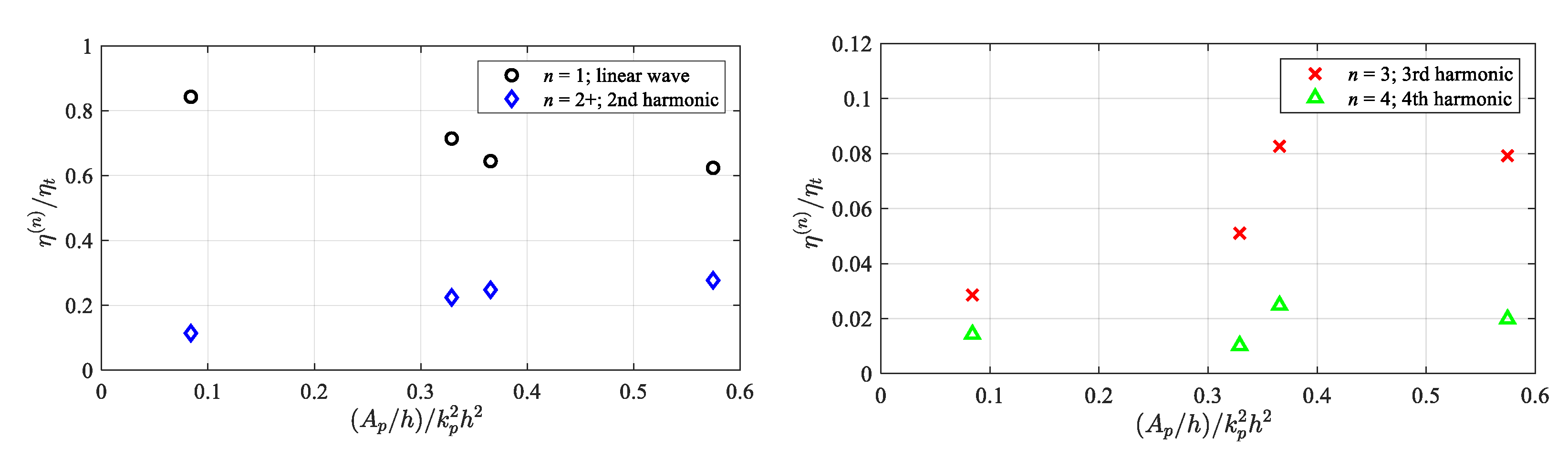
3.2. Harmonic Structure of Nonlinear Waves
4. Extreme Wave Loads on the Vertical Cylinder
4.1. Impact Force on a Vertical Truncated Cylinder
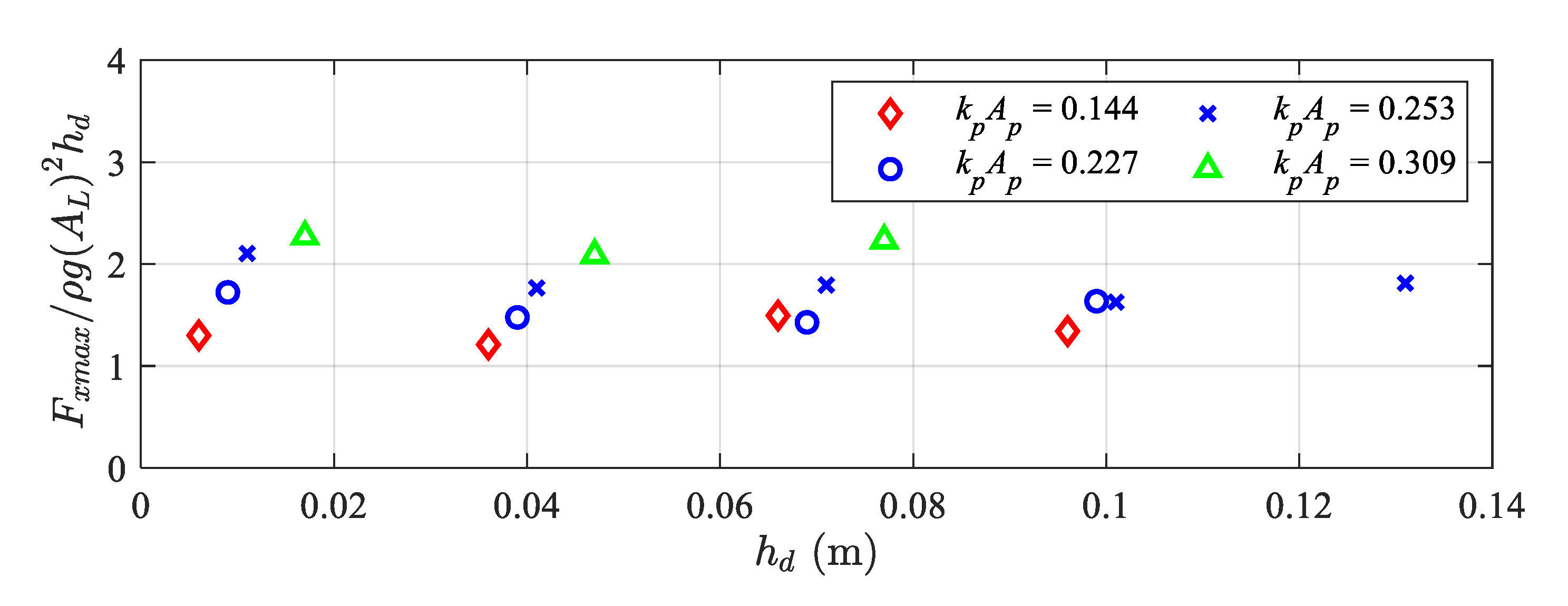
4.2. On the Scaling of Peak Horizontal Impact Forces
5. Conclusions
- The four-phase separation method is found to work well even for long shallow-water waves of strong nonlinearity. The extracted harmonic structure of the wave fields is still apparent, and the nth harmonic wave scales with the nth power of the envelope of the linear wave component.
- The four-phase separation method, in tandem with the iterative technique, works well for generating the desired focused wave groups even in the nearly shallow water regime. The known issue of downshifting in both spatial and temporal domains is resolved.
- The relative contribution from the fundamental wave decreases with the increasing Ursell number, while the contributions from the higher-order harmonics increase, and both arrive at their corresponding saturation levels at larger Ursell numbers. The Ursell number indicates the wave nonlinearity in the long-wave regime, i.e., weighting the respective importance of the nonlinear and shallow-water effects.
- Both horizontal and vertical impact forces are found to increase with the increasing inundation level, while the effect from the wave steepness is relatively small. The Santo scaling, i.e., ρg(AL)2hd, is introduced for non-dimensionalizing the peak horizontal force, which works very well. A reasonably good collapse in data is observed, indicating that the ‘destruction of momentum’ argument may still be applicable to structures with curved surfaces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbr. | Abbreviation(s) |
| TLP | Tension-leg platform |
| GBS | Gravity-based structure |
| CFD | Computational fluid dynamics |
| MOERI | Maritime and Ocean Engineering Research Institute |
| WG | Wave gauge |
| Ur | Ursell number |
| JONSWAP | The Joint North Sea Wave Observation Project |
| FFT | Fast Fourier transform |
| RMSE | Root-mean-square error |
References
- Wienke, J.; Oumeraci, H. Breaking wave impact force on a vertical and inclined slender pile—Theoretical and large-scale model investigations. Coast. Eng. 2005, 52, 435–462. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Newman, J.N.; Vinje, T. Nonlinear wave loads on a slender vertical cylinder. J. Fluid Mech. 1995, 289, 179–198. [Google Scholar] [CrossRef]
- Malenica, Š.; Molin, B. Third-harmonic wave diffraction by a vertical cylinder. J. Fluid Mech. 1995, 302, 203–229. [Google Scholar] [CrossRef]
- Grue, J.; Bjørshol, G.; Strand, Ø. Higher Harmonic Wave Exciting Forces on a Vertical Cylinder; Institute of Mathematics, University of Oslo Preprint: Oslo, Norway, 1993; Volume 2, ISBN 82-553-0862-8. [Google Scholar]
- Chaplin, J.R.; Rainey, R.C.T.; Yemm, R.W. Ringing of a vertical cylinder in waves. J. Fluid Mech. 1997, 350, 119–147. [Google Scholar] [CrossRef]
- Grue, J.; Huseby, M. Higher-harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 2002, 24, 203–214. [Google Scholar] [CrossRef]
- Paulsen, B.T.; Bredmose, H.; Bingham, H.B.; Jacobsen, N.G. Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 2014, 755, 1–34. [Google Scholar] [CrossRef]
- Taylor, R.E.; Chau, F.P. Wave Diffraction Theory—Some Developments in Linear and Nonlinear Theory. J. Offshore Mech. Arct. Eng. 1992, 114, 185–194. [Google Scholar] [CrossRef]
- Lee, C.H.; Newman, J.N. Computation of wave effects using the panel method. In Numerical Models in Fluid–Structure Interaction; WIT Press: Southampton, UK, 2005; pp. 211–251. [Google Scholar]
- Yang, C.; Ertekin, R.C. Numerical simulation of nonlinear wave diffraction by avertical cylinder. Trans. ASME J. Offshore Mech. Arct. Eng. 1992, 114, 36–44. [Google Scholar] [CrossRef]
- Bai, W.; Eatock Taylor, R. Numerical simulation of fully nonlinear regular and focused wave diffraction around a vertical cylinder using domain decomposition. Appl. Ocean Res. 2007, 29, 55–71. [Google Scholar] [CrossRef]
- Chen, L.F.; Zang, J.; Taylor, P.H.; Stagonas, D.; Buldakov, E.; Simons, R. Numerical investigation of unsteady hydrodynamic loads on a vertical cylinder in waves and sheared currents. In Proceedings of the 31st International Workshop on Water Waves and Floating Bodies, Ann Arbor, MI, USA, 3–6 April 2016. [Google Scholar]
- Jian, W.; Cao, D.; Lo, E.Y.; Huang, Z.; Chen, X.; Cheng, Z.; Gu, H.; Li, B. Wave runup on a surging vertical cylinder in regular waves. Appl. Ocean. Res. 2017, 63, 229–241. [Google Scholar] [CrossRef]
- Chen, L.F.; Zang, J.; Taylor, P.H.; Sun, L.; Morgan, G.C.J.; Grice, J.; Orszaghova, J.; Ruiz, M.T. An experimental decomposition of nonlinear forces on a surface-piercing column: Stokes-type expansions of the force harmonics. J. Fluid Mech. 2018, 848, 42–77. [Google Scholar] [CrossRef] [Green Version]
- Kamath, A.; Chella, M.A.; Bihs, H.; Arntsen, Q.A. Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Eng. 2016, 128, 105–115. [Google Scholar] [CrossRef]
- Qu, S.; Liu, S.; Ong, M.C. An evaluation of different RANS turbulence models for simulating breaking waves past a vertical cylinder. Ocean Eng. 2021, 234, 109195. [Google Scholar] [CrossRef]
- Ghadirian, A.; Bredmose, H. Pressure impulse theory for a slamming wave on a vertical circular cylinder. J. Fluid Mech. 2019, 867, R1. [Google Scholar] [CrossRef]
- Cooker, M.J.; Peregrine, H. Pressure-impulse theory for liquid impact problems. J. Fluid Mech. 1995, 297, 193–214. [Google Scholar] [CrossRef]
- Wood, D.J.; Peregrine, D.H. Two and three-dimensional pressure-impulse models of wave impact on structures. Coast. Eng. 1998, 1, 1502–1515. [Google Scholar]
- Korobkin, A. Non-classical boundary conditions in water-impact problems. In IUTAM Symposium on Fluid–Structure Interaction in Ocean Engineering, Proceedings of the IUTAM Symposium, Hamburg, Germany, 23–26 July 2007; Springer: Berlin/Heidelberg, Germany, 2008; pp. 167–178. [Google Scholar]
- Cooker, M.J. A theory for the impact of a wave breaking onto a permeable barrier with jet generation. J. Eng. Maths 2013, 79, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Santo, H.; Taylor, P.H.; Dai, S.S.; Day, A.H.; Chan, E.S. Wave-in-deck experiments with focused waves into a solid deck. J. Fluids Struct. 2020, 98, 103139. [Google Scholar] [CrossRef]
- Tromans, P.S.; Anatruk, A.; Hagemeijer, P. New model for the kinematics of large ocean waves application as a design wave. In Proceedings of the First International Offshore and Polar Engineering Conference, Edinburgh, UK, 11 August 1991; pp. 64–71. [Google Scholar]
- Fitzgerald, C.; Taylor, P.H.; Eatock Taylor, R.; Grice, J.; Zang, J. Phase manipulation the harmonic components of ringing forces on a surface-piercing column. Proc. R. Soc. A 2014, 470, 20130847. [Google Scholar] [CrossRef]
- Chen, L.F.; Taylor, P.H.; Ning, D.Z.; Cong, P.W.; Wolgamot, H.; Draper, S.; Cheng, L. Extreme runup events around a ship-shaped floating production, storage and offloading vessel in transient wave groups. J. Fluid Mech. 2021, 911, A40. [Google Scholar] [CrossRef]
- Taylor, P.H.; Williams, B.A. Wave statistics for intermediate depth water: New waves symmetry. J. Offshore Mech. Arct. Eng. 2004, 126, 54–59. [Google Scholar] [CrossRef]
- Christou, M.; Ewans, K. Field measurements of rogue water waves. J. Phys. Oceanogr. 2014, 44, 2317–2335. [Google Scholar] [CrossRef]
- Santo, H.; Taylor, P.H.; Day, A.H.; Nixon, E.; Choo, Y.S. Current blockage and extreme forces on a jacket model in focused wave groups with current. J. Fluid Struct. 2018, 78, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Zang, J.; Chen, L.F.; Eatock Taylor, R.; Taylor, P.H. Regular waves onto a truncated circular column: A comparison of experiments and simulations. Appl. Ocean Res. 2016, 59, 650–662. [Google Scholar] [CrossRef] [Green Version]
- Ning, D.Z.; Zhao, X.L.; Teng, B.; Johanning, L. Wave diffraction from a truncated cylinder with an upper porous sidewall and an inner column. Ocean Eng. 2017, 130, 471–481. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, Y.; Liu, H. An experimental study of run-up and loads on a vertical truncated cylinder in a solitary wave. Ocean Eng. 2021, 219, 108346. [Google Scholar] [CrossRef]
- Ocean Engineering Committee. Final Report and Recommendations to the 27th ITTC; Ocean Engineering Committee: Copenhagen, Denmark, 2014. [Google Scholar]
- Chen, L.F.; Zang, J.; Hillis, A.J.; Morgan, G.C.J.; Plummer, A.R. Numerical investigation of wave-structure interaction using OpenFOAM. Ocean Eng. 2014, 88, 91–109. [Google Scholar] [CrossRef] [Green Version]
- Stansberg, C.T.; Baarholm, R.; Kristiansen, T.; Hansen, E.W.M.; Rortveit, G. Extreme wave amplification and impact loads on offshore structures. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2005; p. OTC-17487-MS. [Google Scholar]
- Baldock, T.; Swan, C.; Taylor, P.H. A Laboratory Study of Nonlinear Surface Waves on Water. Trans. Roy. Soc. A Math. Phys. Eng. Sci. 1996, 354, 649–676. [Google Scholar]
- Ning, D.Z.; Liang, C.; Chen, L.F.; Zhang, C.W. Numerical investigation on the propagation and evolution of focused waves over a sloping bed. Ocean Eng. 2022, 25, 111035. [Google Scholar] [CrossRef]
- Chen, L.F.; Stagonas, D.; Santo, H.; Buldakov, E.; Simons, R.R.; Taylor, P.H.; Zang, J. Numerical modelling of interactions of waves and sheared currents with a surface piercing vertical cylinder. Coast. Eng. 2019, 145, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Gurley, K.R.; Kareem, A. Numerical experiments in ringing of offshore systems under viscous loads. In Proceedings of the 14th International Conference on Offshore and Arctic Engineering, Florence, Italy, 16–20 June 1996; p. 484. [Google Scholar]
- Beji, S. Applications of Morison’s Equation to Circular Cylinders of Varying Cross-Sections and Truncated Forms. Ocean Eng. 2019, 187, 106156. [Google Scholar] [CrossRef]
- Stoker, J.J. Water Waves: The Mathematical Theory with Applications; Interscience Publ., Inc.: New York, NY, USA, 1957. [Google Scholar]






| Tp (s) | h (m) | kp (m−1) | Ap (m) | R (m) | kpR | kpAp | h/λp | Ur |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.35 | 4.41 | 0.07 | 0.0825 | 0.364 | 0.309 | 0.246 | 0.084 |
| 1.5 | 2.53 | 0.09 | 0.208 | 0.227 | 0.141 | 0.329 | ||
| 1.5 | 2.53 | 0.10 | 0.208 | 0.253 | 0.141 | 0.366 | ||
| 2 | 1.80 | 0.08 | 0.149 | 0.144 | 0.100 | 0.575 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Guo, X.; Yang, Y.; Lu, Y.; Chen, L. Extreme Wave Loading on a Vertical Circular Cylinder. Appl. Sci. 2023, 13, 8784. https://doi.org/10.3390/app13158784
Liu S, Guo X, Yang Y, Lu Y, Chen L. Extreme Wave Loading on a Vertical Circular Cylinder. Applied Sciences. 2023; 13(15):8784. https://doi.org/10.3390/app13158784
Chicago/Turabian StyleLiu, Shi, Xinran Guo, Yi Yang, Yatao Lu, and Lifen Chen. 2023. "Extreme Wave Loading on a Vertical Circular Cylinder" Applied Sciences 13, no. 15: 8784. https://doi.org/10.3390/app13158784




