Dynamics of Semiconductor Laser Coupled with Two External Cavities

Abstract

An investigation into the dynamic states and relative intensity noise of laser diodes subjected to double optical feedback has been conducted. We employed modified and improved time-delay rate equations to account for double external optical feedback. The dynamic states and noise of lasers will be investigated using bifurcation diagrams of the output photon number, its temporal variations, and the intensity noise of the laser. This analysis considers feedback strengths due to the double external cavity and their spacing from the front facet of the laser with and without phase due to feedback. The results reveal that considering phase causes significant variations in laser intensity and a phase shift in the temporal variations of the laser output. This results in relative intensity noise suppression and a frequency shift in the intensity noise spectrum. These findings represent new contributions to our understanding of the reliance of lasing frequency shift on the phase due to feedback, regardless of whether feedback originates from a single or double external cavity. We investigated the optimal conditions corresponding to stable dynamic states of the laser with the lowest noise level. Additionally, we identified conditions that result in chaotic dynamics, where the spectrum does not convey information about the laser system. These insights have potential applications in chaotic and secure optical data encryption.

1. Introduction

Laser diodes, known as LDs, offer numerous advantages when compared to other types of lasers [1]. These benefits include their compact size, cost-effectiveness, and the ability to control their output by adjusting the injected current. As a result, LDs play a crucial role as light sources in various aspects, such as fiber-optic communications and data processing.

However, a common challenge faced by many applications is experiencing external optical feedback (OFB) [2]. This feedback occurs when laser radiation reflects off an external reflector and re-enters the laser cavity. Understanding the impact of OFB is crucial, as it can significantly alter the laser’s behavior, leading to various modes of operation [3].

One notable consequence of OFB is the induction of chaotic dynamics, characterized by irregularities in the laser’s output and a loss of coherence [2]. This effect becomes particularly pronounced under conditions of moderate OFB and when the distance between the laser and reflector is extended, resulting in increased noise levels and reduced coherency.

Previous research mainly focused on LD behavior under a single OFB, which describes this phenomenon by introducing a term of time delay into the laser rate equation [4]. However, this model had limitations and was applicable only to situations with weak to moderate OFB. A theoretical model of time delay applicable over any strength of OFB, accounting for multiple round-trips and optical phases due to OFB, has been presented in Ref. [5], which was applied in investigating the dynamics and noise of pumping LDs used in fiber amplifier systems [5,6]. Moreover, the impacts of nonlinear gain, radiative and non-radiative lifetime, linewidth enhancement factor (LEF), and combined optical phase on the operation states and relative intensity noise (RIN) of 0.1550 μm InGaAsP/InP time-delayed LD have been studied [7,8,9].

To address more complex scenarios where LDs encounter external OFB from two reflectors, such as in fiber-optic communication systems, additional research is needed. This double OFB, typically a result of reflections on both facets of an optical fiber, has applications in encrypted systems of data, generating secured signals that do not reveal any data about the system itself [10]. Pal et al. investigated experimentally and theoretically the dynamics of the LD subjected to two filtered OFBs from two separate external cavities. They found that a second filtered OFB allows versatile manipulation of the LD frequency and provides an extra set of control parameters to get a stable laser [11].

In this paper, we extended a model in Ref. [5] based on the existing time-delay rate equation model from single OFB to encompass double OFB scenarios. This is completed using a traveling-wave approach to propagate the laser in the double cavities and their reflections between the laser front facet and the external reflectors [12]. After that, we propose a modified time delay term to describe double OFB and include it in the LD rate equation. This expansion represents a novel work in the investigations of OFB in LDs and their implementations in communication systems and other applications. LDs are, for instance, widely used in optical communication systems, including fiber-optic communication networks, where they serve as optical transmitters for data transmission. Another example is Optical Data Storage where LDs are used in devices such as CD and DVD players, as well as in Blu-ray technology, for reading and writing data on optical discs. The common issue for all these applications is the distortion of the signal as a result of OFB-induced signal distortion. OFB can, for instance, introduce timing errors and jitters in the laser output, which can lead to issues with data synchronization and the precise writing or reading of data on optical storage media. This can result in difficulty in accurately positioning the laser spot on the storage medium. Excessive OFB can cause data integrity problems. When writing data to optical storage media, any fluctuations in the laser power or position due to feedback can result in data being written incorrectly or with errors. Similarly, during data retrieval, the feedback-induced noise can lead to difficulty in accurately reading the stored data. In extreme cases, OFB-induced power fluctuations can lead to excessive heating of the media or optical components, potentially causing physical damage to the storage medium or laser diode.

In addition to the traveling wave approach, a numerical solution for the enhanced time-delay rate equation model by assigning arbitrary lengths to the external cavities will be introduced [13,14,15]. Using very fine time integration in combination with a long integration time interval of several microseconds will result in a stable solution. With the help of this solution, we will study the operational aspects, dynamic behavior, and noise characteristics of the semiconductor laser further. This exploration will involve categorizing these features based on the bifurcation diagram (BD) of the output power of the LD and the RIN power spectrum in the laser signal [16]. The dynamics of the laser under double OFB are characterized using various tools, including the time variations of the emitted photons and RIN. Our investigation will span various values of external OFB strengths originating from double external cavities, along with variations in their distance from the laser’s facet.

We aim to identify the optimal conditions that result in stable laser operation with low noise for use in optical fiber communications. Additionally, we will identify the conditions that lead to chaotic dynamics, where the RIN spectrum does not reveal information about the laser system. This chaotic behavior holds potential significance in the realm of secure optical data encryption. Another application of our research is to better understand certain feedback processes and the resulting feedback noise, as these are the main limitations of Fiber-To-The-Home (FTTH) systems—for instance, to propose noise reduction solutions without the need for expensive optical isolators [17]. Using feedback control can involve adjusting the laser parameters or using them to minimize the impact of the feedback on system performance. In addition, optical attenuators can reduce the power of the feedback signal, which can help in reducing its impact on the laser, and the application of anti-reflective coatings to optical components can reduce the amount of reflection within the optical system, thereby minimizing the potential for feedback. The results of this work have a high impact on researching these topics further.

Our improved model of double OFB can be used with LDs operating in single and multi-longitudinal modes, including various types of LDs. We categorize the laser’s behavior based on output power and RIN power spectrum, considering two distinct external cavity lengths and optical phase due to OFB [18].

We present an investigation of the dynamic states and RIN of LDs subject to double OFB. We used modified and improved time delay rate equations for the LDs to consider double external OFB [12]. The dynamic states and noise of the LDs will be determined using the output photon number BD, its temporal variations, and the RIN of the LD with OFB strengths from the double OFB, as well as their spacing from the laser facet and with and without optical phase due to OFB. The LD dynamics are studied within two regions: short and long double external cavities. The simulated results show that the single OFB LD changes its state from continuous wave (CW) to periodic oscillation (PO), period doubling (PD), coherence collapse, and chaotic operation. In a short double external cavity region, LD draws from each of the operations with the single OFB to a route-to-CW state. This route-to-CW state is a reflection of the identical route-from-chaos to the identical operation with a single OFB. In a long double OFB regime, increased double OFB strength takes the LD to a route-to-chaos. In comparison with a single OFB case, the double OFB external cavity produces smoother, more chaotic RIN power spectra, which have no specific relationship with the resonance frequencies of the external cavities. Considering optical phase due to OFB in single OFB and double OFB cavities causes significant intensity suppression and phase shift in the temporal photon output of the LD changes. This intensity suppression and phase shift induce RIN suppression and a frequency shift in the RIN spectrum. This dependence of the lasing frequency shift on the optical phase due to OFB is noticed for the first time in this article. RIN suppression is close to the solitary laser noise level when LD operates in the regimes of CW and PO. Double OFB and optical phase due to OFB lead the LD dynamic states to get better, i.e., the dynamic states change to a better state such as CW or PO.

This paper proceeds with an explanation of LD operation states and dynamics with double OFB, outlines numerical calculation procedures, presents simulations with short and long double OFB, and concludes with key findings.

2. Time-Delay Model of Two-Reflector OFB

A model of the rate equation, which includes multiple round-trips in the external cavity and optical phase due to OFB, has been established [5]. The model is extended to study the theoretically dynamic states of the LDs subject to double external OFB [12]. An improved rate equation of LD with double OFB from two external cavities for photon numbers, phase, and carrier numbers is formulated as follows:

$$\frac{dS}{dt}=\frac{1}{2}\left[G-G_{th}\right] S+\frac{a\xi }{V}N+F_S$$

(1)

$$\frac{d\theta }{dt}=\frac{1}{2}\alpha \frac{a\xi }{V}\left(N-\overline{N}\right)-\frac{c}{n_D{L}_D}\varphi +F_{\theta }$$

(2)

$$\frac{dN}{dt}=\frac{I}{e}-\frac{N}{{\tau }_s}-\frac{a\xi }{V}\left(N-N_g\right)S+F_N$$

(3)

$$G=\frac{a\xi }{V}\left(N-N_g\right)S-BS,$$

(4)

where G is the optical gain, a is the slope of the optical gain with the changes in carrier number N, ξ is the conferment factor, V is the active region volume, $\overline{N}$ is the N time-averaged value, α is the LEF, I is the injection current, τ_s is the electron lifetime due to spontaneous emission, and N_g is the carrier number at transparency. The universal constant e defines the electron charge, and B is the nonlinear gain coefficient, respectively [19,20,21]. The threshold gain is given using

$$G_{th}=G_{thD}-\frac{c}{n_D{L}_D}\ln \left|U\right|,$$

(5)

where G_thD is the threshold gain [21]:

$$G_{thD}=\frac{c}{n_D}\left[\kappa +\frac{1}{2L_D}\ln \frac{1}{R_f{R}_b}\right],$$

(6)

where k, L_D, R_f, and R_b are the internal loss, laser cavity length, and front and back facet reflectivity, respectively. The function U expressing the double OFB in the rate equations is given using [12]:

$$\begin{array}{ll}U=& 1-K_{ex1}\sqrt{\frac{S\left(t-{\tau }_1\right)}{S\left(t\right)}}{e}^{j\left[\theta \left(t-{\tau }_1\right)-\theta \left(t\right)-\omega {\tau }_1\right]}\\ & -K_{ex2}\sqrt{\frac{S\left(t-{\tau }_2\right)}{S\left(t\right)}}{e}^{j\left[\theta \left(t-{\tau }_2\right)-\theta \left(t\right)-j\omega {\tau }_2\right]}\end{array}$$

(7)

where ω is the angular frequency of the laser emission, [θ(t − τ₁) − θ(t)] and [θ(t − τ₂) − θ(t)] are the optical phase deviations due to chirping induced by delay in external cavity 1 and external cavity 2, respectively. K_ex1 and K_ex2 are the OFB strengths from the single external cavity and double external cavity, respectively, and are determined with the front facet reflectivity, first reflector reflectivity, and second reflector reflectivity, respectively [12]:

$$K_{ex1}=\left(1-R_f\right)\frac{\sqrt{R_{ex1}}}{\sqrt{R_f}}$$

(8)

$$K_{ex2}=\left(1-R_f\right)\left(1-R_{ex1}\right)\frac{\sqrt{R_{ex2}}}{\sqrt{R_f}}$$

(9)

Figure 1 illustrates a model scheme of semiconductor lasers subjected to double OFB. The laser emitted from the front travels a round-trip in the cavity between the front and first reflector, R_ex1. Then, a round-trip is made between the front facet and double reflector R_ex2, which then re-enters the laser cavity. That is, there are time delays τ₁ and τ₂ between the laser reflected by the front of the laser facet into the cavity of the laser and the laser entered back from single and double reflectors, respectively [12]. By supposing L_ex1 and L_ex2 to be the lengths of the single and double external cavities, respectively, and the external cavity refractive index n_ex, the feedback laser has time delays of

$${\tau }_1=\frac{2n_{ex1}{L}_{ex1}}{c}, \mathrm{and} {\tau }_2=\frac{2n_{ex}{L}_{ex2}}{c}$$

(10)

The Langevin noise sources F_S(t), F_N(t), and F_θ(t), are Gaussian probability distributions with their correlation functions, $〈F_x(t) F_y(t\prime )〉=V_{xy} \delta (t-t\prime )$, x, y = S, N or θ, and have zero mean values, $〈F_S(t)〉=〈F_N(t)〉=〈F_{\theta }(t)〉=0$. Where $\delta (t-t\prime )$ is Dirac’s δ function and V_xy is the correlation variance [22,23,24,25,26]. Adding noise sources to the rate equations induces fluctuations on the photon and carrier numbers due to spontaneous emission.

3. Numerical Calculations

The LD dynamics with double OFB are studied numerically by integrating the rate Equations (1)–(3) using the fourth-order Runge Kutta method [27]. AlGaAs LD emitting at a wavelength of 0.780 μm parameters was used in the calculations, where the numerical values of this LD are given in Ref. [12]. The corresponding threshold current I_thD = 22.5 mA, and the threshold gain G_thD = 2.82 × 10¹¹ s⁻¹. In this article, a short external cavity has been used in the first external cavity L_ex1 = 3 cm, whereas two lengths are considered to be the second external cavity of L_ex2 = 3.5 × 10⁻² m (the short cavity) and 10⁻¹ m (approaches to the long cavity). The refractive index of these external cavities is filled with air (n_ex = 1.0). The resonance frequency separations of the external cavities are $f_{ex1}=1.0/{\tau }_1=5 \mathrm{GHz}$ and $f_{ex2}=1.0/{\tau }_2=4.286 \mathrm{GHz}$. The states are investigated in terms of the strength of the OFB coefficients (intensity) K_ex1 and K_ex2. The integration time step was selected as 5 ps and was used over a period of 5 μs, for which the operation reached a steady state. The phase φ of the OFB is given using

$$\varphi ={\tan }^{-1}\frac{\mathrm{Im}U}{\mathrm{Re}U}+p\pi$$

(11)

where p is an integer and is changed continuously for time evolution since the solution of the arc tangent is defined in the range of –π/2.0 to +π/2.0 in the simulation.

The values $\overline{S}$ and $\overline{N}$ of the photon and carrier number are specified from the steady-state solutions of the rate equation of the solitary laser [12]:

$$\overline{S}=\frac{I-I_{thD}}{e{G}_{thD}}$$

(12)

$$\overline{N}=\frac{N_{thD}+\frac{V}{a\xi }B\overline{S}}{\overline{S}+1}$$

(13)

where N_thD is the threshold carrier number.

The spectra of the RIN are then calculated from the output photon number fluctuations δS(t) = S(t) − $\overline{S}$, obtained instantaneously using fast Fourier transform [28,29]:

$$RIN=\frac{1}{{\overline{S}}^2}\left\{\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}\delta S(t)\delta S(t+\tau )e^{j\omega \tau }d\tau }\right]dt}\right\}=\frac{1}{{\overline{S}}^2}\left\{\frac{1}{T}{\left|{\displaystyle \underset{0}{\overset{T}{\int }}\delta S(\tau )e^{-j\omega \tau }d\tau }\right|}^2\right\}$$

(14)

where $\overline{S}$ is the dc-value of the photon number S(t), which is timely averaged and also numerically calculated. The RIN simulations were carried out as the steady state reached to t ≈ 3~5 μs.

4. Numerical Simulation Results and Discussions

We will start by showing the dynamic states of the laser induced with a single external cavity. The double OFB impacts on the LD dynamic states are then demonstrated by adding a second reflector to the external cavity. This is conducted by investigating the changes happening in each dynamical state produced with the single external cavity.

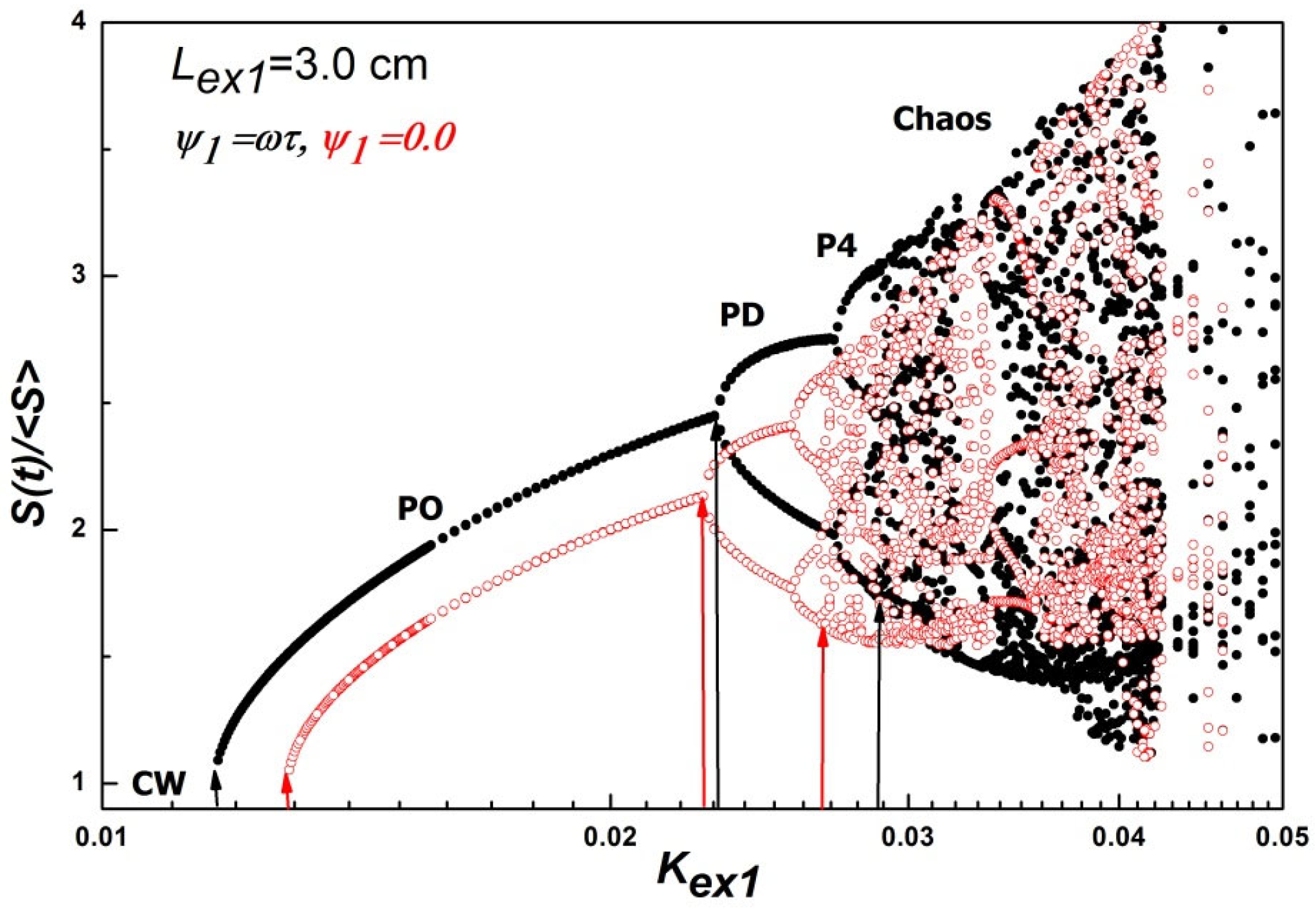
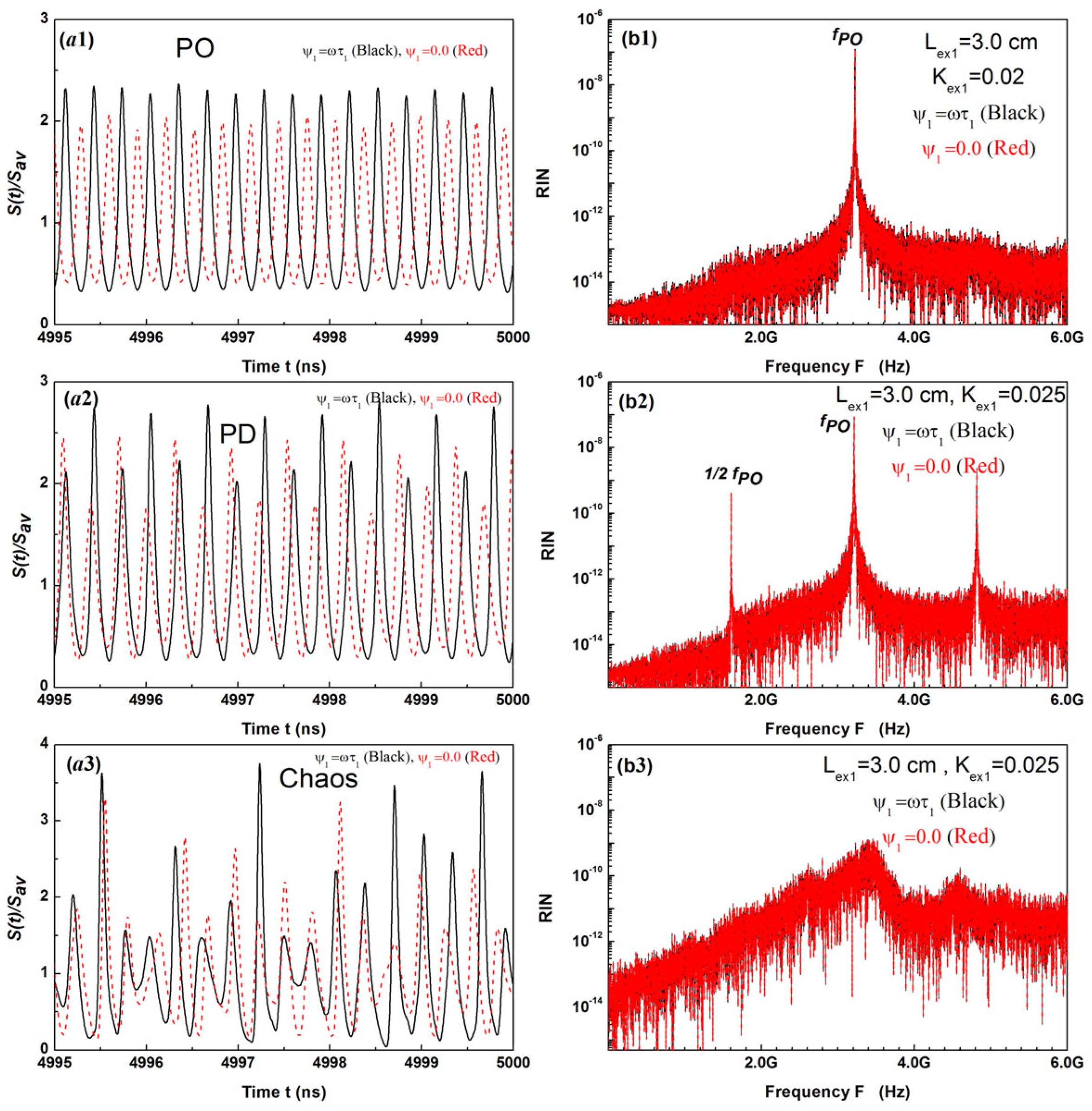
4.1. Laser Dynamic States under Single External Cavity

LD dynamic states induced via the single external cavity at two values of optical phase ψ₁ = 0.0 (red color) and ωτ₁ (black color) are shown in Figure 2. The dynamic states are calculated with BD of the photon number S(t), peak value, with the OFB strength K_ex1. Abdulrhmann et al. investigated the influence of including the noise sources in the rate equations on the amplitude of pulsation and found that it is larger when counting the noise sources in the rate equations [6]. Since including the noise sources in the rate equations has a very little variation on the dynamic states induced via OFB, especially in the transition border to another state [6]. Langevin noise sources are omitted from the rate Equations (1)–(3) in the calculations of the BDs to get a clear vision of the dynamic states of the laser. The LD continues oscillating with the CW state for sufficiently small values of OFB strength K_ex1, which is represented by no points in the figure. When K_ex1 goes beyond the HB point (pointed by the first arrow) of K_ex1 = 0.0129 and 0.0117 in the case of optical phase ψ₁ = 0.0 and ωτ₁, respectively, the LD dynamic state is identified with PO output for relaxation oscillations undamped. This PO is of the one-period kind with frequency increases with an increase in K_ex1. The POs continue up to K_ex1 = 0.0227 and 0.0231, with optical phases ψ₁ = 0.0 and ωτ₁, respectively. Beyond the PO regime, the bifurcation diagram shows two branches indicating the appearance of oscillations with period doubling (PD) (pointed by the second arrow). When K_ex1 > 0.027 and 0.029 and optical phase ψ₁ = 0.0 and ωτ₁, respectively, the PD oscillation bifurcates more and shows many random points and tours, which represents a chaotic dynamic state (pointed by the third arrow). The shown PD route-to-chaos recognizes the LD with a short external cavity of f_ex/f_r > 1.0, as shown in Ref. [30]. By reducing the optical phase ψ₁ to zero the strength of the LD is decreased, and the dynamic states are shifted toward increasing the OFB intensity K_ex1 up to the PO region, which leads to more stability, as shown in Ref. [10]. However, after the PO region, the dynamical regimes such as PD and chaos start to appear at lower values of K_ex1. As shown in the figure, reducing the optical phase ψ₁ from ωτ₁ to 0.0 has no effect on the route-to-chaos, which keeps the PD route-to-chaos.

In the regime when OFB K_ex1 = 0.042–0.05, the laser starts to be attracted to a less chaotic or coherence collapse region, and this is due to entering the laser with a strong OFB, which induces stability in the dynamic states of the laser [5,6].

Examples of the different dynamic states of the single external cavity laser shown in Figure 2 are characterized in Figure 3, when optical phase ψ₁ = 0.0 and ψ₁ = ωτ₁; namely, the PO, PD, and chaos at OFB strength K_ex1 = 0.02, 0.025, and 0.04, respectively. Figure 3 plots the photon numbers S(t)/S_AV time variations and the corresponding RIN power spectrum, which is calculated using the fast Fourier transform of S(t) using Equation (14). The intensity of S(t)/S_av is decreased, and the phase is shifted by decreasing the optical phase ψ₁ from ωτ₁ to zero in all laser states, as shown in Figure 3(a1–a3). The effect of varying optical phase ψ₁ due to OFB on the laser fluctuations has been noticed in Refs. [9,11,31] and confirmed experimentally in Ref [11,31]. The reduction in the intensity of S(t)/S_av is shown in Figure 3b as a little reduction of RIN. As found in Figure 3(b1), RIN shows a sharp peak at PO frequency f_PO = 3.221 GHz and its higher harmonic peaks, which represent uniform periodic oscillations with the relaxation frequency ~ f_r = 3.22 GHz. The RIN power spectrum in the PD dynamic state is distinguished by two sharp peaks at PD frequency f_PD = 3.2 GHz and its half harmonic, as shown in Figure 3(b2). An unequal time type of S(t) variations represents the chaotic operation as displayed in Figure 3(b3). These inequalities in the output of the LD are created due to operating the LD unstably with two conditions: one of them identifies the LD with a frequency of f_Laser = 3.4 GHz and the other to the compound cavity with a frequency of f_Comb = 4.6 GHz [9].

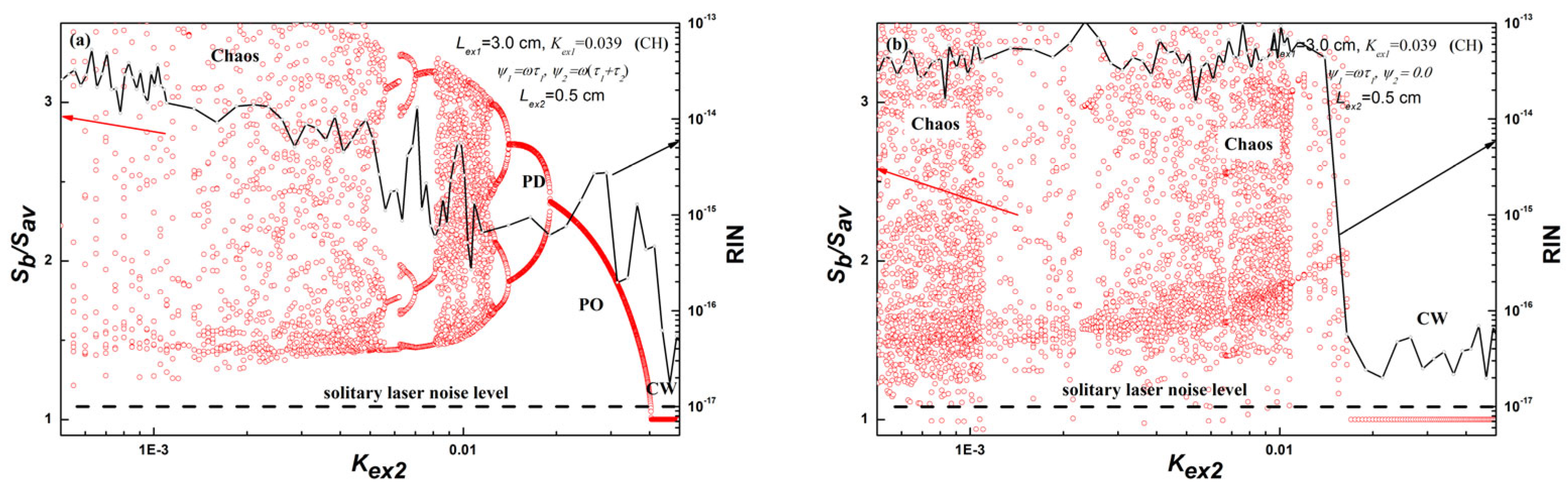
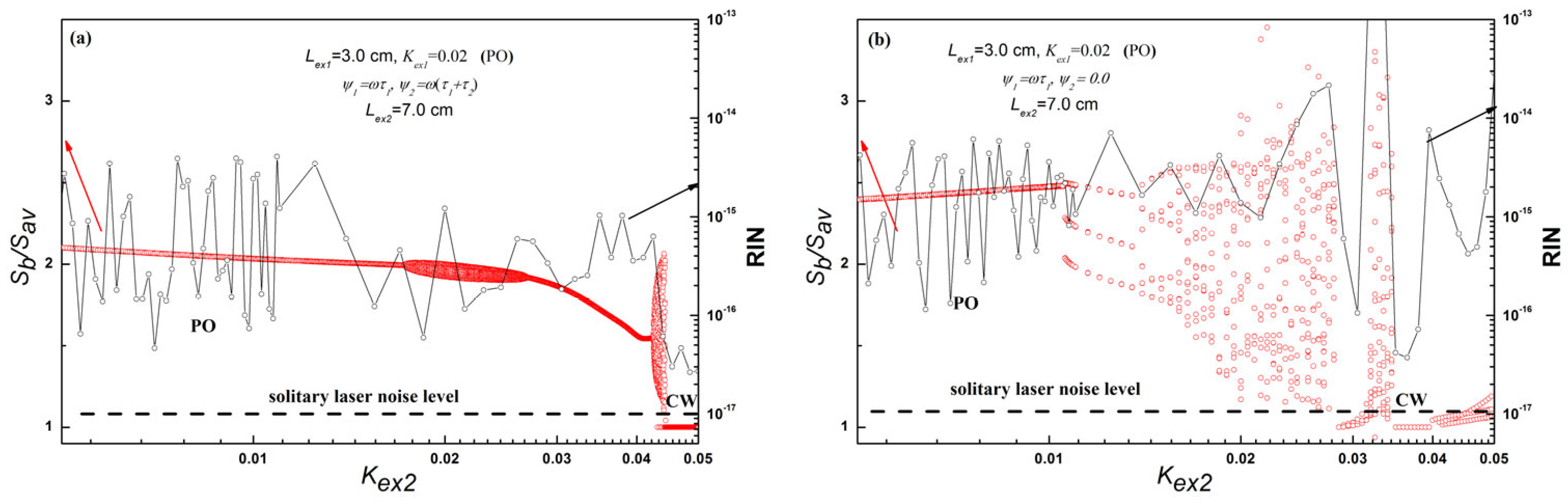
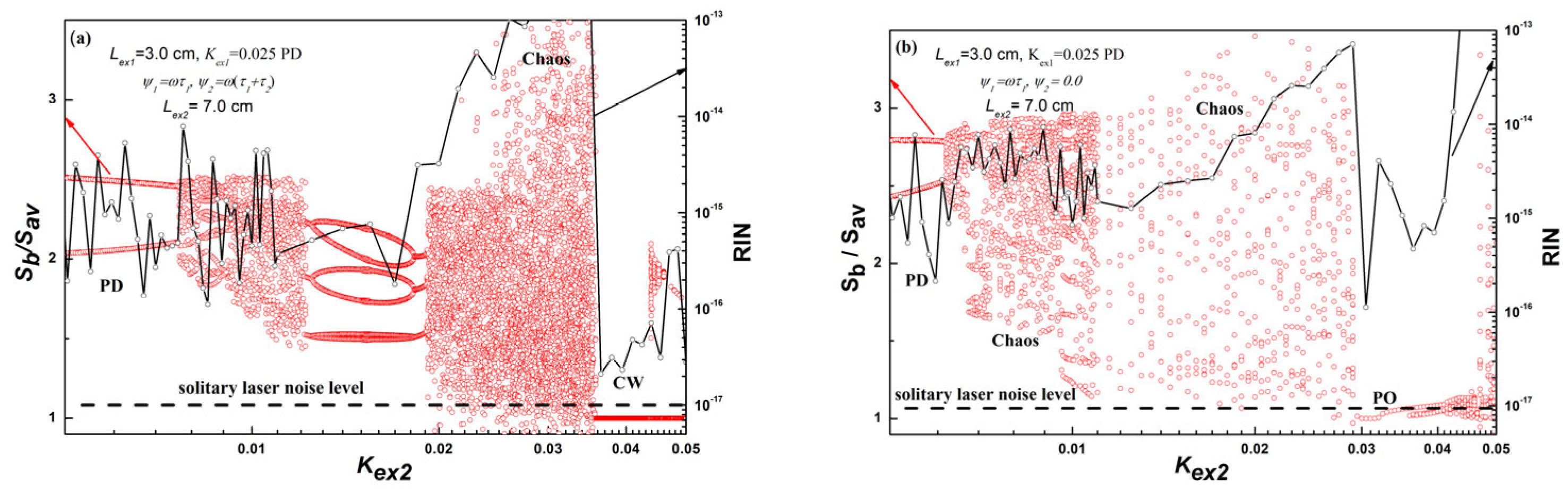
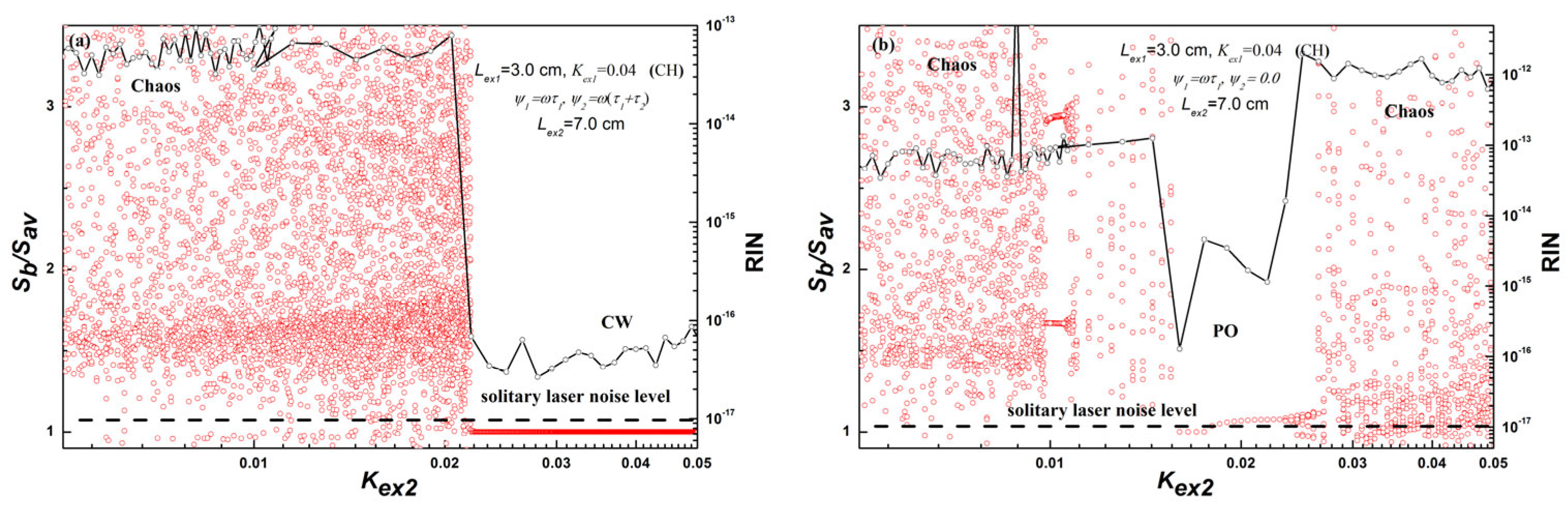
4.2. Laser Dynamic States under Double External Cavity

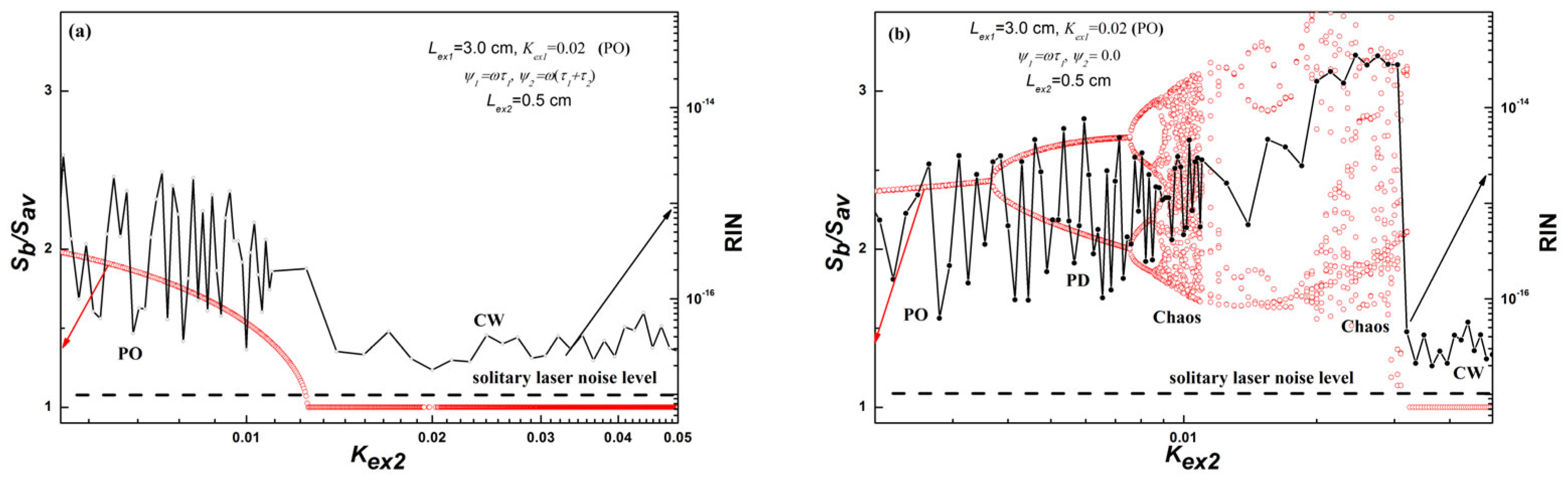
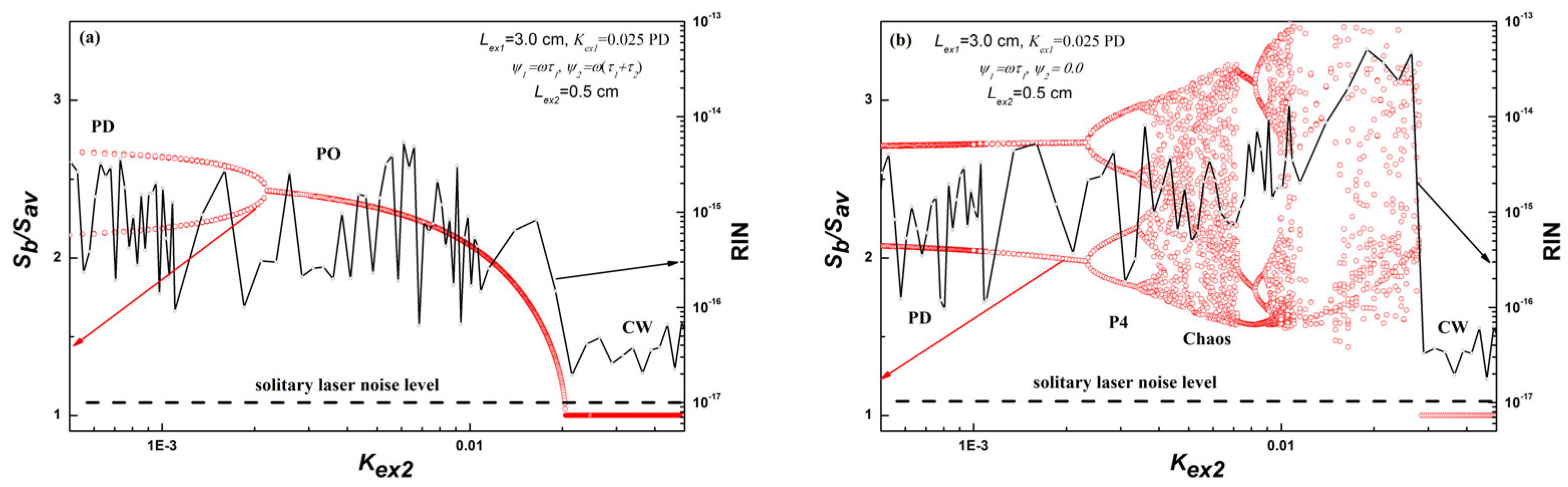
4.2.1. Region of Short Double OFB (L_ex2 = 3.5 × 10⁻² m)

To investigate the impact of the double external cavity on the dynamic states and RIN of the laser, bifurcation diagrams are used. We will start by assuming that the distance between the first and second reflectors is 5 × 10⁻³ m, making the cavity of the double OFB in the short cavity region (L_ex2 = 3.5 × 10⁻² m). Dynamic states of lasers with short external cavities are highly influenced by the number of round-trips in short external cavities [32]. In this paper, we consider the number of round-trips in our simulations. Figure 4a, Figure 5a and Figure 6a plot the bifurcation diagrams and the corresponding average Low-frequency RIN (f < 10 MHz) spectrum versus OFB intensity K_ex2 with optical phase ψ₂ = ω(τ₁ + τ₂) when the single OFB strength is set to dynamic states corresponding to PO, PD, and chaos states at single OFB strength K_ex1 = 0.02, 0.025, and 0.04, respectively.

The shown figures are characterized by three features at each dynamic state: (1) the laser dynamic state in the weak OFB region begins with the dynamic state of a single OFB and (2) increases in the strength of the double OFB K_ex2, leading the LD to a route-to-CW (more stable dynamics). Finally, (3) this route-to-CW is a reflector to the identical route-from-CW to a pertinent dynamic at this level of single OFB strength K_ex1 in the bifurcation diagrams of Figure 2 under a single external cavity.

When the optical phase ψ₂ = 0.0, the LD dynamic states in the presence of double OFB are shown in Figure 4b, Figure 5b and Figure 6b. Figures show that reducing the optical phase ψ₂ to 0.0 moves the laser dynamic state to unstable states and changes the route-to-CW when ψ₂ = ω(τ₁ + τ₂) to the route-to-chaos state at ψ₂ = 0.0. The width of the CW dynamic is wider as ψ₂ = ω(τ₁ + τ₂) than that as ψ₂ = 0.0, as shown in Figure 4. Figure 5 shows the same scenario but in the PD state, where, by increasing the double OFB strength K_ex2, the dynamic states transfer from the PD state to tour and chaotic states, which is the route to the chaos state. Figure 6 shows the dynamic states of the double external cavity at (K_ex1 = 0.04, chaos), the chaos state is directly the route to the CW dynamic state, and the CW state width is wider as ψ₂ = 0.0 than that as ψ₂ = ω(τ₁ + τ₂).

In the same Figure 4, Figure 5 and Figure 6 and on the right Y-axis, the average RIN at Low-frequency (f < 10 MHz) versus the double cavity OFB intensity K_ex2 corresponds to the BDs shown. Figure 4a shows the Low-frequency RIN in the PO regime; as shown in the figure, it is almost in the range of 10⁻¹⁵ to 10⁻¹⁴ and decreases to approach a solitary laser noise level (dashed line) with increasing the double OFB strength K_ex2. As ψ₂ = 0.0, Figure 4b displays RIN enhancement when dynamic states transfer from PO, PD, and chaos regimes till reaching the CW state. The level of the RIN is reduced near the level of solitary laser noise. Figure 5b and Figure 6a,b show the highest level of the RIN, which occurs almost in the chaos regime. We notice that by reducing the optical phase ψ₂ to 0.0, the RIN displays a lower level than that as of ψ₂ = ω(τ₁ + τ₂) in the CW, PO, and PD regimes.

As shown in the figures, when the optical phases ψ₁ = ωτ₁, and ψ₂ = ω(τ₁ + τ₂), the dynamic of the LD is more stable than that as ψ₁ = ωτ₁, and ψ₂ = 0.0, and the RIN suppresses to a level near the solitary laser noise, especially when the laser operates in the CW or PO regime. Figures show that the double external cavity leads to stabilizing the irregular states produced by the single external cavity and keeps the stable CW state, which reduces the RIN to lower levels near solitary laser noise level. That leads to improvements in the properties of the LD, especially in applications such as optical communication systems and others. The RIN corresponding to unstable operation states can be stabilized as rising double OFB strength K_ex2 and optical phase ψ₂, which helps in planning lasers at best dynamics and low noise level. Impacts of optical phase and double OFB strength K_ex2 on the RIN with adapting laser design to adjust values of K_ex2 and ψ₂ are presented here and have not been investigated before. It may be helpful in increasing/decreasing the stability/RIN of LDs, respectively.

The chaotic dynamic state under double OFB is important in many applications, such as secure communication systems. In this section, we have an interest in investigating the output photon number S(t)/S_av, time change, and the corresponding chaos dynamic RIN spectral characteristics under double OFB when K_ex1 = 0.04 and K_ex2 = 0.005 and at optical phase ψ₁ = ωτ₁, ψ₂ = 0.0, and ω(τ₁ + τ₂). Figure 7a plots the variations of S(t)/S_av, which are intensity-reduced and phase-shifted by increasing the optical phase ψ₂ from zero to ω(τ₁ + τ₂), which is similar to single OFB Figure 3(a3). The reduction of the intensity of S(t)/S_av is translated into a decrease of RIN in Figure 7b. The RIN spectrum shows more enhanced peaks than the chaotic RIN with a single OFB shown in Figure 3(b3). The values of the peak frequency have no relationships and are random. The highest peak frequency is 3.4 GHz, which is equal to a single OFB peak frequency. Increasing the optical phase ψ₂ from zero to ω(τ₁ + τ₂) causes phase shift and suppression in the intensity of the RIN by about one order of magnitude.

4.2.2. Region of Long Double OFB (L_ex2 = 10⁻¹ m)

The impacts of double OFB on the dynamic states and the corresponding average Low-frequency RIN when f < 10 MHz of laser in a long external cavity will be investigated. We set the distance between the first and second reflectors at 7 × 10⁻² m, making the double OFB cavity approach the region of the long external cavity (L_ex2 = 10⁻¹ m). Figure 8, Figure 9 and Figure 10 plot the bifurcation diagrams and the corresponding average Low-frequency RIN (f < 10 MHz) when the single OFB induces the same dynamic states as Figure 4, Figure 5 and Figure 6. The figures also indicate that the dynamics of the LD begin with the same dynamic of the LD with a single OFB in the region of weak OFB strength (at small K_ex2)—in both cases, when ψ₂ = 0.0 and ω(τ₁ + τ₂). However, the increase in the double OFB intensity of K_ex2 does not take the laser to a route-to-CW. It takes it to a route-to-chaos, as occurred in the case when ψ₂ = 0.0 in Figure 4b, Figure 5b and Figure 6b. The chaos dynamics range of K_ex2 is narrowest at K_ex1 = 2 × 10⁻² and ψ₂ = 0.0, which agree with PO subject to single OFB, and widest at K_ex1 = 4 × 10⁻², and ψ₂ = 0.0 that agree with chaos dynamic state under single OFB. On the contrary, Figure 10a shows similar behavior as shown in Figure 6a: the rise in the double OFB intensity K_ex2 takes the LD to a route-to-CW state when ψ₂ = ω(τ₁ + τ₂) and attracts the laser to a route-to-chaos state at ψ₂ = 0.0, which is cleared in Figure 10b. The figures show that these routes to the chaos state do not mirror the congruent path from CW to the relevant dynamic at single OFB strength K_ex1 in the bifurcation diagrams of Figure 2 under single OFB. The figures show that variations of PO frequency f_PO with K_ex2 increase with increasing double OFB strength K_ex2 through each dynamic state (PO, PD, and chaos) when ψ₂ = 0.0 and ω(τ₁ + τ₂), as mentioned in Ref. [12].

In Figure 8, Figure 9 and Figure 10 and on the right Y-axis, the average Low-frequency RIN (f < 10 MHz) variation with the double cavity OFB intensity K_ex2 corresponds to BDs shown in the same figures. The RIN, as ψ₂ = 0.0, enhances to higher noise levels when dynamic states transfer from PO and PD to the chaos regime and never approach the solitary laser noise level (dashed line). Figures show that when the optical phase ψ₂ = 0.0, the RIN displays a lower level than that as ψ₂ = ω(τ₁ + τ₂).

As shown in the figures, when the optical phases ψ₁ = ωτ₁, and ψ₂ = ω(τ₁ + τ₂), the dynamic states of the laser are more stable than when ψ₁ = ωτ₁, and ψ₂ = 0.0, and the RIN decreases to levels near quantum noise. Figure 4, Figure 5 and Figure 6 (short external cavity regime) in comparison with Figure 8, Figure 9 and Figure 10 (long external cavity regime) show that the double external cavity leads to setting the irregular states produced by the single external cavity and keeping the stable CW. This reduces the RIN to lower levels near the solitary laser noise level. This leads to improvements in the properties of the LD, especially in applications such as optical communication systems and others. The simulated results show that the RIN, which corresponds to unstable states of the LD, may be stabilized by operating the laser in a short external cavity regime and increasing the double OFB intensity K_ex2 and optical phase ψ₂. This overall helps in designing lasers with high dynamics and low noise levels. The impacts of the optical phase and double OFB K_ex2 on the RIN, with an adapting laser design to adjust the values of K_ex2 and ψ₂, are introduced for the first time. This can be useful in increasing/decreasing stability/RIN of lasers, respectively.

Figure 11 plots the temporal variation of S(t)/S_av and the corresponding chaos RIN spectral characteristics under double OFB of the long external cavity when K_ex1 = 0.029 and K_ex2 = 0.018, and K_ex1 = 0.04 and K_ex2 = 0.015, at optical phase ψ₁ = ωτ₁, ψ₂ = 0.0 and ω(τ₁ + τ₂). Figure 11(a1,a2) show an intensity-suppression and phase shift in the fluctuations of S(t)/S_AV on the increasing of the optical phase ψ₂ from zero to ω(τ₁ + τ₂), which is the same as the chaos state in single OFB and double OFB with short external cavities as shown in Figure 3(a3) and Figure 7a, respectively. The suppression and phase shift of the fluctuations of S(t)/S_AV due to increasing optical phase ψ₂ from zero to ω(τ₁ + τ₂) are translated in Figure 11(b1,b2) into suppression and frequency shift of the RIN spectrum. By comparison, the chaotic RIN spectra in Figure 3(b3) and Figure 7b with the spectra in Figure 11(b1,b2) are smoother, with two weaker and broader peaks. Figure 11(b2) shows that the frequency of the higher peak is 3.6 GHz and 3.8 GHz, as ψ₂ = 0.0 and ω(τ₁ + τ₂), which is higher than the stated peak in the single OFB chaos RIN in Figure 3(b3) by 400 MHz. The lower peak is found at 6.5 GHz and 6.3 GHz, as ψ₂ = 0.0 and ω(τ₁ + τ₂), and has no relation to the primary peak frequency, as shown in Figure 11(b2). Moreover, these two peak frequencies are not related to the resonance frequencies of the external cavities, f_ex1 = 5 GHz and f_ex2 = 4.286 GHz, of the laser. That means no information related to the optical system shape can be obtained from the RIN spectra. This characteristic indicates that the RIN power spectrum of the chaotic dynamic state with a double OFB in the long external cavity is unequal to that describing the single OFB. Therefore, the laser with double OFB and a long external cavity may be utilized to obtain smooth chaos signals used in a secure communication system.

5. Conclusions

We presented a numerical investigation of the dynamics, states, and RIN of LDs operating under a double OFB by providing our previous model of a single OFB external cavity. The dynamics of the LD were studied within two regions: the short double external cavity (3.5 × 10⁻² m) and the long double cavity (10⁻¹ m). In the single OFB cavity, the first reflector has been set at 3 × 10⁻² m far from the LD front facet, which agrees with a PD route-to-chaos. The simulations show that the LD turns its state into POs, PD, and then a chaotic state. In the regime of a short double external cavity, the LD is taken from each of the states with a single OFB to a route-to-CW state. This route-to-CW is a reflection of the identical route-from-chaos to the identical state with a single OFB. In long double OFB, the rise in double OFB strength takes the LD to a route-to-chaos. In comparison with a single OFB case, the double OFB external cavity produces smoother chaotic RIN with two broad and weak peaks at frequencies = 3.6, 3.8, and 6.5, 6.3 GHz, as ψ₂ = 0.0 and ω(τ₁ + τ₂), respectively. These frequencies have no relation to the resonance frequencies of the external cavities. This kind of chaos can be used in a secure communication system. By considering the optical phase due to OFB in single OFB and double OFB cavities, it causes significant intensity suppression and phase shift in the LD output temporal changes. This intensity suppression and phase shift induced RIN suppression and a frequency shift in the RIN spectrum. These simulation results on the impacts of the optical phase due to double OFB on the lasing frequency shift in the RIN spectra are new contributions and have not been investigated before. The RIN is reduced near the solitary noise level as LD operates in the CW and PO regimes. Considering the double OFB and optical phase due to OFB, it causes a change in the dynamic states of the LD from a chaotic state to a more stable CW or PO. The dynamic states of LDs can get better by considering the effects of double OFB and optical phase due to OFB, which leads to a better drawing and a best-performance LD.