On the Regional Temperature Series Evolution in the South-Eastern Part of Romania
Abstract
:1. Introduction
- To evaluate the variability of the temperature series in the region.
- When applying the proposed methods, one determines the regional trend of the data series. If the available set of time series (recorded at different locations) is homogenous, and one wants to evaluate the series value at a point where it is unknown, this value can be chosen to be equal to that of the regional trend in the studied period.
2. Methodology and Data Series
2.1. Methodology
- For each row j of X (j = 1, …, m), compute the difference between the maximum and the minimum values, call it amplitude, and denote it as Aj.
- For each j (j = 1, …, m), divide the interval between the minimum and maximum values on row j in nj intervals of the same length that contain enough values. The number of intervals, nj, is chosen based on the user experience and/or a number of trials.
- For each j (j = 1, …, m), choose the interval with the highest number of elements (call this number frequency) among those formed in the previous step. Denote this interval by Ijmax and its number of elements fjmax.
- Build the ‘Regional series’ whose values are the mean of the elements in all Ijmax.
- Represent the chart of the ‘Regional series’ in Cartesian coordinates, where the Ox is the time axis and Oy is the axis containing the values of the ‘Regional series.’
- Estimate the goodness of fit by computing MAE and MSE and build their charts. The MAE and MSE are computed using the errors obtained as the differences between the recorded values (at each station) and the ‘Regional series’ values.
- At stage 2, nj is not necessarily the same for each row in the matrix. For a small number of series, it is recommended to use the same nj. The number of values in an interval depends on the number of the series. At least ten series should be considered for building the regional series, and at least two values must be contained in each interval. Three values should be the minimum for a higher number of series to avoid intervals containing only extreme values or outliers.
- If at stage 3 in MPPM there are many intervals with the maximum frequency, it is recommended to run the next steps of the algorithm for each case. The ‘Regional series’ will be that with the minimum MAE and MSE. This approach offers a better fit of the ‘Regional series’ than the original one, which only considered the interval whose average value was the closest to the average value of the data recorded at a specific moment. We name MPPM with this improvement, Method I.
- Compute_Amplitude step: compute the extreme values for each year and then the amplitude.
- Amplitude Representation step: draw the chart of amplitude.
- Compute the regional series: for each year, choose the number of intervals, compute the number of elements in each interval, select the interval with the highest number of elements, and compute the average of the elements in this interval.
- Collect the results in the Data Processing from Matlab destination tables (containing MAE and MSE).
- Draw the charts of ‘Regional series’, MAE, and MSE.
- Export to file: the modeling output is exported to the xlsx. files.
- A.
- Set the number of clusters, n, for clustering the recorded series set.
- B.
- Select the cluster that contains the lowest number of time series, determine the columns in the matrix X containing the values of these series, and remove them from X. Denote by Xc the new matrix.
- C.
- Compute the average value of the elements in each row of the matrix Xc. Denote by the average of the elements in the row j of Xc.
- D.
- Build the ‘Regional series’ with the values from the previous step.
- E.
- Represent the ‘Regional series’ chart in Cartesian coordinates, where Ox is the time axis and Oy contains the values of the ‘Regional series’.
- F.
- Estimate the goodness of fit by computing MAE and MSE as in MPPM and draw the MAE and MSE charts (as time series).
- If two clusters contain the same number, the cluster with the best separation property is selected.
- In [34], the k-means algorithm was utilized in Method II for clustering. Agglomerative hierarchical clustering was used in this study.
- In the agglomerative clustering, each cluster is initially formed by a point (in this case, a station). At the next stage, the dissimilarity between every pair of points is computed using a distance (Euclidean, here). Then, the linking criterion to merge different clusters is determined. The single, complete, average, and Ward criteria were used in our experiments. The next stage, the best clustering was chosen on the basis of the value of the agglomerative coefficient [48]. Since the closer the agglomerative coefficient to is 1, the better the clustering, the Ward method was selected among the four mentioned criteria. The process continues until all the objects are linked together. The last step is choosing the cut-off value to acquire the number of clusters [49].
- We chose to apply the hierarchical clustering for the following reasons [50]:
- a.
- In the k-means algorithm, the number of clusters, k, must be specified in advance. In the hierarchical clustering it must not be pre-specified.
- b.
- In k-means, since the k is randomly chosen, the resulting clusters may differ, whereas in the hierarchical clustering, they are always the same.
- c.
- The k-means method assigns records to each cluster for finding disjunct clusters of spherical shape on the basis of distance. Hierarchical clustering easily handles any similarity forms or distance. It was shows that when using Euclidean distance (as in the case of modeling meteorological data), hierarchical clustering outperforms the k-means algorithm.
- d.
- Hierarchical clustering can be applied to any type of attributes.
- Choosing the optimum number of clusters, n, is an optimization problem. Since the choice of n is essential for performing Method II, 30 methods were run (among which Scott [51], Mariott [52], Hubert [53], Friedmann [54], silhouette [55], gap [56]) using the NbClust package in R [57] to determine the optimum number of clusters. For example, if 14 methods indicated n = 2, 10 methods indicated n = 3, and 6 gave n = 4, on the basis of the majority principle, the optimal number of clusters was selected to be 2, followed by 3. Therefore, to compare the outputs of the two methods, the first was run with two and three intervals, and the second with two and three clusters. Worked examples for both methods are presented in [41,42].
- Use the NbClust package in R to determine the number of clusters.
- Use the dplyr package in R to determine the clusters.
- Select the cluster with the highest number of elements. With the series from this cluster, build a matrix Xc.
- Compute the ‘Regional series’ whose elements are the averages from each line of Xc
- Compute MAE and MSE and export the result as an xlsx. file.
2.2. The Studied Region and the Data Series
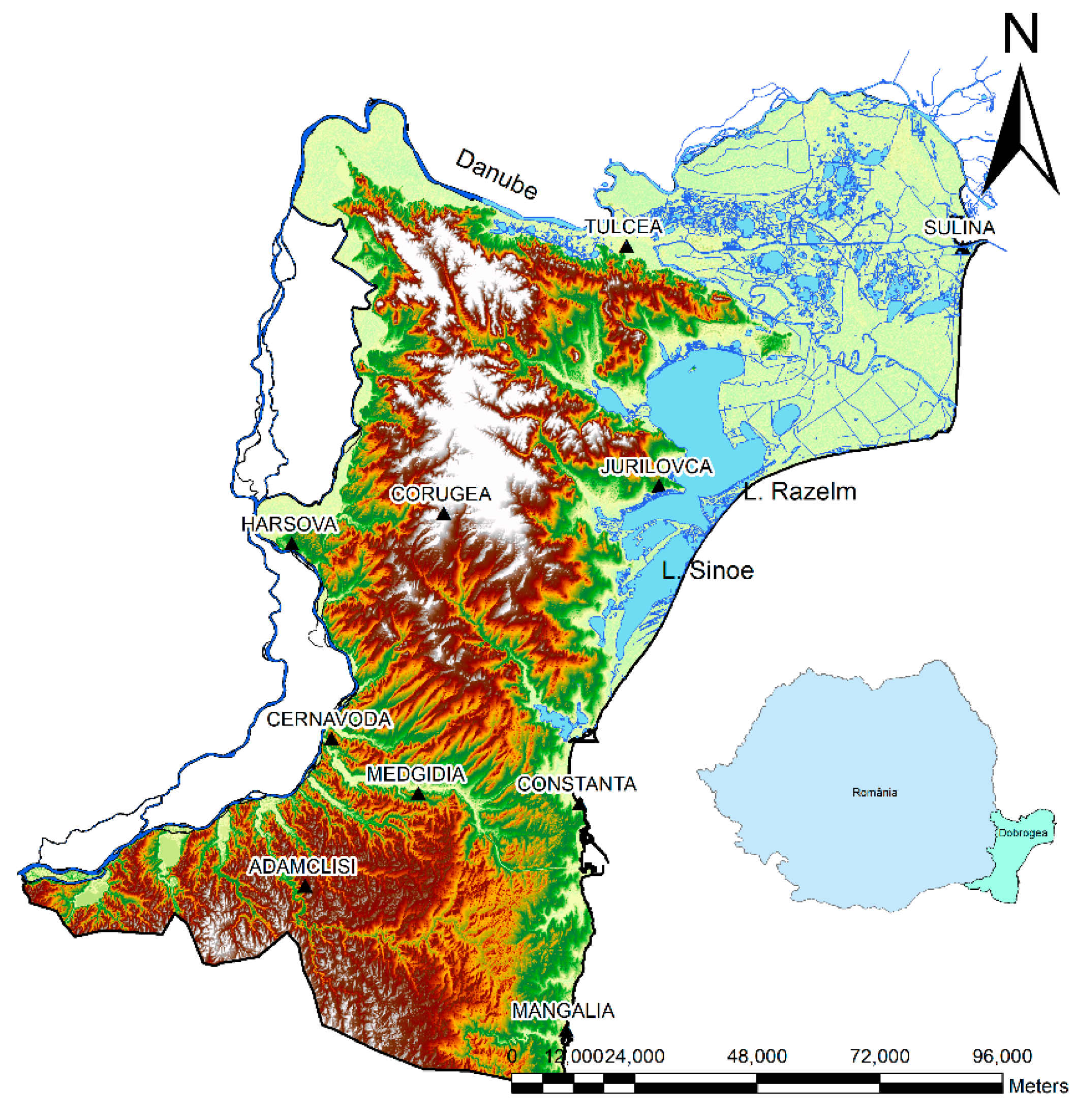
3. Results and Discussion
3.1. Results and Discussion for the Minimum Temperatures Series
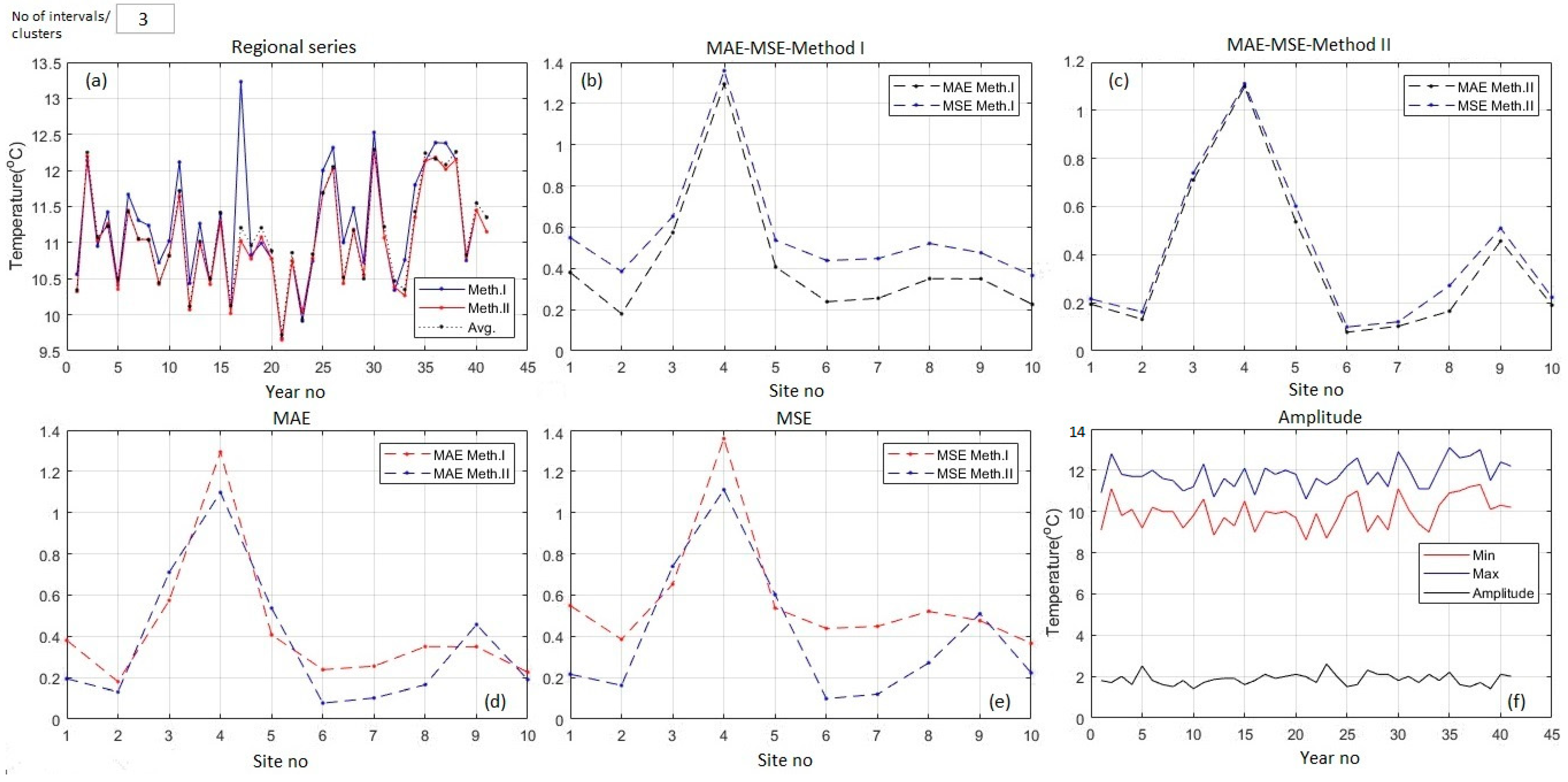
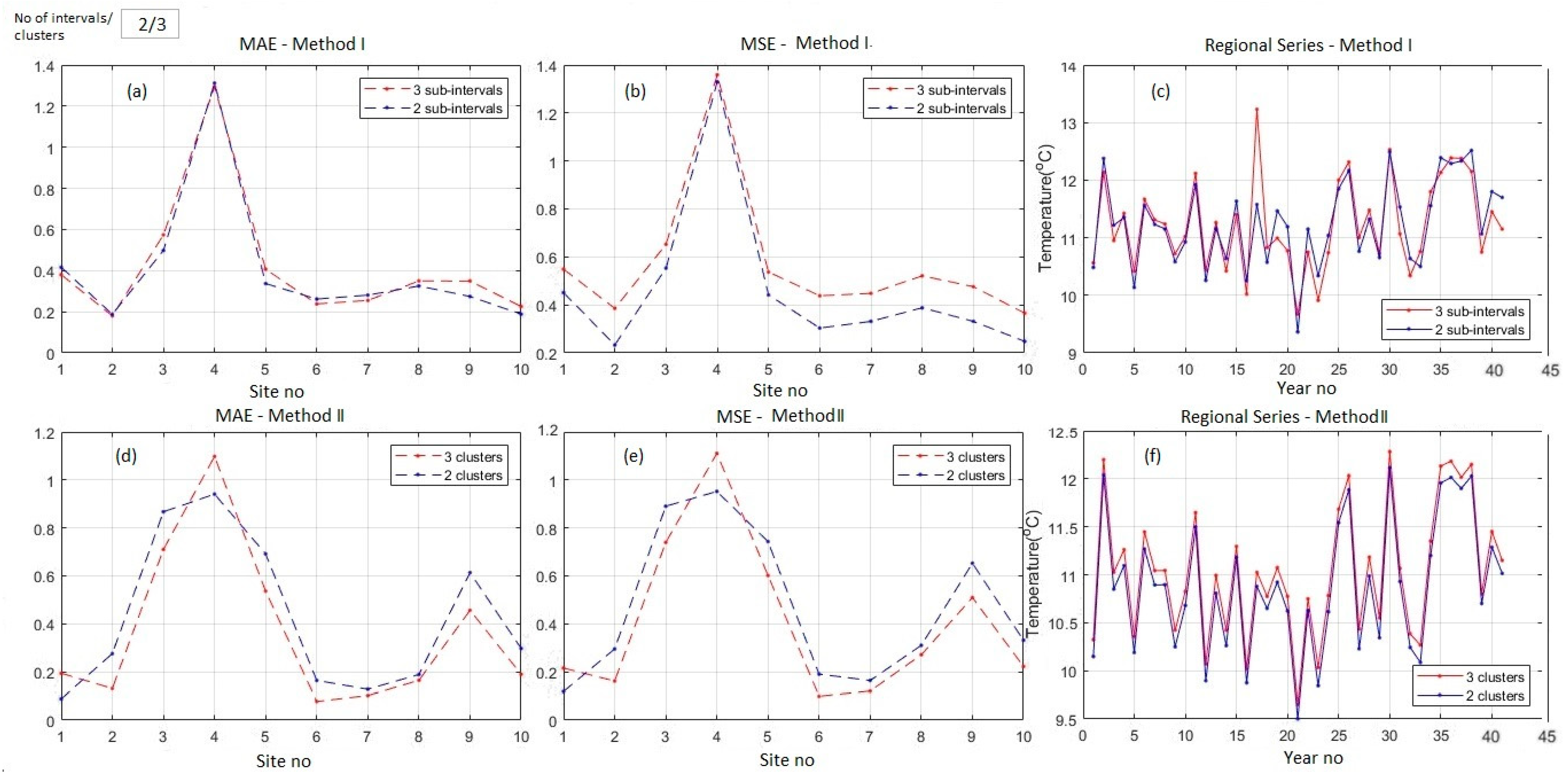
3.2. Results and Discussion for the Average Temperatures Series
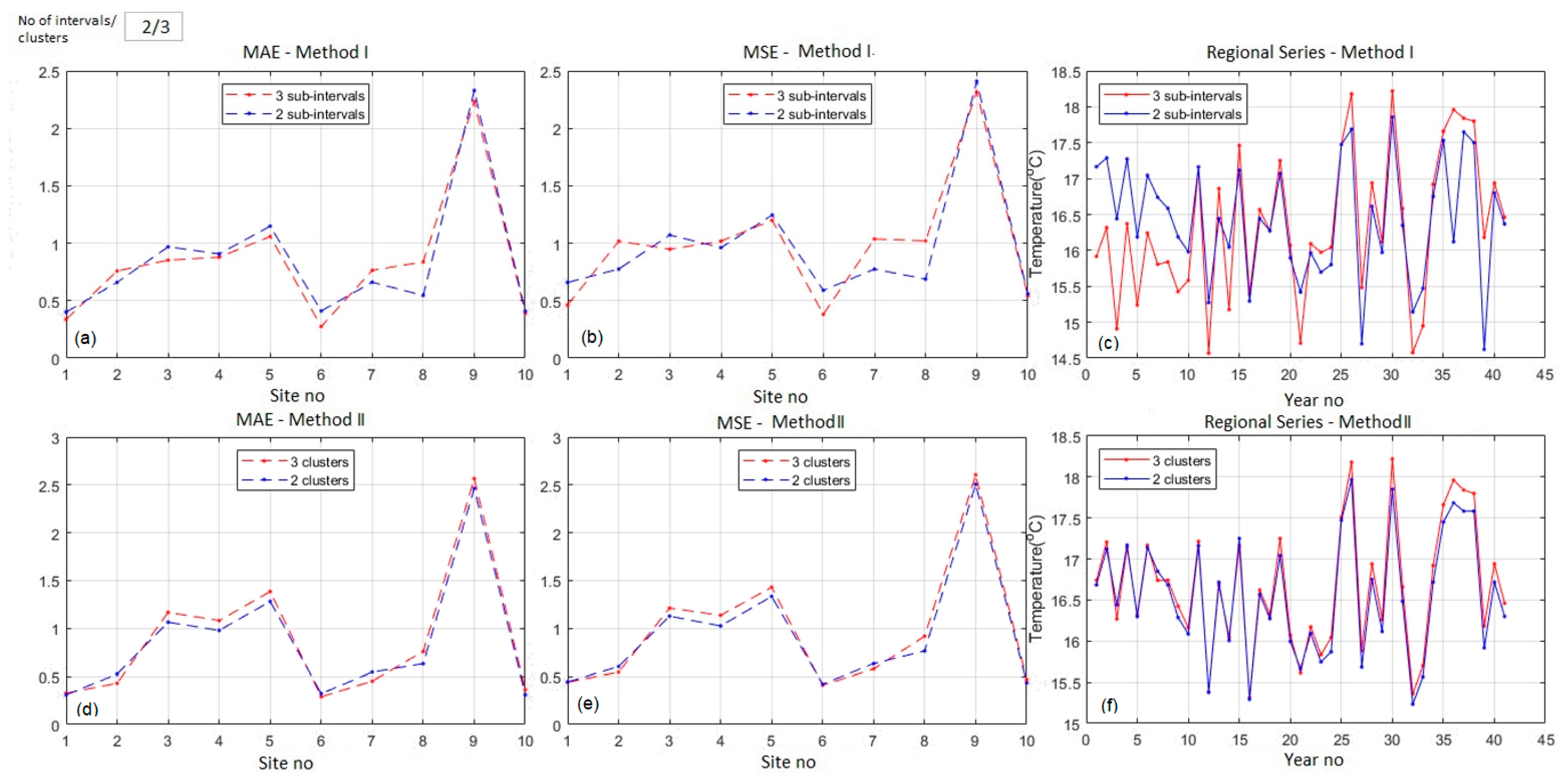
3.3. Results and Discussion for the Maximum Temperatures Series
3.4. Comparison of the Regional Series with the Values from the ROCADA Database
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Emadia, M.; Shahriarib, A.R.; Sadegh-Zadeha, F.; Seh-Bardana, B.J.; Dindarlou, A. Geostatistics-based spatial distribution of soil moisture and temperature regime classes in Mazandaran province, northern Iran. Arch. Acker Pfl. Boden. 2016, 62, 502–522. [Google Scholar] [CrossRef]
- Javari, M. Comparison of interpolation methods for modeling spatial variation of precipitation in Iran. Int. J. Environ. Sci. Ed. 2017, 12, 1037–1054. [Google Scholar]
- Chen, S.; Guo, J. Spatial interpolation techniques: Their applications in regionalizing climate-change series and associated accuracy evaluation in Northeast China. Geomat. Nat. Haz. Risk 2017, 8, 689–705. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, D.; Kilik, F. Geostatistical Approach for Spatial Interpolation of Meteorological Data. An. Acad. Bras. Ciênc. 2016, 88, 2121–2136. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Li, Y. Spatial interpolation of temperature in the United States using residual kriging. Appl. Geogr. 2013, 44, 112–120. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Thiessen, A.H. Precipitation for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar]
- Chiles, J.-P.; Delfiner, P. Geostatistics. Modeling Spatial Uncertainty, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ly, S.; Charles, C.; Degre, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotech. Agr. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Szolgay, J.; Parajka, J.; Kohnova, S.; Hlavcova, K. Comparison of mapping approaches of design annual maximum daily precipitation. Atmos. Res. 2009, 92, 289–307. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Băutu, A.; Băutu, E. Particle Swarm Optimization for the Inverse Distance Weighting Distance method. Appl. Sci. 2020, 10, 2054. [Google Scholar] [CrossRef] [Green Version]
- Șerban, C.; Bărbulescu, A.; Dumitriu, C.S. Maximum precipitation interpolation using an evolutionary optimized IDW algorithm. IOP Conf. Ser. Earth Env. Sci. 2022, 958, 012006. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Șerban, C.; Indrecan, M.-L. Improving spatial interpolation quality. IDW versus a genetic algorithm. Water 2021, 13, 863. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; J. Wiley & Sons: Hoboken, NY, USA, 1993. [Google Scholar]
- Wadoux, A.M.J.-C.; Odeh, I.O.A.; McBratney, A.B. Overview of Pedometrics, in Reference Module in Earth Systems and Environmental Sciences, Elsevier, 2021. Available online: https://doi.org/10.1016/B978-0-12-822974-3.00001-X (accessed on 22 February 2023).
- Wong, A.H.; Kwon, T.J. Development and Evaluation of Geostatistical Methods for Estimating Weather Related Collisions: A Large-Scale Case Study. Transport. Res. Rec. 2021, 2675, 828–840. [Google Scholar] [CrossRef]
- Erdin, R.; Frei, C.; Künsch, H.R. Data Transformation and Uncertainty in Geostatistical Combination of Radar and Rain Gauges. J. Hydrometeorol. 2013, 13, 1332–1346. [Google Scholar] [CrossRef]
- Szentimrey, T.; Bihari, Z.; Szalai, S. Comparison of Geostatistical and Meteorological Interpolation Methods (What is What?). In Spatial Interpolation for Climate Data. The Use of GIS in Climatology and Meteorology; Dobesch, H., Dumolard, P., Dyras, I., Eds.; ISTE Ltd.: London, UK, 2007; pp. 45–56. [Google Scholar]
- Dumitrescu, A.; Birsan, M.-V. ROCADA: A gridded daily climatic dataset over Romania (1961–2013) for nine meteorological variables. Nat. Hazards 2015, 78, 1045–1063. [Google Scholar] [CrossRef]
- Mamara, A.; Anadranistakis, M.; Argiriou, A.A.; Szentimrey, T.; Kovacs, T.; Bezesc, A.; Bihari, Z. High resolution air temperature climatology for Greece for the period 1971–2000. Meteorol. Appl. 2017, 24, 191–205. [Google Scholar] [CrossRef] [Green Version]
- Gofa, F.; Mamara, A.; Anadranistakis, M.; Flocas, H. Developing Gridded Climate Data Sets of Precipitation for Greece Based on Homogenized Time Series. Climate 2019, 7, 68. [Google Scholar] [CrossRef] [Green Version]
- Szentimrey, T. Multiple Analysis of Series for Homogenization (MASH v1.02). Available online: http://www.dmcsee.org/uploads/file/330_1_mishmanual.pdf (accessed on 24 February 2023).
- Szentimrey, T.; Bihari, Z. Meteorological Interpolation based on Surface Homogenized Data Basis (MISH v3.02). Available online: http://www.dmcsee.org/uploads/file/331_2_mashmanual.pdf (accessed on 24 February 2023).
- Praveen, B.; Talukdar, S.; Shahfahad; Mahato, S.; Mondal, J.; Sharma, P.; Islam, A.R.M.T.; Rahman, A. Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches. Sci. Rep. 2020, 10, 10342. [Google Scholar] [CrossRef]
- Patra, J.P.; Mishra, A.; Singh, R.; Raghuwanshi, N.S. Detecting rainfall trends in twentieth century (1871–2006) over Orissa State, India. Clim. Change 2012, 111, 801–817. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Dumitriu, C.S.; Maftei, C. On the Probable Maximum Precipitation Method. Rom. J. Phys. 2022, 67, 801. [Google Scholar]
- Chatterjee, S.; Khan, A.; Akbari, H.; Wang, Y. Monotonic trends in spatio-temporal distribution and concentration of monsoon precipitation (1901–2002), West Bengal, India. Atmos. Res. 2016, 182, 54–75. [Google Scholar] [CrossRef]
- Zittis, G.; Bruggeman, A.; Lelieveld, J. Revisiting future extreme precipitation trends in the Mediterranean. Weather Clim. Extremes 2021, 34, 100380. [Google Scholar] [CrossRef] [PubMed]
- Huerta, G.; Sanso, B.; Stroud, J.R. A spatiotemporal model for Mexico city ozone levels. J. R. Stat. Soc. Ser. C 2004, 53, 231–248. Available online: https://www.jstor.org/stable/3592538 (accessed on 20 March 2022). [CrossRef] [Green Version]
- Lund, R.; Shao, Q.; Basawa, I. Parsimonious periodic time series modelling. Aust. NZ J. Stat. 2006, 48, 33–47. [Google Scholar] [CrossRef]
- Du, Z.; Wu, S.; Kwan, M.P.; Zhang, C.; Zhang, F.; Liu, R. A spatiotemporal regression-kriging model for space-time interpolation: A case study of chlorophyll-a prediction in the coastal areas of Zhejiang, China. Int. J. Geogr. Inf. Sci. 2018, 32, 1927–1947. [Google Scholar] [CrossRef]
- Im, H.K.; Rathouz, P.J.; Frederick, J.E. Space-time modelling of 20 years of daily air temperature in the Chicago metropolitan region. Environmetrics 2009, 20, 494–511. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Nalder, I.A.; Wein, R.W. Spatial interpolation of climatic normals: Test of a new method in the Canadian boreal forest. Agric. For. Meteor. 1998, 92, 211–225. [Google Scholar] [CrossRef]
- Wang, J.-F.; Reis, B.Y.; Hu, M.-G.; Christakos, G.; Yang, W.-Z.; Sun, Q.; Li, Z.-J.; Li, X.-Z.; Lai, S.-J.; Chen, H.-Y.; et al. Area Disease Estimation Based on Sentinel Hospital Records. PLoS ONE 2011, 6, e23428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, C.-D.; Wang, J.-F.; Hu, M.-G.; Li, Q.-X. Interpolation of missing temperature data at meteorological stations using P- BSHADE. J. Clim. 2013, 26, 7452–7463. [Google Scholar] [CrossRef]
- Xu, C.; Wang, J.; Li, Q. A New Method for Temperature Spatial Interpolation Based on Sparse Historical Stations. J. Clim. 2018, 31, 1757–1770. [Google Scholar] [CrossRef]
- Singh, G.; Soman, B. Spatial Interpolation using Inverse Distance Weighing (IDW) in R. Available online: https://rpubs.com/Dr_Gurpreet/interpolation_idw_R (accessed on 11 July 2022).
- Graler, B.; Pebesma, E.; Hevelink, G. Spatio-Temporal Interpolation Using Gstat. Available online: https://cran.r-project.org/web/packages/gstat/vignettes/spatio-termpoal-kriging.pdf (accessed on 11 July 2022).
- Spatiotemporal Interpolation Using Ensemble, ML. Available online: https://opengeohub.github.io/spatial-prediction-eml/spatiotemporal-interpolation-using-ensemble-ml.html (accessed on 11 July 2022).
- Bărbulescu, A. A new method for estimation the regional precipitation. Water Resour. Manag. 2016, 30, 33–42. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Nazzal, Y.; Howari, F. Statistical analysis and estimation of the regional trend of aerosol size over the Arabian Gulf Region during 2002–2016. Sci. Rep. 2018, 8, 9571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bărbulescu, A. On the spatio-temporal characteristics of the aerosol optical depth in the Arabian Gulf zone. Atmosphere 2022, 13, 857. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Postolache, F.; Dumitriu, C.Ș. Estimating the Precipitation Amount at Regional Scale Using a New Tool, Climate Analyzer. Hydrology 2021, 8, 125. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kruskal-Wallis Test. Available online: https://www.statsdirect.com/help/default.htm#nonparametric_methods/kruskal_wallis.htm (accessed on 12 June 2022).
- Yudha Wijaya, C. Breaking down the Agglomerative Clustering Process. Available online: https://towardsdatascience.com/breaking-down-the-agglomerative-clustering-process-1c367f74c7c2 (accessed on 12 June 2022).
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Difference between K Means and Hierarchical Clustering. Available online: https://www.geeksforgeeks.org/difference-between-k-means-and-hierarchical-clustering/ (accessed on 20 March 2022).
- Scott, A.J.; Symons, M.J. Clustering Methods Based on Likelihood Ratio Criteria. Biometrics 1971, 27, 387–397. [Google Scholar] [CrossRef] [Green Version]
- Marriot, F.H.C. Practical Problems in a Method of Cluster Analysis. Biometrics 1971, 27, 501–514. [Google Scholar] [CrossRef]
- Hubert, L.J.; Arabie, P. Comparing Partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Friedman, H.P.; Rubin, J. On Some Invariant Criteria for Grouping Data. J. Am. Stat. Assoc. 1967, 62, 1159–1178. [Google Scholar] [CrossRef]
- Rousseeuw, P. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Lafitte, P. Traité D’informatique Geologique; Masson & Cie: Paris, France, 1972. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly spaced data. In Proceedings of the 1968 ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Maftei, C.; Bărbulescu, A. Statistical analysis of climate evolution in Dobrudja region. Lect. Notes Eng. Comput. Sci. 2008, 2, 1082–1087. [Google Scholar]
- Mocanu-Vargancsik, C.A.; Bărbulescu, A. Study of the Temperature’s Evolution Trend on the Black Sea Shore at Constanta. J. Phys. Conf. Ser. 2019, 1297, 012010. [Google Scholar] [CrossRef]
- Bărbulescu, A. Modeling temperature evolution. Case study. Rom. Rep. Phys. 2016, 68, 798. [Google Scholar]
- Bărbulescu, A. Models for temperature evolution in Constanta area (Romania). Rom. J. Phys 2016, 61, 676–686. [Google Scholar]
- Bărbulescu, A.; Deguenon, J. About the variations of precipitation and temperature evolution in the Romanian Black Sea Littoral. Rom. Rep. Phys. 2015, 67, 625–637. [Google Scholar]
- Bărbulescu, A.; Băutu, E. Mathematical models of climate evolution in Dobrudja. Theor. Appl. Climatol. 2010, 100, 29–44. [Google Scholar] [CrossRef]
- Dumitriu, C.S.; Bărbulescu, A.; Maftei, C. IrrigTool—A New Tool for Determining the Irrigation Rate Based on Evapotranspiration Estimated by the Thornthwaite Equation. Water 2022, 67, 2399. [Google Scholar] [CrossRef]
- Maftei, C.; Bărbulescu, A.; Rugină, S.; Nastac, C.D.; Dumitru, I.M. Analysis of the arbovirosis potential occurrence in Dobrogea, Romania. Water 2021, 13, 374. [Google Scholar] [CrossRef]
- Bărbulescu, A.; Postolache, F. New approaches for modeling the regional pollution in Europe. Sci. Total Environ. 2021, 753, 141993. [Google Scholar] [CrossRef] [PubMed]








| Series | Minimum Series | Average Series | Maximum Series | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Station | Signific. | Q | B | Signific. | Q | B | Signific. | Q | B |
| Adamclisi | + | 0.015 | 6.37 | 0.015 | 10.55 | * | 0.023 | 15.93 | |
| Cernavoda | *** | 0.084 | 4.06 | 0.013 | 10.84 | −0.013 | 17.21 | ||
| Constanta | * | 0.024 | 8.06 | + | 0.020 | 11.40 | * | 0.025 | 15.05 |
| Corugea | *** | 0.078 | 3.04 | + | 0.018 | 9.60 | −0.014 | 15.70 | |
| Harsova | *** | 0.076 | 3.84 | 0.013 | 10.70 | −0.015 | 17.36 | ||
| Jurilovca | *** | 0.097 | 3.93 | 0.014 | 10.67 | ** | −0.031 | 16.62 | |
| Mangalia | * | 0.020 | 7.68 | + | 0.019 | 11.27 | 0.016 | 14.98 | |
| Medgidia | * | 0.024 | 6.03 | 0.013 | 10.70 | * | 0.026 | 15.90 | |
| Sulina | + | 0.018 | 9.00 | 0.017 | 11.25 | * | 0.025 | 13.73 | |
| Tulcea | −0.003 | 6.76 | 0.017 | 10.85 | 0.013 | 16.19 | |||
| Method I | Method II | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | ||||||
| n | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | |
| Site No. | |||||||||
| 1 | 0.77 | 1.32 | 0.92 | 1.67 | 0.84 | 1.43 | 1.00 | 1.73 | |
| 2 | 1.14 | 0.41 | 1.80 | 0.66 | 0.50 | 0.29 | 0.58 | 0.32 | |
| 3 | 1.98 | 3.01 | 2.17 | 3.20 | 2.61 | 3.19 | 2.65 | 3.33 | |
| 4 | 1.96 | 0.93 | 2.44 | 1.17 | 1.34 | 0.76 | 1.40 | 0.78 | |
| 5 | 1.70 | 2.75 | 1.95 | 2.95 | 2.32 | 2.90 | 2.38 | 3.06 | |
| 6 | 0.74 | 1.20 | 0.89 | 1.52 | 0.69 | 1.28 | 0.83 | 1.56 | |
| 7 | 1.34 | 0.31 | 1.98 | 0.69 | 0.70 | 0.14 | 0.81 | 0.19 | |
| 8 | 1.22 | 0.57 | 1.69 | 0.76 | 0.56 | 0.57 | 0.64 | 0.65 | |
| 9 | 2.80 | 3.82 | 2.96 | 4.01 | 3.42 | 4.00 | 3.47 | 4.13 | |
| 10 | 0.75 | 1.43 | 1.01 | 1.82 | 0.94 | 1.53 | 1.18 | 1.91 | |
| Average | 1.44 | 1.58 | 1.78 | 1.85 | 1.39 | 1.61 | 1.50 | 1.77 | |
| Method I | Method II | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | ||||||
| n | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | |
| Site No. | |||||||||
| 1 | 0.41 | 0.38 | 0.45 | 0.55 | 0.09 | 0.19 | 0.12 | 0.22 | |
| 2 | 0.19 | 0.18 | 0.23 | 0.38 | 0.27 | 0.13 | 0.30 | 0.16 | |
| 3 | 0.50 | 0.57 | 0.55 | 0.65 | 0.87 | 0.71 | 0.89 | 0.74 | |
| 4 | 1.31 | 1.29 | 1.33 | 1.36 | 0.94 | 1.10 | 0.95 | 1.11 | |
| 5 | 0.34 | 0.41 | 0.44 | 0.54 | 0.69 | 0.53 | 0.74 | 0.60 | |
| 6 | 0.26 | 0.24 | 0.30 | 0.44 | 0.16 | 0.08 | 0.19 | 0.10 | |
| 7 | 0.28 | 0.25 | 0.33 | 0.45 | 0.13 | 0.11 | 0.16 | 0.12 | |
| 8 | 0.32 | 0.35 | 0.39 | 0.52 | 0.19 | 0.17 | 0.31 | 0.27 | |
| 9 | 0.27 | 0.35 | 0.33 | 0.47 | 0.61 | 0.46 | 0.65 | 0.51 | |
| 10 | 0.19 | 0.23 | 0.25 | 0.36 | 0.30 | 0.19 | 0.33 | 0.22 | |
| Average | 0.41 | 0.43 | 0.46 | 0.57 | 0.43 | 0.37 | 0.46 | 0.41 | |
| Method I | Method II | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | ||||||
| n | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | |
| Site No. | |||||||||
| 1 | 0.40 | 0.37 | 0.66 | 0.46 | 0.31 | 0.33 | 0.44 | 0.44 | |
| 2 | 0.66 | 0.76 | 0.77 | 1.02 | 0.53 | 0.43 | 0.60 | 0.54 | |
| 3 | 0.97 | 0.85 | 1.07 | 0.95 | 1.07 | 1.17 | 1.13 | 1.21 | |
| 4 | 0.91 | 0.88 | 0.96 | 1.02 | 0.98 | 1.09 | 1.03 | 1.14 | |
| 5 | 1.15 | 1.06 | 1.25 | 1.19 | 1.28 | 1.38 | 1.33 | 1.43 | |
| 6 | 0.41 | 0.27 | 0.59 | 0.38 | 0.32 | 0.29 | 0.42 | 0.41 | |
| 7 | 0.66 | 0.76 | 0.77 | 1.04 | 0.55 | 0.46 | 0.63 | 0.58 | |
| 8 | 0.55 | 0.84 | 0.69 | 1.02 | 0.63 | 0.76 | 0.76 | 0.92 | |
| 9 | 2.33 | 2.23 | 2.41 | 2.32 | 2.46 | 2.56 | 2.51 | 2.61 | |
| 10 | 0.41 | 0.39 | 0.56 | 0.54 | 0.31 | 0.36 | 0.44 | 0.47 | |
| Average | 0.84 | 0.84 | 0.97 | 0.99 | 0.84 | 0.88 | 0.93 | 0.99 | |
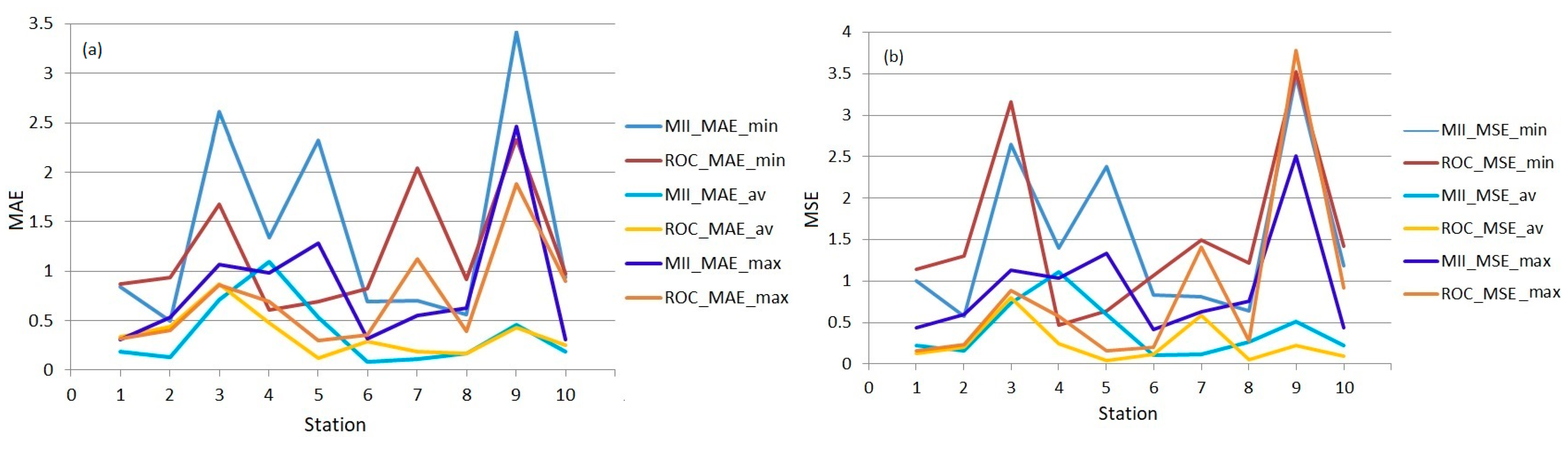
| Min | Average | Max | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | MAE | MSE | |||||||
| Site No. | MII | ROC | MII | ROC | MII | ROC | MII | ROC | MII | ROC | MII (2) | ROC |
| 1 | 0.84 | 0.87 | 1.00 | 1.14 | 0.19 | 0.34 | 0.22 | 0.13 | 0.31 | 0.32 | 0.44 | 0.16 |
| 2 | 0.50 | 0.94 | 0.58 | 1.30 | 0.13 | 0.44 | 0.16 | 0.20 | 0.53 | 0.40 | 0.60 | 0.23 |
| 3 | 2.61 | 1.68 | 2.65 | 3.16 | 0.71 | 0.87 | 0.74 | 0.80 | 1.07 | 0.86 | 1.13 | 0.88 |
| 4 | 1.34 | 0.61 | 1.40 | 0.47 | 1.10 | 0.48 | 1.11 | 0.24 | 0.98 | 0.69 | 1.03 | 0.58 |
| 5 | 2.32 | 0.69 | 2.38 | 0.64 | 0.53 | 0.12 | 0.60 | 0.04 | 1.28 | 0.30 | 1.33 | 0.16 |
| 6 | 0.69 | 0.82 | 0.83 | 1.07 | 0.08 | 0.29 | 0.10 | 0.12 | 0.32 | 0.36 | 0.42 | 0.20 |
| 7 | 0.70 | 2.04 | 0.81 | 1.49 | 0.11 | 0.19 | 0.12 | 0.59 | 0.55 | 1.12 | 0.63 | 1.41 |
| 8 | 0.56 | 0.92 | 0.64 | 1.22 | 0.17 | 0.17 | 0.27 | 0.05 | 0.63 | 0.39 | 0.76 | 0.28 |
| 9 | 3.42 | 2.34 | 3.47 | 3.52 | 0.46 | 0.43 | 0.51 | 0.22 | 2.46 | 1.88 | 2.51 | 3.78 |
| 10 | 0.94 | 0.97 | 1.18 | 1.42 | 0.19 | 0.25 | 0.22 | 0.09 | 0.31 | 0.90 | 0.44 | 0.92 |
| Average | 1.39 | 1.18 | 1.49 | 1.54 | 0.37 | 0.36 | 0.41 | 0.25 | 0.84 | 0.72 | 0.93 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bărbulescu, A. On the Regional Temperature Series Evolution in the South-Eastern Part of Romania. Appl. Sci. 2023, 13, 3904. https://doi.org/10.3390/app13063904
Bărbulescu A. On the Regional Temperature Series Evolution in the South-Eastern Part of Romania. Applied Sciences. 2023; 13(6):3904. https://doi.org/10.3390/app13063904
Chicago/Turabian StyleBărbulescu, Alina. 2023. "On the Regional Temperature Series Evolution in the South-Eastern Part of Romania" Applied Sciences 13, no. 6: 3904. https://doi.org/10.3390/app13063904






