Evaluation of System Identification Methods for Free Vibration Flutter Derivatives of Long-Span Bridges
Abstract
:1. Introduction
2. Aerodynamic Phenomena
2.1. Limited Amplitude Phenomena
2.1.1. Vortex-Induced Vibrations (VIVs)
2.1.2. Buffeting
2.2. Divergent Amplitude Phenomena
2.2.1. Classical Flutter
2.2.2. Galloping
2.2.3. Torsional Flutter
2.2.4. Torsional Divergence
3. Methods of Aerodynamic Analysis
3.1. Wind Tunnel Testing
3.2. Theodorsen Theory for Flat Plate
3.3. Numerical Methods
4. System Identification Methods
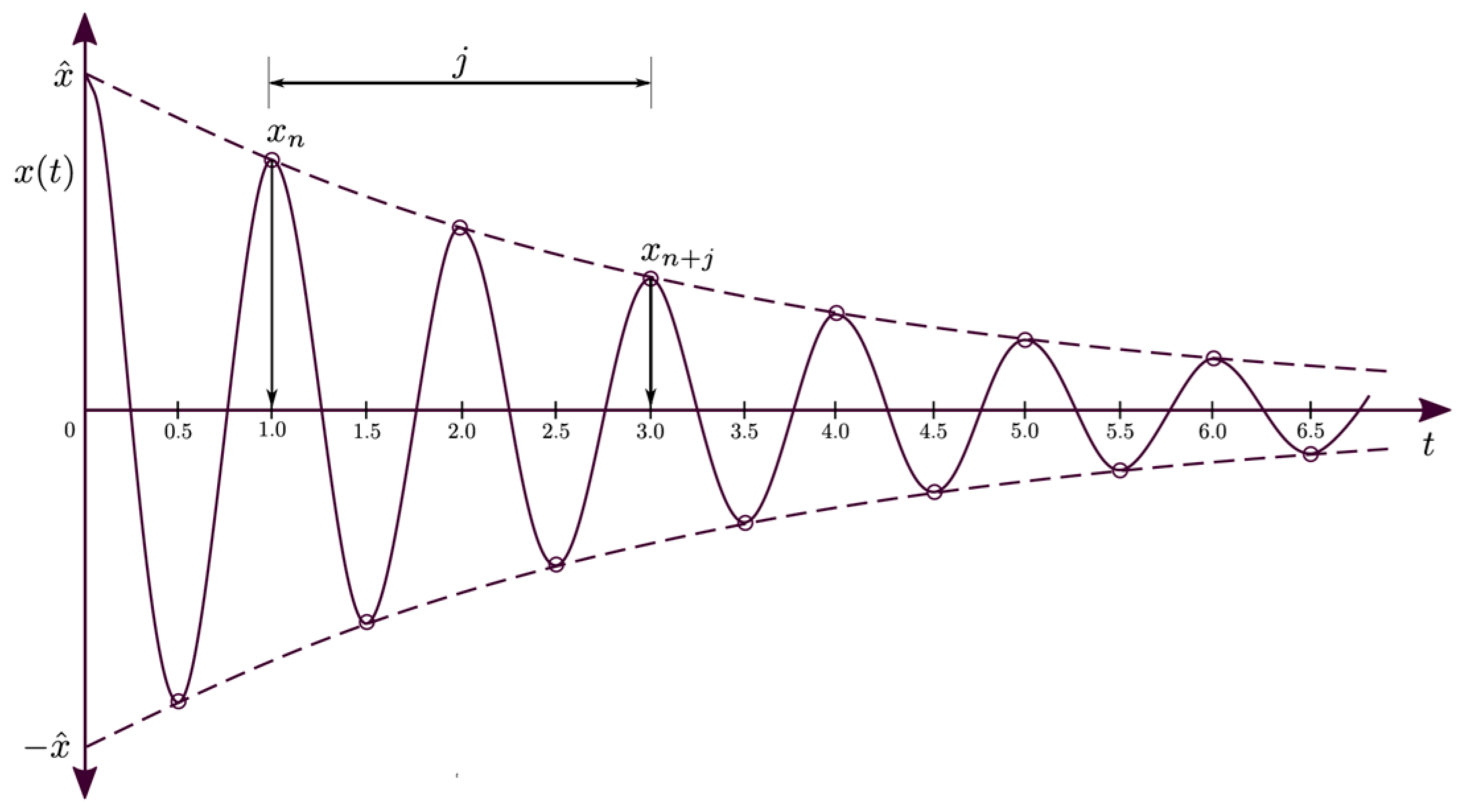
4.1. Logarithmic Decrement Method (LDM)
4.2. Hilbert Transform Method (HTM)
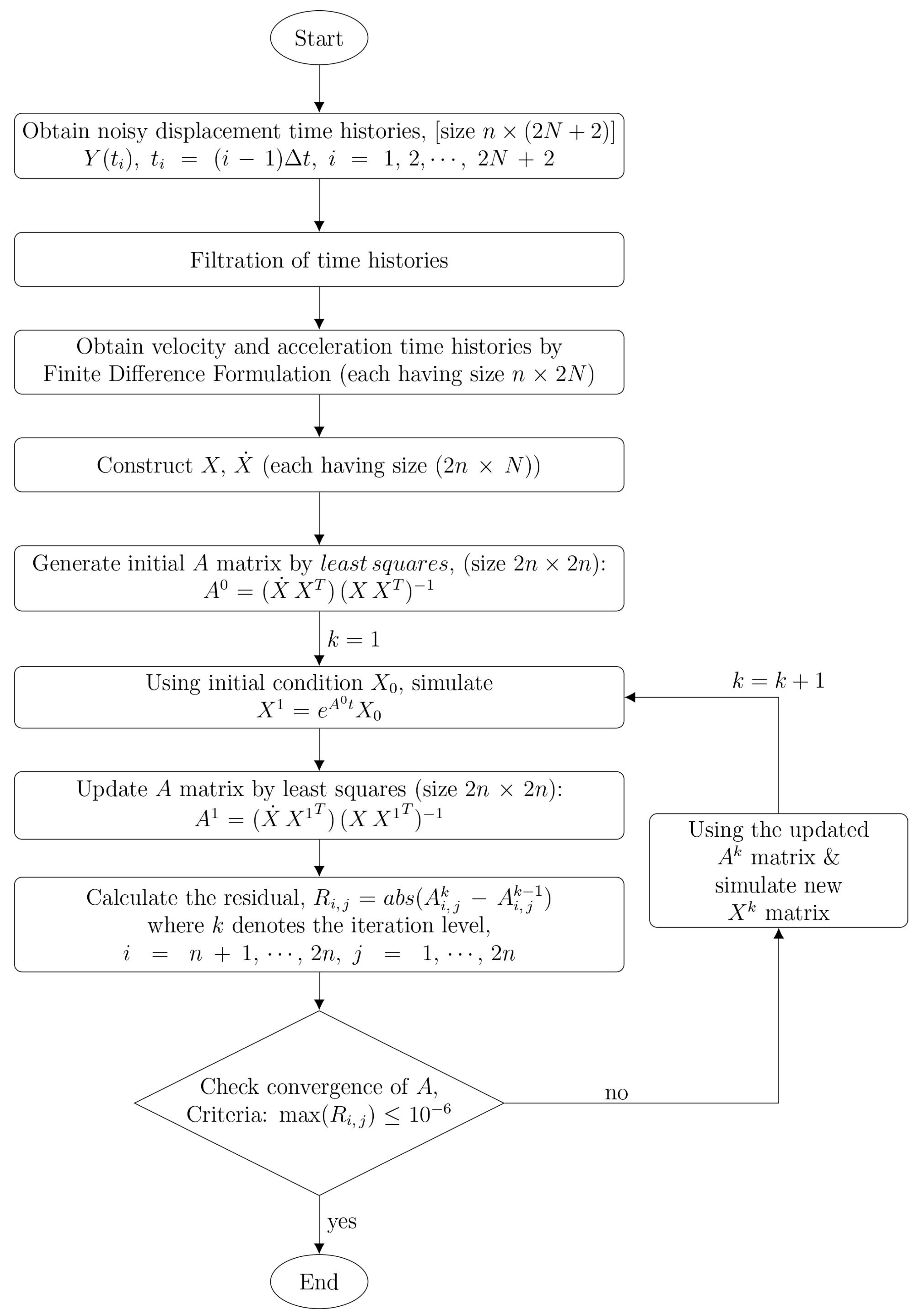
4.3. Iterative Least Squares (ILS)
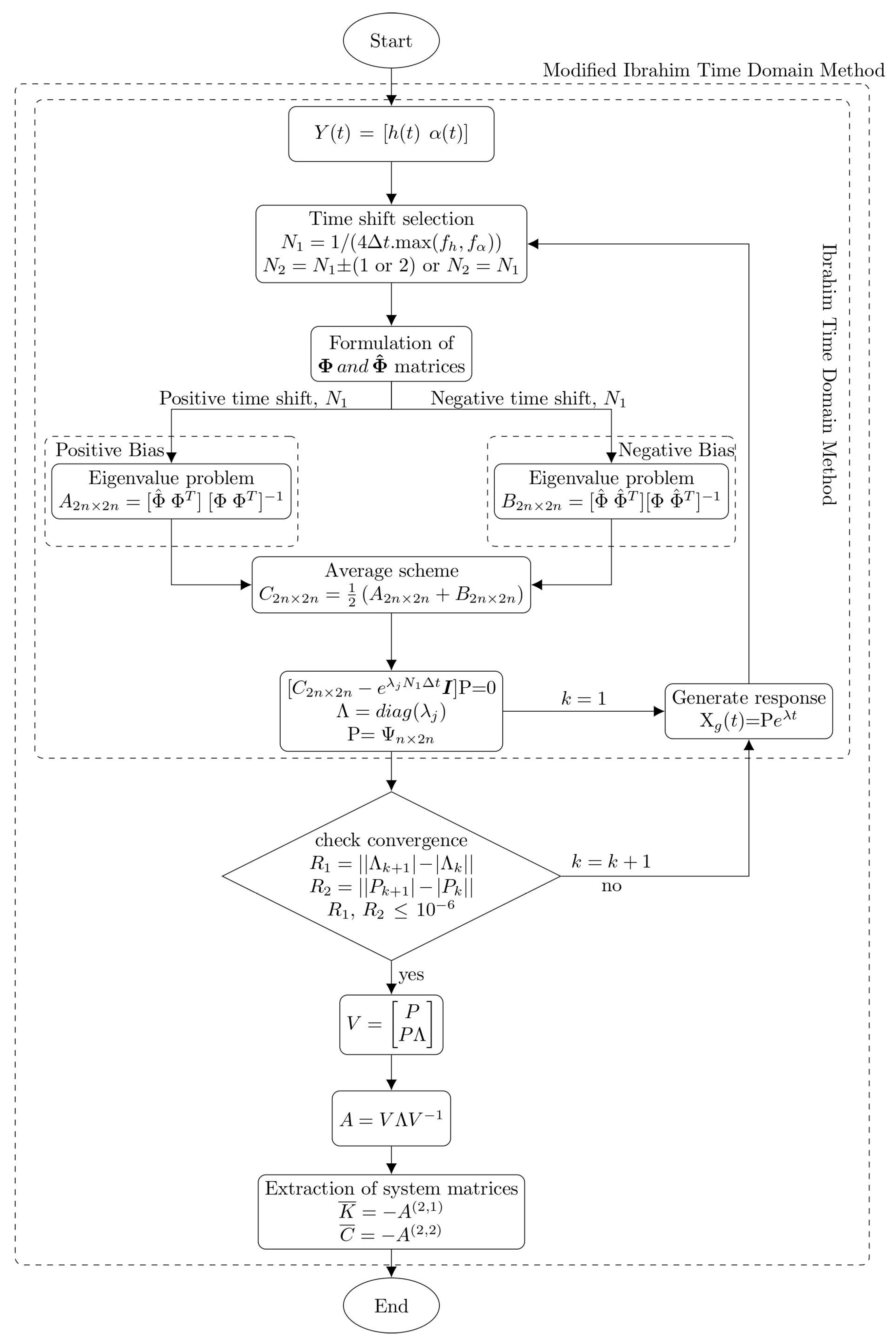
4.4. Modified Ibrahim Time Domain (MITD) Method
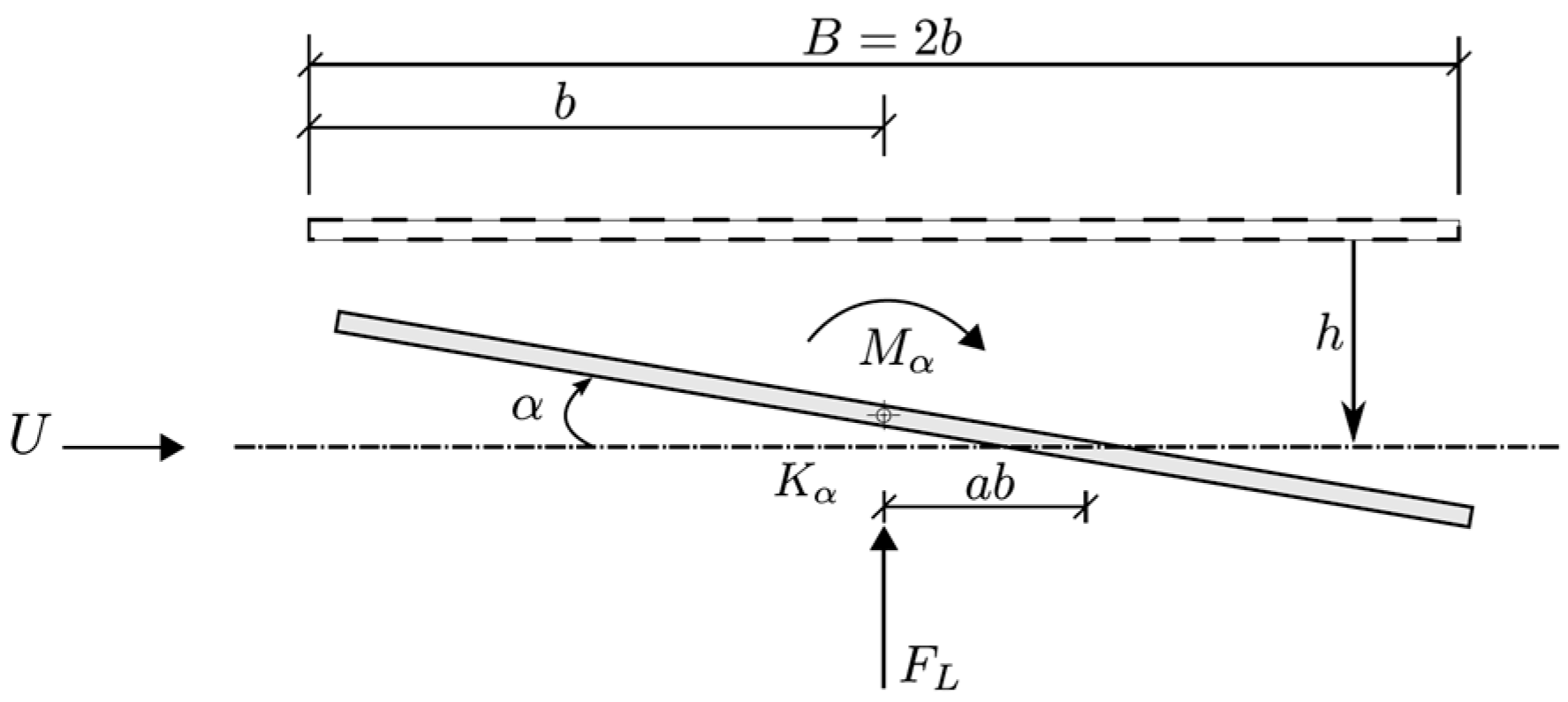
5. Experimental Program
5.1. Bridge Section Model for Wind Tunnel Test
5.2. Bauhaus-Universität Weimar Wind Tunnel Facility
5.3. Free Vibration Test Setup Arrangement
5.4. Test Setup Assembly
5.4.1. Single-Degree-of-Freedom Assembly
5.4.2. Two-Degree-of-Freedom Assembly
6. Experimental Procedure
- ■
- Check and adjust the horizontal position of the section model to zero angles of attack.
- ■
- Displace the section vertically, torsionally, or both using electromagnets.
- ■
- Generate wind flow of the desired velocity using a fan motor (range 0–20 m/s).
- ■
- Record vertical and torsional response of the section using accelerometers.
- ■
- Release the section and record the acceleration response until the motion is damped.
- ■
- Repeat the procedure for each experiment. The rotation angle is measured before releasing the section at higher wind speeds; the section experiences static aerodynamic moment, which can cause deflection in the section.
7. Signal Processing:
7.1. Single-Degree-of-Freedom Acceleration Response
7.2. Single-Degree-of-Freedom Displacement Response
7.3. Two-Degree-of-Freedom Acceleration Response
7.4. Two-Degree-of-Freedom Displacement Responses
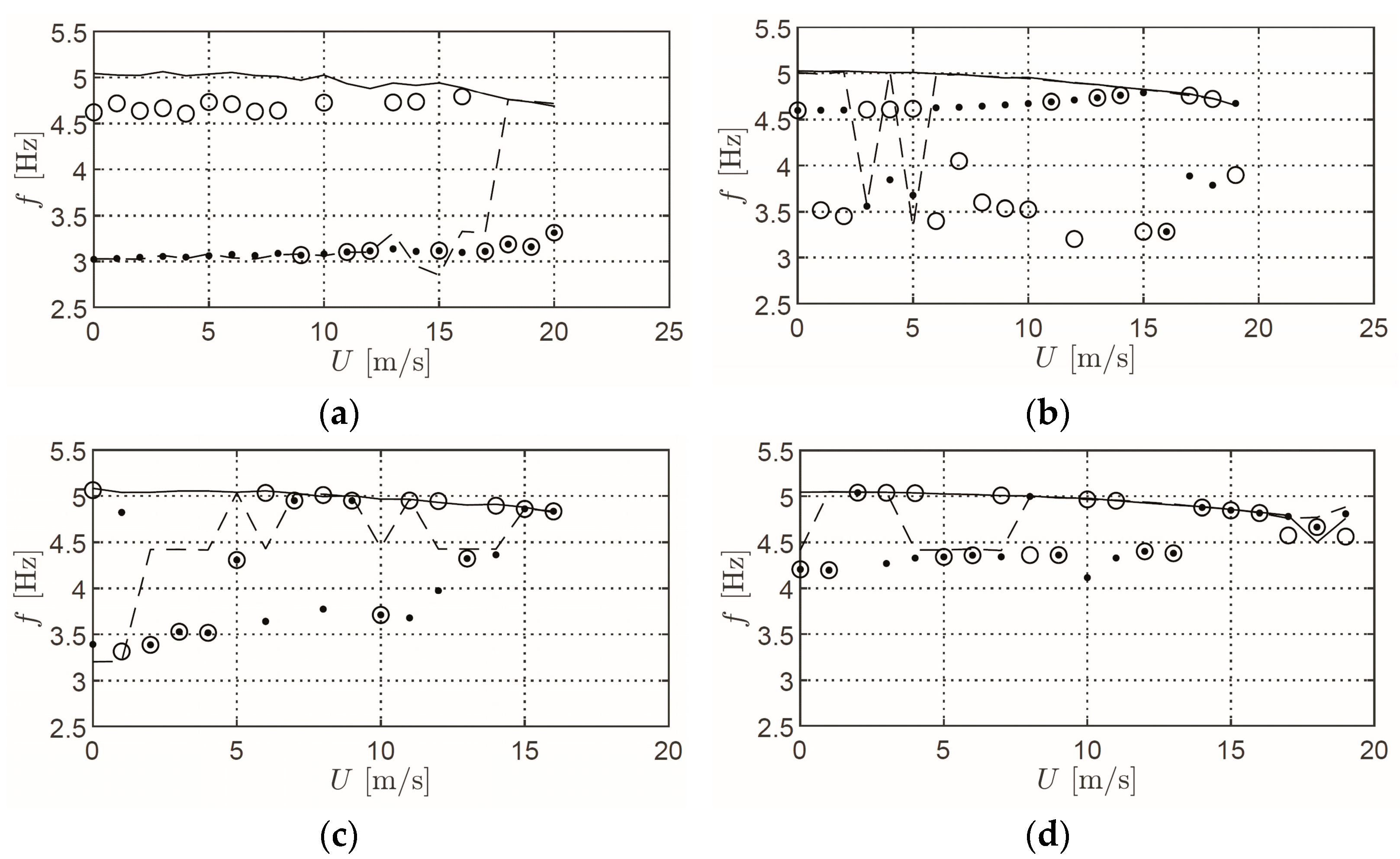
8. Results and Discussions
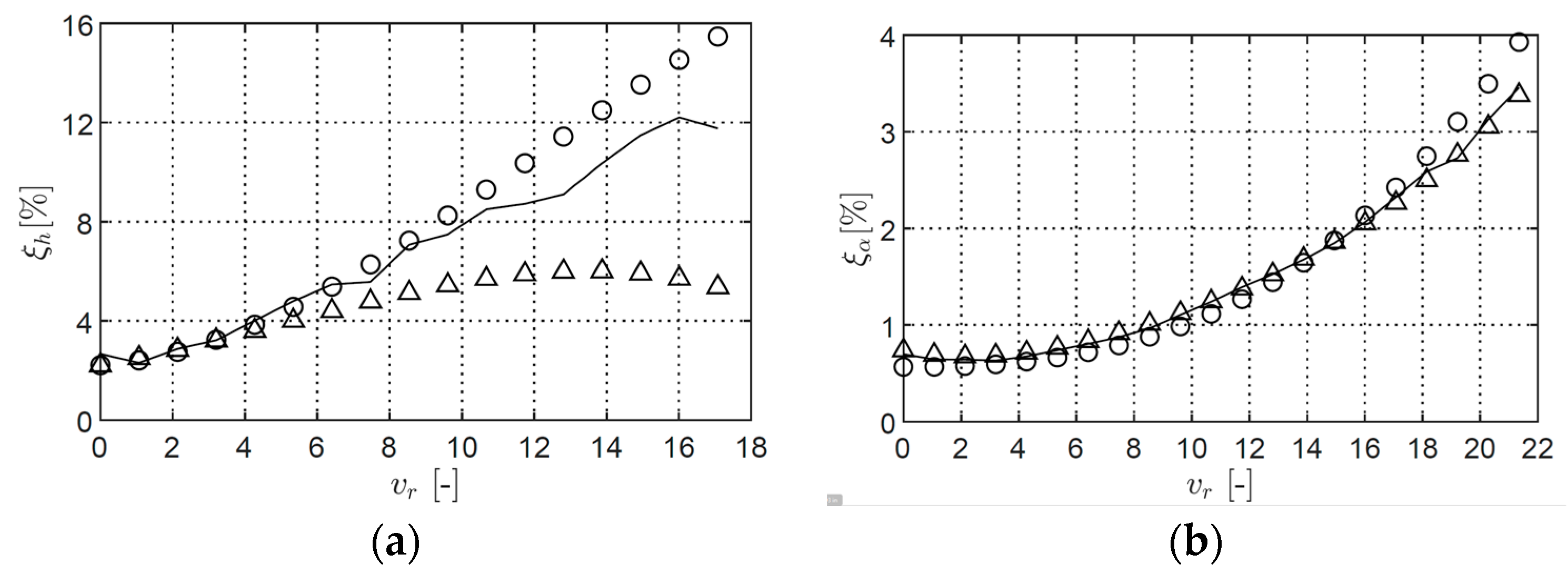
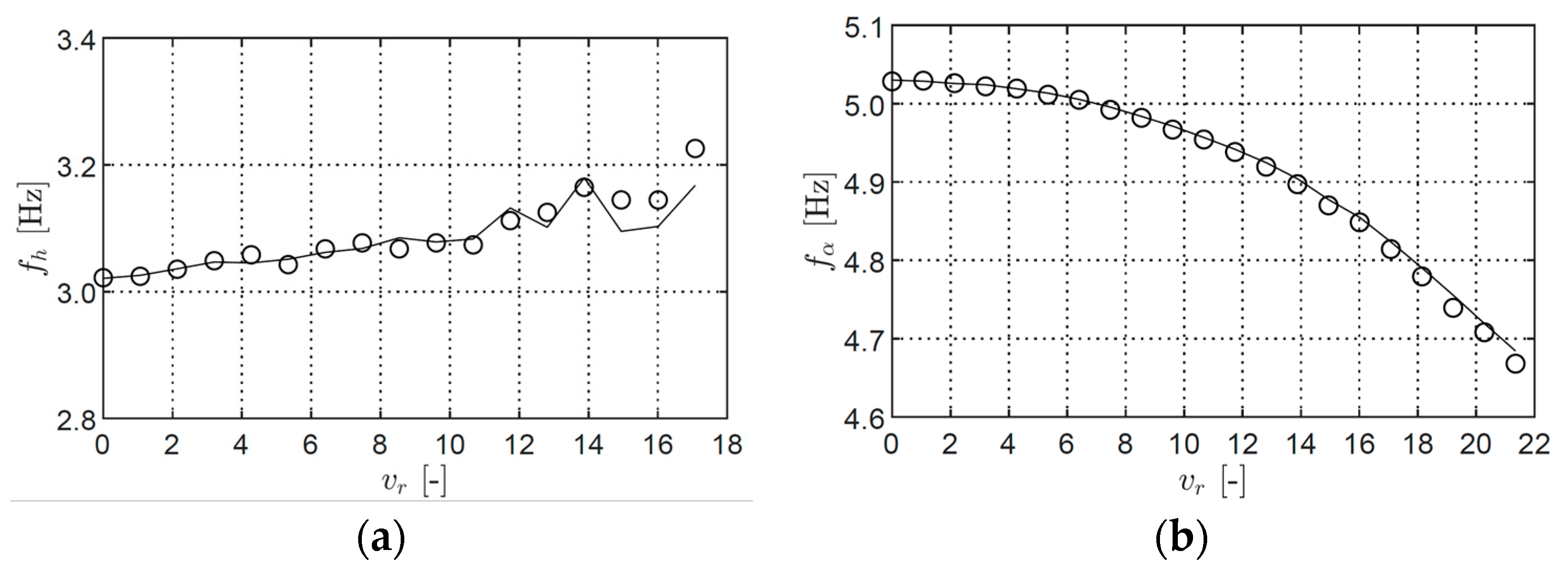
Identification of Stiffness and Damping
9. Identification of Flutter Derivatives from SDOF Tests
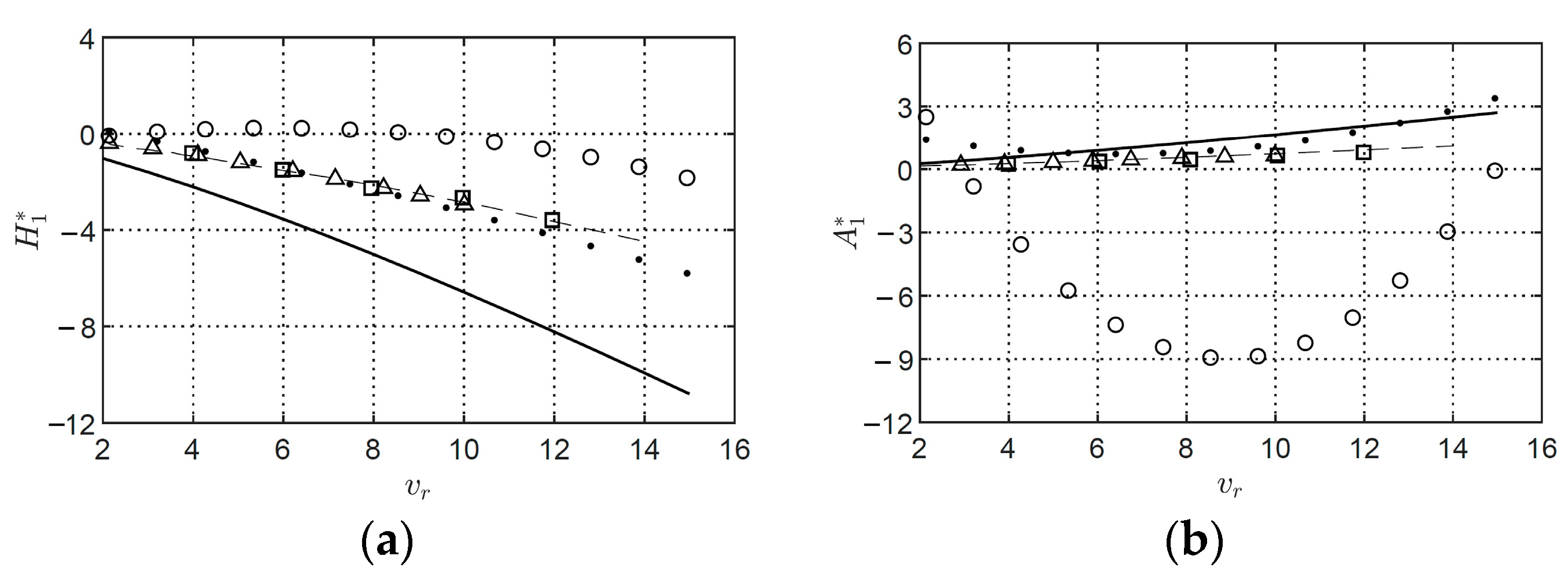
9.1. Flutter Derivatives Using the Hilbert Transform Method, Logarithmic Decrement Method, and Exponential Decay Curve Method
9.2. Flutter Derivatives Using the MITB and ILS Methods
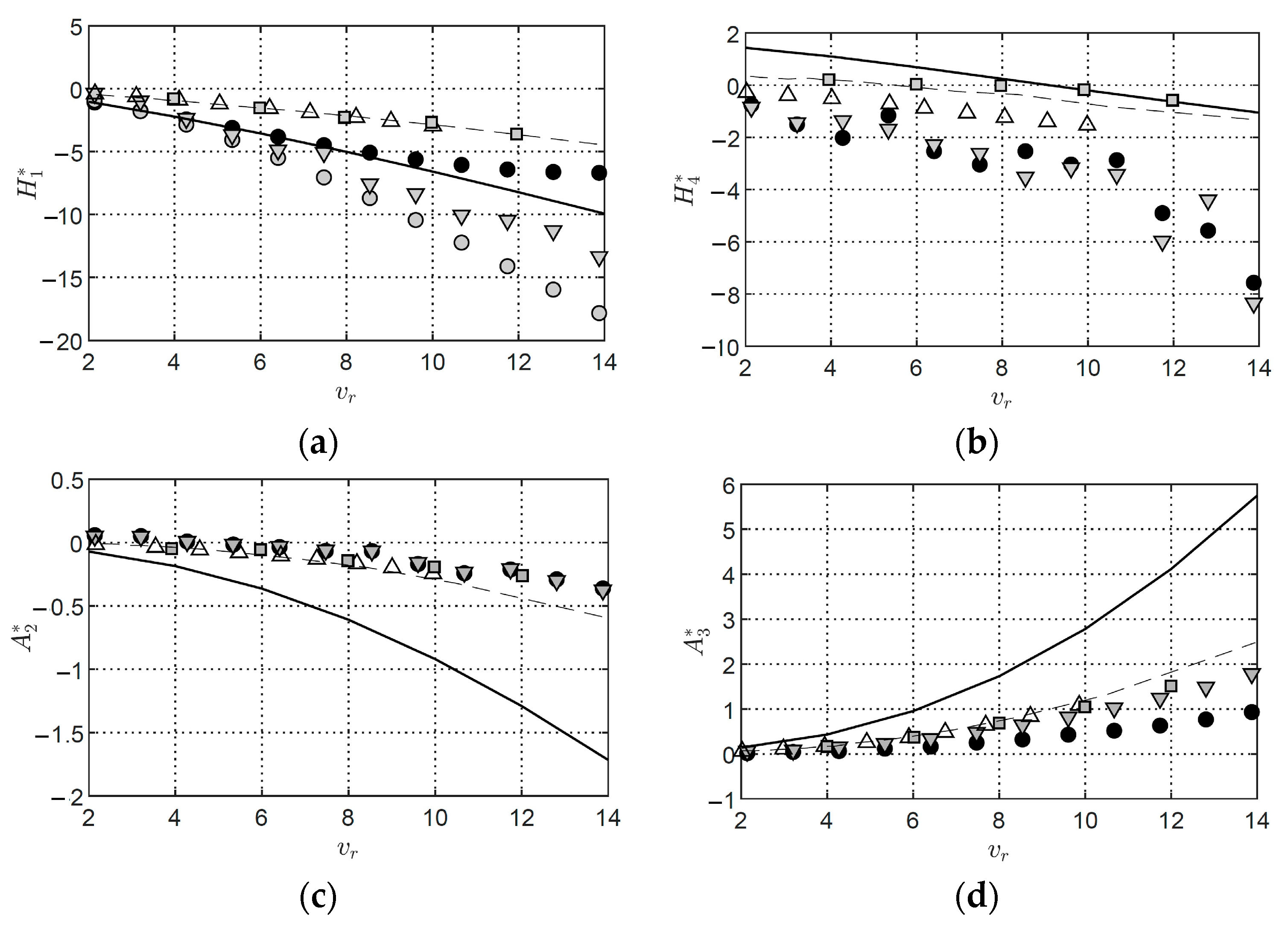
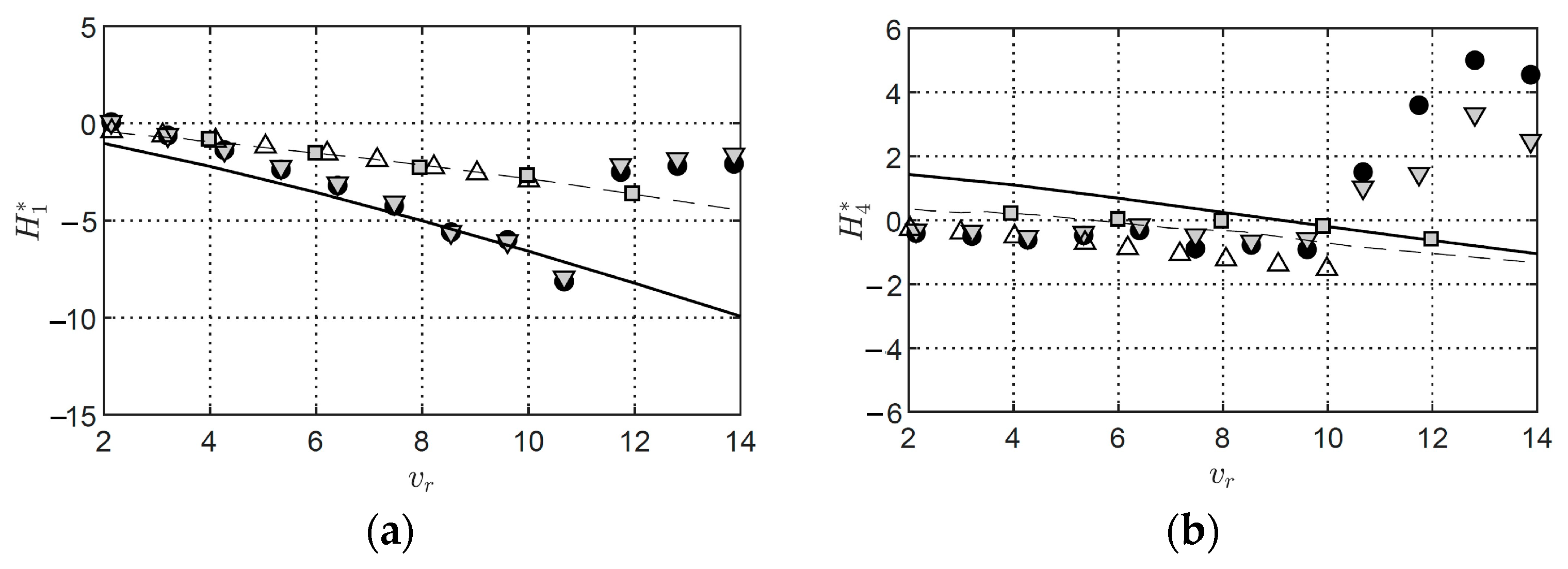
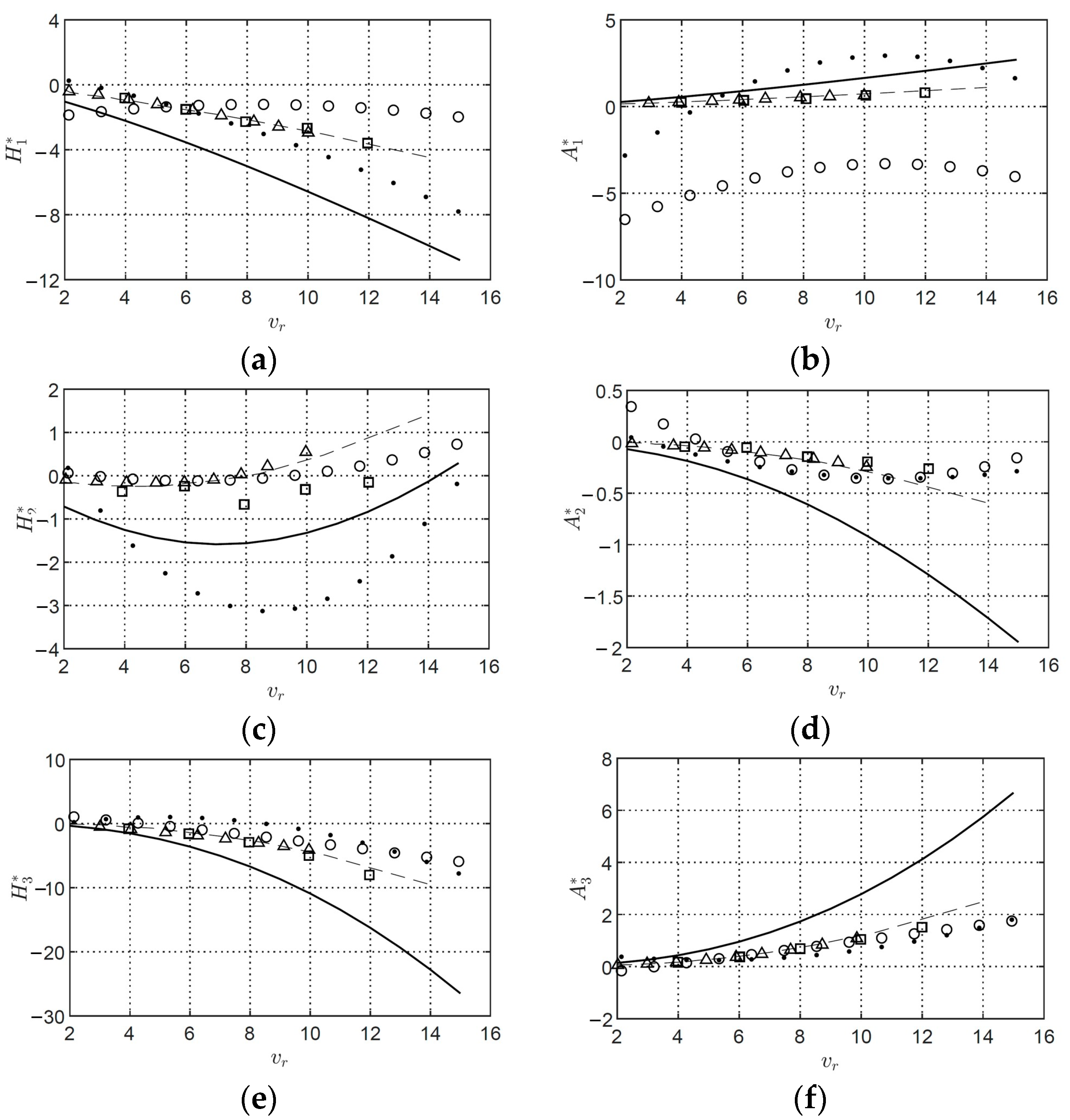
10. Identification of Flutter Derivatives from 2DOF Tests
10.1. Flutter Derivatives from MITD Method
10.2. Flutter Derivatives from ILS Method
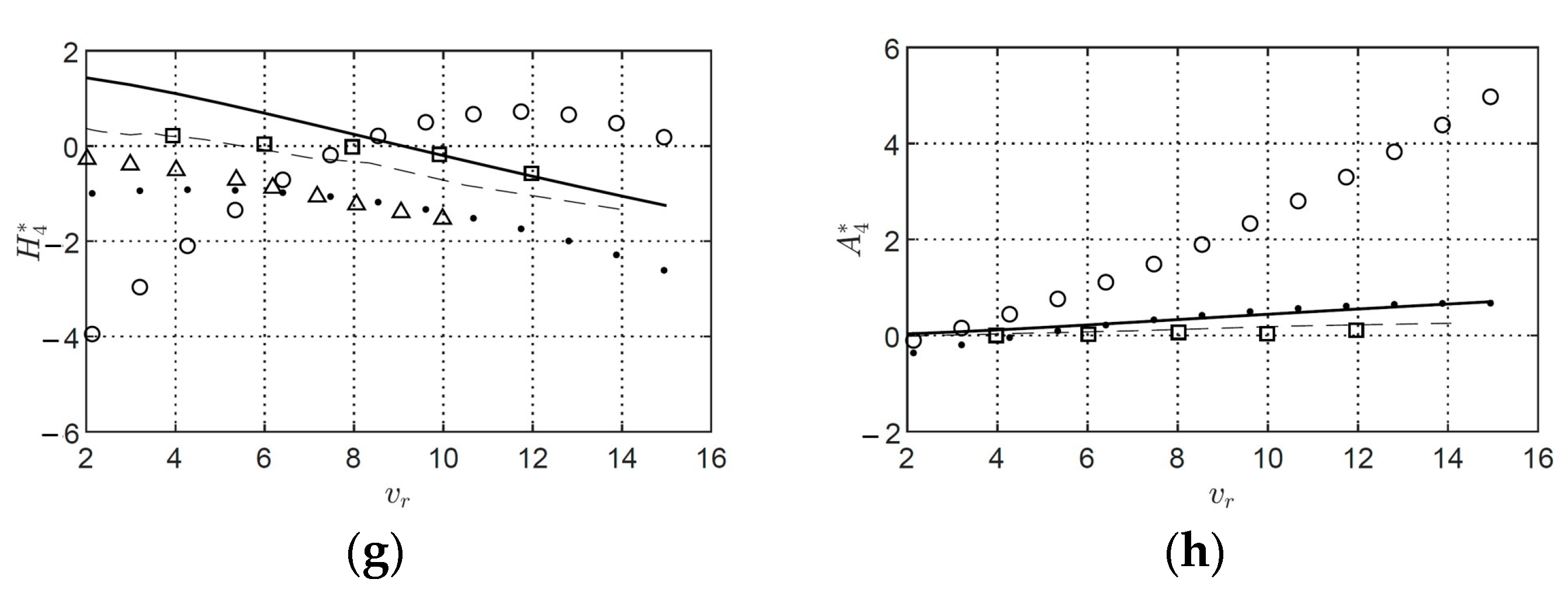
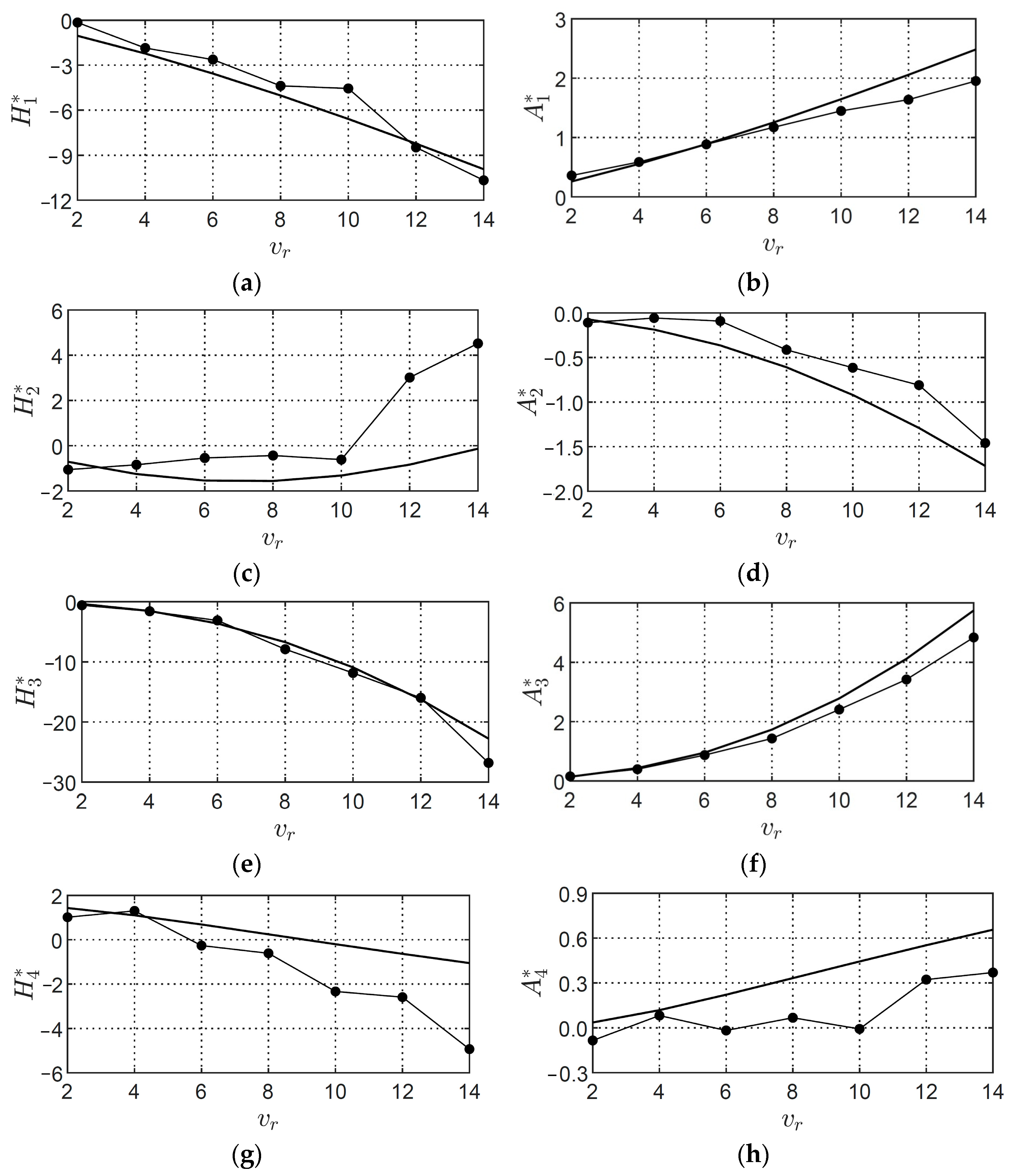
11. Numerical Identification of Flutter Derivatives Using VXFlow
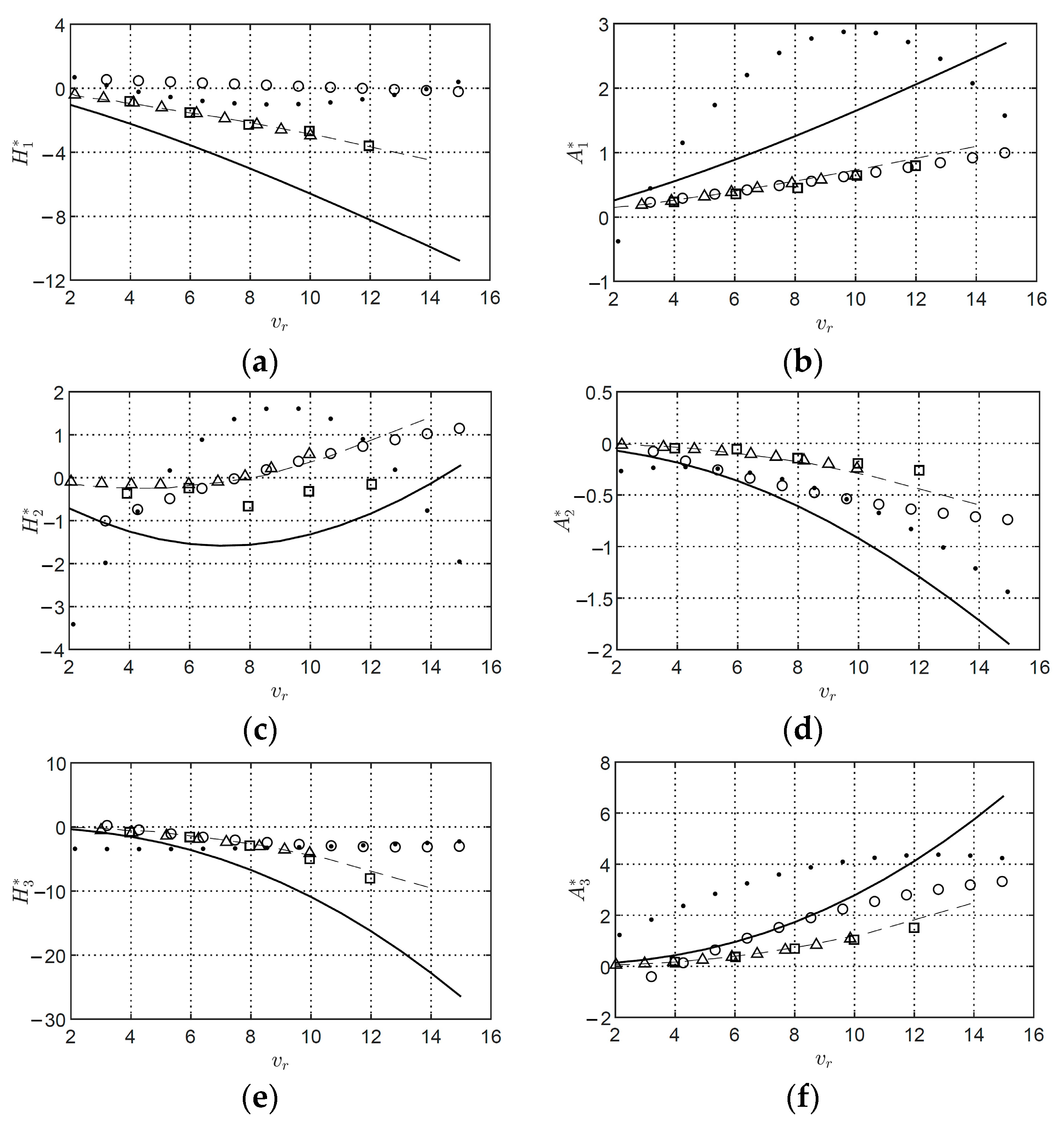
12. Validation of the Flutter Derivatives Extracted Using the MITD, ILS, and CFD Methods
13. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, K.; Javed, A.; Mustafa, A.E.; Saleem, A. Blast-Loading Effects on Structural Redundancy of Long-Span Suspension Bridge Using a Simplified Approach. Pract. Period. Struct. Des. Constr. 2022, 27, 04022024. [Google Scholar] [CrossRef]
- Ge, Y.J.; Xiang, H.F. Computational models and methods for aerodynamic flutter of long-span bridges. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1912–1924. [Google Scholar] [CrossRef]
- Hameed, A.; Rasool, A.M.; Ibrahim, Y.E.; Afzal, M.F.U.D.; Qazi, A.U.; Hameed, I. Utilization of Fly Ash as a Viscosity-Modifying Agent to Produce Cost-Effective, Self-Compacting Concrete: A Sustainable Solution. Sustainability 2022, 14, 11559. [Google Scholar] [CrossRef]
- Su, Y.; Di, J.; Li, S.; Jian, B.; Liu, J. Buffeting Response Prediction of Long-Span Bridges Based on Different Wind Tunnel Test Techniques. Appl. Sci. 2022, 12, 3171. [Google Scholar] [CrossRef]
- Afzal, M.F.U.D.; Matsumoto, Y.; Nohmi, H.; Sakai, S.; Su, D.; Nagayama, T. Comparison of Radar Based Displacement Measurement Systems with Conventional Systems in Vibration Measurements at a Cable Stayed Bridge, Osaka, Japan, August 2016. Available online: https://www.researchgate.net/publication/307932143 (accessed on 17 March 2023).
- Yu, H.; Xu, F.; Ma, C.; Zhou, A.; Zhang, M. Experimental research on the aerodynamic responses of a long-span pipeline suspension bridge. Eng. Struct. 2021, 245, 112856. [Google Scholar] [CrossRef]
- Javed, A.; Krishna, C.; Ali, K.; Afzal, M.F.U.D.; Mehrabi, A.; Meguro, K. Micro-Scale Experimental Approach for the Seismic Performance Evaluation of RC Frames with Improper Lap Splices. Infrastructures 2023, 8, 56. [Google Scholar] [CrossRef]
- Hua, X.; Wang, C.; Li, S.; Chen, Z. Experimental investigation of wind-induced vibrations of main cables for suspension bridges in construction phases. J. Fluids Struct. 2020, 93, 102846. [Google Scholar] [CrossRef]
- Ma, C.M.; Duan, Q.S.; Liao, H.L. Experimental investigation on aerodynamic behavior of a long span cable-stayed bridge under construction. KSCE J. Civ. Eng. 2018, 22, 2492–2501. [Google Scholar] [CrossRef]
- Cardenas, C.S.; Mantawy, I.M.; Azizinamini, A. Repair of Timber Piles Using Ultra-High-Performance Concrete: Investigation of Load Transfer and Load-Carrying Capacity. Transp. Res. Rec. J. Transp. Res. Board 2022, 036119812211211. [Google Scholar] [CrossRef]
- Ashraf, S.; Ali, M.; Shrestha, S.; Hafeez, M.A.; Moiz, A.; Sheikh, Z.A. Impacts of climate and land-use change on groundwater recharge in the semi-arid lower Ravi River basin, Pakistan. Groundw. Sustain. Dev. 2022, 17, 100743. [Google Scholar] [CrossRef]
- Arvan, P.A.; Arockiasamy, M. Energy-Based Approach: Analysis of a Vertically Loaded Pile in Multi-Layered Non-Linear Soil Strata. Geotechnics 2022, 2, 549–569. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, L.; Dong, M.; Sun, H. Analysis of wind-induced vibration of fluid-structure interaction system for isolated aqueduct bridge. Eng. Struct. 2013, 46, 28–37. [Google Scholar] [CrossRef]
- Javed, A.; Sadeghnejad, A.; Rehmat, S.; Yakel, A.; Azizinamini, A. Magnetic Flux Leakage (MFL) Method for Damage Detection in Internal Post-Tensioning Tendons; Florida International University: Miami, FL, USA, 2021. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, Z.; Zhu, S.; Hao, J.; Wang, J. Experimental Study of Mitigation of Wind-Induced Vibration in Asymmetric Cable-Stayed Bridge Using Sharp Wind Fairings. Appl. Sci. 2022, 12, 242. [Google Scholar] [CrossRef]
- Zhu, L.D.; Wang, M.; Wang, D.L.; Guo, Z.S.; Cao, F.C. Flutter and buffeting performances of Third Nanjing Bridge over Yangtze River under yaw wind via aeroelastic model test. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1579–1606. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, H.; Mo, W.; Li, Y. Flutter performance of box girders with different wind fairings at large angles of attack, Wind and Structures. Int. J. 2021, 32, 509–520. [Google Scholar] [CrossRef]
- Laima, S.; Li, H.; Chen, W.; Ou, J. Effects of attachments on aerodynamic characteristics and vortex-induced vibration of twin-box girder. J. Fluids Struct. 2018, 77, 115–133. [Google Scholar] [CrossRef]
- Tacoma Narrows Bridge (Sturdy Gertie)—HistoricBridges.org, (n.d.). Available online: https://historicbridges.org/bridges/browser/?bridgebrowser=washington/tacomanarrowsbridge/ (accessed on 6 March 2023).
- Ge, Y.; Zhao, L.; Cao, J. Case study of vortex-induced vibration and mitigation mechanism for a long-span suspension bridge. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104866. [Google Scholar] [CrossRef]
- Alamdari, M.M.; Rakotoarivelo, T.; Khoa, N.L.D. A spectral-based clustering for structural health monitoring of the Sydney Harbour Bridge. Mech. Syst. Signal Process. 2017, 87, 384–400. [Google Scholar] [CrossRef]
- Mustafa, A.E.; Javed, A.; Ali, K. Safety Assessment of Cables of Suspension Bridge under Blast Load. Struct. Congr. 2022 2022, 2022, 79–93. [Google Scholar] [CrossRef]
- Javed, A.; Mantawy, I.M.; Azizinamini, A. 3D-Printing of Ultra-High-Performance Concrete for Robotic Bridge Construction. SAGE J. 2021, 2675, 307–319. [Google Scholar] [CrossRef]
- Fei, H.; Deng, Z.; Dan, D. Vertical Vibrations of Suspension Bridges: A Review and a New Method. Arch. Comput. Methods Eng. 2021, 28, 1591–1610. [Google Scholar] [CrossRef]
- Larsen, A.; Larose, G.L. Dynamic wind effects on suspension and cable-stayed bridges. J. Sound Vib. 2015, 334, 2–28. [Google Scholar] [CrossRef]
- Weber, F.; Maślanka, M. Frequency and damping adaptation of a TMD with controlled MR damper. Smart Mater. Struct. 2012, 21, 055011. [Google Scholar] [CrossRef]
- Fujino, Y.; Siringoringo, D. Vibration mechanisms and controls of long-span bridges: A review. Struct. Eng. Int. 2013, 23, 248–268. [Google Scholar] [CrossRef]
- Battista, R.C.; Pfeil, L.S. Reduction of vortex-induced oscillations of Rio–Niterói bridge by dynamic control devices. J. Wind. Eng. Ind. Aerodyn. 2000, 84, 273–288. [Google Scholar] [CrossRef]
- Larsen, A.; Danish Maritime Institute. Aerodynamics of Large Bridges: Proceedings of the First International Symposium on Aerodynamics of Large Bridges; Routledge: Copenhagen, Denmark, 1992. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter. 1949; NASA Technical Reports Server (NTRS). Available online: https://ntrs.nasa.gov/citations/19930090935 (accessed on 6 March 2023).
- Assessment of Numerical Prediction Models for Aeroelastic Instabilities of Bridges. Available online: https://www.researchgate.net/publication/325165262_Assessment_of_Numerical_Prediction_Models_for_Aeroelastic_Instabilities_of_Bridges (accessed on 6 March 2023).
- Chowdhury, A.G.; Sarkar, P.P. Identification of Eighteen Flutter Derivatives of an Airfoil and a Bridge Deck. Wind. Struct. 2004, 7, 187–202. [Google Scholar] [CrossRef]
- Chowdhury, A.G.; Sarkar, P.P. A new technique for identification of eighteen flutter derivatives using a three-degree-of-freedom section model. Eng. Struct. 2003, 25, 1763–1772. [Google Scholar] [CrossRef]
- Sarkar, B.P.P.; Member, A.; Jones, N.P.; Scanlan, R.H.; Member, H. Identification of aeroelastic parameters of flexible bridges. J. Eng. Mech. 1994, 120, 1718–1742. [Google Scholar] [CrossRef]
- Kavrakov, I.; Morgenthal, G. A synergistic study of a CFD and semi-analytical models for aeroelastic analysis of bridges in turbulent wind conditions. J. Fluids Struct. 2018, 82, 59–85. [Google Scholar] [CrossRef] [Green Version]
- Cassaro, M.; Cestino, E.; Frulla, G.; Marzocca, P.; Pertile, M. Experimental Determi-nation of Aeroelastic Derivatives for a Small-Scale Bridge Deck. Int. J. Mech. 2018, 12, 67–68. Available online: https://hal.science/hal-02315065 (accessed on 6 March 2023).
- Larsen, A. Aerodynamic aspects of the final design of the 1624 m suspension bridge across the Great Belt. J. Wind. Eng. Ind. Aerodyn. 1993, 48, 261–285. [Google Scholar] [CrossRef]
- Frandsen, J.B. Simultaneous Pressures and Accelerations Measured Full-Scale on the Great Belt East Suspension Bridge. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 95–129. [Google Scholar] [CrossRef]
- Bauhaus-Universität Weimar: Research Equipment. Available online: https://www.uni-weimar.de/en/civil-engineering/chairs/modelling-and-simulation-of-structures/research/research-equipment/ (accessed on 6 March 2023).
- Yang, C.; Xia, Y. A novel two-step strategy of non-probabilistic multi-objective optimization for load-dependent sensor placement with interval uncertainties. Mech. Syst. Signal Process. 2022, 176, 109173. [Google Scholar] [CrossRef]
- Yang, C.; Ouyang, H. A novel load-dependent sensor placement method for model updating based on time-dependent reliability optimization considering multi-source uncertainties. Mech. Syst. Signal Process. 2022, 165, 108386. [Google Scholar] [CrossRef]
- Larsen, A.; Walther, J.H. Discrete vortex simulation of flow around five generic bridge deck sections. J. Wind. Eng. Ind. Aerodyn. 1998, 77, 591–602. [Google Scholar] [CrossRef]
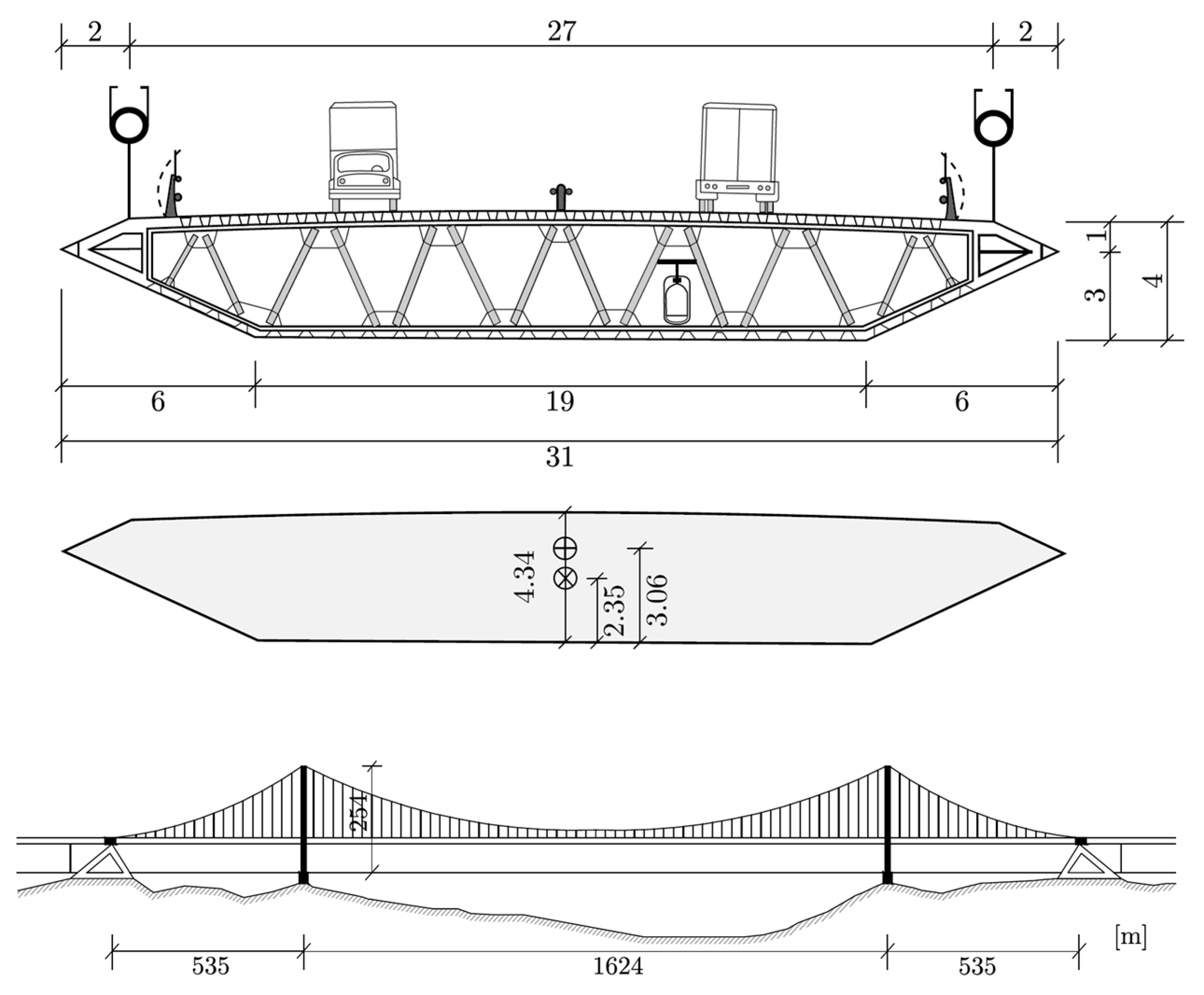

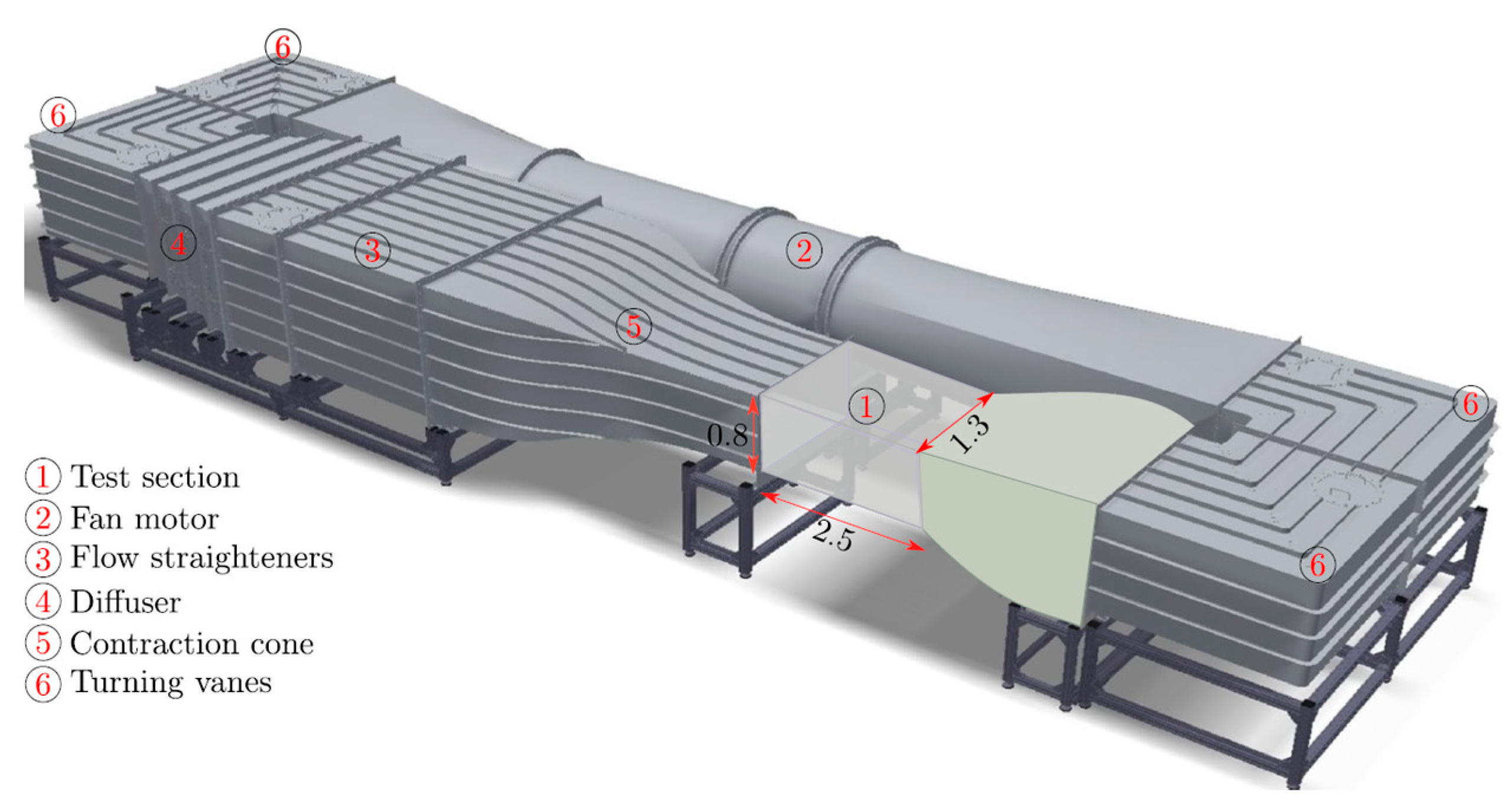
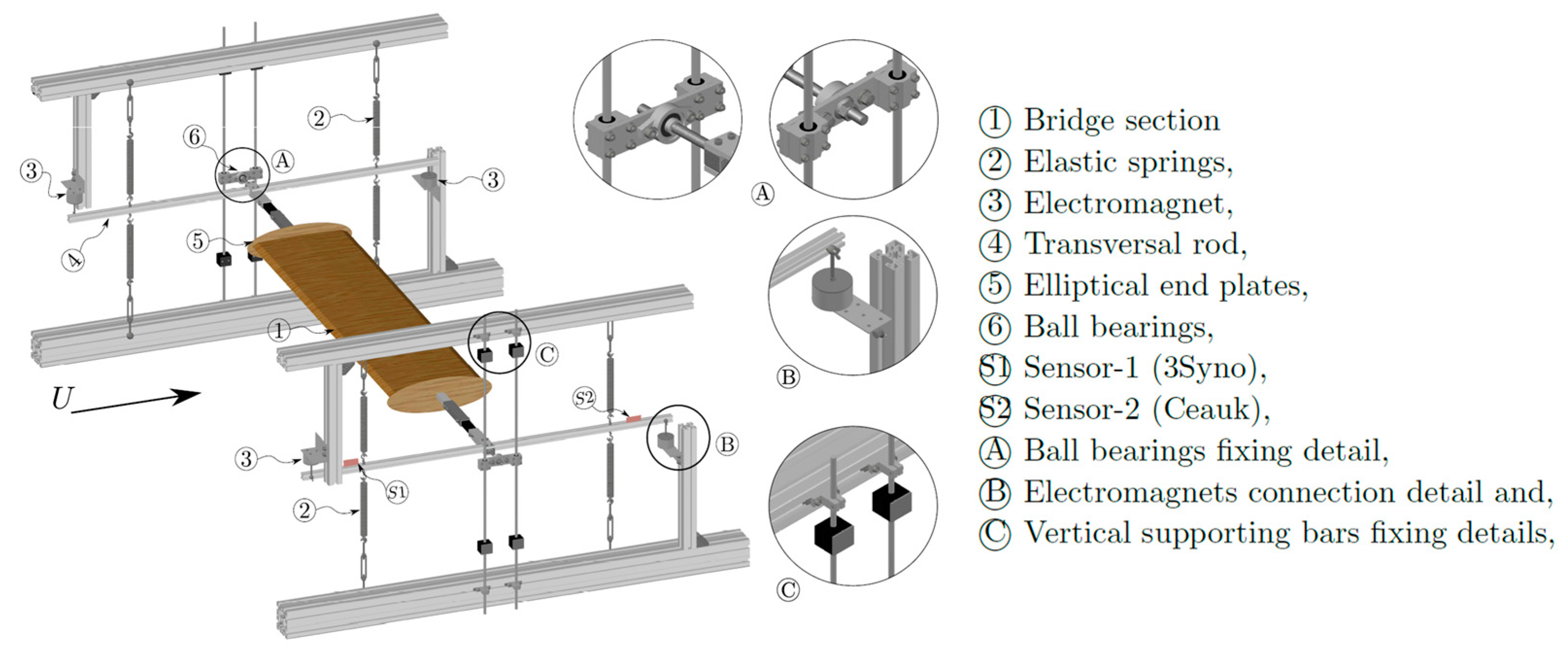
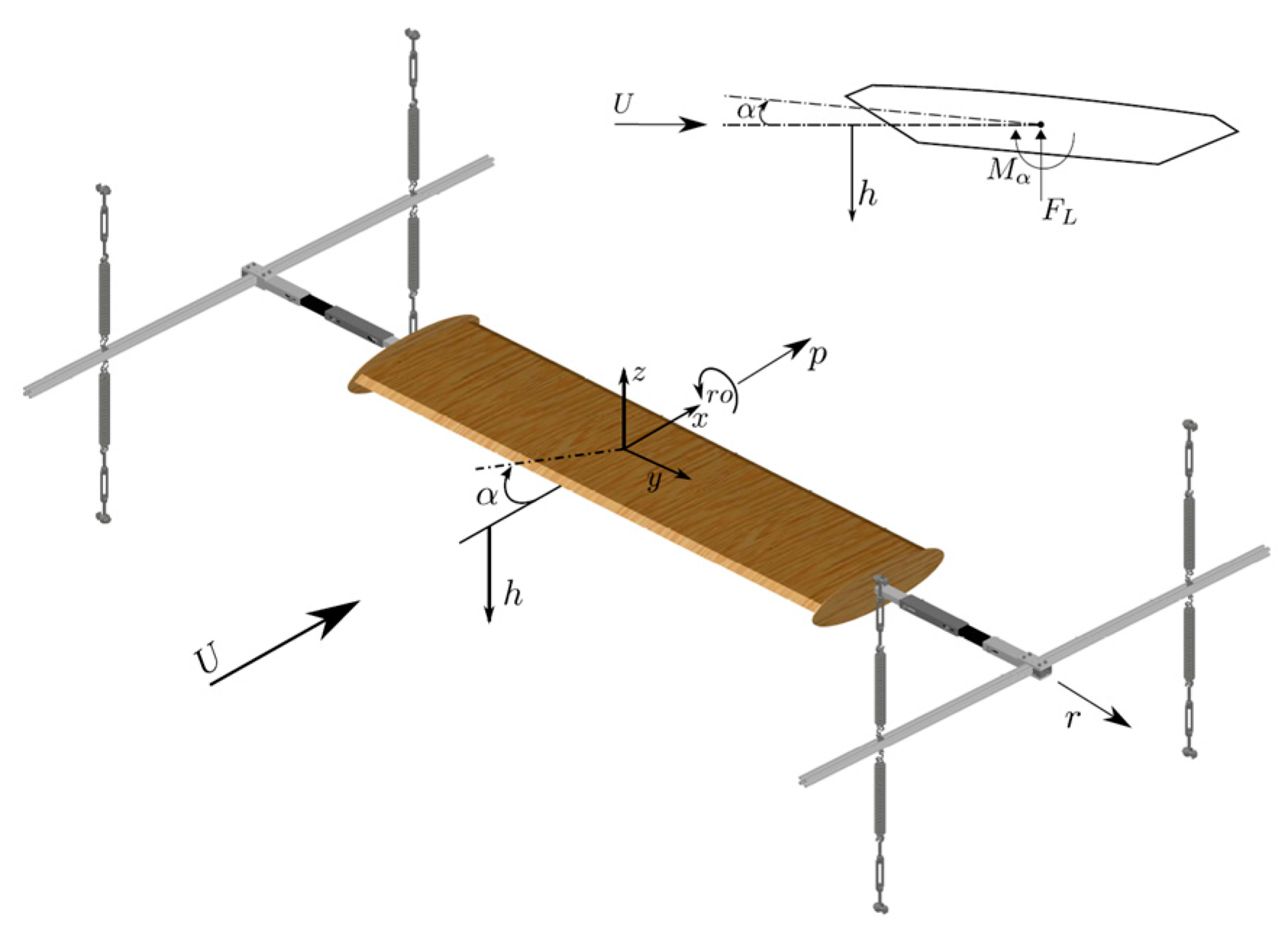



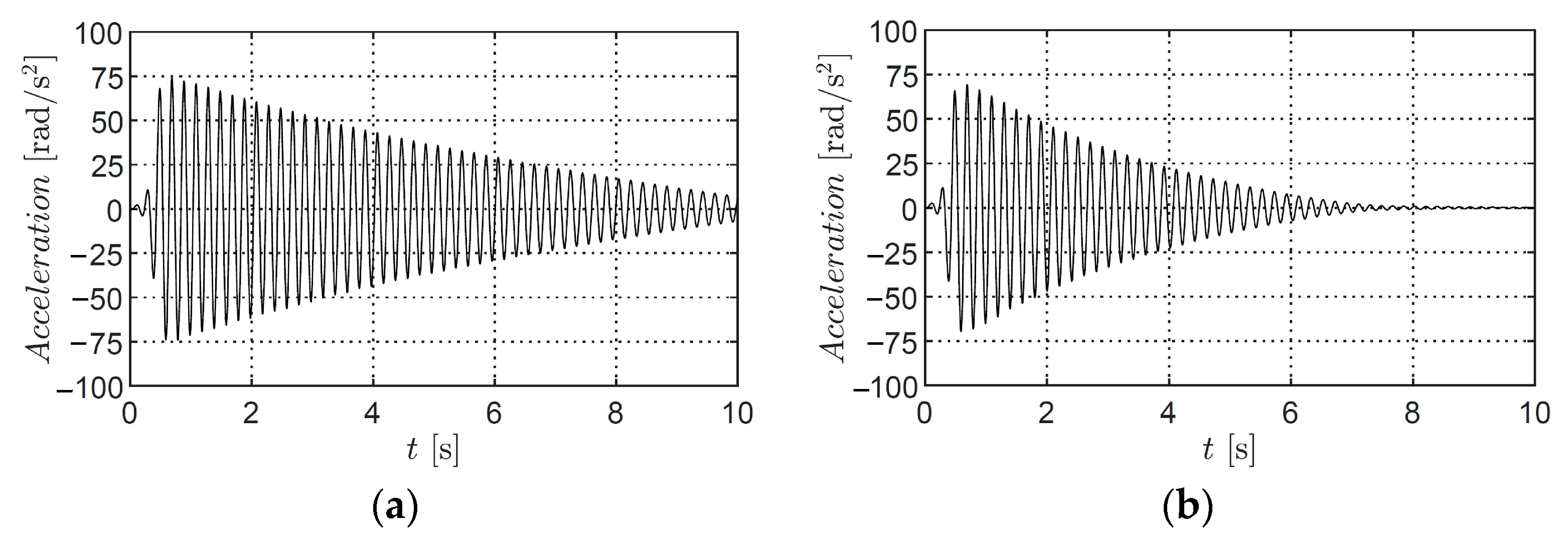
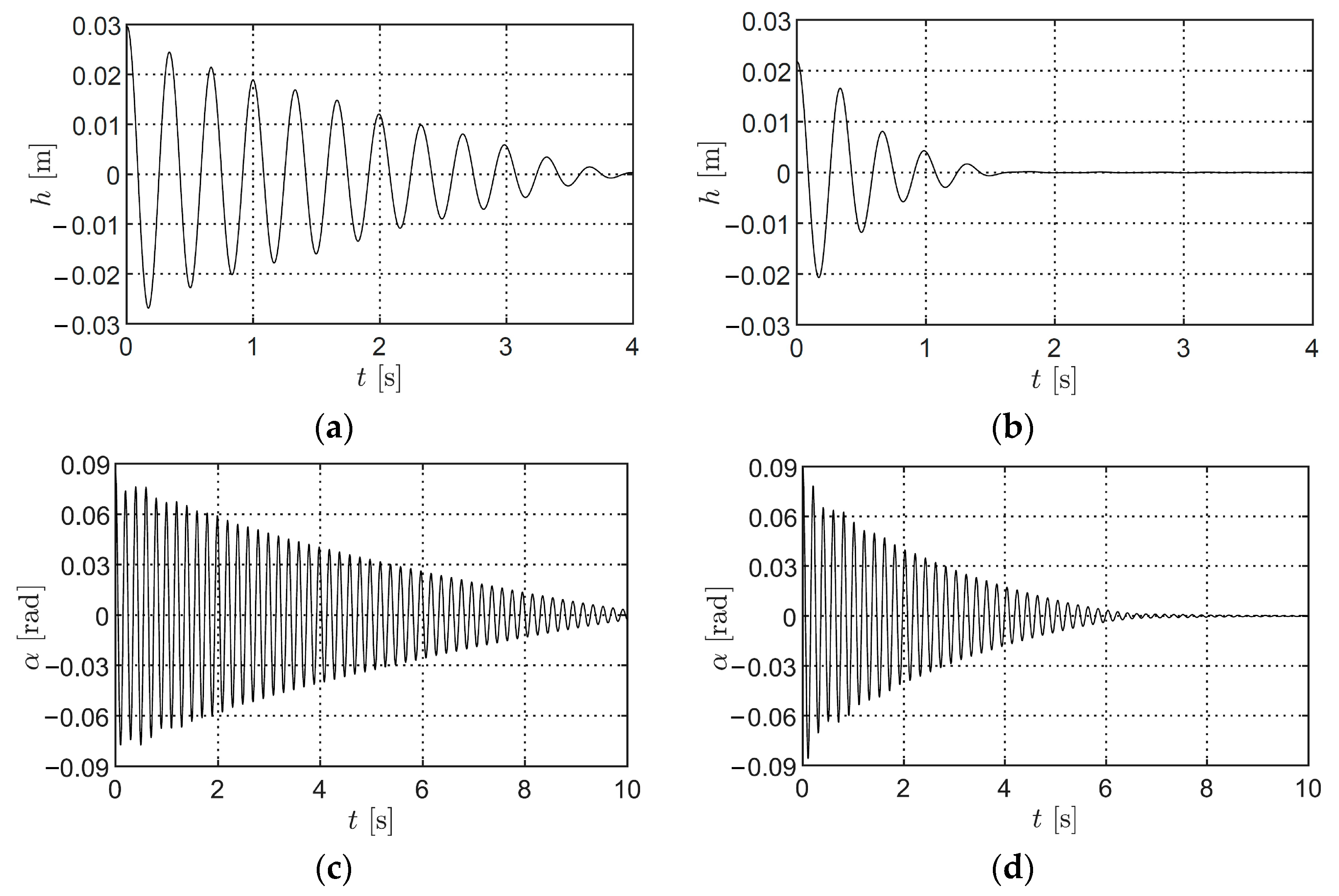

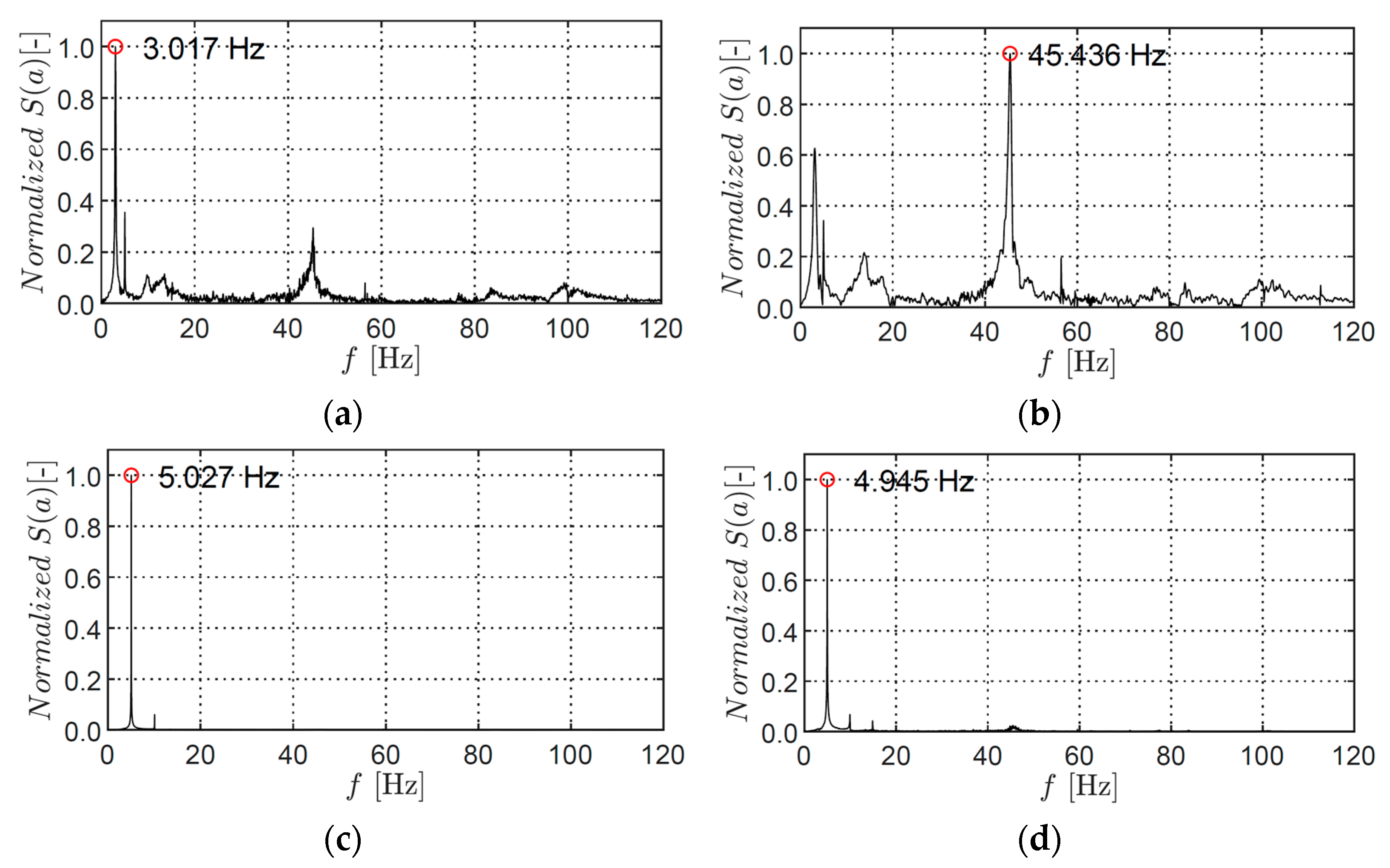
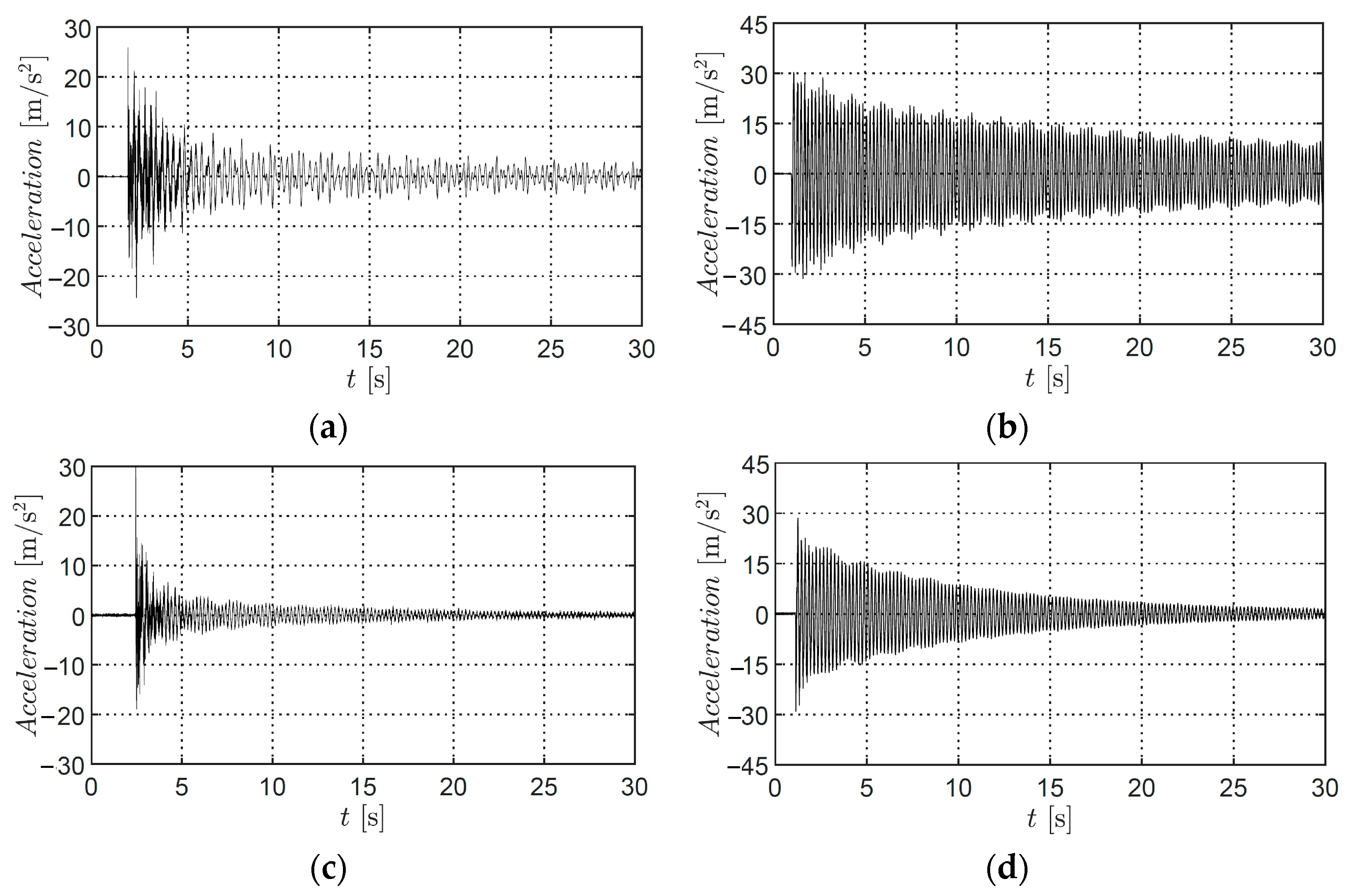
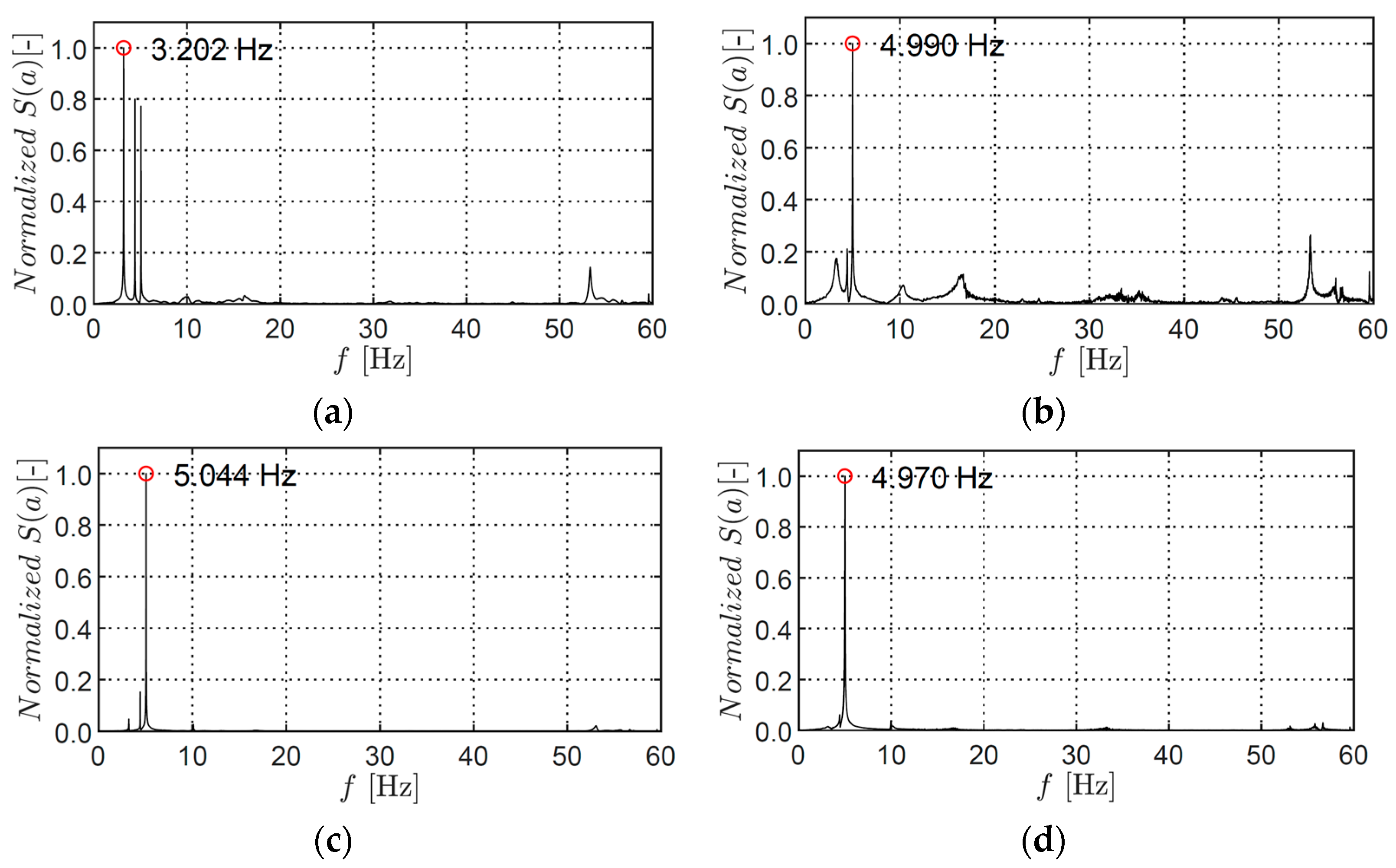
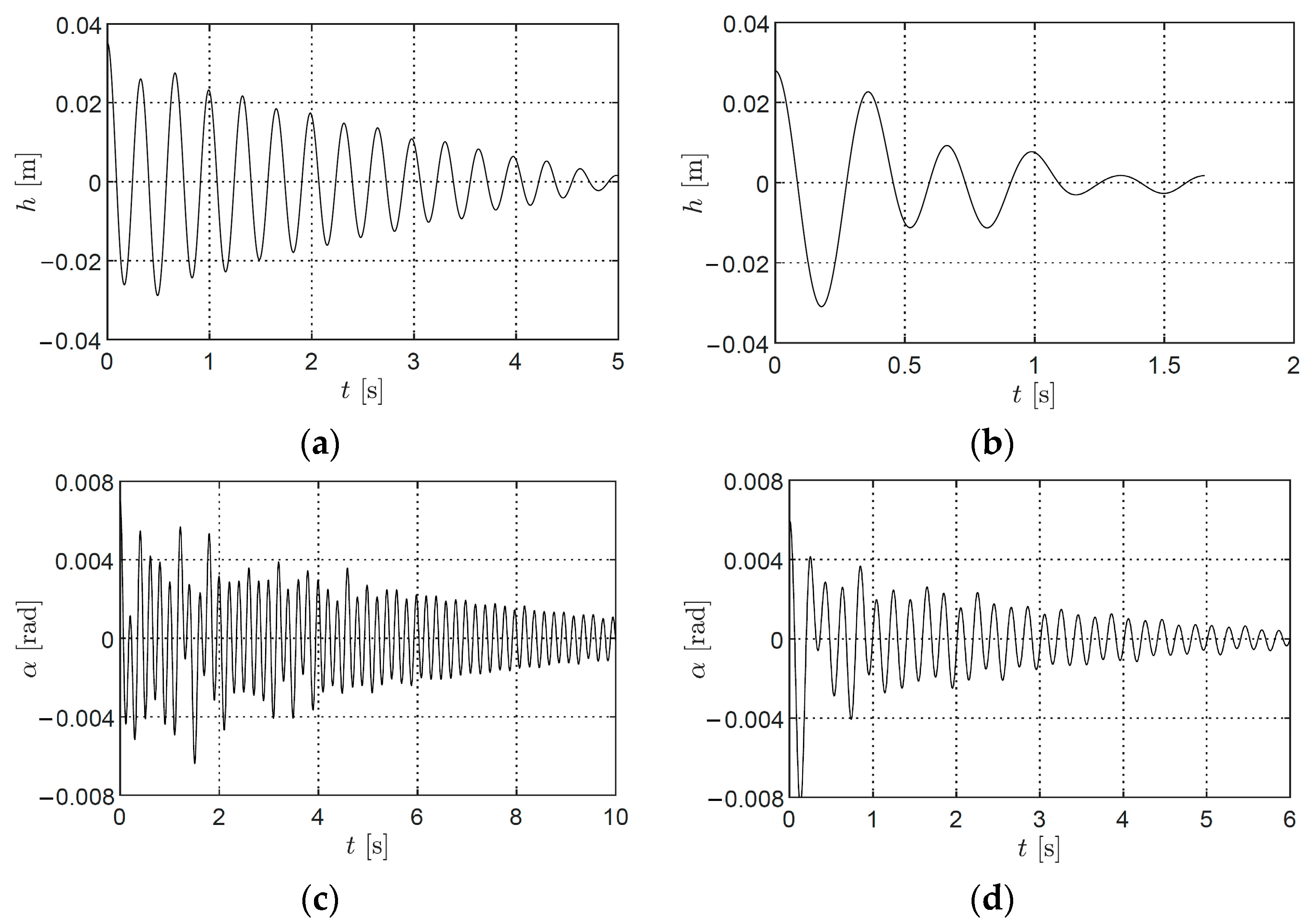
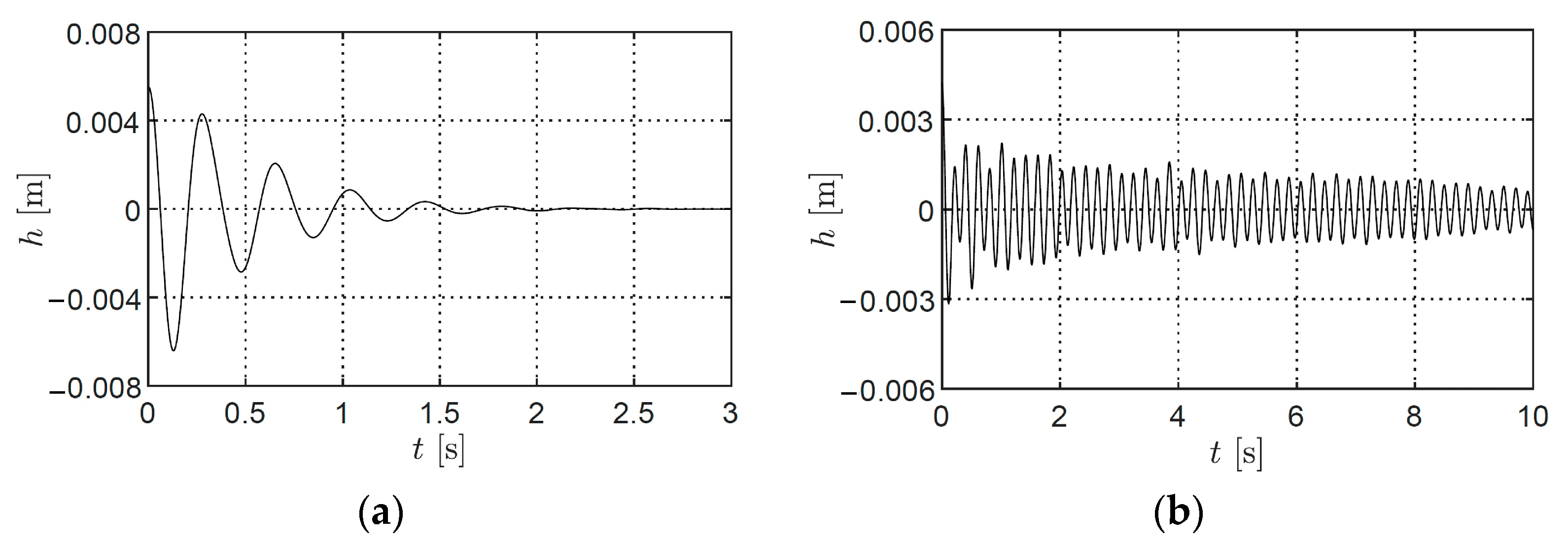
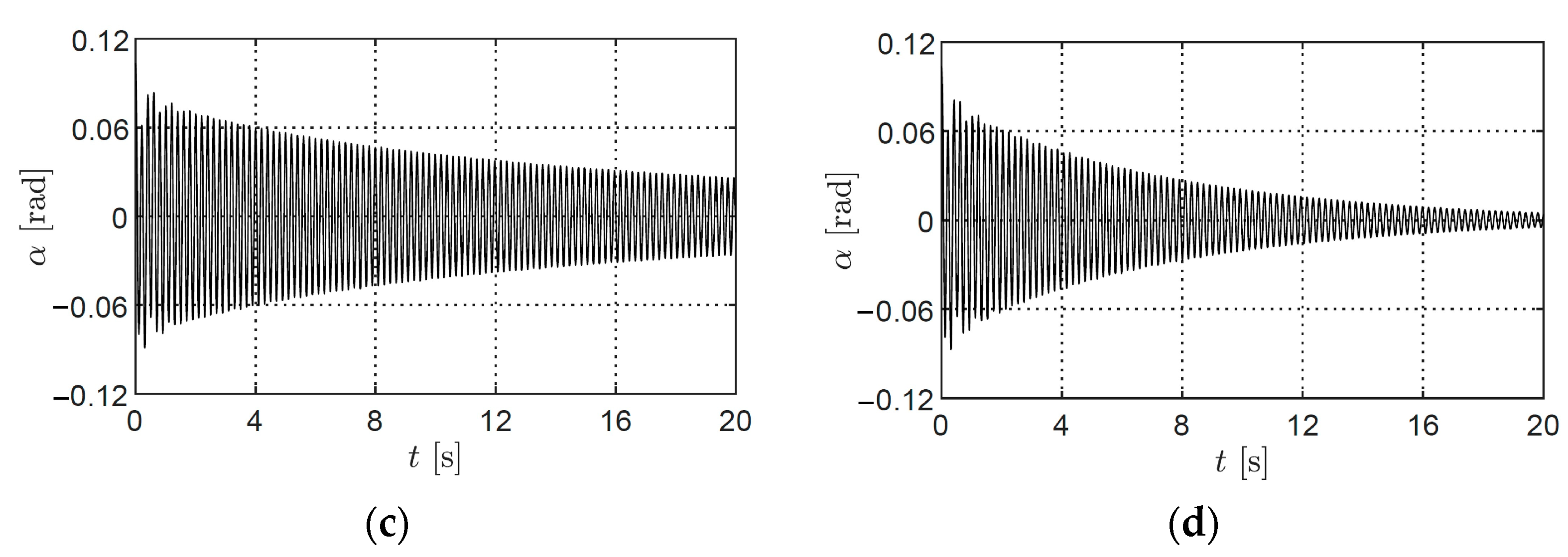



| Structural Parameter | Symbol | Value |
|---|---|---|
| Total span | lspan | 2694 m |
| Deck width | B | 31 m |
| Deck depth | D | 4.4 m |
| Mass | M | 22.74 t/m |
| Mass moment of inertia | I | 2.47 × 103 tm2/m |
| First vertical frequency | fh | 0.10 Hz |
| First torsional frequency | fa | 0.78 Hz |
| B (m) | mh (kg) | Iα (kgm2) | fh (Hz) | fα (Hz) | * kg/m3 | ξh (%) | ξα (%) |
|---|---|---|---|---|---|---|---|
| Logarithmic Decrement Method | |||||||
| 0.31 | 4.348 | 0.0906 | 3.022 | 5.028 | 1.145 | 2.208 | 0.738 |
| Exponential Curve Decay Method | |||||||
| 0.31 | 4.348 | 0.0906 | 3.022 | 5.028 | 1.145 | 2.216 | 0.567 |
| Hilbert Transform Method | |||||||
| 0.31 | 4.348 | 0.0906 | 3.021 | 5.030 | 1.145 | 2.670 | 0.698 |
| B (m) | mh (kg) | Iα (kgm2) | fh (Hz) | fα (Hz) | * kg/m3 | ξh (%) | ξα (%) |
|---|---|---|---|---|---|---|---|
| Test Setup 1 | |||||||
| 0.31 | 4.348 | 0.0906 | 3.017 | 5.027 | 1.145 | 1.83 | 0.22 |
| Test Setup 2 | |||||||
| 0.31 | 3.825 | 0.1256 | 3.202 | 5.044 | 1.145 | 1.75 | 0.49 |
| Motion | Stiffness Matrix | Damping Matrix | ||
|---|---|---|---|---|
| Setup 1 | ||||
| Heave-Dominant | 361.09 | −0.8605 | 0.698 | −0.0421 |
| −11.517 | 984.73 | 0.1694 | 0.1783 | |
| Pitch-Dominant | 491.62 | 0.4308 | 0.2169 | −0.0099 |
| 1036.9 | 9928.83 | −31.79 | 0.1751 | |
| Setup 2 | ||||
| Heave-Dominant | 454.06 | −3.61 | 0.2117 | −0.0896 |
| −13.63 | 1011.6 | 0.1871 | 0.174 | |
| Pitch-Dominant | 698.76 | 1.078 | 0.9287 | −0.0614 |
| 4.947 | 1003.8 | 0.1224 | 0.0734 | |
| Motion | Stiffness Matrix | Damping Matrix | ||
|---|---|---|---|---|
| Setup 1 | ||||
| Heave-Dominant | −360.567 | 5.885 | −0.8407 | −0.3517 |
| 18.667 | −979.77 | −0.5524 | −0.6884 | |
| Pitch-Dominant | −461.608 | −0.7175 | −3.731 | 0.0305 |
| 969.21 | −978.34 | −75.761 | −0.0806 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awan, M.S.; Javed, A.; Afzal, M.F.U.D.; Vilchez, L.F.N.; Mehrabi, A. Evaluation of System Identification Methods for Free Vibration Flutter Derivatives of Long-Span Bridges. Appl. Sci. 2023, 13, 4672. https://doi.org/10.3390/app13084672
Awan MS, Javed A, Afzal MFUD, Vilchez LFN, Mehrabi A. Evaluation of System Identification Methods for Free Vibration Flutter Derivatives of Long-Span Bridges. Applied Sciences. 2023; 13(8):4672. https://doi.org/10.3390/app13084672
Chicago/Turabian StyleAwan, Muhammad Saqlain, Ali Javed, Muhammad Faheem Ud Din Afzal, Luis Federico Navarro Vilchez, and Armin Mehrabi. 2023. "Evaluation of System Identification Methods for Free Vibration Flutter Derivatives of Long-Span Bridges" Applied Sciences 13, no. 8: 4672. https://doi.org/10.3390/app13084672








