Efficient Zero-Sequence Impedance Measurement in Autotransformers Using Low-Voltage Excitation
Abstract
:1. Introduction
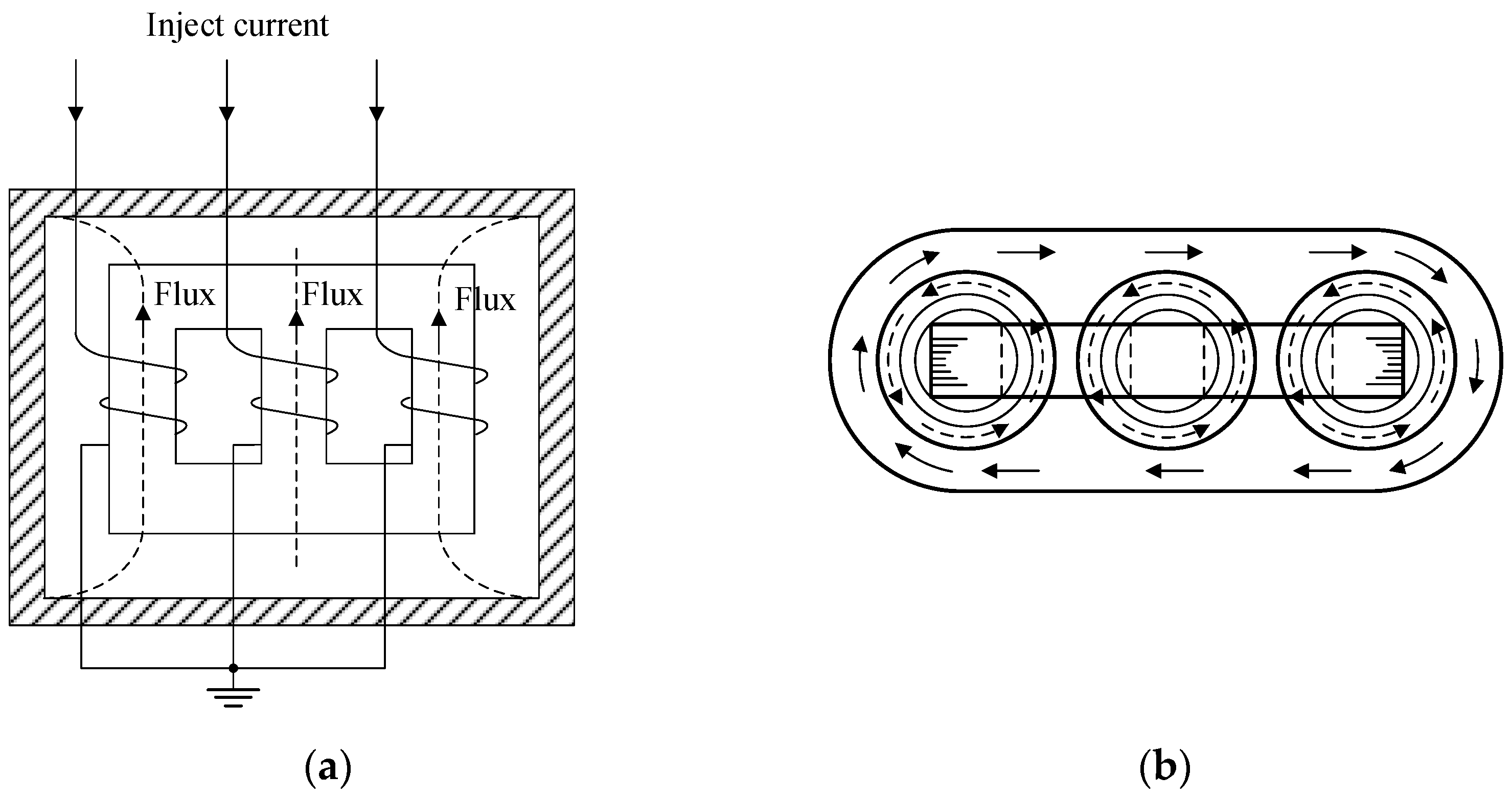
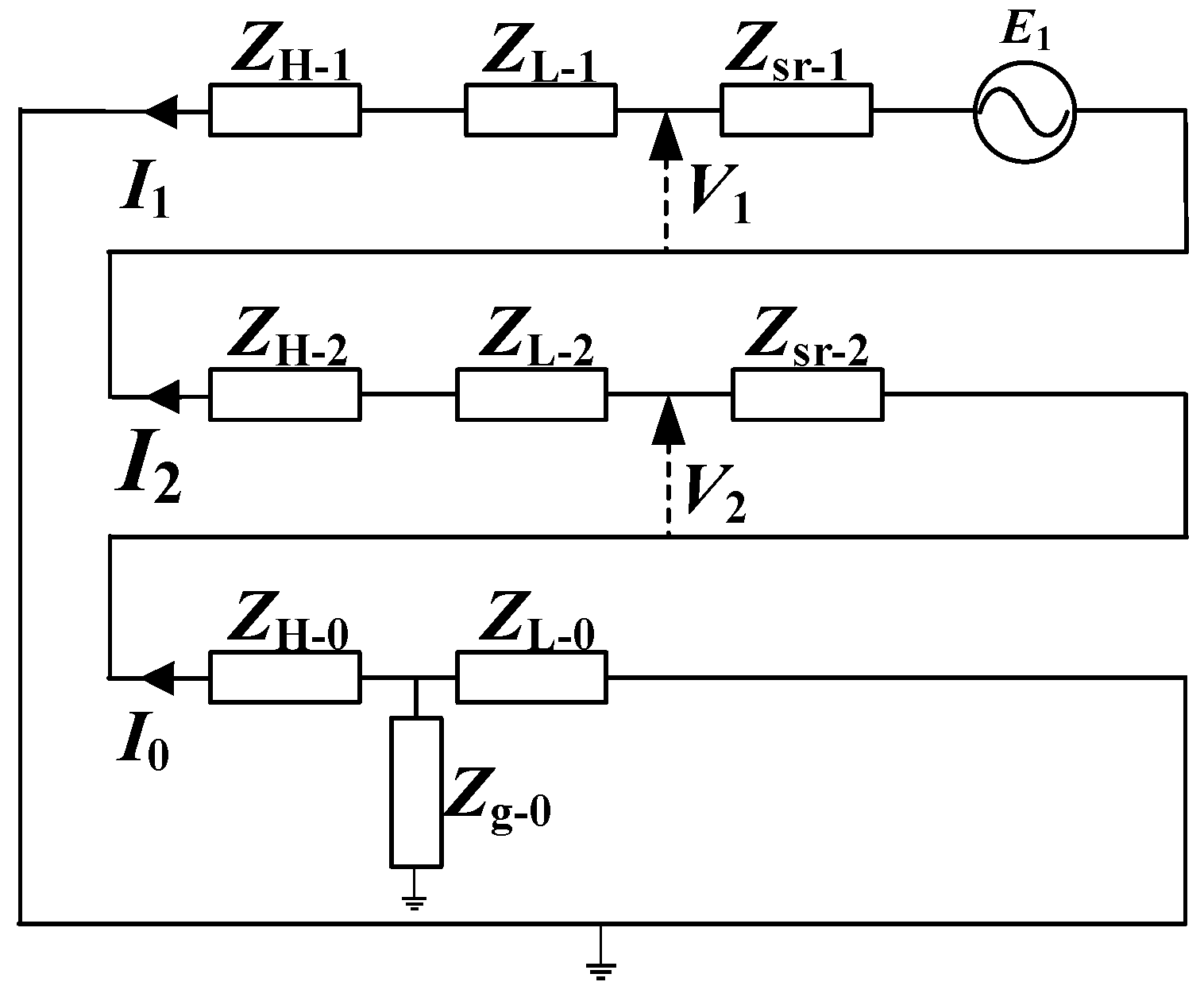
2. YNa Autotransformer Zero-Sequence Impedance Field Test Method
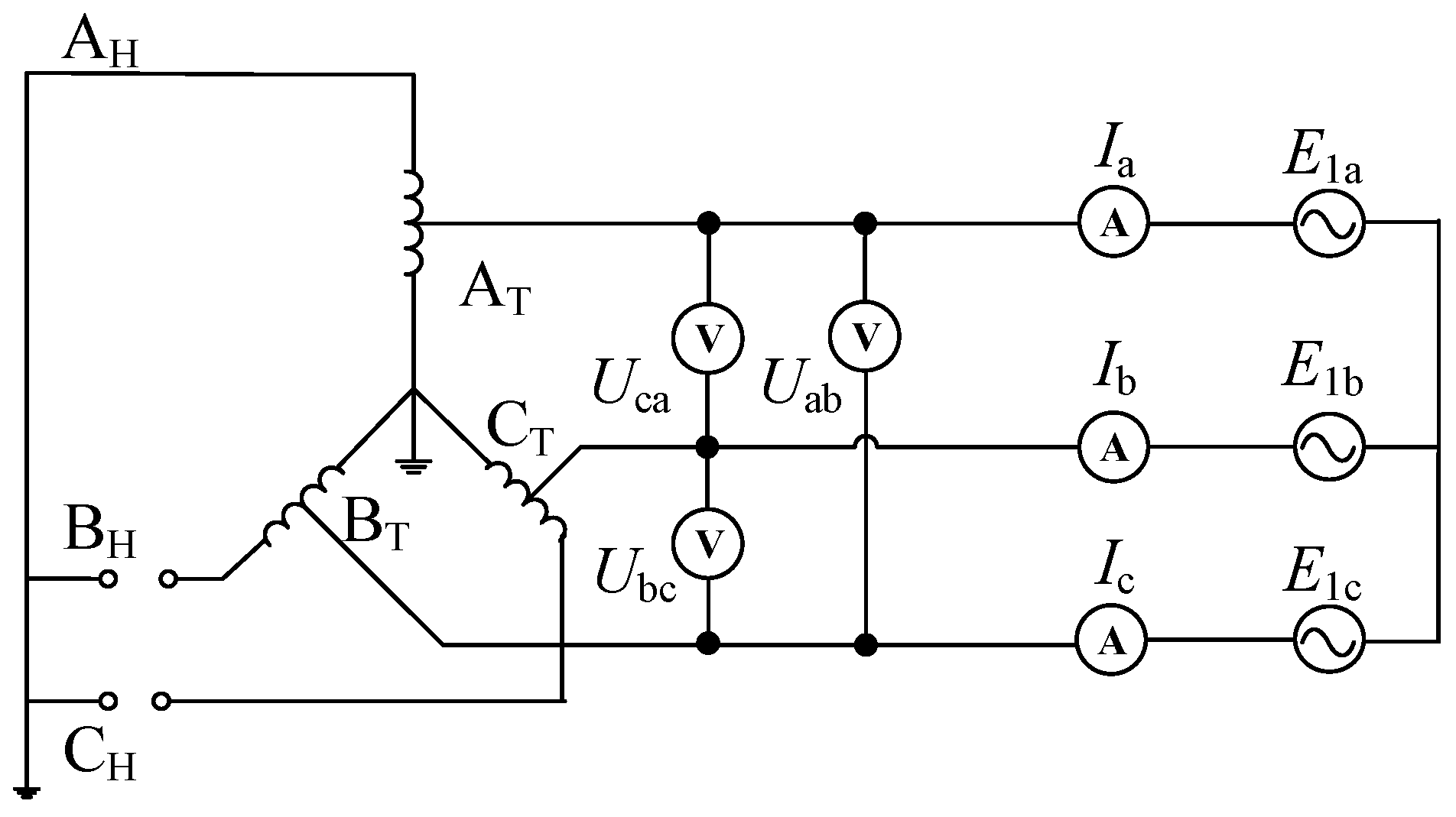
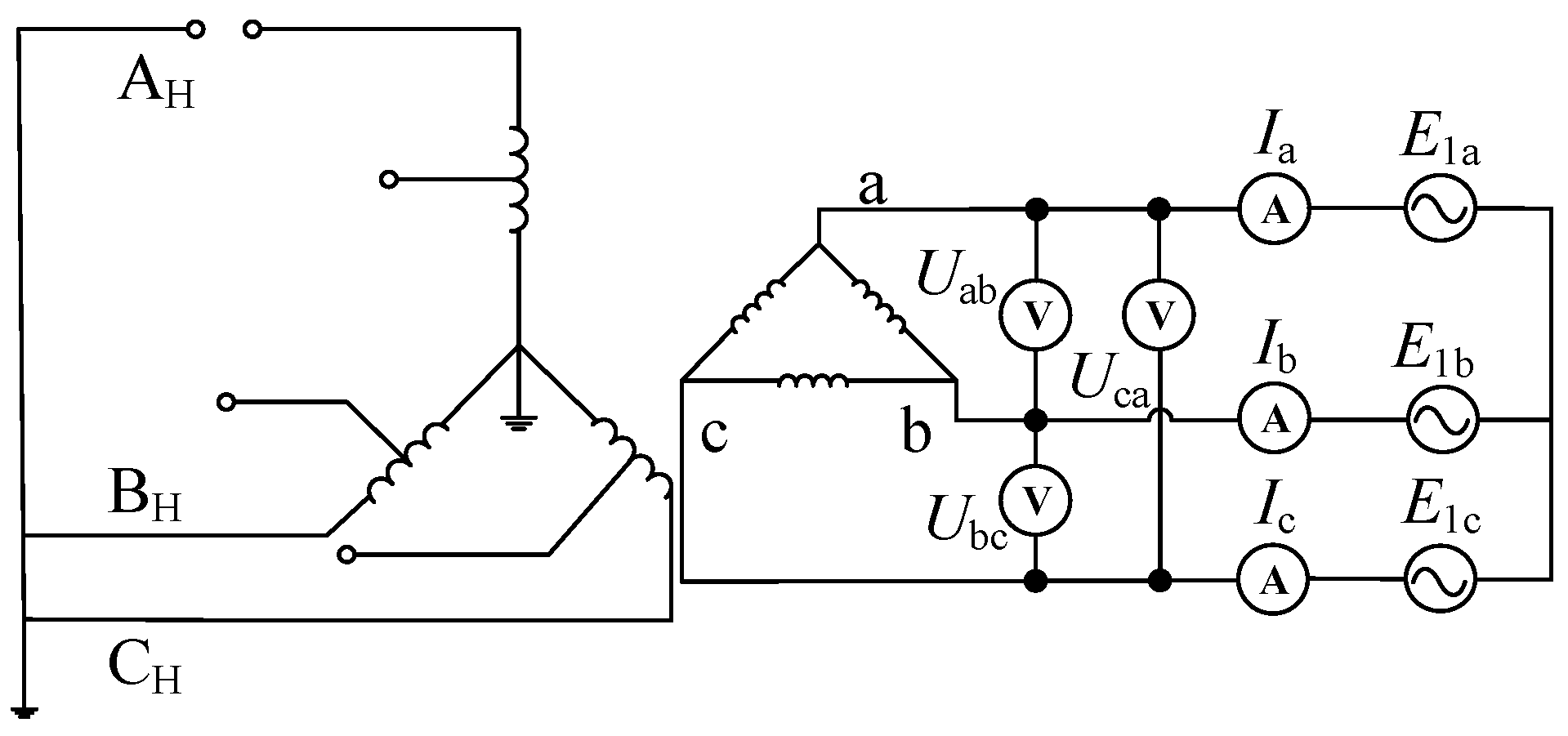
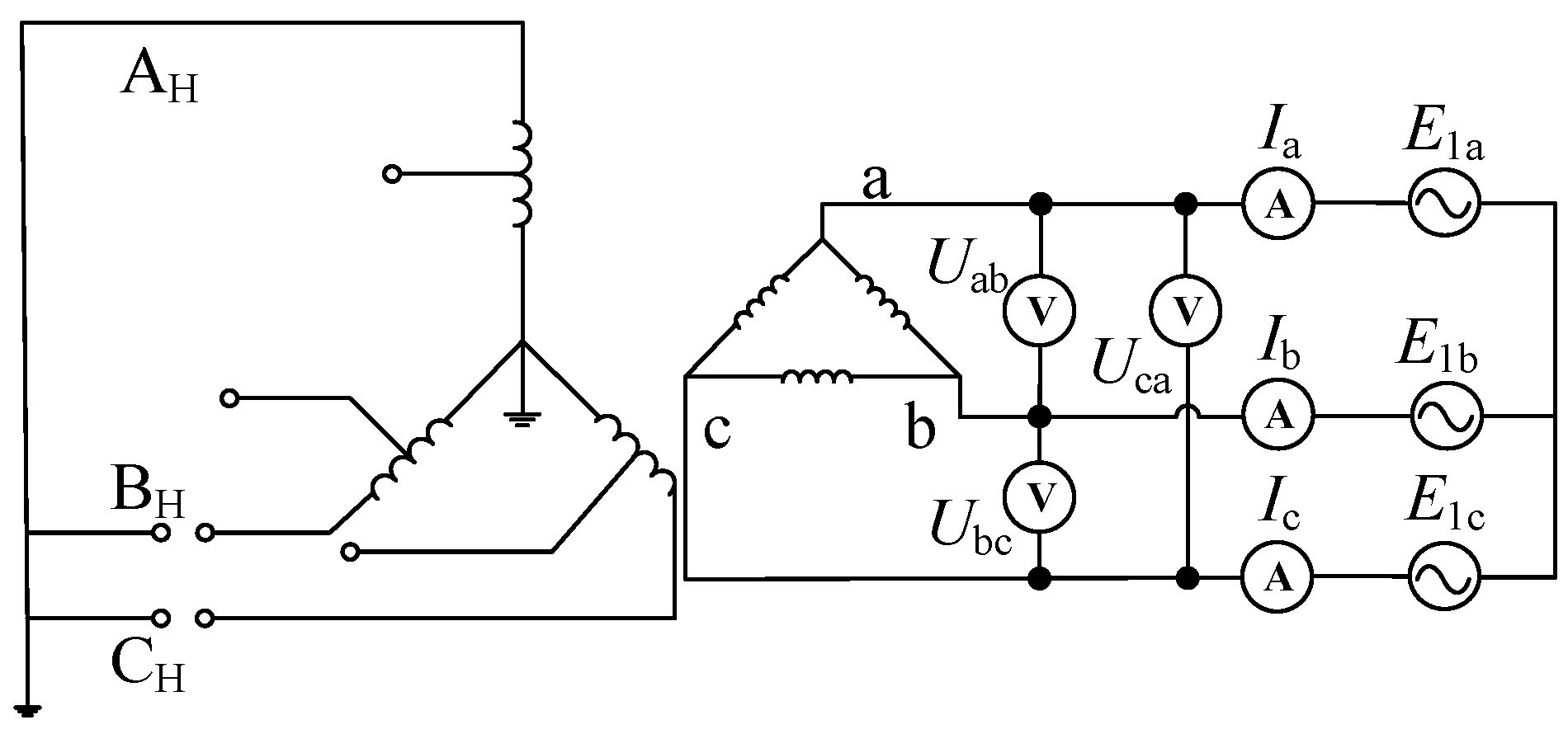
2.1. One-Phase Disconnection Test on the High-Voltage Side
2.2. One-Phase Disconnection Test on Low-Voltage Side
2.3. Two-Phase Disconnection Test on the High-Voltage Side
2.4. Two-Phase Disconnection Test on the Low-Voltage Side
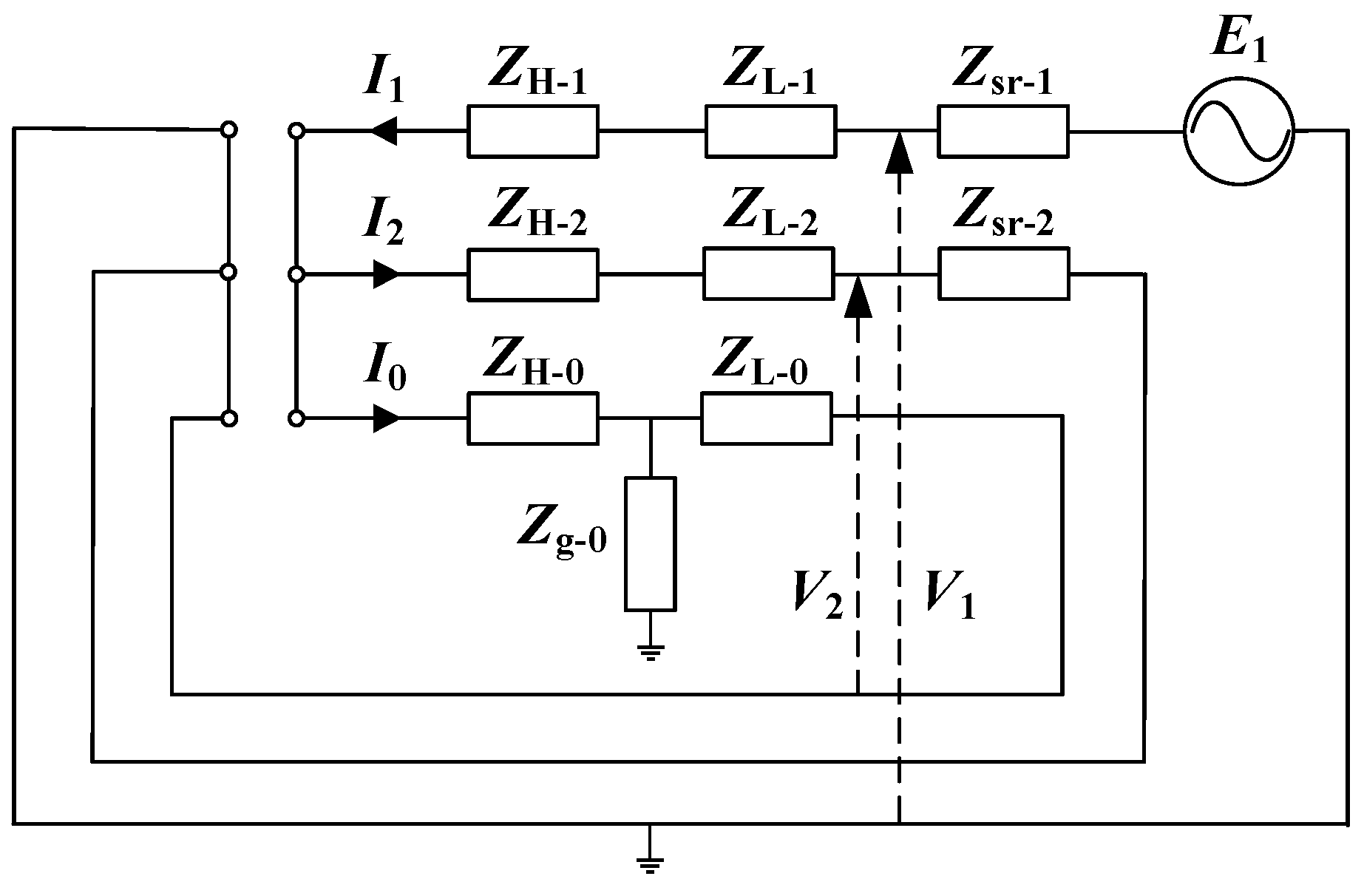
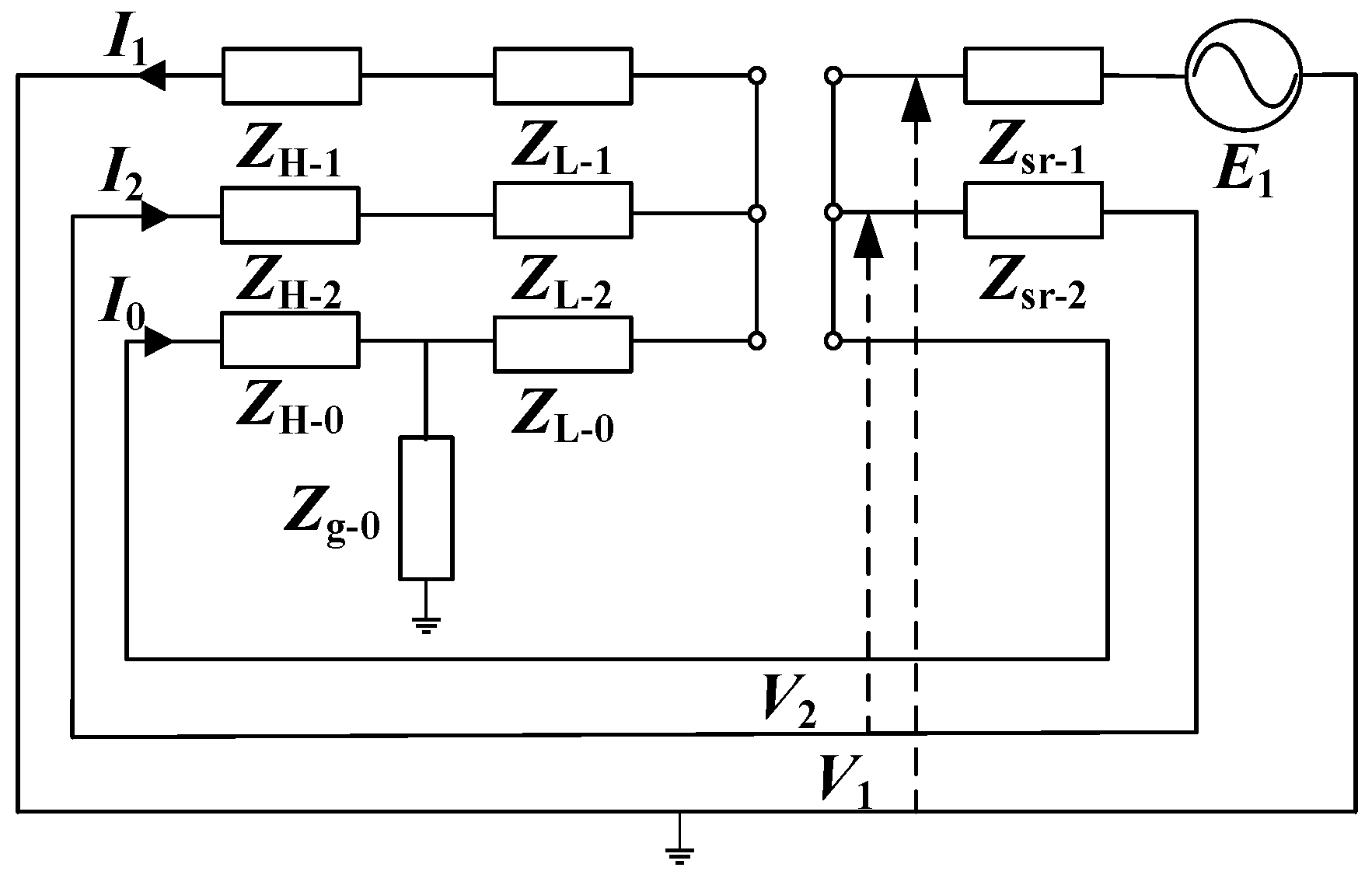
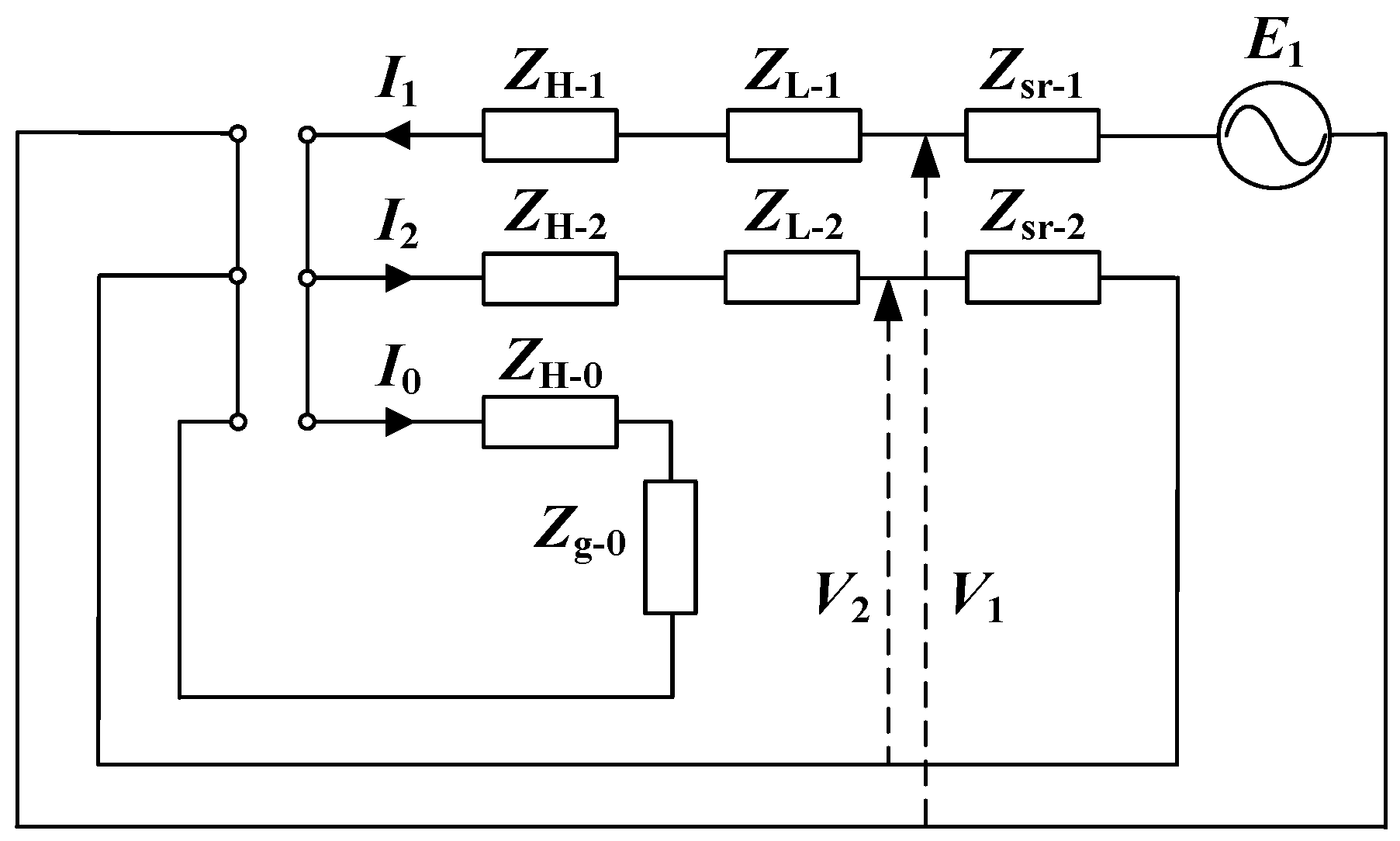
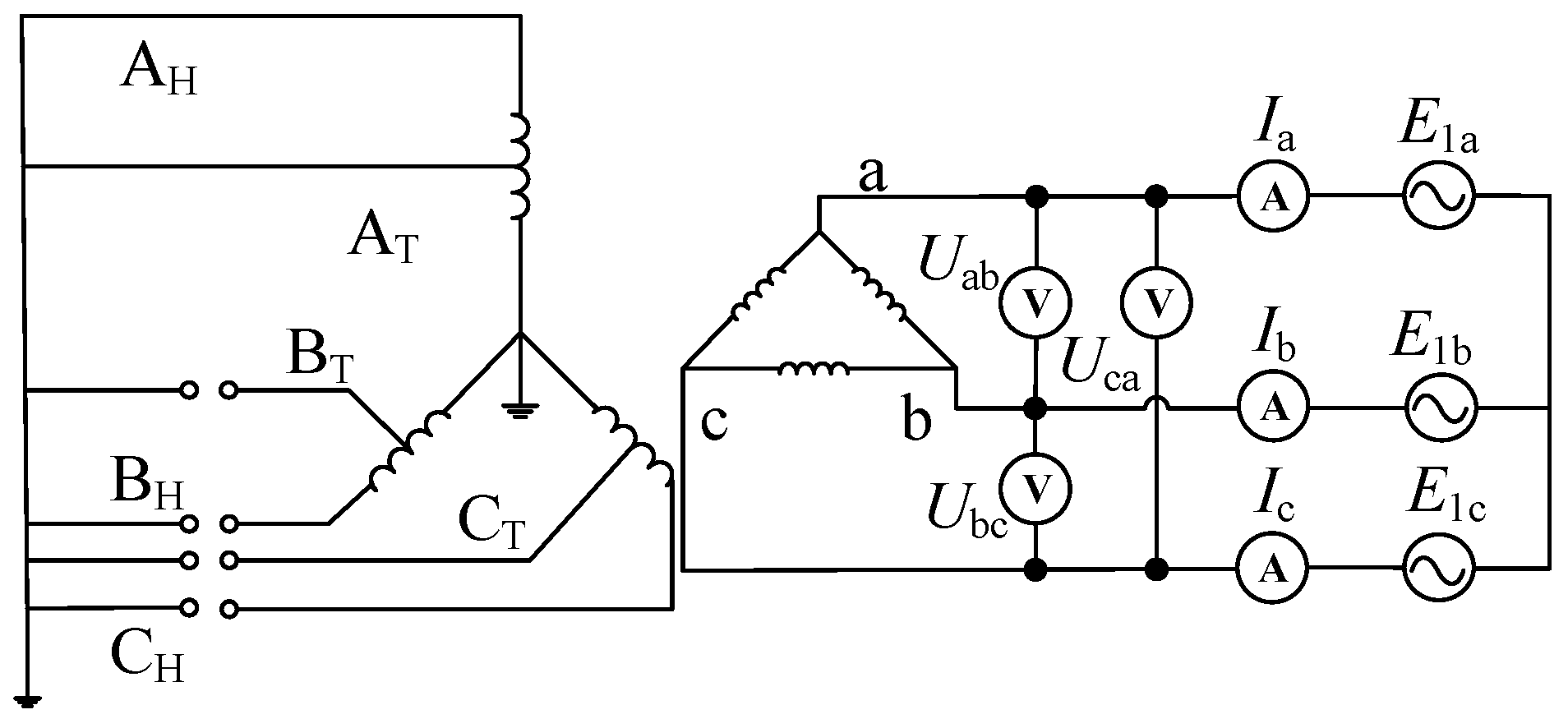
3. YNa0d11 Three-Winding Autotransformer Zero-Sequence Impedance Field Test Method
3.1. One-Phase Disconnection Test
- (1)
- Tset 1: Positive-sequence excitation on the low-voltage side; while one phase of the high-voltage winding is disconnected, the other two phases are short circuited to earth and the medium-voltage winding is completely disconnected.
- (2)
- Tset 2: Positive-sequence excitation on the low-voltage side; while one phase of the medium-voltage winding is disconnected, the other two phases are short circuited to earth and the high-voltage winding is completely disconnected.
- (3)
- Tset 3: Positive-sequence excitation on the low-voltage side; while one phase of the medium- and the high-voltage winding is disconnected, the other two phases are short circuited to earth.
3.2. Two-Phase Disconnection Test
- (1)
- Test 4: Positive-sequence excitation is injected on the low-voltage side; the high-voltage side winding is grounded in one phase and disconnected in two phases and the low-voltage side winding is completely disconnected.
- (2)
- Test 5: Positive-sequence excitation is injected on the low-voltage side; the medium-voltage side winding is grounded in one phase and disconnected in two phases and the high-voltage side winding is completely disconnected.
- (3)
- Test 6: Positive-sequence excitation is injected on the low-voltage side and both high- and medium-voltage windings are single-phase grounded and two-phase disconnected.
4. Simulation Verification
4.1. Double-Winding Autotransformer One-Phase and Two-Phase Disconnection Test
4.2. YNa0d11 Autotransformer One-Phase and Two-Phase Disconnection Test
5. Conclusions
- (1)
- Using the disconnection test to measure the zero-sequence impedance of the transformer to be tested, the test power supply is placed on the low-voltage side of the transformer, reducing the difficulty and complexity of the test and reducing the cost of the test while enabling the field measurement of the zero-sequence impedance of autotransformers.
- (2)
- According to the proposed method, the test results were simulated and compared to the standard measurement method. Although there were some errors, the overall error was less than 3%, which proved the practicality of the proposed method, which could be used in engineering practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
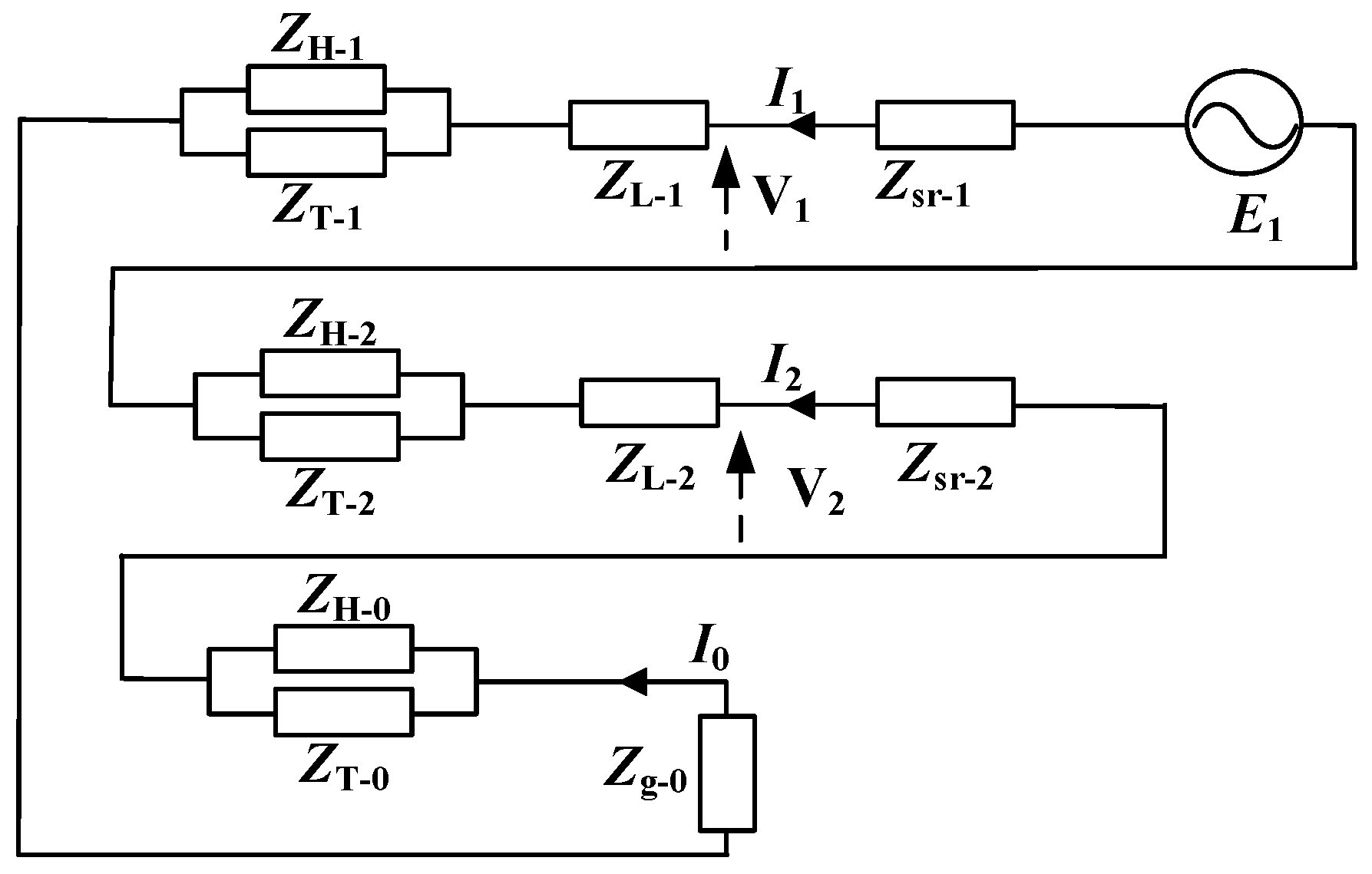
Nomenclature
| Variables | Explanation |
| I1, I2, I0 | Positive-, negative-, and zero-sequence components of current I |
| V1, V2, V0 | Positive-, negative-, and zero-sequence components of voltage V |
| Z1, Z2, Z0 | Positive-, negative-, and zero-sequence components of impedance Z |
| ZH-1, ZH-2, ZH-0 | Positive-, negative-, and zero-sequence components of high-voltage impedance ZH |
| ZL-1, ZL-2, ZL-0 | Positive-, negative-, and zero-sequence components of low-voltage impedance ZL |
| Zg-0 | Zero-sequence excitation impedance |
| , , | Line current between two different phases |
| , , | Line voltage between two different phases |
References
- Wang, J.; He, B. Novel Step-Up Topologies of Zigzag Autotransformer. Electronics 2021, 10, 3071. [Google Scholar] [CrossRef]
- Nina, S.; Bozidar, F.-G.; Marijan, P. Impact of autotransformer inrush currents on differential protection operation. Electr. Power Syst. Res. 2023, 220, 109309. [Google Scholar]
- Das, S.; Ananthan, S.N.; Santoso, S. Estimating zero-sequence impedance of three-terminal transmission line and Theveninimpedance using relay measurement data. Prot. Control Mod. Power Syst. 2018, V3, 373–382. [Google Scholar]
- Fang, T.; Qian, Y.; Guo, C.; Song, C.; Wang, Z.; Luo, J.; Quanke, B.A. Reasearch on transformer fault diagnosis based on a beetle antennae search optimized support vector machine. Power Syst. Prot. Control 2020, 48, 90–96. [Google Scholar]
- Oves, A.G.; Mehrdad, M.; Mehdi, E.-A. A fault data based method for zero-sequence impedance estimation of mutually coupled transmission lines. IEEE Trans. Power Deliv. 2021, 36, 2768–2776. [Google Scholar]
- He, Q.; He, G.; Li, Z.; Lin, M.; Zhang, G.; Li, X. Pilot protection based on zero-sequence current resistance-capacitance component for large-scale inverter-interfaced power stations. Sustainability 2022, 14, 13268. [Google Scholar] [CrossRef]
- Aristotelis, M.T.; Vassilis, C.N. Setting zero-sequence compensation factor in distance relays protecting distribution systems. IEEE Trans. Power Deliv. 2018, 33, 1236–1246. [Google Scholar]
- Yuan, D.; Yin, Z.; Wang, S.; Duan, N. Multi-level transient modeling of the aeronautic asymmetric 18-pulse phase-shifting auto-transformer rectifier in full-cycle design. IEEE Trans. Transp. Electrif. 2022, 8, 3759–3770. [Google Scholar] [CrossRef]
- IEEE Std C57.12.90; IEEE Standard Test Code for Liquid-Immersed Distribution, Power, and Regulating Transformers. IEEE: New York, NY, USA, 2010.
- Liang, H.; Li, H.; Wang, G. A single-phase-to-ground fault detection method based on the ratio fluctuation coefficient of the zero-sequence current and Voltage differential in a distribution network. IEEE Access 2023, 11, 7297–7308. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Jimerson, R.E.; Swift, K.; Garcia, R. Positive- and zero-sequence impedance estimation of YNyn0+d-connected main power transformers in wind power applications. CSEE J. Power Energy Syst. 2021, 7, 57–65. [Google Scholar]
- Bogomolov, V.; Lovo, Y.; Kokhan, P. Fault current levels in 220 and 500 kV autotransformer circuits. Electr. Technol. 1981, 2, 30–37. [Google Scholar]
- Kamel, M.; Saeed, H.; Karrar, A.; Eltom, A.H. On-site low voltage determination of zero-sequence impedances for station auxiliary transformers. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Ramos, A.; Burgos, J.C.; Moreno, A.; Sorrentino, E. Determination of Parameters of Zero-Sequence Equivalent Circuits for Three-Phase Three-Legged YNynd Transformers Based on Onsite Low-Voltage Tests. IEEE Trans. Power Deliv. 2013, 28, 1618–1625. [Google Scholar] [CrossRef]
- Allcock, R.; Holland, S.; Haydock, L. Calculation of zero phase sequence impedance for power transformers using numerical methods. IEEE Trans. Magn. 1995, 31, 2048–2051. [Google Scholar] [CrossRef]
- Wu, Q.; Jazebi, S.; de Leon, F. Parameter Estimation of Three-Phase Transformer Models for Low-Frequency Transient Studies from Terminal Measurements. IEEE Trans. Magn. 2017, 53, 8107108. [Google Scholar] [CrossRef]
- Saeed, H.; Kamel, M.; Karrar, A.; Eltom, A.H.; Bowman, M. On-Site Low Voltage Determination of Zero-Sequence Impedances for Power Transformers. IEEE Trans. Power Deliv. 2020, 35, 1048–1057. [Google Scholar] [CrossRef]
- Chapman, S.J. Electric Machinery Fundamentals; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]



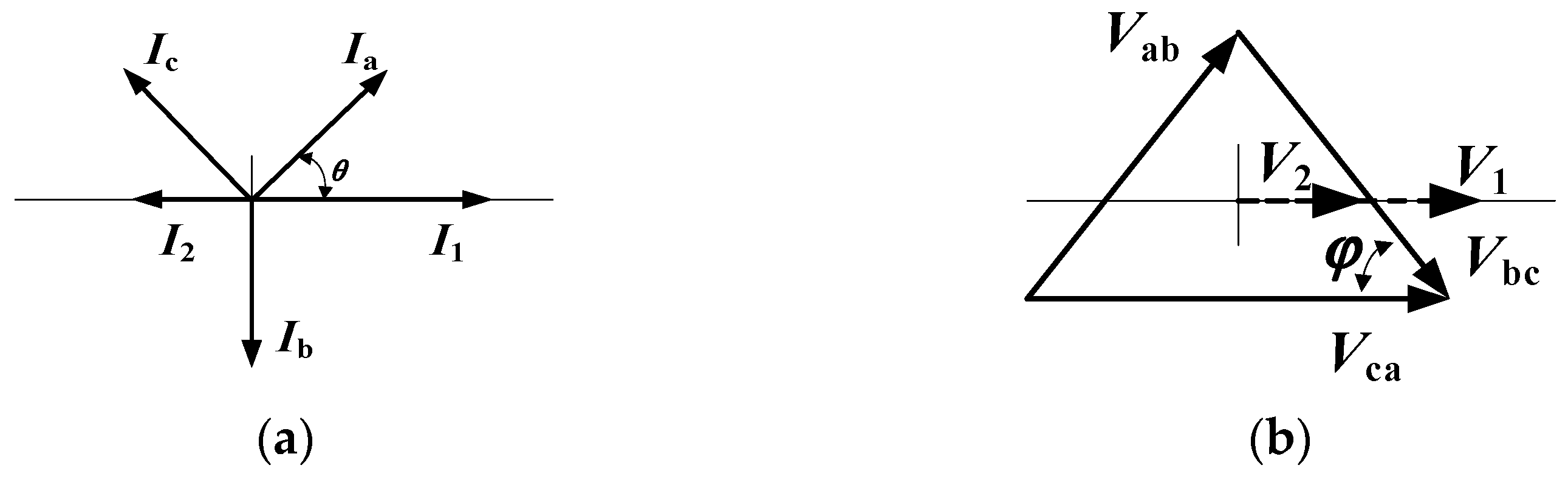




| Transformer Type | Size | Cost | Applicability |
|---|---|---|---|
| Conventional transformer | Larger | Higher | General load |
| Autotransformer | Smaller | Cheaper | Large-capacity load |
| Capacity/kVA | No-Load Loss/kW | Load Loss/kW | Short Circuit Impedance % | |
|---|---|---|---|---|
| YNa0 autotransformer | 31,500 | 45 | 157 | 13 |
| YNa0d11 autotransformer | 63,000 | 30 | 132 | 9 (High-Medium) 28 (High-Low) 20 (Medium-Low) |
| Standard Test Measured Value | One-Phase Disconnection Test | ||
|---|---|---|---|
| High-Voltage | Low-Voltage | ||
| V0 | 1443 V | - | |
| 3I0 | 33.58 A | - | |
| Vab | - | 379.4 V | 399.8 V |
| Vbc | - | 350.9 V | 414.6 V |
| Vca | - | 385.6 V | 385.1 V |
| Iab | - | 13.51 A | 13.78 A |
| Ibc | - | 22.98 A | 23.65 A |
| Ica | - | 13.88 A | 13.95 A |
| (%) | 9.58 | 9.76 | 9.38 |
| error | - | 1.88% | −2.01% |
| Standard Test Measured Value | Two-Phase Disconnection Test | ||
|---|---|---|---|
| High-Voltage | Low-Voltage | ||
| V0 | 1443 V | - | - |
| 3I0 | 33.58 A | - | - |
| Vab | - | 358.3 V | 402.7 V |
| Vbc | - | 400 V | 0 V |
| Vca | - | 361.3 V | 390.3 V |
| Ia | - | 17.66 A | 17.64 A |
| Ib | - | 0.522 A | 0 A |
| Ic | - | 0.522 A | 0 A |
| (%) | 9.58 | 9.65 | 9.69 |
| error | - | 0.73% | 1.15% |
| Standard Test Measured Value | Disconnection Test | |||
|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | ||
| V0 | 1926 V | - | - | - |
| 3I0 | 449.9 A | - | - | - |
| Vab | - | 316.4 V | 319.3 V | 321.7 V |
| Vbc | - | 315.2 V | 317.1 V | 319.4 V |
| Vca | - | 396.3 V | 396.4 V | 398.2 V |
| Ia | - | 37.5 A | 39.3 A | 41.4 A |
| Ib | - | 42.7 A | 45.2 A | 48.5 A |
| Ic | - | 38.8 A | 38.6 A | 41.8 A |
| (%) | 24.8 | 25.1 | - | - |
| (%) | 16.8 | - | 17.3 | - |
| (%) | 17.2 | - | - | 17.5 |
| Error | - | 1.19% | 2.97% | 1.74% |
| Standard Test Measured Value | Disconnection Test | |||
|---|---|---|---|---|
| Test 4 | Test 5 | Test 6 | ||
| V0 | 1926 V | - | ||
| 3I0 | 449.9 A | - | ||
| Vab | - | 384.3 V | 378.4 V | 378.2 V |
| Vbc | - | 400 V | 400 V | 398 V |
| Vca | - | 396.2 V | 394.6 V | 383.5 V |
| Ia | - | 41.7 A | 63.3 A | 68.6 A |
| Ib | - | 0 A | 0 A | 0 A |
| Ic | - | 41.5 A | 63.1 A | 68.6 A |
| (%) | 24.8 | 24.9 | - | - |
| (%) | 16.8 | - | 17.1 | - |
| (%) | 17.2 | - | - | 17.5 |
| Error | - | 0.40% | 1.78% | 1.74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Fang, J.; Wang, H.; Huang, Q.; Hong, H.; Lin, X.; Zhou, N. Efficient Zero-Sequence Impedance Measurement in Autotransformers Using Low-Voltage Excitation. Appl. Sci. 2024, 14, 215. https://doi.org/10.3390/app14010215
Zhang M, Fang J, Wang H, Huang Q, Hong H, Lin X, Zhou N. Efficient Zero-Sequence Impedance Measurement in Autotransformers Using Low-Voltage Excitation. Applied Sciences. 2024; 14(1):215. https://doi.org/10.3390/app14010215
Chicago/Turabian StyleZhang, Min, Jian Fang, Hongbin Wang, Qingdan Huang, Haicheng Hong, Xiang Lin, and Niancheng Zhou. 2024. "Efficient Zero-Sequence Impedance Measurement in Autotransformers Using Low-Voltage Excitation" Applied Sciences 14, no. 1: 215. https://doi.org/10.3390/app14010215




