Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator
Abstract
:1. Introduction
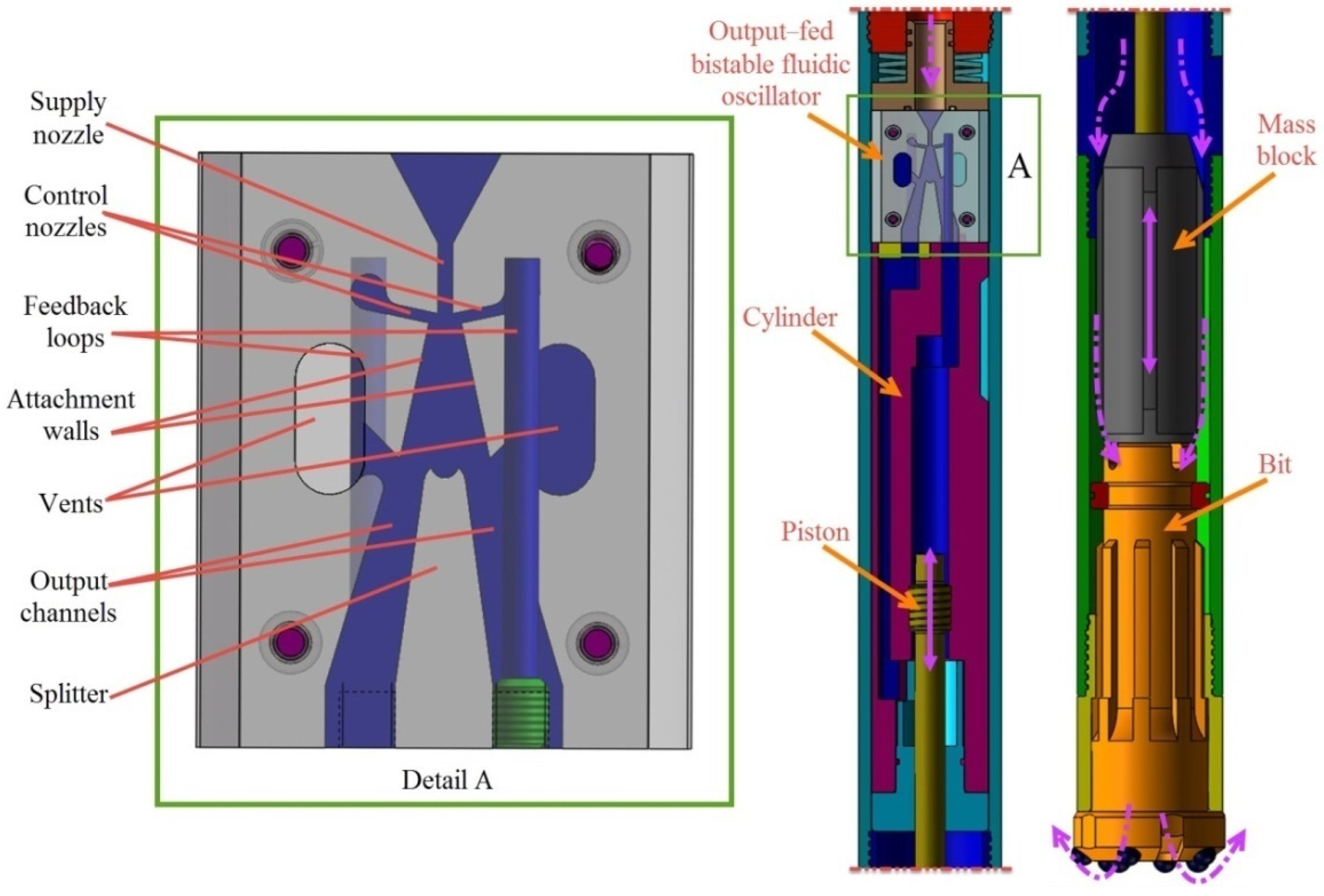
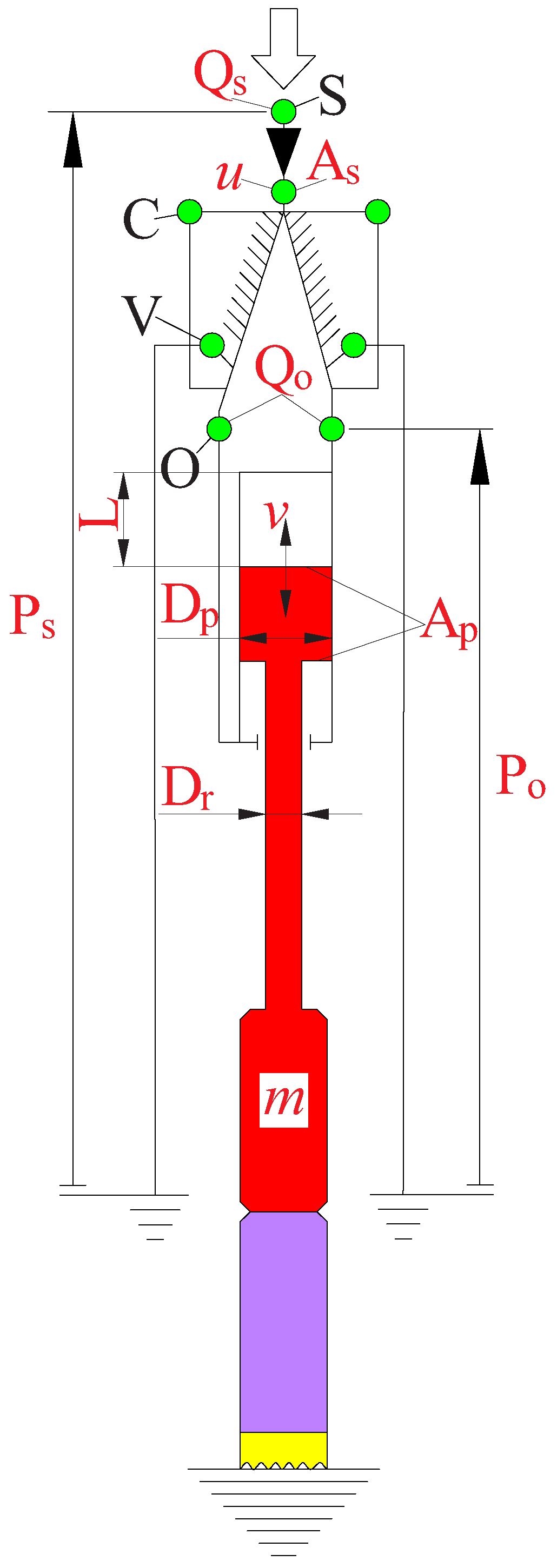
2. Description of the Fluidic Hammer
3. Numerical Procedure
3.1. SpecifiedDimensions of Output-Fed Bistable Fluidic Oscillator
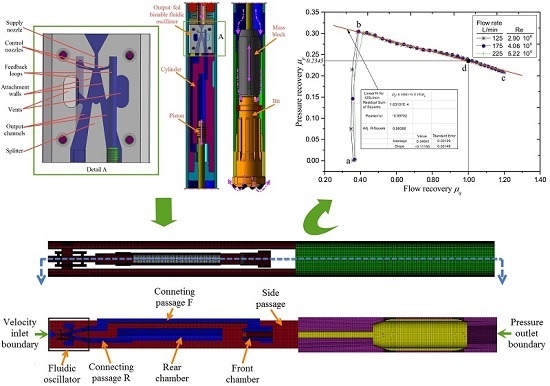
3.2. Methodology of Simulation and Computational Domains
3.3. Mathematical Formulationfor Dynamic Mesh Modeling
3.4. Boundary Conditions and Solving Strategies
4. Results and Discussion
4.1. Performance Analysis Related to the Flow Behavior
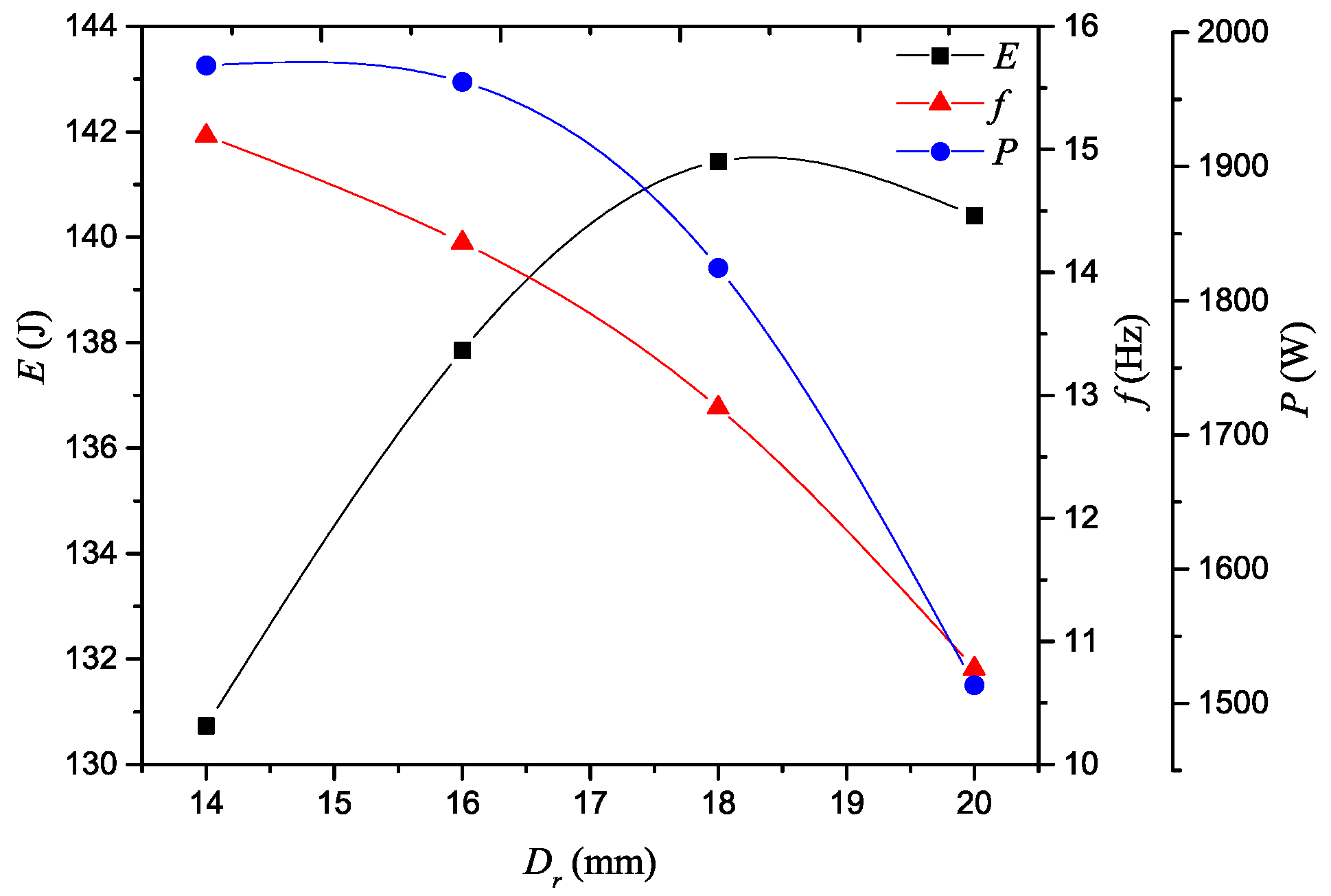
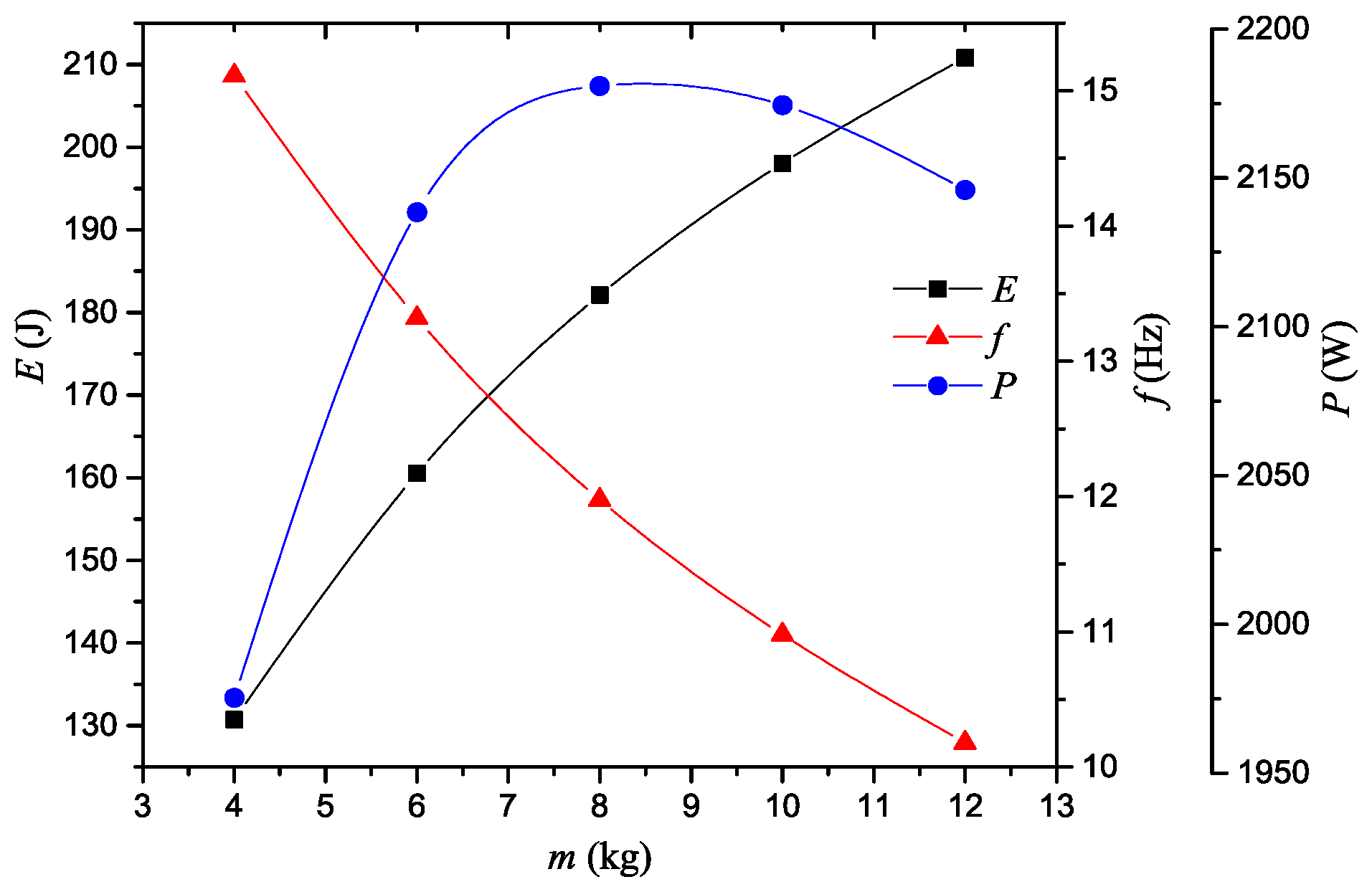
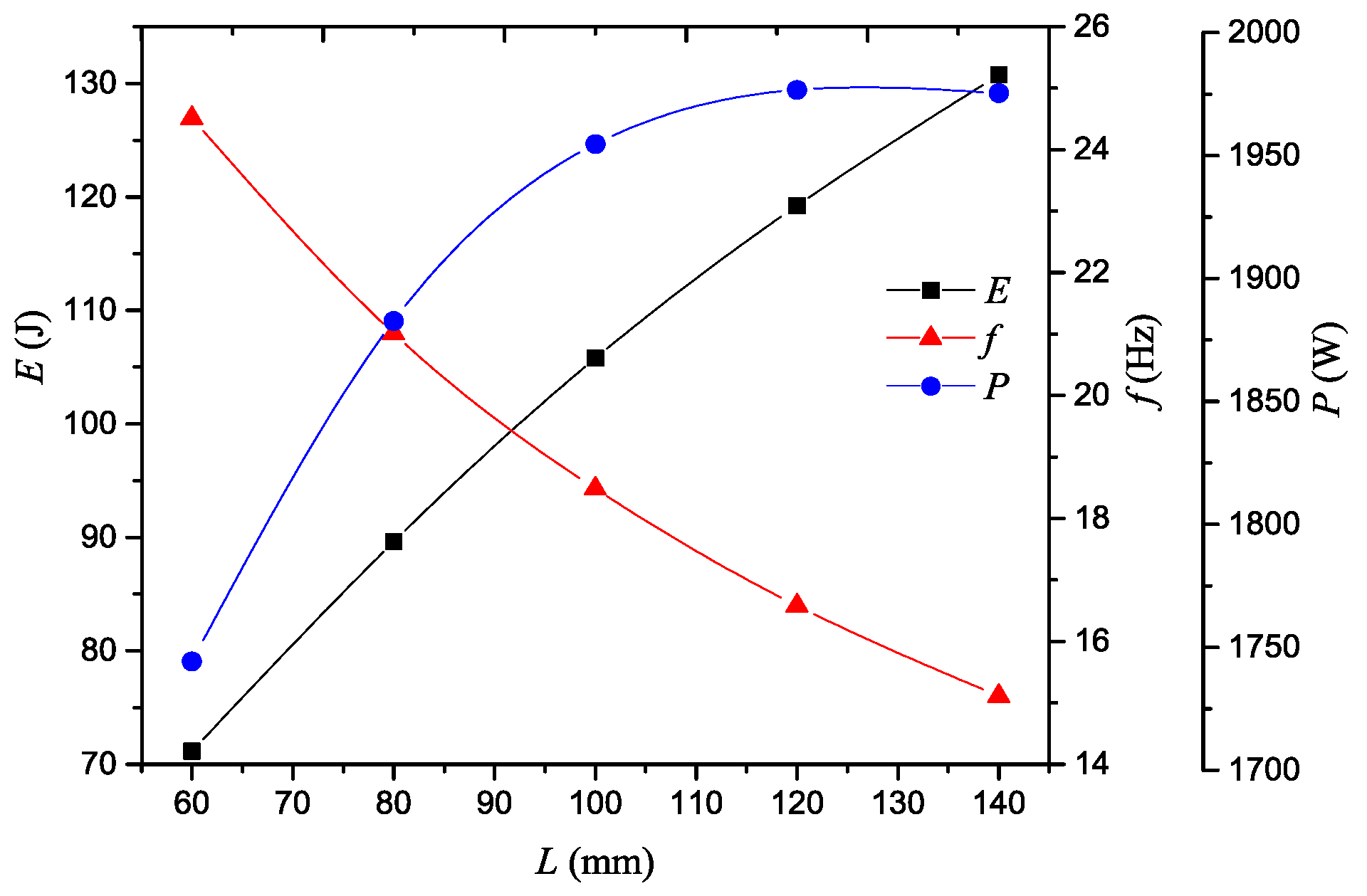
4.2. The Effect of Parameters of the Impact Body on the Performance of Fluidic Hammers
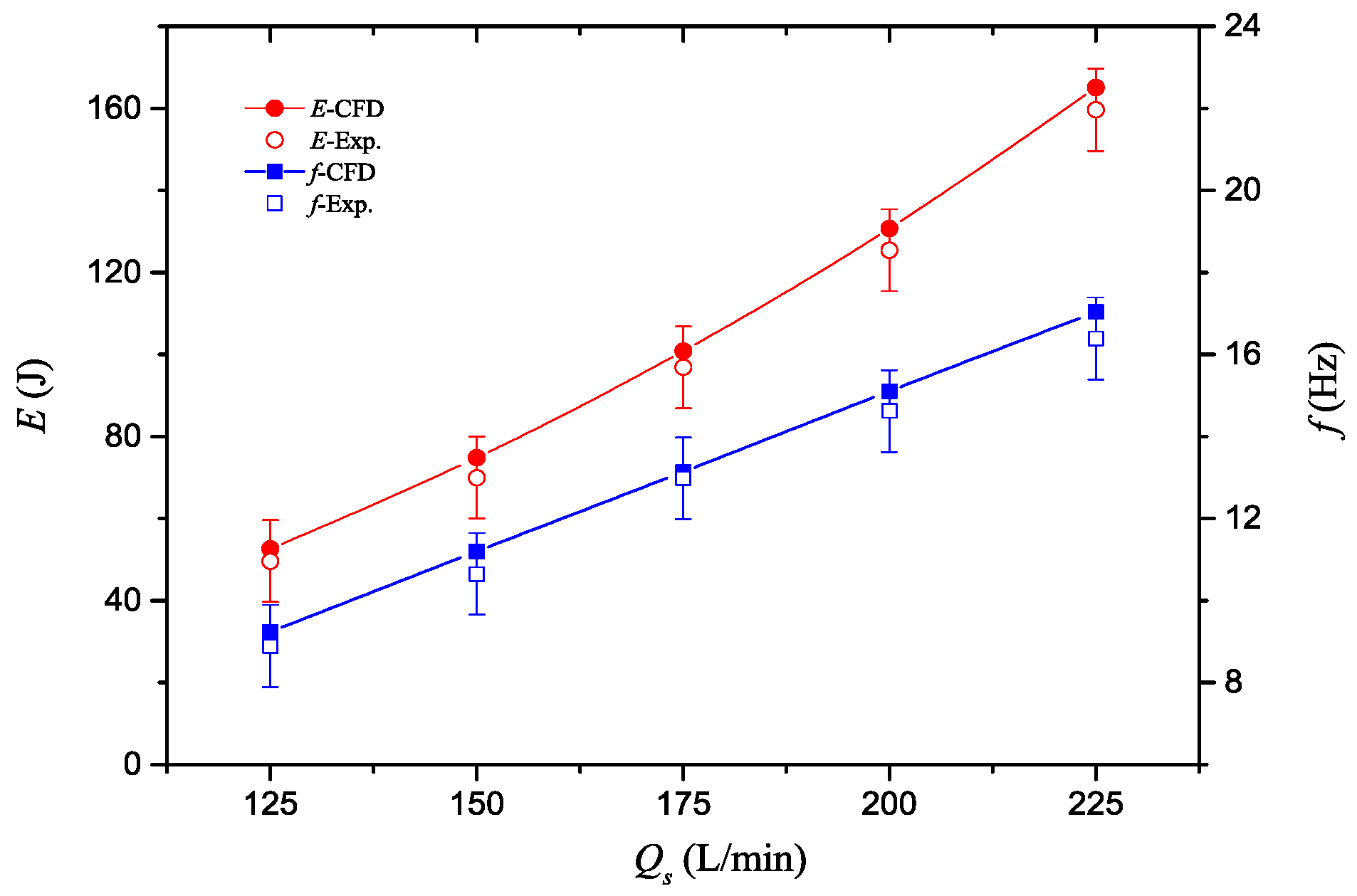
4.3. Experimental Validation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Coanda, H. Device for Deflecting a Stream of Elastic Fluid Projected into an Elastic Fluid. U.S. Patent 2,052,869, 1 September 1936. [Google Scholar]
- Wang, H.; Beck, S.B.M.; Priestman, G.H.; Boucher, R.F. Fluidic pressure pulse transmitting flowmeter. Chem. Eng. Res. Des. 1997, 75, 381–391. [Google Scholar] [CrossRef]
- Nakayama, A.; Kuwahara, F.; Kamiya, Y. A two dimensional numerical procedure for a three dimensional internal flow through a complex passage with a small depth. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 863–871. [Google Scholar] [CrossRef]
- Dummer, G.W.A.; Robertson, J.M. Fluidic Components and Equipment; Pergamon: London, UK, 1968. [Google Scholar]
- Warren, R.W. Fluid Oscillator. U.S. Patent 3,016,066, 9 January 1962. [Google Scholar]
- Warren, R.W. Negative Feedback Oscillator. U.S. Patent 3,158,166, 24 November 1964. [Google Scholar]
- Tesař, V.; Smyk, E. Fluidic low-frequency oscillator with vortex spin-up time delay. Chem. Eng. Process. 2015, 90, 5–15. [Google Scholar] [CrossRef]
- Shakouchi, T. A New Fluidic Oscillator, Flowmeter, without Control Port and Feedback Loop. J. Dyn. Syst. 1989, 111, 535–539. [Google Scholar] [CrossRef]
- Morris, N.M. An Introduction to Fluid Logic; McGraw: New York, NY, USA, 1973. [Google Scholar]
- Wright, P.H. The Coanda Meter—A fluidic digital gas flowmeter. J. Phys. E 1980, 13, 433–436. [Google Scholar] [CrossRef]
- Jeon, M.K.; Kim, J.H.; Noh, J.; Kim, S.H.; Park, H.G.; Woo, S.I. Design and characterization of a passive recycle micromixer. J. Micromech. Microeng. 2005, 15, 346–350. [Google Scholar] [CrossRef]
- Lee, G.B.; Kuo, T.Y.; Wu, W.Y. A novel micromachined flow sensor using periodic flapping motion of a planar jet impinging on a V-shaped plate. Exp. Therm. Fluid Sci. 2002, 26, 435–444. [Google Scholar] [CrossRef]
- Groisman, A.; Enzelberger, M.; Quake, S.R. Microfluidic memory and control devices. Science 2003, 300, 955–958. [Google Scholar] [CrossRef] [PubMed]
- Tesař, V. Fluidic Oscillator with Bistable Jet-Type Amplifier. EP Patent 2,554,854 A2, 6 February 2013. [Google Scholar]
- Tesař, V.; Peszynski, K. Strangely behaving fluidic oscillator. In Proceedings of the European Physical Journal Web of Conferences, Hradec Králové, Czech Republic, 20–23 November 2012; Volume 45.
- Tesař, V.; Zhong, S.; Rasheed, F. New Fluidic-Oscillator Concept for Flow-Separation Control. AIAA. J. 2015, 51, 397–405. [Google Scholar] [CrossRef]
- He, J.F.; Yin, K.; Peng, J.M.; Zhang, X.X.; Liu, H.; Gan, X. Design and feasibility analysis of a fluidic jet oscillator with application to horizontal directional well drilling. J. Nat. Gas Sci. Eng. 2015, 27, 1723–1731. [Google Scholar] [CrossRef]
- Xue, L.; Li, B.M.; Wang, Z.M.; Li, B.J. Ultrahigh-Pressure-Jet-Assisted Drilling Technique: Theory and Experiment. J. Can. Petrol. Technol. 2012, 51, 276–282. [Google Scholar] [CrossRef]
- Luo, Y.J.; Peng, J.M.; Sun, M.Z.; Sun, Q.; Ji, T.; Bo, K. Anice-valve-based pressure-coring system for sampling naturalhydrate-bearing sediments: Proof-of-concept laboratorystudies. J. Nat. Gas Sci. Eng. 2015, 27, 1462–1469. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, J.; Sun, M.; Gao, Q.; Wu, D. Development of applicable ice valves for ice-valve-based pressure corer employed in offshore pressure coring of gas hydrate-bearing sediments. Chem. Eng. Res. Des. 2016, 111, 117–126. [Google Scholar] [CrossRef]
- Peng, J.M.; Yin, Q.L.; Li, G.L.; Liu, H.; Wang, W. The effect of actuator parameters on the critical flow velocity of a fluidic amplifier. Appl. Math. Model. 2013, 37, 7741–7751. [Google Scholar] [CrossRef]
- Peng, J.M.; Zhang, Q.; Li, G.L.; Chen, J.W.; Gan, X.; He, J.F. Effect of geometric parameters of the bistable fluidic amplifier in the liquid-jet hammer on its threshold flow velocity. Comput. Fluids 2013, 82, 38–49. [Google Scholar] [CrossRef]
- Furlan, R.; Silva, M.L.P.D.; Simoes, E.W.; Leminski, R.E.B.; Aviles, J.J.S. Visualization of internal liquid flow interactions in meso planar structures. Flow Meas. Instrum. 2006, 17, 298–302. [Google Scholar] [CrossRef]
- Yamamoto, K.; Hiroki, F.; Hyodo, K. Self-sustained oscillation phenomena of fluidic flowmeters. J. Vis. 1999, 1, 387–396. [Google Scholar] [CrossRef]
- Uzol, O.; Camci, C. Experimental and computational visualization and frequency measurements of the jet oscillation inside a fluidic oscillator. J. Vis. 2002, 5, 263–272. [Google Scholar] [CrossRef]
- Tesař, V.; Bandalusena, H.C.H. Bistable diverter valve in microfluidics. Exp. Fluids 2011, 50, 1225–1233. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zou, J.; Fu, X.; Yang, H.Y. Study on hydrodynamic vibration in fluidic flowmeter. J. Zhejiang Univ. Sci. A 2007, 8, 1422–1428. [Google Scholar] [CrossRef]
- Khelfaoui, R.; Colin, S.; Orieux, S.; Caen, R.; Baldas, L. Numerical and experimental analysis of monostable mini- and micro-oscillators. Heat Transf. Eng. 2011, 30, 121–129. [Google Scholar] [CrossRef]
- Tesař, V.; Hung, C.H.; Zimmerman, W.B. No-moving-part hybrid-synthetic jet actuator. Sens. Actuator A Phys. 2006, 125, 159–169. [Google Scholar] [CrossRef]
- Ansys Inc. Fluent User’s Guide, Release 6.3.26; Ansys Inc.: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Chattopadhyay, H.; Kundu, A.; Saha, B.K.; Gangopadhyay, T. Analysis of flow structure inside a spool type pressure regulating valve. Energy Convers. Manag. 2012, 53, 196–204. [Google Scholar] [CrossRef]
- Wu, D.Z.; Li, S.Y.; Wu, P. CFD simulation of flow-pressure characteristics of a pressure control valve for automotive fuel supply system. Energy Convers. Manag. 2015, 101, 658–665. [Google Scholar] [CrossRef]
- Mousavian, S.M.; Najafi, A.F. Numerical simulations of gas–liquid–solid flows in a hydrocyclone separator. Arch. Appl. Mech. 2009, 79, 395–409. [Google Scholar] [CrossRef]
- Fan, B.W.; Pan, J.F.; Tang, A.K.; Pa, Z.H.; Zhu, Y.J.; Xue, H. Experimental and numerical investigation of the fluid flow in a side-ported rotary engine. Energy Convers. Manag. 2015, 95, 385–397. [Google Scholar] [CrossRef]
- Tesař, V. Mechanism of pressure recovery in jet-type actuators. Sens. Actuator A Phys. 2009, 152, 182–191. [Google Scholar] [CrossRef]
- Tuomas, G. Water Powered Percussive Rock Drilling: Process Analysis, Modeling and Numerical Simulation. Ph.D.Thesis, University of Lulea Tekniska, Lulea, Sweden, 2004. [Google Scholar]
- Franca, L.F.P. A bit-rock interaction model for rotary-percussive drilling. Int. J. Rock Mech. Min. Sci. 2011, 48, 827–835. [Google Scholar] [CrossRef]
- Melamed, Y.; Kiselev, A.; Gelfgat, M.; Dreesen, D.; Blacic, J. Hydraulic hammer drilling technology: Developments and capabilities. J. Energy Resour. Technol. 2000, 122, 1–7. [Google Scholar] [CrossRef]
- Lehmann, F.; Reich, M. Development of alternative drive concepts for downhole hammers in deep drilling operations—A feasibility study. Oil Gas Eur. Mag. 2013, 39, 119–128. [Google Scholar]






| Bs (mm) | 2.1 |
|---|---|
| Ds | 6Bs |
| Bc | 0.8Bs |
| S | 0.5Bs |
| ls | 10Bs |
| lv | 0.5Bs |
| R1 | 1Bs |
| R2 | 1.5Bs |
| 24° |
| Case No. | Dp (mm) | Dr (mm) | m (kg) | L (mm) |
|---|---|---|---|---|
| 1 | 25 | 14 | 4 | 140 |
| 2 | 26 | 14 | 4 | 140 |
| 3 | 27 | 14 | 4 | 140 |
| 4 | 28 | 14 | 4 | 140 |
| 5 | 29 | 14 | 4 | 140 |
| 6 | 25 | 16 | 4 | 140 |
| 7 | 25 | 18 | 4 | 140 |
| 8 | 25 | 20 | 4 | 140 |
| 9 | 25 | 22 | 4 | 140 |
| 10 | 25 | 14 | 6 | 140 |
| 11 | 25 | 14 | 8 | 140 |
| 12 | 25 | 14 | 10 | 140 |
| 13 | 25 | 14 | 12 | 140 |
| 14 | 25 | 14 | 4 | 60 |
| 15 | 25 | 14 | 4 | 80 |
| 16 | 25 | 14 | 4 | 100 |
| 17 | 25 | 14 | 4 | 120 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Peng, J.; Ge, D.; Bo, K.; Yin, K.; Wu, D. Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator. Appl. Sci. 2016, 6, 305. https://doi.org/10.3390/app6100305
Zhang X, Peng J, Ge D, Bo K, Yin K, Wu D. Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator. Applied Sciences. 2016; 6(10):305. https://doi.org/10.3390/app6100305
Chicago/Turabian StyleZhang, Xinxin, Jianming Peng, Dong Ge, Kun Bo, Kun Yin, and Dongyu Wu. 2016. "Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator" Applied Sciences 6, no. 10: 305. https://doi.org/10.3390/app6100305
APA StyleZhang, X., Peng, J., Ge, D., Bo, K., Yin, K., & Wu, D. (2016). Performance Study of a Fluidic Hammer Controlled by an Output-Fed Bistable Fluidic Oscillator. Applied Sciences, 6(10), 305. https://doi.org/10.3390/app6100305