Health Condition Evaluation for a Shearer through the Integration of a Fuzzy Neural Network and Improved Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
2. Literature Review
2.1. Relevant Studies on Shearer Health Condition
2.2. Relevant Improvements for Fuzzy Neural Network
2.3. Discussion
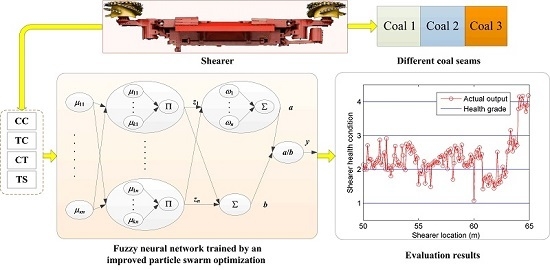
3. The Proposed Approach
3.1. Fuzzy Neural Network (FNN)
3.2. Improved Particle Swarm Optimization Algorithm
3.3. Optimizing the Parameters of FNN with IPSO
- Step 1
- Initialize the particle swarm size M, the maximum of generations tmax, the maximum inertial weight αmax, the minimum inertial weight αmin, c1 and c2, r1 and r2, [Vmin, Vmax], the number of input variables k, the number of neurons in the hidden layer n, H, and set D = 2kn + n, t = 1;
- Step 2
- Update the velocity Vi and position Xi of each particle according to Equations (6) and (7), respectively. Synchronously, update the inertial weight α according to Equation (8);
- Step 3
- The individual best Pi is compared with each particle; if Pi is worse than the fitness value of each particle, then Pi is updated as current position;
- Step 4
- The global best Pg is compared with individual best Pi of each particle; if Pg is worse than Pi, then Pg is updated as current position;
- Step 5
- If the convergence criteria or one of the stopping criteria (generally, a sufficiently good fitness or maximum iteration is met) is satisfied, go to step 7;
- Step 6
- The group fitness variance δ2 is calculated through Equations (9) and (10). If δ2 < H, the velocity and position of the premature particles are updated according to Equations (11) and (7), and the inertial weight α is updated according to Equation (8), go back to Step 3; otherwise, go back to Step 2. Let t = t + 1; and
- Step 7
- The optimal parameters c, σ, and ω of the FNN model can be obtained.
4. Experiment and Discussion
4.1. Sample Data Preparation
4.2. Experiment Results
5. Field Application
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hadi Hoseinie, S.; Ataei, M.; Khalokakaie, R.; Ghodrati, B.; Kumar, U. Reliability analysis of drum shearer machine at mechanized longwall mines. J. Qual. Maint. Eng. 2012, 18, 98–119. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.B.; Tan, C.; Liu, X.H. A novel approach for coal seam terrain prediction through information fusion of improved D–S evidence theory and neural network. Measurement 2014, 54, 140–151. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.B.; Liu, X.H.; Tan, C.; Xu, J.; Zheng, K.H. Multi-sensor data fusion identification for shearer cutting conditions based on parallel quasi-Newton neural networks and the Dempster-Shafer theory. Sensors 2015, 15, 28772–28795. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.F.; Sheu, J.J. Modeling and prediction of retardance in citric acid coated ferrofluid using artificial neural network. J. Magn. Magn. Mater. 2016, 407, 201–208. [Google Scholar] [CrossRef]
- Li, F.J.; Qiao, J.F.; Han, H.G.; Yang, C.L. A self-organizing cascade neural network with random weights for nonlinear system modeling. Appl. Soft Comput. 2016, 42, 184–193. [Google Scholar] [CrossRef]
- He, Y.Y.; Mirzargar, M.; Kirby, R.M. Mixed aleatory and epistemic uncertainty quantification using fuzzy set theory. Int. J. Approx. Reason. 2015, 66, 1–15. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.B.; Liu, X.H.; Yang, Y.W.; Zhang, L. A novel adjustment method for shearer traction speed through integration of T-S cloud inference network and improved PSO. Comput. Intel. Neurosc. 2014. [Google Scholar] [CrossRef] [PubMed]
- Gholamrezaei, M.; Ghorbanian, K. Application of integrated fuzzy logic and neural networks to the performance prediction of axial compressors. Proc. Inst. Mech. Eng. A J. Power 2015, 229, 928–947. [Google Scholar] [CrossRef]
- Young, C.C.; Liu, W.C.; Chung, C.E. Genetic algorithm and fuzzy neural networks combined with the hydrological modeling system for forecasting watershed runoff discharge. Neural Comput. Appl. 2015, 26, 1631–1643. [Google Scholar] [CrossRef]
- Chang, C.L.; Liu, H.C. Applying the Back-Propagation Neural Network model and fuzzy classification to evaluate the trophic status of a reservoir system. Environ. Monit. Assess. 2015, 187, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.M.; Xu, M.H. Fault diagnosis of coal electrical shearer based on quantum neural. Appl. Mech. Mater. 2014, 574, 452–456. [Google Scholar] [CrossRef]
- Gao, F.; Xiao, L.J.; Zhong, W.Y.; Liu, W. Fault diagnosis of shearer based on fuzzy inference. Appl. Mech. Mater. 2011, 52, 1577–1580. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Chen, L.C.; Zhang, Y.J.; Zhao, Z.J. Study of fault diagnosis for shearer based on fuzzy decision tree. Microcomput. Inf. 2009, 25, 94–96. [Google Scholar]
- Fu, J.C.; Wang, H.Y. The study of chirplet’s diagnosis about fault in mechanical on electric traction shearer under the multi-scale. In Proceedings of the 2012 International Conference on Electronics, Communications and Control, Harbin, China, 16–18 August 2013; pp. 1267–1270.
- Niu, K.; Wang, Z.B.; Liu, J.; Zhu, W. Application of OPC interface technology in shearer remote monitoring system. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; pp. 137–140.
- Tan, K.H. Squirrel cage induction generator system using wavelet Petri fuzzy neural network control for wind power applications. IEEE Trans. Power Electron. 2016, 31, 5242–5254. [Google Scholar] [CrossRef]
- Shinde, S.; Kulkarni, U. Extracting classification rules from modified fuzzy min–max neural network for data with mixed attributes. Appl. Soft Comput. 2016, 40, 364–378. [Google Scholar] [CrossRef]
- Loussifi, H.; Nouri, K.; Braiek, N.B. A new efficient hybrid intelligent method for nonlinear dynamical systems identification: The Wavelet Kernel Fuzzy Neural Network. Commun. Nonlinear Sci. 2016, 32, 10–30. [Google Scholar] [CrossRef]
- Liu, Y.T.; Lin, Y.Y.; Wu, S.L.; Chuang, C.H.; Lin, C.T. Brain dynamics in predicting driving fatigue using a recurrent self-evolving fuzzy neural network. IEEE Trans. Neur. Net. Lear. 2016, 27, 347–360. [Google Scholar] [CrossRef] [PubMed]
- Affonso, C.; Sassi, R.J.; Barreiros, R.M. Biological image classification using rough-fuzzy artificial neural network. Expert Syst. Appl. 2015, 42, 9482–9488. [Google Scholar] [CrossRef]
- Lin, C.J.; Wu, C.F.; Lin, H.Y.; Yu, C.Y. An Interactively recurrent functional neural fuzzy network with fuzzy differential evolution and its applications. Sains Malays. 2016, 44, 1721–1728. [Google Scholar]
- Leksakul, K.; Holimchayachotikul, P.; Sopadang, A. Forecast of off-season longan supply using fuzzy support vector regression and fuzzy artificial neural network. Expert Syst. Appl. 2015, 118, 259–269. [Google Scholar] [CrossRef]
- Lin, F.J.; Lu, K.C.; Ke, T.H.; Yang, B.H.; Chang, Y.R. Reactive power control of three-phase grid-connected PV system during grid faults using Takagi–Sugeno–Kang probabilistic fuzzy neural network control. IEEE Trans. Ind. Electron. 2015, 62, 5516–5528. [Google Scholar] [CrossRef]
- Liu, J.J.; Mao, L.L.; Ku, J.F.; He, J.; Fan, L.L. THz spectroscopy detection method for GMOs based on adaptive particle swarm optimization. Opt. Quant. Electron. 2016, 48. [Google Scholar] [CrossRef]
- Fathi, M.; Rodriguez, V.; Fontes, D.B.M.M.; Alvarez, M.J. A modified particle swarm optimisation algorithm to solve the part feeding problem at assembly lines. Int. J. Prod. Res. 2016, 54, 878–893. [Google Scholar] [CrossRef]
- Tsekouras, G.E.; Tsimikas, J. On training RBF neural networks using input-output fuzzy clustering and particle swarm optimization. Fuzzy Set. Syst. 2013, 221, 65–89. [Google Scholar] [CrossRef]
- Cheng, C.T.; Niu, W.J.; Feng, Z.K.; Shen, J.J.; Chau, K.W. Daily reservoir runoff forecasting method using artificial neural network based on quantum-behaved particle swarm optimization. Water 2015, 7, 4232–4246. [Google Scholar] [CrossRef]
- Lin, L.; Guo, F.; Xie, X.L.; Luo, B. Novel adaptive hybrid rule network based on TS fuzzy rules using an improved quantum-behaved particle swarm optimization. Neurocomputing 2015, 149, 1003–1013. [Google Scholar] [CrossRef]
- Li, D.; Wang, W.; Ismail, F. Fuzzy neural network technique for system state forecasting. IEEE Trans. Cybern. 2013, 43, 1481–1494. [Google Scholar]










| Notation | Variable |
|---|---|
| x1 | Cutting motor current (CC) |
| x2 | Traction motor current (TC) |
| x3 | Cutting part temperature (CT) |
| x4 | Traction speed (TS) |
| y | The health grade of shearer |
| Dataset Number | Notation | Training Samples | Testing Samples |
|---|---|---|---|
| 1 | S1 | 300 | 100 |
| 2 | S2 | 400 | 100 |
| 3 | S3 | 500 | 100 |
| 4 | S4 | 600 | 100 |
| 5 | S5 | 700 | 100 |
| 6 | S6 | 800 | 100 |
| Models | Indices | Datasets | |||||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | ||
| IPSO-FNN | MSE | 0.0089 | 0.0085 | 0.0079 | 0.0074 | 0.0084 | 0.0085 |
| MAE | 0.0653 | 0.0619 | 0.0536 | 0.0516 | 0.0571 | 0.0556 | |
| MAPE | 2.41% | 2.23% | 2.09% | 2.05% | 2.14% | 2.11% | |
| TIC | 0.0109 | 0.0095 | 0.0083 | 0.0075 | 0.0086 | 0.0088 | |
| TT (s) | 5.75 | 6.81 | 8.18 | 8.96 | 9.62 | 10.95 | |
| PSO-FNN | MSE | 0.0098 | 0.0093 | 0.0089 | 0.0081 | 0.0093 | 0.0092 |
| MAE | 0.0715 | 0.0684 | 0.0617 | 0.0608 | 0.0622 | 0.0624 | |
| MAPE | 2.86% | 2.74% | 2.55% | 2.51% | 2.57% | 2.54% | |
| TIC | 0.0129 | 0.0112 | 0.0094 | 0.0081 | 0.0090 | 0.0092 | |
| TT (s) | 5.23 | 6.78 | 7.54 | 8.67 | 9.77 | 10.23 | |
| GA-FNN | MSE | 0.0097 | 0.0094 | 0.0091 | 0.0079 | 0.0089 | 0.0091 |
| MAE | 0.0719 | 0.0708 | 0.0671 | 0.0611 | 0.0629 | 0.0622 | |
| MAPE | 2.89% | 2.83% | 2.68% | 2.55% | 2.61% | 2.56% | |
| TIC | 0.0133 | 0.0104 | 0.0091 | 0.0083 | 0.0092 | 0.0094 | |
| TT (s) | 5.86 | 7.01 | 7.97 | 8.84 | 10.12 | 11.08 | |
| FNN | MSE | 0.0135 | 0.0115 | 0.0109 | 0.0095 | 0.0102 | 0.0106 |
| MAE | 0.0912 | 0.0901 | 0.0841 | 0.0810 | 0.0853 | 0.0846 | |
| MAPE | 3.65% | 3.52% | 3.48% | 3.29% | 3.36% | 3.34% | |
| TIC | 0.0157 | 0.0124 | 0.0108 | 0.0101 | 0.0112 | 0.0110 | |
| TT (s) | 12.85 | 14.22 | 15.14 | 16.20 | 17.13 | 18.78 | |
| BPNN | MSE | 0.0128 | 0.0112 | 0.0106 | 0.0096 | 0.0097 | 0.0098 |
| MAE | 0.0901 | 0.0867 | 0.0855 | 0.0816 | 0.0844 | 0.0837 | |
| MAPE | 3.64% | 3.53% | 3.50% | 3.31% | 3.40% | 3.39% | |
| TIC | 0.0148 | 0.0121 | 0.0106 | 0.0098 | 0.0106 | 0.0104 | |
| TT (s) | 11.55 | 13.95 | 15.66 | 16.53 | 17.64 | 18.94 | |
| SVR | MSE | 0.0125 | 0.0119 | 0.0102 | 0.0097 | 0.0096 | 0.0098 |
| MAE | 0.0894 | 0.0867 | 0.0806 | 0.0768 | 0.0759 | 0.0761 | |
| MAPE | 3.56% | 3.52% | 3.49% | 3.26% | 3.22% | 3.31% | |
| TIC | 0.0134 | 0.0125 | 0.0101 | 0.0098 | 0.0101 | 0.0099 | |
| TT (s) | 12.02 | 13.85 | 14.64 | 15.95 | 17.01 | 17.58 | |
| Algorithms | Training Phase | Testing Phase | |||
|---|---|---|---|---|---|
| MSE | MAPE (%) | TT (s) | MSE | MAPE (%) | |
| PSO | 0.0056 | 2.24 | 8.67 | 0.0081 | 2.51 |
| QPSO | 0.0051 | 1.91 | 9.11 | 0.0076 | 2.09 |
| OLB-QPSO | 0.0039 | 1.81 | 10.24 | 0.0069 | 1.98 |
| LPSO | 0.0042 | 1.83 | 10.67 | 0.0071 | 2.01 |
| Proposed IPSO | 0.0047 | 1.86 | 8.96 | 0.0074 | 2.05 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, L.; Wang, Z.; Liu, Z.; Liu, X.; Tan, C.; Xu, R. Health Condition Evaluation for a Shearer through the Integration of a Fuzzy Neural Network and Improved Particle Swarm Optimization Algorithm. Appl. Sci. 2016, 6, 171. https://doi.org/10.3390/app6060171
Si L, Wang Z, Liu Z, Liu X, Tan C, Xu R. Health Condition Evaluation for a Shearer through the Integration of a Fuzzy Neural Network and Improved Particle Swarm Optimization Algorithm. Applied Sciences. 2016; 6(6):171. https://doi.org/10.3390/app6060171
Chicago/Turabian StyleSi, Lei, Zhongbin Wang, Ze Liu, Xinhua Liu, Chao Tan, and Rongxin Xu. 2016. "Health Condition Evaluation for a Shearer through the Integration of a Fuzzy Neural Network and Improved Particle Swarm Optimization Algorithm" Applied Sciences 6, no. 6: 171. https://doi.org/10.3390/app6060171
APA StyleSi, L., Wang, Z., Liu, Z., Liu, X., Tan, C., & Xu, R. (2016). Health Condition Evaluation for a Shearer through the Integration of a Fuzzy Neural Network and Improved Particle Swarm Optimization Algorithm. Applied Sciences, 6(6), 171. https://doi.org/10.3390/app6060171