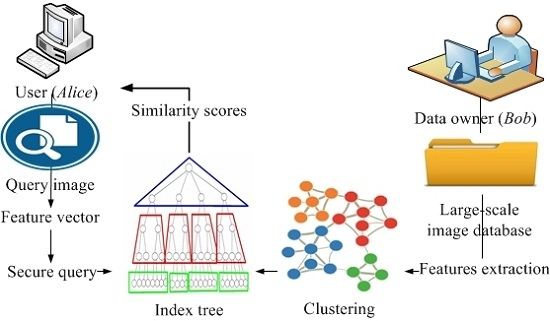
4.2. Problem Statement
The common notations listed in
Table 1 are used throughout this paper. Our proposed scheme includes two parties, namely,
Alice and
Bob, each of whom has a collection of images. We assume that the images of both parties are private. Given an image
I of
Alice, we are interested in determining whether
Bob’s collection contains an image similar to
I without disclosing
Bob’s database to
Alice and vice versa. We evaluate the similarity of two images under the SURF local feature vector model, in which each image is represented as a set of vectors. Let
denote the set of
m images in
Bob’s collection. Without disclosing
I to
Bob and
D to
Alice, our objective is to find a set of images in
D similar to
I without disclosing the matching results to
Bob. We term such protocol as SEPIM. Formally, SEPIM is defined as
SEPIM returns the
M similarity scores
to
Alice instead of returning the actual images. At another time,
Alice can retrieve the similar image from
Bob. To evaluate the similarity between two images, each party initially extracts the feature vectors for each image in its own collection. Several metrics are used to evaluate the similarity between the sets of the two feature vectors such as Euclidean distance and cosine similarity [
8]. The cosine similarity (CSIM) between vectors
and
of size
n can be defined as follows:
where
is the Euclidian length of vector
v, and is defined as the following:
Given normalized vectors
and
, cosine similarity can be written as:
Given two images, and , of the two feature vector sets and , respectively. Algorithm 1 illustrates how the distance between two feature vector sets can be measured through the cosine similarity without preserving privacy.
| Algorithm 1 Insecure Image Distance Calculation |
| Input: two feature vectors and of two images. |
| All vectors
and are of the same size n. |
| Output: : distance between and . |
|
| For to k do |
| Compute
as in Equation (5) |
| For to p do |
| Compute
as in Equation (5) |
|
|
| End for//j |
| |
| End for//k |
|
Table 2 shows a trivial example for
Alice image, which is represented by a set of three vectors of size 5. The first three columns are the feature vectors, while the last three columns are their corresponding normalized versions. Similarly,
Table 3 illustrates the collection of
Bob, which consists of two images. In addition, this table is interpreted in the same way as
Table 2.
To compute the distance between Alice’s image and the first image in Bob’s collection, we have to compute distance between the feature vector sets and . Thus, the distance between and can be calculated as follows:
= = (0.1766 + 0.1067 + 0.1918)/3 = 0.1584.
We note that these calculations are based on minimum cosine values of corresponding vectors sets. We also note that we compute distance between vectors using the dot product, which is equivalent to cosine distance since we assume feature vectors are normalized. Similarly, the distance between and is . Thus, we can conclude that the second image in Bob’s collection is more similar to Alice’s image than the first one because it has a shorter distance.
As shown in the above example, the main step in evaluating similarity between two images is the dot product between their corresponding normalized vectors. Therefore, once we know how to calculate the dot product in a privacy-preserving manner, we can calculate the distance between any two images without sharing their contents.
In the following subsection, we will demonstrate a homomorphic encryption-based protocol [
32] for computing the dot product operation in a privacy-preserving mode. We then show how to utilize such a protocol as a tool in designing our proposed SEPIM.
4.3. Secure Dot Product Based on Homomorphic Encryption
Homomorphic encryption is a probabilistic public key encryption [
9,
32]. Let
and
be the encryption and decryption functions in this system with public key
pk and private key
pr. Without private key
pr, no adversary can guess the plaintext
x in polynomial time. Furthermore,
has a semantic security [
33] property, which means no adversary can compute any function of the plaintext from the ciphertext set. Interestingly, the full homomorphic encryption has two amazing properties, namely: additive and multiplicative. Additive property allows adding two encrypted numbers, i.e.,
. Given a constant
c and a ciphertext
, the multiplicative property works as follows:
. In this paper, we adopt Paillier’s system [
34] for the practical implementation because of its efficiency.
Let
u and
v be secure vectors of
Alice and
Bob, respectively.
Both vectors are of the same size
n. Below, we show how homomorphic encryption can be used to compute the secure dot product between
u and
v. At the beginning,
Alice encrypts her private vector component-wise, i.e.,
, and sends the encrypted vector
z to
Bob. Upon receiving
z,
Bob computes the encrypted component-wise product between
z and
v based on the multiplicative property, (i.e.,
). He then sums up these products based on the additive homomorphic property to compute the encrypted dot product
EDot such as:
. After receiving
EDot from
Bob,
Alice uses her private key
pr to decrypt it and to obtain the plaintext value of
, i.e.,
. Note that
Alice’s private vector
u is not revealed to
Bob because only encrypted values of
u are sent to
Bob. Therefore, without prior knowledge of
Alice’s private key, neither
u vector nor matching plaintext can be recovered by semi-trusted
Bob or any adversary. Thus, this method meets the requirement of second scenario as explained in
Section 1 with respect to privacy-preserving.